
Metody Matematyczne w Elektrotechnice
®
1
Zmienne stanu
Prowadz
ą
cy: dr in
ż
. Tomasz Sikorski
Instytut Podstaw Elektrotechniki i Elektrotechnologii
Wydział Elektryczny
Politechnika Wrocławska
1.
Wprowadzenie .........................................................................................................................................................................................................................2
2.
Przykład opisu układu za pomocą zmiennych stanu ...............................................................................................................................................................6
2.1
Formułowanie równania stanu.........................................................................................................................................................................................6
2.2
Elementy rozwiązania równania stanu ..........................................................................................................................................................................10
2.3
Wykorzystanie transformaty Laplace’a w wyznaczaniu zmiennych stanu ...................................................................................................................18
2.4
Wykorzystanie wartości własnych macierzy stanu do badania stabilności układu .......................................................................................................22
2.5
Wykorzystanie macierzy stanu do wyznaczania odpowiedzi impulsowej układu ........................................................................................................23

Metody Matematyczne w Elektrotechnice
®
2
1. Wprowadzenie
Stanem obwodu w chwili t
0
nazywamy zespół wielko
ś
ci, które razem ze znajomo
ś
ci
ą
wszystkich sygnałów
wej
ś
ciowych (tj.
ź
ródeł napi
ę
cia i
ź
ródeł pr
ą
du), pozwalaj
ą
przewidzie
ć
jednoznacznie zachowanie si
ę
układu w ka
ż
dej chwili t>t
0
tzn. pozwalaj
ą
na jednoznaczne okre
ś
lenie wszystkich sygnałów wyj
ś
ciowych
(napi
ęć
i pr
ą
dów) wszystkich elementów obwodu.
Zmiennymi stanu nazywamy taki układ wielko
ś
ci, który jednoznacznie opisuje stan obwodu. Wielko
ś
ci te
nazywane s
ą
zmiennymi stanu lub współrz
ę
dnymi stanu, a wektor b
ę
d
ą
cy zbiorem n zmiennych stanu
nazywamy wektorem stanu.
W obwodach elektrycznych stan obwodu jednoznacznie opisuj
ą
ładunku na kondensatorach, a zatem
równie
ż
napi
ę
cia na kondensatorach, oraz strumienie cewek czyli równie
ż
pr
ą
dy płyn
ą
ce przez cewki.
Wielko
ś
ci te przyjmiemy za zmienne stanu.
Dla obwodów nie zawieraj
ą
cych oczek osobliwych oraz w
ę
złów (rozci
ęć
) osobliwych liczba zmiennych
stanu jest równa liczbie elementów zachowawczych tj. liczbie kondensatorów i cewek. W ogólno
ś
ci o ilo
ś
ci
zmiennych stanu
ś
wiadczy rz
ą
d obwodu (liczba stopni swobody)
LC
L
C
n
n
n
n
=
− −
gdzie
LC
n
– całkowita liczba kondensatorów i cewek,
L
n
- liczba niezale
ż
nych w
ę
złów osobliwych,
C
n
-
liczba niezale
ż
nych oczek osobliwych.

Metody Matematyczne w Elektrotechnice
®
3
Dla n zmiennych stanu mo
ż
emy sformułowa
ć
n równa
ń
ró
ż
niczkowych pierwszego rz
ę
du lub jedno
równanie n-tego rz
ę
du. To drugie podej
ś
cie jest podstaw
ą
metody klasycznej rozwi
ą
zywania obwodów w
stanach przej
ś
ciowych, daj
ą
ce rozwi
ą
zanie dla jednej zmiennej, b
ę
d
ą
cej podstaw
ą
rozwi
ą
zywanego
równania n-tego rz
ę
du. W metodzie zmiennych stanu wykorzystamy układ n równa
ń
pierwszego
stopnia.
Oznaczmy zmienne stanu za pomoc
ą
( ) ( ) ( )
( )
1
2
3
n
x t ,x t ,x t ...x t
, a odpowiadaj
ą
cy im kolumnowy
wektor zmiennych stanu o wymiarach nx1 jako:
( )
( )
( )
( )
1
2
...
n
x t
x t
t
x t
=
X
nx1
Oznaczmy wymuszenia tj. niesterowane
ź
ródła napi
ę
ciowe i pr
ą
dowe przez
( ) ( ) ( )
( )
1
2
3
n
u t ,u t ,u t ...u t
, a
odpowiadaj
ą
cy im kolumnowy wektor wymusze
ń
o wymiarach px1 jako:
( )
( )
( )
( )
1
2
...
p
u t
u t
t
u
t
=
U
px1

Metody Matematyczne w Elektrotechnice
®
4
Pisz
ą
c układ równa
ń
Kirchhoffa dla danego obwodu mo
ż
emy tak przekształci
ć
zale
ż
no
ś
ci z równaniami
pierwszego rz
ę
du by otrzyma
ć
form
ę
, gdzie z lewej strony wyst
ę
puj
ą
pierwsze pochodne zmiennych stanu,
a z drugiej zmienne stanu i wymuszenia. Jest to tzw. posta
ć
normalna równania stanu.
( )
( )
( )
d
t
t
t
dt
=
+
X
AX
BU
b
ą
d
ź
( )
( )
( )
' t
t
t
=
+
X
AX
BU
Macierze
A
i
B
w obwodzie liniowym maj
ą
elementy stałe, liczbowe, stanowi
ą
ce kombinacje
elementów obwodu.
Przy czym:
A
jest macierz
ą
kwadratow
ą
o wymiarach nxn i zwana jest macierz
ą
stanu,
B
jest macierz
ą
prostok
ą
tn
ą
o wymiarach nxp i zwana jest macierz
ą
wymusze
ń
.
Pełen opis obwodu, zawieraj
ą
cy informacje o napi
ę
cia na cewkach, rezystorach czy pr
ą
dach płyn
ą
cych
przez kondensatory, mo
ż
na sformułowa
ć
drugim równaniem, opartym na zmiennych stanu. Równanie to
jest równaniem algebraicznym i nazywane jest równaniem odpowiedzi.
( )
( )
( )
t
t
t
=
+
Y
CX
DU
gdzie
( )
( )
( )
( )
1
2
...
q
y t
y t
t
y t
=
Y
qx1 – wektor odpowiedzi

Metody Matematyczne w Elektrotechnice
®
5
Przy czym:
C
jest macierz
ą
prostok
ą
tn
ą
o wymiarach qxn i zwana jest macierz
ą
odpowiedzi,
D
jest macierz
ą
prostok
ą
tn
ą
o wymiarach qxp i zwana jest macierz
ą
transmisyjn
ą
.
Równanie stanu i równanie odpowiedzi tworz
ą
par
ę
równa
ń
, które w pełni opisuj
ą
stan obwodu w
warunkach dynamicznych.
Charakterystyczn
ą
cech
ą
metody zmiennych stanu jest mo
ż
liwo
ść
jednoczesnego wyznaczania
zmienno
ś
ci w czasie wszystkich wielko
ś
ci uznanych za zmienne stanu. Ponadto metoda ta umo
ż
liwia
analiz
ę
obwodów ró
ż
nej klasy, tj. liniowych i nieliniowych oraz stacjonarnych i niestacjonarnych. I wreszcie
oparcie równa
ń
tylko na pierwszej pochodnej, a tak
ż
e specjalna struktura równa
ń
wektorowo-macierzowa,
stwarza dobre warunki do aplikacji metody zmiennych stanu przy u
ż
yciu komputerów.
Metody Matematyczne w Elektrotechnice
®
6
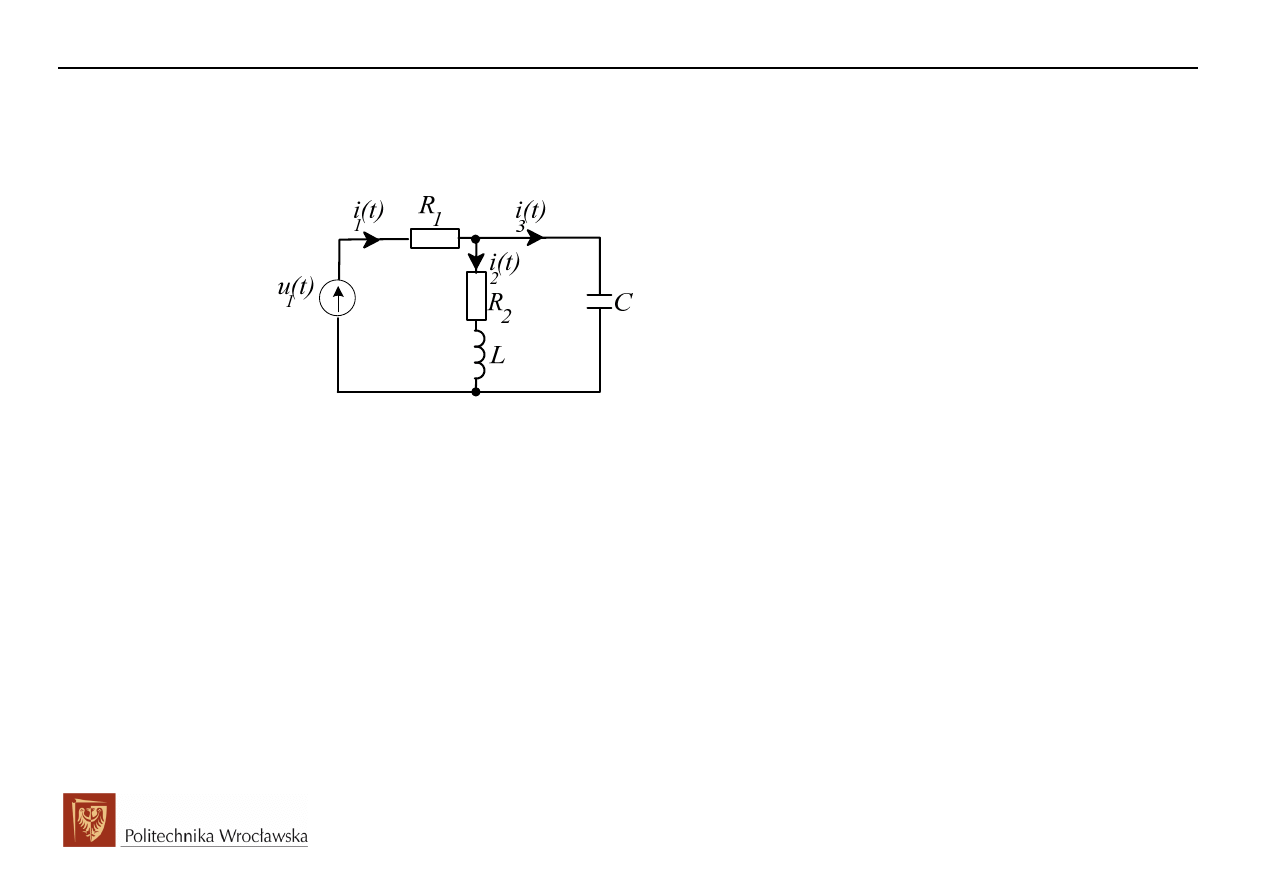
2. Przykład opisu układu za pomoc
ą
zmiennych stanu
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
2.1 Formułowanie równania stanu
Formułowanie równania zmiennych stanu oraz równania odpowiedzi poka
ż
emy na przykładzie.
Stwierdzamy brak oczek oraz w
ę
złów osobliwych, a wi
ę
c rz
ą
d obwodu równy jest liczbie elementów
zachowawczych, n=2, i tyle
ż
samo wyznaczymy zmiennych stanu.
Spodziewamy si
ę
:
( )
( )
( )
1
2
x t
t
x t
=
X
nx1=2x1;
A
nxn=2x2;
( )
( )
1
t
u t
=
U
px1=1x1;
B
nxp=2x1
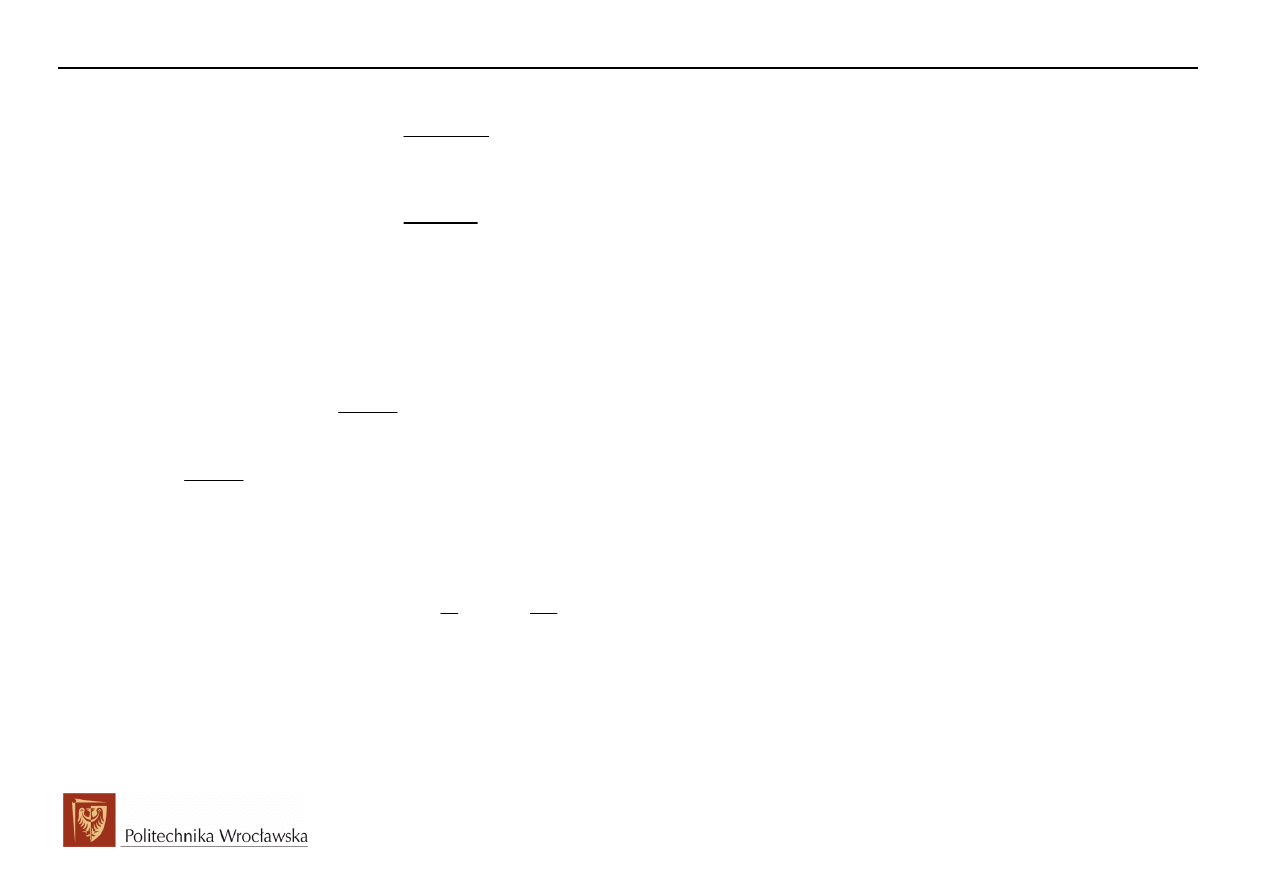
Metody Matematyczne w Elektrotechnice
®
7
( )
( )
( )
( )
( )
( ) ( )
( )
( )
( )
1
3
1
2
2
2
2
C
'
C
'
L
du
t
x t
u
t
i t
C
C x
t
dt
di t
x t
i t
u
t
L
L x
t
dt
=
→
=
= ⋅
=
→
=
= ⋅
Punktem wyj
ś
cia do wyznaczenia równania stanu jest układ równa
ń
Kirchhoffa:
( ) ( ) ( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
2
1
1 1
2 2
2
2 2
C
i t
i t
i t
di t
u t
R i t
R i t
L
dt
di t
R i t
L
u
t
dt
=
+
=
+
+
+
=
;
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
1
2
1
'
1
1 1
2
2
2
'
2
2
2
1
1
2
i t
x t
Cx
t
u t
R i t
Lx t
R x t
Lx t
R x t
x t
=
+
→
=
+
+
+
=
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
'
1
1 2
1
1
2
2
2
'
'
2
2
2
2
1
2
1
2
1
u t
R x t
R Cx
t
Lx t
R x t
R
Lx t
R x t
x t
x t
x t
x t
L
L
=
+
+
+
+
=
→
=
−

Metody Matematyczne w Elektrotechnice
®
8
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
2
1
1 2
1
1
1
2
2
2
'
2
2
1
2
1
1
R
u t
R x t
R Cx t
L
x t
x t
R x t
L
L
R
x t
x t
x t
L
L
=
+
+
−
+
→
=
−
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 2
2
2
2
2
'
1
1
1
1
'
2
2
1
2
1
R x t
R x t
R x t
u t
R Cx t
x t
R
x t
x t
x t
L
L
−
=
+
+
+
→
=
−
( )
( )
( )
( )
( )
( )
( )
'
1
1
1
1 2
1
'
2
2
1
2
1
R Cx t
x t
R x t
u t
R
x t
x t
x t
L
L
= −
−
+
→
=
−
( )
( )
( )
( )
( )
( )
( )
'
1
1
2
1
1
1
'
2
2
1
2
1
1
1
1
x t
x t
x t
u t
R C
C
R C
R
x t
x t
x t
L
L
→
= −
−
+
→
=
−

Metody Matematyczne w Elektrotechnice
®
9
Posta
ć
normalna równania stanu w postaci wektorowo macierzowej:
( )
( )
( )
( )
( )
'
1
1
1
1
1
'
2
2
2
1
1
1
1
0
x t
x t
R C
C
R C
u t
x t
x t
R
L
L
−
−
=
+
−
( )
( )
( )
1
2
x t
t
x t
=
X
nx1=2x1;
wektor zmiennych stanu
1
2
1
1
1
R C
C
R
L
L
−
−
=
−
A
nxn=2x2;
macierz stanu;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
=
−
A
( )
( )
1
t
u t
=
U
px1=1x1;
wektor wymusze
ń
1
1
0
R C
=
B
nxp=2x1
macierz wymusze
ń
;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
=
B

Metody Matematyczne w Elektrotechnice
®
10
2.2 Elementy rozwi
ą
zania równania stanu
Je
ś
li rozpatrywa
ć
dynamik
ę
pracy obwodu elektrycznego tj. wykorzysta
ć
równanie stanu do analizy
obwodu w stanie nieustalonym, konieczna jest znajomo
ść
stanu pocz
ą
tkowego w chwili komutacji t=t
0
.
Okre
ś
la to wektor stanu pocz
ą
tkowego, tj. wektor stanu dla t=t
0
.
( )
( )
( )
1
0
2
0
0
0
...
n
x t
x t
x t
=
X
nx1
Rozwi
ą
zanie równania stanu
( )
( )
( )
' t
t
t
=
+
X
AX
BU
w ogólnym zapisie ma posta
ć
:
( )
(
)
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
τ
τ τ
−
−
=
+
∫
A
A
X
X
BU
Natomiast wektor odpowiedzi
( )
( )
( )
t
t
t
=
+
Y
CX
DU
, w ogólnym zapisie reprezentuje równanie:
( )
(
)
( )
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
t
τ
τ τ
−
−
=
+
+
∫
A
A
Y
C
X
C
BU
DU
fragment
(
)
( )
0
0
t t
e
t
−
A
X
zale
ż
y od wektora stanu pocz
ą
tkowego, wyst
ę
puje tylko przy stanie
pocz
ą
tkowy niezerowym,
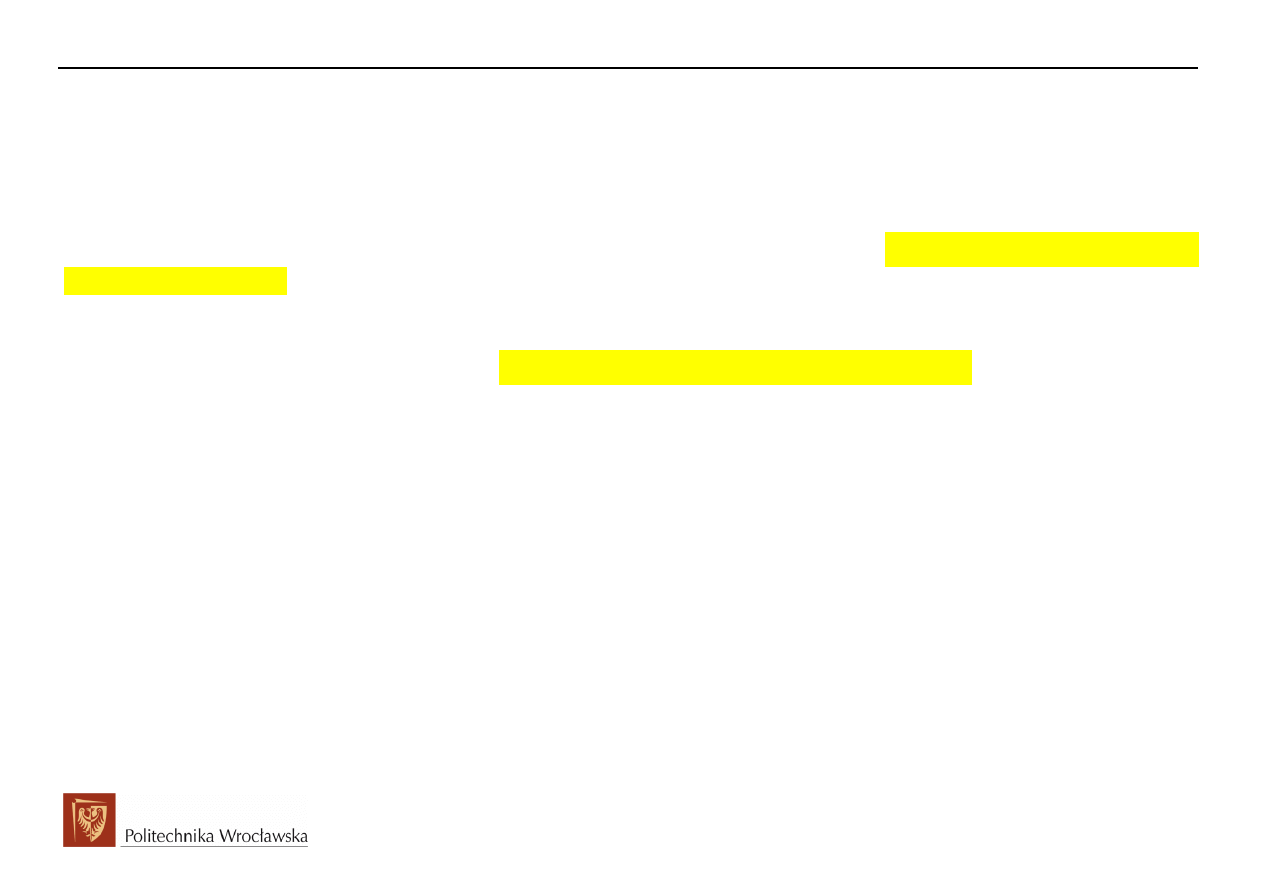
Metody Matematyczne w Elektrotechnice
®
11
fragment
( )
( )
0
t
t
t
e
d
τ
τ τ
−
∫
A
BU
, b
ą
d
ź
( )
( )
0
t
t
t
e
d
τ
τ τ
−
∫
A
C
BU
jest splotem dwóch funkcji macierzowych i
reprezentuje działanie wymusze
ń
.
Charakterystycznym elementem obu równa
ń
jest macierz
( )
t
e
A
zwana macierz
ą
podstawow
ą
lub
tranzycyjn
ą
układu. Kluczowe znaczenie dla rozwi
ą
zania równania stanu b
ę
dzie miała umiej
ę
tno
ść
wyznaczenia macierzy podstawowej.
Pewnym kierunkiem jest wykorzystanie metody rozwini
ę
cia w szereg sko
ń
czony
( )
t
e
A
ze wzgl
ę
du na
kwadratow
ą
macierz
A
przy danym rz
ę
dzie obwodu n.
( )
( )
( )
1
0
n
t
k
k
k
g
e
t
β
−
=
=
=
∑
A
A
A
Rozwini
ę
cie to wykorzystuje twierdzenie twierdzenie Cayleya-Hamiltona, które mówi, i
ż
ka
ż
da macierz
kwadratowa spełnia swoje równanie charakterystyczne, co oznacza:
( )
( )
0
0
g
g
λ
=
→
=
A
dla pierwiastków równania charakterystycznego.
Dla rozpatrywanego przykładu n=2, st
ą
d rozwini
ę
cie przyjmie posta
ć
:
( )
( )
( )
( )
1
0
1
1
t
g
e
t
t
β
β
=
=
+
A
A
A
gdzie 1 oznacza diagonaln
ą
macierz jednostkow
ą
nxn.

Metody Matematyczne w Elektrotechnice
®
12
Macierz stanu, po podstawieniu danych, wynosi
1
1
1
1
−
−
=
−
A
, co pozwala przedstawi
ć
rozwini
ę
cie
macierzy podstawowej w zapisie wektorowo-macierzowym:
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
−
−
−
−
=
=
+
=
+
−
−
A
A
Do
wyznaczenie
współczynników
rozkładu
( ) ( )
0
1
,
t
t
β
β
wykorzystamy
poj
ę
cie
równania
charakterystycznego macierzy stanu
A
(kwadratowej) i wywodz
ą
cych si
ę
z tego równania warto
ś
ci
własne macierzy stanu.
Maj
ą
c dan
ą
macierz kwadratow
ą
A
mo
ż
emy wyznaczy
ć
wielomian charakterystyczny tej macierzy jako:
( )
[
]
det
1
g
λ
λ
=
−
A
gdzie 1 oznacza diagonaln
ą
macierz jednostkow
ą
nxn.
Nast
ę
pnie równanie:
( )
[
]
0
det
1
0
g
λ
λ
=
→
−
=
A
jest równaniem charakterystycznym macierzy
A
, a wywodz
ą
ce si
ę
z tego równania pierwiastki
nazywamy pierwiastkami charakterystycznymi b
ą
d
ź
warto
ś
ciami własnymi macierzy kwadratowej
A
.
Metody Matematyczne w Elektrotechnice
®
13
Spróbujmy wi
ę
c wyznaczy
ć
macierz podstawow
ą
( )
t
e
A
w nast
ę
puj
ą
cych operacjach:
wyznaczenie równania charakterystycznego macierzy
A
wyznaczenie pierwiastków równania charakterystycznego (warto
ś
ci własnych macierzy
A
)
na podstawie rozwini
ę
cia w szereg sko
ń
czony macierzy podstawowej, wykorzysta
ć
warto
ś
ci własne
do wyznaczenia współczynników rozwini
ę
cia tej macierzy w szereg
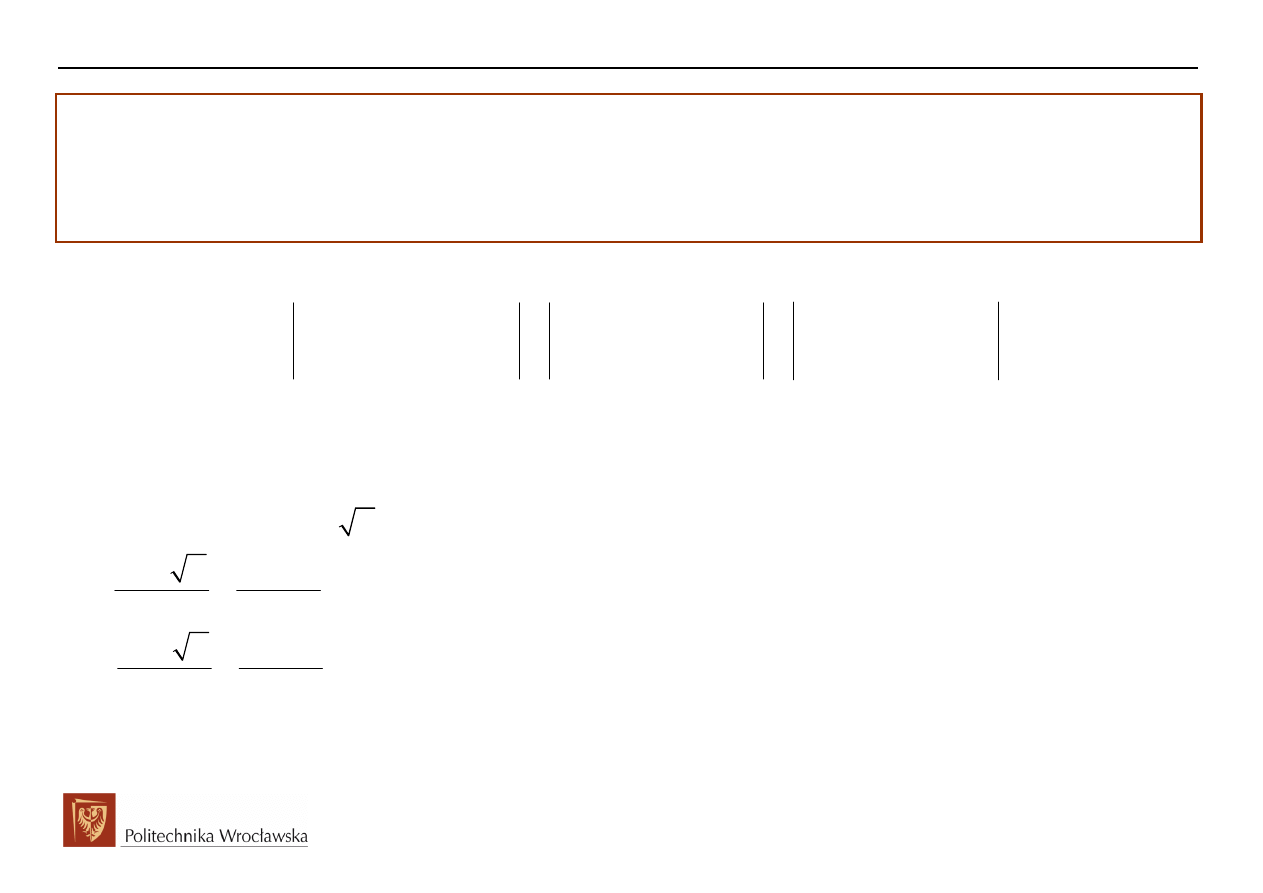
Wyznaczenie równania charakterystycznego macierzy
A
( )
[
]
(
)
(
)
1
1
1
1
1
0
1
1
0
det
1
1
1
1
1
0
1
1
1
0
g
λ
λ
λ
λ
λ
λ
λ
− −
−
−
−
−
−
=
−
=
−
=
−
=
− −
−
−
A
( ) (
)
2
2
1
1
2
2
g
λ
λ
λ
λ
= +
+ =
+
+
Wyznaczenie pierwiastków równania charakterystycznego (warto
ś
ci własnych macierzy
A
)
( )
2
2
1
2
0
2
2
0
4
4 8
4;
2
2
2
1
1
2
2
2
2
1
1
2
2
g
b
ac
j
b
j
j
b
j
j
λ
λ
λ
λ
λ
=
→ +
+ =
∆ = −
= − = −
∆ =
− + ∆ − +
=
=
= − +
− − ∆ − −
=
=
= − −

Metody Matematyczne w Elektrotechnice
®
14
Wyznaczanie macierzy podstawowej przez wyznaczenia współczynników rozwini
ę
cia tej macierzy
w szereg sko
ń
czony.
Przypomnijmy posta
ć
rozwini
ę
cia:
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
−
−
−
−
=
=
+
=
+
−
−
A
A
Jednocze
ś
nie przy warto
ś
ciach własnych macierzy (dla pierwiastków równania charakterystycznego)
( )
( )
( )
0
0
i
t
i
g
g
e
g
λ
λ
λ
=
→
=
→
=
A
czyli:
( )
( )
0
1
t
e
t
t
λ
β
β
λ
=
+
(dla pierwiastków równania charakterystycznego)
to przy danych pierwiastkach
( )
( )(
)
( )
( )(
)
1
2
1
0
1
2
0
1
1
1
1
1
1
1
1
1
t
t
j
e
t
t
j
j
e
t
t
j
λ
λ
λ
β
β
λ
β
β
= − +
→
=
+
− +
= − −
→
=
+
− −
Otrzymamy dwie informacje przy dwóch poszukiwanych współczynnikach rozwini
ę
cia (funkcji zmiennej t):
(
)
( )
( )(
)
(
)
( )
( )(
)
1
1
0
1
1
1
0
1
1
1
1
1
j t
j t
e
t
t
j
e
t
t
j
β
β
β
β
− +
− −
=
+
− +
=
+
− −

Metody Matematyczne w Elektrotechnice
®
15
Przez obustronne odj
ę
cie stronami uzyskamy:
(
)
(
)
( )
( )(
)
( )
( )(
)
(
)
( )
(
)
( )
( )
1
1
1
1
0
1
0
1
1
1
1
1
1
1
1
2
2sin
2
sin
j t
j t
t
jt
jt
t
t
e
e
t
t
j
t
t
j
e
e
e
j
t
e
j
t
j
t
t
e
t
β
β
β
β
β
β
β
− +
− −
−
−
−
−
−
=
+
− +
−
−
− −
−
=
=
→
=
Przez obustronne zsumowanie stronami uzyskamy:
(
)
(
)
( )
( )(
)
( )
( )(
)
(
)
( )
( )
(
)
( )
( )
(
)
( )
( )
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
1
1
1
2
2
2 cos
2
cos
cos
sin
j t
j t
t
jt
jt
t
t
t
t
e
e
t
t
j
t
t
j
e
e
e
t
t
e
t
t
t
t
e
t
t
e
t
e
t
β
β
β
β
β
β
β
β
β
β
− +
− −
−
−
−
−
−
−
+
=
+
− +
+
+
− −
+
=
−
=
−
→
=
+
=
+
Ostatecznie:
( )
1
sin
t
t
e
t
β
−
=
;
( )
(
)
0
cos
sin
t
t
e
t
t
β
−
=
+
Szukana macierz podstawowa
( )
t
e
A
wzgl
ę
dem macierzy
A
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
−
−
−
−
=
=
+
=
+
−
−
A
A
( )
( )
(
)
(
)
cos
sin
0
sin
sin
0
cos
sin
sin
si
cos
sin
si
n
n
cos
t
t
t
t
t
t
t
t
t
t
t
e
t
t
e
t
e
t
g
e
e
t
t
e
e
t
e
t
e
t
e
t
e
t
t
−
−
−
−
−
−
−
−
−
−
+
−
−
=
=
+
=
+
−
−
A
A

Metody Matematyczne w Elektrotechnice
®
16
---------------------------------------------------------------------------------------------------------------------------------------------
UWAGA:
Metoda rozwini
ę
cia w szereg sko
ń
czony jest szczególnie przydatna, gdy macierz kwadratowa
A
ma
wielokrotne warto
ś
ci własne. Np. niech pierwiastek
i
λ
ma krotno
ść
2
i
m
=
.Nale
ż
y wtedy dla tej warto
ś
ci
własnej, oprócz równania
( )
i
t
i
e
g
λ
λ
=
,zapisa
ć
dodatkowe równanie
( )
i
i
i
t
i
d
d
e
g
dt
d
λ
λ λ
λ λ
λ
λ
=
=
=
UWAGA:
Istniej
ą
jeszcze inne metody wyznaczania macierzy podstawowej
( )
t
e
A
:
zastosowanie wzoru interpolacyjnego Sylevestera
metoda przekształce
ń
macierzowych z u
ż
yciem nieosobliwej macierzy przekształce
ń
1
−
=
D
P
AP
---------------------------------------------------------------------------------------------------------------------------------------------
Wracaj
ą
c do głównego równania mo
ż
emy wyznaczy
ć
wektor stanu:
( )
(
)
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
τ
τ τ
−
−
=
+
∫
A
A
X
X
BU
Dla przypadku t
0
=0 oraz zerowych warunków pocz
ą
tkowych, wektor stanu okre
ś
la równanie:
( )
( )
( )
0
t
t
t
e
d
τ
τ τ
−
=
∫
A
X
BU
czyli splot funkcji macierzowych.

Metody Matematyczne w Elektrotechnice
®
17
W danym zadaniu:
( )
( )
1
t
u t
=
U
px1=1x1;
wektor wymusze
ń
1
1
0
R C
=
B
nxp=2x1
macierz wymusze
ń
;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
=
B
( )
( )
(
)
(
)
(
)
(
)
( )
1
0
cos
sin
1
sin
cos
0
t
t
t
t
t
e
u
d
t
t
τ
τ
τ
τ
τ
τ
τ
− −
−
−
−
−
=
⋅
⋅
−
−
∫
X
B
ą
d
ź
ze wzgl
ę
du na przemienno
ść
splotu
( )
( )
(
)
(
)
1
0
0
cos
sin
1
sin
cos
0
t
t
t
t
t
t
t
e
t
d
e
u t
d
t
t
τ τ
τ
τ
−
=
−
=
⋅
−
∫
∫
A
X
BU
( )
(
)
(
)
(
)
1
0
1
0
1
0
cos
cos
sin
sin
t
t
t
t
t
t
e
t
u t
d
t
t
e
u t
d
t
e
t
u t
d
τ
τ
τ
τ
τ
τ
−
−
−
⋅
−
=
⋅
−
=
⋅
−
∫
∫
∫
X
UWAGA:
Wyznaczanie zmiennych stanu jest efektywniejsze przy wykorzystaniu transformaty Laplace’a w
poł
ą
czeniu z metoda przekształce
ń
macierzowych.

Metody Matematyczne w Elektrotechnice
®
18
2.3 Wykorzystanie transformaty Laplace’a w wyznaczaniu zmiennych stanu
Powró
ć
my do postaci normalna równania stanu.
( )
( )
( )
d
t
t
t
dt
=
+
X
AX
BU
b
ą
d
ź
( )
( )
( )
' t
t
t
=
+
X
AX
BU
i dokonajmy obustronnie transformacji Laplace’a:
( )
( )
( )
( )
( )
( )
( )
( )
(
) ( )
( )
( )
( ) (
)
( )
( )
( )
0
0
0
1
0
1
s
s
1
1
s
t
s
s
s
s
s
t
s
s
s
t
s
s
s
t
s
−
−
−
=
+
→
−
=
+
→
−
=
+
→
=
−
+
→
=
X
X
AX
BU
X
AX
BU
X
A X
BU
X
X
A
BU
X
X
P
R
Niech
(
)
1
s
=
−
P
A
, a
( )
( )
0
s
t
=
+
R
BU
X
W omawianym przykładzie
( )
( )
( )
( )
( )
'
1
1
1
1
1
'
2
2
2
1
1
1
1
0
x t
x t
R C
C
R C
u t
x t
x t
R
L
L
−
−
=
+
−

Metody Matematyczne w Elektrotechnice
®
19
( )
( )
( )
1
2
x t
t
x t
=
X
nx1=2x1;
wektor zmiennych stanu
1
2
1
1
1
R C
C
R
L
L
−
−
=
−
A
nxn=2x2;
macierz stanu;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
=
−
A
( )
( )
1
t
u t
=
U
px1=1x1;
wektor wymusze
ń
1
1
0
R C
=
B
nxp=2x1
macierz wymusze
ń
;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
=
B
Po podstawieniu danych:
( )
( )
( )
( )
( )
'
1
1
1
'
2
2
1
1
1
1
1
0
x t
x t
u t
x t
x t
−
−
=
+
−

Metody Matematyczne w Elektrotechnice
®
20
Po przej
ś
ciu do dziedziny operatorowej
( ) (
)
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
0
0
1
0
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1
0
0
t
s
s
s
t
s
s
s
s
U s
s
t
s
U s
−
−
=
=
−
+
=
−
−
+
→ = − =
−
=
−
−
+
→ =
+
→ =
=
⋅
=
X
X
A
BU
X
P
R
P
A
R
BU
X
R
BU
Dalej:
1
1
det
T
−
=
⋅
P
P
D
P
gdzie:
( )
( )
( )
( )
( )
( )
(
)(
) ( )( )
1 1
1 2
22
21
2 1
2 2
12
11
2
11
22
12
21
1
1
1
1
1
1
1
1
1
1
1
1
det
1
1
1
1
2
2
transpose
T
p
p
s
s
s
s
p
p
p p
p p
s
s
s
s
+
+
+
+
−
−
+
− −
+
−
=
=
→
=
−
+
+
−
−
=
−
= +
+ −
− = +
+
P
P
D
D
P
St
ą
d:
1
2
1
1
1
1
1
1
det
2
2
T
s
s
s
s
−
+
−
=
⋅
=
+
+
+
P
P
D
P
( )
( )
( )
1
1
1
0
0
U s
s
U s
=
=
⋅
=
R
BU
Wektor transformat Laplaca zmiennych stanu dla danego przykładu:
( )
( )
1
1
2
1
1
1
1
1
2
2
0
s
U s
s
s
s
s
−
+
−
=
=
⋅
+
+
+
X
P
R
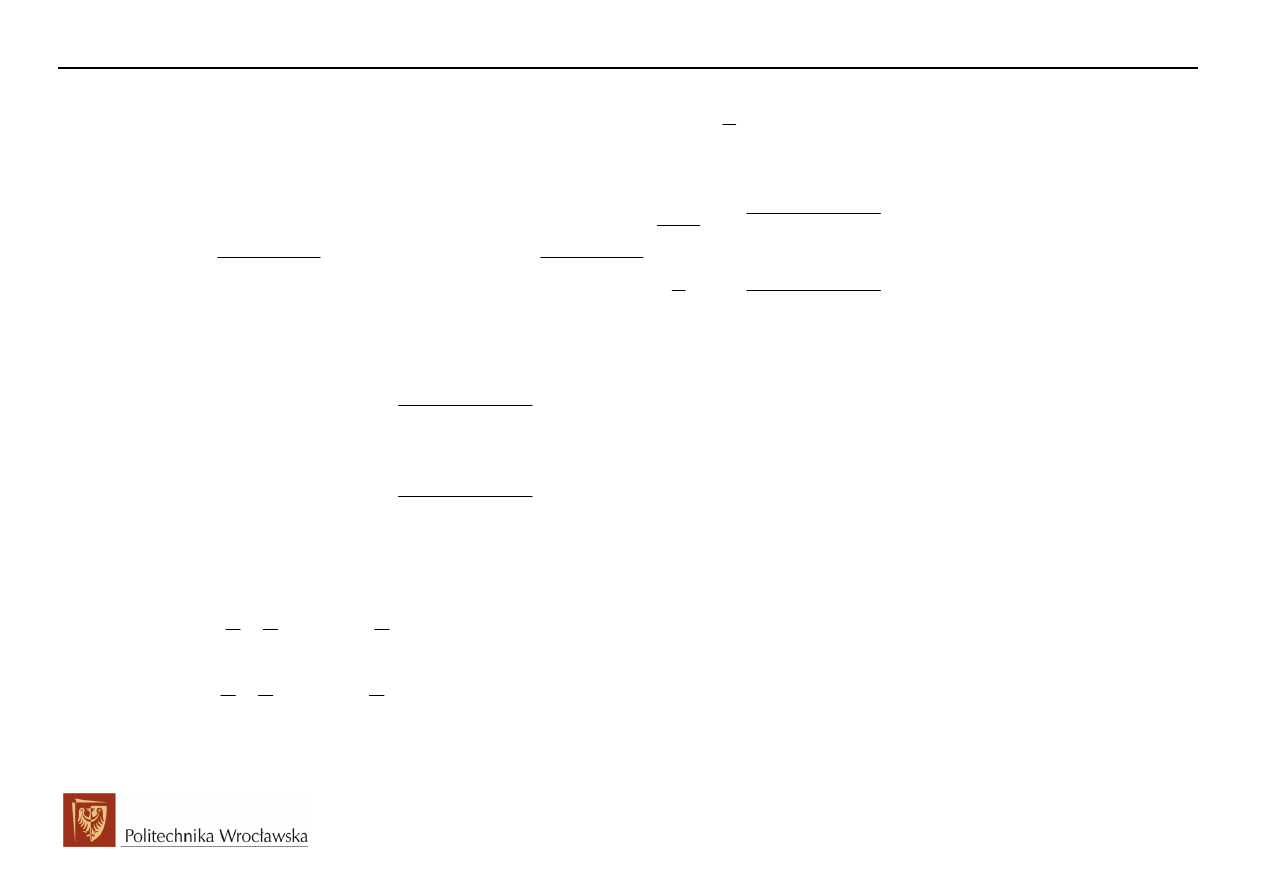
Metody Matematyczne w Elektrotechnice
®
21
Je
ś
li wymuszeniem b
ę
dzie np. napi
ę
cie stałe E=1V to
( )
1
1
U s
s
=
Wtedy:
( )
(
)
(
)
2
1
2
2
2
1
1
2
2
1
1
1 /
1
1
1
1
0
1
1
2
2
2
2
2
2
s
s
s s
s
s
s
s
s
s
s
s
s
s
s
s s
s
−
+
+
+
+
+
−
=
=
⋅
=
=
+
+
+
+
+
+
+
X
P
R
Poszukiwane zmienne stanu:
( )
( )
{
}
( )
( )
(
)
(
)
1
2
1
1
2
1
2
1
2
2
1
2
2
s
s s
s
x t
t
s
x t
s s
s
−
−
−
+
+
+
=
=
+
+
L
L
L
X
X
Rozwi
ą
zanie:
( )
( )
( )
1
1
1
1
cos
sin
1
2
2
2
t
t
C
x t
u
t
e
t
e
t
t
−
−
=
=
−
+
( )
( )
( )
2
1
1
1
cos
sin
1
2
2
2
t
t
L
x t
i t
e
t
e
t
t
−
−
=
=
−
−

Metody Matematyczne w Elektrotechnice
®
22
2.4 Wykorzystanie warto
ś
ci własnych macierzy stanu do badania stabilno
ś
ci układu
Mo
ż
emy stwierdzi
ć
czy system jest stabilny bez wyznaczania zmiennych stanu i badani ich przebiegu.
Otó
ż
o stabilno
ś
ci układu mo
ż
emy wnioskowa
ć
na podstawie poło
ż
enia warto
ś
ci własnych macierzy stanu
A
tj. pierwiastków równania charakterystycznego.
Układ jest stabilny, je
ś
li wszystkie warto
ś
ci własne macierzy stanu maj
ą
cz
ęś
ci rzeczywiste
mniejsze od zera
{ }
Re
0
i
λ
<
W omawianym przypadku
{ }
{ }
1
1
2
2
1
1
Re
1 0
1
1
Re
1 0
j
j
λ
λ
λ
λ
= − +
→
= − <
= − −
→
= − <
ś
wiadczy o stabilno
ś
ci układu.
Metody Matematyczne w Elektrotechnice
®
23
2.5 Wykorzystanie macierzy stanu do wyznaczania odpowiedzi impulsowej układu
Rozwa
ż
my w omawianym przykładzie jedno wej
ś
cie i jedno wyj
ś
cie.
Wtedy równanie odpowiedzi
( )
( )
( )
t
t
t
=
+
Y
CX
DU
b
ą
d
ź
:
( )
(
)
( )
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
t
τ
τ τ
−
−
=
+
+
∫
A
A
Y
C
X
C
BU
DU
zawiera
ć
b
ę
dzie elementy:
( )
( )
1
t
y t
=
Y
qx1=1x1;
wektor odpowiedzi
( )
( )
( )
1
2
x t
t
x t
=
X
nx1=2x1;
wektor zmiennych stanu
[
]
11
12
c
c
=
C
qxn=1x2;
macierz odpowiedzi
dla przypadku 1WYJ
[
] [
]
11
12
1 0
c
c
=
=
C
( )
( )
1
t
u t
=
U
px1=1x1;
wektor wymusze
ń
[ ]
11
d
=
D
qxp=1x1
macierz transmisyjna

Metody Matematyczne w Elektrotechnice
®
24
Z wcze
ś
niejszy wyprowadze
ń
:
1
2
1
1
1
R C
C
R
L
L
−
−
=
−
A
nxn=2x2;
macierz stanu;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
=
−
A
1
1
0
R C
=
B
nxp=2x1
macierz wymusze
ń
;
dla danych
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
=
B
( )
cos
sin
sin
cos
t
t
t
t
t
e
t
e
t
e
t
e
t
e
−
−
−
−
=
−
A
nxn=2x2;
macierz podstawowa (tranzycyjna)
Dla systemu z jednym wej
ś
ciem i jednym wyj
ś
ciem wielko
ść
( )
t
e
A
C
B
równa jest odpowiedzi impulsowej.
Dla systemu o p wej
ść
i q wyj
ść
wielko
ść
( )
t
e
A
C
B
jest macierz
ą
o wymiarze pxq , gdzie element (i,j) tej
macierzy jest funkcj
ą
odpowiedzi impulsowej i-tego wyj
ś
cia na impuls Diraca na j-tym wej
ś
ciu, przy
pozostałych sygnałach wej
ś
ciowych równych zeru.

Metody Matematyczne w Elektrotechnice
®
25
W badanym przypadku jednowej
ś
ciowego i jednowyj
ś
ciowego układu odpowied
ź
impulsowa wyniesie:
( )
[
]
( )
1
1
1 0
cos
sin
cos
0
0
cos
sin
sin
cos
t
t
t
t
t
t
t
t
e
e
t
e
t
e
e
t
e
t
e
t
t
e
t
h t
−
−
−
−
−
−
−
=
⋅
⋅
=
−
⋅
=
=
−
A
C
B
Wyszukiwarka
Podobne podstrony:
MM ETK W04 zmiennestanu id 3442 Nieznany
MM ETK W02 skladowesymetryczne 03
PiS15 W03 Zmienne losowe II 2012
003 zmienne systemowe
Badanie korelacji zmiennych
prąd zmienny malej czestotliwosci (2)
FiR Zmienne losowe1
RBD W03
PRZEPUKLINA PĘPOWINOWA, WYTRZEWIENIE MM
4 operacje na zmiennych I
Wyklad 2 zmiennosc standaryzacja 5 III 2014 b
W03 Orbitale wodoru
Zmienne 2
ćw 5 analiza współzależności zmiennych
więcej podobnych podstron