1
TEORIA PREFERENCJI KONSUMENTA
1. Użyteczność kardynalna i porządkowa
2. Nowoczesna teoria preferencji konsumenta
3. Twierdzenia dotyczące funkcji użyteczności
4. Maksymalizacja użyteczności
WPROWADZENIE DO TEORII
KONSUMENTA I POPYTU RYNKOWEGO
1. Funkcje popytu konsumenta: przedstawienie graficzne
2. Funkcja popytu
3. Uogólnione funkcje popytu
4. Funkcje popytu Cobb-Douglasa
5. Funkcje popytu rynkowego
ELASTYCZNOŚĆ FUNKCJI POPYTU
INDYWIDUALNEGO I RYNKOWEGO
1. Definicja elastyczności
2. Elastyczność funkcji popytu liniowej i nieliniowej
3. Elastyczność i przychody całkowite
4. Przychody całkowite, przeciętne i krańcowe wzdłuż
nieliniowych krzywych popytu
2
TEORIA PREFERENCJI KONSUMENTA
Użyteczność kardynalna i porządkowa
Użyteczność interpretowana jest jako pewien
dający się
zmierzyć
poziom zadowolenia, jaki konsument osiąga dzięki
konsumpcji dobra (Jeremi Bentham).
Użyteczność traktowano jako mierzalną zgodnie z
przyjętymi standardami. Dzięki temu można porównywać ją
między osobami i można również dodawać użyteczności
poszczególnych jednostek.
Wskaźnik, podobnie do użyteczności, jeśli przypisuje
wartości liczbowe określany jest mianem kardynalnego.
Wskaźnik użyteczności kardynalnej umożliwia porównywanie
użyteczności poszczególnych jednostek.
Koncepcja użyteczności jest użyteczna jako sposób
przedstawienia preferencji konsumenta względem koszyków
dóbr. Jedyne, czego potrzebujemy aby skonstruować
wskaźnik użyteczności, to reguła przypisująca większe liczby
do koszyków bardziej preferowanych. Wskaźnik jest
porządkowy, jeśli przedstawia sposób uporządkowania
koszyków konsumpcyjnych.
3
Nowoczesna teoria preferencji konsumenta
W nowoczesnej teorii wskaźnik użyteczności jest
przedstawieniem porządkowych preferencji konsumenta.
Aby przyjrzeć się bliżej tej teorii przyjmijmy, że mamy
tylko dwa dobra: X oraz Y. Konsumenci porządkują koszyki z
dobrami konsumpcyjnymi i dokonują wyboru. Każdy koszyk
zawiera x jednostek dobra X i y jednostek dobra Y.
Twierdzenia dotyczące preferencji konsumenta (zgodne z
własnościami liczb rzeczywistych)
Aby przedstawić preferencje konsumenta dotyczące
koszyków dóbr przy wykorzystaniu wskaźnika wyrażonego za
pomocą liczb rzeczywistych, musimy przyjąć założenia
dotyczące tych preferencji, które są zgodne z własnościami
liczb rzeczywistych.
Twierdzenie 1:
Preferencje są spójne (zupełne)
.
W odniesieniu do każdej pary koszyków A i B, konsument
może dokonać każdego z następujących trzech porównań:
1. A jest preferowane względem B (A
P
B).
2. B jest preferowane względem A (B
P
A).
3. A jest obojętne względem B (A
I
B).
Uporządkowanie koszyków zrobione przez konsumenta
określamy mianem uporządkowania preferencji.
4
TWIERDZENIE 2:
Preferencje są zwrotne
Jeżeli konsument ma do wyboru dwa identyczne koszyki,
czyli A = B pod każdym względem, to jest mu obojętne, który
z nich wybierze. Oznacza to, że jeśli A i B są takie same, to
konsument oceni je tak samo.
TWIERDZENIE 3:
Preferencje są przechodnie
Jeżeli konsument preferuje A względem B oraz B względem
C, to konsument preferuje A względem C: A
P
B i B
P
C
⇒
A
P
C.
Jeśli natomiast konsumentowi jest obojętne A czy B oraz B
czy C, to konsumentowi jest obojętne A czy C:A
I
B i B
I
C
⇒
A
I
C.
Z tego twierdzenia wynika, że preferencje konsumenta są
wewnętrznie zgodne.
TWIERDZENIE 4:
Preferencje są ciągłe.
Jeżeli koszyk A jest preferowany względem B, a koszyk C
jest dostatecznie blisko koszyka B (B jest granicą C), to
również A jest preferowany względem C:A
P
B i C
→
B
⇒
A
P
C.
Twierdzenia 1 – 4 wzięte razem stanowią podstawowe cechy
liczb rzeczywistych, z których chcemy skorzystać przy
konstruowaniu wskaźników użyteczności:
Twierdzenie 1 głosi, że każdemu punktowi na osi liczbowej
przyporządkowana jest pewna wartość.
Twierdzenie 2 głosi, że dwa identyczne punkty na osi
liczbowej mają identyczną wartość.
Twierdzenie 3 głosi, że jeżeli x jest większe od y i y jest
większe od z, to x musi być większe od z.
Twierdzenie 4 głosi, że jeżeli x > y na osi liczbowej, to
istnieje liczba y’ (między x I y), taka, że x > y’.
5
Jeżeli preferencje nie spełniają pierwszych trzech
warunków, to nie możemy ich przedstawić za pomocą liczb
rzeczywistych, nawet porządkowo.
Wszystkie cztery twierdzenia są konieczne I wystarczające
dla istnienia liczbowej reprezentacji.
Taką funkcyjną zależność przypisującą liczby koszykom
nazywamy funkcją użyteczności. Dla dwóch dóbr można ją
zapisać w postaci: U = U(x, y).
Nienasycenie i malejąca krańcowa stopa substytucji (MRS)
Następne dwa założenia umożliwiają ekonomistom korzystać
z rachunku optymalizacyjnego przy ograniczeniu w celu
analizowania wyboru konsumenta.
TWIERDZENIE 5:
Preferencje charakteryzuje
nienasycenie.
Konsument ma dwa koszyki, A i B, takie że X w A równa się X
w B, ale Y w A jest większe od Y w B. W takiej sytuacji
konsument zawsze preferuje A względem B. Podobnie, jeżeli
Y w A równa się Y w B, ale X w A jest większe niż X w B, to
konsument preferuje A względem B.
Innymi słowy, jeżeli A równa się B w jednym wymiarze, ale
jest większe od B w innym wymiarze, to A jest preferowane
względem B („więcej znaczy lepiej”).
Twierdzenie 6 można sformułować na wiele sposobów.
Podstawą jest to, że krzywe obojętności są gładkie i wypukłe
względem początku układu współrzędnych.
Aby wprowadzić to twierdzenie, zdefiniujemy pojęcie
określane mianem
krańcowej stopy substytucji
wzdłuż
krzywej obojętności.
6
Pojedynczą krzywą obojętności można opisać funkcją:
y = f(x,
U
). Nachylenie krzywej obojętności definiujemy
więc:
0
=
dU
dx
dy
.
Natomiast krańcową stopę substytucji Y na X definiujemy
jako ujemne nachylenie krzywej obojętności:
MRS
yx
≡
0
=
−
dU
dx
dy
.
Wiemy, że warunkiem wystarczającym przy optymalizacji
przy liniowym ograniczeniu jest to aby powierzchnia funkcji
celu była wypukła względem początku układu współrzędnych.
Aby krzywe obojętności miały ten kształt muszą mieć ujemne
nachylenie (pierwsze pochodne) i dodatnie drugie pochodne:
0
0
<
=
dU
dx
dy
,
0
0
2
2
>
=
dU
dx
y
d
.
Tłumacząc to na MRS możemy powiedzieć, że jeżeli
nachylenie jest ujemne, to MRS jest dodatnie. Jeżeli druga
pochodna jest dodatnia, to nachylenie MRS musi być ujemne:
0
0
>
−
=
=
dU
yx
dx
dy
MRS
,
(
)
0
0
)
(
2
2
<
−
=
−
=
+
dU
dx
y
d
dx
dy
dx
d
MRS
dx
d
.
Tak więc MRS jest malejące.
TWIERDZENIE 6:
Krzywe obojętności charakteryzują
malejące krańcowe stopy substytucji
.
MRS i użyteczność krańcowa (MU)
MRS możemy również przedstawić jako stosunek MUs. Po
pierwsze, rozważmy ogólną postać funkcji użyteczności
U(x, y) i zapiszmy jej różniczkę zupełną:
7
dy
y
U
dx
x
U
dU
∂
∂
+
∂
∂
=
,
gdzie:
x
U
∂
∂
= użyteczność krańcowa X (MU
x
)
y
U
∂
∂
= użyteczność krańcowa Y (MU
y
).
Wiemy, że wzdłuż krzywej obojętności użyteczność jest
stała, czyli dU = 0:
0
0
=
+
⇒
∂
∂
+
∂
∂
=
=
dy
MU
dx
MU
dy
y
U
dx
x
U
dU
y
x
.
Dlatego:
yx
dU
y
x
MRS
dx
dy
MU
MU
=
−
=
=0
.
8
Maksymalizacja użyteczności
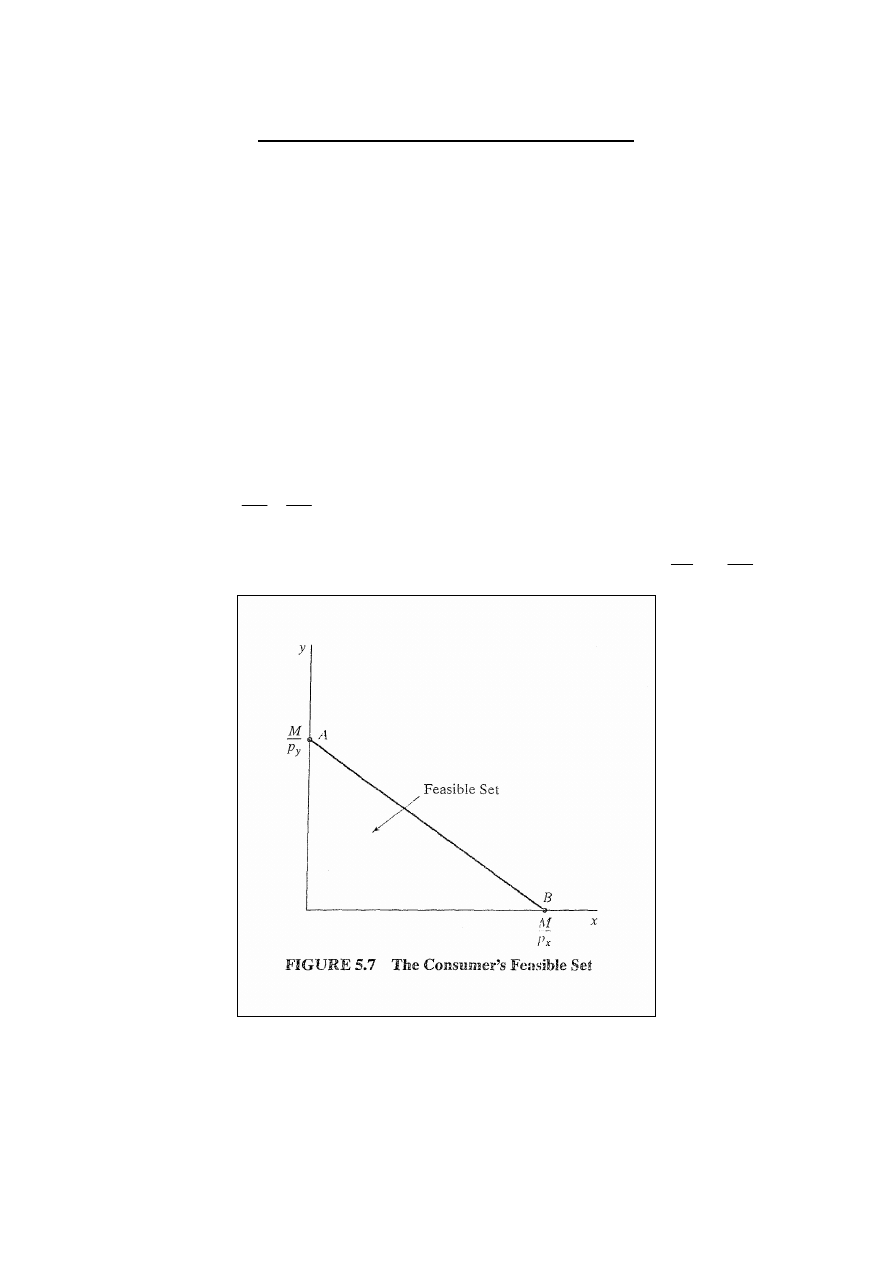
Zbiór osiągalny koszyków konsumpcyjnych jest to zbiór,
który nie jest zbyt drogi przy danym ograniczeniu
budżetowym konsumenta (rys. 5.7).
p
x
= cena dobra X
p
y
= cena dobra Y
M = dochód konsumenta.
Wydatki na konsumpcję muszą być mniejsze lub równe
dochodowi konsumenta: p
x
x + p
y
y ≤ M.
Przyjmujemy, że cały dochód jest wydawany na dwa dobra:
p
x
x + p
y
y = M.
Dlatego:
x
p
p
p
M
y
y
x
y
−
=
nazywamy ograniczeniem budżetowym.
Nachylenie linii ograniczenia budżetowego wynosi:
y
x
p
p
dx
dy
−
=
.
9
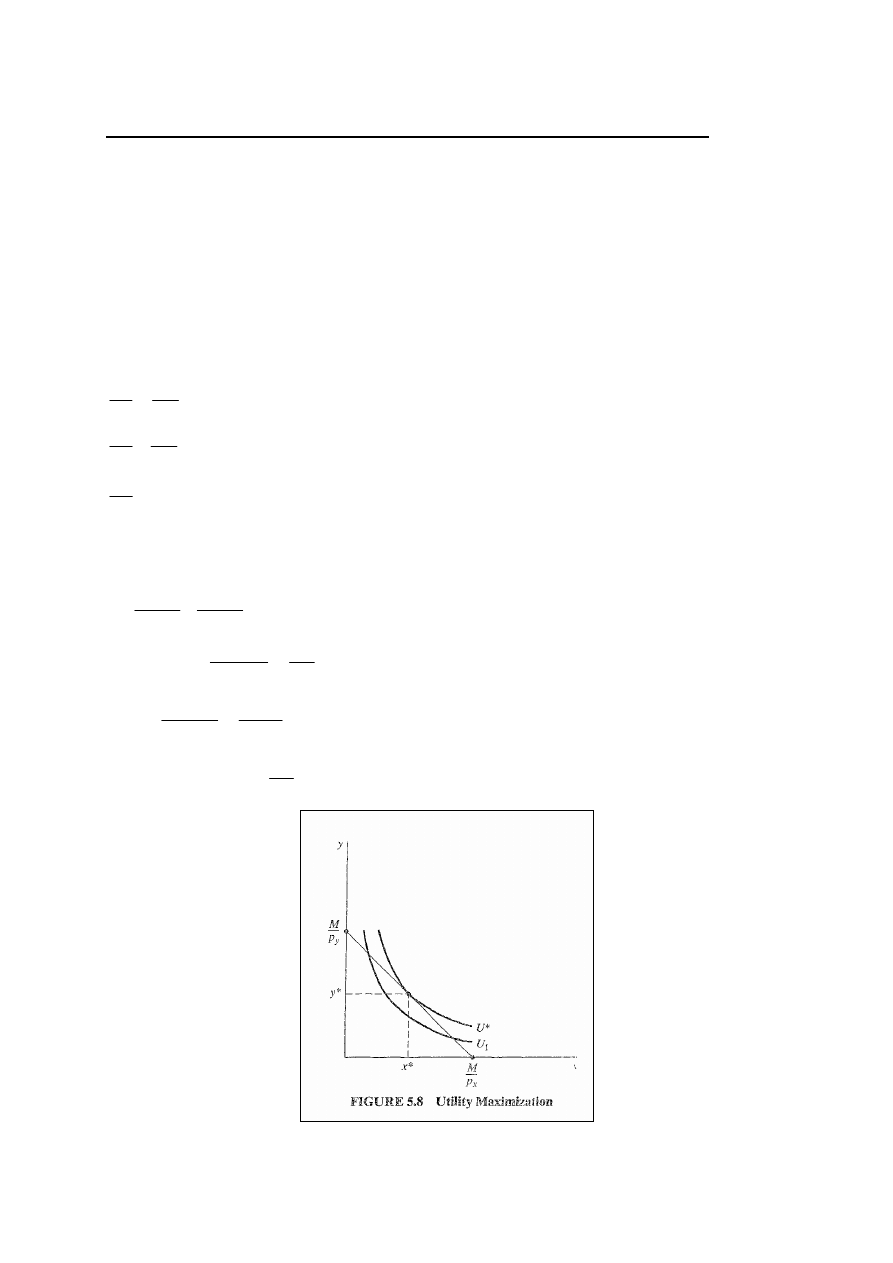
Problem konsumenta maksymalizacji przy ograniczeniu
Uogólniając problem konsumenta polega na (rys. 5.8):
maksymalizacji U = U(x, y) : funkcja celu
przy ograniczeniu: M ≥ p
x
x + p
y
y : ograniczenie budżetowe
Przyjmując, że ograniczenie przyjmuje postać równania
możemy zapisać Lagrangian:
( )
(
)
y
p
x
p
M
y
x
U
y
x
−
−
+
=
ℑ
λ
,
.
Warunki pierwszego rzędu:
0
=
−
∂
∂
=
∂
∂ℑ
x
p
x
U
x
λ
0
=
−
∂
∂
=
∂
∂ℑ
y
p
y
U
y
λ
0
=
−
−
=
∂
∂ℑ
y
p
x
p
M
y
x
λ
.
Rozwiązujemy dla
λ
z pierwszych dwóch warunków
pierwszego rzędu:
y
x
p
y
U
p
x
U
∂
∂
=
∂
∂
=
/
/
λ
.
Dlatego:
y
x
p
p
y
U
x
U
=
∂
∂
∂
∂
/
/
.
Ale:
yx
y
x
MRS
MU
MU
y
U
x
U
=
=
∂
∂
∂
∂
/
/
.
A więc:
y
x
yx
p
p
MRS
=
.
10
WPROWADZENIE DO TEORII
KONSUMENTA I POPYTU RYNKOWEGO
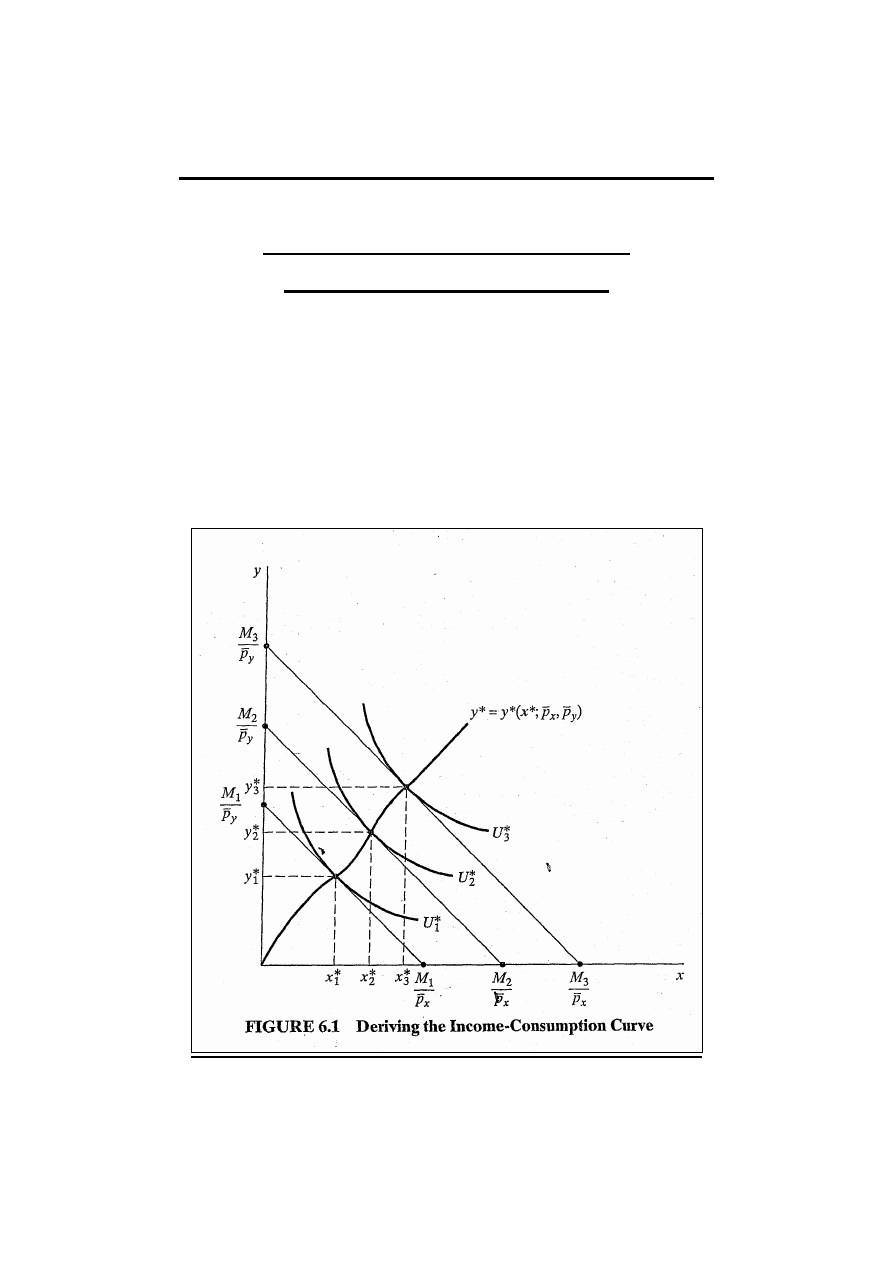
Funkcje popytu konsumenta:
przedstawienie graficzne
W teorii konsumenta warunek jednakowych nachyleń
zrównuje MRS ze stosunkiem cen. Z tego warunku możemy
wyprowadzić funkcję w przestrzeni xy opisującą wybór
konsumenta maksymalizujący użyteczność przy każdym
poziomie dochodu i stałych cenach. Ekonomiści nazywają tę
funkcję krzywą ekspansji dochodowej (rys. 6.1).
11
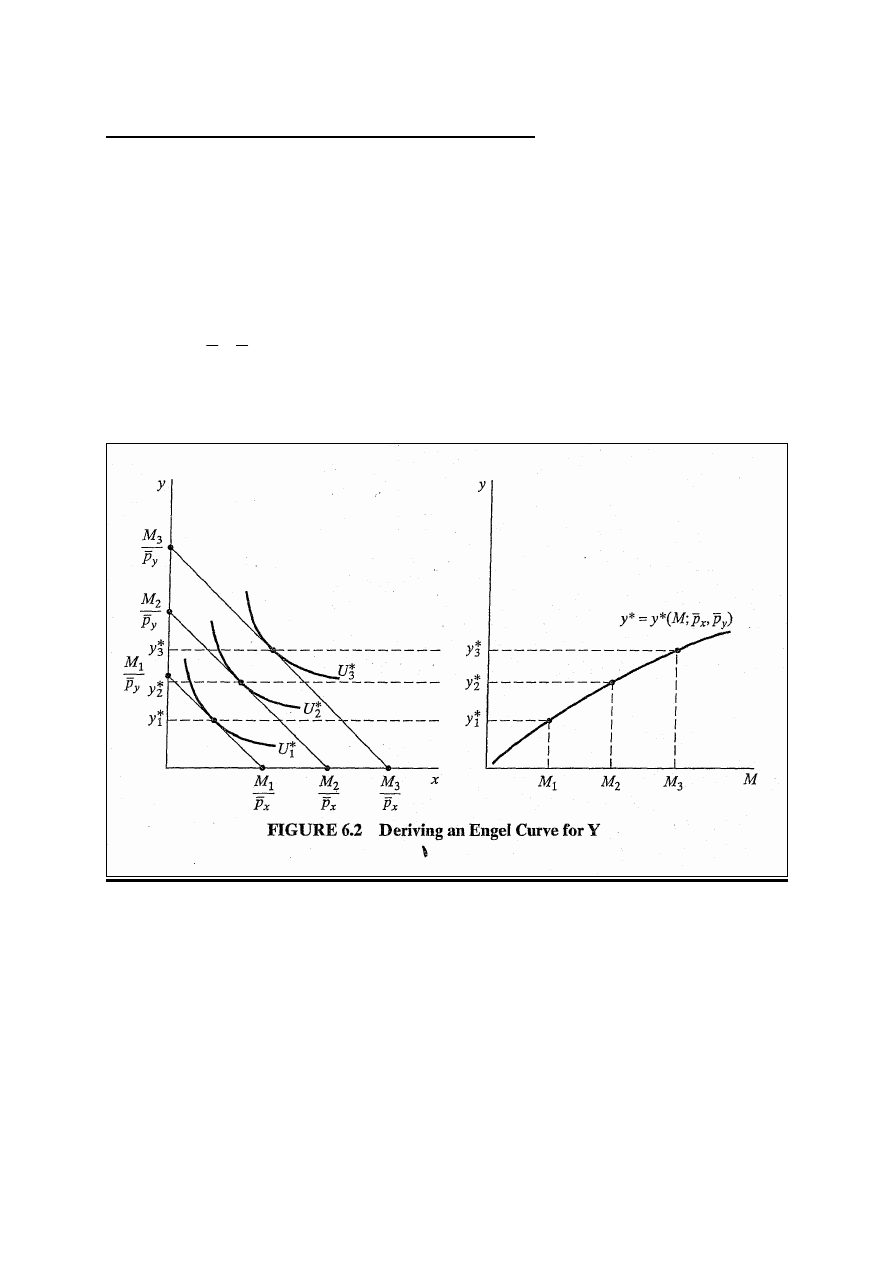
Wielkość popytu jako funkcja dochodu
Aby wyznaczyć wielkość popytu jako funkcję dochodu przy
stałych cenach, bierzemy punkty z krzywej ekspansji
dochodowej i streszczamy zależność między dochodem i x*
(y*) jako zmienną zależną. Dochód jest zmienną niezależną.
Na przykład, wyprowadźmy wykres y jako funkcji dochodu
przy założeniu, że x jest zawsze wybrany optymalnie:
(
)
y
x
p
p
M
y
y
,
;
*
*
=
.
Ekonomiści nazywają ten wykres krzywą Engla (rys.6.2).
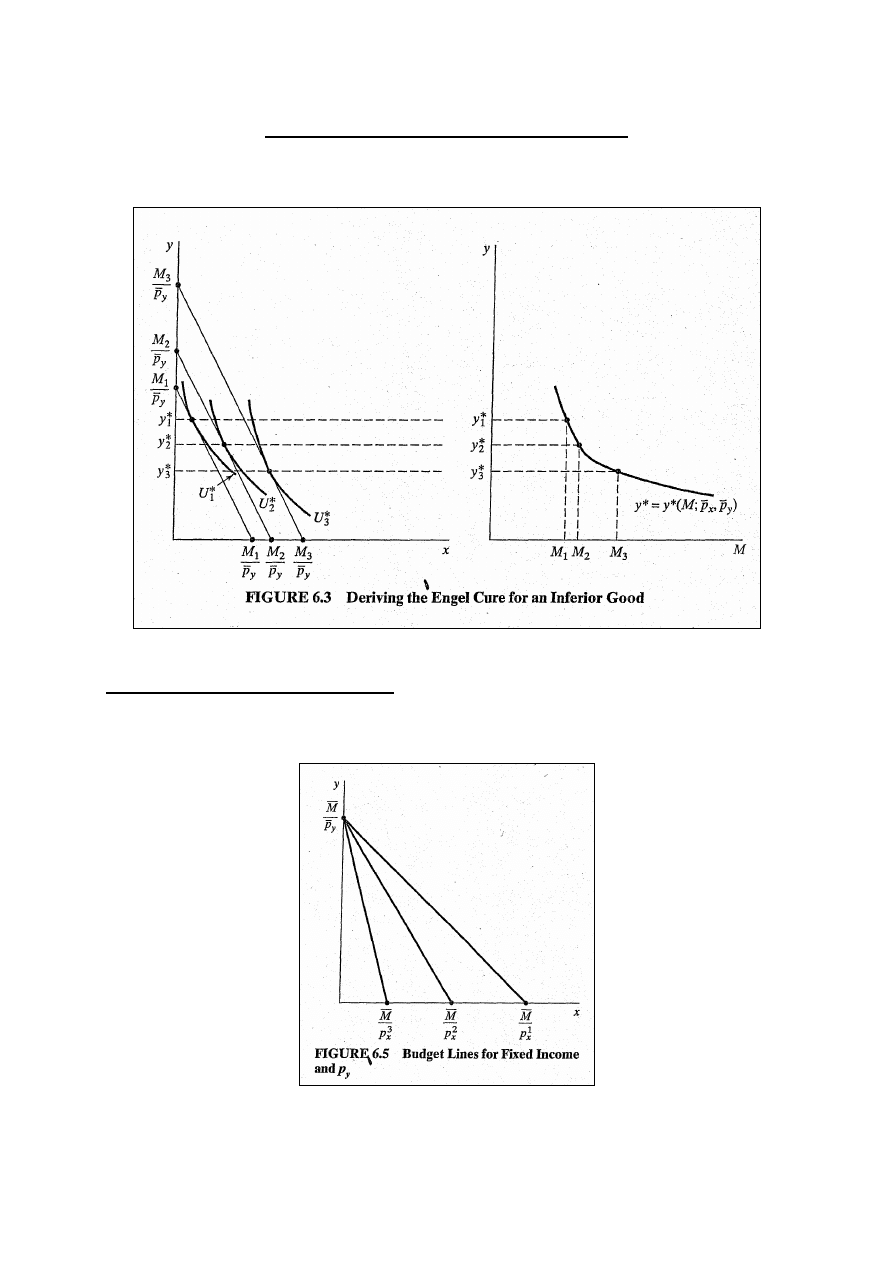
12
Dobra normalne i niższego rzędu
Rys. 6.3
Krzywa ekspansji cenowej
Rys. 6.5: zbiór linii ograniczenia budżetowego.
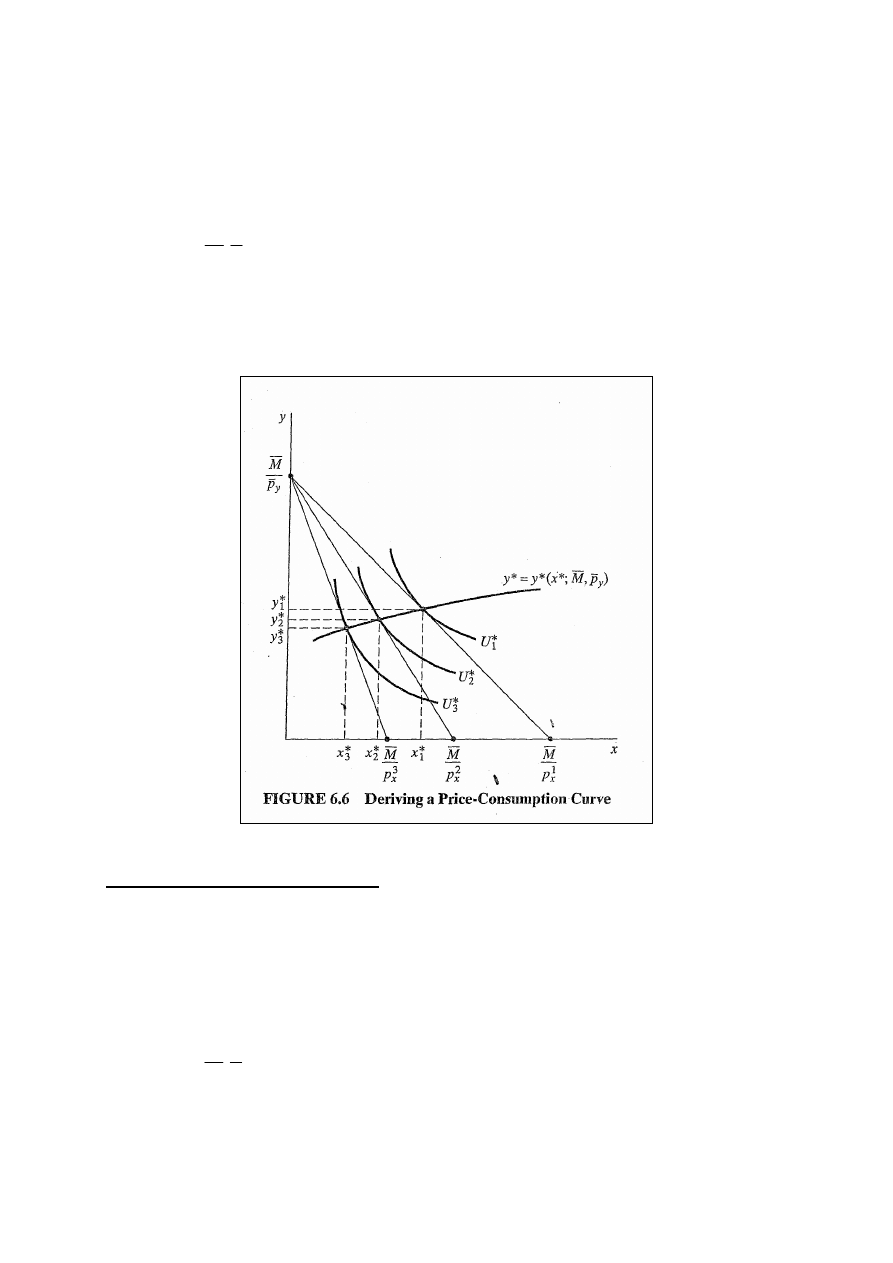
13
Jeżeli określimy wybór maksymalizujący użyteczność dla
każdej linii ograniczenia budżetowego, to będziemy mogli
wyznaczyć jeszcze jedną funkcję y* i x* przy zmieniającej
się p
x
i stałym dochodzie i stałej p
y
:
(
)
y
p
M
x
y
y
,
*;
*
*
=
.
Ekonomiści nazywają tą funkcję krzywą ekspansji cenowej.
(Rys. 6.6).
Normalna krzywa popytu
Mając wyznaczoną krzywą ekspansji cenowej możemy
określić wielkość popytu X jako funkcję ceny tego dobra.
Bierzemy punkty krzywej i przenosimy je na wykres, na
którym x jest zmienną zależną a p
x
jest zmienną niezależną
przy p
y
i dochodzie stałym:
(
)
y
x
p
M
p
x
x
,
;
*
*
=
.
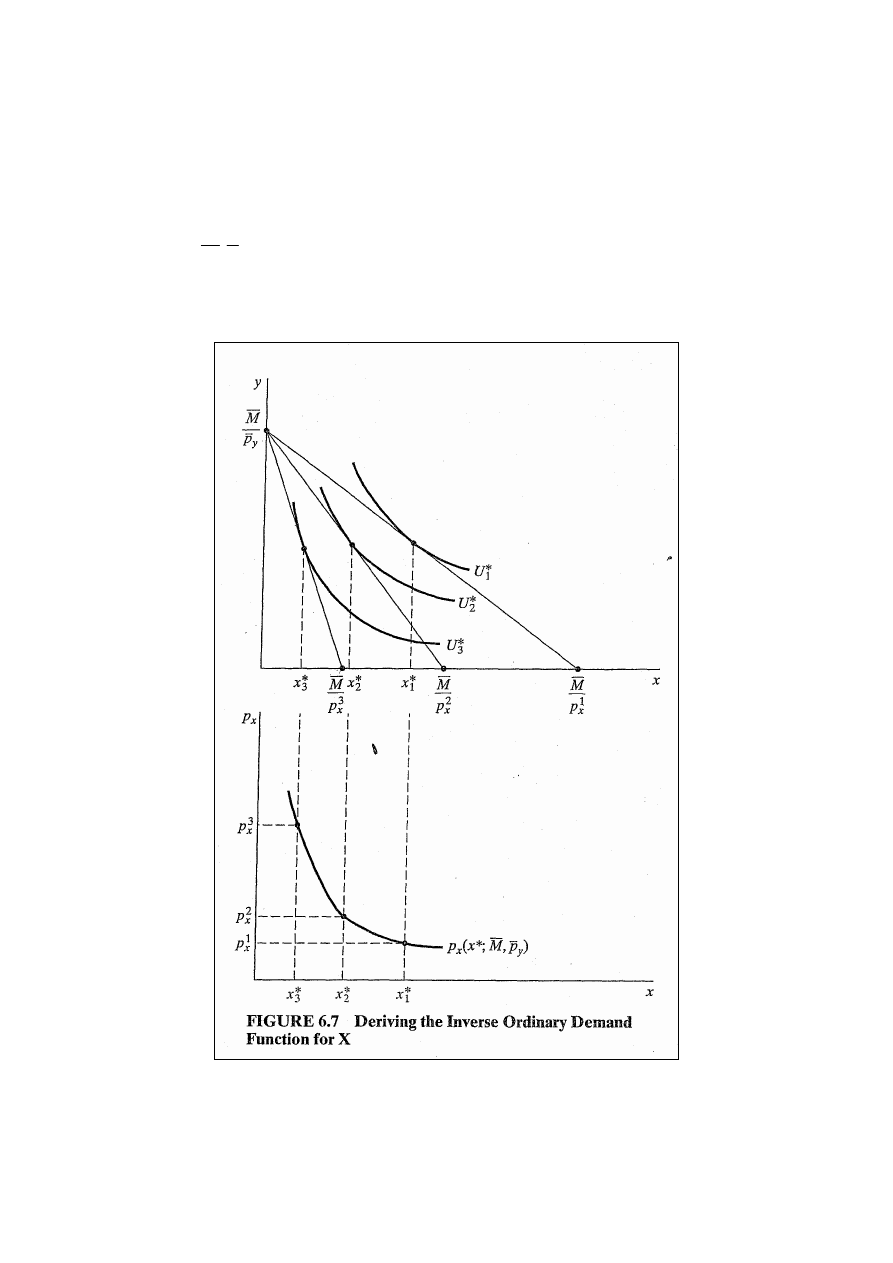
14
Otrzymaną funkcję nazywamy funkcją popytu zwyczajnego
na X. Przekształćmy jednak otrzymany wykres w taki sposób
aby cena znalazła się na osi pionowej, a wielkość popytu na
poziomej, otrzymamy wtedy funkcję popytu odwrotnego:
(
)
y
x
p
M
x
p
p
,
*;
*
=
.
Rys. 6.7.
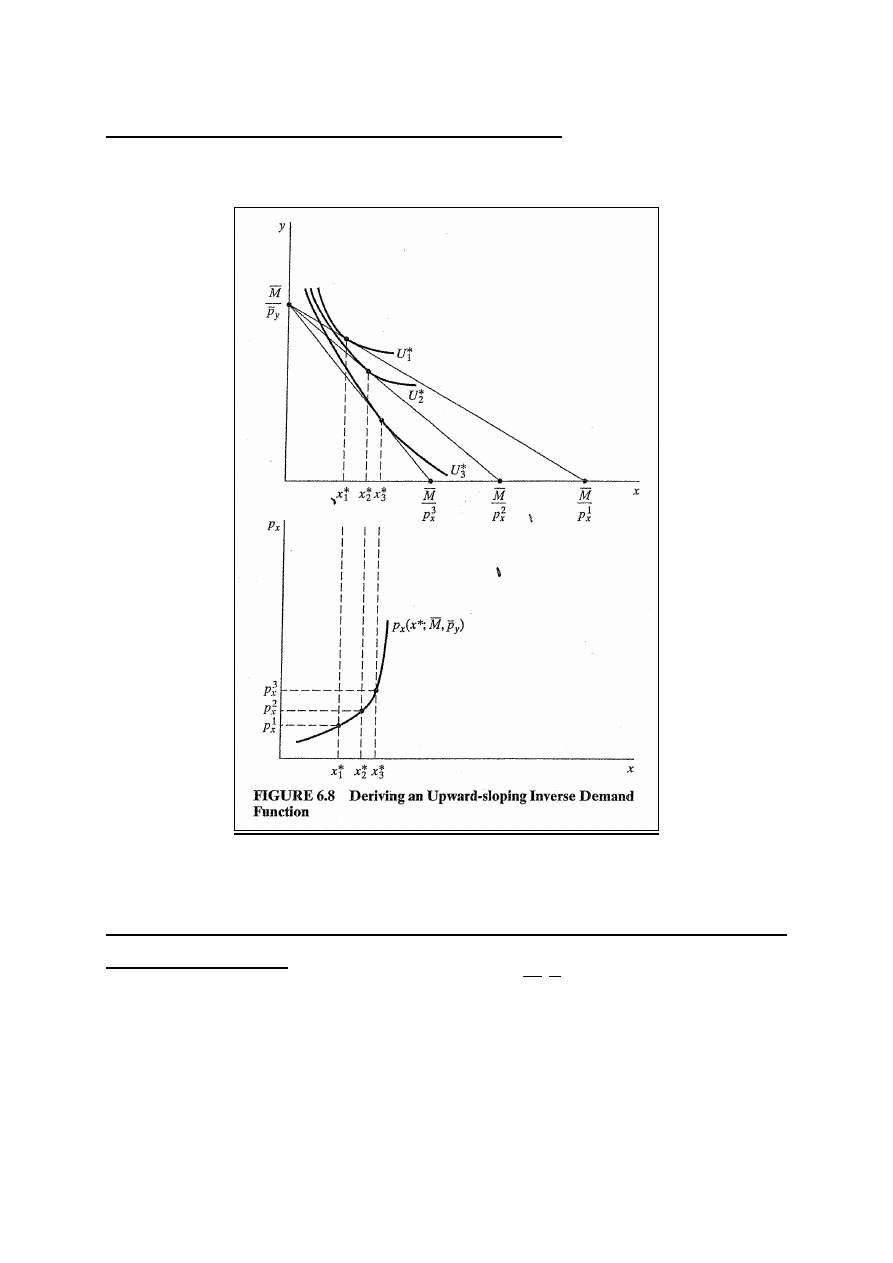
15
Krzywa popytu opadająca i wznosząca się
Rys. 6.8.
Funkcje popytu mieszanego: dobra substytucyjne i
komplementarne
Funkcja popytu mieszanego:
(
)
y
x
p
M
p
y
y
,
;
*
*
=
Substytuty brutto (rys. 6.9) – gdy dochód jest stały, a
użyteczność zmienia się.
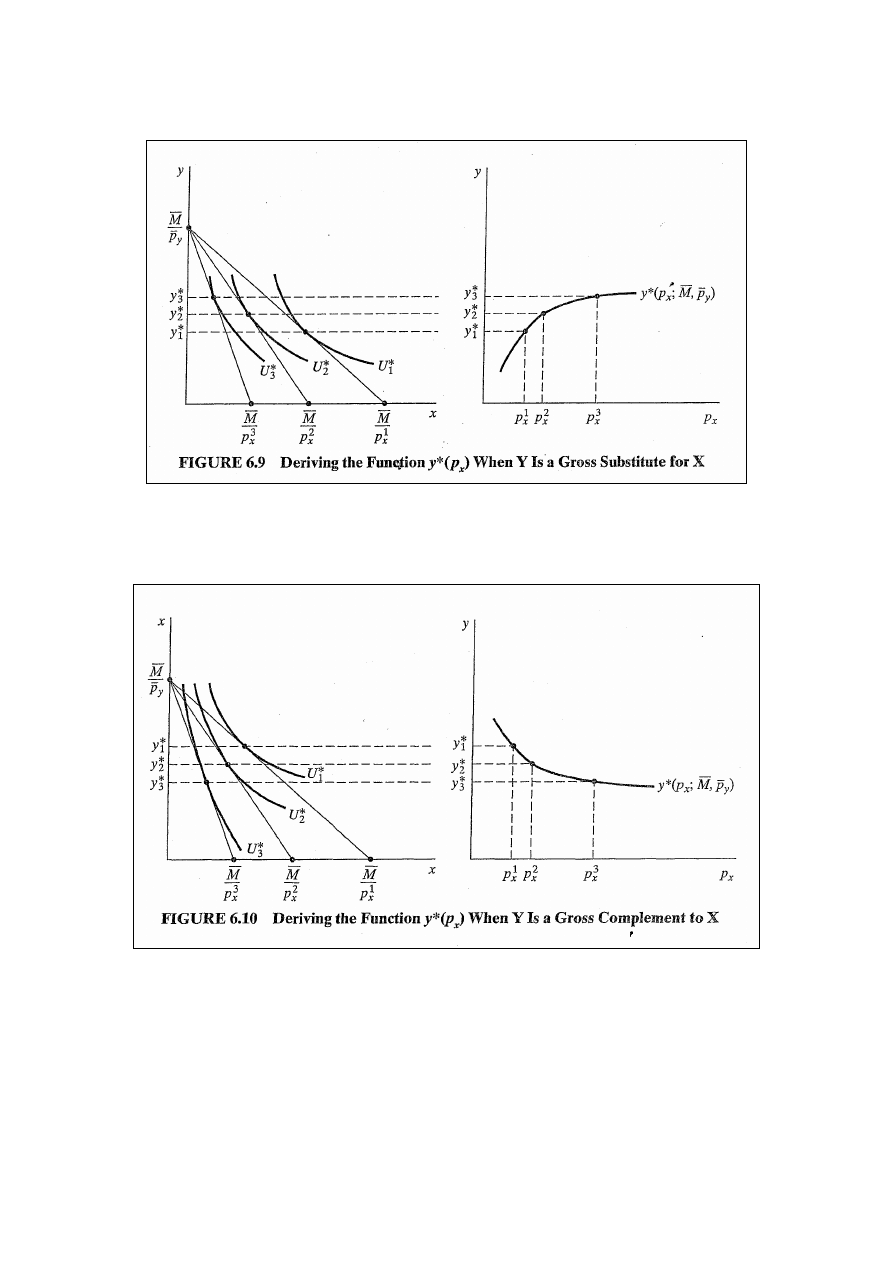
16
Dobra komplementarne brutto (rys. 6.10)
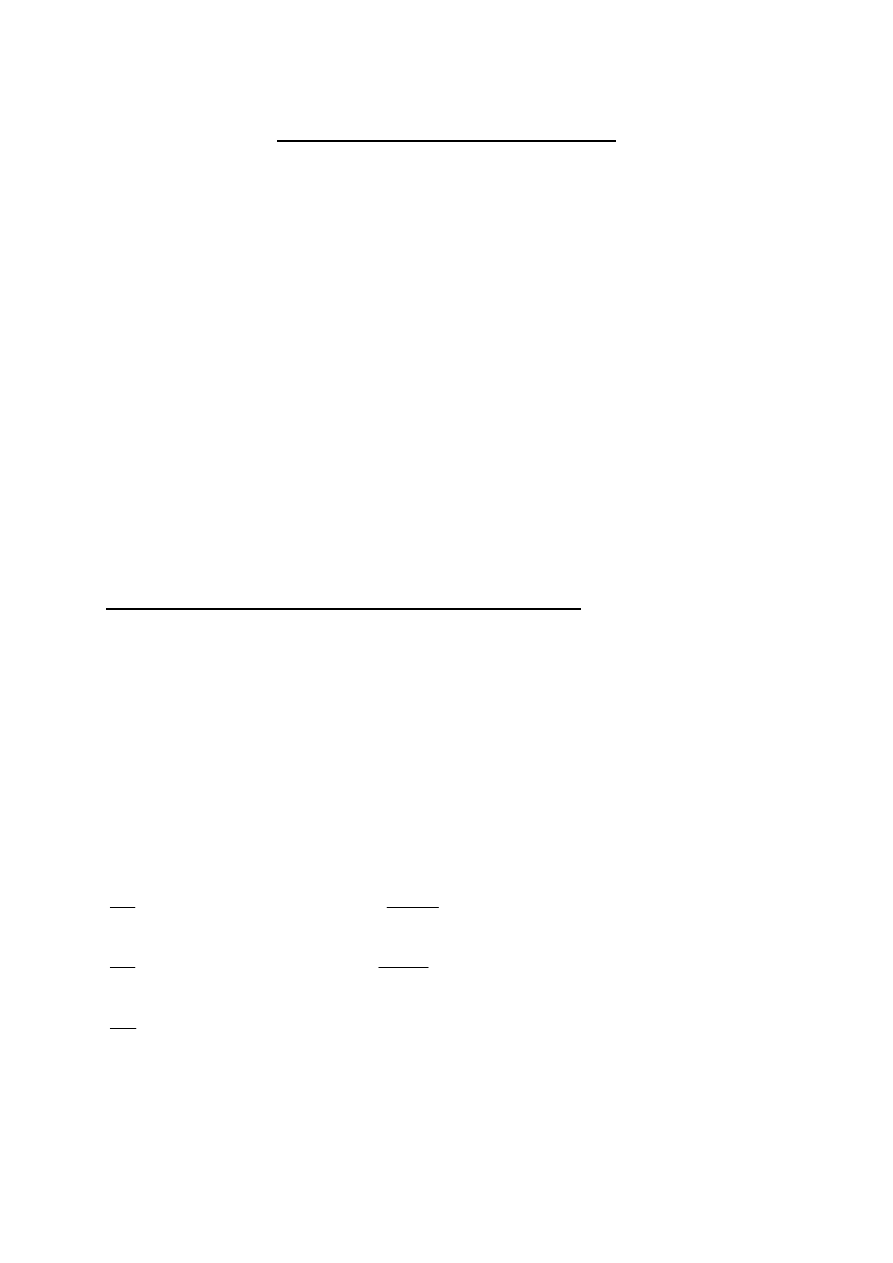
17
Uogólnione funkcje popytu
Aby matematycznie wyprowadzić wyrażenia na funkcje
popytu, które przedstawiliśmy graficznie, zaczynamy od
maksymalizacji użyteczności:
(
U
=
xy
+
x
+
y
,
x
,
y
≥ 0)
przy ograniczeniu budżetowym:
(
M
=
p
x
x
+
p
y
y
).
Z problemu maksymalizacji możemy wyprowadzić wyrażenie
na wielkość popytu jako funkcję wszystkich cen i dochodu.
Nazywamy ją uogólnioną funkcją popytu. Z tej funkcji
możemy wyprowadzić funkcję popytu zwyczajnego, krzywą
Engla, funkcje popytu mieszanego dzięki uczynieniu
poszczególnych cen i dochodu zmienną.
Wyprowadzenie uogólnionej funkcji popytu
Funkcja użyteczności konsumenta:
U = xy + x + y, x, y ≥ 0.
Problem maksymalizacji użyteczności konsumenta:
max
U
=
xy
+
x
+
y
p.w.
M
-
p
x
x
-
p
y
y
= 0
Funkcja Lagrange’a:
L
=
xy
+
x
+
y
+ λ(
M
-
p
x
x
-
p
y
y
)
Warunki pierwszego rzędu:
x
x
p
y
p
y
x
L
1
*
*
0
*
1
*
+
=
⇒
=
−
+
=
∂
∂
λ
λ
y
y
p
x
p
x
y
L
1
*
*
0
*
1
*
+
=
⇒
=
−
+
=
∂
∂
λ
λ
0
*
*
=
−
−
=
∂
∂
y
p
x
p
M
L
y
x
λ
Zrównujemy wartośćλ* z pierwszych dwóch warunków
pierwszego rzędu:
18
(
)
1
*
1
*
1
*
1
*
+
=
+
⇒
+
=
+
x
p
p
y
p
x
p
y
y
x
y
x
Możemy teraz wyprowadzić krzywą ekspansji dochodowej
rozwiązując powyższe wyrażenie dla y:
(
)
1
1
*
*
−
+
=
x
p
p
y
y
x
Wstawiamy je do trzeciego warunku pierwszego rzędu:
(
)
y
x
x
y
x
x
x
y
x
y
x
p
p
M
x
p
p
p
x
p
x
p
M
x
p
p
p
x
p
M
+
−
=
⇒
=
+
−
−
−
⇒
=
−
+
−
−
2
0
0
1
1
*
Tym sposobem otrzymujemy uogólnioną postać funkcji
popytu:
x
y
x
p
p
p
M
x
2
*
+
−
=
Aby wyznaczyć uogólnioną funkcję popytu na Y, wstawiamy
wyrażenie na x* do wyrażenia na krzywą ekspansji
dochodowej:
y
x
y
y
y
y
x
y
y
x
x
y
x
y
x
p
p
p
M
y
p
p
p
p
p
p
p
M
p
p
p
M
p
p
y
2
*
2
2
2
2
2
1
1
2
*
+
−
=
⇒
−
+
+
−
=
−
+
+
−
=
(8)
Wyprowadzenie funkcji popytu jednej zmiennej
Aby teraz wyprowadzić funkcje popytu będące funkcjami
jednej zmiennej zaczynamy od przyjęcia jako stałe,
(parametry) wszystkie zmienne niezależne, a następnie
pojedynczo pozwalamy im się zmieniać. A więc z uogólnionych
funkcji popytu:
x
y
x
p
p
p
M
x
2
*
+
−
=
i
y
x
y
p
p
p
M
y
2
*
+
−
=
19
Krzywe Engla:
x
y
x
p
p
p
M
x
2
*
+
−
=
i
y
x
y
p
p
p
M
y
2
*
+
−
=
Funkcje popytu zwyczajnego:
x
y
x
p
p
p
M
x
2
*
+
−
=
i
y
x
y
p
p
p
M
y
2
*
+
−
=
Funkcje popytu mieszanego:
x
y
x
p
p
p
M
x
2
*
+
−
=
i
y
x
y
p
p
p
M
y
2
*
+
−
=
Funkcje popytu Cobb-Douglasa
Ważne jest aby posługiwać się funkcjami popytu, które są
homogeniczne stopnia 0 względem wszystkich cen i dochodu.
Szczególną funkcją użyteczności, z której można
wyprowadzić bardzo proste funkcje popytu jest uogólniona
funkcja użyteczności Cobb-Douglasa.
U
=
x
α
y
β
,
x
,
y
> 0
Wyprowadzenie funkcji popytu
max
U
=
x
α
y
β
p.w.:
M
–
p
x
y
–
p
y
y
≥ 0.
Nie musimy stosować ograniczeń nieujemnych, gdyż krzywe
obojętności są hiperbolami równoosiowymi asymptotycznymi
względem osi. To eliminuje możliwość rozwiązań brzegowych.
Przyjmując więc, że ograniczenie budżetowe ma postać
równania, Lagrangian jest następujący:
L
=
x
α
y
β
+ λ(
M
–
p
x
x
–
p
y
y
)
20
Warunki pierwszego rzędu:
( ) ( )
( ) ( )
x
x
p
y
x
p
y
x
x
L
β
α
β
α
α
λ
λ
α
*
*
*
0
*
*
*
1
1
−
−
=
⇒
=
−
=
∂
∂
( ) ( )
( ) ( )
y
y
p
y
x
p
y
x
y
L
1
1
*
*
*
0
*
*
*
−
−
=
⇒
=
−
=
∂
∂
β
α
β
α
β
λ
λ
β
0
*
*
=
−
−
=
∂
∂
y
p
x
p
M
L
y
x
λ
Rozwiązując dla λ*:
( ) ( )
( ) ( )
( )
( )
y
x
y
x
p
y
p
x
p
y
x
p
y
x
1
1
1
1
*
*
*
*
*
*
*
−
−
−
−
=
⇒
=
=
β
α
β
α
λ
β
α
β
α
Krzywa ekspansji dochodowej:
*
*
x
p
p
y
y
x
α
β
=
Wstawiając
*
*
x
p
p
y
y
x
α
β
=
trzeciego warunku pierwszego rzędu:
0
*
*
=
−
−
x
p
p
p
x
p
M
y
x
y
x
α
β
Czyli,
(
)
x
x
p
M
x
M
x
p
α
β
α
β
/
1
*
*
1
+
=
⇒
=
+
Przekształcając:
+
α
β
1
aby otrzymać
+
α
β
α
I odwracając
otrzymane wyrażenie otrzymujemy uogólnioną funkcję
popytu na X:
(
)
x
p
M
x
β
α
α
+
=
*
Wstawiając
(
)
x
p
M
x
β
α
α
+
=
*
do równania
*
*
x
p
p
y
y
x
α
β
=
, uogólniona
funkcja popytu na Y:
(
)
(
)
y
x
y
x
y
x
p
M
p
M
p
p
x
p
p
y
β
α
α
β
α
α
α
β
α
β
+
=
+
=
=
*
*
21
Odnotujmy interesujące cechy charakterystyczne
otrzymanych funkcji popytu. Po pierwsze, wykładnik każdego
z dóbr podzielony przez sumę wykładników przedstawia
udział w dochodzie wydatków na każde z dóbr:
α
/(α+β) udział w dochodzie wydatków na x*
β
/(α+β) udział w dochodzie wydatków na y*
Ponadto funkcje popytu mogą być przekształcone do postaci
liniowych dzięki wykorzystaniu logarytmów.
Rynkowe funkcje popytu
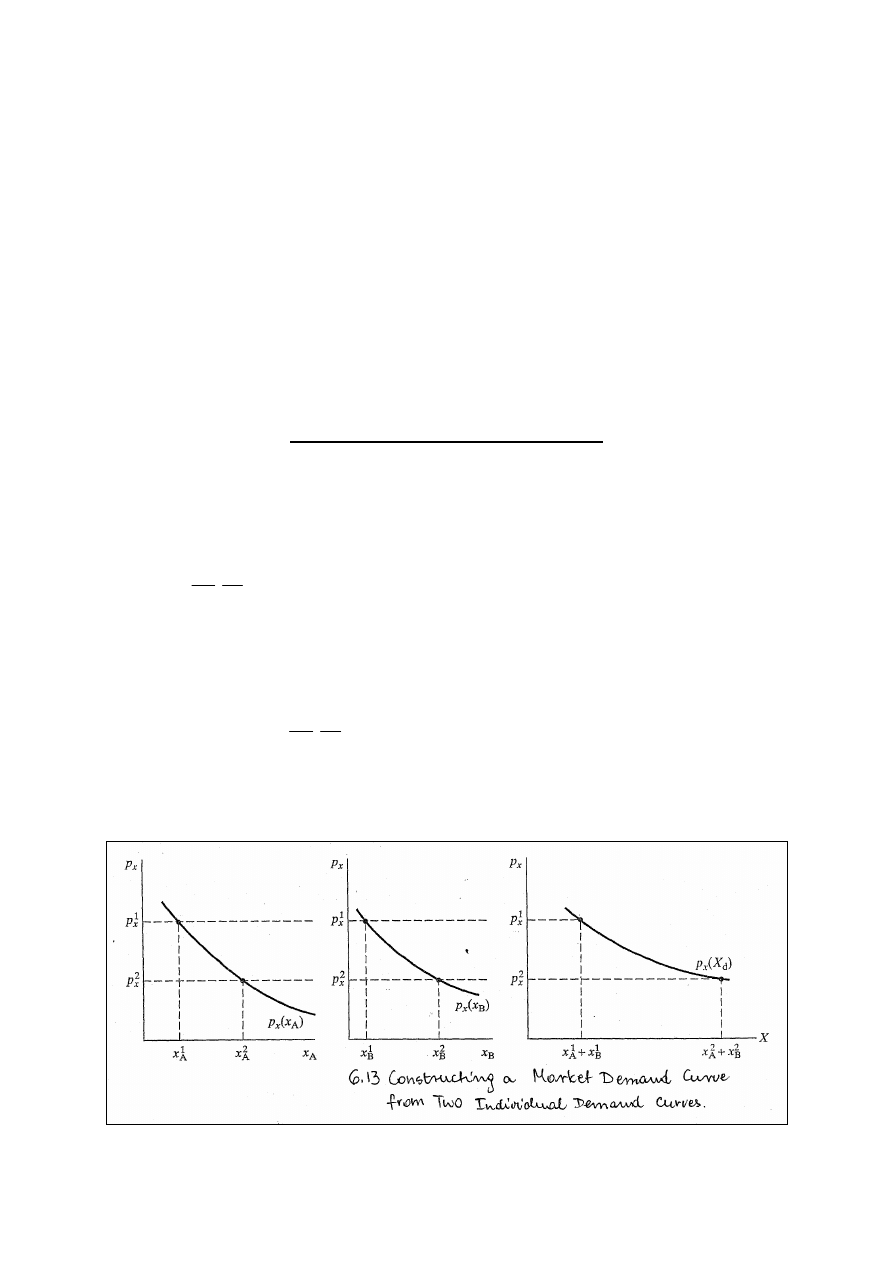
Funkcja popytu rynkowego przedstawia całkowite wielkości
popytu na danym rynku zgłaszane przez wszystkich
konsumentów przy każdej cenie. Otrzymujemy ją dzięki
zsumowaniu funkcji indywidualnych popytów. Jeżeli więc
(
)
y
i
x
i
i
p
M
p
x
x
;
;
=
jest funkcją popytu zwyczajnego na X osoby
i’s, to funkcję popytu rynkowego otrzymujemy sumując
wszystkie funkcje popytu indywidualnego dla wszystkich n
osób:
(
)
y
i
x
n
i
i
n
i
i
d
p
M
p
x
x
X
;
;
1
1
∑
∑
=
=
=
=
(Rys.6.13).
22
ELASTYCZNOŚĆ FUNKCJI POPYTU
INDYWIDUALNEGO I RYNKOWEGO
Definicja elastyczności
Elastyczność cenowa popytu, elastyczność dochodowa
popytu, mieszana elastyczność cenowa popytu.
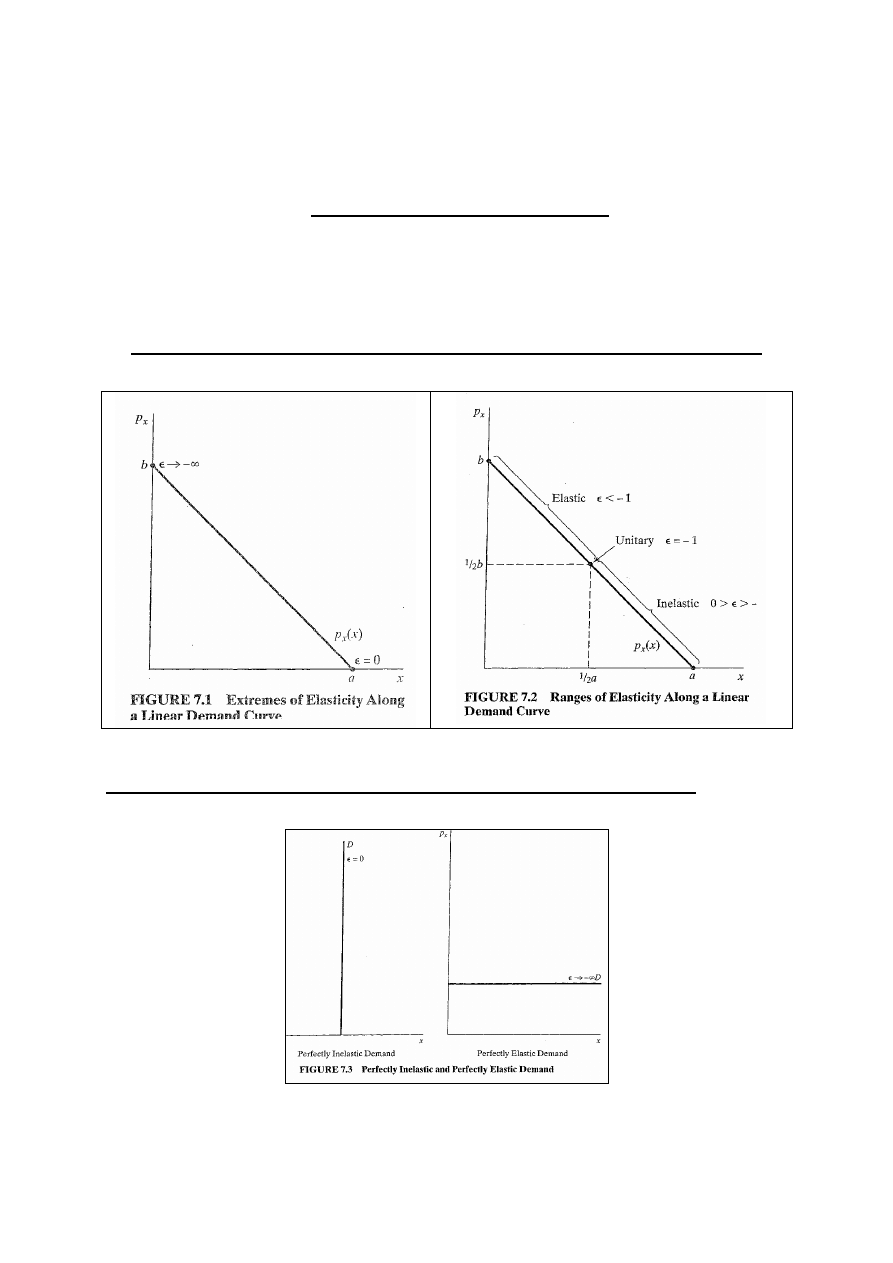
Elastyczność funkcji popytu liniowej i nieliniowej
Rys. 7.1, Rys. 7.2.
Popyt doskonale elastyczny i doskonale nieelastyczny
Rys. 7.3
23
Funkcje popytu o stałej elastyczności
Wzdłuż nieliniowych funkcji popytu elastyczność może być
stała lub różna w każdym punkcie wykresu. Zaczniemy od
funkcji funkcje o stałej elastyczności, w przypadku której w
każdym punkcie wykresu elastyczność jest taka sama. Dzieje
się tak, gdyż zmiana nachylenia wykresu zawsze równa się
zmianie stosunku p
x
/x. Uogólniona postać funkcji popytu o
stałej elastyczności jest następująca:
x = A(p
x
)
-k
gdzie A i k są dodatnimi stałymi.
( )
1
−
−
−
=
k
x
x
p
kA
dp
dx
Dlatego pomnożenie przez p
x
/x:
( )
( )
( )
k
p
A
p
p
kA
x
p
p
kA
k
x
x
k
x
x
k
x
d
−
=
−
=
−
=
−
−
−
−
−
1
1
ε
.
Z tego równania wynika, że:
k > 1, popyt jest wszędzie elastyczny;
k = 1, popyt jest wszędzie jednostkowo elastyczny;
k < 1, popyt jest wszędzie nieelastyczny;
Inne nieliniowe funkcje popytu mają różne elastyczności w
poszczególnych punktach wykresów.
24
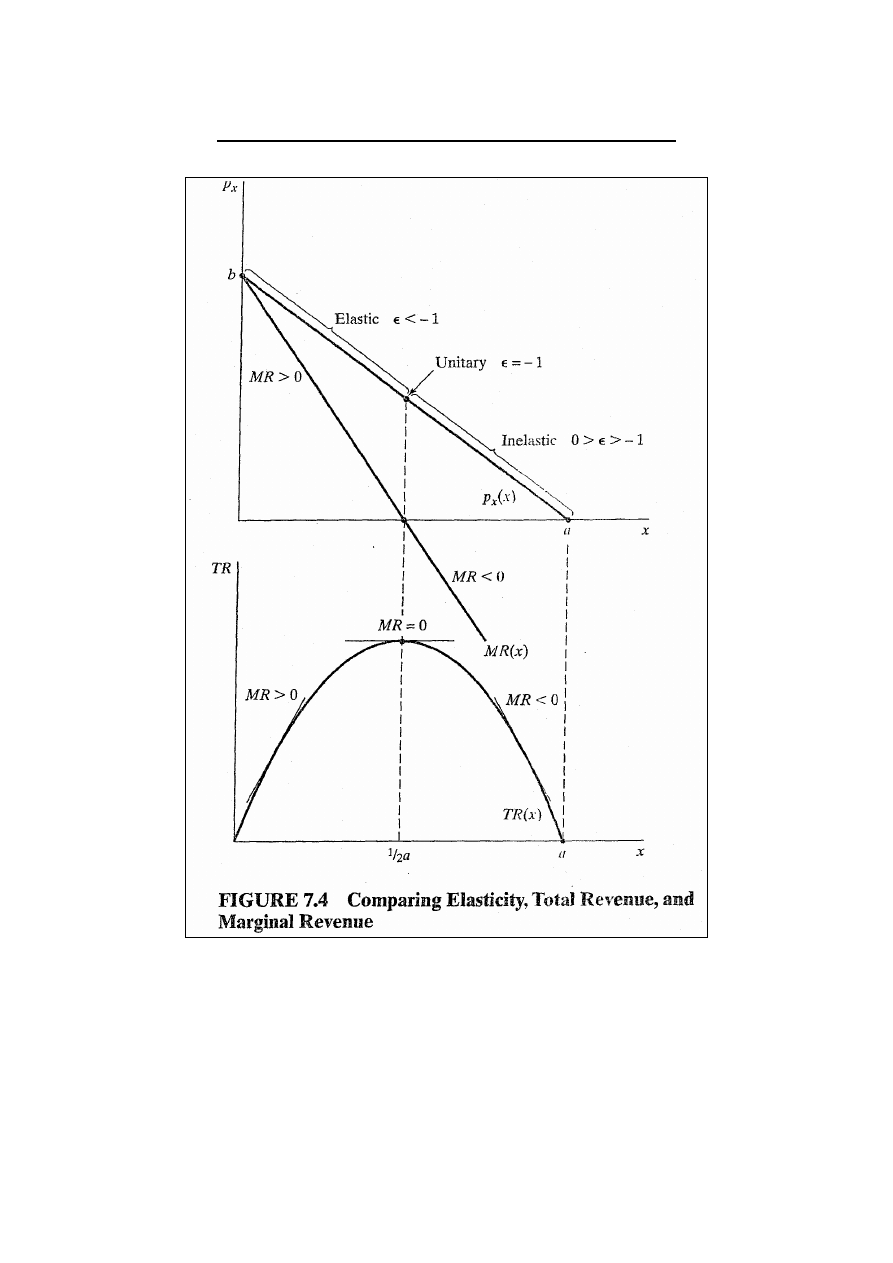
Elastyczność i przychody całkowite
Rys. 7.4
25
Przychody całkowite, przeciętne i krańcowe wzdłuż
nieliniowych krzywych popytu
Nieliniowe krzywe popytu mogą mieć stałe lub zmieniające
się elastyczności. W przypadku funkcji popytu o stałej
elastyczności MR mogą być dodatnie, 0, lub ujemne. Z tego
wynika, że TR albo rosną, są stałe, albo maleją wraz ze
wzrostem x.
( )
k
x
k
x
A
x
p
p
A
x
/
1
−
−
=
⇒
=
k
k
k
x
A
x
A
x
TR
/
1
1
/
1
/
1
1
−
−
−
=
=
x
k
p
k
A
x
k
MR
−
=
−
=
−
1
1
1
1
/
1
.
Z ostatniego równania wynika, że jeżeli k > 1 (popyt
elastyczny), MR są dodatnie; jeżeli k = 1 (jednostkowo
elastyczny) MR wynoszą 0; i jeżeli k < 1 (nieelastyczny), MR
są ujemne.