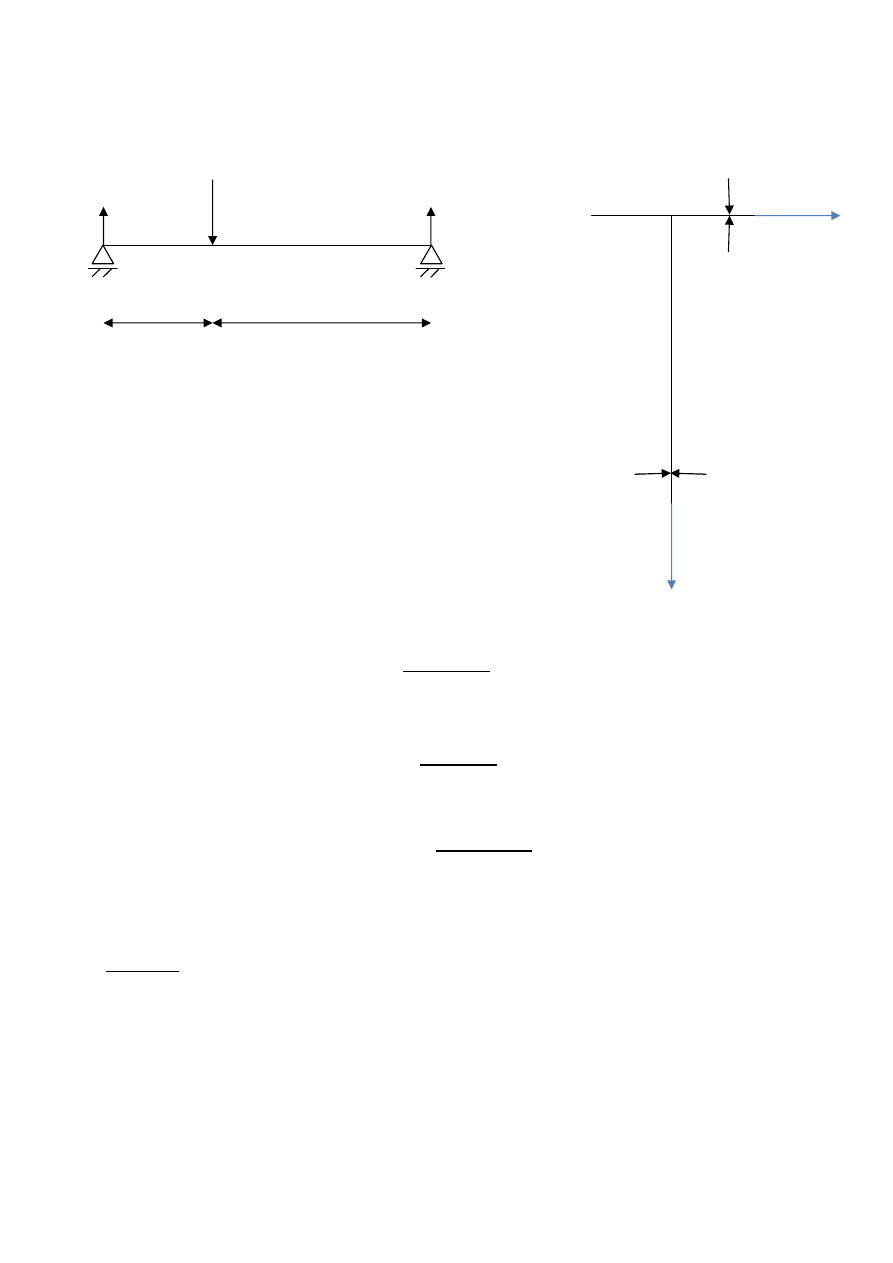
Opracował: Czerwiec 

 

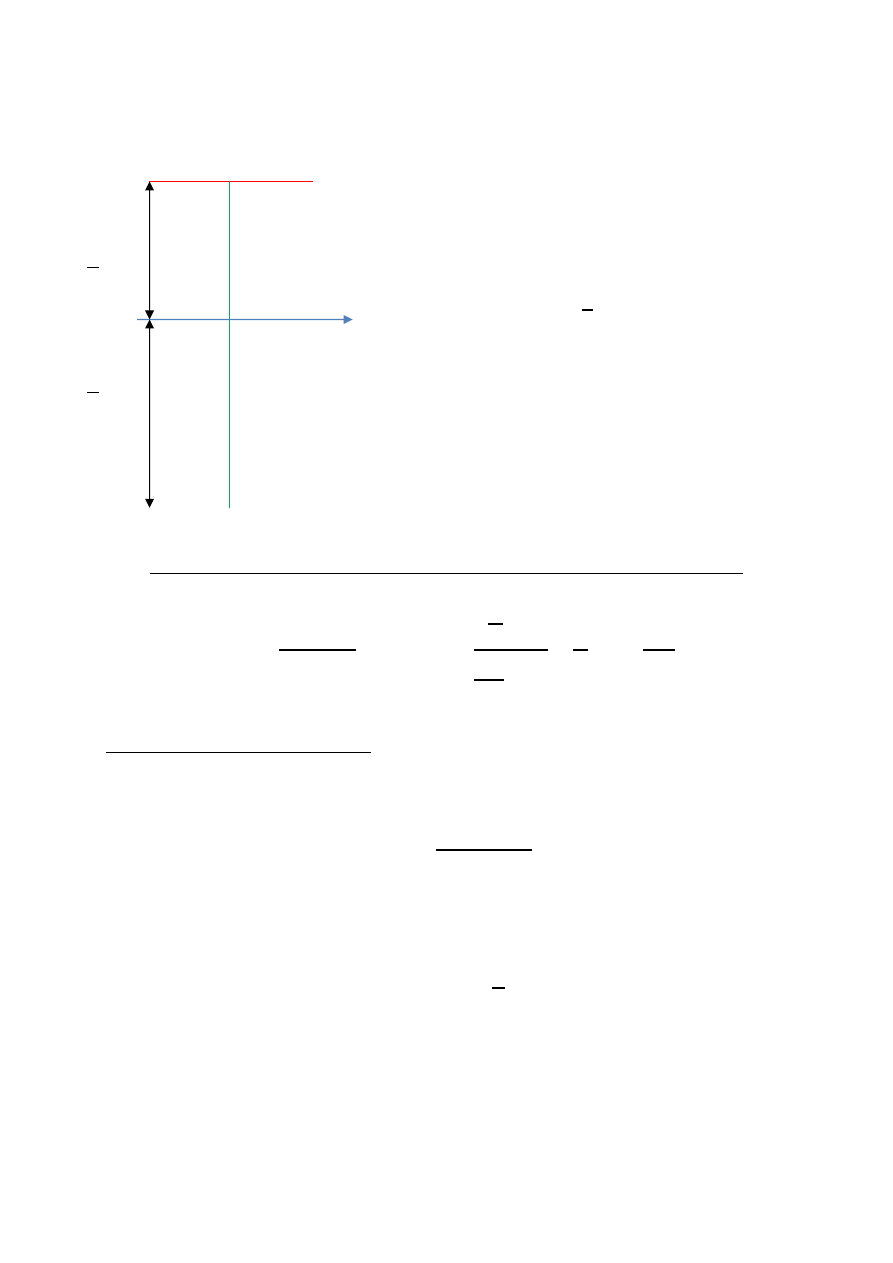
Dla belki obciążonej i przekroju poprzecznym jak na rys. poniżej wyznaczyć 

Ϭ

gmax

 oraz 

τ

max. 

 

 

 

 

 

 

 

 

 

 

 

 

 

Rozwiązanie: 

Dwa podstawowe wzory, które potrzebujemy do rozwiązania zadania to: 

Ϭ

௚௠௔௫

=

ܯ

௚௠௔௫

ܫ

௭௖

∗ ߩ

௠௔௫

 

߬

௠௔௫ୀ

ܶ

௠௔௫

∗ ܵ

ܫ

௭௖

∗ ܷ

 

Poszczególne elementy powyższych wzorów postaram się wyjaśnić podczas liczenia. 

Obliczamy 

Ϭ

ࢍ࢓ࢇ࢞

: 

•

 

Liczymy maksymalny moment gnący(M

gmax

), najpierw sprawdzamy czy w kartkach ksero nie 

ma takiej belki jak w zadaniu. Akurat takiej belki nie ma, więc liczymy na piechotę. 

 

 

B 

A 

R

A 

R

B 

P

 

2/3l

 

1/3l

 

a

 

2a

 

z

 

y

 

t

 

3t

 

Opracował: Czerwiec 

 

W tym celu musimy kolejno policzyć reakcje, siły tnące i momenty. 

ߑ݌݅ݕ = 0: ܴ

஺

− ܲ + ܴ

஻

= 0 

ߑܯ

஺

= 0: ܲ ∗

1

3 ݈ − ܴ

஻∗

݈ = 0 

ܴ

஺

=

2

3 ܲ

 

ܴ

஻

=

1

3 ܲ

 

Wyznaczamy siły tnące i momenty w przedziałach 

ݔ ∈ ቀ0,

ଵ
ଷ

݈ቁ ; ݔ ∈ (

ଵ
ଷ

݈, ݈) 

ܶ(ݔ) = ൞

2

3 ܲ                               ݔ ∈ (0,

1

3 ݈)

2

3 ܲ − ܲ = −

1

3 ܲ       ݔ ∈ (

1

3 ݈, ݈)

 ൢ 

 

ܯ(ݔ) = ൞

2

3 ܲ ∗ ݔ                               ݔ ∈ (0,

1

3 ݈)

2

3 ܲ ∗ ݔ − ܲ ∗ (ݔ −

1

3 ݈)       ݔ ∈ (

1

3 ݈, ݈)

 ൢ 

Podstawiamy do momentów, skrajne wartości przedziałów za x. Patrzymy która z wartości po 

podstawieniu jest największa, bo to właśnie jej szukamy(M

gmax

).  

 

 

 

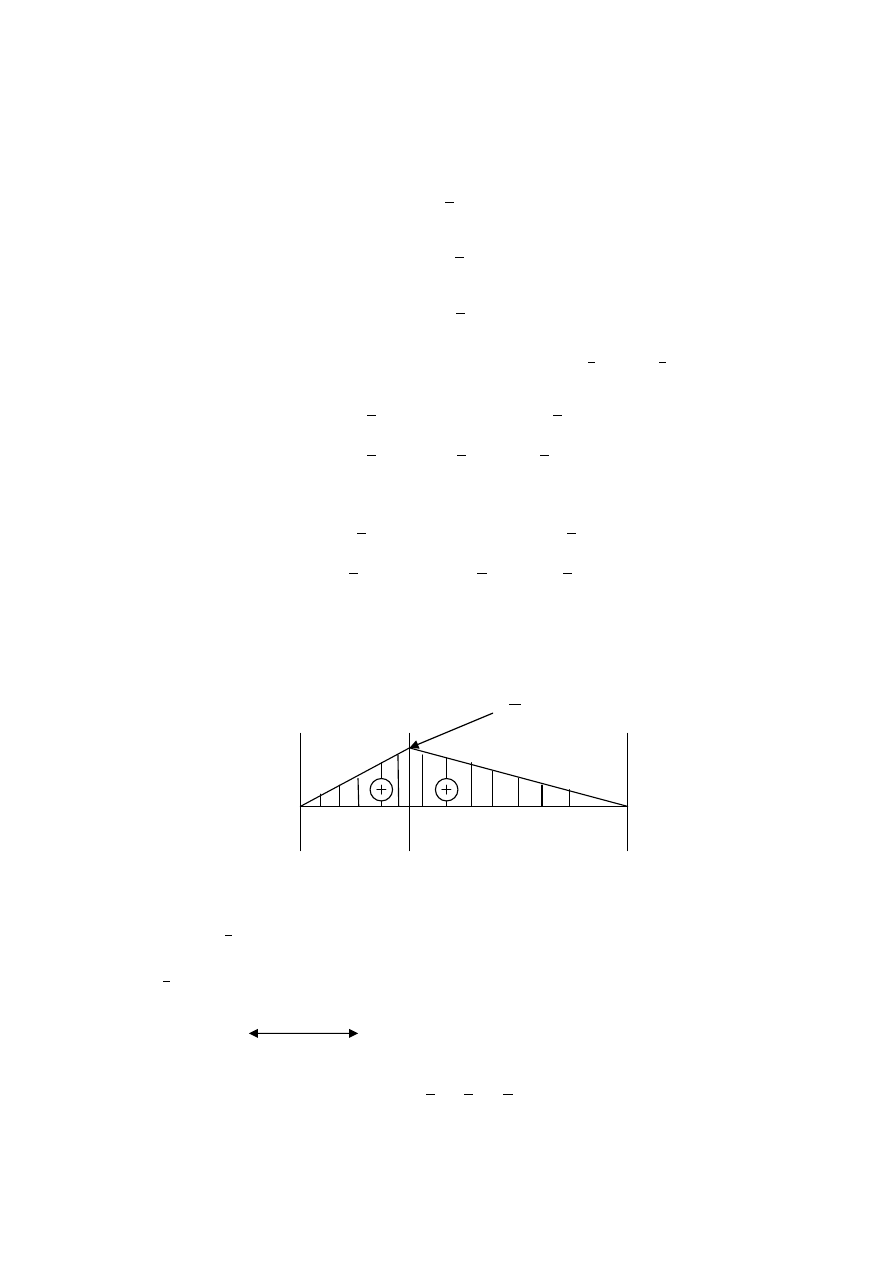
M(x) 

 

Jest jeszcze małe uproszczenie przy liczeniu momentu maksymalnego: liczymy T(x) i mnożymy przez 

długość przedziału, np.: 

przedział  

ݔ ∈ (0,

ଵ
ଷ

݈) 

 

T(x) =

ଶ
ଷ

ܲ 

długość przedziału: 

 

 

ۻ

܏ܕ܉ܠ

=

2

3 ܲ ∗

1

3 ݈ =

૛

ૢ ࡼ࢒

 

Nie zawsze można stosować to uproszczenie ale nie pamiętam w jakich przypadkach nie można. =) 

2

9 ݈ܲ

 

1/3l

 

Opracował: Czerwiec 

 

•

 

Liczymy moment bezwładności przekroju poprzecznego względem osi na której znajduję się 

środek ciężkości, czyli 

I

zc.

 

ܫ

௭௖

= ܫ

௭

− ݕ

௖

ଶ

∗ ܣ 

 

 

Moment bezwładności 

współrzędna śr. ciężkości  

pole powierzchni 

 

 

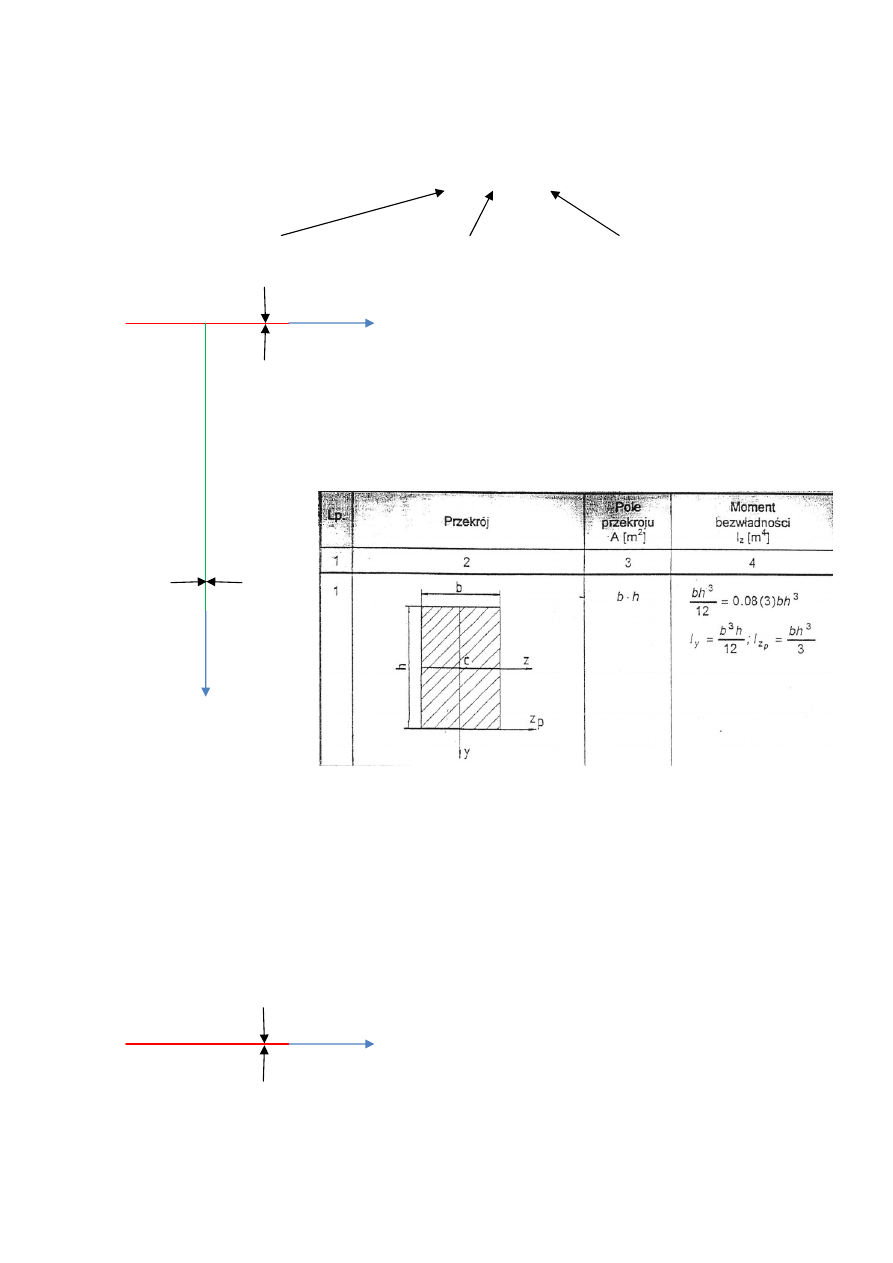
Jeszcze raz nasz przekrój dla przypomnienia. 

- Moment bezwładności 

I

z

 liczymy patrząc na przekrój 

figury u nas mamy dwa prostokąty (

czerwony

 i 

zielony

). Szukamy sobie w kartkach ksero wzorków 

dla prostokąta (skan poniżej). 

 

 

 

 

 

 

 

 

 

Moment bezwładności całej figury będzie sumą momentu 

czerwonego

 i 

zielonego

 prostokąta. 

Moment bezwładności zależy od tego względem jakiej osi jest liczony: 

- może być liczony względem osi z

c

 czyli przechodzącej przez środek ciężkości lub z

p

 czyli osi 

podstawowej która zazwyczaj jest na krawędzi figury 

 

 

 

Czerwony

 prostokąt ma grubość t <<a czyli bardzo małą. Wystarczy wyobrazić sobie kreskę nie da się 

dorysować osi na jej krawędzi, bo jest zbyt cienka stąd wzór dla osi przechodzącej przez środek 

ciężkości. 

a

 

2a

 

z

 

y

 

t

 

3t

 

a

 

z = z

c 

t

 

Opracował: Czerwiec 

 

Z kserówki mamy wzór: 

ܫ

௭

=

ܾℎ

ଷ

12

 

Wysokość i szerokość z wzoru zmieniamy na takiej jakie są w zadania czyli b = a, h = t 

ܫ

௭

=

ܽݐ

ଷ

12

 

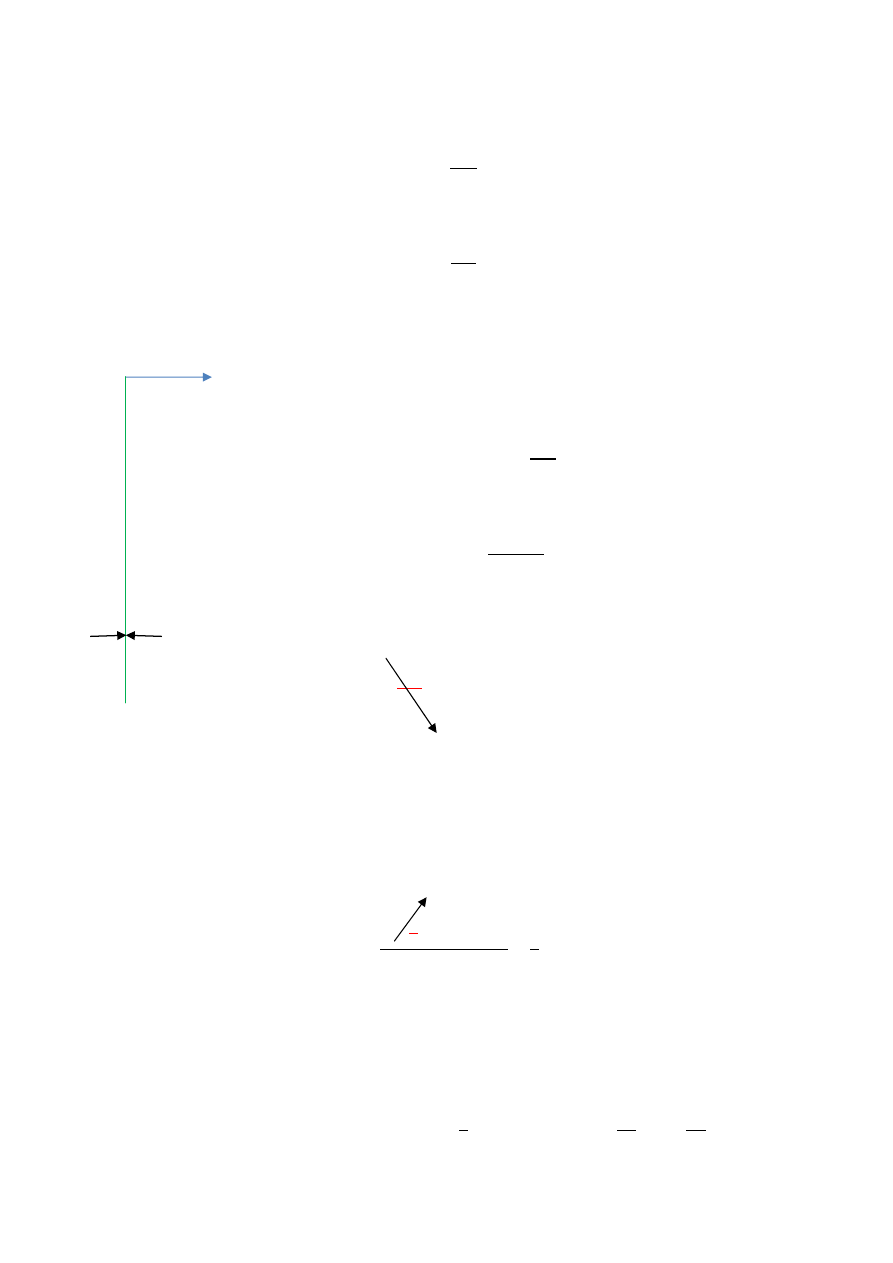
Teraz kolejny prostokąt: 

 

 

Dla 

zielonego

 prostokąta oś z nie jest osią przechodzącą przez 

środek ciężkości dlatego używamy wzoru: 

ܫ

௭

=

ܾℎ

ଷ

3

 

Gdzie: b=3t, h= 2a 

ܫ

௭

=

3ݐ(2ܽ)

ଷ

3

= 8ݐܽ

ଷ

 

 

Suma momentów bezwładności: 

ܫ

௭

=

ܽݐ

ଷ

12

+

8ݐܽ

ଷ

= 8ݐܽ

ଷ

 

 

 

 

- Liczymy współrzędną 

y

c

 środka ciężkości: 

 

ݕ

௖

=

at ∗ t2

+

2a ∗ 3t ∗ a

a ∗ t

+

2a ∗ 3t

=

6

7 a

 

- Pole powierzchni mamy z mianownika wyrażenia powyżej: 

ܣ = 7ܽݐ 

Podstawiamy nasze obliczenia do wzoru na 

I

zc

: 

ࡵ

ࢠࢉ

= ܫ

௭

− ݕ

௖

ଶ

∗ ܣ =

8ݐܽ

3

−

ቀ

6
7

a

ቁ

2

∗ 7ܽݐ = 8ݐܽ

3

−

36

7

ݐܽ

3

=

૛૙

ૠ

࢚ࢇ

૜

 

2a

 

3t

 

z = z

p 

= 0 gdyż t jest bardzo małe

 

0 

 

Opracował: Czerwiec 

 

•

 

Zostało jeszcze najdalej oddalone włókno od osi obojętnej(przechodzącej przez śr. ciężkości) 

ߩ

௠௔௫

 

 
 

Patrzymy jaka jest największa odległość od osi z

c

 do skrajnego 

punktu przekroju: 

 

 

 

 

 

 

 

Mamy wszystko co potrzeba do obliczenia naprężeń od zginania podstawiamy do wzoru: 

Ϭ

ࢍ࢓ࢇ࢞

=

ܯ

௚௠௔௫

ܫ

௭௖

∗ ߩ

௠௔௫

=

2

9 ݈ܲ

20

7 ݐܽ

ଷ

∗

8

7 ܽ =

ૡ

ૢ૙ ࢚ࢇ

૛

 

Następna część zadania czyli obliczanie 

࣎

࢓ࢇ࢞

: 

Dla przypomnienia wzorek: 

߬

௠௔௫ୀ

ܶ

௠௔௫

∗ ܵ

ܫ

௭௖

∗ ܷ

 

•

 

Zaczynamy od

 

ܶ

௠௔௫

 

które z jak wiemy z wcześniejszych obliczeń maksymalne jest w 

pierwszym przedziale naszej belki i wynosi:

 

ࢀ

࢓ࢇ࢞

=

૛

૜ ࡼ 

 

 
 
 

 

 

z

c 

6

7 ܽ

 

8

7 ܽ

 

8

7 ܽ

 

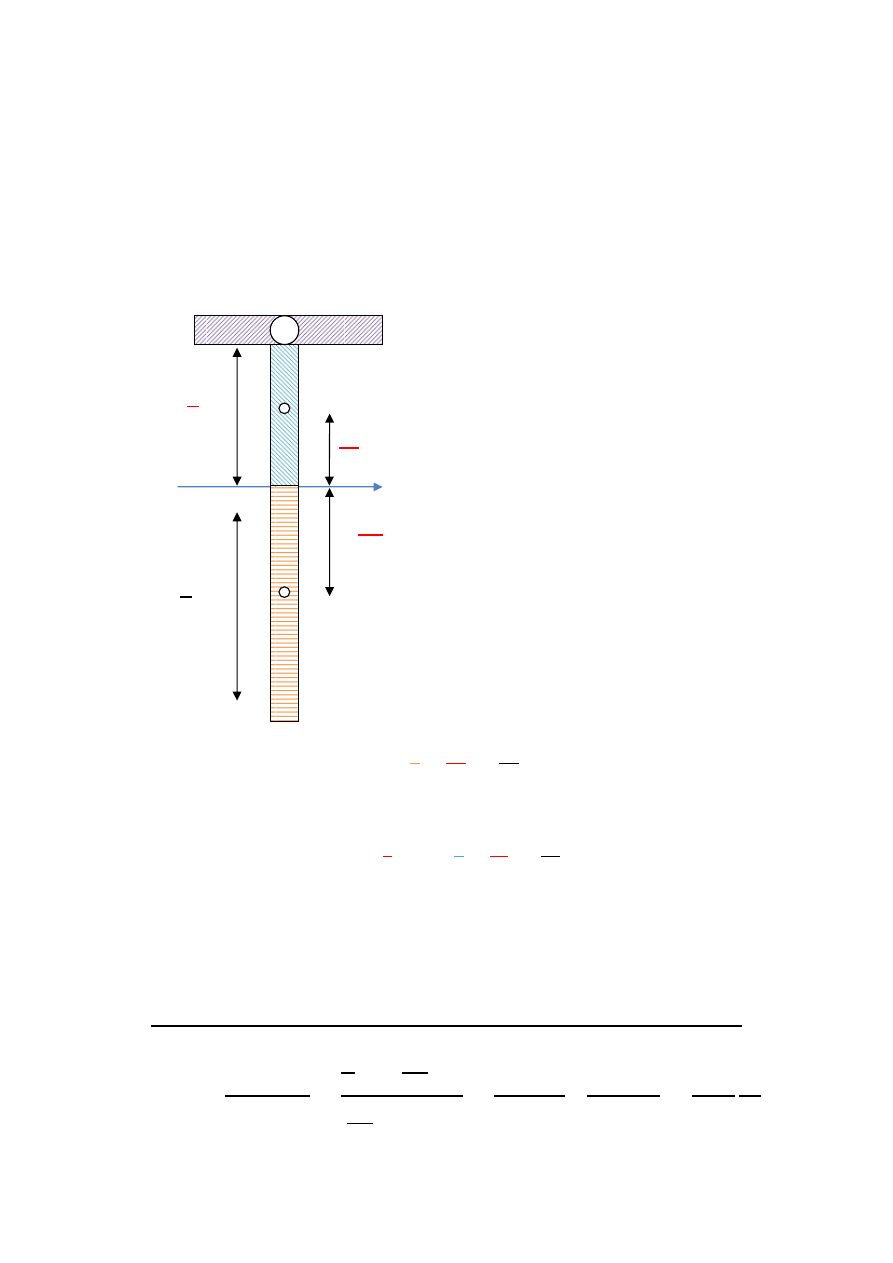
Opracował: Czerwiec 

 

•

 

Liczymy moment statyczny (

S

) dla przekroju:

 

 

Moment statyczny wyraża się wzorem

 

 

ࡿ = ࢖࢕࢒ࢋ ࢖࢕࢝࢏ࢋ࢘ࢠࢉࢎ࢔࢏ ∗ ࢕ࢊ࢒ࢋࢍ࢒࢕࢙ࢉ ࢙࢘࢕ࢊ࢑ࢇ ࢉ࢏ࢋࢠ࢑࢕࢙ࢉ࢏ ࢕ࢊ ࢕࢙࢏ ࢠ

ࢉ

 

 

Przekrój belki w powiększeniu: 

 

 

 

 

 

 

 

 

 

 

 

 

ܵ =

૜ܜ ∗

ૡ

ૠ a

∗

ૡ

૚૝ ܉

=

ૢ૟

૝ૢ ܉

૛

ܜ

 

lub 

ܵ =

܉ ∗ ܜ

∗

6

7 a

+

૜ܜ ∗

૟

ૠ a

∗

6

14 a

=

ૢ૟

૝ૢ ܉

૛

ܜ 

•

 

I

zc

 

mamy obliczoną przy pierwszej części zadania.

 

•

 

Liczymy sumę szerokości 

U

 włókien na osi 

z

c

:

 

Mamy jedno włókno o szerokości 

3t, więc: 

ࢁ = ૜࢚ 

Mamy wszystko co potrzeba do obliczenia naprężeń od ścinania podstawiamy do wzoru: 

࣎

࢓ࢇ࢞ୀ

ܶ

௠௔௫

∗ ܵ

ܫ

௭௖

∗ ܷ =

2

3 ܲ  ∗

96

49 a

ଶ

t

20

7 ݐܽ

ଷ

∗ 3ݐ

=

64a

ଶ

pt

49 ∗

7

60ݐ

ଶ

ܽ

ଷ

=

૚૟

૚૙૞

ܘ

܉ܜ 

a

 

t

 

3t

 

z

c 

6

7 ܽ

 

8

7 ܽ

 

ૡ

૚૝ ࢇ

 

s

c 

s

c 

s

c 

6

14 ܽ

 

3t