1

Ruch obrotowy, bryła sztywna

– poziom rozszerzony

Zadanie 1. (11 pkt)

Źródło: CKE 2005 (PR), zad. 28.



     

 

        

    

    

             

          

           

       

  

           

          

       












   

        





Zadanie 1.1 (6 pkt)

2

     



 

  

            

            

            

              

             
 















  

           

         



















Zadanie 1.3 (2 pkt)

Zadanie 1.2 (3 pkt)

3

Zadanie 2. (12 pkt)

Źródło: CKE 2008 (PR), zad. 1.

Egzamin maturalny z fizyki i astronomii

Poziom rozszerzony

2

Rozwiązanie zadaĔ naleĪy zapisaü w wyznaczonych miejscach pod treĞcią zadania.

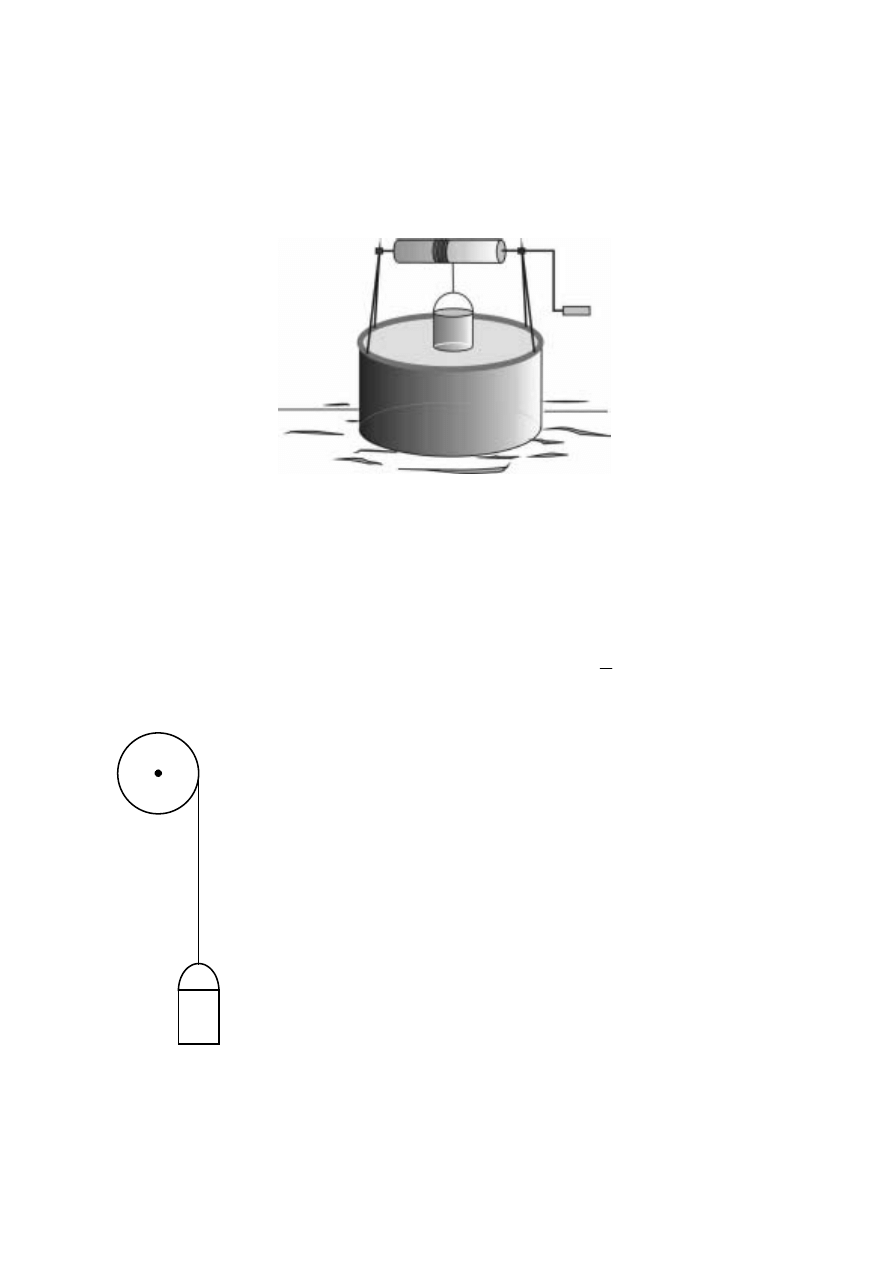
Zadanie 1. Beczka (12 pkt)

Do hurtowni chemicznej przywieziono transport blaszanych beczek z gipsem. W celu

wyáadowania beczek z samochodu poáoĪono pochylniĊ, tworząc w ten sposób równiĊ

pochyáą. WysokoĞü, z jakiej beczki staczaáy siĊ swobodnie bez poĞlizgu wynosiáa 100 cm.

Beczki byáy ĞciĞle wypeánione gipsem, który nie mógá siĊ przemieszczaü, i miaáy ksztaát

walca o Ğrednicy 40 cm. Masa gipsu wynosiáa 100 kg.

W obliczeniach przyjmij wartoĞü przyspieszenia ziemskiego równą 10 m/s

2

, a beczkĊ

potraktuj jak jednorodny walec. MasĊ blachy, z której wykonano beczkĊ pomiĔ.

Moment bezwáadnoĞci walca, obracającego siĊ wokóá osi prostopadáej do podstawy walca
i przechodzącej przez jej Ğrodek, jest równy

2

2

1 mr

I

.

Zadanie 1.1 (2 pkt)

Uzupeánij rysunek o pozostaáe siáy dziaáające na beczkĊ podczas jej swobodnego staczania.

Zapisz ich nazwy.

Zadanie 1.2 (2 pkt)

Oblicz wartoĞü siáy nacisku beczki na równiĊ podczas staczania, jeĪeli kąt nachylenia

pochylni do poziomu wynosi 30

o

.

Į = 30

o

Į = 60

o

sin Į

0,50

0,87

cos Į

0,87

0,50

tg Į

0,58

1,73

ctg Į

1,73

0,58

F

g

Zadanie 2.1 (2 pkt)

Zadanie 2.2 (2 pkt)

4

Egzamin maturalny z fizyki i astronomii

Poziom rozszerzony

3

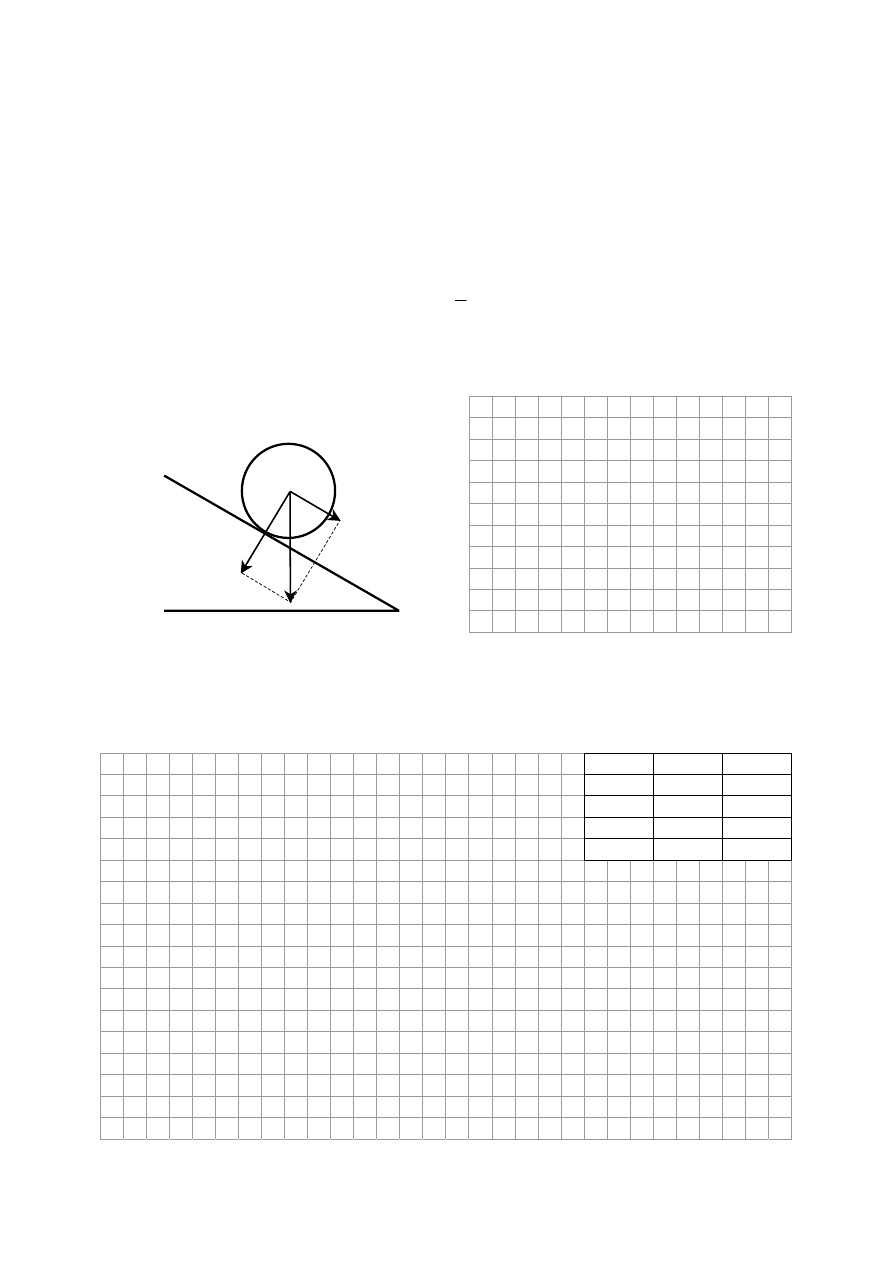
Zadanie 1.3 (4 pkt)

WykaĪ, Īe wartoĞü prĊdkoĞci liniowej beczki po stoczeniu siĊ z pochylni jest równa 3,65 m

s

.

Zadanie 1.4 (2 pkt)

Oblicz, korzystając ze związku pomiĊdzy energią i pracą, zasiĊg toczenia siĊ beczki

po poziomej trawiastej powierzchni. Przyjmij, Īe podczas toczenia siĊ beczki po trawie dziaáa

na nią staáa siáa oporu o wartoĞci 50 N, a wartoĞü prĊdkoĞci liniowej beczki po stoczeniu siĊ
z pochylni jest równa 3,65 m

s

.

Zadanie 1.5 (2 pkt)

WykaĪ, Īe zmiana zawartoĞci beczki z gipsu na cement (o innej niĪ gips masie), równieĪ

ĞciĞle wypeániający beczkĊ, nie spowoduje zmiany wartoĞci przyspieszenia kątowego, z jakim

obraca siĊ beczka wokóá osi prostopadáej do podstawy beczki i przechodzącej przez jej

Ğrodek.

Nr zadania

1.1. 1.2. 1.3. 1.4. 1.5.

Maks. liczba pkt

2

2

4

2

2

Wypeánia

egzaminator! Uzyskana liczba pkt

Zadanie 2.3 (4 pkt)

Zadanie 2.4 (2 pkt)

Zadanie 2.5 (2 pkt)