1
BADANIE
KINETYKI
REAKCJI
HYDROLIZY
SACHAROZY
KATALIZOWANEJ PRZEZ INWERTAZĘ Z DROŻDŻY
Cel ćwiczenia:
Celem ćwiczenia jest badanie kinetyki reakcji hydrolizy sacharozy
katalizowanej przez enzym – inwertazę oraz wyznaczenie stałej Michaelisa dla
tej reakcji.
Podstawy teoretyczne:
Enzymy są białkami posiadającymi zdolność do niezwykle efektywnego
katalizowania reakcji organicznych. Przyśpieszenie reakcji odbywa się poprzez
obniżenie bariery aktywacji, które jest skutkiem tworzenia niskoenergetycznych
kompleksów enzymu z substratem (ES). Wiązanie substratu zachodzi w miejscu
zwanym miejscem aktywnym enzymu. Na skutek utworzenia się kompleksu ES
tworzy się konkurencyjna w stosunku do reakcji niekatalizowanej ścieżka
reakcyjna, w której energia stanu przejściowego jest niższa niż dla reakcji
zachodzącej przy braku enzymu. Jeden z najszybciej działających enzymów,
anhydraza węglanowa katalizuje reakcję przeniesienia CO
2
z tkanek do krwi.
Enzym ten przyśpiesza reakcję 10
7
razy w stosunku do reakcji niekatalizowanej.
Miarą aktywności enzymów jest maksymalna liczba obrotów, która określa
liczbę aktów reakcyjnych, w które wchodzi cząsteczka enzymu na jednostkę
czasu w warunkach pełnego wysycenia enzymu substratem. W tabeli nr 1
zestawiono przykładowe wartości liczby obrotów.
Tabela 1.
ENZYM
LICZBA OBROTÓW
K
M
/ µ
µ
µ
µM
ANHYDRAZA WĘGLANOWA
600000
8000
PENICYLINAZA
2000
50
CHYMOTRYPSYNA
100
5000
POLIMERAZA DNA I
15
LIZOZYM
0,5
6
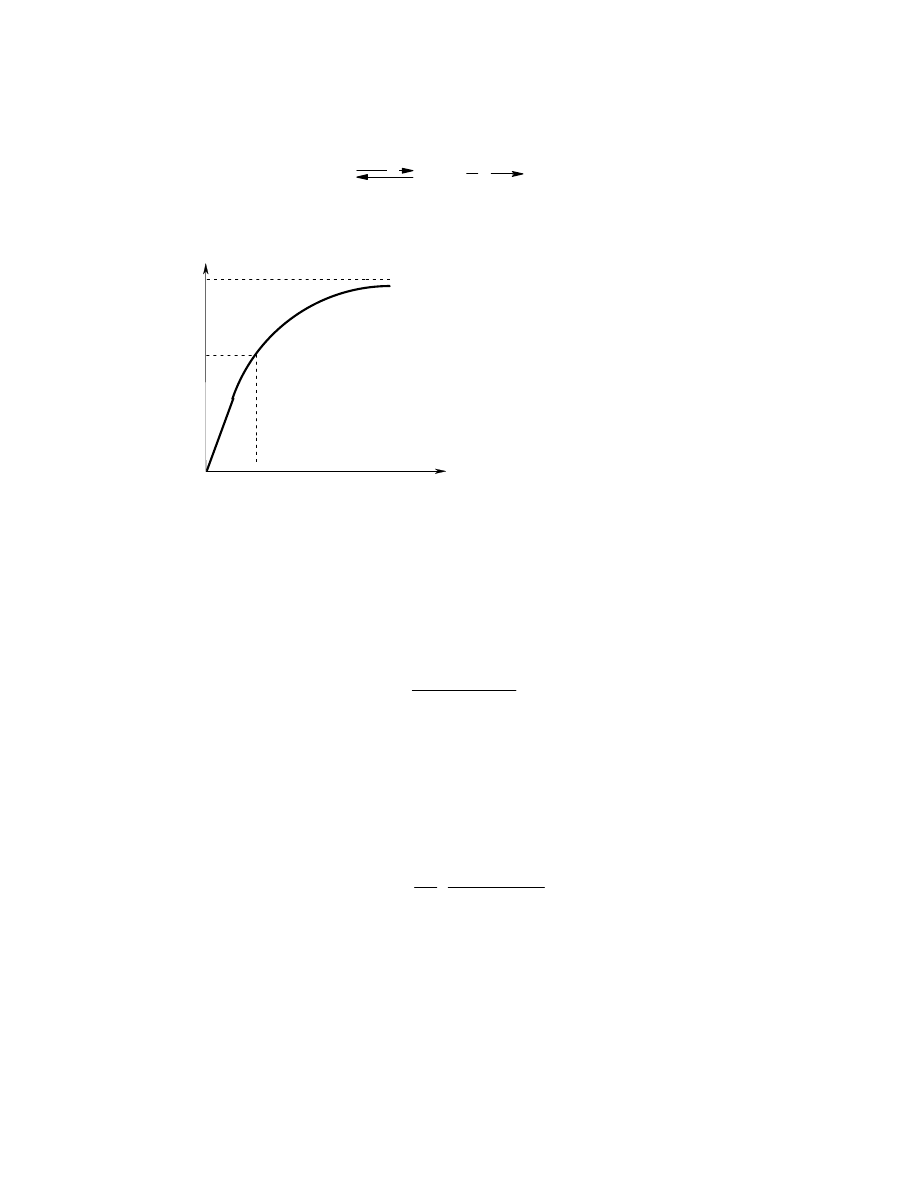
Dla wielu enzymów szybkość katalizy zmienia się ze stężeniem substratu. Przy
stałym stężeniu enzymu szybkość zależy prawie liniowo od stężenia substratu,
jeśli jest ono małe. Przy dużych stężeniach substratu, szybkość prawie nie
zależy od stężenia (Rys 1). W roku 1913 L. Michaelis i M. Menten
zaproponowali
model
odpowiadający
przedstawionej
charakterystyce
kinetycznej. Zakłada on, że reakcja jest dwuetapowa: w pierwszym etapie
tworzy się kompleks ES występujący w równowadze z substratami E i S, w
2
drugim etapie kompleks ES jest rozkładany do produktu z odtworzeniem
cząsteczki wolnego enzymu E:
E + S
ES
k
k
a
a'
k
b
E + P
Rys. 1. Zależność szybkości reakcji enzymatycznej od stężenia substratu
V
max
V
max
/2
V
C
substr
K
M
Odwołując się do przybliżenia stanu stacjonarnego można napisać wyrażenie
opisujące wypadkową szybkość tworzenia ES:
sybkość tworzenia ES = k
a
[E][S] – k
a’
[ES] – k
b
[ES] = 0
stąd:
[ES] =
[E][S]
a
k
k
a'
b
+
k
Całkowite stężenie enzymu [E
0
] jest sumą stężeń enzymu wolnego [E] i
związanego [ES]. Ponieważ ilość wprowadzonego enzymu jest niewielka,
stężenie wolnego substratu [S] jest praktycznie równe jego stężeniu
całkowitemu a więc można pominąć różnicę między [S] a [S] + [ES] stąd:
[ES] =
[E] [S]
a
k
k
a'
b
+
k
0
+ k
a
[S]
Przy założeniu, że etap określony stałą szybkości k
b
jest najwolniejszy, szybkość
reakcji wyrażona jest równaniem:
V = k
b
[ES] = k[E
0
]
3
gdzie:
k =
k [ S]
b
[ S] + K
M
Stała K
M
zwana stałą Michaelisa (patrz tab. 1) jest określona jako:
k
k
a'
b
+
k
a
M
K
=
(Wykazać, że jeśli k
b
<< k
a’
, jest ona równa stałej dysocjacji kompleksu [ES]).
Jeśli [S] >> K
M
to wtedy reakcja przebiega z szybkością maksymalną, gdzie:
V
MAX
= k
b
[E
0
]
a stała k
b
zwana jest maksymalną liczbą obrotów.
Łatwo udowodnić, że szybkość reakcji V przy dowolnym stężeniu substratu jest
powiązana z V
MAX
relacją:
M
V =
[ S]
[ S] + K
V
MAX
Równanie powyższe stanowi podstawę analizy kinetyki reakcji enzymatycznych
metodą wykresu Lineweavera-Burka. Po odwróceniu równania otrzymuje się
zależność:
1/V = 1/V
max
+ (K
M
/V
MAX
)[S]
-1
Po przedstawieniu powyższej zależności w układzie liniowym, można
wyznaczyć wartości K
M
oraz k
b
.
Opis metody:
Roztwory związków optycznie czynnych (jak np. sacharozy, glukozy,
fruktozy) posiadają właściwość skręcania płaszczyzny polaryzacji światła. Kąt
skręcenia jest wprost proporcjonalny min. do stężenia substancji optycznie
czynnej. Zmiany stężeń reagentów można śledzić obserwując zmiany
skręcalności optycznej roztworów w czasie. Wykorzystuje się przy tym to, że
sacharoza jest optycznie prawoskrętna, powstająca glukoza również, natomiast
fruktoza w silniejszym stopniu skręca płaszczyznę polaryzacji światła w lewo.
Dlatego podczas reakcji obserwuje się zmianę wartości kąta skręcenia w lewo.
4
W trakcie zajęć przeprowadza się dwie serie pomiarowe przy różnych
stężeniach sacharozy. Szybkość początkową reakcji wyznacza się z zależności
kąta skręcenia płaszczyzny polaryzacji w funkcji czasu. Stałą Michaelisa
wyznacza się graficznie z równania Lineweavera-Burka.
Aparatura i odczynniki:
2 cylindry 50 ml
3 pipety
stoper
roztwór sacharozy w buforze octanowym (pH=4,8)
roztwór inwertazy w wodzie
polarymetr półcieniowy
Wykonanie pomiarów:
1. Ustawić termostat na 25
0
C
2. Odważyć na wadze analitycznej 13,6600 – 13,7000 g sacharozy i
rozpuścić ją w buforze octanowym tak aby otrzymać 100 ml roztworu
(kolba miarowa 100 ml).
3. Do cylindra z korkiem pobrać pipetą 20 ml roztworu sacharozy w buforze
octanowym.
4. Do drugiego cylindra pobrać pipetą 20 ml roztworu enzymu.
5. Włączyć transformator do sieci i zapalić lampę sodową.
6. Umieścić oba cylindry w termostacie na 10 –15 minut.
7. Nastawić okular polarymetru na najwyższą ostrość i wprawić się w
nastawianiu analizatora na jednakowe zaciemnienie obu pól (patrz
instrukcja przyrządu).
8. Wyjąć oba cylindry z termostatu.
9. Wlać roztwór enzymu do roztworu sacharozy włączając jednocześnie
stoper (stoper powinien zostać włączony w momencie wlania pierwszej
kropli enzymu).
10. Zamknąć cylinder korkiem i wymieszać zawartość (nie wytrząsać!).
11. Otrzymany roztwór wlać do rurki polarymetrycznej z płaszczem grzejnym
tak, aby utworzyła się wypukła powierzchnia cieczy, a następnie
szkiełkiem ściąć menisk tak, aby nie było pęcherzyków powietrza.
12. Umieścić rurkę w polarymetrze i po 1 minucie od zmieszania roztworów
ustawić analizator na jednakowe zaciemnienie obu pól a następnie
odczytać wartość kąta skręcenia płaszczyzny polaryzacji światła z
dokładnością do 0,05
0
. Wykonać 7 pomiarów kąta skręcenia co 2 min.
Nastawianie analizatora rozpocząć pół minuty wcześniej. Musi być ono
wykonane w określonym czasie (sam odczyt można zrobić nieco później).
5
13. W międzyczasie umyć dokładnie cylindry wodą i w jednym z nich
umieścić ponownie 20 ml roztworu enzymu a w drugim 15 ml roztworu
sacharozy w buforze octanowym oraz 5 ml buforu.
14. Umieścić oba cylindry w termostacie na 10 –15 minut.
15. Wykonać ponownie czynności jak w pkt. 8-12.
16. Następnie wykonać analogicznie kolejne 2 serie pomiarów stosując
odpowiednio 10 ml roztworu sacharozy w buforze octanowym oraz 10 ml
buforu i 5 ml roztworu sacharozy w buforze i 15 ml buforu
17. Zmierzyć skręcalność wyjściowego roztworu sacharozy.
18. Po zakończeniu pomiarów wyłączyć termostat i lampę sodową oraz umyć
dokładnie wodą naczynia i rurkę.
Opracowanie wyników:
1.
Sporządzić wykresy zależności kąta skręcenia płaszczyzny polaryzacji
ś
wiatła w funkcji czasu i wyznaczyć z nich szybkość początkową
reakcji (skorzystać z załączonej krzywej wzorcowej zależności kąta
skręcenia płaszczyzny polaryzacji światła mieszaniny reakcyjnej w
funkcji stężenia sacharozy).
2.
Sporządzić wykres 1/V = f(1/S) i w oparciu o niego wyznaczyć
wartość stałej Michaelisa K
M
.
3.
Sformułować wnioski.
LITERATURA:
1.
P. W. Atkins – Chemia Fizyczna- PWN
2.
L. Stryer – Biochemia - PWN
6
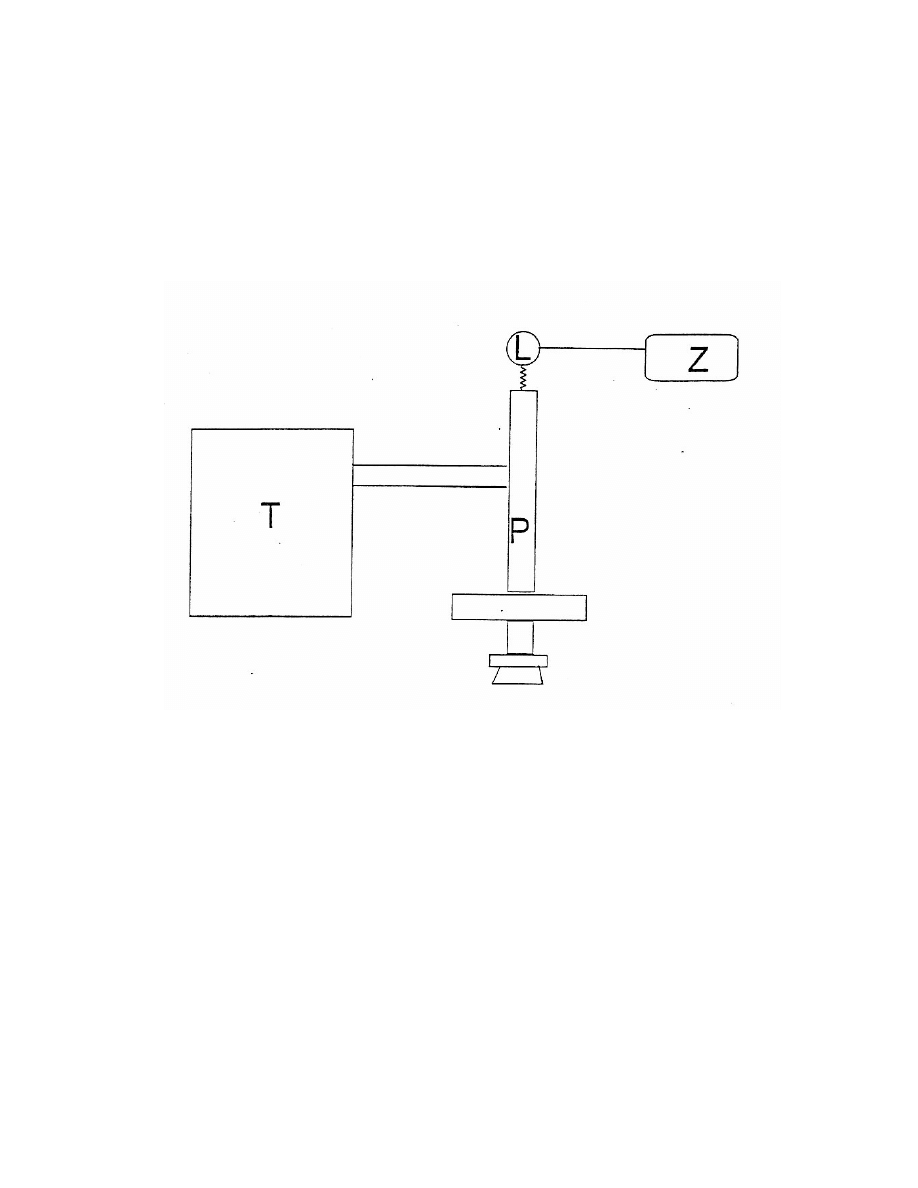
SCHEMAT ZESTAWU:
Z- zasilacz lampy sodowej
L – lampa sodowa
P – polarymetr półcieniowy
T- termostat
POLARYMETR PÓŁCIENIOWY
1. Polaryzator (pryzmat Nicola)
2. Miejsce na umieszczenie rurki polarymetrycznej
3. Analizator
4. Pokrętło nastawiania analizatora
5. Pokrętło ostrości pola
6. Okular
7. Skala skręcenia kąta polaryzacji
8. Światło sodowe
7
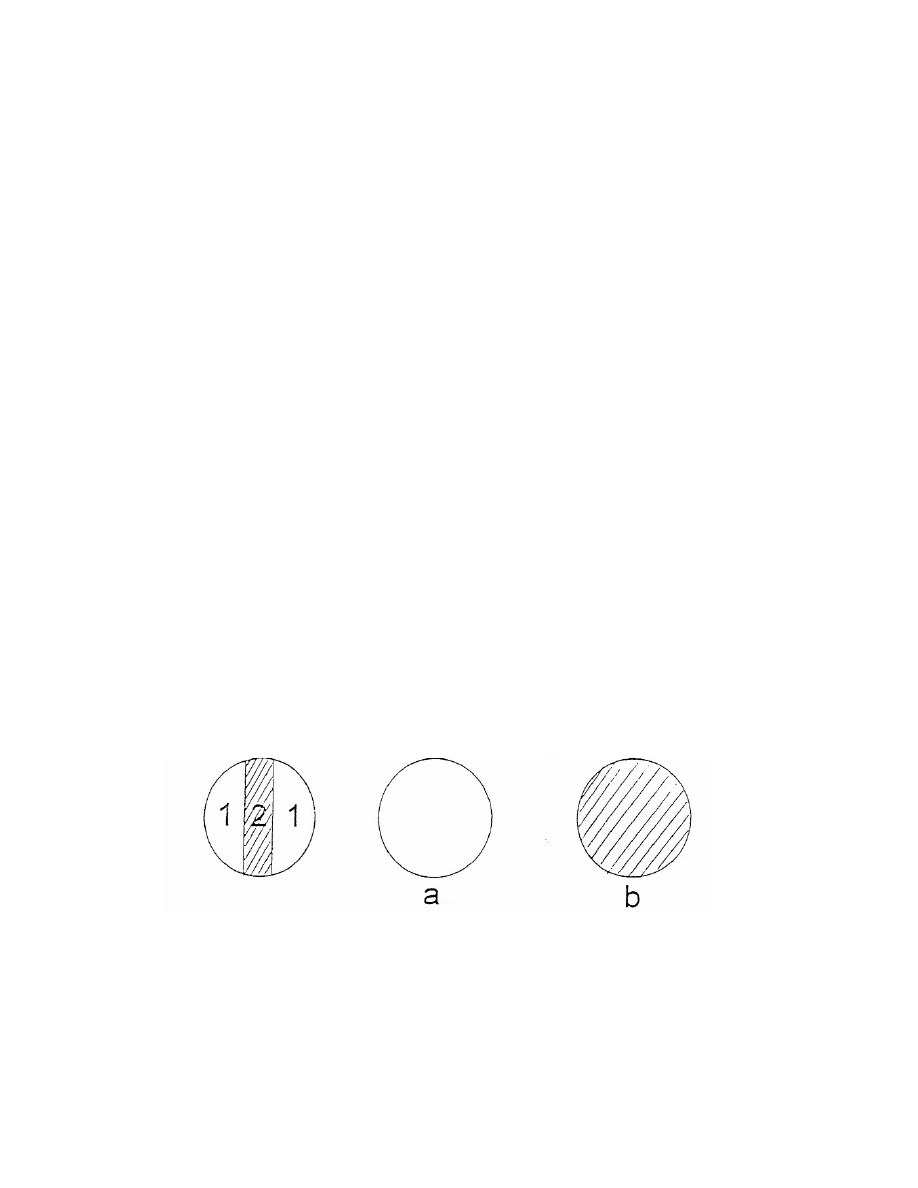
Pomiar kąta skręcenia płaszczyzny polaryzacji światła polega na ustawieniu
pokrętłem analizatora takiego położenia, w którym występuje jednakowe
zaciemnienie obydwu pól w chwili pomiaru.
1 – pierwsze pole
a) nastawienie niewłaściwe
2- drugie pole
b) nastawienie właściwe
8
Jednakowe oświetlenie obydwu pól występuje dla dwu odmiennych kątów:
jedno dla maksymalnej jasności (a), drugie dla minimalnej (b). Właściwe jest
to drugie.