Robert Maniura

Sprawozdanie z ćwiczenia nr 14: Kinetyka reakcji inwersji sacharozy

1. Wstęp teoretyczny:

Niektóre substancje, zwane optycznie czynnymi, wykazują zdolność skręcania płaszczyzny drgań liniowo spolaryzowanego światła, które przez nie przechodzi . Własność tę nazywamy aktywnością optyczną . Niekiedy substancja jest optycznie czynna tylko w stanie krystalicznym, jak np. kwarc; świadczy to, że jej aktywność optyczna jest spowodowana specyficznym ułożeniem cząsteczek w sieci kryształu. Znamy jednak wiele związków chemicznych, które są optycznie czynne także są w stanie ciekłym, gazowym lub roztworach. W takich przypadkach aktywność optyczna jest wynikiem przestrzennej konfiguracji cząsteczek danej substancji. Cząsteczki mające tę cechę nazywamy dyssymetrycznymi. Zdolność skręcania płaszczyzny światła spolaryzowanego przez substancję optycznie czynną charakteryzuje skręcalność optyczna . Jest ona funkcją długości fali światła użytego do pomiaru skręcalności i zależy nieco od temperatury, a w przypadku roztworów substancji optycznie czynnych - także od rozpuszczalnika. Dla roztworów skręcalność właściwą definiujemy wzorem :
gdzie:  oznacza obserwowany kąt skręcenia; d - wyrażoną w dm grubość warstwy roztworu, przez którą przechodzi spolaryzowane światło, c - stężenie podane w gramach badanej substancji na 100 cm³ roztworu .

Skręcalność optycznie czynnej substancji jest zależna od długości fali spolaryzowanego światła . Zależność tę nazywamy dyspersją skręcalności optycznej . W zakresach widma dostatecznie odległych od pasm absorbcji elektronowej substancji, dyspersję skręcalności optycznej opisuje równanie:
. W równaniu tym  jest długością fali światła przechodzącego przez substancję, _oi - długością fali odpowiadającą maksimum i - tego „aktywnego” pasma absorpcyjnego badanej substancji, K_i zaś - stałą charakterystyczną dla tego pasma. W najprostszych przypadkach wystarcza uwzględnić wpływ jednego tylko pasma absorbcji, przez co wzór poprzedni upraszcza się do postaci podanej przez P. Drudego:

Wykorzystując kąt skręcania a (zmierzony doświadczalnie) można obliczyć stałą szybkości reakcji inwersji sacharozy:

gdzie: t - czas; c_o - stężenie początkowe; c_k - stężenie po upływie czasu t;

Podstawiając:

gdzie:
- początkowa skręcalność optyczna;
- skręcalność optyczna po czasie t;
- kąt skręcania całkowicie zinwertowanej sacharozy, otrzymujemy:

zamieniając logarytm naturalny na logarytm dziesiętny:

2. Opracowanie wyników:

Aby obliczyć stałą szybkości reakcji inwersji sacharozy korzystam z następującej zależności:

gdzie:
- początkowa skręcalność optyczna;
- skręcalność optyczna po czasie t;
- kąt skręcania całkowicie zinwertowanej sacharozy (
= -2,0); t - czas;

Na podstawie podanych zależności obliczam stałą szybkości reakcji inwersji sacharozy. Rezultaty obliczeń zostały umieszczone w tabeli.

t [min]	t [s]			k [s^-1]
0,0	0,0	= 12,3
5,0	300,0	12,00	1,55E-02	1,19E-04
10,0	600,0	11,20	3,48E-02	1,33E-04
15,0	900,0	11,00	4,14E-02	1,06E-04
20,0	1200,0	10,50	5,84E-02	1,12E-04
25,0	1500,0	10,00	7,62E-02	1,17E-04
30,0	1800,0	9,20	1,06E-01	1,36E-04
50,0	3000,0	7,00	2,01E-01	1,54E-04
80,0	4800,0	5,30	2,92E-01	1,40E-04

Na podstawie uzyskanych rezultatów obliczam wartość średnią szybkości reakcji:

k_śr = 1,45
[s^-1]

W przypadku małej liczby pomiarów średnia może różnić się dość znacznie od wartości prawdziwej. Dlatego wygodniej jest wtedy określić przedział, w którym wartość rzeczywista znajduje się z dużym prawdopodobieństwem. Taki przedział nazywamy przedziałem ufności. Wyznaczam przedział ufności dla prawdopodobieństwa 95% (p = 0,95 ; α = 0,05)

μ = X ⁺ t * s

gdzie: X - średnia arytmetyczna; t - wartość funkcji Studenta, wartość współczynnika „t” dla prawdopodobieństwa 95% (dla 8 pomiarów), t = 2,365 dla K = n - 1 = 7

s - odchylenie standardowe średniej arytmetycznej, obliczane ze wzoru:

s =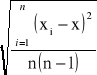

gdzie: x_i - kolejne wyniki; x - średnia arytmetyczna wyników; n - ilość wyników (n=5).

s =

Obliczony przedział ufności dla stałej szybkości reakcji jodowania acetonu:

k =
[ s^-1 ]

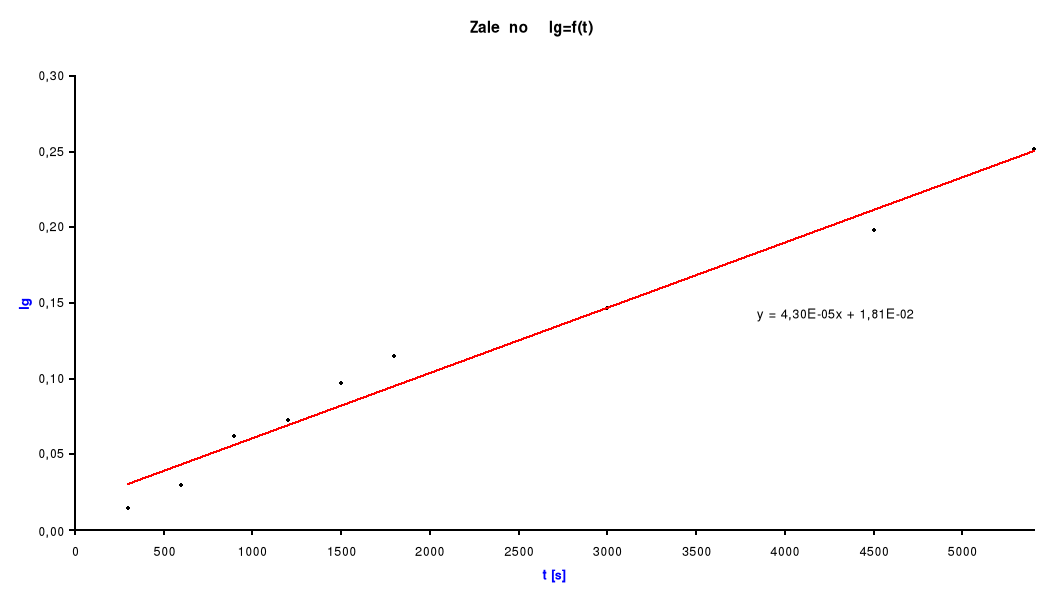
Następnie wykreślam wykres zależności
od czasu t [s].

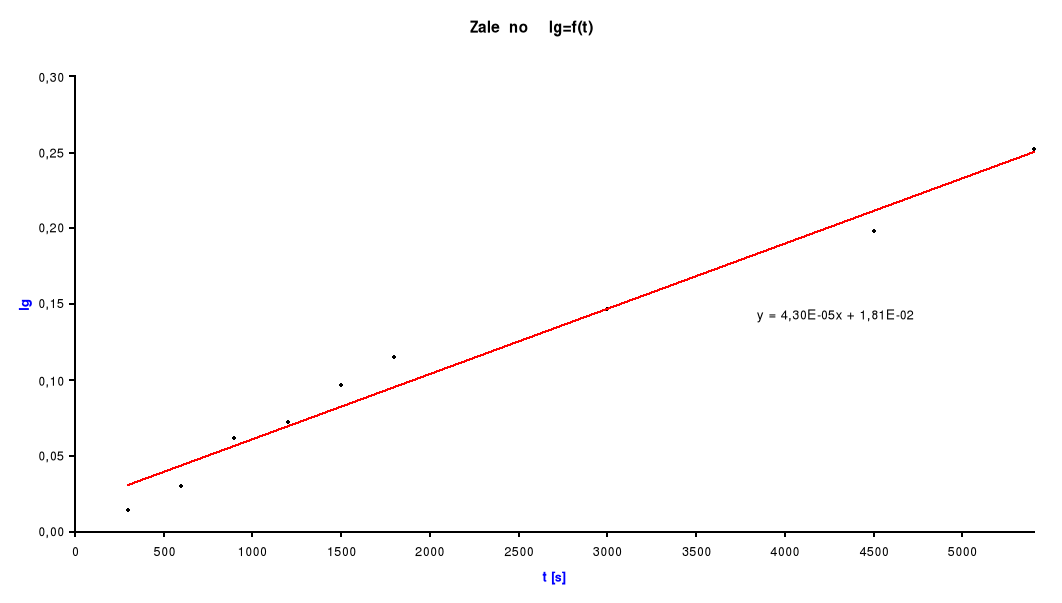
Metodą regresji liniowej wyznaczam k:

y = ax + b a =
b =

Błędy :

x = t[s]	y =	x^2	y^2
300	1,47	90000	2,2
600	3,00	360000	9,0
900	6,21	810000	3,9
1200	7,23	1440000	5,2
1500	9,69	2250000	9,4
1800	1,15	3240000	1,3
3000	1,47	9000000	2,2
4500	1,98	20250000	3,9
5400	2,52	29160000	6,3

= 19200;
= 0,988;
= 66600000;
= 3,7
;
= 3210,707786;

a'=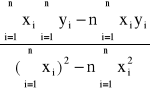
= 4,30
; b'=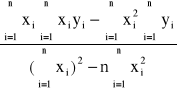
= 1,81

yi'	d = (yi - yi')	d^2
-0,00520	1,00520	1,010426
0,00770	0,99230	0,984663
0,02060	0,97940	0,959233
0,03349	0,96651	0,934135
0,04639	0,95361	0,909371
0,05929	0,94071	0,884939
0,11088	0,88912	0,790537
0,17537	0,82463	0,680021
0,21406	0,78594	0,617704

=7,7710;

S_b' =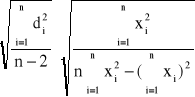
S_b' = 0,57

S_a' =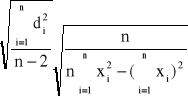
S_a' = 2,1

Obliczam k z zależności k od współczynnika a, który mam z zależności liniowej y = ax +b a =

= kt z tego wynika, że 2,303a = k

k = 2,303a

k =
= 1,0
[s^-1]

Wyznaczam skręcalność właściwą sacharozy korzystając z zależności:

gdzie: [] - skręcalność właściwa;  - kąt płaszczyzny skręconej ( = 2,5⁰); c - stężenie w [g/100 cm³] (c = 20 g/100 cm³); d - grubość próbki (d = 0,19009 dm)

Wartość tablicowa skręcalności właściwej wynosi 66⁰, więc błąd wynosi 0,38 %

3. Wnioski:

Przeprowadzone doświadczenie miało na celu sprawdzenie czy reakcja inwersji sacharozy ma charakter autokatalityczny. Uzyskane wyniki potwierdzają tezę, iż reakcja inwersji sacharozy ma autokatalityczny charakter i jest katalizowana kwasem. Graficzny obraz reakcji inwersji sacharozy wskazuje na liniową zależność, co potwierdza powyższe wnioski. Głównym źródłem błędów były niedokładności związane z pomiarem objętości cieczy oraz naważki sacharozy.

Stałą szybkości inwersji sacharozy wyznaczyłam dwoma sposobami: wartość obliczona k =
[s^-1] i wartość wyznaczona metodą regresji liniowej k = 1,0
[s^-1]. Wyznaczone w różny sposób stałe szybkości reakcji inwersji sacharozy różnią się nieznacznie, co dodatkowo świadczy o słuszności zastosowanej metodyki pomiarowej.

1

2

---