1

Wojciech Klityński
Paweł Targosz
Metoda procesów przejściowych

Wstęp

Metoda procesów przejściowych TEM (transient electromagnetic) nazywana

najczęściej TDEM (time-domain electromagnetic method, metoda elektromagnetyczna w

domenie czasu) należy do grupy metod elektromagnetycznych (EM) rozpoznania ośrodka

geoelektrycznego.

Podobnie jak tradycyjna metoda elektrooporowa (DC resistivity) służy do określenia

oporności właściwej ośrodka geologicznego i jest stosowana najczęściej w wersji pionowych

sondowań a rzadziej w wersji profilowań. Metoda TDEM znana jest od kilkudziesięciu lat

jednak wraz z rozwojem techniki, szczególnie elektroniki i komputerowych technik

interpretacyjnych jej efektywność, a co za tym idzie znaczenie w rozpoznaniu ośrodka

geoelektrycznego wzrasta, zwłaszcza, że jest często bardziej efektywna od metody

elektrooporowej. Szczególnie ważne jest to, że metoda ta nie wymaga systemu pomiarowego

o tak dużych rozmiarach jak w metodzie elektrooporowej, gdzie głębokość penetracji zależy

od rozmiaru układu pomiarowego (rozstawu) i jest kilkakrotnie mniejsza od tego rozstawu.

W metodzie procesów przejściowych wykorzystuje się fakt, że pole elektromagnetyczne

ź

ródeł impulsowych w tzw. strefie bliskiej nie zależy od odległości nadajnik-odbiornik

dlatego pomiary może realizować cewka odbiorcza w pętli nadawczej (tzw. central loop) co

daje przewagę w metodyce pomiarowej w stosunku do metod: elektrooporowej czy CSAMT

(Control Source Audio Magnetotelluric), gdzie rozmiary układu pomiarowego dla osiągnięcia

określonego zasięgu głębokościowego muszą być dużo większe (Klityński, Miecznik, 1998).

System pomiarowy w metodzie TDEM składa się z nadajnika i pętli nadawczej (transmitter

loop) i odbiornika (receiver) oraz cewki odbiorczej lub rzadziej pętli odbiorczej.

Głębokość badań w metodzie TDEM wynosi najczęściej od dziesiątków do ok. 1000

metrów (i więcej) i zależy m. in. od rozmiaru pętli nadawczej, mocy nadajnika i poziomu

zakłóceń w obszarze pomiarowym. Głębokość penetracji można zwiększyć nawet do 10 km

stosując specjalną metodykę pomiarową i nadajniki wysokiej mocy (Keller et al., 1984).

Metoda TDEM charakteryzuje się największą poprzeczną i pionową rozdzielczością w

kartowaniu dobrze przewodzących struktur (wśród wszystkich elektromagnetycznych metod

(Krivochieva S., Chouteau M., 2001). Zwykle dokładność pomiaru w tej metodzie jest bardzo

duża (Keller, G.V.,1997).

2

Metoda TDEM ma szerokie zastosowanie m.in. w rozpoznawaniu ośrodka

hydrogeologicznego w tym kartowaniu kontrastu opornościowego wód kwaśnych i

zasolonych z jednej strony a wód słodkich z drugiej strony (Krivochieva S., Chouteau M.,

2001), określaniu geometrii wód podziemnych (Papadopoulos et al., 2004), w kartowaniu

kontrastów opornościowych związanych z występowaniem wód geotermalnych, lokalizacji

skupień rud siarczków charakteryzujących się wysoką przewodnością zlokalizowanych w

ośrodku o niskiej przewodności, w poszukiwaniu struktur dobrze przewodzących związanych

z występowaniem uranu, diamentu i rud metali (Chow-Son Chen and Shuhjong Tsao, 2001),

w kartowaniu struktur geologicznych związanych z występowaniem węgla kamiennego, w

kartowaniu granic pomiędzy zmarzliną a ośrodkiem nie zamarzniętym, w kompleksie z

innymi metodami geofizycznymi: z metodą elektrooporową, z metodą magnetotelluryczną

(Krivochieva S., Chouteau M., 2003) oraz CSAMT i jako dodatkowa z metodą sejsmiczną.

W Polsce metoda TDEM nie została jeszcze zastosowana na szerszą skalę. Zwrócono

jednak uwagę na możliwości jej stosowania w rozpoznaniu morfologii podłoża

prekambryjskiego na Zapadlisku Przedkarpackim (Klityński, Miecznik, 1998). Obszar ten

charakteryzuje się budową tektoniczną typu blokowego, gdzie głębokość zalegania

powierzchni rozgraniczającej miocen od wysokooporowego prekambru jest stosunkowo mała.

Rejon ten budzi zainteresowanie ze względu na możliwości występowania złóż bituminów

zarówno w utworach miocenu jak i prekambru.

Przedstawiono również w Polsce możliwości zastosowania metody procesów

przejściowych w kompleksie z metodą elektrooporową przy monitorowaniu migracji

zanieczyszczeń w warstwie wodonośnej (Antoniuk et al., 1991).

1. Podstawy teoretyczne

Metody elektromagnetyczne wykorzystują sztuczne źródła generujące pole

elektromagnetyczne (oprócz metody magnetotellurycznej - MT), tak więc należą do metod

aktywnych. Wszystkie te metody są metodami powierzchniowymi. System pomiarowy w

metodzie pasywnej (MT) składa się tylko z rejestratora (receiver). Źródło pola MT jest

naturalne i dla częstotliwości od ok. 1 do 10

3

Hz znajduje się w jonosferze, a dla często-

tliwości od 10

-5

do 1 Hz w magnetosferze. W przedziale częstotliwości od. ok. 0.5 do 5 Hz

sygnał jest jednak słabszy co manifestuje się często słabą jakością danych w tym zakresie

częstotliwości (tzw. dead band) (Simpson F., Bahr K., 2005). Głębokość penetracji w

metodzie MT zależy od częstotliwości

(

)

)

(Hz

f

i tzw. uśrednionej oporności ośrodka

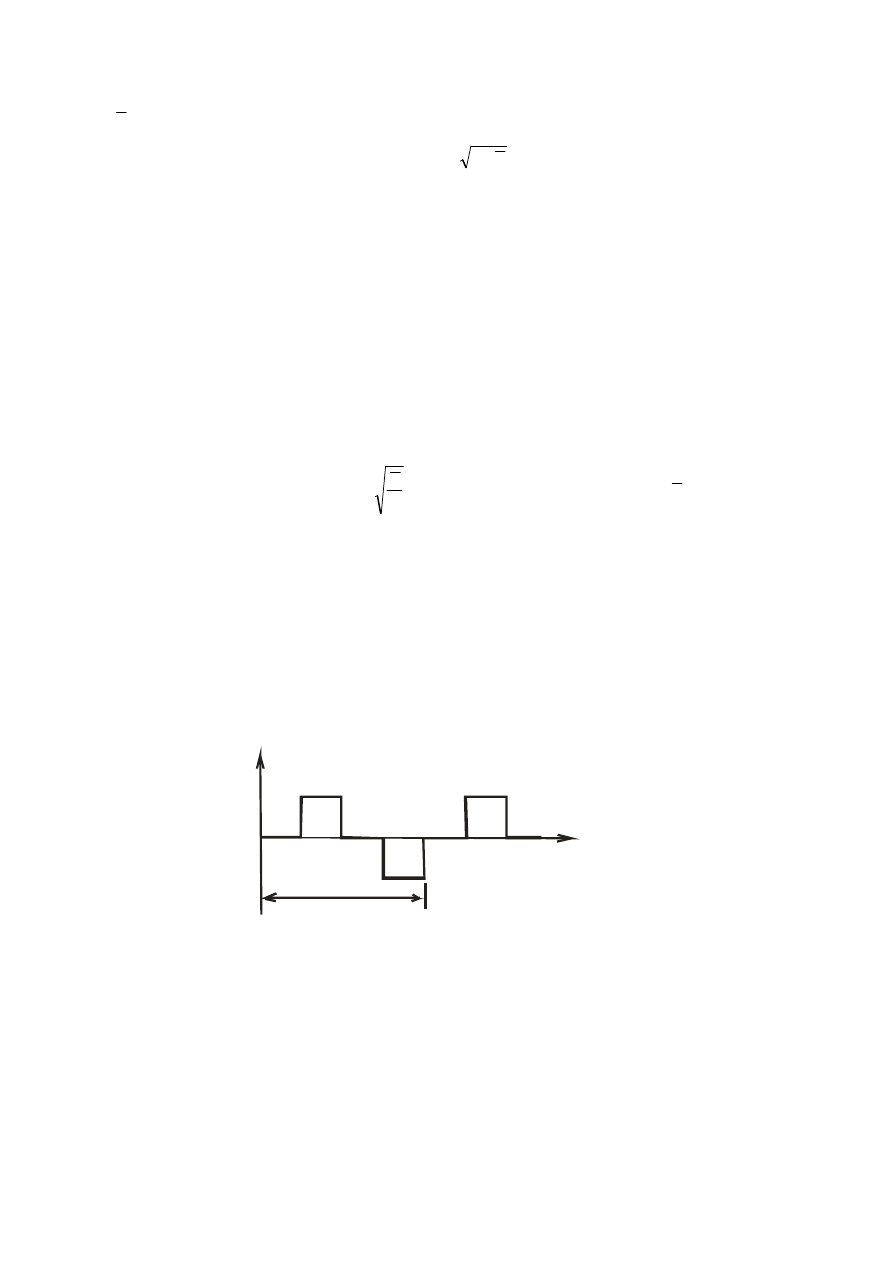
3

[ ]

(

)

m

Ω

ρ

(oporności ekwiwalentnej półprzestrzeni dla badanego ośrodka) i może być w

przybliżeniu określona wzorem:

( )

ρ

δ

⋅

≈

T

T

500

(gdzie -

]

[

/

1

sek

f

T

=

). Zasięg

głębokościowy metody MT wynosi więc od kilkudziesięciu metrów do kilkuset km (Simpson

F., Bahr K., 2005).

W przypadku metod aktywnych pole EM jest generowane za pomocą sztucznego

ź

ródła (transmitter). System pomiarowy składa się ze źródła pola EM (pole pierwotne) i

rejestratora wtórnego pola EM. Metody elektromagnetyczne mogą być podzielone na dwie

grupy: FDEM (frequency-domain electromagnetic, metoda elektromagnetyczna w domenie

częstotliwości)

oraz

TDEM

(time-domain

electromagnetic

method,

metoda

elektromagnetyczna w domenie czasu). W metodach FDEM zmiana prądu źródłowego w

czasie ma charakter quasisinusoidalny. W takim przypadku głębokość penetracji zależy od

częstotliwości fali EM

( )

f

f

ρ

δ

⋅

≈

500

i oporności uśrednionej ośrodka

[ ]

(

)

m

Ω

ρ

. Zasięg

głębokościowy w metodzie FDEM jest jednak mniejszy niż w przypadku metody MT i

wynosi od kilku do kilkuset (i więcej) metrów (Kauffann A.A., Keller G.V, 1983).

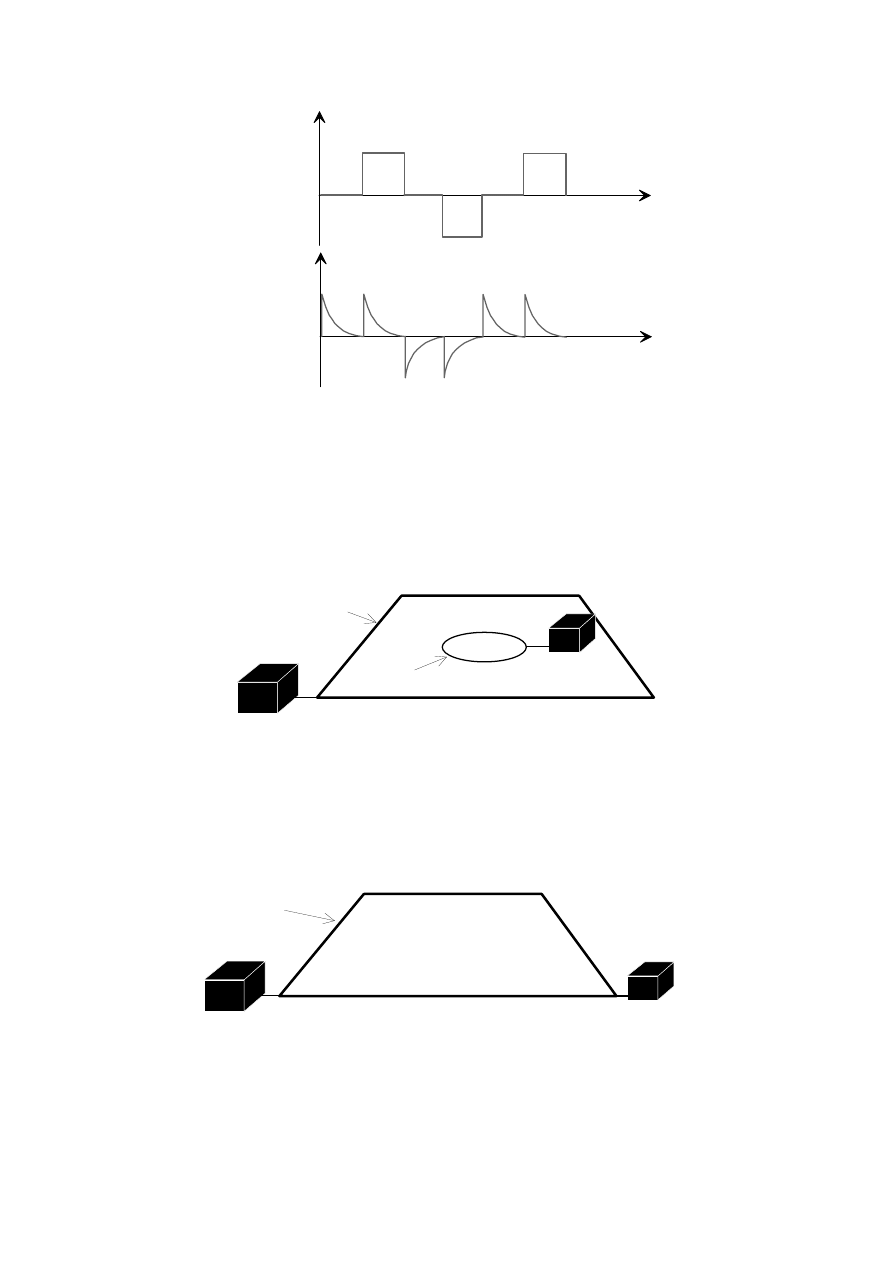
W metodzie TDEM prąd źródłowy (okresowy) ma najczęściej symetryczny kształt

prostokątny. Po każdej drugiej ćwiartce okresu prąd jest gwałtownie redukowany do zera

(rys. 1), a głębokość penetracji zależy od czasu jaki upłynął od wyłączenia prądu w pętli

nadawczej (Keller G.V., 1997).

T/4

T/4

T/4

T/4

T/4

T=okres
zwykle ok. 1 msec

Prąd pętli nadawczej
(zwykle kilka Amperów)

Rys. 1. Postać prądu pętli nadawczej w metodzie TDEM

Metody elektromagnetyczne to metody w których generowane są zmienne w czasie

prądy elektryczne w ziemi. Penetrację ośrodka geologicznego umożliwia wykorzystanie

zjawiska indukcji elektromagnetycznej. Zmienne w czasie pole magnetyczne jest wytwarzane

na powierzchni ziemi przy użyciu cewki (coil) albo pętli (loop) czyli przewodników

odpowiednio ukształtowanych (kabli przewodzących) umieszczonych na powierzchni ziemi.

4

Najczęściej stosowana jest jednak pętla nadawcza o kształcie kwadratu (o boku L[m]).

Odbiornik

stanowi

najczęściej

cewka

odbiorcza.

Podstawowym założeniem metod EM jest spełnienie równań Maxwella:

Prawo Gaussa:

η

=

⋅

∇

D

r

(źródłem pola elektrycznego są ładunki)

Prawo Faradya:

t

B

E

∂

∂

−

=

×

∇

r

r

(zmienne w czasie

( )

t

pole magnetyczne

( )

B

r

wytwarza wirowe pole elektryczne

( )

E

r

)

Prawo Gaussa dla pola

magnetycznego:

0

=

⋅

∇

B

r

(pole magnetyczne jest bezźródłowe)

Prawo Ampere’a

Maxwella:

t

D

j

H

∂

∂

+

=

×

∇

r

r

r

(przepływający prąd (

−

j

r

gęstość prądu) oraz

zmienne pole elektryczne wytwarzają wirowe pole

magnetyczne)

gdzie:

D

r

- indukcja elektryczna

[

]

2

/

m

C

,

B

v

- indukcja magnetyczna

[ ]

T

,

E

r

- natężenie pola elektrycznego

[

]

m

V

/

,

H

r

- natężenie pola magnetycznego

[

]

m

A

/

,

j

r

- gęstość prądu

[

]

2

/

m

A

,

η

- gęstość ładunku

[

]

3

/

m

C

,

⋅

∇

- operator dywergencji,

×

∇

- operator rotacji.

W ośrodkach liniowych:

E

D

r

r

⋅

=

ε

a

H

B

r

r

⋅

=

µ

gdzie:

ε

- przenikalność elektryczna,

µ

przenikalność magnetyczna.

Równania Maxwella mogą być sprowadzone do równań falowych dla pola

elektrycznego

( )

E

r

i magnetycznego

( )

H

r

:

0

2

2

2

=

∂

∂

−

∂

∂

−

∇

t

E

t

E

E

r

r

r

µε

µσ

oraz

5

0

2

2

2

=

∂

∂

−

∂

∂

−

∇

t

H

t

H

H

r

r

r

µε

µσ

x

z

y

Rys. 2. Kartezjański układ współrzędnych

Dla warstwowanej półprzestrzeni

( )

z

ρ

ρ

=

i w układzie Kartezjańskim (ośrodek 1D):

0

2

2

2

2

=

∂

∂

−

∂

∂

−

∂

∂

t

H

t

H

z

H

x

x

x

µε

µσ

Dla pól harmonicznie zmiennych (założenie metod EM w domenie częstotliwości):

t

i

x

x

e

z

H

H

ω

ω

−

⋅

=

)

,

(

gdzie

f

π

ω

2

=

- częstość pola, powyższe równanie można przekształcić

do postaci:

0

1

2

2

=

⋅













−

+

x

x

H

i

i

dz

H

d

σ

ωε

ωµσ

Dla metod EM (niskie częstotliwości):

1

/

<<

σ

ωε

(zachowanie fali EM w

przewodniku) pozostaje tylko składnik

t

∂

∂

stąd otrzymujemy tzw. równanie dyfuzji:

0

2

2

=

∂

∂

−

∂

∂

t

H

z

H

x

x

µσ

lub dla pól harmonicznie zmiennych

0

2

2

=

⋅

+

x

x

H

i

dz

H

d

ωµσ

.

Jak widać transport energii w metodach EM jest rządzony dyfuzją, a nie propagacją

falową.

Zgodnie z prawem Faradaya zmienne pole magnetyczne generuje zmienne pole

elektryczne, które z kolei wytwarza prąd elektryczny. W związku z tym w metodach EM

pierwotne zmienne pole magnetyczne wytwarza wtórne prądy elektryczne wewnątrz Ziemi.

Wielkość tych wtórnych prądów wyidukowanych w Ziemi zależy od rozkładu przewodności

elektrycznej













=

ρ

σ

1

[

]

m

mS /

penetrowanego ośrodka. Rejestrator służy do pomiaru

zmiennego pola magnetycznego wytworzonego przez wtórne prądy elektryczne.

6

Jak

wcześniej

wyjaśniono

najważniejszym

zjawiskiem

w

metodach

elektromagnetycznych jest zjawisko indukcji i rządzi nimi równanie dyfuzji.

To decyduje o rozdzielczości metod EM, która nie jest tak duża jak w przypadku

metody sejsmicznej, gdzie decydującą rolę odgrywają zjawiska falowe (równanie falowe). To

również decyduje o zasięgu głębokościowym metod EM określonym przez tzw. efekt

naskórkowy (skin effect). Zasięg głębokościowy jest tutaj określony przez tzw. głębokość dla

skin efektu:

σ

σ

ωµ

δ

⋅

≈

=

f

o

503

2

gdzie

[ ]

Hz

f

to częstotliwość pola EM,

f

⋅

⋅

=

π

ω

2

to

częstość pola EM a

[

]

m

H

o

/

10

4

7

−

⋅

⋅

=

π

µ

to przenikalność magnetyczna próżni z kolei

[

]

1

−

Ω

m

σ

to przewodność właściwa ośrodka (Nagendra Pratap Singh and Toru Mogi, 2003).

W metodzie procesów przejściowych (TDEM) pole elektromagnetyczne jest

generowane przez impuls prądowy lub sygnał przejściowy wzdłuż kabla rozłożonego na

powierzchni ziemi (pętla nadawcza). To generuje zmienne pole magnetyczne wewnątrz ziemi.

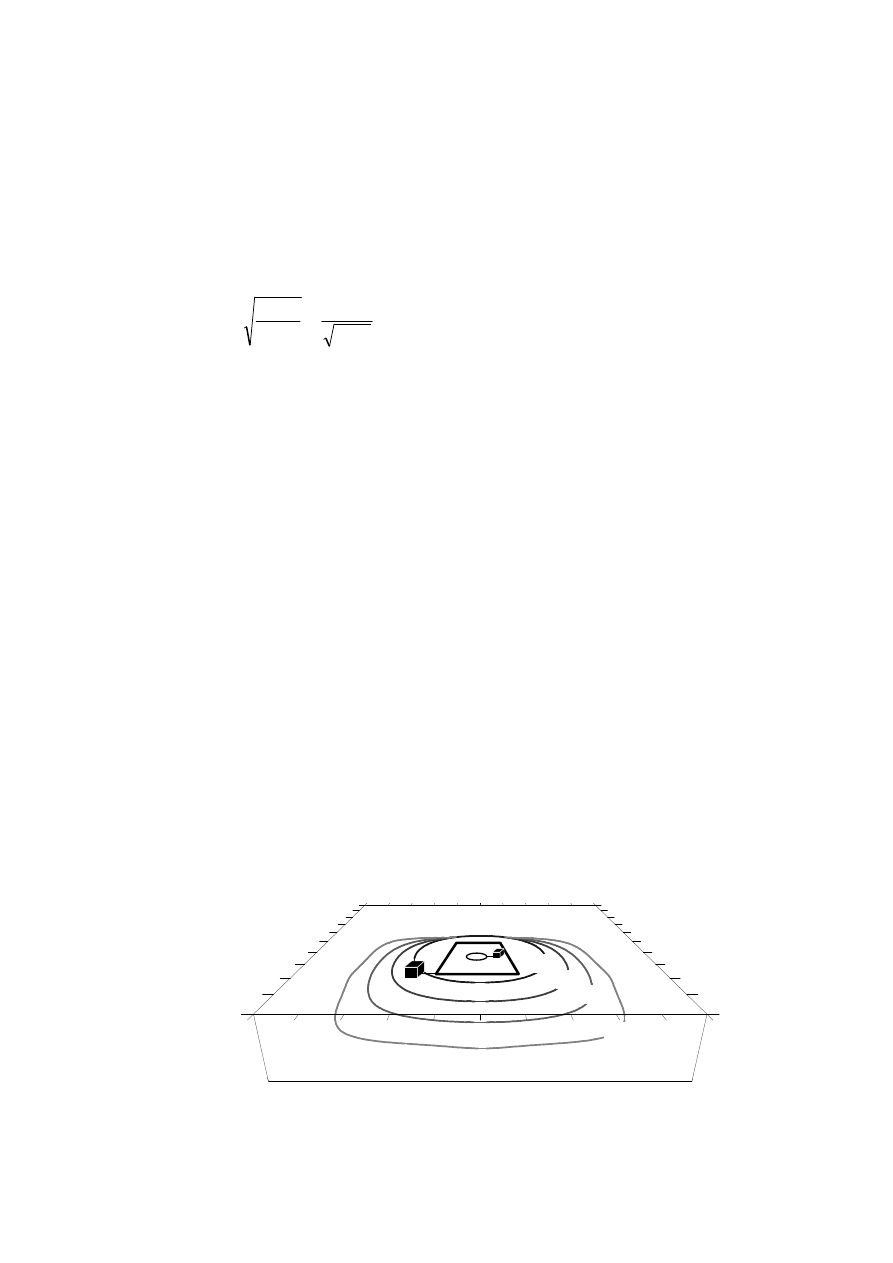
Początkowo indukowany prąd koncentruje się bezpośrednio pod powierzchnią ziemi poniżej

pętli nadawczej. Potem dyfunduje w czasie w dół (rys. 3). Tak więc zasięg pola EM się

powiększa, następuje jednak tłumienie, które jest coraz większe w miarę przesuwania się w

głąb Ziemi. „Tempo” dyfuzji zależy od przewodności ośrodka. W wysokooporowym ośrodku

tempo dyfuzji jest szybkie. W przewodzącym ośrodku prąd dyfunduje wolniej. Zmiennemu

polu elektrycznemu wyidukowanemu z którym związane są prądy wirowe zgodnie z

równaniami Maxwella towarzyszy zmienne pole magnetyczne. Pole magnetyczne „wraca” na

powierzchnię ziemi „niosąc ze sobą informację” o rozkładzie przewodności tego ośrodka.

Wtórne zmienne pole magnetyczne pochodzące od wtórnych prądów wirowych

rozprzestrzenia się wolno w porównaniu z tempem ustalania się pierwotnego pola

magnetycznego.

(a)

(b)

(c)

(d)

(a) zaraz po wł

ą

czeniu

(b) (c) (d) stopniowo (po czasie)

Rys. 3 Zachowanie prądu przejściowego w Ziemi

7

W metodzie procesów przejściowych mierzone jest wtórne pole magnetyczne i czas

opóźnienia (t), czyli czas jaki upłynął od wyłączenia prądu w pętli nadawczej (Keller,

G.V.,1997). Geometria rozkładu przewodności, a więc głębokość i przewodność, są

odzwierciedlone przez wartości wtórnego pola magnetycznego. Głębokość penetracji zgodnie

z zasadą dyfuzji zależy od oporności i czasu (t). Tak więc nie ma teoretycznie limitu na tę

głębokość. Praktyczny limit jest jednak podyktowany najmniejszą możliwą do zmierzenia

amplitudą sygnału. Zasięg głębokościowy zależy więc od geometrii układu pomiarowego (w

tym rozmiaru pętli nadawczej), wielkości mocy użytej w pętli nadawczej, czułości odbiornika

i panujących w otoczeniu zakłóceń i może wynieść od kilku metrów do około tysiąca metrów,

a dla specjalnych źródeł nawet do 10 km (Keller G.V. et al., 1984).

Zasięg głębokościowy w metodzie TDEM zależy od czasu (t[s]) (jego maksymalna

wartość) i od średniej oporności ośrodka

[ ]

(

)

m

Ω

ρ

:

( )

[ ]

m

t

2

/

1

3

.

503

ρ

δ

⋅

⋅

=

(Parasnis, 1986).

Z kolei wg danych firmy Phoenix zasięg głębokościowy wynosi: D=

[ ]

ms

t

⋅

⋅

ρ

500

[m].

Maksymalny czas dla którego poziom sygnału jest wystarczający do jego rejestracji

zależy od rozmiaru pętli nadajnika, mocy źródła oraz poziomu zakłóceń. Tak więc zasięg

głębokościowy bezpośrednio zależy od czasu (t) jaki upływa od wyłączenia prądu w pętli

nadawczej, a pośrednio od w/w czynników. Poziom zakłóceń ( Nm ) wynosi zwykle od

8

10

−

do

10

10

−

[V/m]. Maksymalny czas rejestracji możemy wyznaczyć z wzoru:

(

)

(

)

5

/

1

3

2

400

/













⋅

⋅

⋅

=

a

t

o

Nm

M

t

ρ

π

µ

[s] (wg danych firmy Phoenix), gdzie

t

M to moment nadajnika =

2

L

I

⋅

[Am

2

],

I to prąd pętli nadawczej [Amper], L to długość pętli nadawczej [metr] a

a

ρ

to oporność ośrodka

[ ]

m

Ω

. Zakładając rozmiary pętli nadawczej (

L

L

×

[m

2

]) wynoszące:

10

10

×

,

20

20

×

,

40

40

×

,

100

100

×

oraz

300

300

×

[m

2]

oraz trzy możliwe poziomy

zakłóceń:

8

10

−

=

Nm

[V/m

2

] ,

9

10

−

=

Nm

[V/m

2

],

10

10

−

=

Nm

[V/m

2

] obliczamy czas

ostatniego rejestrowanego sygnału oraz odpowiadający zasięg głębokościowy (D=

[ ]

ms

t

a

⋅

⋅

ρ

500

[m]) (patrz tabele niżej).

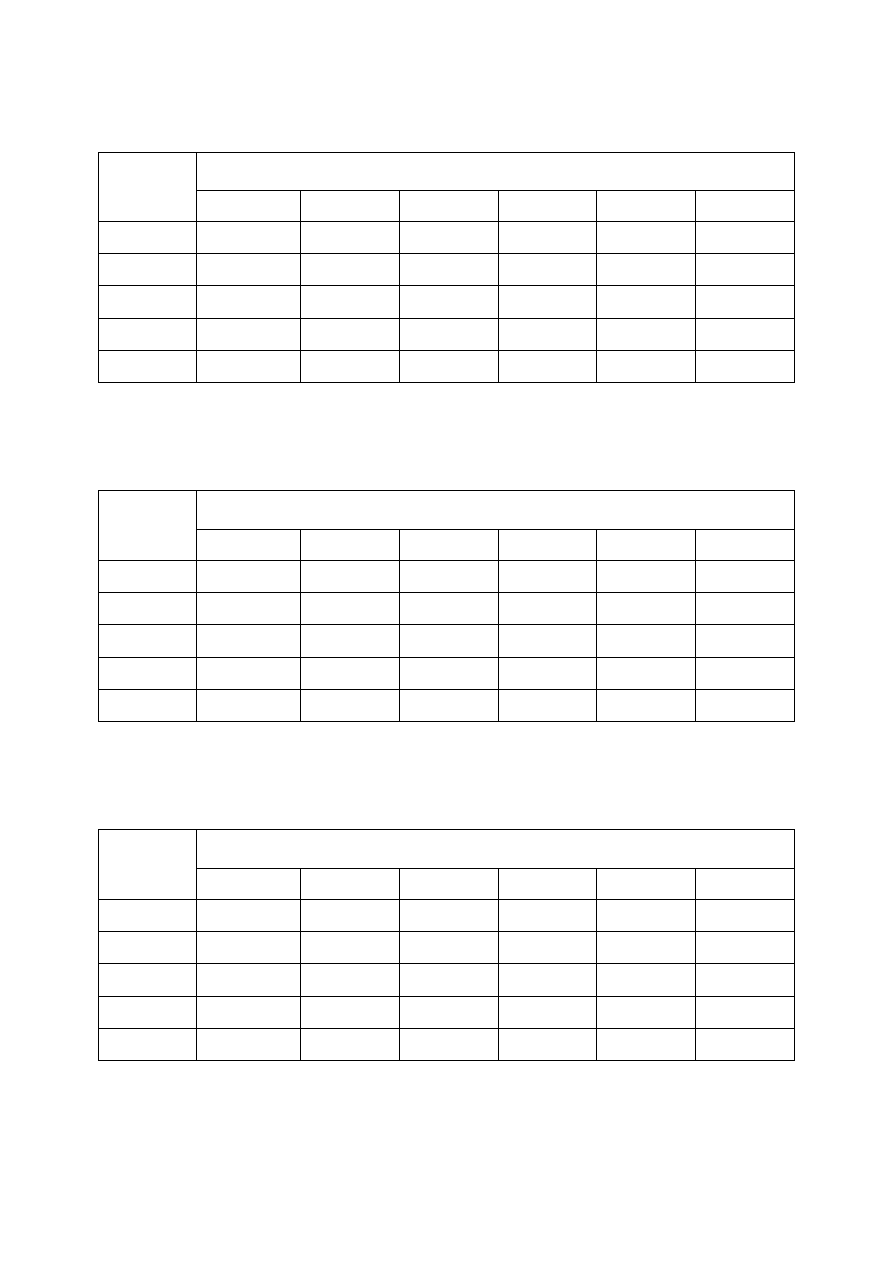
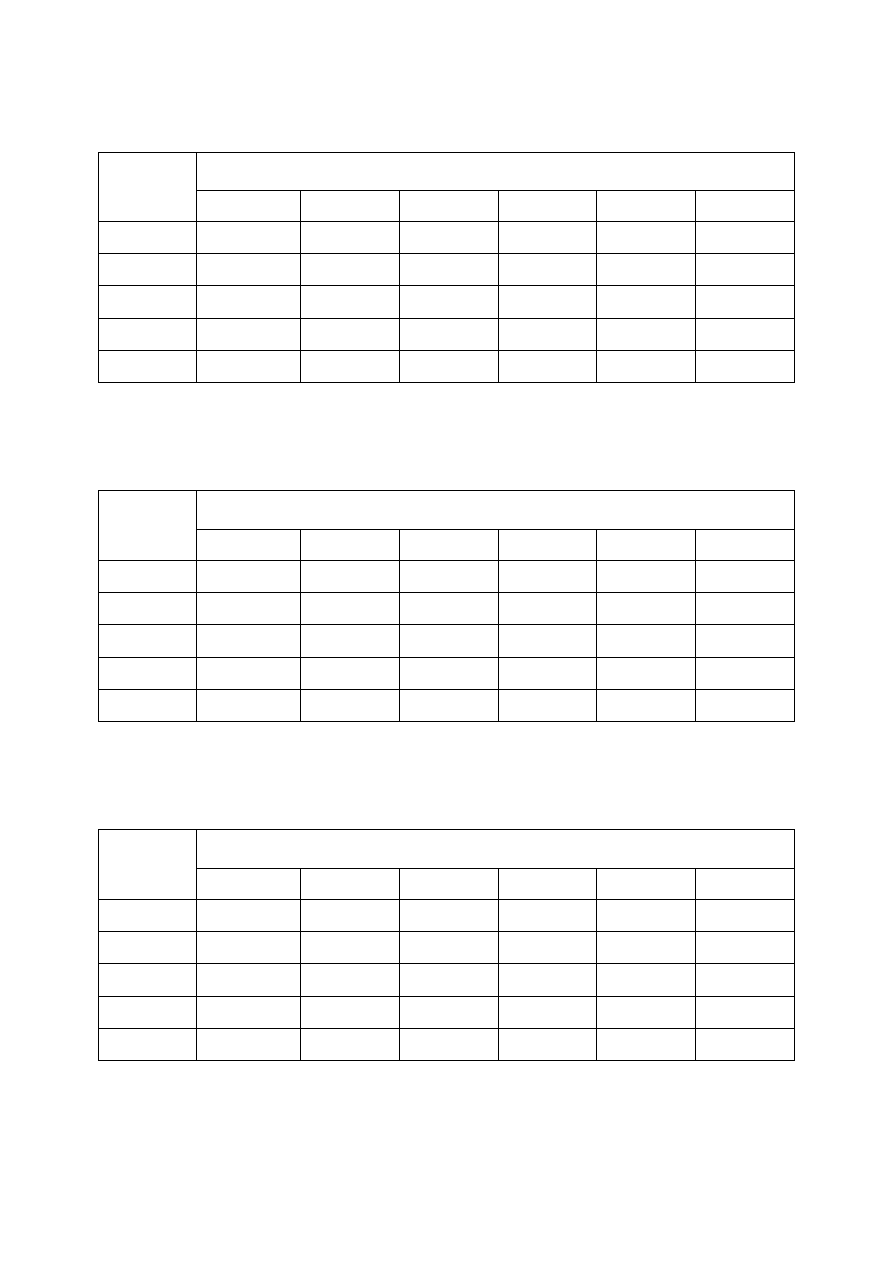
8

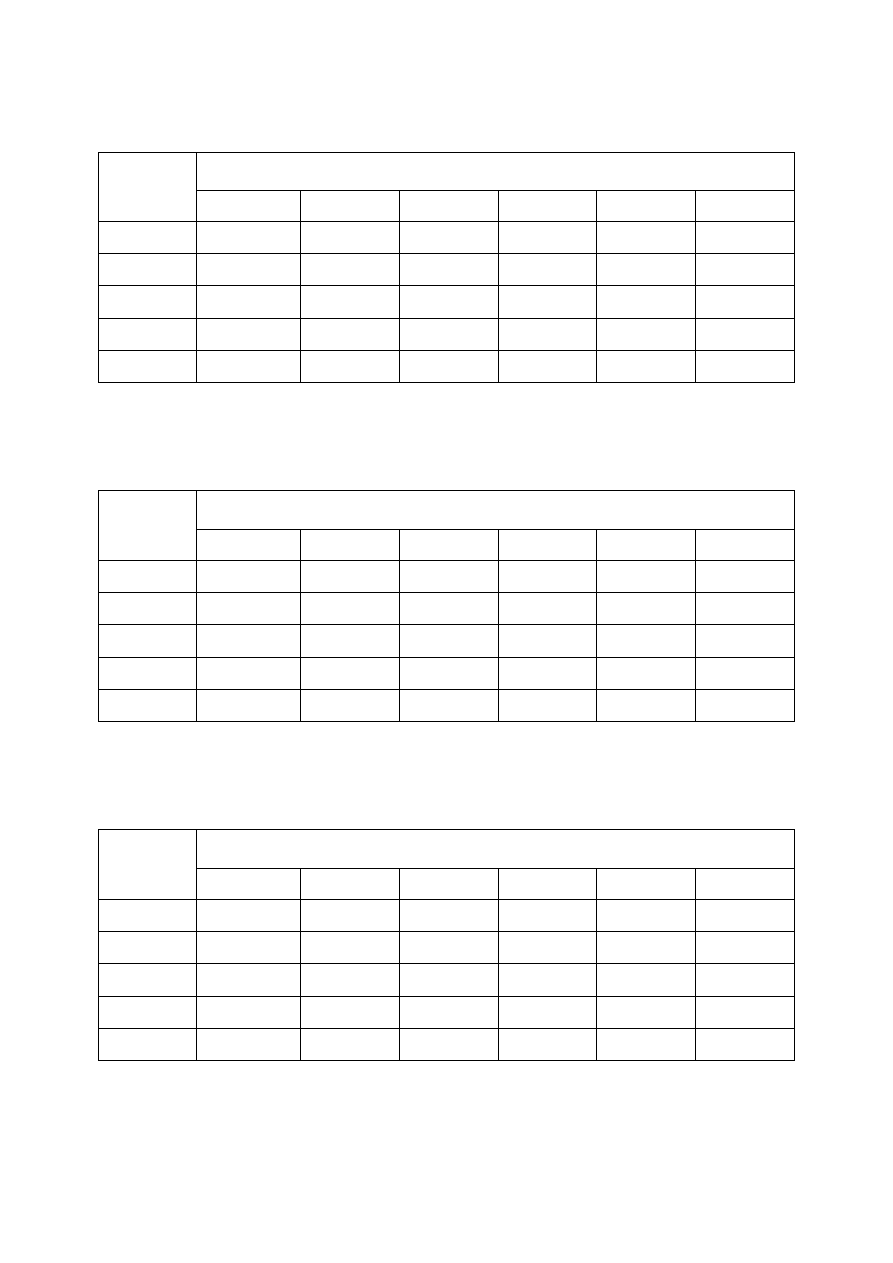
Tabela 1. Czas ostatniego rejestrowanego sygnału dla

10

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

10

10

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

15,12

8,72

5,76

3,80

2,19

1,45

100

10

×

19,95

11,51

7,59

5,01

2,89

1,91

100

20

×

*

26,32

15,19

10,02

6,61

3,82

2,52

100

40

×

*

34,73

20,04

13,22

8,72

5,03

3,32

100

50

×

37,97

21,91

14,46

9,54

5,50

3,63

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 2. Zasięg głębokościowy (D) dla

10

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

10

10

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

122,95

147,68

169,64

194,86

234,06

268,86

100

10

×

141,23

169,64

194,86

223,84

268,86

308,84

100

20

×

*

162,24

194,86

223,84

257,13

308,84

354,76

100

40

×

*

186,36

223,84

257,13

295,36

354,76

407,52

100

50

×

194,86

234,06

268,86

308,84

370,95

426,11

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

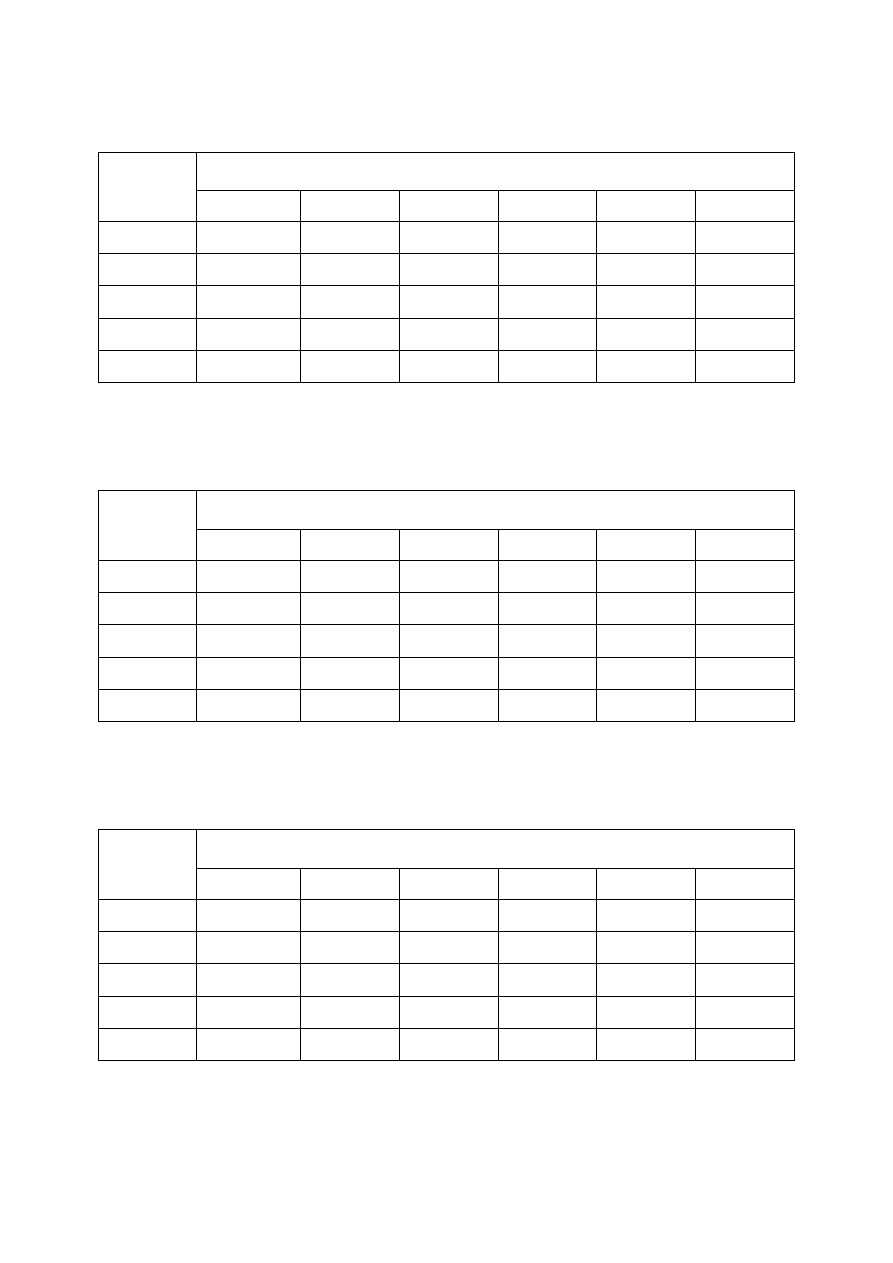
Tabela 3. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

10

10

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

6,02

3,47

2,29

1,51

0,87

0,58

100

10

×

7,94

4,58

3,02

1,99

1,15

0,76

100

20

×

*

10,48

6,05

3,99

2,63

1,52

1,00

100

40

×

*

13,83

7,98

5,26

3,47

2,00

1,32

100

50

×

15,12

8,72

5,76

3,80

2,19

1,45

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

9

Tabela 4. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

10

10

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

77,58

93,18

107,04

122,95

147,68

169,64

100

10

×

89,11

107,04

122,95

141,23

169,64

194,86

100

20

×

*

102,36

122,95

141,23

162,24

194,86

223,84

100

40

×

*

117,58

141,23

162,24

186,36

223,84

257,13

100

50

×

122,95

147,68

169,64

194,86

234,06

268,86

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 5. Czas ostatniego rejestrowanego sygnału dla

8

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

10

10

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

2,40

1,38

0,91

0,60

0,35

0,23

100

10

×

3,16

1,82

1,20

0,79

0,46

0,30

100

20

×

*

4,17

2,41

1,59

1,05

0,60

0,40

100

40

×

*

5,50

3,18

2,10

1,38

0,80

0,53

100

50

×

6,02

3,47

2,29

1,51

0,87

0,58

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 6. Zasięg głębokościowy dla

8

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

10

10

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

100

5

×

48,95

58,79

67,53

77,58

93,18

107,04

100

10

×

56,23

67,53

77,58

89,11

107,04

122,95

100

20

×

*

64,59

77,58

89,11

102,36

122,95

141,23

100

40

×

*

74,19

89,11

102,36

117,58

141,23

162,24

100

50

×

77,58

93,18

107,04

122,95

147,68

169,64

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

10

Tabela 7. Czas ostatniego rejestrowanego sygnału dla

10

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

20

20

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

26,32

15,19

10,02

6,61

3,82

2,52

400

10

×

34,73

20,04

13,22

8,72

5,03

3,32

400

20

×

*

45,83

26,45

17,45

11,51

6,64

4,38

400

40

×

*

60,47

34,89

23,02

15,19

8,77

5,78

400

50

×

66,11

38,15

25,17

16,61

9,58

6,32

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 8. Zasięg głębokościowy (D) dla

10

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

20

20

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

162,24

194,86

223,84

257,13

308,84

354,76

400

10

×

186,36

223,84

257,13

295,36

354,76

407,52

400

20

×

*

214,07

257,13

295,36

339,28

407,52

468,11

400

40

×

*

245,90

295,36

339,28

389,73

468,11

537,72

400

50

×

257,13

308,84

354,76

407,52

489,48

562,26

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 9. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

20

20

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

10,48

6,05

3,99

2,63

1,52

1,00

400

10

×

13,83

7,98

5,26

3,47

2,00

1,32

400

20

×

*

18,24

10,53

6,95

4,58

2,64

1,74

400

40

×

*

24,07

13,89

9,17

6,05

3,49

2,30

400

50

×

26,32

15,19

10,02

6,61

3,82

2,52

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

11

Tabela 10. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

20

20

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

102,36

122,95

141,23

162,24

194,86

223,84

400

10

×

117,58

141,23

162,24

186,36

223,84

257,13

400

20

×

*

135,07

162,24

186,36

214,07

257,13

295,36

400

40

×

*

155,15

186,36

214,07

245,90

295,36

339,28

400

50

×

162,24

194,86

223,84

257,13

308,84

354,76

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 11. Czas ostatniego rejestrowanego sygnału dla

8

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

20

20

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

4,17

2,41

1,59

1,05

0,60

0,40

400

10

×

5,50

3,18

2,10

1,38

0,80

0,53

400

20

×

*

7,26

4,19

2,77

1,82

1,05

0,69

400

40

×

*

9,58

5,53

3,65

2,41

1,39

0,92

400

50

×

10,48

6,05

3,99

2,63

1,52

1,00

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 12. Zasięg głębokościowy (D) dla

8

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

20

20

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

400

5

×

64,59

77,58

89,11

102,36

122,95

141,23

400

10

×

74,19

89,11

102,36

117,58

141,23

162,24

400

20

×

*

85,22

102,36

117,58

135,07

162,24

186,36

400

40

×

*

97,90

117,58

135,07

155,15

186,36

214,07

400

50

×

102,36

122,95

141,23

162,24

194,86

223,84

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

12

Tabela 13. Czas ostatniego rejestrowanego sygnału dla

10

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

40

40

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

45,83

26,45

17,45

11,51

6,64

4,38

1600

10

×

60,47

34,89

23,02

15,19

8,77

5,78

1600

20

×

*

79,79

46,04

30,38

20,04

11,57

7,63

1600

40

×

*

105,28

60,76

40,08

26,45

15,26

10,07

1600

50

×

115,11

66,43

43,83

28,91

16,69

11,01

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 14. Zasięg głębokościowy (D) dla

10

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

40

40

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

214,07

257,13

295,36

339,28

407,52

468,11

1600

10

×

245,90

295,36

339,28

389,73

468,11

537,72

1600

20

×

*

282,47

339,28

389,73

447,68

537,72

617,68

1600

40

×

*

324,47

389,73

447,68

514,25

617,68

709,53

1600

50

×

339,28

407,52

468,11

537,72

645,87

741,91

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

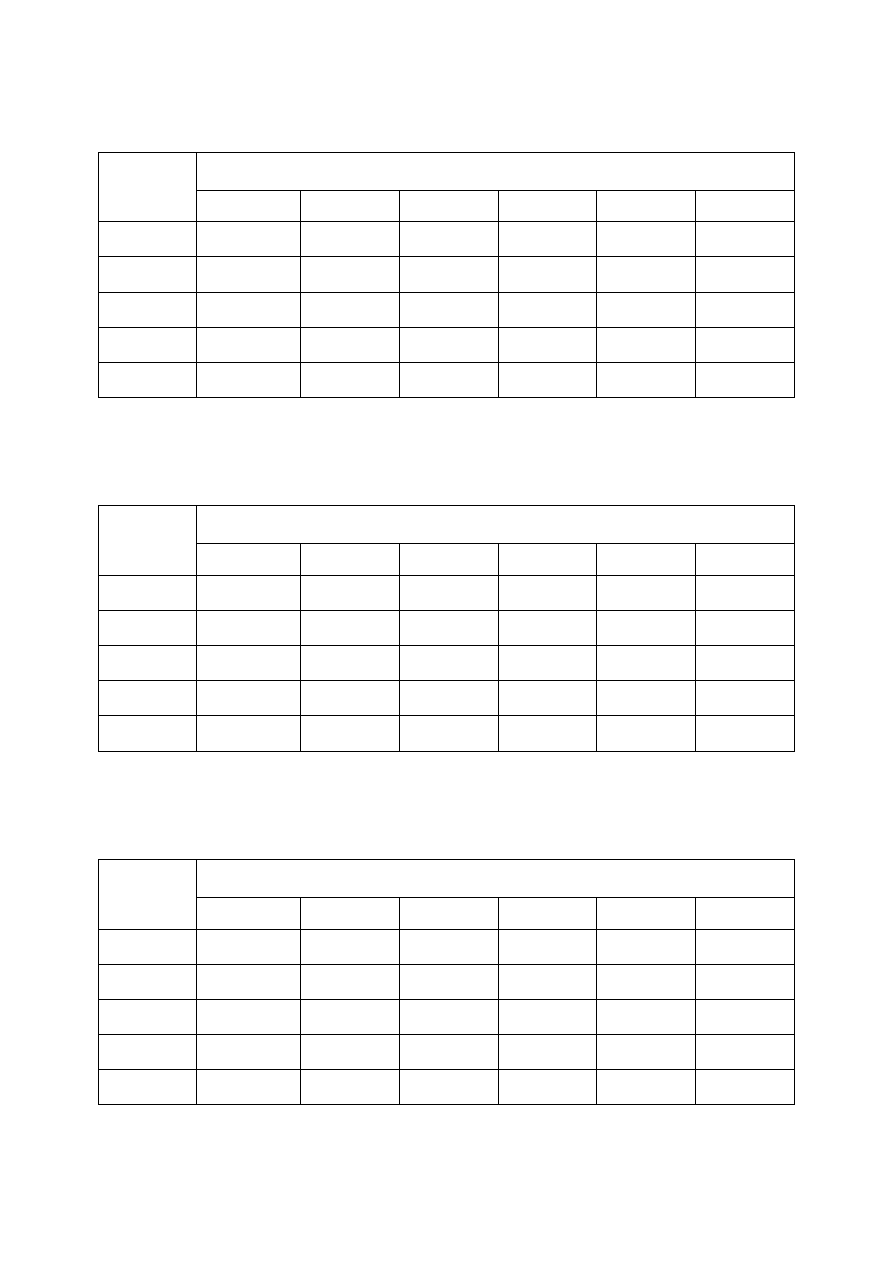
Tabela 15. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

40

40

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

18,24

10,53

6,95

4,58

2,64

1,74

1600

10

×

24,07

13,89

9,17

6,05

3,49

2,30

1600

20

×

*

31,76

18,33

12,09

7,98

4,60

3,04

1600

40

×

*

41,91

24,19

15,96

10,53

6,08

4,01

1600

50

×

45,83

26,45

17,45

11,51

6,64

4,38

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

13

Tabela 16. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

40

40

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

135,07

162,24

186,36

214,07

257,13

295,36

1600

10

×

155,15

186,36

214,07

245,90

295,36

339,28

1600

20

×

*

178,23

214,07

245,90

282,47

339,28

389,73

1600

40

×

*

204,73

245,90

282,47

324,47

389,73

447,68

1600

50

×

214,07

257,13

295,36

339,28

407,52

468,11

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 17. Czas ostatniego rejestrowanego sygnału dla

8

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

40

40

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

7,26

4,19

2,77

1,82

1,05

0,69

1600

10

×

9,58

5,53

3,65

2,41

1,39

0,92

1600

20

×

*

12,65

7,30

4,81

3,18

1,83

1,21

1600

40

×

*

16,69

9,63

6,35

4,19

2,42

1,60

1600

50

×

18,24

10,53

6,95

4,58

2,64

1,74

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 18. Zasięg głębokościowy (D) dla

8

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

40

40

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

1600

5

×

85,22

102,36

117,58

135,07

162,24

186,36

1600

10

×

97,90

117,58

135,07

155,15

186,36

214,07

1600

20

×

*

112,45

135,07

155,15

178,23

214,07

245,90

1600

40

×

*

129,17

155,15

178,23

204,73

245,90

282,47

1600

50

×

135,07

162,24

186,36

214,07

257,13

295,36

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

14

Tabela 19. Czas ostatniego rejestrowanego sygnału dla

10

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

100

100

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

95,38

55,04

36,31

23,96

13,83

9,12

4

10

10

×

125,86

72,63

47,92

31,61

18,24

12,04

4

10

20

×

*

166,07

95,84

63,23

41,71

24,07

15,88

4

10

40

×

*

219,13

126,46

83,43

55,04

31,76

20,96

4

10

50

×

239,59

138,26

91,22

60,18

34,73

22,91

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 20. Zasięg głębokościowy (D) dla

10

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

100

100

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

308,84

370,95

426,11

489,48

587,92

675,35

4

10

10

×

354,76

426,11

489,48

562,26

675,35

775,77

4

10

20

×

*

407,52

489,48

562,26

645,87

775,77

891,13

4

10

40

×

*

468,11

562,26

645,87

741,91

891,13

1023,63

4

10

50

×

489,48

587,92

675,35

775,77

931,80

1070,35

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

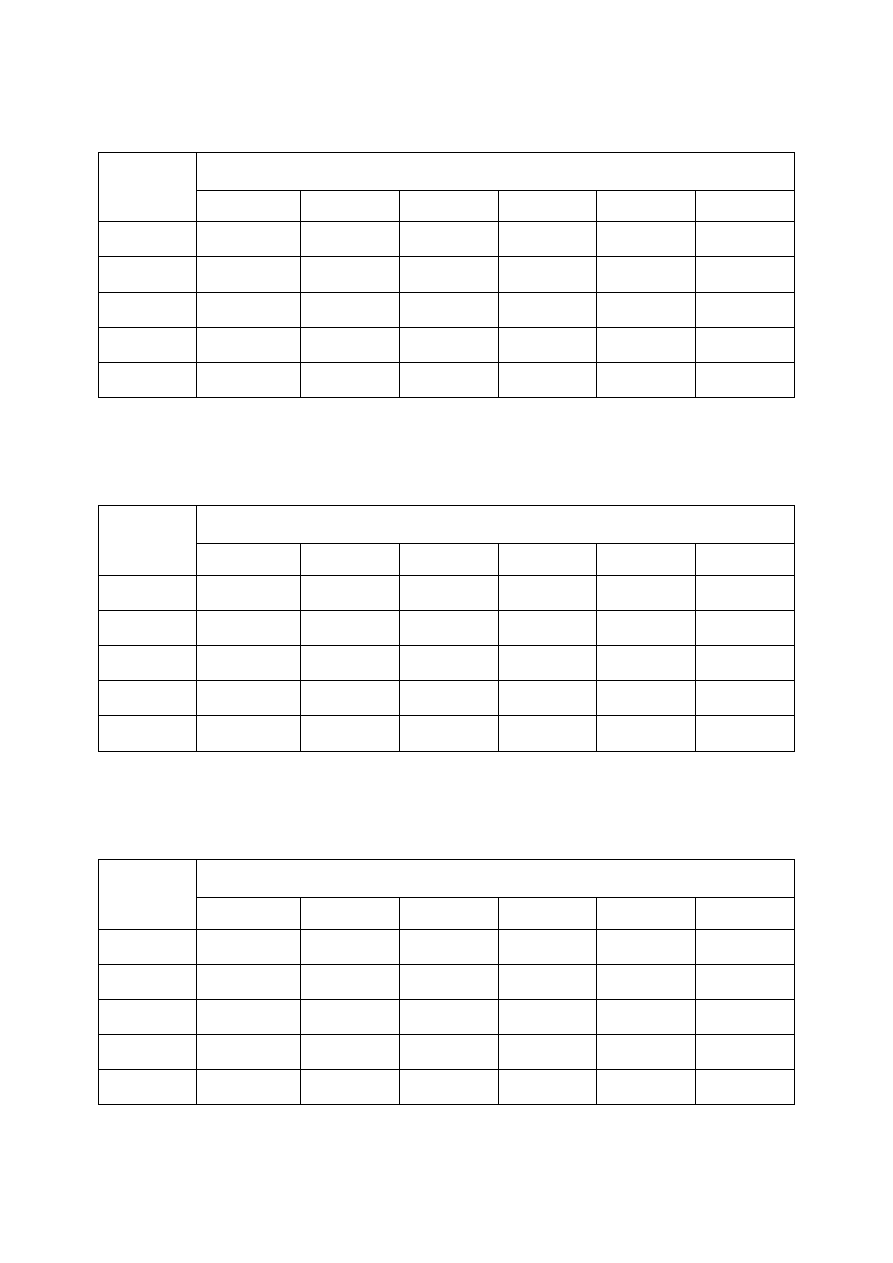
Tabela 21. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

100

100

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

37,97

21,91

14,46

9,54

5,50

3,63

4

10

10

×

50,10

28,91

19,08

12,59

7,26

4,79

4

10

20

×

*

66,11

38,15

25,17

16,61

9,58

6,32

4

10

40

×

*

87,24

50,34

33,21

21,91

12,65

8,34

4

10

50

×

95,38

55,04

36,31

23,96

13,83

9,12

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

15

Tabela 22. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

100

100

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

194,86

234,06

268,86

308,84

370,95

426,11

4

10

10

×

223,84

268,86

308,84

354,76

426,11

489,48

4

10

20

×

*

257,13

308,84

354,76

407,52

489,48

562,26

4

10

40

×

*

295,36

354,76

407,52

468,11

562,26

645,87

4

10

50

×

308,84

370,95

426,11

489,48

587,92

675,35

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 23. Czas ostatniego rejestrowanego sygnału dla

8

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

100

100

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

15,12

8,72

5,76

3,80

2,19

1,45

4

10

10

×

19,95

11,51

7,59

5,01

2,89

1,91

4

10

20

×

*

26,32

15,19

10,02

6,61

3,82

2,52

4

10

40

×

*

34,73

20,04

13,22

8,72

5,03

3,32

4

10

50

×

37,97

21,91

14,46

9,54

5,50

3,63

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 24. Zasięg głębokościowy (D) dla

8

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

100

100

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

5

×

122,95

147,68

169,64

194,86

234,06

268,86

4

10

10

×

141,23

169,64

194,86

223,84

268,86

308,84

4

10

20

×

*

162,24

194,86

223,84

257,13

308,84

354,76

4

10

40

×

*

186,36

223,84

257,13

295,36

354,76

407,52

4

10

50

×

194,86

234,06

268,86

308,84

370,95

426,11

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

16

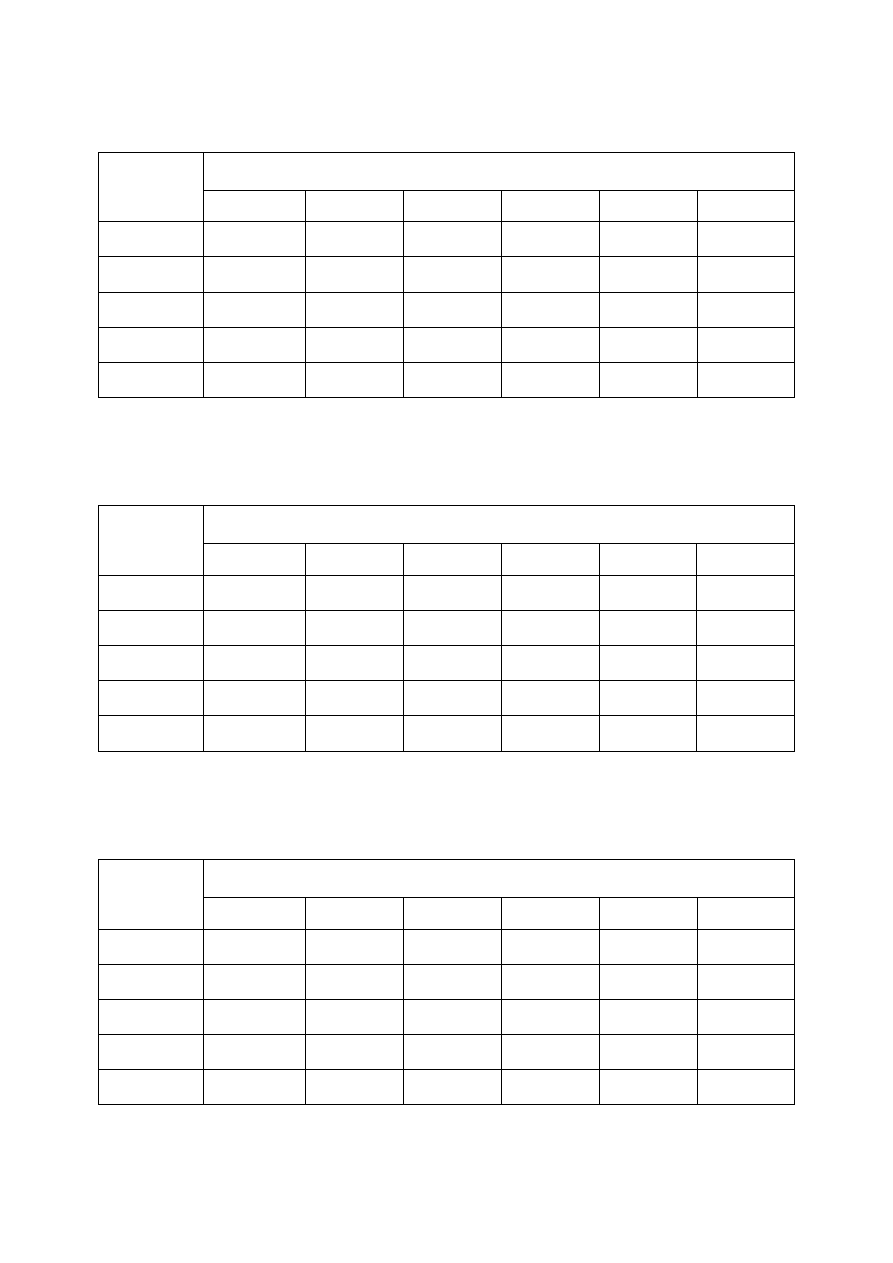
Tabela 25. Czas ostatniego rejestrowanego sygnału dla

10

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

300

300

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

229,70

132,56

87,45

57,70

33,30

21,97

4

10

9

10

⋅

×

303,09

174,91

115,40

76,13

43,93

28,99

4

10

9

20

⋅

×

*

399,93

230,79

152,27

100,46

57,97

38,25

4

10

9

40

⋅

×

*

527,71

304,53

200,92

132,56

76,50

50,47

4

10

9

50

⋅

×

576,98

332,96

219,67

144,93

83,64

55,18

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 26. Zasięg głębokościowy (D) dla

10

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

300

300

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

479,27

575,66

661,26

759,59

912,37

1048,03

4

10

9

10

⋅

×

550,54

661,26

759,59

872,54

1048,03

1203,87

4

10

9

20

⋅

×

*

632,40

759,59

872,54

1002,29

1203,87

1382,89

4

10

9

40

⋅

×

*

726,44

872,54

1002,29

1151,33

1382,89

1588,52

4

10

9

50

⋅

×

759,59

912,37

1048,03

1203,87

1446,00

1661,02

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 27. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

300

300

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

91,45

52,77

34,82

22,97

13,26

8,75

4

10

9

10

⋅

×

120,66

69,63

45,94

30,31

17,49

11,54

4

10

9

20

⋅

×

*

159,22

91,88

60,62

39,99

23,08

15,23

4

10

9

40

⋅

×

*

210,09

121,24

79,99

52,77

30,45

20,09

4

10

9

50

⋅

×

229,70

132,56

87,45

57,70

33,30

21,97

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

17

Tabela 28. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

300

300

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

302,40

363,22

417,23

479,27

575,66

661,26

4

10

9

10

⋅

×

347,37

417,23

479,27

550,54

661,26

759,59

4

10

9

20

⋅

×

*

399,02

479,27

550,54

632,40

759,59

872,54

4

10

9

40

⋅

×

*

458,35

550,54

632,40

726,44

872,54

1002,29

4

10

9

50

⋅

×

479,27

575,66

661,26

759,59

912,37

1048,03

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 29. Czas ostatniego rejestrowanego sygnału dla

8

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

300

300

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

36,41

21,01

13,86

9,14

5,28

3,48

4

10

9

10

⋅

×

48,04

27,72

18,29

12,07

6,96

4,59

4

10

9

20

⋅

×

*

63,38

36,58

24,13

15,92

9,19

6,06

4

10

9

40

⋅

×

*

83,64

48,27

31,84

21,01

12,12

8,00

4

10

9

50

⋅

×

91,45

52,77

34,82

22,97

13,26

8,75

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 30. Zasięg głębokościowy (D) dla

8

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

300

300

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

9

5

⋅

×

190,80

229,18

263,25

302,40

363,22

417,23

4

10

9

10

⋅

×

219,17

263,25

302,40

347,37

417,23

479,27

4

10

9

20

⋅

×

*

251,76

302,40

347,37

399,02

479,27

550,54

4

10

9

40

⋅

×

*

289,20

347,37

399,02

458,35

550,54

632,40

4

10

9

50

⋅

×

302,40

363,22

417,23

479,27

575,66

661,26

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

18

Jak widać z wyżej przedstawionych wyników obliczeń na zasięg głębokościowy w

metodzie procesów przejściowych wpływa wiele czynników takich jak poziom zakłóceń,

oporność badanego ośrodka, moc źródła, rozmiar pętli nadawczej oraz czas pomiaru.

Analizując w/w wyniki obliczeń widać, że poziom zakłóceń w obszarze badań ma ogromne

znaczenie. Dla niewielkiej pętli nadawczej (

2

10

10

m

×

) i dla średniej oporności ośrodka

wynoszącej 10

Ω

m przy niskim poziomie zakłóceń (

2

10

/

10

m

V

−

) dla prądu wynoszącego 40

Amperów zasięg głębokościowy może wynieść ok. 260 metrów. Przy wysokim poziomie

zakłóceń

2

8

/

10

m

V

−

zasięg głębokościowy spada do ok. 100 metrów (tabele 1-2).

Im większy rozmiar pętli nadawczej tym zasięg głębokościowy metody TDEM jest większy.

Dla pętli (

2

20

20

m

×

), średniej oporności ośrodka 10

Ω

m i średniego poziomu zakłóceń

(

2

9

/

10

m

V

−

) oraz dla prądu 40 Amperów zasięg ten wynosi ponad 200 metrów (tabele 9 i

10). W takich samych warunkach dla pętli nadawczej o rozmiarach (

2

40

40

m

×

) zasięg

głębokościowy rośnie do ponad 290 metrów (tabele 15 i 16), a dla dużych pętli tj.

2

100

100

m

×

i

2

300

300

m

×

zasięgi głębokościowe rosną do odpowiednio 426 metrów (tabele

21 i 22) i do 660 metrów (tabele 27 i 28).

Najdłuższe czasy ostatniego rejestrowanego sygnału dla średniego poziomu zakłóceń

(

2

9

/

10

m

V

−

) dla prądu wynoszącego 50 Amperów uzyskuje się dla układu

2

300

300

m

×

i dla

niskiej oporności (2

Ω

m). Wartość tego czasu osiąga 230 ms. Mimo krótszego czasu

ostatniego rejestrowanego sygnału (ok. 22 ms) przy dużej oporności ośrodka (100

Ω

m)

uzyskuje się większy zasięg głębokościowy (1050 metrów wobec 480 metrów, patrz tabele

27-28). Dla niewielkich pętli nadawczych (

2

10

10

m

×

i

2

20

20

m

×

) maksymalne rejestrowane

czasy mogą wynieść od kilku do kilkudziesięciu ms, a zasięgi głębokościowe od ok.

kilkudziesięciu metrów do ponad 500 metrów w zależności od oporności ośrodka, mocy

ź

ródła i poziomu zakłóceń (tabele 1-12).

Są to typowe przedziały penetracji dla metody TDEM. Oczywiście dla większych pętli

nadawczych można uzyskać większe zasięgi głębokościowe np. dla pętli nadawczej o

rozmiarach

2

500

500

m

×

(to największe jakie się stosuje) dla średniego poziomu zakłóceń

(

2

9

/

10

m

V

−

) zasięg głębokościowy może przekroczyć dla dużych oporności nawet 2000

metrów, a dla dużej mocy osiąga wartość ok. 1000 metrów (tabele 31 i 32). Jak wcześniej

wspomniano dla specjalnych źródeł i układów pomiarowych (z dużym offsetem) można

osiągnąć dużo większy zasięg głębokościowy, nawet do 10000 metrów (Keller et al., 1984).

19

Tabela 31. Czas ostatniego rejestrowanego sygnału dla

9

10

−

=

Nm

[V/m

2

] oraz dla

rozmiaru pętli nadawczej

500

500

×

m

(w milisekundach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

25

5

⋅

×

345,65

199,47

131,60

86,82

50,10

33,06

4

10

25

10

⋅

×

456,09

263,20

173,65

114,57

66,11

43,62

4

10

25

20

⋅

×

*

601,82

347,30

229,13

151,17

87,24

57,56

4

10

25

40

⋅

×

*

794,10

458,26

302,34

199,47

115,11

75,94

4

10

25

50

⋅

×

868,24

501,05

330,57

218,09

125,86

83,03

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

Tabela 32. Zasięg głębokościowy (D) dla

9

10

−

=

Nm

[V/m

2

] oraz dla rozmiaru pętli

nadawczej

500

500

×

m

(w metrach)

oporność

a

ρ

[ ]

m

Ω

t

M

[Am

2

]

2

5

10

20

50

100

4

10

25

5

⋅

×

587,92

706,17

811,18

931,80

1119,20

1285,63

4

10

25

10

⋅

×

675,35

811,18

931,80

1070,35

1285,63

1476,80

4

10

25

20

⋅

×

*

775,77

931,80

1070,35

1229,51

1476,80

1696,39

4

10

25

40

⋅

×

*

891,13

1070,35

1229,51

1412,34

1696,39

1948,64

4

10

25

50

⋅

×

931,80

1119,20

1285,63

1476,80

1773,82

2037,58

(*) – 20, 40 [Amperów] – dla aparatury V8 (Phoenix)

20

2. Technika i metodyka pomiarów

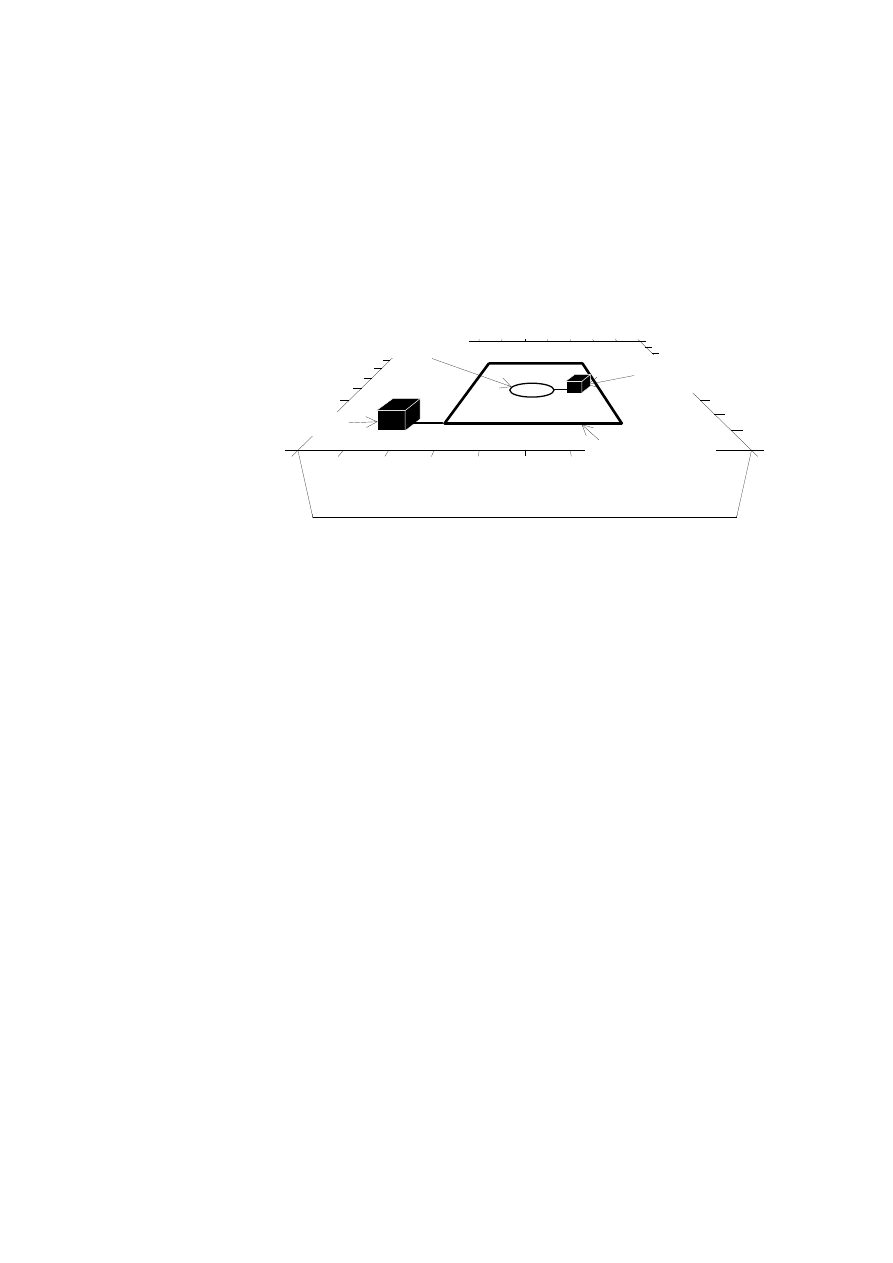
Typowy system pomiarowy dla metody TDEM składa się z nadajnika (transmitter-Tx)

i zwykle kwadratowej pętli nadawczej wykonanej z przewodnika umieszczonego na

powierzchni

ziemi,

odbiornika

(receiver-Rx)

i

zwykle

cewki

odbiornika

(rys. 4).

Cewka odbiornika
(Receiver Coil)

Odbiornik
(Receiver)

P

ę

tla nadawcza

(Transmitter loop)

Nadajnik
(Transmitter)

Rys. 4. Typowy układ pomiarowy dla metody TDEM

Rozmiar pętli nadawczej jest uzależniony od potrzebnej głębokości penetracji. Dla

płytkiego zasięgu głębokościowego (mniej niż 40 metrów) rozmiar pętli (boku kwadratu)

wynosi zwykle od 5 do 10 metrów. Dla niewielkich pętli nadawczych (krótkie pętle, small

loop), o rozmiarach np. 10, 20, 40 m, z układem centralnym (central loop, patrz rys. 6)

głębokość badań może osiągnąć od 4 do 5 krotności średnicy pętli nadawczej. Dla głębokości

penetracji do 1000 m i więcej konieczne jest stosowanie pętli nadawczej o rozmiarach do

kilkuset metrów (długie pętle, long loop), np. 300 m, a nawet 500 metrów. W celu

osiągnięcia dużego zasięgu (do 10 km) konieczne jest stosowanie układu z odsunięciem pętli

nadawczej od cewki pomiarowej (offset loop) nawet do kilkudziesięciu km, ze źródłem o

momencie ok. miliona Amper na metr i więcej (Keller G.V. et al., 1984).

Odbiornikiem w metodzie TDEM jest wielozwojowa cewka zlokalizowana na

powierzchni ziemi zwykle w środku pętli nadawczej (central loop). W takim przypadku, gdy

wyznaczamy krzywą oporności pozornej w funkcji czasu (t), czyli krzywą sondowania, to

punkt pomiarowy znajduje się w punkcie centralnym pętli nadawczej.

Napięcie cewki odbiorczej ma przebieg przedstawiony na rys. 5.

21

T/4

T/4

T/4

T/4

N

a

p

i

ę

c

ie

o

d

b

io

rn

ik

a

T/4

T/4

T/4

T/4

P

r

ą

d

p

ę

tl

i

n

a

d

a

w

c

z

e

j

T/4

T/4

czas

czas

Rys. 5. Postać napięcia cewki odbiorczej

Układy pomiarowe stosowane w metodzie TDEM to układy dla których uzyskuje się:

I. Pojedyncze krzywe sondowań TDEM (vertical sounding array) (Kenneth L. Zonge, 1992)

(mierzona jest tutaj składowa

z

H

):

1. cewka pomiarowa znajduje się w środku pętli nadawczej (central-loop/in loop):

Cewka odbiornika

Odbiornik

P

ę

tla nadajnkia

Nadajnik

Tx

Rx

Rys. 6. Układ pomiarowy w metodzie TDEM z cewką odbiornika znajdującą się w środku
pętli nadawczej

2. jako nadajnika i odbiornika używa się tej samej pętli (zwykle długiej: 100 – 300 metrów)

(central loop/single loop):

Odbiornik

P

ę

tla nadajnkia

i odbiornika

Nadajnik

Tx

Rx

Rys. 7. Układ pomiarowy w metodzie TDEM ze wspólną pętlą odbiornika i pętlą nadajnika

3. odbiornik i nadajnik to różne pętle przesunięte względem siebie na powierzchni ziemi

(loop-offset). Zwykle odległość między odbiornikiem i nadajnikiem jest niewielka i wynosi

kilkadziesiąt metrów do kilometra (small offset):

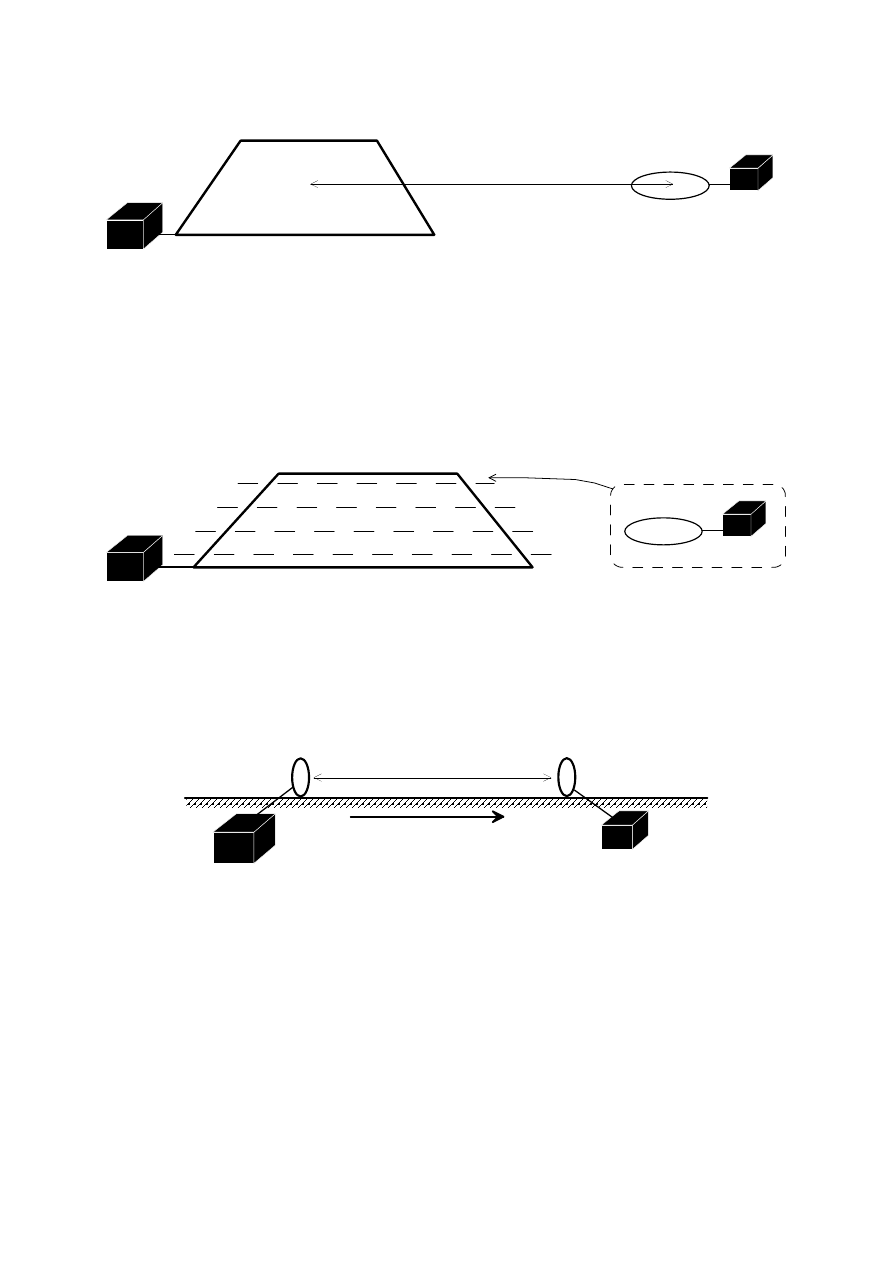
22

P

ę

tla nadajnkia

Nadajnik

Tx

Cewka odbiornika

Odbiornik

Rx

Odległo

ść

pomi

ę

dzy

p

ę

tl

ą

nadajnika i cewk

ą

odbiornika

Rys. 8. Układ pomiarowy w metodzie TDEM z odbiornikiem i nadajnikiem przesuniętych
względem siebie

II. Druga wersja układów to układy profilowe (profilling arrays) (Kenneth L. Zonge, 1992):

1. długa pętla nadawcza (nieruchoma) i cewka odbiorcza poruszająca się wzdłuż profilu

prostopadłego do jednego ramienia pętli nadawczej (fixed-loop) (mierzona składowa

z

H

):

Nieruchoma p

ę

tla nadawcza

Nadajnik

Tx

Cewka odbiornika

Odbiornik

Rx

profile poprzeczne

Ruchomy odbiornik

Rys. 9. Układ pomiarowy profilowy w metodzie TDEM z odbiornikiem ruchomym i
nadajnikiem nieruchomym przesuniętych względem siebie

2. cewka nadawcza i odbiorcza o podobnych rozmiarach poruszają się w pewnej odległości

wzdłuż profilu (mierzona składowa

z

H

):

Nadajnik

Tx

Cewka
odbiornika

Odbiornik

Rx

Kierunek profilu

Cewka

nadajnika

Stała odległo

ść

pomi

ę

dzy

nadajnikiem i odbiornikiem

Rys. 10. Układ pomiarowy profilowy w metodzie TDEM z ruchomym odbiornikiem i

nadajnikiem przesuniętych względem siebie ze stałą odległością

3. LOTDEM (long offset TDEM) z dużą odległością pomiędzy pętlą nadawczą a cewką

odbiorczą (rzędu km i kilkudziesięciu km). Pętla nadawcza ma zwykle duże rozmiary (np.

100 metrów i więcej). Mierzy się tutaj składowe

x

H ,

y

H i

z

H

i uzyskuje obraz 3-D na

pewnej głębokości. Duże odległości pomiędzy nadajnikiem i odbiornikiem stosowane są w

bardzo głębokich badaniach (Keller G.V. et al., 1984).

23

Najczęściej stosowane układy pomiarowe w metodzie procesów przejściowych to

układy dla których uzyskuje się pojedyncze krzywe sondowań. Są to układy z cewką

odbiornika znajdującą się w pętli nadawczej lub z odbiornikiem i nadajnikiem nieznacznie

przesuniętych względem siebie.

Pomimo niedużych odległości nadajnik – odbiornik (a nawet „zerowych” w przypadku

układu central loop) metoda TDEM pozwala na osiągnięcie zasięgu głębokościowego do

kilkuset a nawet tysięcy metrów. Jest tutaj wykorzystana właściwość pola magnetycznego

ź

ródła impulsowego, gdzie zmiany czasowe pionowej składowej wektora indukcji

magnetycznej w strefie bliskiej nie zależą od odległości nadajnik – odbiornik (Klityński,

Miecznik, 1998). Taka właściwość pola nie występuje ani w metodzie elektrooporowej, gdzie

rozstaw układu pomiarowego musi być wielokrotnie większy od głębokości penetracji ani w

metodach elektromagnetycznych w domenie częstotliwości, gdzie odległość nadajnik

odbiornik dla takich zasięgów głębokościowych musi być znaczna. Realizacja sondowań

metodą procesów przejściowych w strefie bliskiej oprócz udogodnień metodycznych daje

istotną korzyść natury interpretacyjnej. Na wartość amplitudy pola elektromagnetycznego w

strefie bliskiej w niewielkim stopniu wpływają boczne – w stosunku do punktu centralnego

układu pomiarowego – niejednorodności badanego ośrodka, co istotnie wpływa na wysoką

dokładność interpretacji krzywych sondowań TDEM (jest to najczęściej interpretacja 1D).

Często jednak wpływy boczne (ośrodek 2D/3D), zjawisko IP czy zjawisko

superparamagnetyzmu powodują zakłócenia krzywych dla układu centralnego i

niejednoznaczności interpretacji 1D danych TDEM. Wówczas stosuje się specjalną metodykę

pomiarową w której wykorzystuje się układy central loop i offset loop jednocześnie .

3. Przetwarzanie danych

Dane zapisywane i przechowywane są w postaci ciągu danych cyfrowych jako rezultat

próbkowania odbiornika układu pomiarowego. Typowe dane mogą zawierać 250-1000

próbek sekundę (Keller, G.V.,1997).

Odbiornik zawiera kilkadziesiąt wąskich bramek pomiarowych (najczęściej 20) na których

mierzona jest amplituda malejącego napięcia na kolejno następujących po sobie bramkach

czasowych (rys. 11).

24

czas

1 2 3 4 5 6

19 20

Rys. 11. Napięcie odbiornika w bramkach czasowych

Bramki czasowe w czasie pomiaru różnią się w celu minimalizacji zakłóceń pomiarowych.

Dla ograniczenia zakłóceń w pomiarach początkowa bramka jest wąska czyli w miejscu w

którym napięcie zmienia się gwałtownie. Później, gdy amplituda niewiele się zmienia bramka

się poszerza.

Okres prądu dla pętli nadawczej wynosi zwykle ok. 1 ms albo mniej. W takim

przypadku kilkusekundowy pomiar może wygenerować tysiące sygnałów przejściowych. Im

dłuższy czas pomiaru tym bardziej poprawia stosunek sygnału do zakłóceń. Jeden impuls nie

da wystarczająco dużo informacji, a wiele impulsów pozwala uzyskać krzywą sondowania

TDEM. Processing zwykle zawiera następujące procedury: dekonwolucji sygnału odbiornika,

tłumienia zakłóceń i normalizacji związanej z geometrią układu. Czasami impulsowe

zakłócenia losowe stanowią duży problem. Takie zakłócenia są ograniczane przy

wykorzystaniu tzw. przetwarzania typu robust. Najważniejszym elementem przetwarzania

danych w metodzie TDEM jest eliminacja zakłóceń przemysłowych. Wykonuje się to m.in.

przez „składanie” kolejnych porcji danych. W rezultacie amplitudy sygnałów użytecznych są

podwójnie wzmacniane, a amplitudy zakłóceń są redukowane. Elementem przetwarzania jest

również zastosowanie filtru dolnoprzepustowego celem uniknięcia zjawiska aliasingu.

Ponieważ system przetwarzania nie jest perfekcyjny używana jest dekonwolucja. Tutaj

najważniejszą rolę odgrywa tzw. „bootstrapping”, gdzie sygnał użyteczny jest oddzielany od

sygnału zakłócającego.

Rejestrowany sygnał zależy nie tylko od rozkładu oporności w Ziemi ale także od geometrii

układu pomiarowego, mocy źródła i czułości odbiornika. Ta zależność jest eliminowana przez

normalizację sygnału na punkcie polowym sygnałem referencyjnym, który kompensuje w.w.

zależności.

W metodzie TDEM wielkością liczoną i interpretowaną podobnie jak w innych metodach

geoelektrycznych jest oporność pozorna

[ ]

m

a

Ω

ρ

. Krzywa sondowania to oporność pozorna

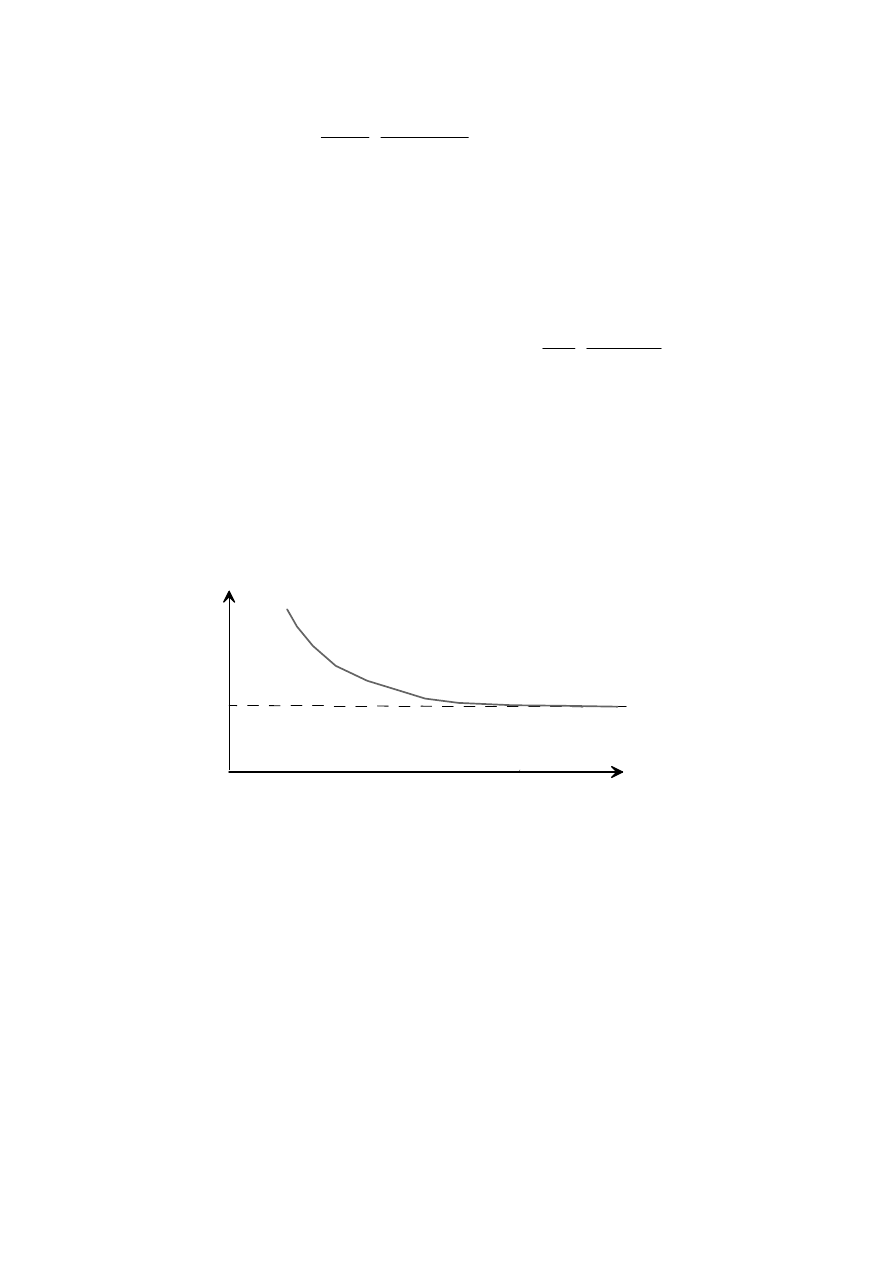
25

w funkcji czasu

( )

t

a

ρ

:

(

)

3

/

2

/

4

.

0

4













⋅

⋅

⋅

⋅

⋅

=

dt

dB

t

M

t

z

t

o

o

a

µ

π

µ

ρ

, gdzie t – czas pomiaru, mierzony od

czasu wyłączenia pola podstawowego,

t

M - moment nadajnika (powierzchnia pętli –

L

2

[m

2

] pomnożona przez wartość prądu – I [A]) i

dt

dB

z

/

- zmiana w czasie pionowej

składowej pola magnetycznego (Kauffman and Keller, 1983). Tak więc mierzona jest

składowa pionowa pola magnetycznego (

z

H

).

Oporność pozorną praktycznie liczy się z wzoru:

3

/

5

3

/

2

/

5

2

4

−

⋅













⋅

⋅

⋅

⋅

=

t

S

U

M

r

t

o

o

a

µ

π

µ

ρ

, gdzie

[ ]

V

U

to napięcie rejestratora,

r

S

- efektywna powierzchnia cewki rejestratora

[ ]

2

m

.

Dla modelu warstwowanego (1D) i dwuwarstwowego, gdy oporności warstw wynoszą

1

ρ

i

2

ρ

, a miąższość pierwszej warstwy wynosi h dla wczesnego czasu (krótkie czasy) krzywa

sondowania wyglądają jak niżej (rys. 12).

log10 (t-czas)

ρ

ρ ρ

log10 ( (t))

ρ

a

1

1

2

>

gał

ąź

opadaj

ą

ca

Rys. 12. Krzywa sondowania w metodzie TDEM dla modelu 1D dwuwarstwowego, gdzie

1

ρ

i

2

ρ

to odpowiednio oporności pierwszej i drugiej warstwy dla wczesnego czasu

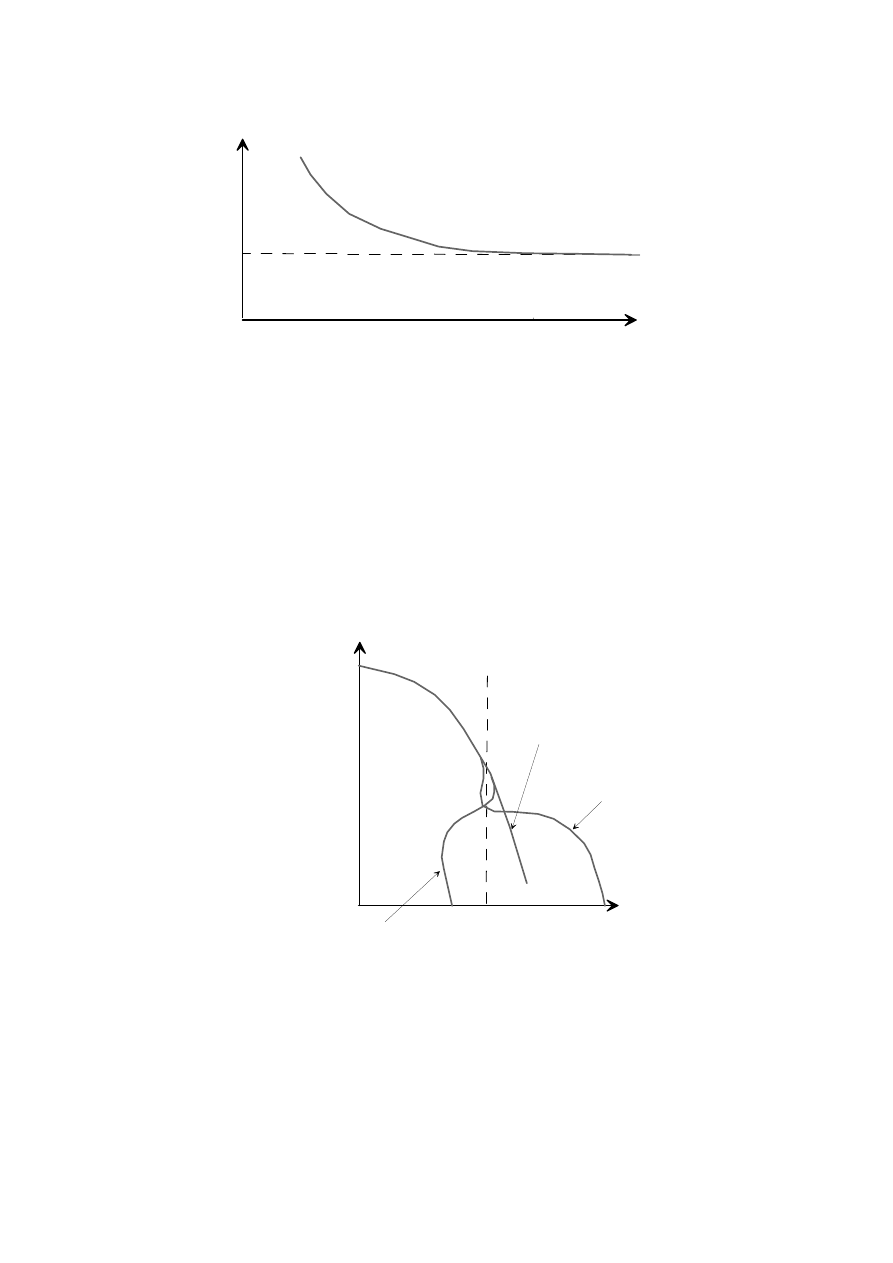
Jak widać występuje tzw. gałąź opadająca nie związana z żadną warstwą. Krzywa ta jest

identyczna jak dla modelu jednorodnej półprzestrzeni o oporności

ρ

(patrz rysunek 13).

26

log10 (t-czas)

ρ

log10 ( (t))

ρ

a

gał

ąź

opadaj

ą

ca

Rys. 13. Krzywa sondowania w metodzie TDEM dla modelu jednorodnej półprzestrzeni o
oporności

ρ

Dla odpowiednio długiego czasu rejestracji (

*

t

t

>

), dla modelu dwuwarstwowego, gdy

1

2

ρ

ρ

>

mierzone napięcie odbiornika będzie mniejsze niż powinno być dla modelu

półprzestrzeni o oporności

1

ρ

(patrz rysunek 14a). W przypadku gdy

1

2

ρ

ρ

<

w

późniejszym czasie (

*

t

t

>

) mierzone napięcie odbiornika będzie większe niż powinno być

dla modelu półprzestrzeni o oporności

1

ρ

(patrz rysunek 14b).

log10 (t-czas)

lo

g

1

0

(

n

a

p

i

ę

c

ie

o

d

b

io

rn

ik

a

)

(t=t*)

log10 ( (t))

model
półprzestrzeni
o oporno

ś

ci:

model
dwuwarstwowy:

model
dwuwarstwowy:

ρ

ρ ρ

1

2

1

>

ρ ρ

2

1

<

ρ

a

a)

b)

Rys. 14. Napięcie odbiornika dla modelów: półprzestrzeni i dwuwarstwowego 1D dla
metody TDEM

Gdy czas rejestracji przekroczy wartość t

*

to krzywe sondowań TDEM dla modelu

dwuwarstwowego wyglądają jak niżej (rys. 15).

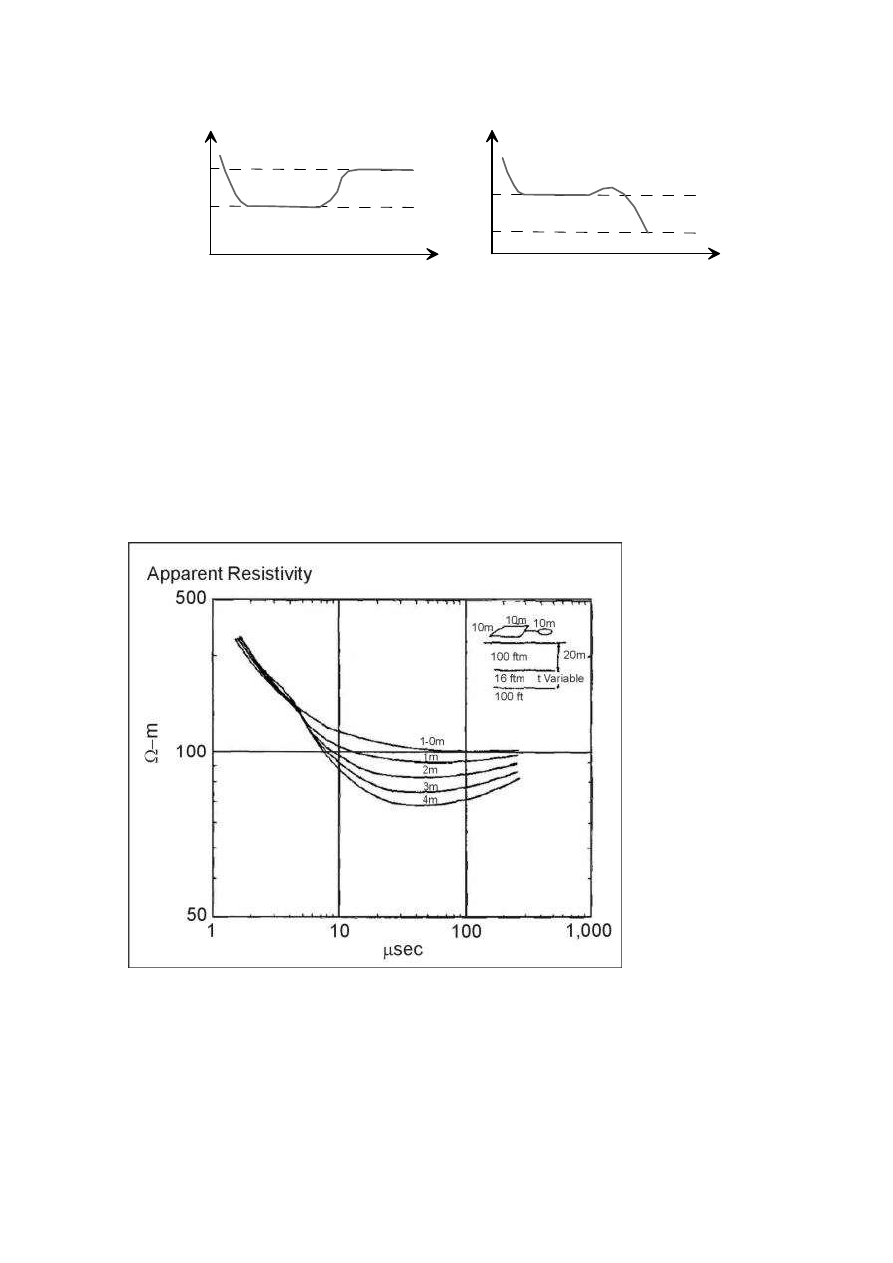
27

log10 (t-czas)

ρ ρ

log10 ( (t))

ρ

a

1

2

>

ρ

1

ρ

2

log10 (t-czas)

ρ ρ

log10 ( (t))

ρ

a

1

2

<

ρ

2

ρ

1

Rys. 15. Krzywe sondowań w metodzie TDEM dla modelu dwuwarstwowego (1D), gdzie

1

ρ

i

2

ρ

to odpowiednio oporności pierwszej i drugiej warstwy

Podsumowując, dla zbyt krótkich czasów rejestracji otrzymujemy krzywą jak dla modelu

półprzestrzeni o oporności

1

ρ

. Aby otrzymać pełną krzywą czas rejestracji musi przekroczyć

wartość graniczną (t>t

*

).

Krzywe sondowań TDEM w zależności od zastosowanego układu pomiarowego (np. central

loop, offset loop) różnią się między sobą np. dla modelu trójwarstwowego wyglądają:

Rys. 16. Krzywe sondowań w metodzie TDEM dla modelu 1D trójwarstwowego (układ
pomiarowy offset loop)

28

1

10

100

1000

µ

sec

100

500

50

Ω

-m

1-0m
1m
2m
3m
4m

10m

10m

10m

100 ftm

16 ftm

100 ftm

20m

t Variable

Rys. 17. Krzywe sondowań w metodzie TDEM dla modelu 1D trójwarstwowego: a -układ

pomiarowy central loop, b – układ pomiarowy offset loop

4. Interpretacja w metodzie TDEM

Zasięg głębokościowy metody TDEM zależy od czasu rejestracji ( t ). Maksymalna

głębokość badań jest jednak określona przez maksymalny czas dla którego jest możliwe

zarejestrowanie napięcia

)

(t

U

. W metodzie TDEM praktycznie niemożliwe jest wydzielenie

warstw o bardzo wysokiej oporności, metoda jest natomiast bardzo efektywna dla warstw o

dobrej przewodności (Giovanni Barrocu & Gaetano Ranieri, 2000). Rozdzielczość metody

TDEM w dużej mierze zależy od rozmiaru pętli nadawczej. Dla bardzo małej pętli (10-15 m)

możliwe jest wydzielenie płytkich warstw o niskich opornościach. Gdy konieczne jest

zapewnienie dużego zasięgu głębokościowego konieczne jest użycie pętli nadawczej dużych

rozmiarów. Wówczas jednak utrudnione jest wydzielenie struktur w płytkich warstwach.

Najbardziej efektywny przedział oporności dla metody TDEM to oporność od niskich

wartości (poniżej 1

Ω

m ) do kilkuset

Ω

m. Miąższość wydzielanych warstw możliwa do

interpretacji dla pętli nadawczej o rozmiarze L wynosi:

10

/

min

L

h

>

a

L

h

3

max

<

(Giovanni

Barrocu & Gaetano Ranieri, 2000).

29

Główną procedurą interpretacyjną stosowaną w metodzie TDEM jest wykorzystanie

algorytmu inwersji przy założeniu modelu jednowymiarowego (1D). Hipotetyczny model 1D

jest konstruowany w procesie interpretacji i dalej liczone są krzywe sondowań TDEM (

( )

t

a

ρ

)

odpowiadające temu modelowi. Model jest zmieniany dopóki nie uzyska się zgodności

danych obserwowanych i teoretycznych (odpowiadających modelowi) z pewną dokładnością.

Zgodność krzywej teoretycznej i polowej uzyskuje się stosując procedury inwersji 1D.

Poniższy rysunek przedstawia przykład inwersji 1D krzywej sondowania TDEM (Rowland

B., 2002).

Rys. 18. Wynik interpretacji 1D danych TDEM (sondowanie TDEM i model geoelektryczny
wynikowy)

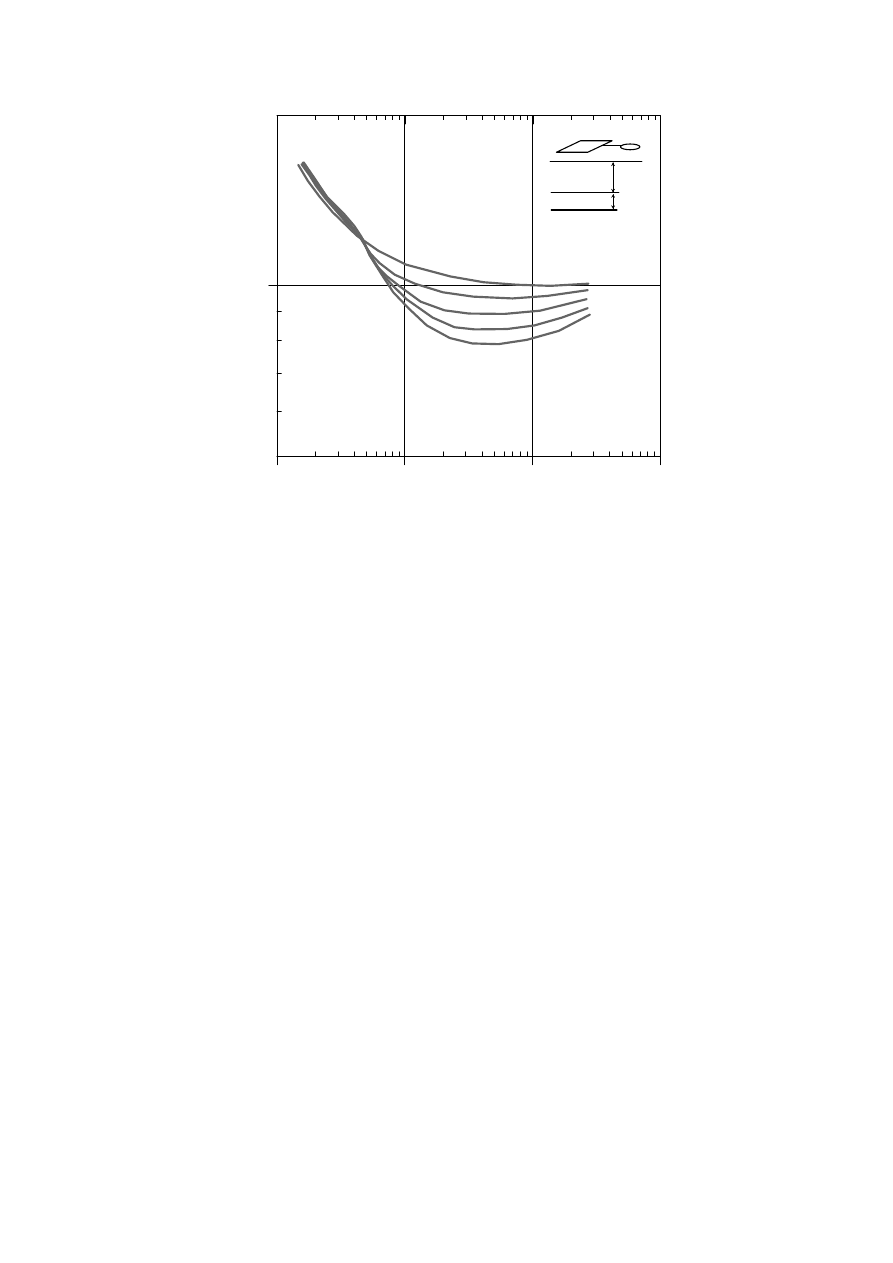
Krzywa oporności pozornej prezentuje model 1D czterowarstwowy. Jak widać gałąź

krzywej

odpowiadająca

krótkiemu

czasowi

rejestracji

jest

gałęzią

opadającą

charakterystyczną dla metody TDEM i nie odpowiadającą żadnej warstwie w modelu 1D.

Oporność pozorna podobnie jak w innych metodach geoelektrycznych nie jest

opornością rzeczywistą. Jest równa oporności właściwej tylko dla modelu jednorodnej

półprzestrzeni. Dla modelu warstwowanego jest złożoną funkcją, która podobnie jak w innych

metodach geoelektrycznych podlega zjawisku ekwiwalencji czyli przypadku w którym dwa

30

lub więcej modeli może generować podobne albo identyczne (w granicach błędu

pomiarowego) krzywe sondowań. W modelu interpretacyjnym 1D (co najmniej 3

warstwowym) dla cienkiej warstwy (środkowej) możemy zwiększać miąższość warstwy i

zmniejszać przewodność i uzyskać równie dobre dopasowanie krzywej teoretycznej i krzywej

polowej. To często wywołuje błędy interpretacyjne. Gdy warstwa geoelektryczna badanego

ośrodka jest bardziej miąższa albo kontrast opornościowy duży to ekwiwalencja stanowi

mniejszy problem. Posiadanie dodatkowych informacji o miąższości lub oporności warstwy

ekwiwalentnej całkowicie eliminuje to zjawisko.

Ponieważ głównym modelem interpretacyjnym wykorzystywanym w metodzie

procesów przejściowych jest model 1D jednym z problemów interpretacji danych TDEM są

struktury geologiczne dwu- i trójwymiarowe (2D/3D). Wpływ trójwymiarowości przy

pomiarze układem central loop jest „uśredniany” istnieje jednak problem niejednoznaczności

interpretacji 1D (najczęściej stosowanej) przy wykorzystaniu układów z offsetem (czyli gdy

konieczne jest uzyskanie odpowiedniej rozdzielczości dla dużych głębokości). Aby uniknąć

wpływu modelu 2D/3D na niejednoznaczność interpretacji krzywych sondowań TDEM

należy odpowiednio lokalizować sondowanie (unikając wpływów bocznych) albo stosować

odpowiednią metodykę pomiarową i interpretacyjną – obok układu offset loop należy

stosować układ central loop (Krivochieva and Chouteou, 2001).

Zjawiskiem, które również wpływa na obniżenie efektywności pomiaru i interpretacji

danych TDEM jest zjawisko polaryzacji wzbudzonej (IP effect – Induction Polarization),

które szczególnie manifestuje się dla układu pomiarowego centralnego. Efekt IP zachodzi

przy występowaniu wysokooporowych przypowierzchniowych warstw przykrywających

warstwy o niższej oporności (Giovanni Barrocu & Gaetano Ranieni, 2000). Zjawisko to

wprowadza zaburzenie na krzywej

( )

t

a

ρ

i stwarza duże problemy w interpretacji danych

TDEM (Descloitres et al., 2000). Zjawisko IP zaburza krzywe sondowań niejednokrotnie

uniemożliwiając efektywną interpretację 1D. Poprawę jednoznaczności interpretacji w takich

przypadkach można uzyskać stosując bardziej skomplikowaną konfigurację pomiaru, czyli

metodykę pomiarową opartą o różne układy pomiarowe – obok układu central loop należy

stosować układ offset loop (Descloitres et al., 2000, Krivochieva and Chouteou, 2001).

Wykonując pomiar i interpretację 1D dla obu układów pomiarowych można uzyskać lepszą

rozdzielczość parametrów uzyskanego modelu geoelektrycznego, ograniczenie wpływu

zakłóceń elektromagnetycznych oraz lepsze rozpoznanie strefy przypowierzchniowej co ma

istotne znaczenie w interpretacji danych TDEM. Obie konfiguracje dostarczają niezależną

31

informację o geologicznych strukturach. Dane uzyskane układem pomiarowym central loop

dostarczają bardziej rzetelną informację o płytkich warstwach, offset loop głębszych

warstwach. Na przykładzie badań w Meksyku prowadzonych w celu określenia warunków

hydrogeologicznych (Chalco-Sub-Basin), gdzie występuje ośrodek trójwymiarowy

(wywołany przez boczne struktury ”zaburzające” ośrodek 1D) prześledzono efektywność

wykorzystania obu układów pomiarowych (Krivochieva and Chouteou, 2001).

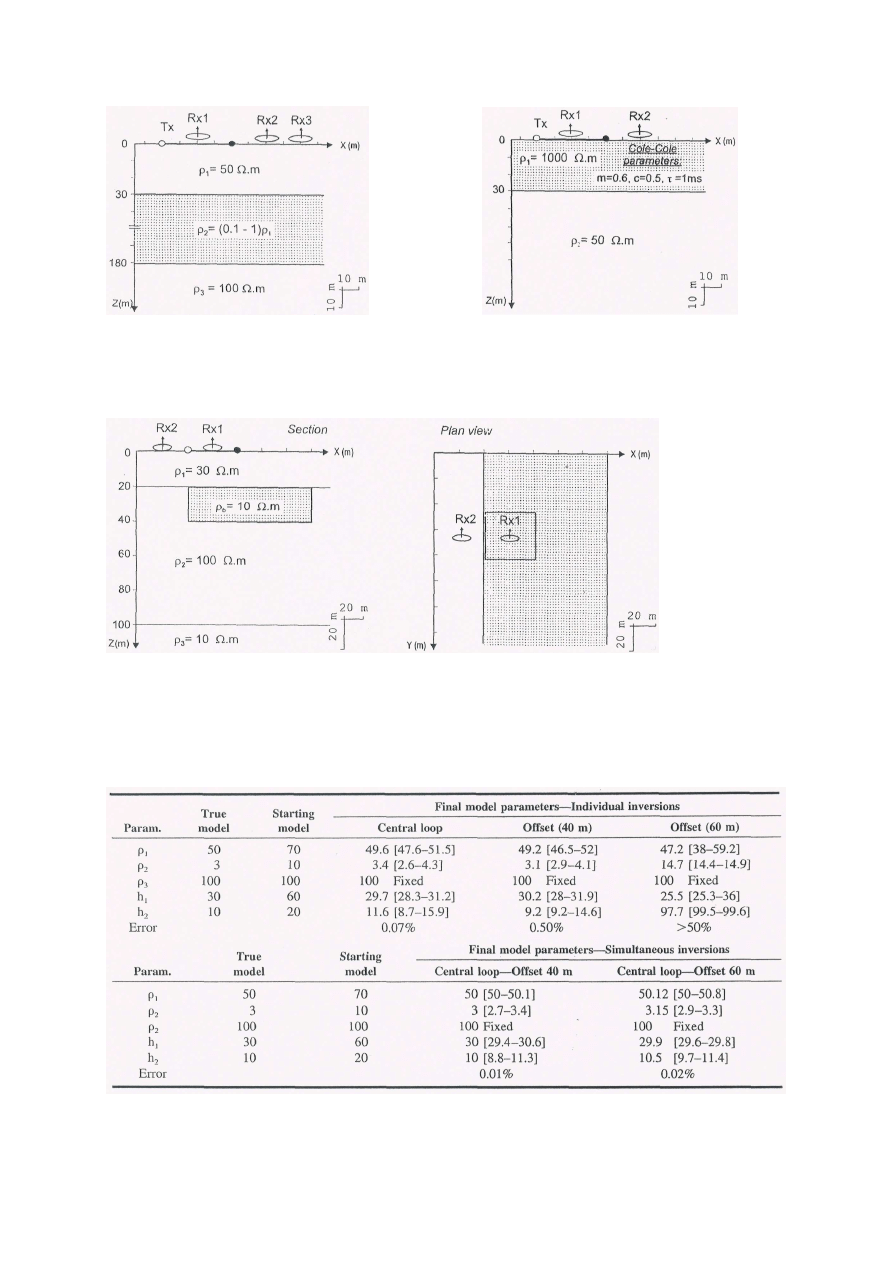
Doświadczenia wykazały, że interpretacja 1D jest bardziej właściwa (w ośrodku 2D/3D), gdy

poziom zakłóceń EM jest niewielki i zmiany oporności w kierunku poziomym niezbyt duże.

W wielu przypadkach układ central loop jest bardziej narażony na zakłócenia EM (zakłócenia

nadajnika, efekt IP, efekt namagnesowania).

W badaniach w Meksyku wykorzystano następującą konfigurację układu pomiarowego:

1.

)

(

)

(

2

2

1

1

c

Rx

c

Rx

−

- oba układy central loop, 2.

)

(

)

(

1

1

2

2

off

Rx

c

Rx

−

- jeden układ central

loop, drugi offset loop, 3.

)

(

)

(

1

1

1

1

off

Rx

c

Rx

−

- central loop i offset loop itd. (Rys. 19).

Tx

1

Tx

2

Tx

3

Rx (c )

1

1

Rx (c )

2

Rx (c )

3

Rx (off )

1

Rx (off )

2

Rx (off )

3

linia profilu

Rys. 19. Konfiguracja składająca się z kombinacji układów central loop i offset loop

Wyniki interpretacji 1D danych syntetycznych dla poniżej opisanych modeli i dla

dwóch układów pomiarowych (Rys. 19) pokazały, że zastosowana metodyka pomiarowa

pozwoliła na znaczną poprawę rozdzielczości i zmniejszenie ekwiwalencji w interpretacji

danych TDEM. Wykonano modelowania dla typowych modelów symulujących ośrodek

hydrogeologiczny (Krivochieva and Chouteou, 2001).

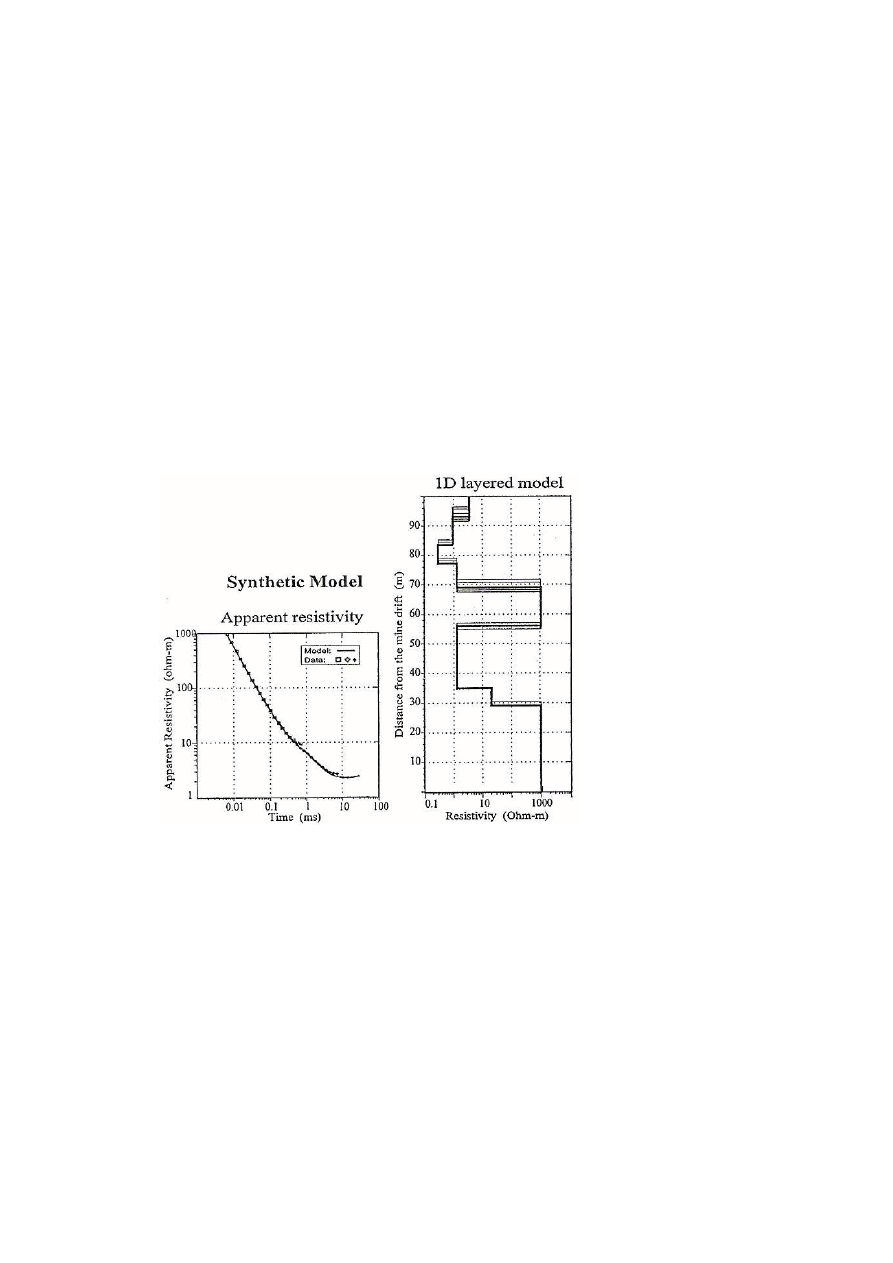
Model A to model ośrodka 3-warstwowego ze zmienną opornością drugiej warstwy (warstwa

niskooporowa,

rys.

20).

Model

B

to

dwuwarstwowy

ośrodek

zawierający

przypowierzchniową warstwę wysokooporową będącą źródłem efektu polaryzacji

wzbudzonej (IP) zalegającą na warstwie niepolaryzującej (rys. 21). Model C zawiera

strukturę 3D umieszczoną w warstwowanym ośrodku (rys. 22).

32

Rys. 20 Model A

Rys. 21 Model B

Rys. 22 Model C

Dla danych syntetycznych odpowiadających modelowi A wykonana została interpretacja 1D

przy wykorzystaniu układu central loop i offset loop (tabela 33).

Tabela 33. Rezultaty jednoczesnej inwersji 1D dla układu central loop i offset loop dla

modelu A (rys. 20)

33

Wyniki interpretacji dla układu central loop wskazują na dobrą dokładność tej interpretacji

dla pierwszej warstwy. Wyinterpretowane oporność i miąższość dla drugiej warstwy są lekko

zawyżone. Dla układu pomiarowego z offsetem 40 metrów otrzymano podobne wyniki

interpretacji, natomiast dla układu z większym offsetem (60 m) oporność wyinterpretowana

drugiej warstwy jest bardzo zawyżona i zmienia się pomiędzy 14.4 a 14.9

Ω

m (podczas gdy

oporność rzeczywista ma wartość 3

Ω

m, rys. 20). Bardzo dobre rezultaty wyników

interpretacji uzyskuje się przy wykorzystaniu kombinacji układów pomiarowych central loop

i offset loop niezależnie od wielkości offsetu (40 i 60 metrów, tabela 33).

Dla modelu B, gdzie pierwsza warstwa jest b. wysokooporowa mamy do czynienia z efektem

IP. W tym przypadku wyniki interpretacji dla układów z offsetem są dużo bliższe modelowi

rzeczywistemu niż dla układu central loop (tabela 34). Dla tego układu wyinterpretowana

miąższość pierwszej warstwy jest zaniżona a oporność tej warstwy traktowana jako oporność

izolatora. Również wyinterpretowana oporność drugiej warstwy jest bardzo zawyżona (tabela

34).

Tabela 34. Rezultaty jednoczesnej inwersji 1D dla układu central loop i offset loop dla

modelu B (rys. 21)

Dla modelu C (rys. 22) gdzie mamy do czynienia ze strukturami 2D/3D najlepsze rezultaty

interpretacji 1D uzyskuje się dla układu central loop (tabela 35). Tutaj układ z offsetem daje

dużo gorsze rezultaty. Z kolei kombinacja dwóch układów (central loop i offset loop) daje

wyniki zadowalające. Widać, że układ central loop jest najmniej podatny na wpływ struktur

2D/3D.

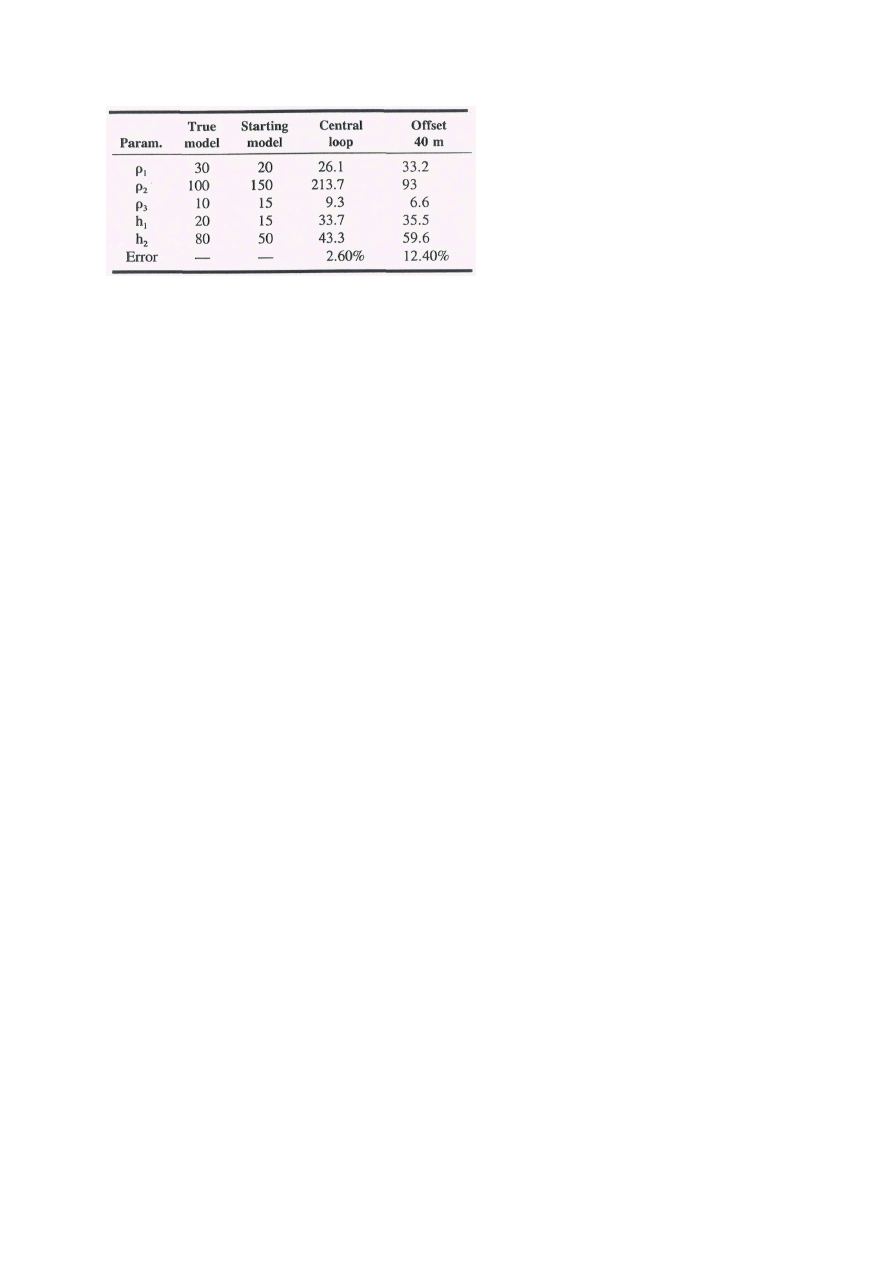
34

Tabela 35. Rezultaty jednoczesnej inwersji 1D dla układu central loop i offset loop dla

modelu C (rys. 22)

Analiza przykładów dla modeli A, B i C wskazuje, że oba układy użyte jednocześnie

pozwalają na bardziej efektywną interpretację dla modelu warstwowanego. Uzyskuje się

również lepszą rozdzielczość wyników interpretacji, redukcję efektu IP przy wykonywaniu

inwersji 1D jednocześnie dla układu central loop i offset loop a także redukcję efektu 2D/3D.

Jak widać kombinacja układów central loop i offset loop jest uniwersalna i taka metodyka

pomiarowa powinna być stosowana dla zapewnienia efektywności i odpowiedniej

rozdzielczości przy rozpoznawaniu zarówno głębokich jak i płytkich struktur (Krivochieva

and Chouteou, 2001).

5. Metoda procesów przejściowych w badaniach kompleksowych

Metoda TDEM to bardzo silne narzędzie służące rozpoznaniu środowiska

geoelektrycznego i może być efektywnie wykorzystywana w kompleksie z innymi metodami

elektromagnetycznymi. Ważne jest, że w tej metodzie eliminowanych jest wiele „zaburzeń”

występujących np. w metodzie MT, takich jak static shift (Jones, 1988) czy szerzej „galvanic

distortion” (Ledo et al., 2002). Dlatego metoda ta często jest używana jako metoda

towarzysząca metodzie MT w celu wprowadzenia poprawki na przesunięcie statyczne (Meju

M.A., 1996, 2002) i uzupełnienia metody MT np. dla zbadania płytkich struktur (Krivochieva

S., Chouteau M., 2003, Manzella A. et al., 2004).

Jednym z zastosowań metody TDEM jest jej wykorzystanie do rozpoznawania

ś

rodowiska hydrogeologicznego wraz z metodą magnetotelluryczną. Przykładem może być

wykorzystanie obu metod na przedmieściach miasta Meksyk (Krivochieva S., Chouteau M.,

2003). Celem badań było zapewnienie wody pitnej dla mieszkańców południowych

przedmieść miasta. Główne cele to: określenie geometrii formacji wodonośnej i określenie

35

przebiegu niżej leżących formacji. Zakres częstotliwości zastosowany w metodzie MT

wynosił od 300 Hz do 0,002 Hz. Metodą TDEM zostały wykonane płytkie badania (40*40,

rozmiar pętli nadawczej) i głębokie sondowania (100*100, rozmiar pętli nadawczej) w

zakresie

s

µ

88

do

ms

70

.

W badanym obszarze miały miejsce silne efekty galwaniczne zakłócające krzywe sondowań

MT. Zastosowana metoda TDEM umożliwiła analizę zjawiska „galvanic distortion” na tym

obszarze i wprowadzenie poprawki przy wykorzystaniu procedur dekompozycji. Dodatkowo

(oprócz zaburzeń galwanicznych) w badanym obszarze występuje zaburzenie danych MT w

przedziale częstotliwości 0,3 do 3 sekund - zaburzenie przez boczne struktury (anizotropia)

znajdujące się na głębokości 500 – 700 metrów. W rozpatrywanym obszarze metoda TDEM

pozwoliła na rozpoznanie trzech pierwszych warstw, co było niemożliwe w przypadku

metody MT. Pierwsza warstwa (miąższość:

m

50

26

−

) to piaskowce-ilaste o oporności

m

Ω

−

26

17

, druga warstwa to wysokooporowe bazalty (miąższość:

m

50

40

−

), trzecia

warstwa to gruba warstwa piaskowcowo-ilasta, poniżej są piaskowce (

m

600

400

−

,

m

Ω

−

30

6

) leżące na bazalcie spękanym ze słodką wodą a głębiej znajduje się

wysokooporowe podłoże. Wykonana została interpretacja 1D danych MT metodą OCCAMA

i inwersja 2D z uwzględnieniem wyników interpretacji danych TDEM dla pierwszych trzech

warstw z wprowadzeniem poprawki na zaburzenia galwaniczne. To umożliwiło efektywne

rozpoznanie i określenie geometrii ośrodka hydrogeologicznego i warstwy wodonośnej oraz

otaczającego środowiska geologicznego. Interpretacja danych MT i TDEM pozwoliła także

na wskazanie stref niskooporowych poniżej bazaltu (gdzie znajduje się warstwa ochronna

zasilona).

Metoda procesów przejściowych ma również zastosowanie w kompleksie z innymi

metodami geofizycznymi np. z metodą sejsmiczną. Przykładem takiego zastosowania jest

użycie obu metod w rozpoznaniu struktur rudnych węglanowo-potasowych w Ameryce

Północnej (Chouteau M. et al., 1997). Mamy tam do czynienia z sekwencją

płaskorównoległych warstw (model 1D) składających się z soli i anhydrytów zawierających

złoża węglanowo-potasowe. Obszar wydobycia znajduje się na głębokości 900-1100 metrów

przy czym pokłady mają grubość od

m

5

5

,

2

−

. Problemem jest tutaj oczywiście głębokość

złoża i jego mała miąższość, problemem górniczym jest również dopływ wody. Efektywność

rozpoznania ośrodka (w tym formacji wodonośnej) zapewniona została dzięki zastosowaniu

kompleksu metod sejsmicznych (sejsmika refrakcyjna i refleksyjna) jak i metod

elektromagnetycznych z których największą rolę odegrała metoda TDEM (w zakresie

36

czasowym od

ms

s

70

6

−

µ

). Metoda TDEM okazała się najlepsza ze względu na głębokość

penetracji i rozdzielczość pionową w rozpoznaniu środowiska hydrogeologicznego. Badania

wykonane zostały z chodnika zlokalizowanego powyżej badanego rejonu. Metoda TDEM

została zastosowana do kartowania formacji wodonośnej, która charakteryzuje się niską

opornością. Efektywność zastosowania metody TDEM (interpretacja 1D) okazała się wysoka

i formacja wodonośna o miąższości ok. m

5 i oporności poniżej

m

Ω

1

określona została w

odległości ok.

m

80

od chodnika. Badania w tym rejonie jak również w podobnym obszarze

górniczym w Brazylii wskazują, że przy zastosowaniu metody TDEM możliwe jest

osiągnięcie dużej rozdzielczości i przy niskiej oporności kompleksu wodonośnego możliwe

jest wykrycie tej warstwy o miąższości ok.

m

5

,

2

w odległości ok.

m

120 od chodnika.

Jak wcześniej wspomniano w Polsce na początku lat 90-tych poprzedniego wieku

zwrócono uwagę na możliwości zastosowania metody procesów przejściowych w kompleksie

z metodą elektrooporową przy monitorowaniu migracji zanieczyszczeń w warstwie

wodonośnej (Antoniuk et al., 1991). Wykazano wówczas, że metoda elektrooporowa daje

bardzo dobre rezultaty w sytuacji gdy warstwa wodonośna występuje we fragmencie K

przekroju geoelektrycznego jako warstwa środkowa. Kolektor nasycony wodą o naturalnej

mineralizacji zaznacza się na krzywych sondowań jako maksimum. Dopływ zanieczyszczeń i

zmniejszenie się oporności warstwy wodonośnej prowadzi najczęściej do zmiany sekwencji

oporności z typu K na Q lub H. W warunkach bardzo małej mineralizacji wody zaznacza się

przewaga metody elektrooporowej w rozpoznaniu tego ośrodka. W warunkach dużej

mineralizacji zaznacza się przewaga metody procesów przejściowych. Wynika to z tego, że w

takim przypadku rosną efekty indukcyjne na których bazuje ta metoda.

Literatura

Antoniuk J., Maćkowski T., Klityński W., 1991, Analiza rozdzielczości krzywych sondowań
elektrooporowych i procesów przejściowych w aspekcie monitorowania zanieczyszczeń wód
podziemnych, materiały konferencyjne, Jaworze, T.2 s.109-126.

Giovani Barrocu & Gaetano Ranieri, 2000, 16

th

Salt Water Intrusion Meeting, Międzyzdroje,

Poland,

12-15 June 2000.

Chauteau M., Philips G., Prugger A., 1997, Mapping and Monitoring Soft rock Mining,
Procedings of Exploration 97: Fourth Decennial International Conference on Mineral
Exploration, p. 927-940.

Chow-Son Chen and Shuhjong Tsao, 2001, Time-Domain Spectral IP and Its Applications in
the Southern Chinkuashih Area, Northern Taiwan, TAO, Vol. 12. No. 4, 483-586.

37

Descloitres M., Guerin R., Albobuy Y., Tabbagh A. and Ritz M., 2000, Improvement in
TDEM sounding interpretation of induced polarization. JA case study in resistive rocks of the
Fogo volcano, Cape Verde Islands, Journal of Applied Geophysics, Vol. 45, Issue 1, p. 1-18.

Jones, A., G., 1988. Static shift of magnetotelluric data and its removal in a sedimentary basin
environment, Geophysics, 53, 967-97.

Kauffman A.A. and Keller G.V., 1983, Frequency and Transient Soundings, Elsevier
Amsterdam, Methods in Geochemistry and Geophysics, No. 16, 685 p.

Keller G.V., Pritchard J.I., Jacobson J.J. and Harthill N., 1984, Megasource Time-domain
Electromagnetic Sounding Methods, Geophysics ol. 49, No. 7, p. 993-1009.

Keller G.V., 1997, Principles of time-domain electromagnetic (TDEM) sounding, The
Leading Edge, April 1997, v. 16 no. 4; p 355-357.

Klityński W., Miecznik J., 1998, Kartowanie podłoża wysokooporowego metodą procesów
przejściowych, Nafta – Gaz, nr 1/1998

Krivochieva S., Chouteau M., 2001, Improvement in 1D TDEM Interpretation by
Simultaneous Inversion of Data from Two Loop Configurations. JEEG, Vol. 6, Issue 1, pp.
19-32.

Krivochieva S., Chouteau M., 2003, Integrating TDEM and MT methods for characterization
and delineation of the Santa Catarina aquifer (Chalco sub-Basin, Mexico), Journal of Applied
Geophysics, Vol. 53, Issue 1, p. 23-43.

Ledo, J., P. Queralt, and J. Pous, 1998. Galvanic Distortion on magnetotelluric data over a
3-D regional structure Geophys. J. Int., 132, 295-301.

Manzella A., Volpi G., Zaja A., Meju M., 2004, Combined TEM-MT investigation of
shallow-depth resistivity structure of Mt Somma-Vesuvius, Journal of Volcanology and
Geothermalresearch 131, p. 19-32.

Meju M.A, 1996, Joint inversion of TDEM and distorted MT soundings: some effective
practical considerations, Geophysics, 61 91, p. 56-65.

Meju M.A, 2002, Geoelectromagnetic exploration for natural resources: models case studies
and Challenges. Surv. Geophysics, 23, p. 133-205.

Nagendra Pratap Singh and Toru Mogi, 2003, Effective skin depth of EM fields due to large
circular loop and electric dipole sources, Earth Planets Space, 55, 301-313.

Papadopoulos, P. Tsourlos, P. Karmis, G. Vargemeziz and G.N. Tsokas, 2004, A TDEM
survey to define local hydrogeological structure In Anthemountas Basin, N. Greece, Journal
of Balkani Geophysical Society, Vol. 7, No. 1, p. 1-11.

Parasnis , D.S., 1986, Principles of applied geophysics: Chapman and Hall, 402 p.

38

Kenneth L. Zonge, 1993, Introduction to TDEM, Practical Geophysics II, Northwest Mining
Association. Zonge Engineering and Mearch Organization Inc, USA.