**.Metoda identyfikacji metodą momentów dla dowolnego u(t)


Należy wyznaczyć

)

(t

g

na podstawie znajomości

)

(t

u

i

)

(t

y

.

Założenia:

-

sygnały

)

(t

u

i

)

(t

y

określone są na przedziale czasu [0-

T];

-

rozważania przeprowadza się dla

∞

→

T

-

dla uproszczenia doboru funkcji aproksymujących wprowadza się funkcję wagi

)

(t

w

Transformata sygnału wejściowego z wagą

)

(t

w

:

( )

( ) ( )

dt

e

t

u

t

w

s

U

st

w

−

∞

∫

=

0

(1)

Transformata sygnału wyjściowego z wagą

)

(t

w

:

( )

( ) ( )

dt

e

t

y

t

w

s

Y

st

w

−

∞

∫

=

0

(2)

Oraz transformata odpowiedzi impulsowej

)

(t

g

z wagą

)

(t

w

:

( )

( ) ( )

dt

e

t

g

t

w

s

G

st

w

−

∞

∫

=

0

(3)

Dla zerowych warunków początkowych:

( )

( ) ( )

s

U

s

G

s

Y

w

w

w

=

(4)

Podstawiamy (1),(2) i (3) do (4):

( ) ( )

( ) ( )

( ) ( )

dt

e

t

u

t

w

dt

e

t

g

t

w

dt

e

t

y

t

w

st

st

st

−

∞

−

∞

−

∞

∫

∫

∫

⋅

=

0

0

0

(5)

Rozwijając w szereg względem st funkcję

st

e

−

otrzymamy:

( )

( ) ( )

( )

( ) ( )

( )

( ) ( )

dt

t

u

t

w

s

m

t

-

dt

t

g

t

w

s

t

-

dt

t

y

t

w

s

n

t

-

m

m

m

m

n

n

n

n

!

1

!

1

!

1

0

0

0

0

0

0

∫ ∑

∫ ∑

∫ ∑

∞

∞

=

∞

∞

=

∞

∞

=













⋅













=













ν

ν

ν

ν

ν

(6)

Definiujemy teraz momenty w postaci:

( ) ( )

.

0,1,2,....

0

=

=

∫

∞

ν

µ

ν

ν

dt

t

g

t

w

t

(7)

( ) ( )

.

0,1,2,....

0

=

=

∫

∞

n

dt

t

y

t

w

t

a

n

n

(8)

( ) ( )

.

0,1,2,....

0

=

=

∫

∞

m

dt

t

u

t

w

t

b

m

m

(9)

Momenty (8) i (9) można obliczyć po wprowadzeniu stosownego w(t).
Uwzględniając (7),(8) i (9) w (6) mamy:

( )

( )

( )

∑

∑

∑

∞

=

∞

=

∞

=

⋅

=

0

0

0

!

1

!

1

!

1

m

m

m

m

n

n

n

n

s

m

b

-

s

-

s

n

a

-

ν

ν

ν

ν

ν

µ

(10)

( )

( )

∑

∑

∞

=

+

+

∞

=

=

0

,

0

!

1

!

1

m

m

m

m

n

n

n

n

s

b

-

s

n

a

-

ν

ν

ν

ν

ν

µ

(11)

podstawiając

n

m

=

+

ν

( )

( ) ( )

∑∑

∑

∞

=

∞

=

+

−

∞

=

−

=

0

0

0

!

!

1

!

1

n

m

n

n

n

n

n

n

s

n

b

-

s

n

a

-

ν

ν

ν

ν

ν

ν

µ

(12)

porównując współczynniki przy tych samych potęgach s :

( )

( ) ( )

∑

∞

=

−

−

=

0

!

!

1

!

1

ν

ν

ν

ν

ν

µ

n

b

-

n

a

-

n

n

n

n

(13)

ostatecznie:

,....

2

,

1

2

1

0

0

=

=













=

−

∞

=

∑

n

,....

,

,

ν

b

ν

n

a

n

n

ν

ν

ν

µ

(14)

Używając równanie (9) można obliczyć:

2

1

0

n

0

0

,....

,

,

b

b

ν

n

a

n

n

n

=













−

=

−

∞

=

∑

ν

ν

ν

µ

µ

(15)

Czyli na tym etapie w oparciu o obliczone wcześniej

ν

−

n

n

b

i

a

można wyliczyć

n

µ

.

Na obecnym etapie mamy policzone

n

µ

. Dalej zostanie przedstawione w jaki sposób w

oparciu o znajomość momentów

n

µ

można wyliczyć

)

(

~

oraz

)

(

~

s

G

t

g

będące aproksymacją

odpowiednio odpowiedzi impulsowej oraz transmitancji badanego obiektu.

Przy tej aproksymacji zadbamy o parę użytecznych szczegółów:
-aby funkcja aproksymująca

)

(

~ t

g

oraz aproksymowana

)

(t

g

miały te same momenty przy

wadze

)

(t

w

:

( ) ( )

n

dt

t

g

t

w

t

≤

≤

=

∫

∞

ν

µ

ν

ν

0

~

0

(16)

-aby funkcje tworzące bazę funkcji

( )

∑

=

=

n

i

i

i

t

C

t

g

0

)

(

~

ϕ

(17)

tworzyły ciąg funkcji ortonormalnych:

( ) ( ) ( )

∫

∞













=

≠

=

0

1

0

j

dla i

j

dla i

dt

t

w

t

t

j

i

ϕ

ϕ

(18)

-współczynniki

i

C należy tak dobrać aby osiągnąć minimum funkcjonału:

( ) ( ) ( )

[

]

dt

t

g

t

g

t

w

I

2

0

~

−

=

∫

∞

(19)

W tym celu wstawiamy do (19) (17) uwzględniając (18) otrzymujemy wyrażenia na

i

C po

Przyrównaniu

0

=

∂

∂

i

C

I

( ) ( ) ( )

.

,.........

2

,

1

,

0

0

=

=

∫

∞

i

dt

t

t

g

t

w

C

i

i

ϕ

(20)

Czyli na tym etapie identyfikacji należy:

Wyznaczyć współczynniki

Wyznaczyć współczynniki

Wyznaczyć współczynniki

Wyznaczyć współczynniki

i

C

dla wyliczonych momentów

dla wyliczonych momentów

dla wyliczonych momentów

dla wyliczonych momentów

ν

µ

dla wybranych

dla wybranych

dla wybranych

dla wybranych

( )

t

i

ϕ

i

i

i

i

( )

t

w

....

1.Aproksymacja wielomianami Laguerra.

Z definicji wielomiany te wyrażają się wzorem:

( )

( )

( ) ( )

[

]

t

i

i

i

t

i

i

e

t

t

d

d

e

i

t

L

t

!

α

α

α

α

α

ϕ

−

=

=

(21)

po różniczkowaniu:

( )

( )

( ) ( )

[

]

t

i

i

i

t

i

i

e

t

t

d

d

e

i

t

L

t

!

α

α

α

α

α

ϕ

−

=

=

(22)

( )

( )

(

)

( )

!

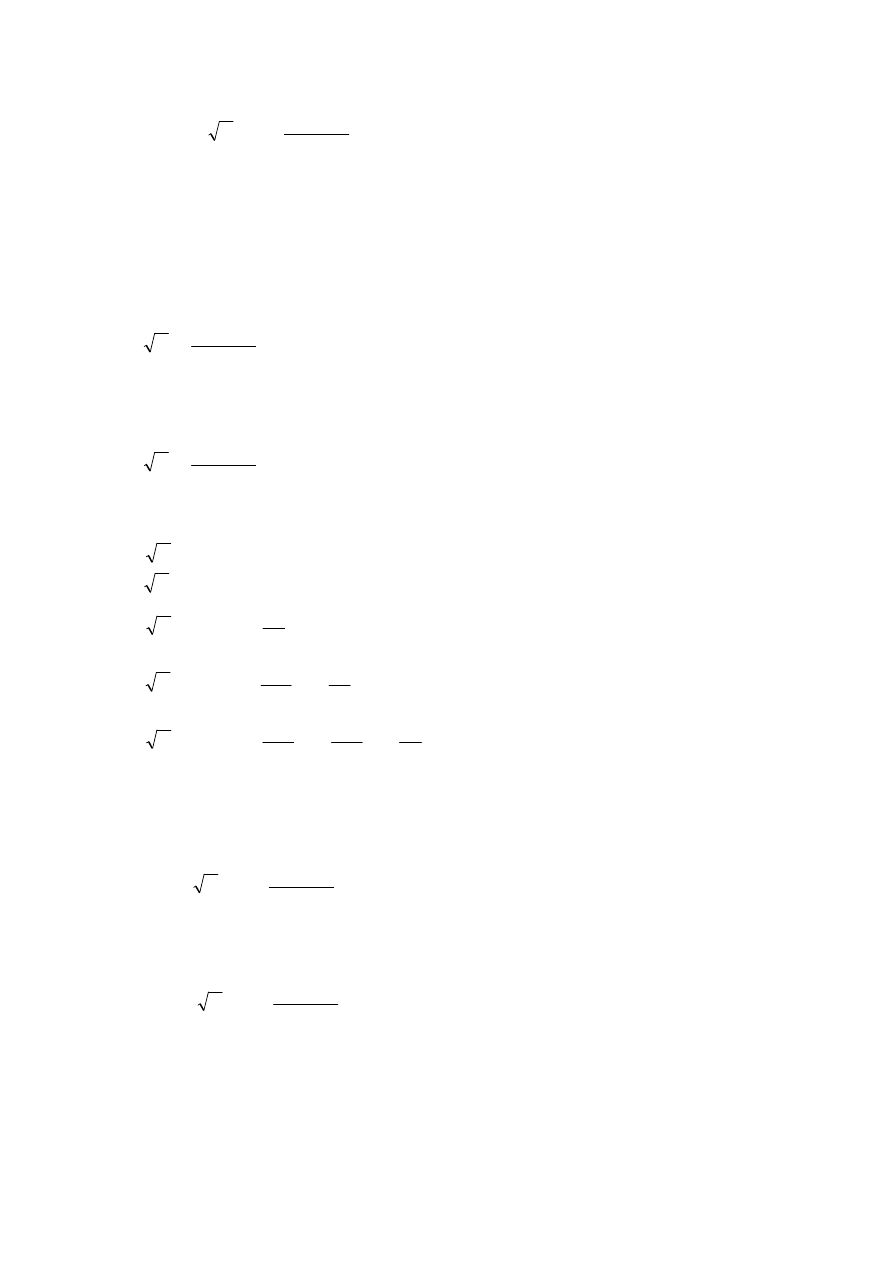
0

j

i

t

j

i

t

L

t

j

i

i

j

i

i

−

−













=

=

−

=

∑

α

α

ϕ

(23)

aby zachodziła ortonormalność funkcję wagi trzeba przyjąć

( )

t

w

w postaci:

( )

t

e

t

w

α

−

=

(24)

uwzględniając (23) w (20):

(

)

( )

( ) ( )

,....,n

,

i

dt

t

t

w

t

g

j

i

j

i

t

C

j

i

i

j

j

i

i

1

0

!

0

0

=













−

−

=

−

∞

=

−

∫

∑

α

α

(25)

podstawiając do (25) relację (7) otrzymujemy:

(

)

( )

,....,n

,

i

j

i

j

i

t

C

i

i

j

j

i

i

1

0

!

0

=













−

−

=

∑

=

−

µ

α

α

(30)

Z (30) możemy wyliczyć kolejne współczynniki

i

C kolejno jako:

C

0

0

µ

α

=

(

)

C

-

1

0

1

αµ

µ

α

=

C

!

2

2

-

2

2

1

0

2













+

=

µ

α

αµ

µ

α

C

!

3

!

2

3

3

-

3

3

2

2

1

0

3













−

+

=

µ

α

µ

α

αµ

µ

α

(31)

C

!

4

!

3

4

!

2

6

4

-

4

4

3

3

2

2

1

0

4













+

−

+

=

µ

α

µ

α

µ

α

αµ

µ

α

Dla tych zależności spełniony jest warunek

( ) ( )

t

g

t

g

~

≈

.

Łącząc wzory (17) i (30) oraz (31):

( )

(

)

( )

!

0

0

j

i

t

j

i

C

t

g

j

i

i

j

n

i

i

−

−













≈

−

=

=

∑

∑

α

α

(32)

Transmitancję określa zatem wzór:

( )

(

)

1

0

0

+

−













≈

−

−

=

=

∑

∑

j

i

j

i

i

j

n

i

i

s

t

j

i

C

s

G

α

α

(33)

2.Aproksymacja funkcjami Laguerra.

( )

( )

( ) ( )

[

]

t

i

i

i

t

i

i

e

t

t

d

d

e

i

t

L

t

2

!

α

α

α

α

α

ϕ

−

=

=

(34)

czyli:

( )

(

)

( )

!

0

2

j

i

t

j

i

e

t

j

i

i

j

t

i

−

−













=

−

=

−

∑

α

α

ϕ

α

(35)

( )

( )

( ) ( )

,....,n

,

i

dt

e

t

t

w

t

g

j

i

j

i

C

t

j

i

i

j

j

i

i

1

0

!

2

0

0

=













−

−

=

−

−

∞

=

−

∫

∑

α

α

α

(36)

( )

( )

,....,n

,

i

j

i

j

i

C

j

i

i

j

j

i

i

1

0

!

0

=













−

−

=

−

=

−

∑

µ

α

α

(37)

( )

(

)

( )

!

0

2

0

j

i

t

j

i

e

C

t

g

j

i

i

j

t

n

i

i

−

−













≈

−

=

−

=

∑

∑

α

α

α

(38)

( )

1

0

2

1

1

2

1

1

+

=













+













−

≈

∑

i

i

n

i

i

s

s

C

s

G

α

α

α

(39)

j

ω

δ

α/2

3. Aproksymacja funkcjami wykładniczymi: