**.Modelowanie zakłóceń przypadkowych

Zadanie : Dany jest szum o parametrach

( )

( ) ( )

( )

y

F

y

f

Φ

R

y

y

yy

yy

→

→

ω

τ

, chcemy ten

szum przekształcić w szum o żądanych parametrach:

( )

( ) ( )

( )

x

F

x

f

Φ

R

x

x

xx

xx

→

→

ω

τ

.

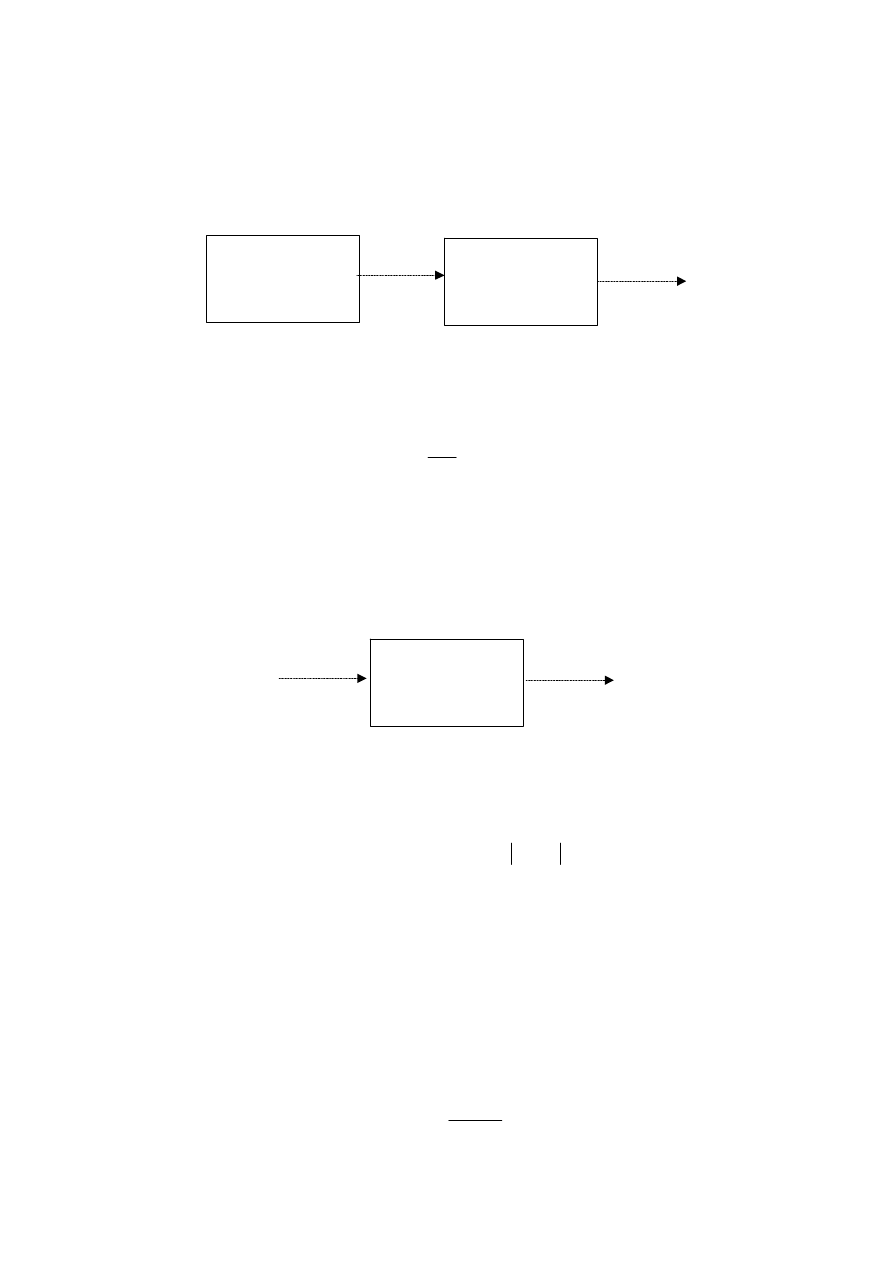
Generator
szumu

Filtr

y(t)

x(t)

1.Aby uzyskać zadaną gęstość widmową należy użyć filtru liniowego dynamicznego w
postaci:

( )

n

m

W

W

s

G

n

l

m

l

<

=

2.aby uzyskać zadaną gęstość prawdopodobieństwa należy użyć bezinercyjnych filtrów
nieliniowych w postaci:

( )

y

g

x

=

ad:a:

y(t)

x(t)

G( j )

ω

Obowiązują zależności:

( ) ( ) ( )

s

Y

s

G

s

X

=

( ) ( ) (

) ( )

( )

( )

ω

ω

ω

ω

ω

ω

xx

xx

xx

Φ

j

G

Φ

j

G

j

G

Φ

2

=

−

=

Ze względu na symetrię i dodatniość funkcji

( )

ω

xx

Φ

Gęstości widmowe aproksymowane

przy pomocy wielomianów są funkcjami parzystych potęg

ω

. Stąd można dokonać rozkładu

na:

( )

( ) (

)

ω

ω

ω

j

F

j

F

Φ

y

y

yy

−

=

( )

( ) (

)

ω

ω

ω

j

F

j

F

Φ

x

x

xx

−

=

Poszukiwaną transmitancję wyznacza się jako:

( )

( )

( )

ω

ω

ω

j

F

j

F

j

G

y

x

=

Przykład:

( )

t

y

- jest białym szumem;

( )

1

=

ω

yy

Φ

zatem

( )

1

=

ω

j

F

y

( )

t

x

ma zadaną gęstość w postaci

( )

2

1

ω

ω

+

=

a

Φ

xx

zatem

( )

ω

ω

j

a

j

F

y

+

=

1

Poszukiwana transmitancja ma postać:

( )

( )

1

1

s

a

s

G

j

a

j

G

+

=

→

+

=

ω

ω

Ad.b.

y(t)

x(t)

g( y )

Obowiązuje zależność:

( )

( )

(

)

y

g

F

y

F

x

y

=

Równanie to ma nieskończoną ilość rozwiązań, jeżeli przyjąć że

( )

y

g

ma być

różnowartościowa a dodatkowo:

( )

0

≥

dy

y

dF

y

równanie ma jedno, jedyne rozwiązanie.

Metoda graficzna rozwiązania równania przedstawiona jest poniżej:

Fy

g(y)

y

x

Fx

1

5

4

2

3