**. Pomiar gęstości prawdopodobieństwa f (hipoteza ergodycznośći) x ( x )

x1

t

X2

t

.........................................................

Xn

t

t

∀ ∈( ,

0 ∞)

t

x

m

= m

x

x

Stacjonarny proces jest procesem ergodycznym jeżeli średnia policzona po zbiorze realizacji jest taka sama dla wszystkich czasów rzeczywistych i dodatkowo jest równa średniej liczonej po czasie dla wszystkich realizacji. Dla ergodycznych procesów stochastycznych, gęstość prawdopodobieństwa i dystrybuantę prawdopodobieństwa można łatwo obliczyć według następujących schematów.

Obliczenie gęstości prawdopodobieństwa: f

x ( x )

X(t)

X+ X

∆

X

T

t

∆t

∆

1

∆t2

∆t3

∆t4 t5

∆t6

k

∑ ∆ t i

lim 1

T →∞

f

= lim

, =

x ( x )

T

T ∆ x ?

∆ x→0

∆ x

Czas obserwacji procesu (horyzont czasowy pomiaru) powinien być wystarczająco długi.

Oznacza to przy używaniu powyższego wzoru dla danego x , zakończenie obliczeń gdy wydłużanie czasu obserwacji nie powoduje zmian f

.

x ( x )

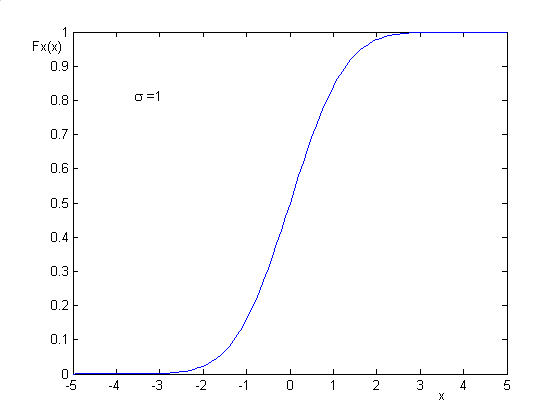
Obliczenie dystrybuanty: F

x ( x )

X(t)

X

∆τ

t

1

∆τ

∆τ

2

3

k

∑ ∆ τ i

F

=

1

lim

x ( x )

T →∞

T

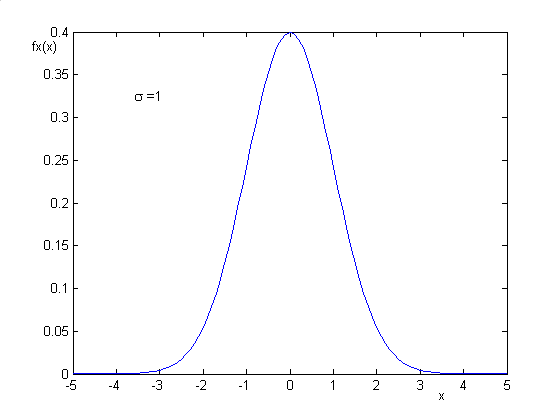
rozkład gaussowski:

( x− mx )

−

f x =

e

σ

x (

)

2

1

2 x

2π σ x

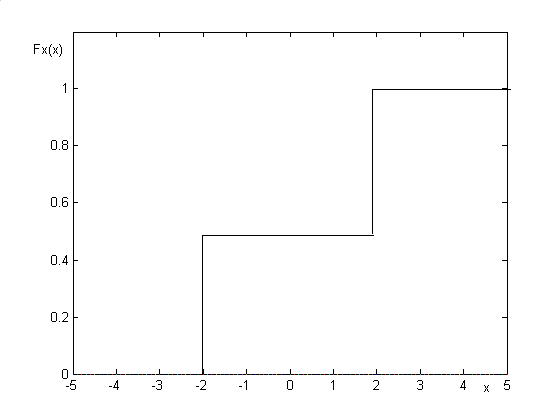
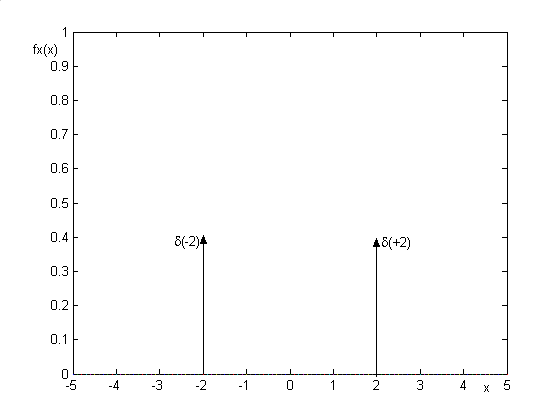
rozkład dwumianowy

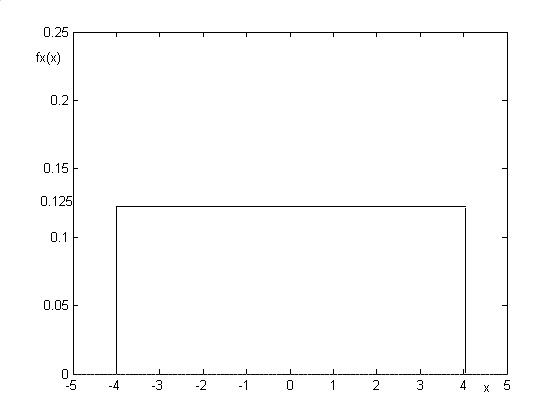
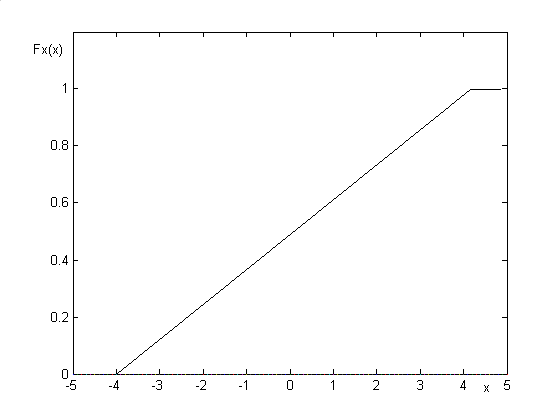
rozkład jednorodny (równomierny)

**. Pomiar gęstości widmowej Φ

xx ( jω )

Bezpośrednie wyliczenie gęstości widmowej własnej lub wzajemnej jest trudne. Łatwiej Jest najpierw wyliczyć odpowiednie funkcje korelacji a następnie obliczyć ich transformaty Fouriera.

Obliczenie funkcji korelacji w oparciu o dane pomiarowe: T

N−K

1

1

R τ =

∫

⋅

+τ ≅

∑

⋅

+

= R

xx ( )

x( t) x( t

) d t

x( n∆) x( n∆ k∆) xx ( k∆)

T

N +1− K n=0

0

k =

,

1

,

0

,

2 .... k

max

R

R

xx (τ ) =

xx (− τ )

R

R

xy (τ ) ≠

xx (− τ )

X(t)

∆t

t

warunki poprawnych obliczeń dla sygnałów ciągłych: T =

? τ

=

?

R

xx τ

=

max

( l im ( ) 0 )

τ →∞

Horyzont czasowy powinien być tak długi aby wydłużanie czasu obliczeń nie powodowało zmian wartości otrzymywanych funkcji korelacji. Maksymalna wartość przesunięcia czasowego, powinna być tak duża aby obejmowała czas w którym występuje funkcja korelacji.

warunki poprawnych obliczeń dla sygnałów próbkowanych z krokiem próbkowania

∆ t :

N =

? k

=

?

∆ t =

?

max

π

2

τmax

π

2

ω g

τ

max ≥ T

=

⇒

k

ω

max =

∆ t ≤ T

=

I

ω

=1+

d

ω

∆ t

g

ω

ω

d

g

d

Obliczenie na podstawie R

,

R

funkcji Φ

,

-metoda trapezów

xx (ω ) Φ xy ( jω ) xx (τ )

xy (τ )

+∞

+∞

+∞

Φ

= ∫

−

= ∫

c

os

− ∫

s

in

xy ( jω )

Rxy (τ )

ω

j τ

e

dτ

Rxy (τ )

(ω τ ) dτ j Rxy(τ ) (ω τ ) dτ

−∞

−∞

−∞

wprowadzamy funkcje T : i

Ti

Ki

t

ti- i

∆

ti

ti+∆i



K 0

τ t

i

< ≤ i − ∆



i

K

K

t

T τ

p τ

τ

t

τ t

i ( )







=  ( )



= − i

i

+ i 1+ i i − ∆ i < < i + ∆

i









2∆

2

i



∆ i 





0 τ ≥ ti + ∆





i



R τ

T τ

xy ( )

n

≅ ∑ i( )

i=1

+∞

+∞

n

+∞

n

n

+∞

n

+∞

Φ

jω

R e ωτ dτ

T c

os ω τ dτ

j

T s

in ω τ dτ

T cos ω τ dτ j T sin ω τ dτ

xy (

)

















= ∫

− j

xy

≅ ∫∑  i

( ) − ∫∑  i ( ) = ∑ ∫ i ( )  −



∑ ∫ i ( ) 

−∞

−∞ i=1



−∞ i=1



i=1  −∞



i=1  −∞



ti −∆

t

i

i + ∆

t

i

i −∆

t

i

i + ∆ i

Φ

jω

K cos ω τ dτ

p t cos ω τ dτ j K sin ω τ dτ

p t sin ω τ dτ

xy (

) n 



n 



≅ ∑

i

+

 ∫

( )

∫ i( ) ( )  − ∑

i

+



 ∫

( )

∫ i( ) ( ) 

i=1  0

t

1

0

i −∆

i=

i





ti −∆ i



ω

ω

Re(

sin t

sin

Φ

jω

K t

xy (

) n 

( i ) (∆ i )

≅ ∑



 i i



ω

ω

1

t

i= 

i

∆ i



ω

ω

Im(

K

cos t

cos

Φ

jω

sign t

( )

K t

xy (

)

n



i

( i ) (∆ i )

≅ −∑



i 

 −

+ i i



ω

ω

ω

1

t

i=



i

∆ i

