**. FFT- szybka transformata Fouriera 1.przedstawienie przebiegów czasowych w dziedzinie częstości ma bardzo duże znaczenie praktyczne (np. rozpoznawanie mowy, obrazów), 2.Przekształcenie całkowe Fouriera ma podstawową wadę, wymaga nieskończonego czasu całkowania.

T

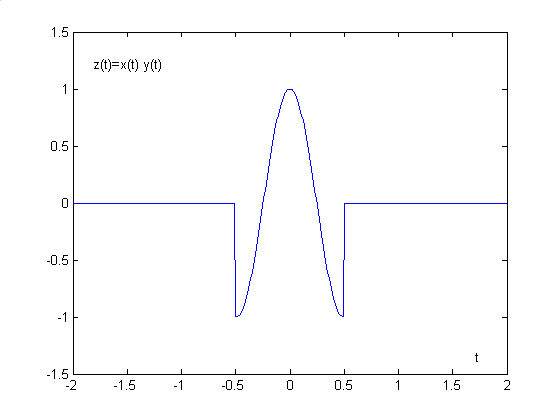
Na rysunkach pokazano wpływ ograniczenia się do czasów skończonych obserwacji (okno Prostokątne) na obserwowany przebieg czasowy.

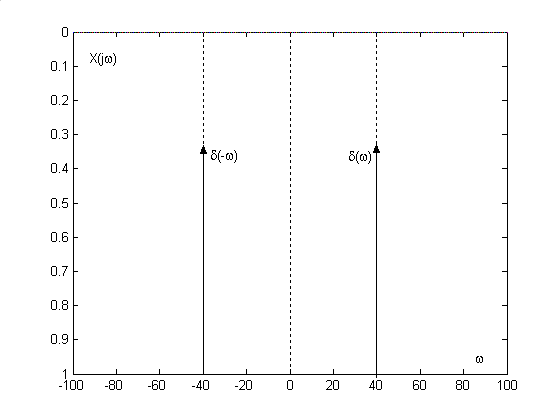
Z ( jω) = X ( jω)∗ Y ( jω) Iloczynowi w dziedzinie czasu odpowiada splot w dziedzinie częstość.

1/T

Mamy już skończony czas obserwacji. Teraz zastąpimy całkowanie, sumowaniem próbkowanego sygnału:

∞

∞

X ( jω) = ∫ x( t) − jω t e

X ( jω) = ∫ x( t) − j t e ω

0

−∞

zamieniamy na sumę przy założeniu że, znane jest N próbek sygnału: π k n

N-

j

X ( jk )

2

1

=

−

∑ x e N k n

= 01 , 2

, ,........ N

.

−1

n=0

Jest to wzór na dyskretne przekształcenie Fouriera.

Podobnie można wyznaczyć odwrotne dyskretne przekształcenie Foruriera: π k n

k-

j

x( n)

1

2

1

=

−

∑ X e N n k

= 01 , 2

, ,........ N

.

−1

N k=0

Aby wyliczyć dyskretną transformatę Fouriera należy obliczyć 2

N wyrażeń typu:

2π

2π k n

− j

− j

W = e

W kn

N

= e N

pomnożyć je przez odpowiednie x oraz zsumować. Bardzo dużo obliczeń. ale jest na to n

bardzo prosty sposób, jeżeli przyjmiemy, że ilość próbek czasowych jest liczbą typu: N = 2 l

l − liczba c

ałałkowi

różnych wartości wyrażeń typu

kn

W

będzie tylko N a nie aż

2

N . I tak jeżeli ilość próbek czasowych x jest np. 128 należy obliczyć tylko 128 różnych kn

W

a nie 16.384 jak w

n

przypadku dowolnym. Liczba mnożeń ogranicza się do: N log N g

dy

= 2 l

N

2

FFT

N log N

log N

10

np.: N = 102

4

2

10

=

wówczas

2

2

=

=

=

= 0

.0098 ≈ 1%

FT

2

N

N

1024

k= 0

k= 1

2

3

1

4

0

n= 0,1,2,3,4,5,6,7

5

7

6

k= 2

k= 3

1,5

6

1

3

2,6

0,4

4

0

7

5

3,7

2

k= 4

k= 5

2

7

5

1,3,5,7

4

0

0,2,4,6

1

3

6

k= 6

k= 7

3,7

6

5

7

2,6

0,4

0

4

1

3

1,5

2

Jak naprawdę obliczać w matlabie: clear all

T=100;

dt=.01;

t=0:dt:T;

k=length(t); % k=10001

q=log2(k); % q=13.2879

r=floor(q); % r=13

l=2^r; % l=8192

m=l/2; % m=4096

w1=5; % częstość w Hz x=sin(2*pi*w1*t); % sinusoida figure(1);plot(x(1:l)); % rysunek1

f=(dt^(-1)*(0:m-1))/l; % skala częstości z=fft(x,l); % fft figure(2);plot(z); % rysunek-motylek p=(z.*conj(z))*l; % gęstość widmowa figure(3);plot(f,p(1:m)); % rysunek3