**.Metoda powierzchni.
Dysponujemy odpowiedzią badanego układu na wymuszenie
( )
t
1
czyli
( )
t
h
.
Jeśli badany obiekt jest liniowy, jego model można zapisać w postaci transmitancji:
( )
m
n
s
a
s
a
s
a
s
a
b
s
b
s
b
s
b
s
b
s
G
n
n
n
n
n
n
m
m
m
m
m
m
>
+
+
+
+
+
+
+
+
+
+
=
−
−
−
−
−
−
−
−
;
1
.......
......
1
1
2
2
1
1
0
1
1
2
2
1
1
Należy w procesie identyfikacji wyznaczyć
n
m
+
+
1
współczynników transmitancji w
oparciu o znajomość
( )
t
h
.
Najpierw wyliczmy:
( )
( )
0
0
0
0
0
lim
lim
b
t
h
s
G
K
t
s
=
=
=
∞
→
→
( )
( )
(
)
( )
1
0
1
1
0
0
0
1
0
1
lim
s
1
lim
lim
a
K
b
t
h
s
G
K
s
G
K
t
s
s
+
−
=
=
−
=
=
∞
→
→
→
( )
( )
(
)
( )
2
0
1
1
2
2
1
1
0
2
0
2
lim
s
1
lim
lim
a
K
a
K
b
t
h
s
G
K
s
G
K
t
s
s
−
+
=
=
−
=
=
∞
→
→
→
..........................
..........................
( )
( )
(
)
( ) ( )
( )
r
r
r
r
r
r
r
t
r
r
s
r
s
r
a
K
a
K
a
K
b
t
h
s
G
K
s
G
K
0
1
2
2
1
1
1
1
0
0
1
.
..........
1
lim
s
1
lim
lim
−
−
−
∞
→
−
−
→
→
−
+
+
−
+
−
=
=
−
=
=
kolejne
i
K można wyliczyć z odpowiedzi
( )
t
h
w następujący sposób:
( )
t
h
K
t
0
0
lim
∞
→
=
( )
( )
(
)
( )
t
h
K
d
h
K
t
h
t
1
1
t
0
0
0
1
lim
;
∞
→
=
−
=
∫
τ
τ
( )
( )
(
)
( )
t
h
K
d
h
K
t
h
t
2
2
t
0
1
1
2
lim
;
∞
→
=
−
=
∫
τ
τ
..........................................
..........................................
( )
( )
(
)
( )
t
h
K
d
h
K
t
h
r
t
r
r
r
r
∞
→
−
−
=
−
=
∫
lim
;
t
0
1
1
τ
τ
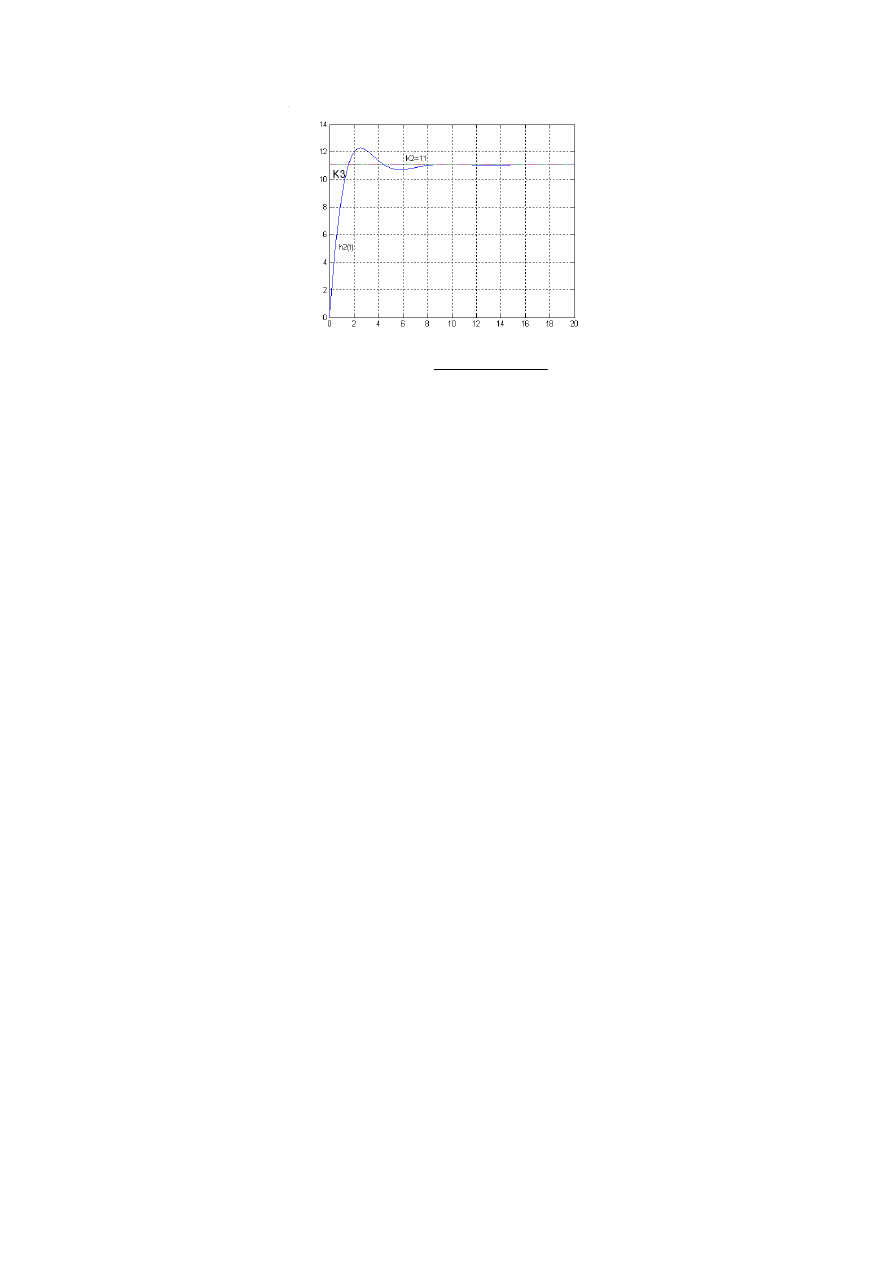
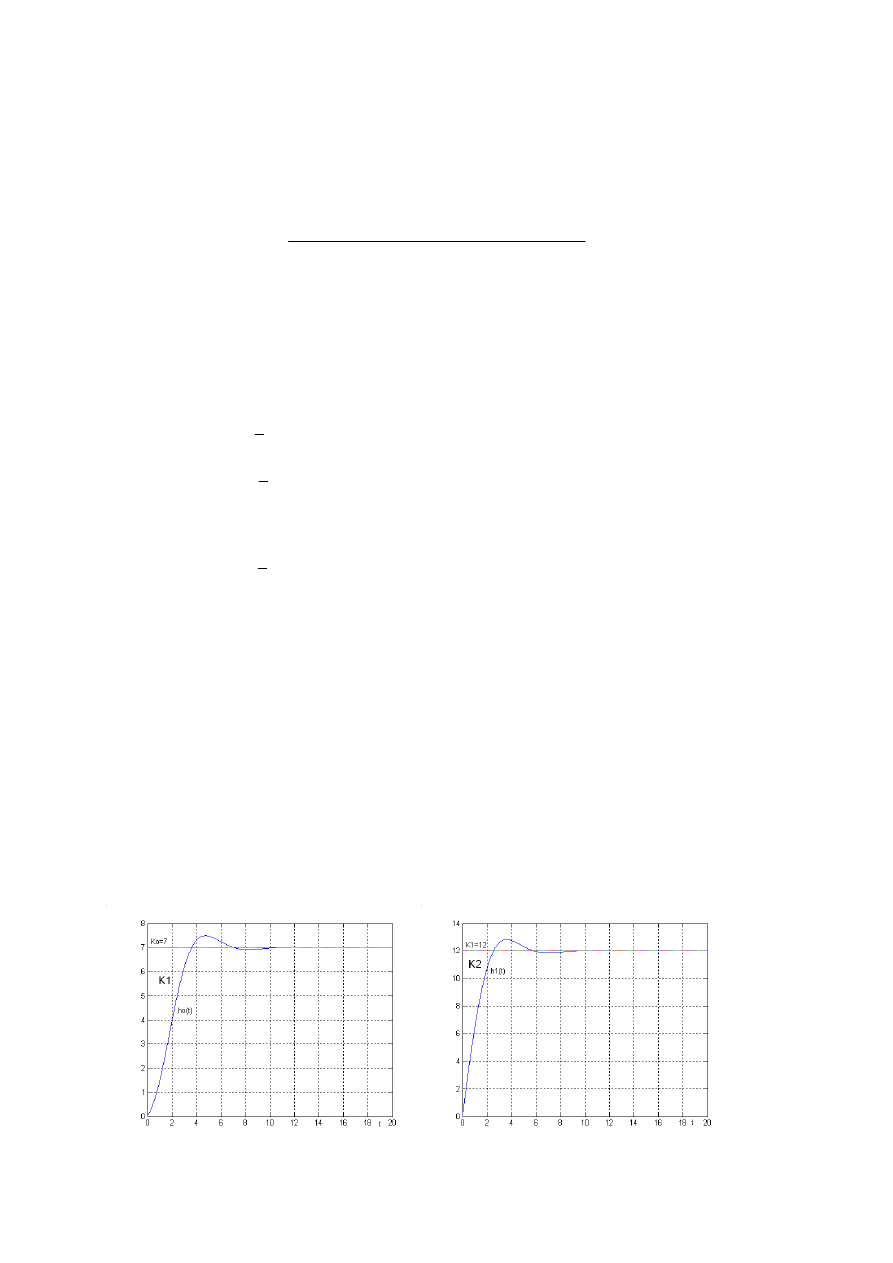
przykład zilustrowano dla m=2 n=3
( )
;
1
2
2
7
2
2
3
2
+
+
+
+
+
=
s
s
s
s
s
s
G
Równania dla m=3 oraz n=4 mają postać:
−
−
=
−
−
−
−
−
−
−
−
−
−
−
−
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
3
2
1
0
4
3
2
1
3
4
5
6
7
2
3
4
5
6
1
2
3
4
5
0
1
2
3
4
0
1
2
3
0
1
2
0
1
0
b
b
b
b
a
a
a
a
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
Aby rozwiązać równania najpierw „wycinamy” z układu równań:
−
−
−
−
=
−
−
−
−
−
−
−
−
7
6
5
4
4
3
2
1
3
4
5
6
2
3
4
5
1
2
3
4
0
1
2
3
K
K
K
K
a
a
a
a
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
K
Po wyliczeniu a można wyliczyć b:
+
−
−
−
−
=
−
−
3
2
1
0
4
3
2
1
0
1
2
0
1
0
3
2
1
0
0
0
0
0
0
0
0
0
0
0
K
K
K
K
a
a
a
a
K
K
K
K
K
K
b
b
b
b
Wyszukiwarka
Podobne podstrony:
Identyfikacja Procesów Technologicznych, 06 Metoda Momentów pelna
Identyfikacja Procesów Technologicznych 05.Metoda momentów
Identyfikacja Procesów Technologicznych, 05 Metoda momentów
Identyfikacja Procesów Technologicznych 06.Metoda Momentów pelna
Identyfikacja Procesów Technologicznych, Identyfikacja parametrycznarekurencyjną metodą najmniejszyc
Identyfikacja Procesów Technologicznych, 02 Eksperyment czynny
Identyfikacja Procesów Technologicznych, 07 Identyfikacja stochastyczna
Identyfikacja Procesów Technologicznych, Identyfikacja charakterystyki statycznej obiektu dynamiczne
Identyfikacja Procesów Technologicznych, Identyfikacja charakterystyk statycznych obiektu dynamiczne
Identyfikacja Procesów Technologicznych 10.FFT
Identyfikacja Procesów Technologicznych 03.Obiekt oscylacyjny
Identyfikacja Procesów Technologicznych 09.Metodya korelacji
Identyfikacja Procesów Technologicznych, Identyfikacja parametryczna obiektu dynamicznego (cz.1 i 2)
Identyfikacja Procesów Technologicznych, Identyfikacja parametryczna obiektów dynamicznych, Nr ?wicz
Identyfikacja Procesów Technologicznych, 12 Generatory przebiegów przypadkowych c d
Identyfikacja Procesów Technologicznych, 11 Generatory przebiegów przypadkowych
Identyfikacja Procesów Technologicznych, Realizacja liniowych modeli dyskretnych z wykorzystaniem si
Identyfikacja Procesów Technologicznych, 08 Pomiar gestosci prawdopodobienstwa
Identyfikacja Procesów Technologicznych 07.Identyfikacja stochastyczna
więcej podobnych podstron