1
ZADANIA Z MATEMATYKI DLA WYDZIAŁÓW IM i ICHiP
Liczby zespolone i funkcje wymierne
1.Znaleźć część rzeczywistą i część urojoną liczby zespolonej
a)
)
3
)(
2
1
(
)
3
2
(
2
i
i
i
z
−
+
−
=
Odp:
−
=
−
=
7
,
0
Im
7
,
1
Re
z
z
; b)
2
19
5
)
1
2
(
+
+
=
i
i
z
Odp:
=
−
=
5
,
1
Im
2
Re
z
z
;
c)
2
)
1
(
)
3
1
)(
3
(
i
i
i
z
+
+
−
+
=
Odp:
=
=
3
Im
1
Re
z
z
; d)
i
i
z
−
+
=
1
3
2
Odp:
−
=
=
5
,
0
Im
5
,
2
Re
z
z
;
2.Znależć postacie trygonometryczne liczb zespolonych
a)
i
z
+
−
=
3
1
oraz
i
z
−
−
=
1
2
a następnie obliczyć :
α
)
3
2
2
1
z
z
Odp:
)
12
5
sin
12
5
cos
(
2
8
π
π
i
+
−
;
β
)
4
2
3
1
z
z
Odp: -2i ;
b)
i
z
2
3
2
1
−
=
oraz
i
z
3
1
2
+
−
=
a następnie obliczyć:
)
α
2
2
3
1
z
z
Odp:
)
3
(
128
i
+
−
; )
β
5
2
2
1
z
z
Odp:
);
3
1
(
4
1
i
+
3.Obliczyć
a)
16
)
3
(
i
−
−
Odp:
)
3
1
(
2
15
i
+
−
;
b)
21
)
3
(
i
+
−
Odp:
;
2
21
i
−
4.Korzystając z postaci kartezjańskiej i trygonometrycznej liczby
i
i
+
+
1
3
1
obliczyć:
12
sin
π
i
12
cos
π
Odp:
2
2
3
1
12
cos
+
=
π
i
2
2
1
3
12
sin
−
=
π
5.Znależć pierwiastki liczby zespolonej i zaznaczyć na płaszczyźnie zespolonej
a)
i
4
3
+
Odp:
i
w
i
w
+
=
∨
−
−
=
2
2
2
1
;
b)
i
12
5
−
−
Odp:
;
3
2
3
2
2
1
i
w
i
w
−
=
∨
+
−
=
c)
i
4
3
8
8
−
−
Odp:
i
w
i
w
i
w
i
w
−
=
∨
−
−
=
∨
+
−
=
∨
+
=
3
3
1
3
3
1
3
2
1
0
;
d)
4
3
i
−
−
Odp:
)]
2
1
24
7
sin(
)
2
1
24
7
[cos(
2
4
π
π
π
π
k
i
k
w
k
+
+
+
=
dla
;
3
,
2
,
1
,
0
=
k
e)
i
3
3
2
2
−
Odp:
)]
3
2
9
5
sin(
)
3
2
9
5
[cos(
4
3
π
π
π
π
k
i
k
w
k
+
+
+
=
dla
;
12
,
0
=
k
f)
3
1
3
−
−
i
i
Odp:
)]
3
2
36
13
sin(
)
3
2
36
13
[cos(
2
6
π
π
π
π
k
i
k
w
k
+
+
+
=
dla
;
2
,
1
,
0
=
k
h)
5
1
−
Odp:
)
5
2
5
1
sin(
)
5
2
5
1
cos(
π
π
π
π
k
i
k
w
k
+
+
+
=
dla
;
4
,
3
,
2
,
1
,
0
=
k
6. Korzystając ze wzorów Newtona i Moivrea wyrazić przez
α
sin
i
α
cos
funkcje
a)
α
3
sin
i
α
3
cos
b)
α
4
sin
i
α
4
cos
7.Zaznaczyć na płaszczyźnie zespolonej zbiory spełniające warunki
a)
2
1
=
+
−
z
i
z
Odp:
i
z
3
1
2
−
−
=
; b)
3
2
)
(
)
(
−
=
−
+
+
i
z
z
i
z
z
i
Odp:
i
z
2
3
1
+
=
;
c)
i
z
z
z
z
2
3
+
=
−
+
Odp:
;
2
2
2
1
i
z
i
z
+
=
∨
+
−
=
d)
i
z
z
+
=
+
2
Odp:
;
4
3
i
z
+
=
2
e)
0
3
)
4
Re(
2
2
2
=
+
+
z
z
z
Odp:
x
y
x
y
2
2
=
∨
−
=
; f)
z
z
z
Im
Re
+
≥
Odp:
2
2
+
−
R
R
;
g)
4
4
3
<
+
−
i
z
Odp:
16
)
4
(
)
3
(
2
2
<
+
+
−
y
x
;
h)
z
z
Im
1
=
−
Odp:
0
1
≥
∧
=
y
x
;
i)
1
Im
2
−
=
z
Odp:
1
2
−
=
xy
; j)
z
z
Re
2
≥
−
Odp:
4
4
2
−
≥
x
y
;
k)
<
<
≥
+
π
π
2
3
)
arg(
2
1
0
)
Re(
2
iz
i
z
Odp:
x
y
≤
<
0
;
l)
<
<
≤
<
π
π
z
z
arg
3
1
2
1
Odp:
a
pierśierśc
wycinek
;
m)
2
1
1
Im
=
z
Odp:
0
1
)
1
(
2
2
≠
∧
=
+
+
z
y
x
;
n)
z
z
Re
1
=
−
Odp:
1
2
2
−
=
x
y
;
8.Rozwiązać równanie algebraiczne
a)
0
5
1
)
2
1
(
2
=
+
+
−
+
i
z
i
z
Odp:
i
z
i
z
−
=
∨
+
−
=
1
3
2
2
1
;
b)
0
)
5
(
)
4
1
(
2
=
+
−
+
+
i
z
i
z
Odp:
;
1
3
2
2
1
i
z
i
z
−
=
∨
−
−
=
c)
0
4
3
2
4
=
−
+
z
z
Odp:
i
z
i
z
z
z
2
2
1
1
4
3
2
1
=
∨
−
=
∨
=
∨
−
=
;
d)
0
9
6
3
=
−
−
z
z
Odp:
;
2
3
2
3
2
3
2
3
3
3
2
1
i
z
i
z
z
+
−
=
∨
−
−
=
∨
=
e)
0
30
13
3
2
3
4
=
+
+
+
+
z
z
z
z
Odp:
i
z
i
z
z
z
2
1
2
1
3
2
4
3
2
1
+
=
∨
−
=
∨
−
=
∨
−
=
;
f)
0
10
7
5
2
3
4
=
+
+
−
−
z
z
z
z
Odp:
;
2
2
2
1
4
3
2
1
i
z
i
z
z
z
+
=
∨
−
=
∨
−
=
∨
−
=
9.Wiedząc, że liczba zespolona:
a)
i
z
+
=
2
1
jest pierwiastkiem równania
,
0
5
4
6
4
2
3
4
=
+
−
+
−
z
z
z
z
znaleźć pozostałe
pierwiastki Odp:
i
z
i
z
i
z
i
z
=
∨
−
=
∨
−
=
∨
+
=
4
3
2
1
2
2
;
b)
i
z
2
1
=
jest pierwiastkiem równania
,
0
20
16
9
4
2
3
4
=
+
+
+
+
z
z
z
z
znaleźć pozostałe
pierwiastki
Odp:
i
z
i
z
i
z
i
z
+
−
=
∨
−
−
=
∨
−
=
∨
=
2
2
2
2
4
3
2
1
;
10.Rozłożyć na ułamki proste funkcję wymierną w zbiorze liczb rzeczywistych i zespolonych
a)
3
2
)
1
(
1
)
(
+
+
=
x
x
x
x
f
Odp:
3
)
1
(
2
1
1
1
)
(
+
−
+
−
=
x
x
x
x
f
;
b)
5
2
4
2
3
2
)
(
2
3
4
2
−
−
+
+
+
+
=
x
x
x
x
x
x
x
f
Odp:
;
5
2
1
16
5
)
1
(
16
3
)
1
(
16
2
)
(
2
+
+
+
−
⋅
+
−
+
+
=
x
x
x
x
x
x
f
c)
2
3
10
2
)
(
3
2
+
−
+
=
x
x
x
x
f
Odp:
;
)
1
(
4
2
2
)
(
2
−
+
+
=
x
x
x
f
d)
8
16
14
6
1
)
(
2
3
4
+
−
+
−
=
x
x
x
x
x
f
Odp:
;
2
2
1
2
1
)
2
(
1
2
1
2
1
2
1
)
(
2
2
+
+
−
⋅
+
−
⋅
+
−
−
=
x
x
x
x
x
x
f
e)
3
4
5
)
(
4
2
+
−
+
=
x
x
x
x
x
f
Odp:
)
3
2
(
2
3
)
1
(
1
)
1
(
2
1
)
(
2
2
+
+
+
−
−
+
−
=
x
x
x
x
x
x
f
;
Macierze i układy równań liniowych
1.Niech będą dane macierze
a)
−
=
1
1
4
0
3
1
A
;
−
=
0
1
2
0
1
0
1
3
1
B
;
−
=
1
1
0
2
4
1
C
α
) Obliczyć
T
C
A 3
2
−
β
)Rozwiązać równanie macierzowe
C
A
X
T
2
3
=
+
γ
) Obliczyć iloczyny macierzy
AC
;
CA
;
AB
;
C
C
T
;
T
CC
3
b)
−
=
1
0
2
2
3
1
A
;
−
=
3
1
2
0
1
3
B
;
−
−
=
1
1
3
1
2
1
1
2
C
;
αααα
) Obliczyć
T
B
A 2
3
−
ββββ
) Rozwiązać równanie macierzowe
B
X
A
T
=
+
3
2
γγγγ
)Obliczyć iloczyny macierzy
AB
;
BA
;
BC
;
C
C
T
;
T
CC .
2.Obliczyć wyznacznik macierzy
=
5
3
4
2
0
1
1
2
1
A
Odp:
3
=
A
a) Stosując rozwinięcie względem pierwszego wiersza.
b) Stosując rozwinięcie względem drugiej kolumny.
3.Korzystając z własności obliczyć wyznacznik
a)
5
3
4
2
0
1
1
2
1
Odp: 3 ; b)
2
0
1
0
2
1
0
3
1
2
1
2
4
3
2
1
−
−
Odp: -40 ; c)
1
2
1
3
1
3
2
1
1
1
1
2
1
1
1
1
−
−
−
−
−
Odp: 33;
d)
1
6
1
5
1
1
4
2
3
−
−
−
−
Odp: -113;
e)
u
z
x
z
y
x
z
x
+
+
1
1
1
Odp: yu; f)
4
1
1
1
2
0
1
2
1
0
2
3
0
4
0
1
−
−
−
Odp: 63;
g)
3
2
1
3
2
1
+
+
+
c
b
a
c
b
a
Odp: 0 ;
h)
3
0
0
2
7
2
1
5
2
0
0
3
5
4
3
1
Odp: -10 ; i)
64
27
8
1
16
9
4
1
4
3
2
1
1
1
1
1
Odp: 12
j)
2
2
2
1
1
1
z
y
x
z
y
x
Odp:
)
)(
)(
(
y
z
x
z
x
y
−
−
−
;
4. Znaleźć macierz odwrotną macierzy za pomocą macierzy dopełnień
a)
−
−
=
1
0
1
2
1
3
1
1
2
A
Odp:
−
−
−
−
=
−
2
1
2
1
2
1
2
1
2
3
2
5
2
1
2
1
2
1
1
A
b)
−
−
=
5
2
3
1
A
Odp:
=
−
1
2
3
5
1
A
c)
=
1
1
2
2
1
0
3
2
1
A
Odp:
−
−
−
−
=
−
1
3
2
2
5
4
1
1
1
1
A
;
d)
=
2
1
5
2
A
Odp:
−
−
=
−
2
1
5
2
1
A
;
5.Rozwiązać równanie macierzowe

4
a)
B
XA
=
dla
−
−
=
1
0
1
2
1
3
1
1
2
A
i
−
=
2
0
1
3
1
2
B
Odp:
−
−
=
2
3
2
1
2
1
3
1
2
X
;
b)
B
AX
=
dla
−
−
=
5
2
3
1
A
i
=
2
3
1
2
B
Odp:
=
4
7
11
19
X
;
Skorzystać z wyników przykładu 4a) i 4b).
c)
B
AX
=
dla
−
=
1
0
0
2
1
0
3
3
1
A
i
=
0
1
1
0
0
1
B
Odp:
−
−
=
0
1
1
2
3
10
X
;
d)
B
XA
=
dla
−
−
=
1
1
0
0
1
1
1
0
1
A
i
−
=
1
0
1
1
2
1
B
Odp:
−
=
0
0
1
2
0
1
X
;
6.Rozwiązać za pomocą wzorów Cramera i metodą macierzową układ równań
a)
=
−
+
=
+
−
=
+
+
9
3
4
8
2
2
17
2
3
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
=
=
=
1
2
4
3
2
1
x
x
x
; b)
=
+
−
=
−
+
=
+
+
2
7
3
4
14
3
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
=
=
=
3
2
1
3
2
1
x
x
x
;
c)
=
−
+
−
=
+
−
=
+
+
5
2
5
3
2
2
3
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
−
=
=
=
1
2
1
3
2
1
x
x
x
; d)
−
=
+
+
−
=
+
−
−
=
+
+
2
4
4
4
2
2
1
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
−
=
=
=
2
2
1
3
2
1
x
x
x
;
Kolokwium I (8p.)
7.Korzystając z definicji obliczyć rząd macierzy
a)
−
−
=
3
1
10
5
0
2
4
2
1
1
2
1
A
Odp: r(A)=2 b)
−
−
−
−
=
4
2
2
2
1
1
2
1
1
A
Odp: r(A)=1
8.Znależć rząd macierzy sprowadzając macierz do postaci bazowej
a)
−
−
−
=
3
3
0
2
4
2
2
0
1
2
1
1
A
b)
−
−
−
=
2
5
3
3
3
1
0
0
1
3
2
2
1
1
1
1
B
c)
−
−
=
8
4
1
0
1
5
2
1
1
0
2
0
1
2
1
3
2
0
1
1
C
Odp: r(A)=3; Odp: r(B)=3 ; Odp:r(C)=2.
5
9.Metodą przekształceń elementarnych rozwiązać układ równań liniowych (sprowadzić
macierz rozszerzoną układu do postaci bazowej i powołać się na twierdzenie Kroneckera-
Capelliego)
a)
=
+
−
=
+
−
=
+
−
−
=
+
+
5
4
2
7
3
3
5
2
2
1
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
Odp:
=
+
−
=
−
=
t
x
t
x
t
x
3
2
1
)
4
(
3
1
)
2
1
(
3
1
; b)
=
−
+
−
=
+
+
=
+
+
=
+
+
14
3
3
2
7
5
5
3
2
2
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
Odp:
−
=
=
=
2
2
1
3
2
1
x
x
x
;
c)
=
+
+
+
−
=
−
+
=
+
+
+
−
=
−
+
−
3
2
5
2
3
1
2
3
4
0
3
2
2
3
4
3
2
1
4
3
1
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Odp:
=
−
=
−
=
=
3
1
2
2
4
3
2
1
x
x
x
x
; d)
=
−
+
=
+
+
=
+
+
−
=
−
+
1
3
2
3
1
2
1
3
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
Odp: sprzeczny;
e)
=
+
+
−
=
+
+
−
=
+
+
−
4
2
3
6
7
3
3
4
4
5
2
4
5
2
3
4
3
2
1
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
Odp:
−
+
−
=
+
−
=
=
=
s
t
x
s
t
x
s
x
t
x
12
18
7
10
15
6
4
3
2
1
f)
=
−
=
+
+
=
+
−
0
0
0
4
2
3
2
3
2
1
3
2
1
x
x
x
x
x
x
x
x
Odp:
=
=
−
=
t
x
t
x
t
x
3
2
1
2
;
g)
=
+
−
=
+
−
=
+
+
5
10
11
4
3
4
3
2
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
=
+
=
−
=
t
x
t
x
t
x
3
2
1
)
2
1
(
5
1
)
7
9
(
5
1
h)
=
+
−
+
=
+
+
+
=
−
−
+
3
5
3
2
3
1
2
4
3
2
1
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
Odp:sprzeczny;
i)
=
+
−
=
+
−
+
=
+
+
−
1
2
5
3
2
2
2
3
2
2
4
3
2
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
x
x
x
Odp:
=
∧
=
−
+
=
−
−
=
s
x
t
x
s
t
x
s
t
x
4
3
2
1
)
2
5
1
(
3
1
)
2
5
(
3
1
;
j)
=
−
−
=
−
=
−
=
+
+
1
1
0
2
2
1
3
2
3
1
3
2
1
x
x
x
x
x
x
x
x
x
Odp:
=
=
=
1
0
1
3
2
1
x
x
x
;
10*.Przedyskutować rozwiązywalność układu równań w zależności od parametru a
R
∈
.
a)
=
+
−
=
+
−
=
+
−
a
x
x
x
x
ax
x
x
x
ax
2
2
3
3
1
1
3
2
1
3
2
1
3
2
1
b)
−
=
+
+
=
+
+
=
+
+
3
3
0
2
4
2
0
3
2
3
2
1
3
2
1
3
2
1
a
x
x
x
ax
x
x
x
x
x
Odp:a) a≠1 i a
≠
2 jedno rozwiązanie b) a
≠
3 jedno rozwiązanie
a=1 nieskończenie rozwiązań a=3 nieskończenie rozwiązań
a=2 układ sprzeczny
Geometria analityczna
1.W równoległoboku ABCD wyrazić wektory
AB i AD przez wektory AC i BD .
2. W trapezie OABC zachodzi warunek
CB
OA
3
=
.
a) Wyrazić wektor OA przez wektory OB i OC .
b) Wyrazić wektor OB przez wektory OA i OC
3.a)Niech wektory u i v o długościach
1
=
u
i
2
=
v
tworzą kąt <(
)
;v
u
=120
o
.
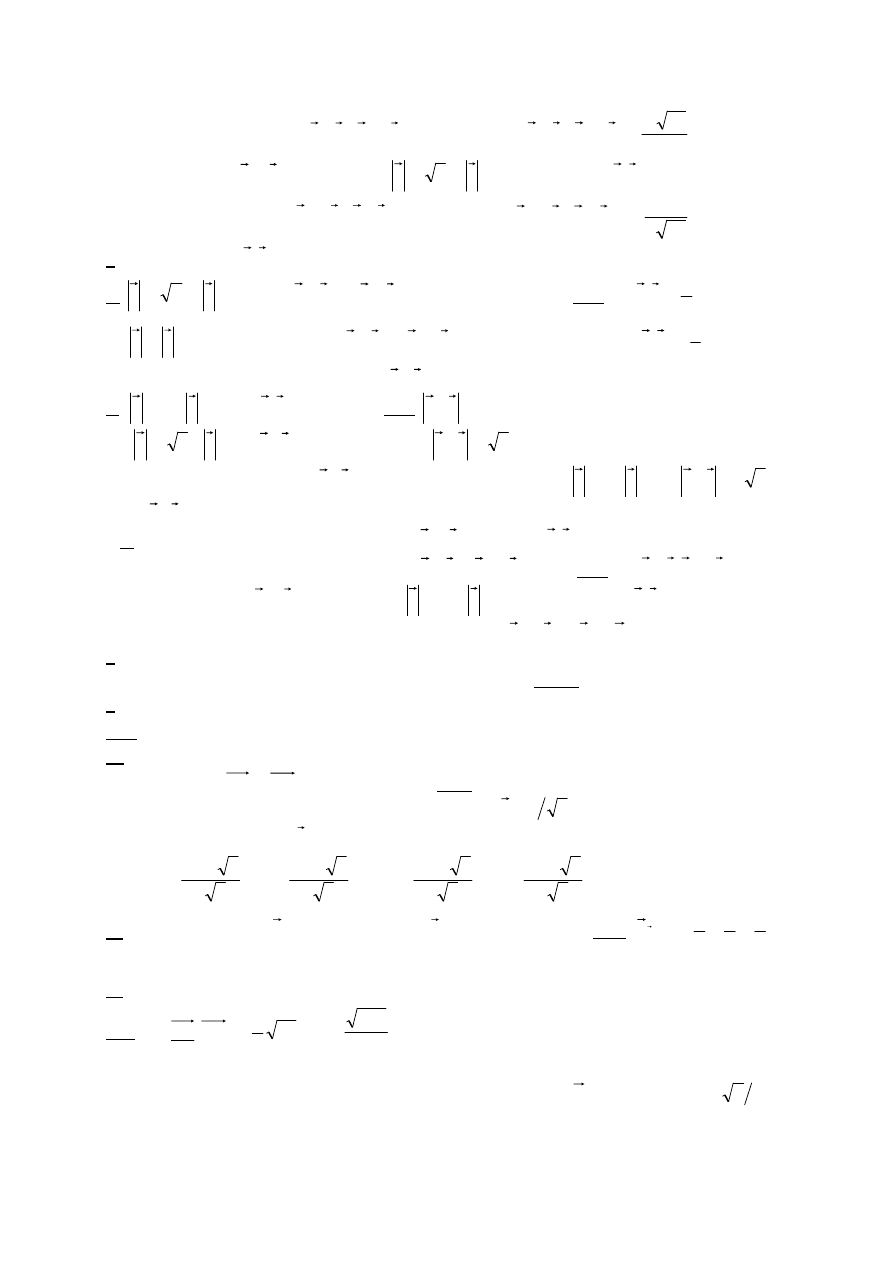
6
Obliczyć cosinus kąta
)
3
2
;
2
(
v
u
v
u
+
−
<
. Odp:
7
21
)
3
2
;
2
(
cos
−
=
+
−
<
v
u
v
u
;
b) Niech wektory u i v o długościach
3
=
u
i
2
=
v
tworzą kąt <(
.
150
)
,
°
=
v
u
Obliczyć cosinus kąta
).
2
,
2
(
v
u
v
u
−
+
<
Odp:
35
2
11
)
2
,
2
(
cos
−
=
−
+
<
v
u
v
u
;
4. Obliczyć kąt
)
,
( v
u
<
wiedząc , że
a)
2
=
u
i
3
=
v
oraz
)
(
v
u
+
o(
3
3
)
=
+
v
u
. Odp:
)
;
( v
u
<
=
π
4
3
.
b)
2
=
=
v
u
oraz , że wektory
v
u
+
2
i
v
u 5
4
−
są prostopadłe.
Odp:
.
3
1
)
,
(
π
=
<
v
u
5. Obliczyć moduł iloczynu wektorowego
v
u
×
wiedząc ,że:
a)
2
=
u
;
3
=
v
;
0
150
)
;
(
=
<
v
u
Odp:
3
=
×
v
u
b)
3
=
u
;
2
=
v
;
3
−
=
v
u o
Odp:
3
=
×
v
u
6. Obliczyć iloczyn skalarny
v
u o wiedząc, że jest ujemny oraz
2
=
u
;
7
=
v
;
3
3
=
×
v
u
.
Odp:
13
−
=
v
u o
.
7.a)Równoległobok rozpięty na wektorach u i v ma pole
10
)
;
(
=
v
u
S
. Obliczyć pole
równoległoboku rozpiętego na wektorach
v
u
+
3
i
.
2
v
u
−
Odp:
70
)
2
;
3
(
=
−
+
v
u
v
u
S
.
b) Dane są wektory u i v o długościach
2
=
u
i
3
=
v
tworzące kąt
.
120
)
,
(
°
=
<
v
u
Znaleźć pole równoległoboku rozpiętego na wektorach
v
u
2
−
i
.
2
3
v
u
+
Odp:
.
24
=
S
8.Znależć współrzędne środka ciężkości trójkąta o wierzchołkach
)
0
,
1
,
2
(
−
−
=
A
,
)
2
,
3
,
1
(
−
−
−
=
B
,
)
1
,
5
,
0
(
−
−
=
C
. Odp:
)
1
,
3
,
1
(
−
−
−
=
S
.
9.Znależć kąty wewnętrzne w trójkącie wierzchołkach
)
1
,
1
,
1
(
=
A
,
)
5
,
0
,
0
(
=
B
,
).
3
,
1
,
2
(
−
=
C
Odp:
o
45
=
α
,
o
45
=
β
,
o
90
=
γ
.
10.Dane są punkty
)
2
,
1
,
(
−
=
m
m
A
;
)
3
,
1
,
3
(
−
−
=
m
B
;
)
1
,
2
,
1
(
−
=
m
C
. Dla jakich wartości
R
m
∈
wektory AB i AC prostopadłe. Odp:
2
1
=
∨
=
m
m
.
11.Dla jakich wartości parametrów a i
b
R
∈
wektor
[
]
b
a
u
,
,
3
1
=
jest wersorem
prostopadłym do wektora
[ ]
1
,
1
,
1
=
v
.
Odp:
)
3
2
3
1
3
2
3
1
(
)
3
2
3
1
3
2
3
1
(
2
2
1
1
−
−
=
∧
+
−
=
∨
+
−
=
∧
−
−
=
b
a
b
a
12.Znależć rzut wektora
[
]
3
,
1
,
2
−
=
a
na wektor
[ ]
5
,
1
,
4
=
b
. Odp:
−
−
−
=
7
5
,
7
1
,
7
4
b
a
.
13.Obliczyć pole trójkąta o wierzchołkach
)
2
,
0
,
0
(
=
A
;
)
1
,
1
,
2
(
=
B
,
)
0
,
1
,
1
(
−
=
C
oraz wysokość
c
h
.
Odp:
35
2
1
)
;
(
=
∆
AC
AB
S
;
6
210
=
c
h
.
14.Znależć wektor prostopadły do płaszczyzny trójkąta o wierzchołkach
),
3
,
2
,
1
(
=
A
),
2
,
3
,
4
(
=
B
)
4
,
2
,
2
(
=
C
oraz obliczyć jego pole. Odp:
]
1
,
4
,
1
[
−
−
=
w
i
.
2
2
3
=
S
15.Obliczyć objętość oraz wysokość
D
h
czworościanu o wierzchołkach

7
a)
)
1
,
0
,
2
(
=
A
,
)
2
,
3
,
1
(
=
B
,
)
0
,
2
,
1
(
−
=
C
,
)
8
,
3
,
2
(
=
D
. Odp:
=
)
;
;
(
AD
AC
AB
V
cz
6
37
;
30
10
37
=
D
h
.
b)
),
1
,
1
,
2
(
−
=
A
),
3
,
1
,
0
(
=
B
)
1
,
3
,
2
(
−
=
C
i
)
2
,
3
,
0
(
=
D
.
Odp:
=
)
;
;
(
AD
AC
AB
V
cz
3
20
;
7
14
5
=
D
h
.
Płaszczyzna i prosta w przestrzeni
1.Znależć postać parametryczną płaszczyzny i równanie płaszczyzny przechodzącej przez punkty
)
4
,
2
,
1
(
−
=
A
;
)
3
,
1
,
2
(
=
B
;
)
5
,
1
,
3
(
−
=
C
. Odp:
H:
+
+
=
+
+
=
+
+
=
s
v
t
u
x
x
s
v
t
u
x
x
s
v
t
u
x
x
3
3
30
3
2
2
20
2
1
1
10
1
⇔
+
−
=
−
−
=
+
+
−
=
s
t
x
s
t
x
s
t
x
4
3
2
4
3
1
3
2
1
; H:
.
0
30
5
7
4
0
)
(
)
(
)
(
3
2
1
30
3
3
20
2
2
10
1
1
=
−
+
+
=
−
+
−
+
−
x
x
x
x
x
w
x
x
w
x
x
w
2.Znależć równanie płaszczyzny przechodzącej przez punkty
)
1
,
2
,
1
(
−
=
A
i
)
3
,
1
,
1
(
−
=
B
oraz
prostopadłej do płaszczyzny
0
1
2
:
3
2
1
=
+
−
+
x
x
x
H
. Odp:
0
17
8
2
5
:
3
2
1
=
−
+
−
Π
x
x
x
.
3.Znależć postać parametryczną, kierunkową i krawędziową prostej przechodzącej przez punkty
)
1
,
1
,
2
(
−
=
A
i
).
3
,
1
,
1
(
−
=
B
Odp:
+
=
+
=
+
=
t
u
x
x
t
u
x
x
t
u
x
x
L
3
30
3
2
20
2
1
10
1
:
⇔
+
=
+
−
=
−
=
t
x
t
x
t
x
2
1
2
1
3
2
3
2
1
;
2
1
2
1
3
2
:
3
2
1
3
30
3
2
20
2
1
10
1
−
=
+
=
−
−
−
=
−
=
−
x
x
x
u
x
x
u
x
x
u
x
x
L
;
=
+
−
=
−
+
0
2
0
1
3
2
:
3
2
2
1
x
x
x
x
L
4.Znależć prostą przechodzącą przez punkt
)
1
,
3
,
2
(
=
A
i prostopadłą do płaszczyzny
0
1
2
3
3
:
3
2
1
=
−
+
−
x
x
x
H
. Odp :
2
1
3
3
3
2
:
3
2
1
−
=
−
−
=
−
x
x
x
L
.
5.Znależć równanie płaszczyzny przechodzącej przez punkt
a)
)
1
,
2
,
3
(
=
A
i prostopadłą do prostej
1
2
1
2
3
:
3
2
1
+
=
−
=
−
x
x
x
L
Odp:
0
5
2
:
3
2
1
=
−
+
−
x
x
x
H
.
b)
)
2
,
4
,
1
(
=
A
i prostopadłą do prostej
.
0
3
2
0
1
2
:
3
1
2
1
=
−
+
=
−
−
x
x
x
x
L
Odp:
.
0
2
4
2
:
3
2
1
=
+
−
+
x
x
x
H
6.Znależć równanie płaszczyzny przechodzącej przez punkty
)
3
,
1
,
2
(
−
=
A
i
)
2
,
4
,
1
(
=
B
oraz
równoległej do wektora
].
5
,
1
,
3
[
=
u
Odp:
.
0
1
8
13
:
3
2
1
=
−
−
+
x
x
x
H
7.Znależć prostą przechodzącą przez punkt
a)
)
1
,
2
,
1
(
−
=
A
i równoległą do prostej
=
−
−
+
=
+
+
−
0
2
2
0
1
2
:
3
2
1
3
2
1
x
x
x
x
x
x
L
Odp:
3
2
1
1
:
2
1
−
=
−
x
x
K
=
5
1
3
+
x
.
b)
)
1
,
1
,
0
(
=
A
i równoległą do prostej
.
0
2
0
1
2
:
3
2
1
3
2
1
=
+
+
+
=
+
−
+
x
x
x
x
x
x
L
Odp:
.
1
1
3
1
2
:
3
2
1
−
=
−
−
=
x
x
x
K
8.Znależć równanie płaszczyzny przechodzącej przez punkt
a)
)
3
,
2
,
1
(
−
=
A
i prostą
3
1
1
3
2
1
:
3
2
1
−
−
=
−
=
+
x
x
x
L
Odp:
0
9
4
2
7
:
3
2
1
=
+
+
−
x
x
x
H
.
b)
)
3
,
7
,
2
(
−
=
A
i prostą
.
0
2
0
3
2
:
3
2
1
3
2
1
=
+
−
=
+
−
+
x
x
x
x
x
x
L
Odp:
.
0
33
23
6
39
:
3
2
1
=
+
+
−
x
x
x
H
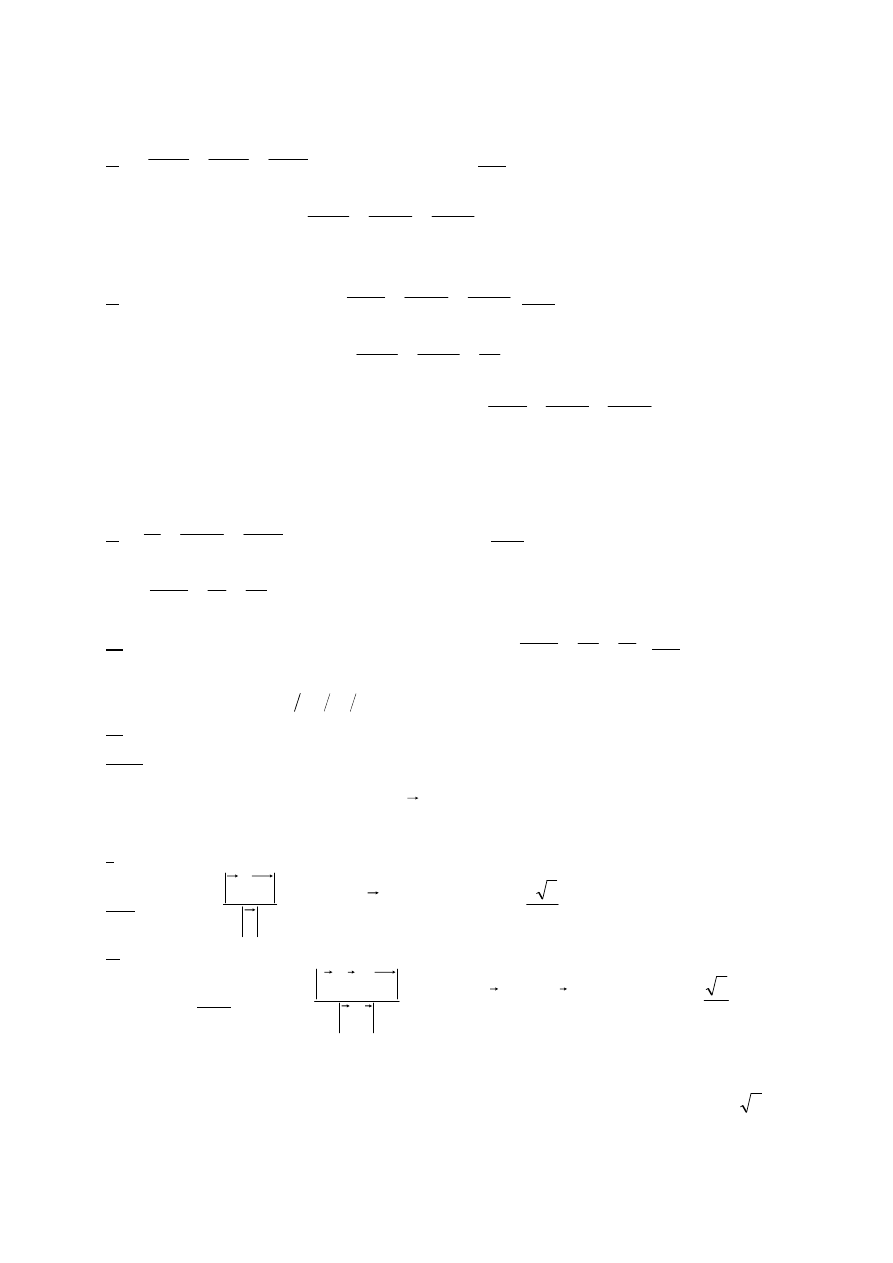
8
9.Wykazać, że proste
1
L
i
2
L
przecinają się. Znaleźć równanie płaszczyzny zawierającej te proste:
a)
1
1
2
1
1
3
:
3
2
1
1
+
=
+
=
+
x
x
x
L
;
=
−
−
=
+
−
0
2
0
4
3
:
3
2
3
1
2
x
x
x
x
L
Odp:
);
1
,
3
,
1
(
−
=
A
0
5
2
:
3
2
1
=
−
+
x
x
x
H
b)
=
−
−
=
+
−
0
1
2
0
2
:
3
2
3
1
1
x
x
x
x
L
;
1
2
1
4
3
2
:
3
2
1
2
−
=
−
=
−
x
x
x
L
. Odp:
);
1
,
3
,
1
(
−
=
A
.
0
5
2
:
3
2
1
=
−
+
x
x
x
H
10.Wykazać, że proste
1
L
i
2
L
są równoległe.Znaleźć równanie płaszczyzny zawierającej te proste,
a)
=
+
+
−
=
−
+
−
0
1
2
0
2
2
:
3
2
1
3
2
1
1
x
x
x
x
x
x
L
i
3
2
1
2
1
1
:
3
2
1
2
−
−
=
−
+
=
−
x
x
x
L
. Odp:
.
0
19
2
9
3
:
3
2
1
=
+
−
+
x
x
x
H
b)
=
−
+
−
=
−
+
−
0
3
3
2
0
2
2
:
3
2
1
3
2
1
1
x
x
x
x
x
x
L
i
.
1
1
3
1
2
:
3
2
1
2
−
=
−
−
=
−
x
x
x
L
Odp:
.
0
5
5
4
:
3
2
1
=
−
+
−
x
x
x
H
11.Znależć równanie płaszczyzny zawierającą prostą
1
2
2
3
3
1
:
3
2
1
1
−
+
=
−
=
−
x
x
x
L
i równoległą do
prostej
=
−
−
+
=
−
+
−
0
5
2
0
3
2
:
3
2
1
3
2
1
2
x
x
x
x
x
x
L
. Odp:
0
51
11
14
13
:
3
2
1
=
+
+
−
x
x
x
H
.
12.Znależć równanie rzutu prostopadłego prostej
L
na płaszczyznę
H
, gdy:
a)
1
1
1
2
1
:
3
2
1
−
−
=
−
−
=
x
x
x
L
i
0
4
3
2
:
3
2
1
=
−
+
−
x
x
x
H
. Odp:
=
−
+
+
=
−
+
−
0
9
4
5
0
4
3
2
:
3
2
1
3
2
1
x
x
x
x
x
x
K
.
b)
1
2
1
1
:
3
2
1
−
=
=
−
−
x
x
x
L
i
.
0
6
3
2
:
3
2
1
=
−
+
+
x
x
x
H
Odp:
.
0
4
2
4
0
6
3
2
:
3
2
1
3
2
1
=
−
−
+
=
−
+
+
x
x
x
x
x
x
K
13.Znależć rzut prostopadły punktu
)
8
,
2
,
1
(
=
A
na prostą
1
1
2
1
:
3
2
1
x
x
x
L
=
−
=
−
. Odp:
)
1
,
1
,
3
(
'
−
=
A
.
14.Znależć rzut prostopadły punktu
)
1
,
2
,
1
(
−
=
A
na prostą przechodzącą przez punkty
)
1
,
1
,
0
(
=
B
i
)
3
,
2
,
1
(
=
C
. Odp:
).
3
1
,
3
2
,
3
1
(
'
−
=
A
15.Znależć punkt symetryczny do punktu
)
1
,
1
,
5
(
=
A
względem płaszczyzny
.
0
2
3
:
3
2
1
=
+
−
x
x
x
H
Odp:
).
1
,
5
,
1
(
'
−
−
=
A
16.Znależć punkt symetryczny do punktu
)
10
,
7
,
2
(
−
=
A
względem płaszczyzny przechodzącej przez
punkt
)
2
,
2
,
3
(
=
P
i prostopadłej do wektora
].
2
,
3
,
1
[
−
=
w
Odp:
).
2
,
11
,
4
(
'
−
−
=
A
17.Obliczyć odległość :
a)punktu
)
3
,
1
,
2
(
−
=
A
od płaszczyzny
0
6
5
4
3
:
3
2
1
=
−
+
−
x
x
x
H
Odp:
)
(
)
(
;
)
;
(
H
w
H
P
w
PA
w
H
A
d
⊥
∧
∈
=
o
.
2
3
3
)
;
(
=
H
A
d
.
b) punktu
)
2
,
1
,
3
(
=
A
od płaszczyzny
H
przechodzącej przez punkty
)
2
,
1
,
4
(
−
=
B
;
)
1
,
0
,
3
(
=
C
;
)
3
,
0
,
1
(
=
D
. Odp:
)
//
(
)
//
(
)
(
;
)
(
)
;
(
H
v
H
u
H
P
v
u
PA
v
u
H
A
d
∧
∧
∈
×
×
=
o
.
2
6
)
;
(
=
H
A
d
.
c) punktu
)
1
,
1
,
5
(
−
=
A
od płaszczyzny
.
0
4
2
2
:
3
2
1
=
+
−
−
x
x
x
H
Odp:
.
3
)
;
(
=
H
A
d
d) punktu
)
0
,
3
,
4
(
=
A
od płaszczyzny
+
=
−
−
=
+
+
=
s
t
x
s
t
x
s
t
x
H
2
3
4
3
2
3
1
:
3
2
1
dla
.
,
R
s
t
∈
Odp:
.
6
)
;
(
=
H
A
d
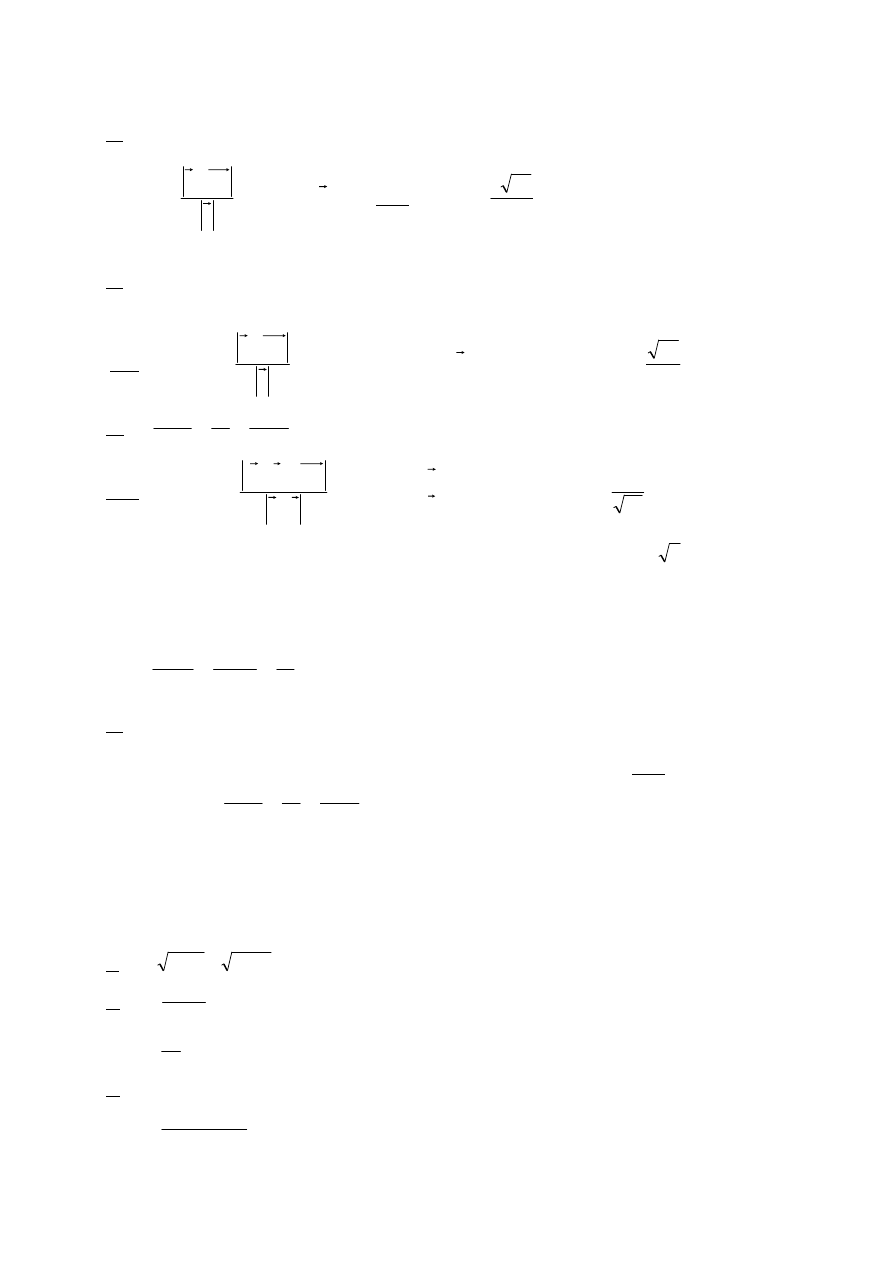
9
18.Obliczyć odległość punktu
)
5
,
4
,
3
(
=
A
od prostej
=
−
+
−
=
+
+
0
2
0
:
3
2
1
3
2
1
x
x
x
x
x
x
L
.
).
//
(
)
(
;
)
;
(
L
u
L
P
u
PA
u
L
A
d
∧
∈
×
=
Odp:
.
2
22
3
)
;
(
=
L
A
d
19.Obliczyć odległość między prostymi:
a)
=
+
=
+
−
+
0
0
1
2
:
2
1
3
2
1
1
x
x
x
x
x
L
i
=
−
+
−
=
−
+
−
0
3
3
2
0
6
3
2
:
3
2
1
3
2
1
2
x
x
x
x
x
x
L
.
Odp:
)
//
//
(
)
(
)
(
;
)
;
(
2
1
2
1
2
1
L
L
u
L
B
L
A
u
AB
u
L
L
d
∧
∈
∧
∈
×
=
.
3
42
)
;
(
2
1
=
L
L
d
b)
1
1
1
1
1
:
3
2
1
1
−
=
=
+
x
x
x
L
i
=
+
−
+
−
=
+
−
+
0
4
2
2
0
3
:
3
2
1
3
2
1
2
x
x
x
x
x
x
L
Odp:
∧
∈
∧
∈
×
×
=
)
//
(
)
(
)
//
(
)
(
;
)
(
)
;
(
2
2
1
1
2
1
L
v
L
B
L
u
L
A
v
u
AB
v
u
L
L
d
o
;
14
10
)
;
(
2
1
=
L
L
d
.
c)
=
−
−
=
+
+
0
1
0
1
:
3
1
2
1
1
x
x
x
x
L
i
=
+
+
=
−
+
0
1
0
:
3
2
3
2
1
2
x
x
x
x
x
L
; Odp:
.
2
)
;
(
2
1
=
L
L
d
d)
=
−
+
=
+
−
0
1
0
:
3
1
3
2
1
1
x
x
x
x
x
L
i
.
3
0
2
2
:
3
2
1
3
2
1
2
=
+
+
=
+
−
x
x
x
x
x
x
L
Odp:
.
1
)
;
(
2
1
=
L
L
d
e)
1
3
2
4
9
:
3
2
1
1
x
x
x
L
=
−
+
=
−
i
=
−
+
=
+
+
0
2
0
14
2
3
:
3
1
2
1
2
x
x
x
x
L
Odp:
.
7
)
;
(
2
1
=
L
L
d
20.Na prostej
=
−
−
+
=
−
+
−
0
1
2
0
2
:
3
2
1
3
2
1
x
x
x
x
x
x
L
znaleźć punkt równoodległy od punktów
)
2
,
1
,
1
(
−
=
A
i
).
2
,
1
,
3
(
=
B
Odp:
).
2
,
1
,
1
(
=
C
21.Na prostej
1
1
2
1
1
:
3
2
1
−
=
=
−
+
x
x
x
L
znaleźć punkt równoodległy od płaszczyzn
0
6
2
3
:
3
2
1
1
=
+
−
+
x
x
x
H
i
0
2
3
2
:
3
2
1
2
=
−
−
+
x
x
x
H
. Odp:
).
2
,
2
,
2
(
−
=
C
Kolokwium II (8p.)
Ciągi liczbowe
1.Zbadać monotoniczność i ograniczoność ciągu:
a)
.
5
2
+
−
+
=
n
n
a
n
Odp: monotonicznie rosnący i ograniczony.
b)
8
3
1
−
+
=
n
n
a
n
Odp: jest monotonicznie malejący dla
3
≥
n
i jest ograniczony.
c)
!
2
n
a
n
n
=
Odp: monotonicznie niemalejący i ograniczony.
d)
n
a
n
n
)
1
(
−
=
Odp: nie jest monotoniczny i nie jest ograniczony.
e)
n
n
n
n
a
n
2
3
5
3
2
2
+
−
+
=
Odp: rosnący i ograniczony.
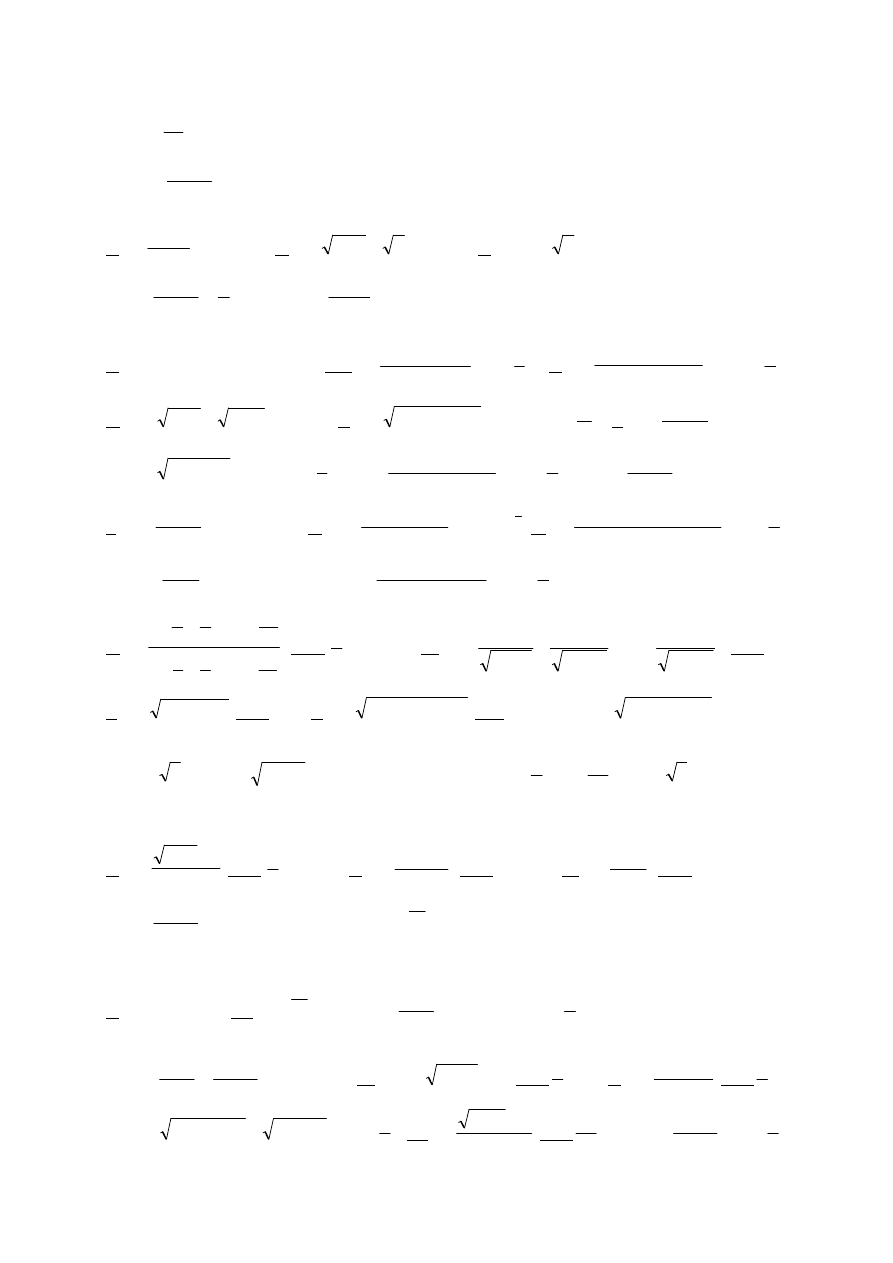
10
f)
!
n
n
a
n
n
=
Odp: rosnący i ograniczony z dołu
g)
1
3
1
2
+
+
=
n
n
n
a
Odp: jest monotonicznie malejący i jest ograniczony
2.Korzystając z definicji granicy ciągu wykazać, że
a)
2
1
1
2
lim
=
+
−
∞
→
n
n
n
; b)
0
)
1
(
lim
=
−
+
∞
→
n
n
n
; c)
−∞
=
−
∞
→
)
1
(
lim
n
n
;
d)
3
2
4
3
3
2
lim
=
−
+
∞
→
n
n
n
; e)
;
1
lim
2
+∞
=
+
∞
→
n
n
n
3.Obliczyć granicę ciągu
a)
)
1
2
(
lim
2
3
+
−
∞
→
n
n
n
. Odp:
.
∞
b)
.
5
2
3
1
2
lim
2
2
3
+
+
+
−
∞
→
n
n
n
n
n
Odp:
3
1
c)
.
4
3
)
2
(
5
4
2
3
4
lim
n
n
n
n
n
⋅
−
−
⋅
⋅
+
⋅
∞
→
Odp:
;
3
2
−
d)
).
2
1
(
lim
+
−
−
∞
→
n
n
n
Odp:
.
0
e)
).
2
3
2
4
(
lim
2
n
n
n
n
−
+
−
∞
→
Odp:
.
2
1
−
f)
.
2
7
1
3
lim
n
n
n
n
−
+
∞
→
Odp:
.
0
g)
)
3
2
9
(
lim
2
n
n
n
n
−
+
∞
→
Odp:
;
3
1
h)
n
n
n
n
n
4
2
3
4
)
3
(
5
4
3
lim
⋅
+
⋅
−
⋅
−
⋅
∞
→
Odp:
;
2
3
i)
3
2
)
1
7
2
5
(
lim
+
→∞
−
−
n
n
n
n
Odp: 0;
j)
.
3
2
1
2
lim
2
3
−
∞
→
+
−
n
n
n
n
Odp:
.
6
−
e
k)
n
n
n
n
n
−
−
+
∞
→
1
3
4
2
3
lim
2
2
Odp:
;
3
2
e
l)
.
2
3
7
3
1
lim
2
n
n
n
−
+
⋅⋅
⋅
+
+
+
∞
→
Odp:
2
3
m)
1
2
)
2
3
(
lim
+
∞
→
+
−
n
n
n
n
Odp:
;
10
−
e
n)
2
...
3
2
1
lim
n
n
n
+
+
+
+
∞
→
Odp:
;
2
1
o)
n
n
n
3
1
9
1
3
1
1
2
1
4
1
2
1
1
lim
+
⋅⋅
⋅
+
+
+
+
⋅⋅
⋅
+
+
+
∞
→
Odp:
3
4
; p)
+
+
⋅⋅
⋅
+
+
+
+
∞
→
n
n
n
n
n
2
2
2
1
2
1
1
1
lim
Odp: 1;
r)
n
n
n
n sin
3
lim
+
∞
→
Odp:1; s)
n
n
n
n
n
5
4
2
3
lim
+
⋅
+
∞
→
Odp: 5; t)
n
n
n
6
3
4
2
lim
⋅
+
⋅
∞
→
Odp: 6;
4*.Wykazać, że istnieje granica ciągu określonego rekurencyjnie
a)
n
n
a
a
a
+
=
=
+
6
,...,
6
1
1
Odp: 3; b)
)
3
(
2
1
,...,
1
1
1
n
n
n
a
a
a
a
+
=
=
+
Odp:
3
;
Granica funkcji w punkcie skupienia i ciągłość funkcji. Asymptoty funkcji.
1.Korzystając z definicji granicy w sensie Heinego obliczyć
a)
x
x
x
1
1
lim
0
−
+
→
Odp:
2
1
b)
2
1
)
1
(
1
lim
−
−
→
x
x
Odp:
∞
−
c)
2
1
lim
2
−
+
→
x
x
Odp:
∞
+
d)
2
4
lim
2
2
−
−
→
x
x
x
Odp: 4 e)
1
1
1
lim
−
→
+
x
x
e
Odp:
∞
+
f)
)
1
2
(
lim
+
−
+∞
→
x
x
Odp:
1
2. Korzystając z definicji granicy w sensie Heinego wykazać , że nie istnieje granica
a)
x
x
sin
lim
+∞
→
b)
1
1
1
2
lim
−
→
x
x
c)
x
x
sin
1
lim
+
→
π
d)
x
arctg
x
1
lim
0
→
3.0bliczyć granice funkcji
a)
−
−
−
→
3
1
1
3
1
1
lim
x
x
x
Odp: -1 b)
)
1
(
lim
2
x
x
x
x
−
+
+∞
→
Odp:
2
1
c)
2
0
cos
1
lim
x
x
x
−
→
Odp:
2
1
d)
)
7
1
2
(
lim
2
2
x
x
x
x
n
−
−
−
−
+∞
→
Odp:
2
5
e)
x
x
x
5
sin
2
4
lim
0
−
+
→
Odp:
20
1
f)
x
x
tg
x
5
sin
2
lim
0
→
Odp:
5
2

11
g)
9
2
3
3
sin
lim
0
+
−
→
x
x
x
Odp:
9
−
h)
x
x
x
x
x
3
sin
3
4
2
sin
2
3
lim
0
+
−
→
Odp:
13
1
−
i)
x
x
x
x
x
3
sin
3
4
2
sin
2
3
lim
+
−
+∞
→
Odp:
4
3
j)
x
x
x
π
sin
1
lim
2
1
−
→
Odp:
π
2
k)
π
π
−
→
x
x
x
sin
lim
Odp:
1
−
l)
x
x
x
+
−
+∞
→
1
1
arcsin
lim
Odp:
2
π
−
n)
x
e
x
x
2
sin
1
lim
3
0
−
→
0dp:
2
3
o)
1
1
2
3
2
lim
+
+∞
→
+
+
x
x
x
x
Odp:
e
p)
x
x
x
x
x
+
−
+
+∞
→
2
3
1
2
3
lim
2
2
Odp:
3
2
e
r)
1
2
2
3
lim
+
+∞
→
+
x
x
x
x
0dp:
0
s)
x
x
e
1
0
1
1
lim
+
+
→
Odp:
0
t)
x
x
e
1
0
1
1
lim
+
−
→
Odp:
1
u)
x
arctg
x
−
−
→
1
1
lim
1
Odp:
2
π
v)
x
arctg
x
−
+
→
1
1
lim
1
Odp:
2
π
−
w)
tgx
x
2
1
2
lim
2
+
−
→
π
Odp:
0
z)
tgx
x
2
1
2
lim
2
+
+
→
π
Odp:
2
4.Zbadać ciągłość funkcji
a)
−
=
−
1
2
6
1
2
)
(
x
x
x
x
f
dla
dla
dla
)
;
2
(
]
2
;
1
[
)
1
;
(
+∞
∈
∈
−∞
∈
x
x
x
b)
−
−
−
=
x
x
x
x
f
4
)
1
(
1
)
(
2
2
dla
dla
dla
)
;
2
[
)
2
;
0
[
)
0
;
(
+∞
∈
∈
−∞
∈
x
x
x
Odp: w punkcie
1
0
=
x
ciągła lewostronnie Odp: w punkcie
2
0
=
x
ciągła prawostronnie
c)
+∞
∪
−
−∞
∈
−
−
∈
=
)
;
1
(
)
1
;
(
1
]
1
;
1
[
2
cos
)
(
x
dla
x
x
dla
x
x
f
π
d)
=
≠
+
=
0
1
0
)
(
4
2
x
dla
x
dla
x
x
x
x
f
Odp: w punkcie
1
0
−
=
x
ciągła prawostronnie Odp: w punkcie
0
0
=
x
ciągła prawostronnie
e)
=
∨
−
=
−
≠
∧
−
≠
−
+
+
=
2
3
5
1
2
3
6
3
)
(
2
x
x
dla
x
x
dla
x
x
x
x
f
f)
=
≠
−
=
0
1
0
cos
1
)
(
2
x
dla
x
dla
x
x
x
f
Odp: nieciągła w punkcie
.
2
=
x
Odp: nieciągła w punkcie x=0
5.Wykazać , że równanie ma w przedziale co najmniej jeden pierwiastek , gdy
a)
0
1
3
3
=
+
−
x
x
dla
)
2
;
1
(
∈
x
b)
0
1
3
5
=
−
−
x
x
dla
)
2
;
1
(
∈
x
6.Wyznaczyć asymptoty funkcji i sporządzić wykres
a)
2
3
)
1
(
)
(
+
=
x
x
x
f
b)
1
)
(
2
−
=
x
x
f
c)
x
x
arctg
x
f
−
=
1
)
(
Odp: asymptota pionowa obustronna Odp: asymptota ukośna w Odp: asymptota pozioma
o równaniu
;
1
−
=
x
asymptota
)
(
−∞
o równaniu
x
y
−
=
równaniu
π
25
,
0
−
=
y
;
ukośna o równaniu
2
−
=
x
y
oraz w
)
(
+∞
o rów.
x
y
=
π
π
5
,
0
)
1
(
5
,
0
)
1
(
−
=
∧
=
+
−
f
f
d)
1
1
)
(
−
=
x
e
x
f
e)
x
x
x
f
1
)
(
−
=
Odp: asymptota pionowa obustronna o równaniu Odp: asymptota pionowa prawostronna
;
0
=
x
asymptota pozioma w
)
(
−∞
o rów:
1
−
=
y
o równaniu
;
0
=
x
asymptota ukośna
oraz w
)
(
+∞
o rów:
0
=
y
w
)
(
+∞
o równaniu
x
y
=
f)
x
x
x
f
1
)
(
2
−
=
Odp: asymptota pozioma w
)
(
−∞
o rów.
1
−
=
y
oraz w
)
(
+∞
o rów.
1
=
y
12
Pochodne funkcji
1.Korzystając z definicji obliczyć pochodną funkcji w punkcie
a)
x
x
f
2
cos
)
(
=
;
R
x
∈
Odp:
x
x
f
2
sin
2
)
(
−
=
′
b)
x
x
f
ln
)
(
=
;
)
;
0
(
∞
∈
x
Odp:
x
x
f
1
)
(
=
′
c)
1
4
)
(
+
=
x
x
f
;
2
0
=
x
Odp:
3
2
)
2
(
=
′
f
d)
1
;
2
1
)
(
=
+
=
o
x
x
x
f
Odp:
9
1
)
1
(
−
=
′
f
e)
+∞
∈
−
−∞
∈
−
=
)
;
1
[
1
)
1
;
(
2
1
2
1
)
(
2
x
dla
x
x
dla
x
x
x
f
;
1
0
=
x
Odp:
2
1
)
1
(
)
1
(
)
1
(
=
′
=
′
=
′
+
−
f
f
f
f)
;
1
)
(
3
−
=
x
x
f
1
=
o
x
Odp:
)
1
(
f
′
-nie istnieje.
2.Obliczyć pochodną funkcji
a)
2
3
)
(
3
3
2
5
+
+
+
=
−
x
x
x
x
f
b)
x
ctgx
tgx
x
f
ln
4
)
(
+
−
=
c)
x
e
x
x
f
2
)
(
−
=
Odp:
4
3
1
4
3
5
)
(
−
−
−
+
=
′
x
x
x
x
f
Odp:
)
1
2
sin
1
(
4
)
(
2
+
=
′
x
x
f
Odp:
x
e
x
x
x
f
3
2
)
(
−
=
′
d)
x
x
x
f
arcsin
ln
)
(
⋅
=
e)
2
1
ln
)
(
x
x
x
f
+
=
f)
x
x
x
x
x
f
cos
sin
cos
sin
)
(
+
−
=
Odp:
2
1
ln
arcsin
)
(
x
x
x
x
x
f
−
+
=
′
Odp:
2
2
2
2
)
1
(
ln
2
1
)
(
x
x
x
x
x
x
f
+
−
+
=
′
Odp:
x
x
x
f
2
sin
1
2
sin
2
)
(
+
=
′
g)
x
arctg
x
f
=
)
(
h)
x
x
f
3
cos
)
(
=
i)
x
e
x
f
sin
)
(
=
Odp:
)
1
(
2
1
)
(
x
x
x
f
+
=
′
Odp:
x
x
x
f
sin
cos
3
)
(
2
⋅
−
=
′
Odp:
x
e
x
x
f
sin
cos
)
(
⋅
=
′
j)
x
x
x
f
−
+
=
1
1
ln
)
(
k)
)
1
(
)
(
2
x
x
arctg
x
f
+
−
=
l)
x
x
x
f
sin
)
(
=
Odp:
1
2
)
(
2
−
=
′
x
x
f
Odp:
)
1
(
2
1
)
(
2
x
x
f
+
=
′
Odp:
)
sin
ln
(cos
)
(
sin
x
x
x
x
x
x
f
x
+
=
′
3.Obliczyć pierwszą i drugą pochodną funkcji
a)
2
2
1
1
)
(
x
x
arctg
x
x
x
f
−
+
−
=
b)
)
1
ln(
)
(
2
+
+
=
x
x
x
f
c)
2
1
arcsin
)
(
x
x
arctgx
x
f
+
−
=
Odp:
2
1
2
)
(
x
x
f
−
=
′
Odp:
1
1
)
(
2
+
=
′
x
x
f
Odp:
0
)
(
=
′
x
f
d)
x
x
x
f
=
)
(
e)
2
arcsin
2
2
1
)
(
2
x
x
x
x
f
+
−
=
f)
x
e
x
x
f
2
)
(
−
=
Odp:
]
1
)
1
[(ln
)
(
2
x
x
x
x
f
x
+
+
=
′′
Odp:
2
2
)
(
x
x
f
−
=
′
Odp:
x
e
x
x
x
x
f
4
)
3
)(
2
(
)
(
−
−
=
′′
4.Wykazać, że funkcja
)
(
x
u
u
=
spełnia równanie różniczkowe
a)
;
1
1
ln
)
(
x
x
u
+
=
u
e
u
x
=
+
′
1
b)
;
2
1
)
(
2
2
x
e
x
u
x
−
−
=
2
2
x
e
u
u
x
−
=
+
′
c)
;
)
(
1
x
xe
x
u
−
=
0
3
=
+
′
−
′′
u
u
x
u
x
d)
x
e
x
u
x
sin
)
(
=
;
0
2
2
=
+
′
−
′′
u
u
u
5.Znaleźć równanie stycznej do krzywej
)
(
x
f
y
=
w punkcie o odciętej
o
x
gdy
13
a)
2
4
8
)
(
x
x
f
+
=
;
2
=
o
x
Odp:
0
4
2
=
−
+
y
x
b)
x
x
x
f
cos
)
(
+
=
;
π
=
0
x
Odp:
1
−
=
x
y
c)
2
1
arcsin
)
(
−
=
x
x
f
;
1
=
o
x
Odp:
)
1
(
2
1
−
=
x
y
d)
x
x
arctg
x
f
+
−
=
1
1
)
(
;
1
=
o
x
Odp:
1
+
−
=
x
y
6.Znaleźć różniczkę funkcji
)
;
(
0
dx
x
df
w punkcie
0
x
na przyroście argumentu
dx
gdy
a)
2
2
1
1
ln
)
(
x
x
x
f
+
−
=
dla
R
dx
x
∈
∧
=
2
1
0
Odp:
dx
dx
df
15
32
)
;
2
1
(
−
=
b)
5
)
(
2
+
=
x
x
f
dla
R
dx
x
o
∈
∧
=
2
Odp:
dx
dx
df
3
2
)
;
2
(
=
c)
arctgx
x
f
=
)
(
dla
1
,
0
1
−
=
∧
−
=
dx
x
o
Odp:
05
,
0
)
1
,
0
:
1
(
−
=
−
−
df
7.Obliczyć przyrost funkcji
)
;
(
0
dx
x
f
∆
i różniczkę funkcji
)
;
(
0
dx
x
df
w punkcie
o
x
na przyroście
argumentu
dx
, gdy
a)
3
1
)
(
x
x
f
+
=
dla
2
,
0
2
=
∧
=
dx
x
o
b)
2
1
1
)
(
x
x
f
+
=
dla
1
,
0
1
−
=
∧
−
=
dx
x
o
Odp;
=
−
+
=
∆
)
(
)
(
)
;
(
o
o
o
x
f
dx
x
f
dx
x
f
0,41 Odp:
0475
,
0
)
(
)
(
)
;
(
−
=
−
+
=
∆
o
o
o
x
f
dx
x
f
dx
x
f
4
,
0
)
(
)
;
(
'
=
=
dx
x
f
dx
x
df
o
o
05
,
0
)
(
)
(
'
−
=
=
dx
x
f
dx
x
df
o
o
8.Korzystając z różniczki
dx
x
f
x
f
dx
x
f
)
(
)
(
)
(
0
0
0
′
+
≈
+
obliczyć przybliżone wartości liczb
a)
3
02
,
8
Odp: 2,002 b)
03
,
0
e
Odp:
03
,
1
c)
96
,
0
arctg
Odp: 0,765
d)
97
,
0
ln
Odp:-0,03 e)
o
31
sin
Odp:
515
,
0
f)
54
,
0
arcsin
Odp: 0,57
9.Korzystając z reguły de l’Hospitala obliczyć granice
a)
2
0
lim
x
arctgx
x
x
−
→
Odp: 0 b)
−
−
→
1
1
ln
1
lim
1
x
x
x
Odp:
2
1
c)
x
tg
x
x
2
)
1
(
lim
1
π
−
→
Odp:
π
2
d)
x
x
x
ln
lim
2
0
+
→
Odp: 0 e)
−
−
→
1
1
1
lim
0
x
x
e
x
Odp:
2
1
f)
+
−
+∞
→
x
arctgx
x
1
1
ln
2
lim
π
Odp:
2
1
g)
( )
x
x
x
2
cos
1
1
lim
π
−
−
→
Odp:1 h)
x
x
arctgx)
2
(
lim
π
+∞
→
Odp:
π
2
−
e
i)
x
x
x
)]
1
[ln(
lim
0
+
→
Odp: 1
j)
x
x
ctgx
ln
1
0
)
(
lim
+
→
Odp:
e
1
k)
x
x
x
sin
0
lim
+
→
Odp: 1 l)
2
1
0
)
2
(cos
lim
x
x
x
→
Odp:
2
1
e
)
∗
m
2
1
0
sin
lim
x
x
x
x
→
Odp:
6
1
−
e
)
∗
n
x
x
arctgx
ln
1
2
lim
−
+∞
→
π
Odp:
e
1
o*)
x
x
x
x
x
2
cos
3
cos
lim
+
+
−∞
→
10..Zapisać wzór Taylora (z resztą Lagrangea) dla funkcji
a)
4
1
)
(
+
=
x
x
f
w punkcie
2
−
=
o
x
i dla
3
=
n
Odp:
3
4
2
)
2
(
)]
2
(
2
[
1
)
2
(
8
1
)
2
(
4
1
2
1
4
1
+
+
+
−
+
+
+
−
=
+
x
x
x
x
x
ϑ
dla
)
;
4
(
+∞
−
∈
x
b)
3
4
)
(
x
x
f
=
w punkcie
1
=
o
x
i dla
4
=
n
Odp:
4
3
8
3
2
3
4
)
1
(
)]
1
(
1
[
1
243
5
)
1
(
81
4
)
1
(
9
2
)
1
(
3
4
1
−
−
+
+
−
−
−
+
−
+
=
x
x
x
x
x
x
θ
dla
)
,
+∞
−∞
∈
x
14
c)
x
x
x
f
cos
)
(
=
w punkcie
2
π
=
o
x
i dla
3
=
n
. Odp: dla
)
,
(
+∞
−∞
∈
x
mamy
3
2
)
2
)](
2
(
2
cos(
3
)
2
(
2
sin(
)
2
(
2
[(
6
1
)
2
(
)
2
(
2
cos
π
π
θ
π
π
θ
π
π
θ
π
π
π
π
−
−
+
−
−
+
−
+
+
−
−
−
−
=
x
x
x
x
x
x
x
x
d)
x
e
x
f
x
sin
)
(
=
w punkcie
0
=
o
x
i dla
4
=
n
Odp:
4
3
2
)
sin(
6
1
3
1
sin
x
x
e
x
x
x
x
e
x
x
θ
θ
−
+
+
=
dla
)
,
(
+∞
−∞
∈
x
11.Obliczyć bezwzględny błąd przybliżenia funkcji wielomianem w podanym przedziale
a)
2
8
1
2
1
1
1
x
x
x
−
+
≈
+
dla
]
1
,
0
[
∈
x
Odp:
16
1
)
1
(
1
16
1
)
0
,
(
3
5
3
≤
+
=
x
x
x
R
θ
dla
]
1
,
0
[
∈
x
b)
3
3
1
x
x
tgx
+
≈
dla
1
,
0
≤
x
Odp:
5
4
6
2
4
1
,
0
)
(
cos
)]
(
sin
2
4
[
)
sin(
4
24
1
)
0
,
(
≤
+
=
x
x
x
x
x
R
θ
θ
θ
dla
1
,
0
≤
x
c)
2
3
9
1
3
1
1
1
x
x
x
−
+
≈
+
dla
]
2
1
,
0
[
∈
x
Odp:
3
3
3
8
3
2
1
81
5
)
1
(
1
81
5
)
0
,
(
⋅
≤
+
=
x
x
x
R
θ
d)
2
2
1
1
cos
x
x
−
≈
dla
2
1
≤
x
Odp:
384
1
2
1
1
24
1
)
cos(
!
4
1
)
0
,
(
4
4
4
=
⋅
⋅
≤
=
x
x
x
R
θ
dla
2
1
≤
x
12.Korzystając ze wzoru Taylora obliczyć przybliżoną wartość liczby i oszacować błąd
przybliżenia
a)
5
,
4
dla
3
=
n
; Odp :
12109375
,
2
5
,
0
32
1
!
2
1
5
,
0
4
1
!
1
1
2
5
,
4
2
≈
⋅
⋅
−
⋅
⋅
+
≈
⋅
≤
+
⋅
⋅
⋅
=
0002442
,
0
)
5
,
0
4
(
8
!
3
5
,
0
3
)
4
;
5
,
4
(
7
3
4
θ
R
121320344
,
2
5
,
4
≈
(kalkulator)
b)
1
,
1
ln
dla
4
=
n
; Odp:
095333
,
0
1
,
0
!
3
2
1
,
0
!
2
1
1
,
0
!
1
1
0
1
,
1
ln
3
2
=
⋅
+
⋅
−
⋅
+
≈
000025
,
0
1
,
0
)
1
,
0
1
(
1
!
4
6
)
0
,
1
;
1
,
1
(
4
4
4
≤
⋅
+
⋅
=
θ
R
(ln1,1=0,095310—kalkulator)
c)
3
,
0
sin
dla
6
=
n
; Odp:
29552025
,
0
3
,
0
!
5
1
3
,
0
!
3
1
3
,
0
!
1
1
3
,
0
sin
5
3
=
⋅
+
⋅
−
⋅
≈
7
6
6
10
3
3
,
0
!
6
)
3
,
0
sin(
)
0
;
3
,
0
(
⋅
≤
⋅
=
θ
R
[ bo
)
3
,
0
)
3
,
0
sin(
≤
θ
]
)
29552021
,
0
3
,
0
(sin
=
d)
4
1
e
dla
5
=
n
; Odp:
7788086
,
0
)
25
,
0
(
!
4
1
)
25
,
0
(
!
3
1
)
25
,
0
(
!
2
1
)
25
,
0
(
!
1
1
1
1
4
3
2
4
≈
−
+
−
+
−
+
−
+
=
e
6
5
5
25
,
0
5
10
1
,
8
!
5
25
,
0
25
,
0
!
5
)
0
;
25
,
0
(
⋅
=
≤
=
−
−
θ
e
R
)
7788008
,
0
1
(
25
,
0
4
kalkulator
e
e
−
=
=
−
13.Zbadać monotoniczność i wyznaczyć ekstrema funkcji f gdy
a)
x
e
x
x
f
1
2
)
(
=
Odp:
2
min
4
1
)
2
1
(
e
f
f
=
=
; maleje w
)
0
,
(
−∞
i
)
2
1
,
0
(
, rośnie w
)
,
2
1
(
+∞
rośnie w
)
0
,
(
−∞
i
)
,
3
2
(
∞
.
b)
x
x
x
f
2
ln
)
(
=
Odp:
;
4
)
(
,
0
)
1
(
2
2
max
min
−
−
=
=
=
=
e
e
f
f
f
f
maleje w
)
1
,
(
2
−
e
rośnie w
)
,
0
(
2
−
e
i
)
,
1
(
+∞
.
c)
x
arctgx
x
f
−
=
)
(
Odp: brak ekstremum; maleje w (-
)
,
+∞
∞
.

15
14.Korzystając z drugiego warunku dostatecznego zbadać czy funkcja
f
ma ekstremum w punkcie
o
x
:
a)
x
x
x
f
−
=
ln
2
)
(
dla
2
=
o
x
Odp:
2
2
ln
2
)
2
(
max
−
=
=
f
f
b)
2
cos
2
)
(
x
x
x
f
+
=
dla
0
0
=
x
Odp:
2
)
0
(
min
=
=
f
f
c)
x
x
x
x
f
1
ln
2
)
(
+
−
=
dla
1
=
o
x
Odp: brak ekstremum
15.Wyznaczyć najmniejszą największą wartość funkcji f w danym przedziale
a)
3
3
)
(
x
x
x
f
−
=
dla
]
8
,
1
[
−
∈
x
Odp:
1
)
0
(
5
)
8
(
max
min
=
=
∧
−
=
=
f
f
f
f
b)
x
x
arctg
x
f
+
−
=
1
1
)
(
dla
]
1
,
0
[
∈
x
Odp:
π
4
1
)
0
(
0
)
1
(
max
min
=
∧
=
=
f
f
f
c)
x
x
x
f
ln
)
(
2
=
dla
]
,
1
[ e
x
∈
Odp:
2
max
min
)
(
0
)
1
(
e
e
f
f
f
f
=
=
∧
=
=
16.Wyznaczyć punkty przegięcia oraz przedziały wypukłości i wklęsłości funkcji
a)
x
e
x
f
1
)
(
−
=
Odp:
;
)
2
1
(
2
−
=
=
e
f
f
p
wypukła w
)
0
,
(
−∞
i
)
2
1
,
0
(
, wklęsła w
)
,
2
1
(
+∞
.
b)
x
x
x
f
ln
)
(
2
=
Odp:
;
2
3
)
(
3
2
3
−
−
−
=
=
e
e
f
f
p
wklęsła w
)
,
0
(
2
3
−
e
, wypukła w
)
,
(
2
3
+∞
−
e
.
c)
2
4
)
(
x
x
x
f
−
=
Odp:
;
0
)
0
(
=
=
f
f
p
wypukła w
),
0
,
2
[
−
wklęsła w (0,2].
17.Zbadać funkcję i narysować wykres
a)
x
e
x
x
f
1
)
4
1
(
)
(
−
=
.Odp: asymptota pionowa prawostronna:
,
0
=
x
asymptota ukośna w (
∞
−
) i
(
∞
+
) :
4
3
+
=
x
y
; rosnąca w
)
0
,
(
−∞
i
);
,
0
(
+∞
,
4
1
)
2
1
(
2
e
f
f
p
=
=
wklęsła w
)
0
,
(
−∞
i
)
2
1
,
0
(
,
wypukła w
).
,
2
1
(
+∞
b)
x
x
x
f
ln
)
(
=
Odp: asymptota pionowa prawostron;na:
,
0
=
x
asymptota ukośna w
0
:
)
(
=
+∞
y
;
,
2
)
(
2
max
e
e
f
f
=
=
rosnąca w
),
,
0
(
2
e
malejąca w
);
,
(
2
+∞
e
,
3
8
)
(
3
4
3
8
−
=
=
e
e
f
f
p
wklęsła w
)
,
0
(
3
8
e
, wypukła w
).
,
(
3
8
+∞
e
c)
2
2
1
1
arcsin
)
(
x
x
x
f
+
−
=
Odp: asymptota pozioma w
)
(
−∞
i
;
2
:
)
(
π
−
=
+∞
y
2
)
0
(
max
π
=
=
f
f
ostrze,
rosnąca w
),
0
,
(
−∞
malejąca w
);
,
0
(
+∞
wypukła w
)
0
,
(
−∞
i
).
,
0
(
+∞
d)
x
xe
x
f
1
)
(
=
Odp: asymptota pionowa prawostronna:
,
0
=
x
asymptota ukośna w
)
(
−∞
i
)
(
+∞
:
;
1
+
=
x
y
,
)
1
(
min
e
f
f
=
=
rosnąca w
)
0
,
(
−∞
i
),
,
1
(
+∞
malejąca w
);
1
,
0
(
wklęsła w
),
0
,
(
−∞
wypukła w
).
,
0
(
+∞
e)
x
x
x
f
ln
)
(
=
Odp: asymptota pionowa prawostronna:
,
0
=
x
asymptota pozioma w
0
:
)
(
=
+∞
y
;
,
1
)
(
max
e
e
f
f
=
=
rosnąca w
),
,
0
(
e
malejąca w
);
,
(
+∞
e
2
3
2
3
2
3
)
(
−
=
=
e
e
f
f
p
, wklęsła w
),
,
0
(
2
3
e
16
wypukła w
).
,
(
2
3
+∞
e
f)
arcctgx
x
x
f
+
=
2
1
)
(
Odp: asymptota ukośna w
π
+
=
−∞
x
y
2
1
:
)
(
i
x
y
2
1
:
)
(
=
+∞
;
,
4
1
2
1
)
1
(
,
4
3
2
1
)
1
(
min
max
π
π
+
=
+
−
=
−
=
f
f
f
rosnąca w
)
1
,
(
−
−∞
i
),
,
1
(
+∞
malejąca w
)
1
,
1
(
−
;
,
2
)
0
(
π
=
=
f
f
p
wklęsła w
),
0
,
(
−∞
wypukła w
).
,
0
(
+∞
Kolokwium III (12p.)
Całka nieoznaczona oraz całka oznaczona właściwa i niewłaściwa.
1.Całkując bezpośrednio obliczyć całki
a)
dx
x
x
x
x
)
2
5
3
(
5
2
4
3
+
+
−
∫
Odp:
;
2
1
4
5
7
4
2
4
4
4
3
C
x
x
x
x
x
x
+
−
+
−
b)
dx
x
x
x
x
)
1
5
sinh
4
sin
1
1
9
(
2
2
2
+
+
+
+
−
−
∫
Odp:
;
5
cosh
4
arcsin
9
C
arctgx
x
ctgx
x
+
+
+
−
−
c)
xdx
ctg
∫
2
Odp:
;
C
x
ctgx
+
−
−
d)
∫
xdx
tg
2
Odp:
C
x
tgx
+
−
;
e)
dx
x
x
x
∫
−
sin
cos
2
cos
Odp:
;
cos
sin
C
x
x
+
−
f)
dx
x
x
x
∫
2
2
cos
sin
2
cos
Odp:
C
tgx
ctgx
+
−
−
;
g)
dx
x
x
∫
+
)
1
(
1
2
2
Odp:
;
1
C
arctgx
x
+
−
−
h)
dx
x
x
x
∫
+
+
)
1
(
)
1
(
2
2
Odp:
C
arctgx
x
+
+
2
ln
;
2.Zapisując funkcję podcałkową jako pochodną funkcji znależć całki
a)
dx
x
∫
2
3
Odp:
;
3
3
ln
2
1
2
C
x
+
⋅
b)
dx
e
x
∫
−
3
Odp:
;
3
1
3
C
e
x
+
−
−
c)
∫
dx
x
4
cos
1
2
Odp:
;
4
4
1
C
x
tg
+
d)
dx
x
∫
−
)
1
5
(
sin
1
2
Odp:
C
x
ctg
+
−
−
)
1
5
(
5
1
;
e)
dx
x
∫
+
2
4
1
1
Odp:
C
x
arctg
+
2
2
1
; f)
dx
x
∫
−
2
3
1
1
Odp:
C
x
+
3
arcsin
3
1
g)
∫
+
dx
x
3
5
4
1
Odp:
C
x
+
+
3
2
)
5
4
(
8
3
h)
dx
x
∫
+
5
)
2
3
(
Odp:
C
x
+
+
6
)
2
3
(
18
1
3.Korzystając ze wzorów na całkowanie przez części lub przez podstawienie obliczyć całki
a)
dx
x
x
∫
3
ln
Odp:
C
x
x
+
+
−
)
2
1
(ln
2
1
2
b)
dx
x
x
∫
ln
Odp:
C
x
x
+
−
)
2
(ln
2
;
c)
dx
x
tgx
∫
+
2
3
cos
3
Odp:
C
tgx
+
+
3
4
)
3
(
4
3
d)
∫
+
x
ctgx
2
sin
1
Odp:
C
x
ctg
ctgx
+
−
−
3
3
2
;
e)
dx
x
x
∫
2
sin
Odp:
;
sin
ln
C
x
xctgx
+
+
−
f)
dx
x
x
∫
2
cos
Odp:
C
x
xtgx
+
+
cos
ln
;
g)
dx
x
tgx
∫
)
ln(cos
Odp:
;
)
ln(cos
ln
C
x
+
−
h)
dx
x
ctgx
∫
)
ln(sin
Odp:
C
x
+
)
ln(sin
ln
;
i)
∫
xdx
arcsin
Odp:
;
1
arcsin
2
C
x
x
x
+
−
+
j)
∫
xarctgxdx
Odp:
;
]
)
1
[(
2
1
2
C
x
arctgx
x
+
−
+
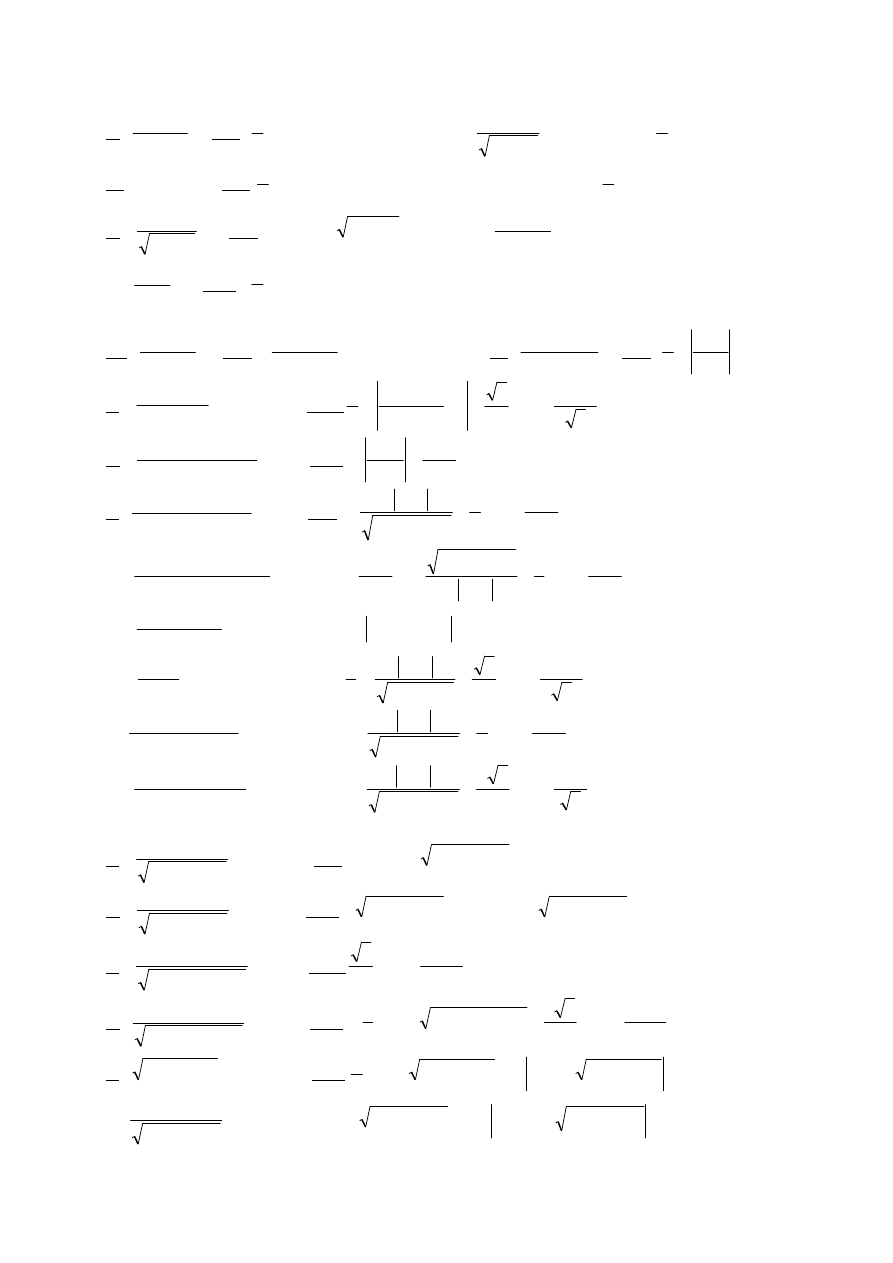
17
k)
dx
e
e
x
x
∫
+
2
4
1
Odp:
;
)
2
(
2
1
C
e
arctg
x
+
l)
dx
e
e
x
x
∫
−
2
4
Odp:
;
)
2
1
arcsin(
C
e
x
+
m)
∫
dx
x)
sin(ln
Odp:
)];
cos(ln
)
[sin(ln
2
1
x
x
x
−
n)
∫
dx
x)
cos(ln
Odp:
)];
cos(ln
)
[sin(ln
2
1
x
x
x
+
o)
dx
e
x
∫
+
2
1
1
Odp:
C
e
e
x
x
+
+
+
−
−
−
)
1
ln(
2
; p)
dx
e
e
x
x
∫
−
+
1
Odp:
C
arctge
x
+
;
r)
dx
x
x
∫
2
2
ln
Odp:
;
)
2
ln
2
(ln
1
2
C
x
x
x
+
+
+
−
s)
dx
x
∫
2
ln
Odp:
C
x
x
x
+
+
−
)
2
ln
2
(ln
2
;
4.Oliczyć całki funkcji wymiernych
a)
dx
x
∫
−
3
)
2
(
1
Odp:
;
)
2
(
2
1
2
C
x
+
−
−
b)
dx
x
x
∫
+
−
3
4
1
2
Odp:
C
x
x
+
−
−
1
3
ln
2
1
;
c)
dx
x
x
x
∫
+
+
1
2
Odp:
C
x
arctg
x
+
+
−
+
+
3
1
2
3
3
1
3
)
1
2
(
ln
2
1
2
;
d)
dx
x
x
x
∫
−
+
−
2
5
4
1
2
3
Odp:
;
1
1
1
2
ln
C
x
x
x
+
−
+
−
−
e)
dx
x
x
x
x
∫
+
+
+
+
5
7
3
5
2
3
Odp:
;
2
1
2
1
4
)
1
(
1
2
ln
2
C
x
arctg
x
x
+
+
+
+
+
+
f)
dx
x
x
x
x
x
∫
+
+
+
−
10
18
7
9
4
2
4
2
Odp:
;
3
1
3
1
1
3
9
)
1
(
ln
1
1
2
C
x
arctg
x
x
x
+
−
+
+
+
−
+
+
−
g)
dx
x
x
x
∫
+
−
−
1
2
2
1
4
2
Odp:
;
)
1
2
(
1
2
2
ln
2
C
x
arctg
x
x
+
−
+
+
−
h)
dx
x
∫
+
1
1
3
Odp:
;
3
1
2
3
3
1
1
ln
3
1
2
C
x
arctg
x
x
x
+
−
+
+
−
+
i)
dx
x
x
x
x
∫
−
+
+
+
5
3
5
3
2
3
Odp:
;
2
1
2
1
5
2
1
ln
2
C
x
arctg
x
x
x
+
+
+
+
+
−
j)
dx
x
x
x
x
∫
+
+
−
−
4
2
4
3
2
3
Odp:
;
3
1
3
3
2
4
2
1
ln
2
C
x
arctg
x
x
x
+
−
−
+
−
+
5.Obliczyć całki funkcji niewymiernych
a)
∫
+
−
5
2
2
x
x
dx
Odp:
;
)
5
2
1
ln(
2
C
x
x
x
+
+
−
+
−
b)
dx
x
x
x
∫
+
−
+
5
2
3
2
2
Odp:
;
)
5
2
1
ln(
7
5
2
2
2
2
C
x
x
x
x
x
+
+
−
+
−
+
+
−
c)
∫
+
+
−
1
2
3
2
x
x
dx
Odp:
;
2
1
3
arcsin
3
3
C
x
+
−
d)
dx
x
x
x
∫
+
+
−
+
1
2
3
1
2
2
2
Odp:
C
x
x
x
x
+
−
+
+
+
−
+
−
2
1
3
arcsin
3
3
5
1
2
3
)
1
(
3
1
2
;
e)
dx
x
x
∫
−
−
1
2
2
Odp:
;
1
2
1
ln
1
2
)
1
(
2
1
2
2
C
x
x
x
x
x
x
+
−
−
+
−
−
−
−
−
f)
dx
x
x
x
∫
+
−
−
5
4
4
3
2
Odp:
1
)
2
(
)
2
(
ln
2
5
4
3
2
2
+
−
+
−
+
+
−
x
x
x
x
+C;
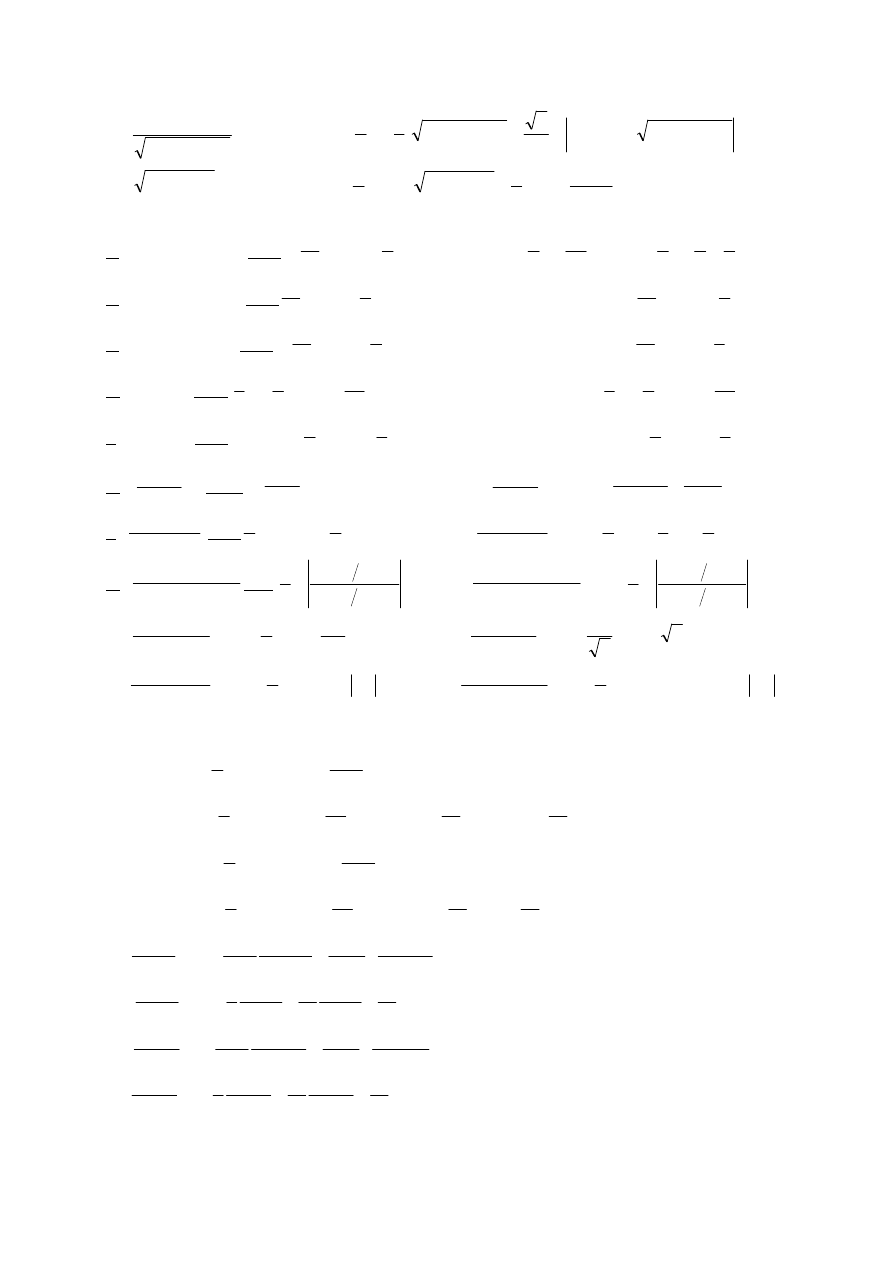
18
g)
dx
x
x
x
∫
+
+
1
2
2
2
2
Odp:
;
1
2
2
)
1
2
(
ln
16
2
1
2
2
)
8
3
4
1
(
2
2
C
x
x
x
x
x
x
+
+
+
+
+
+
+
+
−
h)
dx
x
x
∫
−
+
2
2
Odp:
;
3
1
2
arcsin
8
9
2
)
2
(
4
1
2
C
x
x
x
x
+
−
+
−
+
−
6.Znaleźć całki funkcji trygonometrycznych
a)
∫
xdx
x
5
cos
3
sin
Odp:
;
2
cos
4
1
8
cos
16
1
x
x
+
−
b)
dx
x
x
3
2
sin
3
sin
∫
Odp:
;
sin
2
1
3
sin
2
3
x
x
−
c)
∫
xdx
x
6
cos
3
cos
Odp:
;
3
sin
6
1
9
sin
18
1
x
x
+
d)
∫
xdx
x
2
cos
5
sin
Odp:
;
2
cos
6
1
7
cos
14
1
x
x
−
−
e)
∫
xdx
x
5
sin
3
sin
Odp:
;
2
sin
4
1
8
sin
16
1
x
x
+
−
f)
∫
xdx
x
6
cos
2
cos
Odp:
;
4
sin
8
1
8
sin
16
1
x
x
+
g)
xdx
∫
4
sin
Odp:
;
4
sin
32
1
2
sin
4
1
8
3
x
x
x
+
−
h)
∫
xdx
4
cos
Odp:
;
4
sin
32
1
2
sin
4
1
8
3
x
x
x
+
+
i)
∫
xdx
5
sin
Odp:
)
cos
5
1
cos
3
2
(cos
5
3
x
x
x
+
−
−
; j)
xdx
∫
5
cos
Odp:
;
sin
5
1
sin
3
2
sin
5
3
x
x
x
+
−
k)
dx
x
x
∫
2
3
sin
cos
Odp:
;
)
sin
sin
1
(
C
x
x
+
+
−
l)
dx
x
x
∫
4
3
cos
sin
Odp:
;
cos
1
cos
3
1
3
C
x
x
+
−
ł)
∫
−
x
dx
cos
3
5
Odp:
;
)
2
2
(
2
1
C
x
tg
arctg
+
m)
∫
+
x
dx
sin
4
5
Odp:
C
x
tg
arctg
+
+
)
4
2
5
(
3
1
3
2
;
n)
∫
+
x
x
dx
cos
4
sin
3
Odp:
;
4
)
2
(
2
1
)
2
(
2
ln
5
1
C
x
tg
x
tg
+
−
+
o)
∫
+
x
x
dx
sin
4
cos
3
Odp:
;
1
)
2
(
3
1
)
2
(
3
ln
5
1
C
x
tg
x
tg
+
−
+
p)
∫
+
x
dx
2
cos
3
1
Odp:
;
)
2
(
2
1
C
tgx
arctg
+
r)
∫
+
x
dx
2
sin
1
Odp:
;
)
2
(
2
1
C
tgx
arctg
+
s)
∫
x
x
dx
cos
sin
3
Odp:
;
ln
2
1
2
tgx
x
ctg
+
−
t)
∫
x
x
dx
3
3
cos
sin
Odp:
;
ln
2
)
(
2
1
2
2
tgx
x
ctg
x
tg
+
−
7.Wyprowadzić wzór rekurencyjny na obliczanie całek i obliczyć
a)
∫
xdx
n
cos
=
∫
−
−
−
+
,
cos
1
cos
sin
1
2
1
xdx
n
n
x
x
n
n
n
dla
,...;
4
,
3
,
2
=
n
;
16
5
cos
sin
16
5
cos
sin
24
5
cos
sin
6
1
cos
3
5
6
C
x
x
x
x
x
x
x
xdx
+
+
+
+
=
∫
b)
,
sin
1
sin
cos
1
sin
2
1
xdx
n
n
x
x
n
xdx
n
n
n
∫
∫
−
−
−
+
−
=
dla
,...;
4
,
3
,
2
=
n
;
16
5
cos
16
5
sin
cos
24
5
sin
cos
6
1
sin
3
5
6
C
x
x
x
x
x
x
xdx
+
+
−
−
−
=
∫
c)
,
sin
1
1
2
sin
cos
1
1
sin
1
2
1
dx
x
n
n
x
x
n
dx
x
n
n
n
∫
∫
−
−
−
−
+
−
−
=
dla
,...;
4
,
3
,
2
=
n
;
15
8
sin
cos
15
4
sin
cos
5
1
sin
1
3
5
6
C
ctgx
x
x
x
x
dx
x
+
−
−
−
=
∫
d)
,
cos
1
1
2
cos
sin
1
1
cos
1
2
1
dx
x
n
n
x
x
n
dx
x
n
n
n
∫
∫
−
−
−
−
+
−
=
dla
,...;
4
,
3
,
2
=
n
;
15
8
cos
sin
15
4
cos
sin
5
1
cos
1
3
5
6
C
tgx
x
x
x
x
dx
x
+
+
+
=
∫
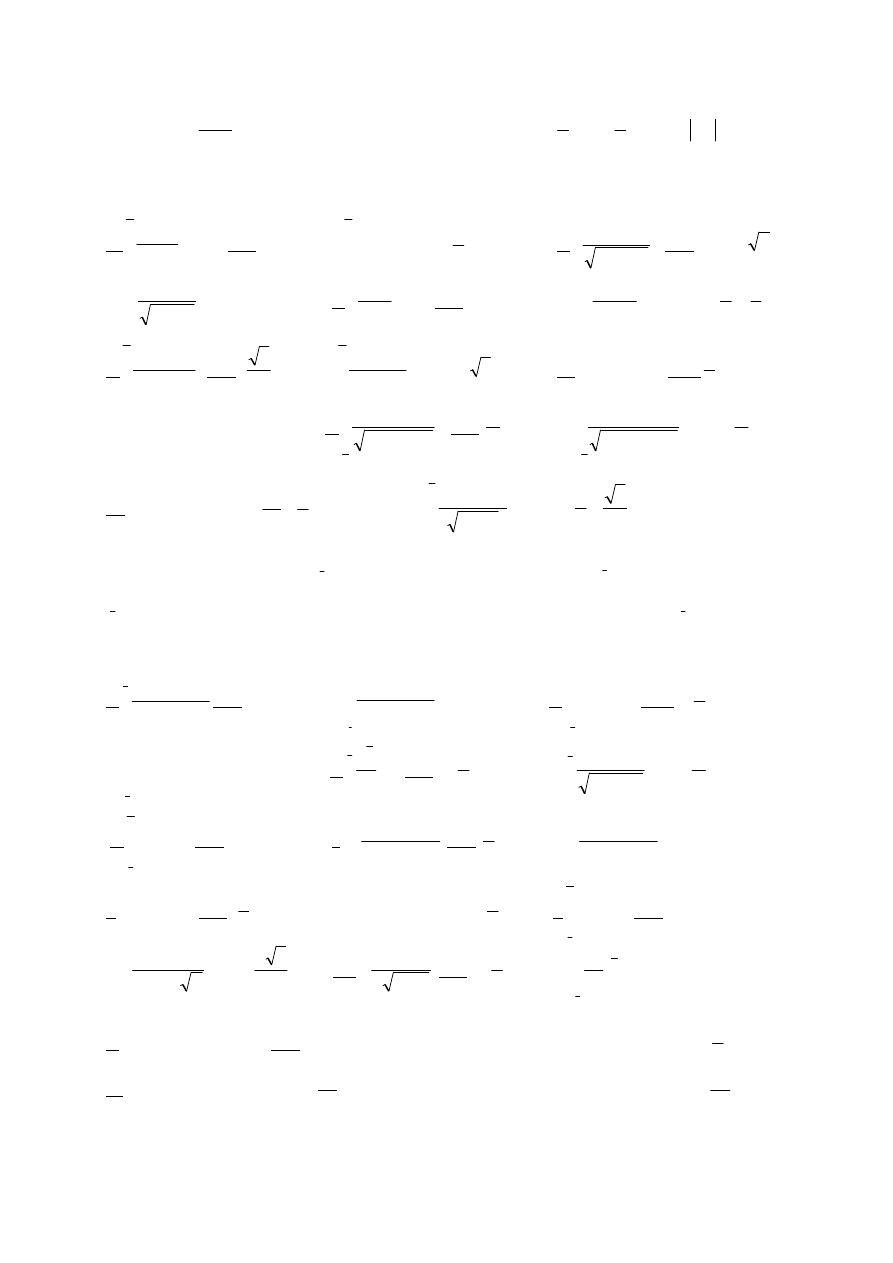
19
e)
∫
∫
−
−
−
−
=
xdx
tg
x
tg
n
xdx
tg
n
n
n
2
1
1
1
, dla
,...;
3
,
2
=
n
;
ln
2
1
4
1
2
4
5
C
tgx
x
tg
x
tg
x
tg
+
−
−
=
∫
f)
,
1
dx
e
x
n
e
x
dx
e
x
x
n
x
n
x
n
∫
∫
−
−
=
dla
,...;
2
,
1
=
n
;
6
6
3
2
3
3
C
e
xe
e
x
e
x
dx
e
x
x
x
x
x
x
+
−
+
−
=
∫
8. Obliczyć całki oznaczone właściwe
a)
∫
+
4
0
2
1
π
x
dx
Odp: 1; b)
∫
4
0
π
tgxdx
Odp:
;
2
ln
2
1
c)
∫
+
a
x
a
dx
0
2
2
Odp:
);
2
1
ln(
+
d)
dx
x
x
∫
−
2
0
2
4
Odp: 2; e)
∫
+
−
1
0
1
1
dx
x
x
Odp:
;
2
ln
2
1
−
f)
dx
x
x
x
∫
+
2
1
3
Odp:
;
5
8
ln
2
1
g)
∫
+
2
0
cos
2
π
x
dx
Odp:
;
9
3
π
h)
∫
+
3
0
sin
1
π
x
dx
Odp:
;
1
3
−
i)
dx
x
x
e
∫
1
2
ln
Odp:
);
1
2
(
9
1
3
+
e
k)
∫
π
0
2
sin xdx
x
Odp:
;
4
2
−
π
l)
∫
−
+
2
2
1
2
3
x
x
dx
Odp:
;
2
π
ł)
∫
−
−
+
1
2
1
2
2
8
x
x
dx
Odp:
;
6
π
m)
∫
1
0
2
arctgxdx
x
Odp:
);
2
ln
1
(
6
1
12
−
−
π
n)
dx
x
x
x
∫
−
2
1
0
2
1
arcsin
Odp:
;
12
3
2
1
π
−
9.Obliczyć całki oznaczone niewłaściwe
∫
∫
+
→
=
b
T
a
T
b
a
dx
x
f
dx
x
f
;
)
(
lim
)
(
;
)
(
lim
)
(
∫
∫
−
→
=
T
a
b
T
b
a
dx
x
f
dx
x
f
∫
∫
∫
+
=
b
a
c
a
b
c
dx
x
f
dx
x
f
dx
x
f
;
)
(
)
(
)
(
;
)
(
lim
)
(
∫
∫
−∞
→
∞
−
=
b
T
T
b
dx
x
f
dx
x
f
∫
∫
+∞
+∞
→
=
=
T
a
a
T
dx
x
f
dx
x
f
;
)
(
lim
)
(
;
)
(
)
(
)
(
∫
∫
∫
+∞
∞
−
+∞
∞
−
+
=
c
c
dx
x
f
dx
x
f
dx
x
f
a)
∫
+
−
2
0
2
6
5x
x
dx
Odp:rozb. b)
∫
+
−
2
1
2
3
4x
x
dx
Odp: rozb. c)
∫
1
0
ln xdx
x
Odp:
;
4
1
−
d)
dx
x
∫
1
0
ln
Odp: -1; e)
dx
x
e
x
∫
−
0
1
3
1
Odp:
;
2
e
−
f)
∫
−
4
2
2
4
x
x
dx
Odp:
;
2
π
g)
∫
4
0
2
π
dx
ctg
Odp: rozb. h)
∫
+∞
−
+
+
1
2
5
4
x
x
dx
Odp:
π
4
3
i)
∫
∞
−
+
−
0
2
3
4
x
x
dx
Odp:
;
2
ln
j)
∫
+∞
−
1
2
dx
e
x
x
Odp:
;
5
e
k)
∫
∞
−
0
2
dx
xe
x
Odp:
;
4
1
−
l)
∫
4
0
2
π
dx
ctg
Odp: rozb.
ł)
∫
+∞
+
1
)
3
(
x
x
dx
Odp:
;
9
3
2
π
m)
∫
−
∞
−
−
5
4
x
x
dx
Odp:
;
5
ln
2
1
−
n)
dx
e
x
x
1
0
3
1
∫
+∞
Odp: rozb.
10. Obliczyć pole obszaru ograniczonego krzywymi o równaniach
a)
,
ln
x
y
=
.
ln
2
x
y
=
Odp:
;
3
e
−
b)
,
2
2
x
x
y
−
=
.
0
=
+
y
x
Odp:
;
2
9
c)
,
0
=
x
).
1
(
2
−
=
y
y
x
Odp:
;
12
1
d)
,
8
2
=
+
x
y
.
0
2
=
−
x
y
Odp:
;
3
64
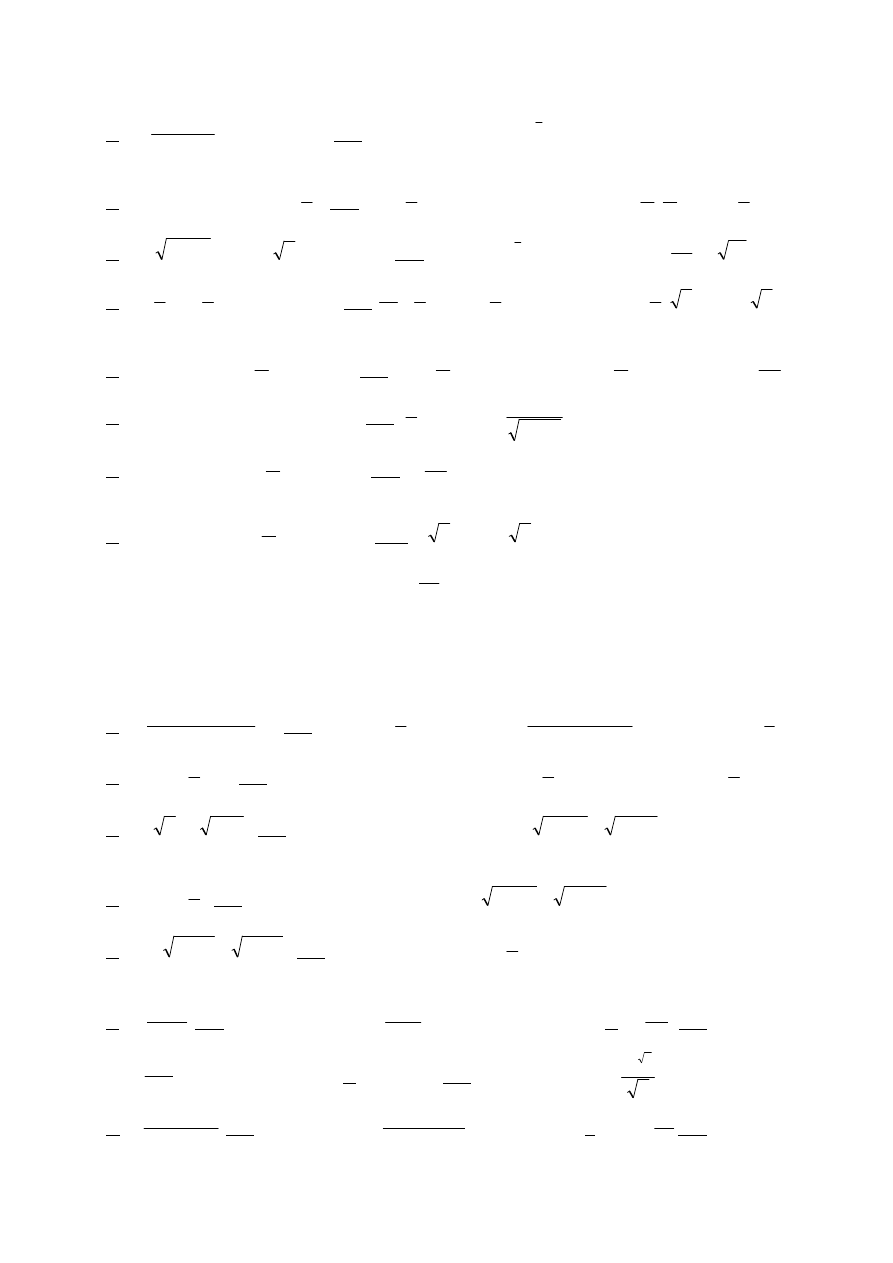
20
e)
,
)
1
(
1
2
+
=
x
x
y
,
0
=
y
.
1
≥
x
Odp:
;
2
ln
1
−
f)
,
2
2
1
x
xe
y
−
=
,
0
=
y
.
0
≥
x
Odp: 1;
11.Obliczyć długość łuku krzywej o równaniu
a)
)
1
ln(
2
x
y
−
=
dla
].
2
1
,
0
[
∈
x
Odp:
;
2
1
3
ln
−
b)
)
ln(sin
1
x
y
+
=
dla
];
2
,
3
[
π
π
∈
x
Odp:
;
3
ln
2
1
c)
x
x
x
y
arcsin
2
+
−
=
dla
];
1
,
0
[
∈
x
Odp: 2; d)
2
3
x
y
=
dla
];
4
,
0
[
∈
x
Odp:
);
1
10
10
(
27
8
−
e)
y
y
x
ln
4
1
2
1
2
−
=
dla
];
,
1
[
e
y
∈
Odp:
;
4
1
2
2
−
e
f)
2
2
1
y
x
=
dla
]
1
,
0
[
∈
x
Odp:
);
2
1
ln(
2
(
2
1
+
+
12.Obliczyć objętość obszaru powstałego przez obrót krzywej
a)
tgx
y
=
dla
]
4
,
0
[
π
∈
x
wokół osi x;Odp:
)
4
1
(
π
π
−
b)
x
y
sin
=
dla
]
2
,
0
[
π
∈
x
wokół osi x; Odp:
2
2
π
c)
x
xe
y
=
dla
]
1
,
(
−∞
∈
x
wokół osi x; Odp:
;
4
1
2
π
e
d)
2
1
1
x
y
+
=
dla
)
,
0
[
∞
∈
x
wokół osi x;
e)
x
y
sin
=
dla
]
2
,
0
[
π
∈
x
wokół osi y;Odp:
);
2
4
(
2
−
π
π
13.Obliczyć pole powierzchni bocznej obszaru powstałego przez obrót krzywej
a)
x
y
sin
=
dla
]
2
,
0
[
π
∈
x
wokół osi x; Odp:
)]
2
1
ln(
2
[
+
+
π
b)
x
y
4
2
=
dla
]
3
,
0
[
∈
x
wokół osi x. Odp:
;
3
56
π
Kolokwium IV (8p.)
Szeregi liczbowe
1.Korzystając z definicji zbadać zbieżność szeregu
a)
∑
∞
=
+
−
1
)
1
2
)(
1
2
(
1
n
n
n
Odp: zbieżny do
2
1
; b)
∑
∞
=
+
−
1
)
1
3
)(
1
3
(
1
n
n
n
Odp: zbieżny do
3
1
;
c)
)
1
1
ln(
1
∑
∞
=
+
n
n
Odp:rozbieżny; d)
n
n
)
3
2
(
1
∑
∞
=
−
Odp: zbieżny do
;
2
1
−
e)
)
1
(
1
1
+
∞
=
+
−
∑
n
n
n
n
n
Odp: zbieżny do 0; f)
)
1
2
3
2
(
1
+
−
+
∑
∞
=
n
n
n
Odp: rozbieżny;
2.Sprawdzić warunek konieczny zbieżności szeregu i wyciągnąć wniosek
a)
)
1
1
ln(
1
∑
∞
=
+
n
n
Odp: może być zbieżny; b)
)
1
2
3
2
(
1
+
−
+
∑
∞
=
n
n
n
Odp: może być zbieżny;
c)
)
1
1
(
2
1
2
−
−
+
∑
∞
=
n
n
n
n
Odp: rozbieżny; d)
∑
∞
=
1
1
sin
n
n
n
Odp: rozbieżny;
3.Korzystając z kryterium całkowego lub porównawczego zbadać zbieżność szeregu
a)
∑
∞
=
2
ln
1
n
n
n
Odp:rozbieżny b)
∑
∞
=
1
2
ln
n
n
n
Odp: rozbieżny; c)
∑
∞
=
1
2
3
n
n
e
n
Odp: zbieżny;
d)
∑
∞
=
1
2
ln
n
n
n
Odp: zbieżny; e)
∑
∞
=
1
n
arcctgn
Odp: rozbieżny f)
∑
∞
=
−
1
n
n
n
e
Odp: zbieżny;
g)
∑
∞
=
+
+
+
1
2
1
3
5
2
n
n
n
n
Odp: rozbieżny h)
∑
∞
=
+
−
+
1
3
1
3
3
1
2
n
n
n
n
Odp: zbieżny i)
∑
∞
=
1
2
1
sin
n
n
n
Odp: rozbieżny;
21
j)
∑
∞
=
1
2
1
n
n
tg
Odp: zbieżny; k)
)
1
1
ln(
1
1
n
n
n
+
∑
∞
=
Odp: zbieżny l)
n
n
n
1
sin
1
1
∑
∞
=
Odp: zbieżny;
{
x
x
≤
sin
dla
;
0
≥
x
π
2
sin
≥
x
dla
];
2
,
0
[
π
∈
x
x
tgx
≥
dla
)
2
,
0
[
π
∈
x
;
x
tgx
π
4
≤
dla
];
4
,
0
[
π
∈
x
1
ln
−
≤
x
x
dla
;
0
≥
x
x
x
≤
+
)
1
ln(
dla
;
0
≥
x
}
4.Korzystając z kryterium d’Alemberta lub kryterium Cauchyego zbadać zbieżność szeregu.
Jeśli
n
n
n
a
a
g
1
lim
+
∞
→
=
oraz
α
)
,
1
<
g
to
∑
n
a
zbieżny bezwzględnie;
β
)
,
1
>
g
to
∑
n
a
rozbieżny.
Jeśli
n
n
n
a
g
∞
→
=
lim
oraz
α
)
,
1
<
g
to
∑
n
a
zbieżny bezwzględnie;
β
)
,
1
>
g
to
∑
n
a
rozbieżny.
a)
∑
∞
=
1
!
3
n
n
n
n
n
Odp: zbieżny; b)
∑
∞
=
1
2
)!
2
(
n
n
n
n
Odp: zbieżny; c)
)!
2
(
)
!
(
)
1
(
2
1
1
n
n
n
n
∑
∞
=
+
−
Odp: zbieżny bezwgl.
d)
2
2
1
)
!
(
4
)
1
(
n
n
n
n
n
n
∑
∞
=
−
Odp:rozb.; e)
∑
∞
=
+
+
1
2
2
)
1
2
(
)
1
(
n
n
n
n
n
Odp: zb.; f)
∑
∞
=
+
1
2
)
1
2
(
n
n
n
n
Odp: zbieżny;
g)
2
)
2
3
(
)
1
(
1
n
n
n
n
n
+
+
−
∑
∞
=
Odp: rozb.; h)
n
n
n
n
n
n
2
)
1
(
)
1
(
2
1
+
−
∑
∞
=
Odp: zb. bezwgl.; i)
n
n
n
)
1
(arcsin
1
∑
∞
=
;
5.Zbadać zbieżność bezwzględną i warunkową szeregu
a)
∑
∞
=
+
−
1
2
1
2
)
1
(
n
n
n
n
Odp: zb.war.; b)
∑
∞
=
−
2
2
ln
)
1
(
n
n
n
n
Odp: zb.bezwgl.; c)
n
n
n
n
n
)
1
2
(
)
1
(
1
+
−
∑
∞
=
Odp: rozb.;
d)
∑
∞
=
+
−
2
1
ln
)
1
(
n
n
n
n
Odp: zb.war. e)
n
n
n
n
ln
)
1
(
1
∑
∞
=
−
Odp: zb. war.; f)
∑
∞
=
+
+
−
1
2
1
2
)
1
(
n
n
n
n
Odp: zb.war.;
g)
∑
∞
=
−
2
ln
)
1
(
n
n
n
n
Odp: zb.war.; h)
∑
∞
=
−
1
4
!
)
1
(
n
n
n
n
Odp: rozbieżny; i)
∑
∞
=
−
1
1
sin
)
1
(
n
n
n
Odp: zb.war.;
6.Wyznaczyć przybliżoną wartość sumy szeregu z dokładnością 0,01, gdy
a)
∑
∞
=
+
−
1
2
1
)
1
(
n
n
n
Odp:
83
,
0
9
=
≈
S
S
; b)
∑
∞
=
+
−
1
1
2
)
1
(
n
n
n
n
Odp:
40
,
0
4
=
≈
S
S
;
c)
∑
∞
=
+
−
1
1
!
2
)
1
(
n
n
n
n
Odp:
;
87
,
0
7
=
≈
S
S
7.Zbadać zbieżność punktową ciągu funkcyjnego
a)
n
n
x
x
f
=
)
(
dla
]
1
,
0
[
∈
x
Odp: zbieżny do funkcji
;
0
1
)
1
,
0
[
0
)
(
=
∈
=
x
dla
x
dla
x
f
b)
2
2
1
)
(
n
x
x
f
n
+
=
dla
)
,
(
+∞
−∞
∈
x
Odp: zbieżny do funkcji
x
x
f
=
)
(
dla
)
,
(
+∞
−∞
∈
x
;
c)
n
x
n
x
f
n
sin
)
(
=
dla
)
,
(
+∞
−∞
∈
x
Odp: zbieżny do funkcji
x
x
f
=
)
(
dla
);
,
(
+∞
−∞
∈
x
d)
x
n
x
n
x
f
n
2
2
1
)
(
+
=
dla
)
,
(
+∞
−∞
∈
x
Odp: zbieżny do funkcji
;
0
0
0
1
)
(
=
≠
=
x
dla
x
dla
x
x
f
e)
)
1
(
)
(
x
n
x
n
x
f
n
−
+
=
dla
)
,
0
(
+∞
∈
x
Odp: zbieżny do funkcji
x
x
f
2
1
)
(
=
dla
)
,
0
(
+∞
∈
x
;
22
8.Korzystając z definicji zbadać zbieżność punktową szeregu funkcyjnego
)
(
1
x
f
n
n
∑
∞
=
dla x
∈
D;
Dla ustalonego
D
x
∈
tworzymy ciąg sum częściowych
)
(
...
)
(
)
(
)
(
2
1
x
f
x
f
x
f
x
S
n
n
+
+
+
=
i
obliczamy
)
(
)
(
lim
x
S
x
S
n
n
=
∞
→
.
a)
∑
∞
=
−
1
2
n
nx
e
dla
)
,
0
(
+∞
∈
x
Odp:zbieżny do funkcji
x
x
e
e
x
S
2
2
1
)
(
−
−
+
=
dla
);
,
0
(
+∞
∈
x
b)
∑
+∞
=
−
−
1
1
2
)
1
(
n
n
x
x
dla
)
1
,
0
(
∈
x
Odp: zbieżny do funkcji
x
x
S
=
)
(
dla
);
1
,
0
(
∈
x
c)
∑
∞
=
+
1
2
2
)
1
(
n
n
x
x
dla
)
,
(
+∞
−∞
∈
x
Odp: zbieżny do funkcji
1
)
(
2
+
=
x
x
S
dla
);
,
(
+∞
−∞
∈
x
9.Znaleźć zakres zbieżności punktowej szeregu funkcyjnego
a)
n
n
x
x
n
)
1
2
(
1
∑
∞
=
+
Dla ustalonego
}
2
1
{
−
−
∈
R
x
obliczamy granicę
1
2
)
(
lim
)
(
+
=
=
∞
→
x
x
x
f
x
g
n
n
n
Gdy g(x)<1 , to szereg jest zbieżny bezwzględnie w zbiorze
);
,
3
1
(
)
1
,
(
+∞
−
∪
−
−∞
b)
∑
∞
=
−
1
)
1
(
n
x
n
n
Odp: zbieżny warunkowo w
]
1
.
0
(
oraz zbieżny bezwzględnie w
);
,
1
(
+∞
c)
∑
∞
=
1
2
sin
2
n
n
n
n
x
Odp: zbieżny bezwzględnie w zbiorze
)
2
6
5
(
)
6
1
,
2
6
1
(
π
π
π
π
π
k
k
+
∪
+
−
;
d)
∑
∞
=
−
1
2
2
n
nx
n
e
Odp: zbieżny bezwzględnie w zbiorze
);
,
(
+∞
−∞
e)
n
n
x
x
n
)
2
3
(
1
∑
∞
=
+
Odp: zbieżny bezwzględnie w zbiorze
)
1
,
2
1
(
−
;
f)
∑
∞
=
1
n
nx
e
nx
Odp: zbieżny bezwzględnie w zbiorze
)
,
0
[
+∞
;
g)
n
n
x
x
n
)
1
1
(
1
1
−
+
∑
∞
=
Odp: zbieżny w zbiorze
]
0
,
(
−∞
;
10.Wyznaczyć promień i znaleźć zakres zbieżności szeregu potęgowego
a)
∑
∞
=
⋅
−
1
2
)
3
(
n
n
n
n
x
Dla ustalonego
R
x
∈
, obliczamy granicę
2
3
)
(
lim
)
(
−
=
=
∞
→
x
x
f
x
g
n
n
n
Gdy
1
)
(
<
x
g
, to szereg zbieżny , a więc
2
3
<
−
x
a stąd
.
2
=
R
Zakres zbieżności
)
5
,
1
[
;
b)
n
n
x
n
n
)
1
(
)
!
(
)!
2
(
1
2
+
∑
∞
=
Dla ustalonego
}
1
{
−
−
∈
R
x
, obliczamy granicę
1
4
)
(
)
(
lim
)
(
1
+
=
=
+
∞
→
x
x
f
x
f
x
g
n
n
n
Gdy
1
)
(
<
x
g
, to szereg zbieżny , a więc
4
1
1
<
+
x
, a stąd
4
1
=
R
.
c)
n
n
n
n
x
n
2
1
1
4
3
⋅
⋅
∑
∞
=
+
Odp: promień
3
3
2
=
R
, zakres zbieżności
)
3
3
2
,
3
3
2
(
−
;
d)
∑
∞
=
+
⋅
2
3
)
1
(
ln
1
n
n
x
x
n
Odp: promień
1
=
R
, zakres zbieżności [-1,1];
23
e)
n
n
n
x
n
)
2
(
!
3
1
+
⋅
∑
∞
=
Odp: promień
+∞
=
R
, zakres zbieżności
)
,
(
+∞
−∞
;
f)
n
n
n
x
n
)
3
2
(
)
1
(
1
−
⋅
−
∑
∞
=
Odp: promień
2
1
=
R
, zakres zbieżności (1,2] ;
g)
∑
∞
=
−
2
ln
)
2
(
n
n
n
n
x
Odp: promień
1
=
R
, zakres zbieżności [1,3] ;
h)
n
n
n
x
n
2
1
4
⋅
∑
∞
=
Odp: promień
2
1
=
R
, zakres zbieżności
)
2
1
,
2
1
(
−
;i)
n
n
x
n
n
)
3
(
!
)!
2
(
1
+
⋅
∑
∞
−
Odp:
promień
0
=
R
, zakres zbieżności punkt {-3};
11.Korzystając ze znanych rozwinięć, rozwinąć w szereg Taylora (Maclaurina) funkcję
a)
2
3
1
)
(
2
+
−
=
x
x
x
f
w p-cie
0
=
o
x
Odp:
n
n
n
x
x
f
)
2
1
1
(
)
(
0
1
∑
∞
=
+
−
=
dla
)
1
,
1
(
−
∈
x
;
b)
2
2
4
)
(
x
x
x
x
f
−
+
+
=
w p-cie
0
=
o
x
Odp:
n
n
n
n
x
x
f
]
2
1
)
1
[(
)
(
0
∑
∞
=
+
−
=
dla
)
1
,
1
(
−
∈
x
;
c)
)
3
4
ln(
)
(
x
x
f
+
=
w p-cie
0
=
o
x
Odp:
1
0
1
1
4
)
1
(
3
)
1
(
4
ln
)
(
+
∞
=
+
+
⋅
+
−
+
=
∑
n
n
n
n
n
x
n
x
f
dla
)
3
4
,
3
4
(
−
∈
x
;
d)
)
2
3
ln(
)
(
x
x
f
+
=
w p-cie
0
=
o
x
Odp:
1
0
1
1
3
)
1
(
2
)
1
(
3
ln
)
(
+
∞
=
+
+
⋅
+
−
+
=
∑
n
n
n
n
n
x
n
x
f
dla
)
2
3
,
2
3
(
−
∈
x
;
e)
2
)
1
(
1
)
(
x
x
f
−
=
w p-cie
0
=
o
x
Odp:
∑
∞
=
−
=
1
1
)
(
n
n
nx
x
f
dla
)
1
,
1
(
−
∈
x
;
f)
2
)
2
(
1
)
(
+
=
x
x
f
w p-cie
0
=
o
x
Odp:
1
1
1
1
2
)
1
(
)
(
−
+
∞
=
+
∑
−
=
n
n
n
n
x
n
x
f
dla
)
2
,
2
(
−
∈
x
;
g)
x
x
f
2
sin
)
(
=
w p-cie
0
=
o
x
Odp:
n
n
n
n
x
n
x
f
2
1
2
1
)!
2
(
2
)
1
(
)
(
−
∞
=
∑
−
=
dla
)
,
(
+∞
−∞
∈
x
;
h)
x
x
f
2
cos
)
(
=
w p-cie
0
=
o
x
Odp:
n
n
n
n
x
n
x
f
2
1
2
1
)!
2
(
2
)
1
(
1
)
(
−
∞
=
∑
−
+
=
dla
)
,
(
+∞
−∞
∈
x
;
i)
x
arctg
x
f
2
)
(
=
w p-cie
0
=
o
x
Odp:
n
n
n
n
x
n
x
f
2
0
1
2
1
2
2
)
1
(
)
(
∑
∞
=
+
+
−
=
dla
)
2
1
,
2
1
(
−
∈
x
;
j)
x
xe
x
f
2
)
(
−
=
w p-cie
0
=
o
x
Odp:
1
0
!
2
)
1
(
)
(
+
∞
=
∑
−
=
n
n
n
n
x
n
x
f
dla
)
,
(
+∞
−∞
∈
x
;
k)
x
x
f
1
)
(
=
w p-cie
2
=
o
x
Odp:
n
n
n
n
x
x
f
)
2
(
2
)
1
(
)
(
0
1
−
−
=
∑
∞
=
+
dla
)
4
,
0
(
∈
x
;
l)
x
e
x
f
=
)
(
w p-cie
1
−
=
o
x
Odp:
n
n
x
n
e
x
f
)
1
(
!
1
1
)
(
0
+
=
∑
∞
=
dla
)
,
(
+∞
−∞
∈
x
;
m)
x
x
f
cos
)
(
=
w p-cie
2
π
=
o
x
Odp:
1
2
0
1
)
2
(
)!
1
2
(
)
1
(
)
(
+
∞
=
+
−
+
−
=
∑
n
n
n
x
n
x
f
π
dla
)
,
(
+∞
−∞
∈
x
;
n)
x
x
f
ln
)
(
=
w p-cie
1
=
o
x
Odp:
1
0
)
1
(
1
)
1
(
)
(
+
∞
=
−
+
−
=
∑
n
n
n
x
n
x
f
dla
)
2
,
0
(
∈
x
;
12.Obliczyć z dokładnością do
3
10
−
całkę, wykorzystując rozwinięcie funkcji podcałkowej w szereg
potęgowy

24
a)
dx
x
x
∫
1
0
sin
Odp:
720
681
; b)
∫
−
5
,
0
0
2
dx
e
x
Odp:
960
523
;
∫
4
2
1
dx
e
x
Odp:
835
,
2
;
UWAGA: Zadania oznaczone tłustym drukiem są zadaniami do rozwiązania w domu.
LITERATURA
T.Jurlewicz, Z.Skoczylas:Algebrai geometria analityczna (definicje, twierdzenia,wzory),OWGiS.
T.Jurlewicz, Z. Skoczylas: Algebra i geometria analityczna (przykłady i zadania), OWGiS.
M.Gewert, Z. Skoczylas: Analiza matematycznaI (definicje, twierdzenia,wzory), OWGiS.
M.Gewert, Z. Skoczylas: Analiza matematycznaI (przykłady i zadania), OWGiS.
M.Gewert, Z. Skoczylas: Analiza matematycznaII (definicje, twierdzenia,wzory), OWGiS.
M.Gewert, Z. Skoczylas: Analiza matematycznaII (przykłady i zadania), OWGiS.
H.Łubowicz, B.Wieprzkowicz: Matematyka. Podstawowe wiadomości teoretyczne i ćwiczenia,
H.Łubowicz, B.Wieprzkowicz: Matematyka. Podstawowe wiadomości teoretyczne i ćwiczenia,
H.Łubowicz, B.Wieprzkowicz: Matematyka. Podstawowe wiadomości teoretyczne i ćwiczenia,
H.Łubowicz, B.Wieprzkowicz: Matematyka. Podstawowe wiadomości teoretyczne i ćwiczenia, OWPW.
G.Decewicz, W.śakowski: Matematyka, część 1.WNT.
W.śakowski,W.Kołodziej:Matematyka, część 2.WNT.
L. Maurin, M. Mączyński, T.Traczyk: Matematyka-podręcznik dla studentów wydziałów chemicznych.
M.Mączyński, J.Muszyński, T.Traczyk, W.śakowski: Matematyka,podręcznik podstawowy dla WST.
ZALICZENIE ĆWICZEŃ I EGZAMINU
4-ry kolokwia w sumie za
36,0p. i aktywność na ćwiczeniach 4,0p. Do uzyskania jest 40,0p.
Oceny : [21;24]-
3,0; [25;28]-3,5; [29;32]-4,0; [33;36]-4,5; [37;40]-5,0
Zaliczenie ćwiczeń jest warunkiem przystąpienia do egzaminu.
ZALICZENIE PRZEDMIOTU
EGZAMIN=CZĘŚĆ ZADANIOWA EGZAMINU + CZĘŚĆ TEORETYCZNA EGZAMINU
Z cześci zadaniowej można uzyskać max
30,0p. zalicza 15,0p.
Z cześci teoretycznej można uzyskać max
30,0p zalicza 15,0p.
Student , który z zaliczenia uzyskał co najmniej 25,0p.oraz zaliczył wszystkie kolokwia może
być zwolniony z części zadaniowej egzaminu.
Wtedy za ten egzamin otrzymuje premię zależną od liczby punktów z zaliczenia ćwiczeń
następująco: 25p.-
15p.; 26p.- 16p.; ……………. ;40p.-30p.
Część teoretyczną można zaliczać na egzaminie lub na organizowanych w trakcie trwania
semestru dwóch repetytoriach.Pierwsze odbędzie się w połowie semestru a drugie pod koniec
semestru. Z każdego repetytorium można uzyskać max 15,0p. zalicza 8,0p.
Na końcową ocenę z przedmiotu składa się suma punktów uzyskanych z zaliczenia, części
zadaniowej egzaminu i części teoretycznej egzaminu, można uzyskać max 1
00p.Zalicza 51p.
ocena końcowa=zaliczenie ćwiczeń+część zadaniowa egzaminu+ część teoretyczna egzaminu
Ocena końcowa przedmiotu:[51;60]-
3,0 [61-70]-3,5 [71;80]-4,0 [81;90]-4,5 [91;100]-5,0.

25
PYTANIA NA REPRTYTORIUM I
1.Definicja modułu i argumentu liczby zespolonej wraz z interpretacją geometryczną. Postać
trygonometryczna i wzór Moivrea. Obliczyć np: a)
10
)
1
(
i
−
; b)
15
)
3
(
i
+
−
2. Definicja pierwiastka liczby zespolonej. Znależć pierwiastki liczby zespolonej np.: a)
3
i
; b)
3
1
−
i zaznaczyć na płaszczyżnie zespolonej.
3.Twierdzenie podstawowe algebry i własność wielomianu zespolonego współczynnikach
rzeczywistych. Znależć rozkład wielomianu na czynniki np.:
20
16
9
4
)
(
2
3
4
+
+
+
+
=
z
z
z
z
z
w
wiedząć, że liczba zespolona
i
z
2
1
=
jest miejscem zerowym tego wielomianu.
4. Definicja wyznacznika macierzy. Własności wyznaczników. Korzystając z własności obliczyć
wyznacznik macierzy…….
5. Definicja macierzy odwrotnej. Metoda wyznaczania macierzy odwrotnej. Znależć macierz odwrotną
macierzy….
6.Definicja rzędu macierzy. Własności rzędu macierzy. Obliczyć rząd macierzy, sprowadzając
macierz do postaci bazowej……
7.Definicja ogólnego układu równań liniowych. Twierdzenie Kroneckera-Capelliego. Zbadać
rozwiązywalność układu równań liniowych sprowadzając układ do postaci bazowej…..
8.Definicja i własności iloczynu skalarnego wektorów. Długość wektora i własności długości
wektora. Definicje wektorów równoległych, prostopadłych, kąta między wektorami i pola trójkąta
rozpiętego na wektorach. Obliczyć kąt miedzy wektorami….
9.Definicja iloczynu wektorowego wektorów wraz z interpretacją geometryczną. Metoda oblicznia
i własności iloczynu wektorowego. Obliczyć pole i wysokość trójkąta o wierzchołkach…..
10.Definicja płaszczyzny w przestrzeni R
3
. Postać parametryczna i kanoniczna płaszczyzny.
Znależć równanie płaszczyzny przechodzącej przez……
11.Podać wzory na odległość punktu od płaszczyzny danej w postaci parametrycznej i kanonicznej
z objaśnieniami. Znależć np.:odległość punktu A=(2,-1,3) od płaszczyzny H: 3x
1
-2x
2
+4x
3
+4=0.
12.Definicja prostej w przestrzeni R
3
. Postać parametryczna, kierunkowa i krawędziowa prostej.
Znależć prostą w tych postaciach przechodzącą przez……
13.Podać wzory na odległość prostych równoległych i skośnych z objaśnieniami. Znależć odległość
między prostymi np.:
=
+
−
+
=
+
+
−
=
−
+
=
−
0
1
0
2
2
:
...
...
2
1
1
2
2
:
3
2
1
3
2
1
2
3
2
1
1
x
x
x
x
x
x
L
i
x
x
x
L
14.Definicja ciągu liczbowego oraz definicje ciągu monotonicznego i ograniczonego. Zbadać
monotoniczność i ograniczoność ciągu….
15.Definicja granicy ciągu . Własności ciągów zbieżnych. Wykazać z definicji,że np.:
a)
3
3
1
2
lim
=
+
+
∞
→
n
n
n
; b)
istnieje
nie
n
n
n
n
..
3
1
)
1
(
lim
−
+
+
⋅
−
∞
→
16.Definicja funkcji różnowartościowej , na zbiór i odwrotnej. Funkcje odwrotne do funkcji
trygonometrycznych wraz z interpretacją geometryczną.
17. Funkcje hiperboliczne i funkcje do nich odwrotne wraz z interpretacją geometryczną.
18.Definicja granicy funkcji w sensie Heinego. Z definicji granicę funkcji obliczyć
np.: a)
x
x
x
x
2
4
lim
2
2
2
−
−
→
b)wykazać, że
x
x
sin
lim
∞
→
nie istnieje
19. Definicja ciągłości funkcji. Własności funkcji ciągłych. Zbadać ciągłość funkcji
a)
=
≠
+
=
0
1
0
)
(
4
2
x
dla
x
dla
x
x
x
x
f
b)
=
≠
−
=
0
1
0
cos
1
)
(
2
x
dla
x
dla
x
x
x
f
20. Definicje asymptot pionowych, poziomych i ukośnych funkcji. Twierdzenie o asymptocie
Ukośnej. Wyznaczyć asymptoty funkcji i sporządzić wykres funkcji
a)
1
1
)
(
−
=
x
e
x
f
; b)
x
x
x
f
1
)
(
2
−
=
; c)
arctgx
x
x
f
−
=
)
(
; d)
x
x
x
f
1
)
(
−
=

26
PYTANIA NA REPETYTORIUM II
1.Definicja pochodnej funkcji wraz z interpretacją geometryczną. Obliczyć z definicji pochodną
funkcji np.: a)
5
2
)
(
+
=
x
x
f
w punkcie x
0
=2; b)
x
x
f
sin
)
(
=
w punkcie
R
x
∈
2.Definicja różniczki funkcji wraz z interpretacją geometryczną. Twierdzenie o przyroście i jego
zastosowania . Korzystając z różniczki obliczyć przybliżoną wartość liczby a)
02
,
9
.;b)
54
,
0
arcsin
3.Podać twierdzenie de L’Hospitala z uwagami. Korzystając z twierdzenia de L’Hospitala obliczyć
granicę a)
x
x
x
ln
lim
2
0
+
→
; b)
)]
1
(
lim
1
−
−∞
→
x
x
e
x
; c)
x
x
ctgx
ln
1
0
)
(
lim
+
→
; d)
x
x
x
sin
0
lim
+
→
; e)
2
1
0
)
2
(cos
lim
x
x
x
→
4.Podać twierdzenie Lagrangea wraz z interpretacją geometryczną. Podać wnioski z tego twierdzenia
i jeden udowodnić.
5)Podać twierdzenie Taylora z objaśnieniami.Zapisać wzór Taylora (z resztą Lagrangea) dla funkcji
a)
x
x
f
ln
)
(
=
w punkcie
1
=
o
x
i dla
3
=
n
c)
x
x
x
f
cos
)
(
=
w punkcie
2
π
=
o
x
i dla
3
=
n
6.Definicja ekstremum funkcji wraz z interpretacją geometryczną. Warunek konieczny na ekstremum
funkcji i uwagi. Podać przykład na to, że jest to tylko warunek konieczny.
7.Podać pierwszy warunek dostateczny na ekstremum.. Korzystając z pierwszego warunku na
ekstremum wyznaczyć ekstrema lokalne funkcji, oraz zbadać monotoniczność funkcji, gdy
a)
x
e
x
x
f
1
2
)
(
=
b)
x
x
x
f
2
ln
)
(
=
c)
x
arctgx
x
f
−
=
)
(
d)
2
2
)
1
2
ln(
2
1
)
(
−
−
=
x
x
x
f
8.Podać drugi warunek dostateczny na ekstremum.Korzystając z drugiego warunku dostatecznego
zbadać czy funkcja
f
ma ekstremum w punkcie
o
x
, gdy
a)
x
x
x
f
−
=
ln
2
)
(
dla
2
=
o
x
; b)
2
cos
2
)
(
x
x
x
f
+
=
dla
0
0
=
x
;
c)
x
x
x
x
f
1
ln
2
)
(
+
−
=
dla
1
=
o
x
9.Podać twierdzenie o przyjmowaniu kresów i twierdzenie o przyjmowaniu wartości pośrednich.
Wyznaczyć najmniejszą i największą wartość funkcji f w danym przedziale
a)
3
3
)
(
x
x
x
f
−
=
dla
]
8
,
1
[
−
∈
x
b)
x
x
arctg
x
f
+
−
=
1
1
)
(
dla
]
1
,
0
[
∈
x
c)
x
x
x
f
ln
)
(
2
=
dla
]
,
1
[ e
x
∈
10.Podać warunek konieczny i dostateczny na punkt przegięcia.Wyznaczyć punkty przegięcia oraz
przedziały wypukłości i wklęsłości funkcji
a)
x
e
x
f
1
)
(
−
=
b)
x
x
x
f
ln
)
(
2
=
c)
2
4
)
(
x
x
x
f
−
=
11.Definicja funkcji pierwotnej. Twierdzenie podstawowe o funkcjach pierwotnych z
dowodem.Definicja całki nieoznaczonej. Wykazać, że funkcja
=
≠
−
=
0
..
...
..........
0
.
..........
0
..
...
1
cos
1
sin
2
)
(
x
dla
x
dla
x
x
x
x
f
nie jest ciągła w punkcie x
0
=0, ale jest całkowalna w zbiorze R.
12. Podać twierdzenia o całkowaniu przez części i podstawienie. Obliczyć całkę
a)
∫
dx
e
x
b)
dx
x
x
arctg
∫
c)
∫
)
ln(cos x
tgx
d)
dx
x
x
∫
arcsin
13.Metody całkowania funkcji wymiernych , trygonometrycznych i niewymiernych. Obliczyć
a)
∫
+
−
5
2
2
x
x
dx
; b)
∫
x
dx
2
3
sin
cos
; c)
∫
x
dx
sin
; d)
dx
x
x
∫
−
+
2
2
27
14.Wyprowadzić wzór rekurencyjny i obliczyć
a)
xdx
n
∫
sin
dla
,...;
4
,
3
,
2
=
n
xdx
∫
4
sin
b)
dx
x
n
∫
sin
1
dla
,...;
4
,
3
,
2
=
n
dx
x
∫
4
sin
1
12.Wstęp do definicji całki oznaczonej. Definicjiacałki oznaczonej właściwej z uwagami.
13.Wlasności całki oznaczonej właściwej. Podać twierdzenia o wartości średniej i główne.
14.Definicja całki oznaczonej niewłaściwej pierwszego rodzaju wraz z interpretacją geometryczną.
Obliczyć całki oznaczone niewłaściwe
a
∫
+∞
−
+
+
1
2
5
4x
x
dx
; b)
∫
∞
−
+
−
0
2
3
4x
x
dx
; c)
∫
+∞
o
arcctgxdx
; d
∫
∞
−
+
0
)
1
(
dx
e
x
x
; e)
dx
x
x
∫
+∞
+
0
6
2
1
15.Definicja całki oznaczonej niewłaściwej drugiego rodzaju wraz z interpretacją.Obliczyć całki
niewłaściwe drugiego rodzaju
a)
∫
+
−
2
1
2
3
4x
x
dx
; b)
dx
x
∫
1
0
ln
; c)
∫
−
4
2
2
4
x
x
dx
; d)
∫
π
π
2
sin x
dx
; e)
∫
4
0
2
π
dx
ctg
16.Zastosowania geometryczne całek wraz z interpretacją geometryczną.
Obliczyć pole obszaru ograniczonego krzywymi o równaniach
a)
,
2
2
x
x
y
−
=
.
0
=
+
y
x
; b)
,
8
2
=
+
x
y
.
0
2
=
−
x
y
Obliczyć długość łuku krzywej o równaniu
a)
x
x
x
y
arcsin
2
+
−
=
dla
];
1
,
0
[
∈
x
b)
y
y
x
ln
4
1
2
1
2
−
=
dla
];
,
1
[ e
y
∈
Obliczyć objętość obszaru powstałego przez obrót krzywej
a)
2
1
1
x
y
+
=
dla
)
,
0
[
∞
∈
x
wokół osi x; b)
x
y
sin
=
dla
]
2
,
0
[
π
∈
x
wokół osi y.
Obliczyć pole powierzchni bocznej obszaru powstałego przez obrót krzywej
a)
x
y
sin
=
dla
]
2
,
0
[
π
∈
x
wokół osi x; b)
x
y
4
2
=
dla
]
3
,
0
[
∈
x
wokół osi x.
17.Definicja szeregu i jego zbieżności. Korzystając z definicji zbadać zbieżność szeregu
a)
∑
∞
=
+
⋅
1
)
1
(
1
n
n
n
; b)
∑
∞
=
+
1
)
1
1
ln(
n
n
; c)
n
n
)
3
2
(
1
∑
∞
=
−
; d)
)
1
2
3
2
(
1
+
−
+
∑
∞
=
n
n
n
19.Podać kryteria całkowe i porównawcze zbieżności szeregu. .Korzystając z kryterium całkowego
lub porównawczego zbadać zbieżność szeregu
a)
∑
∞
=
1
2
ln
n
n
n
; b)
∑
∞
=
1
2
ln
n
n
n
; c)
∑
∞
=
1
n
arcctgn
; d)
∑
∞
=
−
1
n
n
n
e
e)
∑
∞
=
+
−
+
1
3
1
3
3
1
2
n
n
n
n
; f)
∑
∞
=
+
−
+
1
2
3
2
1
2
n
n
n
n
20. Podać kryteria zbieżności szeregu d’Alamberta i Cauchyego. Korzystając z kryterium d’Alemberta
lub kryterium Cauchyego zbadać zbieżność szeregu.
a)
∑
∞
=
1
2
)!
2
(
n
n
n
n
; b)
)!
2
(
)
!
(
2
1
n
n
n
∑
∞
=
; c)
2
2
1
)
!
(
4
n
n
n
n
n
∑
∞
=
; d)
∑
∞
=
+
+
1
2
2
)
1
2
(
)
1
(
n
n
n
n
n
; e)
2
)
2
3
(
1
n
n
n
n
+
+
∑
∞
=
;f)
2
)
1
(
2
1
n
n
n
n
n
+
∑
∞
=
21.Podać definicję zbieżności bezwzględnej i warunkowej szeregu. Zbadać zbieżność bezwzględną i
warunkową szeregu
a)
∑
∞
=
−
2
2
ln
)
1
(
n
n
n
n
; b)
n
n
n
n
n
)
1
2
(
)
1
(
1
+
−
∑
∞
=
; c)
∑
∞
=
+
−
2
1
ln
)
1
(
n
n
n
n
; d)
∑
∞
=
+
+
−
1
2
1
2
)
1
(
n
n
n
n
;e)
∑
∞
=
−
1
4
!
)
1
(
n
n
n
n
Wyszukiwarka
Podobne podstrony:
mata zadania zadania id 765851 Nieznany
mata zadania cw3 id 765850 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
więcej podobnych podstron