15

1

K A T E D R A F I Z Y K I S T O S O W A N E J

_________________________________________

P R A C O W N I A F I Z Y K I

Ć

w. 15. Wyznaczanie ciepła topnienia lodu

Wprowadzenie

Materia w przyrodzie na Ziemi występuje w trzech stanach skupienia (fazach) – jako gazy,

ciecze, i ciała stałe (do wystąpienia czwartego stanu materii - plazmy - konieczne są warunki
szczególne, np. błyskawice). Przez fazę rozumie się zbiór wszystkich części danego układu o
jednakowych własnościach fizycznych i jednakowym składzie chemicznym, oddzielonych od
pozostałych części układu powierzchnią rozdziału.

Różnice własności fizycznych tych stanów skupienia wynikają z odmiennej budowy

mikroskopowej. Możliwe jest przejście substancji z jednej fazy do innej, ale dzieje się to wówczas
gdy średnia energia kinetyczna cząsteczek przekroczy określoną wartość energii wiązania danej
fazy. Przejścia takie są odwracalne.

W stanie gazowym cząsteczki są daleko od siebie i słabo ze sobą oddziałują. Gaz nie ma spręży-

stości postaci ani sprężystości objętości, przyjmuje kształt i objętość naczynia w którym się znajduje.

W cieczach wzajemne oddziaływanie cząsteczek jest dużo silniejsze, lecz oddziaływania te nie

wiążą ich jeszcze w konkretnym położeniu w przestrzeni. Cząsteczki wykonują drgania wokół
chwilowych położeń równowagi, ciecze posiadają sprężystość objętości.

Z ciałem stałym mamy do czynienia wówczas, gdy charakteryzuje sie ono sprężystością postaci,

tzn. dąży do zachowania swojego kształtu. Z punktu widzenia struktury mikroskopowej
charakterystyczne jest to, że każdy atom wykonuje drgania wokół swojego stałego położenia
równowagi. Ze względu na rozmieszczenie atomów (lub cząsteczek) w przestrzeni, ciała stałe
dzielimy na bezpostaciowe (amorficzne) lub krystaliczne. W ciałach amorficznych (np. szkło,
smoła, żywice) atomy są rozłożone w przestrzeni zupełnie przypadkowo i nieregularnie.
Podgrzewając takie ciała przy przejściu do stanu ciekłego obserwuje się ich stopniowe mięknięcie
w pewnym przedziale temperatur.

Zupełnie inaczej wygląda sytuacja w przypadku kryształów. Charakteryzują sie one określonym

rozmieszczeniem elementów w przestrzeni, przy czym mamy do czynienia z regularnym
powtarzaniem w przestrzeni identycznych struktur o kształcie równoległościanów. Mówimy o sieci
periodycznej, zawierającej grupę atomów związanych z każdym węzłem sieci lub umieszczonej w
każdym podstawowym równoległościanie. Takie jednoznaczne przypisanie atomów bazowych do
sieci krystalicznej powoduje, że mówimy o strukturze krystalicznej. Najbardziej powszechna
występująca w warunkach ziemskich odmiana lodu I posiada ułożenie atomów odpowiadające
heksagonalnej sieci krystalicznej.

Cechą charakterystyczną powoli schładzanych czystych kryształów jest ściśle określona

temperatura topnienia (równa temperaturze krzepnięcia). Oznacza to, że dostarczając ciepło do ciała
powodujemy jego przejście ze stanu stałego w stan ciekły bez zmiany temperatury. Dopiero gdy
całe ciało zamieni sie w ciecz, następuje dalszy wzrost temperatury. Zachowanie takie na
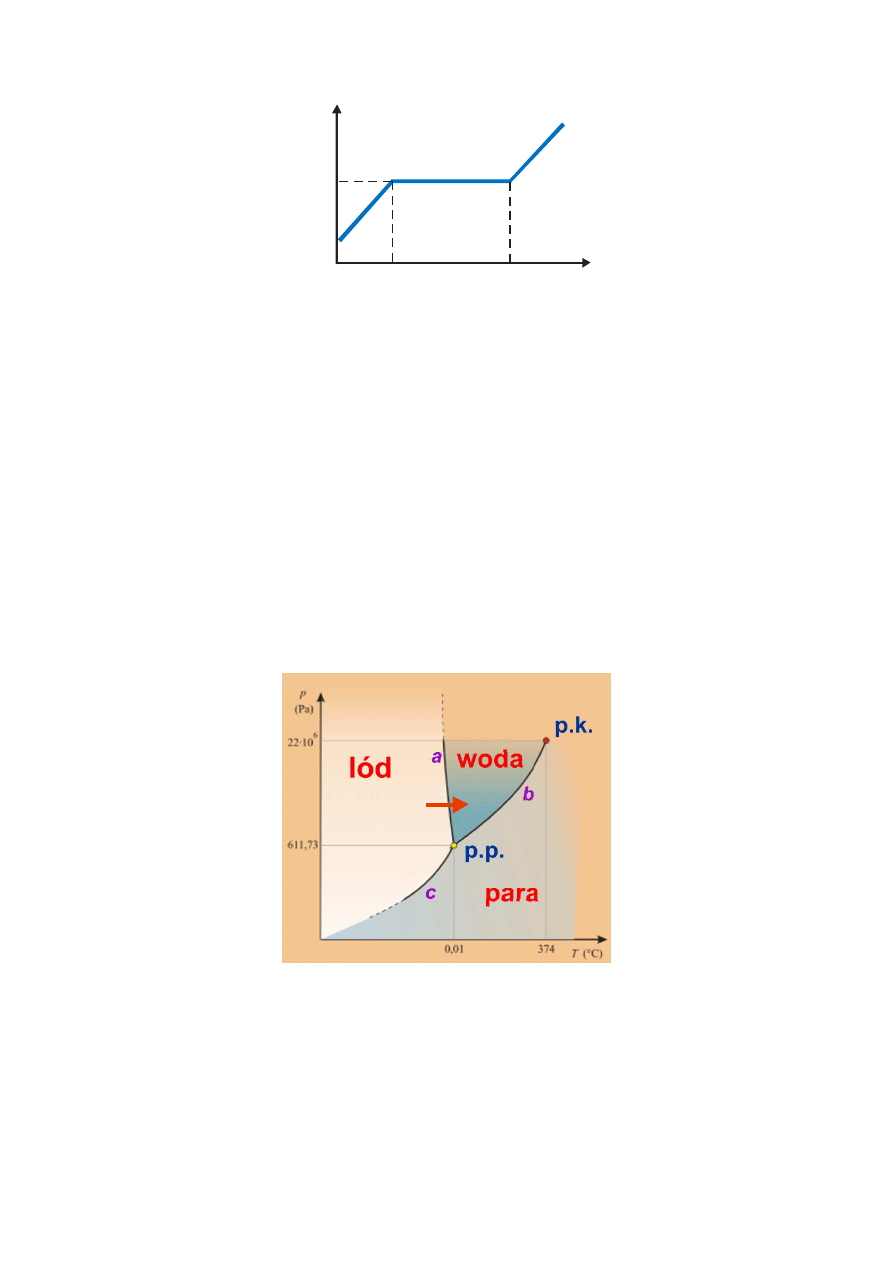
przykładzie lodu przedstawia rysunek 1.

Ilość energii Q, którą należy dostarczyć jednostkowej masie ciała, aby przeprowadzić ją w stan

ciekły bez zmiany temperatury nazywa się ciepłem topnienia c

t

i mierzona jest w J/kg:

m

Q

c

t

=

.

(1)

2

∆

Q

T

0 C

o

Lód

Topnienie lodu

Woda

Rys. 1. Zależność temperatury od dostarczonego ciepła dla lodu pod normalnym ciśnieniem w pobliżu temperatury

topnienia.

Każda faza jest trwała w określonych warunkach ciśnienia i temperatury. W pewnych warunkach

dana substancja może występować jednocześnie nawet w kilku fazach, co nazywane jest równowa-
gą termodynamiczną albo równowagą fazową. Lecz naruszenie warunków równowagi powoduje
przemianę fazową. Warunki trwałości różnych faz wygodnie jest przedstawić na wykresie
fazowym. Widoczne są na nim zarówno zakresy trwałości różnych faz danej substancji, jak
i krzywe równowagi fazowej, przy przekroczeniu których mamy do czynienia z przemianą fazową.

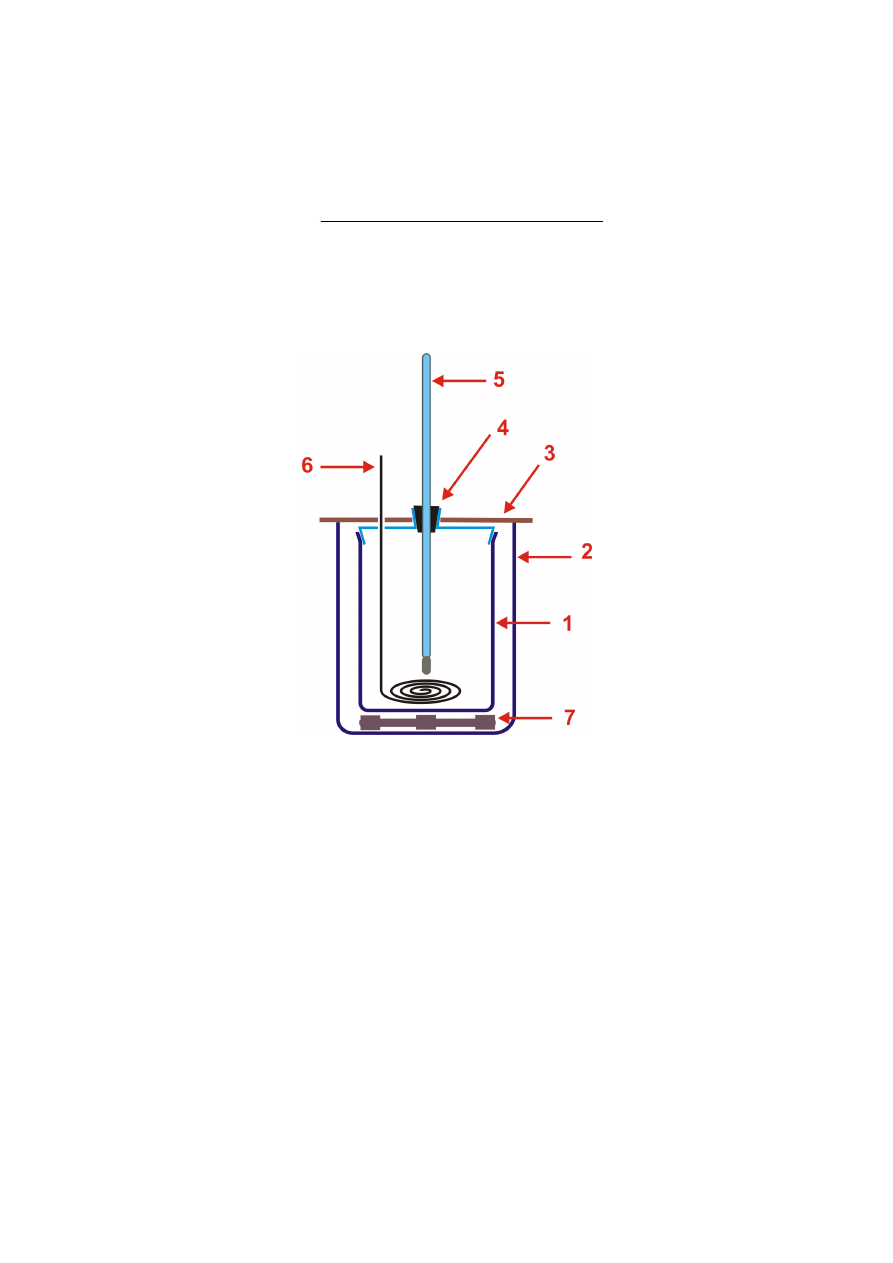
Jako przykład wspomnianego obrazowania faz posłuży wykres fazowy wody przedstawiony na

rysunku 2. Krzywa a obrazuje punkty równowagi fazowej pomiędzy lodem a wodą. Krzywa b
zawiera punkty równowagi pomiędzy wodą a parą nasyconą, co jednocześnie jest zależnością
temperatury wrzenia cieczy od ciśnienia zewnętrznego. Krzywa c przedstawia równowagę
pomiędzy lodem a parą nasyconą realizowaną w procesie sublimacji i resublimacji. Punkt spotkania
trzech krzywych zwany punktem potrójnym wody określa parametry ciśnienia i temperatury, przy
których w równowadze współistnieją trzy fazy – lód, woda i para nasycona. W temperaturze
powyżej temperatury punktu krytycznego, H

2

O może istnieć tylko w postaci gazowej, niezależnie

od wywieranego ciśnienia.

Rys. 2. Wykres fazowy wody. Zaznaczono krzywe równowagi faz oraz obszary trwałości faz. Strzałką zaznaczono

przejście fazowe lodu w wodę realizowane w ćwiczeniu; p.p. – punkt potrójny wody; p.k. – punkt krytyczny.

Podczas przemiany fazowej następuje zawsze skokowa zmiana własności fizycznych ciała, które

tej przemianie podlega. Przemianom pierwszego rodzaju (np. zmiany stanu skupienia) towarzyszy
zawsze pochłonięcie lub wydzielenie pewnej ilości ciepła oraz skokowa zmiana gęstości i funkcji
stanu układu (energii wewnętrznej, entalpii, entropii).

Przy przemianach drugiego rodzaju nie wydziela się ani nie pochłania żadna ilość ciepła.

Gęstość oraz funkcje stanu układu zmieniają się w sposób ciągły, natomiast skokowo zmieniają sie

3

takie parametry ciała jak: pojemność cieplna, współczynnik rozszerzalności cieplnej, współczynnik
ś

ciśliwości. Przykładem przejść fazowych drugiego rodzaju może być przejście ferromagnetyka

w paramagnetyk (punkt Curie) czy przejście materiału w stan nadprzewodnictwa.

Krzywe równowagi fazowej dla przemian pierwszego rodzaju opisane są za pomocą równania

Clapeyrona – Clausiusa:

p

c

V

V

T

dp

dT

)

(

1

2

−

=

,

(2)

gdzie: dT - zmiana temperatury przemiany fazowej spowodowana zmianą ciśnienia dp; T - tempe-
ratura przemiany; V

1

- objętość ciała w 1 fazie; V

2

- objętość ciała w 2 fazie; c

p

- ciepło przemiany.

Zazwyczaj podczas topnienia ciała stałego dT/dp jest większe od zera, co oznacza że przy

wzroście ciśnienia wzrasta również temperatura topnienia. Jeśli jednak wzór ten odniesiemy do
topnienia lodu, to sytuacja wygląda inaczej. Ponieważ V

2

– V

1

< 0 (objętość powstałej wody jest

mniejsza od objętości stopionego lodu), więc również dT/dp < 0, co oznacza że ze wzrostem
ciśnienia temperatura topnienia lodu maleje (około 0,007K / 1atm). Widoczne jest to na wykresie
fazowym wody (rys. 2).

Ciepło topnienia lodu ma jedną z największych wartości w naturze, natomiast woda ma

największe ciepło właściwe. Jest to niezwykle ważna własność ze względu na możliwość
łagodzenia szybkości zmian temperatury w przyrodzie, zwłaszcza w okresie wiosennym.

Metoda pomiaru

Ideą ćwiczenia jest wyznaczenie spadku temperatury wody po rozpuszczeniu się w niej kostki

lodu o temperaturze początkowej równej temperaturze topnienia w warunkach normalnych, tj.
273,15 K. Pomiar masy ciał biorących udział w wymianie ciepła oraz znajomość ich ciepeł
właściwych pozwala na obliczenie ciepła topnienia lodu. Pomiary, w których ciała wymieniają
ciepło przeprowadza sie w urządzeniu zwanym kalorymetrem (rys. 3), którego budowa pozwala na
prawie adiabatyczny przebieg procesów (ograniczenie wymiany ciepła z otoczeniem).

Jeśli rozpatrzymy topnienia lodu o temperaturze początkowej T

o

= 273,15 K, to podczas tego

procesu powstaje najpierw woda o temperaturze równej temperaturze lodu aż do całkowitego jego
stopienia. Pobierana jest przy tym z otoczenia energia cieplna w ilości:

Q

t

= m·c

t

,

(3)

gdzie: m - masa lodu; c

t

- ciepło topnienia lodu.

W ćwiczeniu kostki lodu są wrzucane do kalorymetru z wodą o temperaturze początkowej T

p

,

zaś po całkowitym rozpuszczeniu lodu ustala sie temperatura końcowa całej wody równa T

k

.

Więc

powstała z lodu woda pobiera ciepło:

Q

w

= m·c

w

·

(T

k

– T

o

) ,

(4)

gdzie: m - masa wody powstałej z lodu równa masie lodu; c

w

- ciepło właściwe wody.

Zatem całkowita ilość pobranego ciepła Q

1

konieczna do stopienia lodu i podgrzania wody

powstałej z jego stopienia jest równa:

Q

1

= m·c

t

+ m·c

w

·

(T

k

– T

o

) .

(5)

Ciałami przekazującymi ciepło jest zarówno woda znajdująca sie w kalorymetrze jak i kalory-

metr (wewnętrzne naczynie), których temperatury są takie same. Przy uprzednio określonych
temperaturach: początkowej - T

p

i końcowej - T

k

, ilość ciepła oddanego Q

2

można zapisać wzorem:

Q

2

= m

w

·c

w

·

(T

p

– T

k

) + m

k

·c

k

·

(T

p

– T

k

) ,

(6)

gdzie: m

w

- masa wody w kalorymetrze; c

w

- ciepło właściwe wody; m

k

- masa kalorymetru; c

k

-

ciepło właściwe kalorymetru.

4

Zgodnie z zasadą bilansu cieplnego ciepło pobrane przez jedne ciała jest równe ciepłu oddanemu
przez inne (Q

1

= Q

2

), zatem:

m·c

t

+ m·c

w

·

(T

k

– T

o

) = m

w

·c

w

·

(T

p

– T

k

) + m

k

·c

k

·

(T

p

– T

k

) .

(7)

Na tej podstawie uzyskujemy wyrażenie pozwalające obliczyć ciepło topnienia lodu:

m

T

T

mc

T

T

c

m

c

m

c

o

k

w

k

p

k

k

w

w

t

)

(

)

(

)

(

−

−

−

⋅

+

=

.

(8)

Wykonanie

ć

wiczenia

1.

Pobrać od prowadzącego zajęcia: kalorymetr (rys. 3), termometr i odważniki.

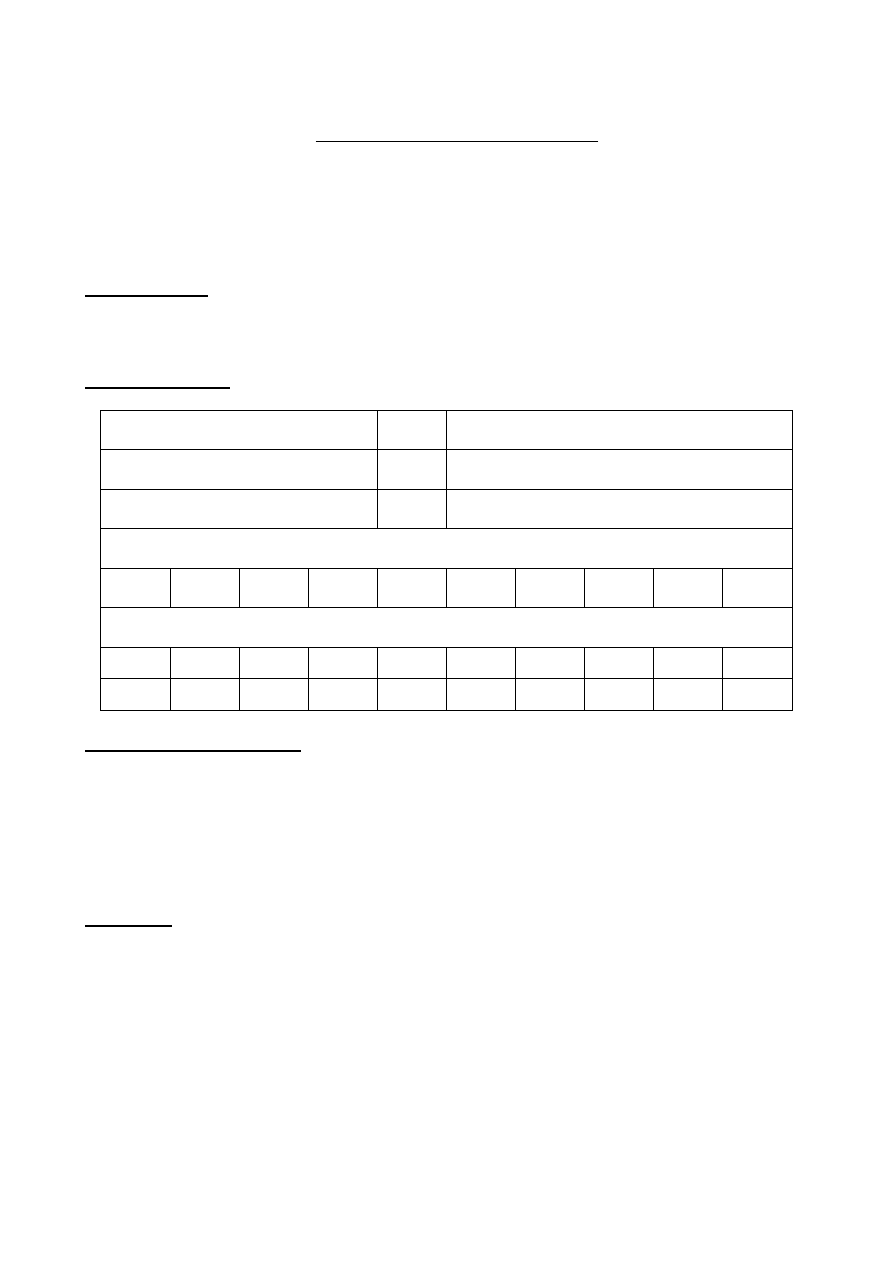
Rys.3. Budowa kalorymetru: 1 – naczynie wewnętrzne z przykrywką; 2 – naczynie zewnętrzne

(osłona adiabatyczna); 3 – dwuczęściowa pokrywa z tworzywa; 4 – korek; 5 – termometr;

6 – mieszadełko; 7 krzyżak dystansujący naczynia.

2.

Zważyć wewnętrzne naczynie kalorymetru z mieszadełkiem (m

k

).

3.

Napełnić naczynie wewnętrzne do połowy wodą o temperaturze zbliżonej do temperatury

otoczenia i zważyć (m

k+w

). Masa wody jest równa: m

w

= m

k+w

– m

k

.

4.

Naczynie wewnętrzne z wodą wstawić do naczynia zewnętrznego, zamknąć przykrywką

z termometrem i okresowo mieszając, przez kilka minut obserwować temperaturę zapisując jej
wartość co minutę.

5.

W międzyczasie wyjąć z zamrażarki 2 kostki lodu, położyć je na bibule i odczekać aż lód

zacznie się topić (bibuła wilgotna). Przyjmujemy, że temperatura lodu jest wówczas równa
temperaturze topnienia w warunkach normalnych (T

o

= 273,15 K).

6.

Osuszyć lód za pomocą bibuły, wrzucić go do kalorymetru z wodą i przykryć zarówno naczynie

wewnętrzne jak i zewnętrzne.

7.

Nadal okresowo mieszając notować temperaturę wody co 30s aż do jej wzrostu. Za temperaturę

początkową T

p

należy przyjąć temperaturę wody tuż przed wrzuceniem lodu, a za temperaturę

końcową T

k

jej najmniejszą wartość po wrzuceniu lodu.

8.

Ponownie zważyć naczynie wewnętrzne kalorymetru (m

k+w+l

). Masa wrzuconego lodu jest

równa; m

= m

k+w+l

- m

k+w

.

9.

Pomiary powtórzyć.

5

10.

Ciepło topnienia lodu obliczyć wg wzoru:

m

T

T

mc

T

T

c

m

c

m

c

o

k

w

k

p

k

k

w

w

t

)

(

)

(

)

(

−

−

−

⋅

+

=

,

gdzie: c

k

- ciepło właściwe kalorymetru; c

w

- ciepło właściwe wody; m- masa lodu; m

w

- masa

wody w kalorymetrze; m

k

- masa kalorymetru.

11. Analizę niedokładności wyznaczenia ciepła topnienia lodu należy przeprowadzić metodą

różniczkową, przyjmując że c

t

= f

(m, m

w

, m

k

, T

p

, T

k

) .

Dane tablicowe:

Ciepło właściwe kalorymetru:

c

k

= 896 J/(kg·K)

Ciepło właściwe wody:

c

w

= 4182 J/(kg·K)

Tabela pomiarowa

Masa kalorymetru

m

k

Masa kalorymetru z wodą

m

k+w

Masa kalorymetru z wodą i lodem

m

k+w+l

Temperatura wody przed wrzuceniem lodu [

o

C]

Temperatura po wrzuceniu lodu [

o

C]

Zagadnienia do kolokwium:

1.

Stany skupienia materii. Podział ciał stałych i ich własności.

2.

Rodzaje przemian fazowych.

3.

Topnienie, ciepło topnienia.

4.

Wykres fazowy wody, punkt potrójny.

5.

Równania Clapeyrona – Clausiusa.

6.

Zasada bilansu cieplnego. Wyprowadzenie wzoru do obliczenia ciepła topnienia lodu.

Literatura:

1. D. Halliday, R. Resnick, J. Walker, Podstawy fizyki, Wydawnictwo Naukowe PWN, Warszawa

2003, tom 2.

2. J. Massalski, M. Massalska, Fizyka dla Inżynierów, WNT, Warszawa 2008, tom 1.