1

KINEMATYKA

Kinematyka



Pojęcia pola prędkości



Strumień objętości i strumień masy



Równanie ciągłości

2

Kinematyka

Kinematyka zajmuje się analitycznym opisem przepływów niezależnie

od przyczyn (sił) jakie ten ruch wywołały.

Główne zadanie polega na określeniu prędkości (

v

) i przyspieszenia

(

a

) dowolnego elementu płynu w dowolnej chwili (

t

)

Klasyfikacja przepływów

Wektorowe pole prędkości ogólnie opisuje funkcja

v

=

v

(

x,y,z,t

)

Różne kryteria klasyfikacji przepływów

Ze względu na zależność od czasu



nieustalone (niestacjonarne)



ustalone (stacjonarne)

Ze względu na ilość współrzędnych



trójwymiarowe (przestrzenne)



dwuwymiarowe (płaskie, osiowosymetryczne,...)



jednowymiarowe

…….

3

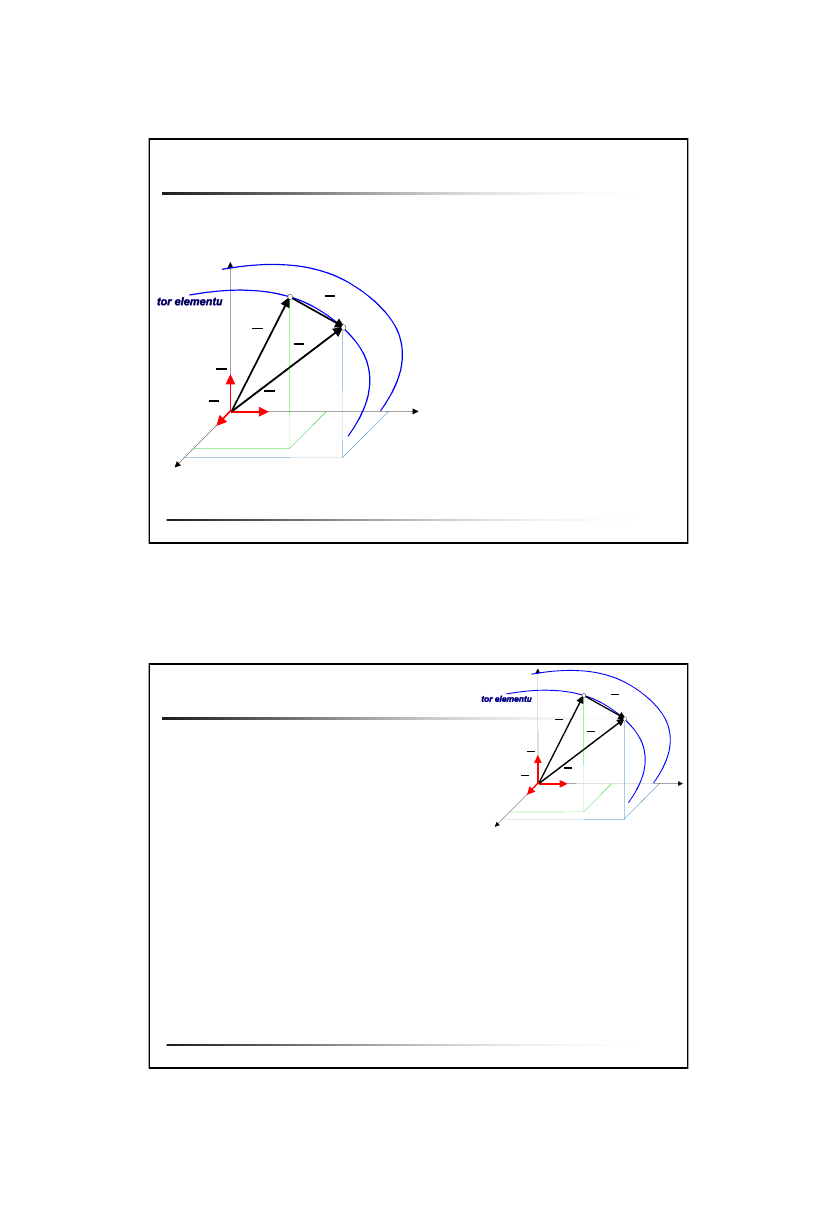
Opis przepływu wg Lagrange’a



Metoda analitycznego opisu

przepływów w której rozpatruje się

ruch elementów płynu wzdłuż ich

torów.



Identyfikacja elementu – za pomocą

współrzędnych w chwili

t

=

t

0

0

0

)

(

r

k

j

i

r









c

b

a

t



Wektor-promień r, określający

położenie elementu w chwili

t>t

0

zależy od

a,b,c,t



a,b,c,t

– zmienne Lagrange’a

x

z

y

O

a

r

i

j

k

b

P (t )

0

0

P(t)

c

0

r

D

r

y

x

z

Opis przepływu wg Lagrange’a



Wektor -promień

)

,

,

,

(

)

,

,

,

(

)

,

,

,

(

)

,

(

0

t

c

b

a

z

z

t

c

b

a

y

y

t

c

b

a

x

x

z

y

x

t















k

j

i

r

r

r



Jeżeli w równaniach zmieniamy

t

to otrzymujemy równania toru

elementu płynu, który w chwili

t

=

t

0

był w punkcie

P

0

(

a,b,c

)



Jeżeli zmieniamy

a,b,c

– to otrzymujemy przestrzenny rozkład

elementów płynu w chwili

t



Indywidualnie traktuje poszczególne elementy płynu, opisując ich

położenie i zmianę stanu zachodzącą w czasie



Stosuje się w przypadkach, gdy istotne jest określenie zmian

parametrów przepływu wzdłuż toru elementu

x

z

y

O

a

r

i

j

k

b

P (t )

0 0

P(t)

c

0

r

D

r

y

x

z

4

Opis przepływu wg Eulera



Polega na badaniu ruchu kolejnych elementów płynu przepływających

przez wybrany punkt przestrzeni



Metoda Eulera – analiza lokalna przepływów



Każda wielkość fizyczna jest przedstawiana w funkcji czasu i

współrzędnych położenia x,y,z

x,y,z,t – współrzędne Eulera

)

,

,

,

(

)

,

(

t

z

y

x

t

v

r

v

v





Pochodna substancjalna



Interesuje nas wyrażenie zmian dowolnej wielkości związanej z elementem

płynu w czasie



Określimy przyspieszenia elementu płynu który w danym momencie czasu

przechodzi przez punkt (x,y,z)



Prędkość elementu płynu jest funkcją



Wektor przyspieszenia jest pochodną zupełną wektora prędkości:

z

y

x

v

z

v

y

v

x

t

dt

dz

z

dt

dy

y

dt

dx

x

t

dt

d



















































v

v

v

v

a

v

v

v

v

v

a

)

),

(

),

(

),

(

(

t

t

z

t

y

t

x

v

v



z

y

x

v

dt

dz

v

dt

dy

v

dt

dx







Dla poruszającego się elementu

płynu jest:

pochodna lokalna

pochodna unoszenia

pochodna substancjalna

5

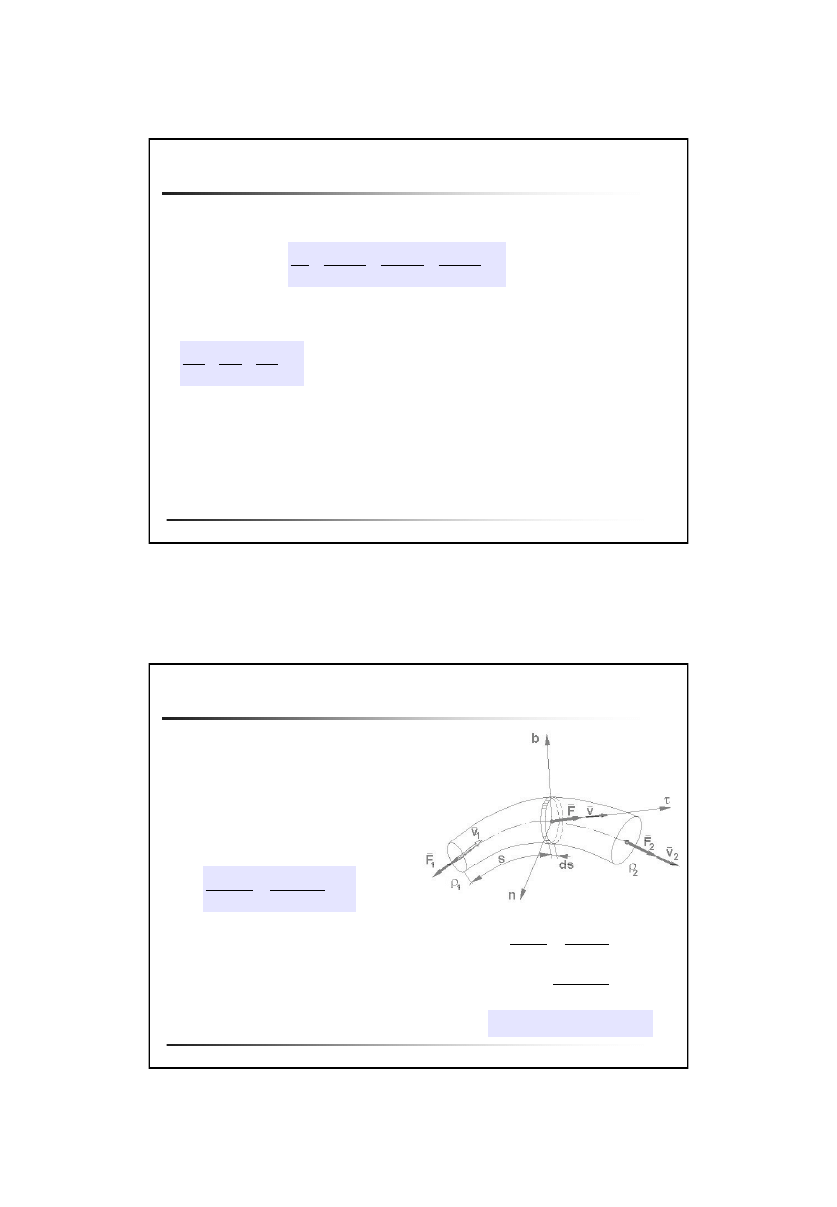
Tor elementu płynu, linia prądu i inne pojęcia.

Tor elementu płynu



Współrzędne Lagrange’a - tor elementu płynu określony

jest bezpośrednio przez równania parametryczne



Współrzędne Eulera – tor elementu płynu opisany jest

przez równania różniczkowe

dt

v

dz

dt

v

dy

dt

v

dx

z

y

x







,

,

Równania musimy scałkować i wyeliminować parametr

t.

Stałe całkowania określa się z warunków brzegowych.

)

,

,

,

(

)

,

,

,

(

)

,

,

,

(

t

c

b

a

z

z

t

c

b

a

y

y

t

c

b

a

x

x







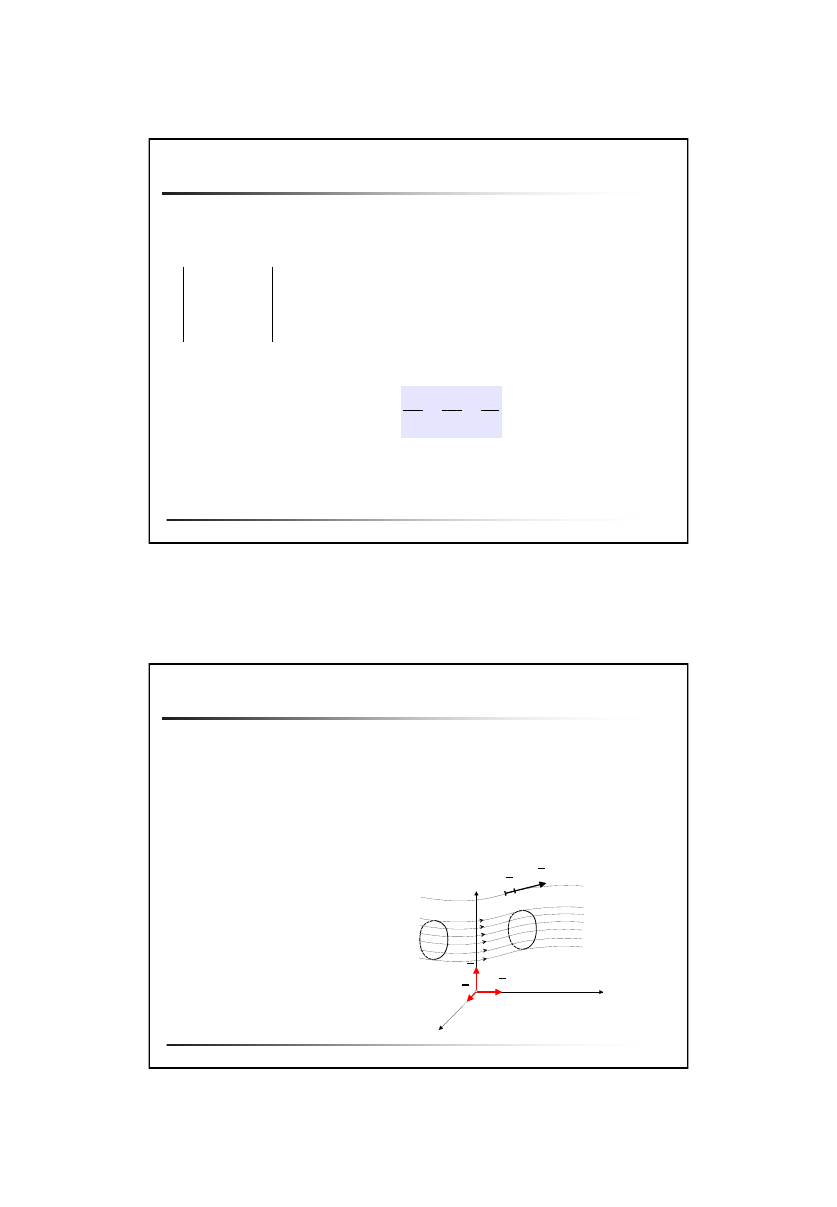
Linia prądu

Linia prądu – linia do której w danej chwili w każdym jej punkcie wektory

prędkości elementów, leżących na tej linii są styczne

x

z

y

O

i

j

k

K

v

ds

z

y

x

v

v

v

dz

dy

dx

d

k

j

i

v

k

j

i

s













6

Linia prądu

Równanie różniczkowe linii prądu

0

k

j

i

k

j

i

0

s

v



















)

(

)

(

)

(

dx

v

dy

v

dz

v

dx

v

dy

v

dz

v

dz

dy

dx

v

v

v

d

y

x

x

z

z

y

z

y

x

0

0

0













dx

v

dy

v

dz

v

dx

v

dy

v

dz

v

y

x

x

z

z

y

z

y

x

v

dz

v

dy

v

dx





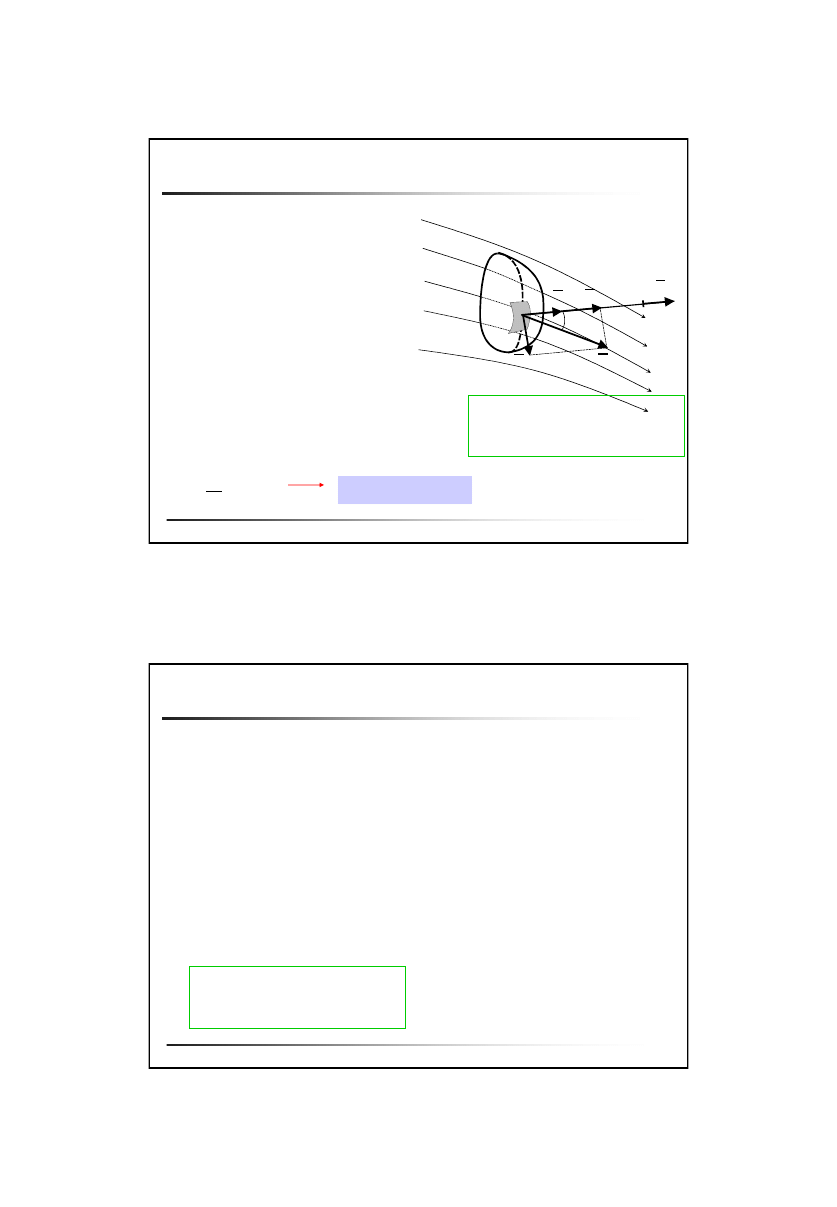
Inne pojęcia

Rurka prądu - zbiór linii prądu poprowadzony przez punkty dowolnego

zamkniętego konturu

Struga - płyn znajdujący się wewnątrz rurki prądu
Struga jednorodna - w każdym punkcie przekroju poprzecznego strugi prędkość,

gęstość, ciśnienie są takie same.

Struga elementarna - jeśli kontur otacza elementarne pole

dF

Powierzchnia prądu - ciągły zbiór linii prądu

x

z

y

O

i

j

k

K

v

ds

7

Strumień objętości przepływu

Powierzchnia F

nie jest powierzchnią prądu

Obliczamy strumień objętości przepływu
przez powierzchnię F

Elementarny strumień objętości
przepływu:

F

dF

v

n



v

t

v

n

dQ

dF

v

dF

v

d

n











cos

F

v

Całkowity strumień objętości
przepływu przez powierzchnię

F

:











F

n

F

dF

v

d

Q

F

v





F

n

śr

dF

v

F

v

1

s

m

F

v

Q

śr

/

3



V

Q





Używane nazwy:
strumień objętości przepływu
objętościowe natężenie przepływu

Strumień masy przepływu

Dla płynów ściśliwych ze względu na zmienną gęstość stosujemy

strumień masy przepływu:

Jeżeli płyn jest nieściśliwy:

]

[

kg/s

dF

v

d

Q

F

n

F

m















F

v

Uwaga na symbole:

m

Q

m





F

v

Q

d

Q

m

sr

F

m



















F

v



Używane nazwy:
strumień masy przepływu
masowe natężenie przepływu

8

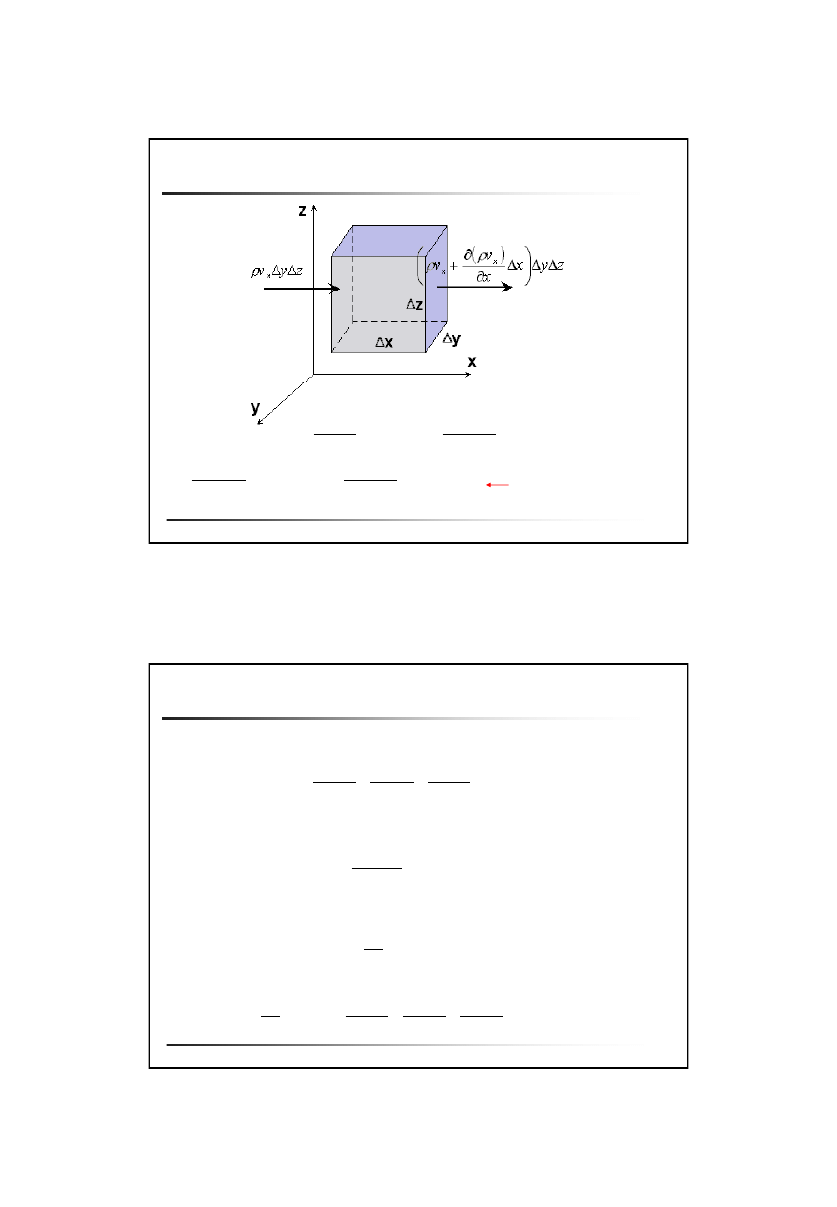
Równanie ciągłości

Vdt

z

v

Vdt

y

v

Vdt

x

v

zdt

y

x

x

v

v

zdt

y

v

z

y

x

x

x

x

D







D







D









D

D













D









D

D

)

(

,

)

(

)

(

)

(













Analogicznie dla

pozostałych kierunków

Równanie ciągłości

Vdt

z

v

y

v

x

v

z

y

x

D































)

(

)

(

)

(







Dla wszystkich trzech kierunków:

Przyrost ilości substancji zmagazynowanej w objętości

D

V

w czasie

dt

:

dt

t

V



D



)

(



Uwzględniając, że objętości

D

V

nie zmienia się w czasie

dt

:

Vdt

t

D







Otrzymane wyrażenia (*) i (**) muszą być sobie równe:

(*)

(**)

Vdt

z

v

y

v

x

v

Vdt

t

z

y

x

D

































D





)

(

)

(

)

(









9

Równanie ciągłości

Słuszne dla płynu idealnego oraz lepkiego

0

)

(

)

(

)

(

























z

v

y

v

x

v

t

z

y

x









0



















z

v

y

v

x

v

z

y

x

Dla przepływu nieściśliwego ustalonego

i nieustalonego

Równanie ciągłości dla nieustalonego przepływu przestrzennego płynu

ściśliwego

Przepływ jednowymiarowy (struga jednorodna)

Struga jednorodna, więc:
prędkość i gęstość w każdym punkcie przekroju

poprzecznego strugi jest jednakowa (w danej chwili)

Równanie ciągłości strugi jednorodnej

w nieustalonym przepływie płynu

ściśliwego:

0

)

(

)

(













s

vF

t

F





Dla płynu nieściśliwego:

0

)

(

)

(













s

vF

t

F

Dla przepływu ustalonego płynu ściśliwego:

0

)

(







s

vF



czyli

const

m

Q

vF

m











10

Równanie ciągłości strugi

Masowe natężenie przepływu płynu ściśliwego w każdym przekroju

poprzecznym strugi ma stałą wartość.

Dla płynu nieściśliwego, możemy stosować objętościowe natężenie

przepływu



W przypadku płynu nieściśliwego prędkość ustalonego przepływu w

strudze zmienia się odwrotnie proporcjonalnie do przekroju strugi



W ruchu ustalonym struga nie może ulec przerwaniu



Jeżeli struga o przekroju

F

i prędkości v

rozdziela się na

n

strug o

przekrojach

F

i

w których płyn porusza się z prędkością v

i

to:

const

Q

vF











n

i

i

i

v

F

Fv

1

Równanie ciągłości strugi

Jeżeli zastosujemy równanie ciągłości do układu krwionośnego możemy stwierdzić dlaczego w
naczyniach włoskowatych prędkość krwi jest bardzo mała (przyjmujemy pewne uproszczenie
złożonego układu).

Średnica aorty wynosi ok. 2,3cm – powierzchnia przekroju poprzecznego F=4 cm

2

Zakładając że przez aortę płynie Q=5 Litrów/minutę to prędkość krwi w aorcie wynosi:

Q=v*F v=Q/F=20,8 cm · s

-1

Zakładając, że całkowita powierzchnia poprzeczna wszystkich naczyń włoskowatych wynosi
F

k

=4800 cm

2

,to średnia prędkość w tych naczyniach wyniesie:

v

k

=Q/F

k

=0,017 cm ·s

-1

.

11