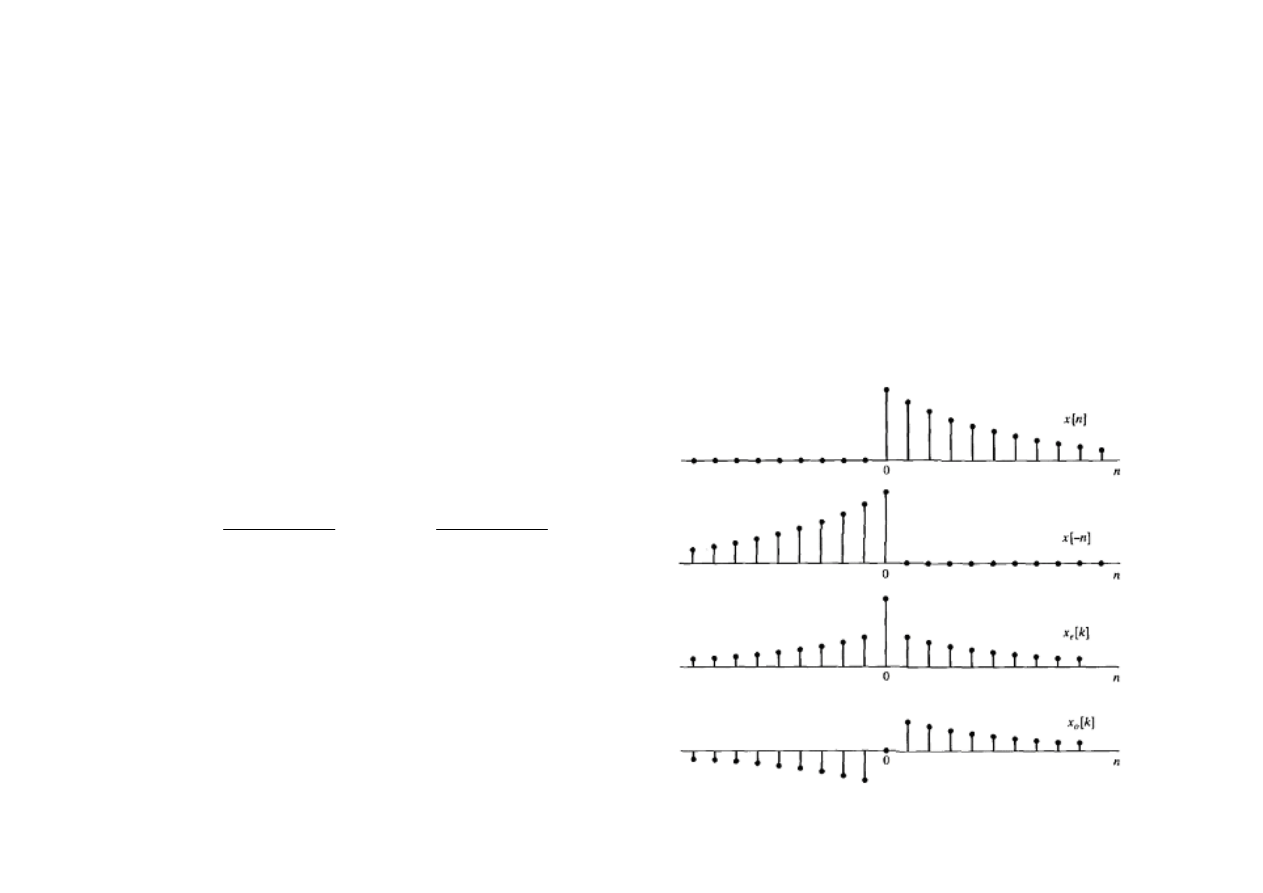
Dyskretna transformata Hilberta
W przypadku ogólnym transformata Fouriera ciągu dyskretnego jest wyznaczana dla
ω
z przedziału o długości
π
2
, np.
π
ω
π
≤
<
−
. Jednak dla ciągu x[n] o wartościach rzeczywistych transformata Fouriera spełnia zależność
ω
j
e
(conjugate symmetric), co oznacza, że wyznaczenie
ω
j
e
X
dla
)
(
*
ω
j
e
X
−
=
)
(
X
)
(
π
ω
≤
≤
0
wyznacza
również wartości
ω
j
dla
)
e
(
X
0
≤
≤
−
ω
π
. Dla ciągu przyczynowego zależność pomiędzy częścią rzeczywistą i
częścią urojoną współczynników Fouriera jest jednoznaczna i jest określana jako transformata Hilberta.
Analiza zależności Hilberta dla współczynników Fouriera ciągu dyskretnego
Dowolny ciąg x[n] można przedstawić w postaci sumy
ciągu parzystego x
e
[n] i nieparzystego x
o
[n]:
]
[
]
[
]
[
n
x
n
x
n
x
+
o
e
=
gdzie:
2
]
[
]
[
]
[
,
2
]
[
]
[
]
[
n
x
n
x
n
x
n
x
n
x
n
x
o
e
−
−
=
−
+
=
Dodatkowo jeśli x[n] jest przyczynowy (tzn. x[n]=0,
n<0) można odtworzyć x[n] z ciągu parzystego x
e
[n]
lub z ciągu nieparzystego dla n>0.
]
[
]
0
[
]
[
]
[
2
]
[
n
x
n
u
n
x
n
x
e
e
δ
−
=
]
[
]
0
[
]
[
]
[
2
]
[
n
x
n
u
n
x
n
x
o
δ
−
=
1
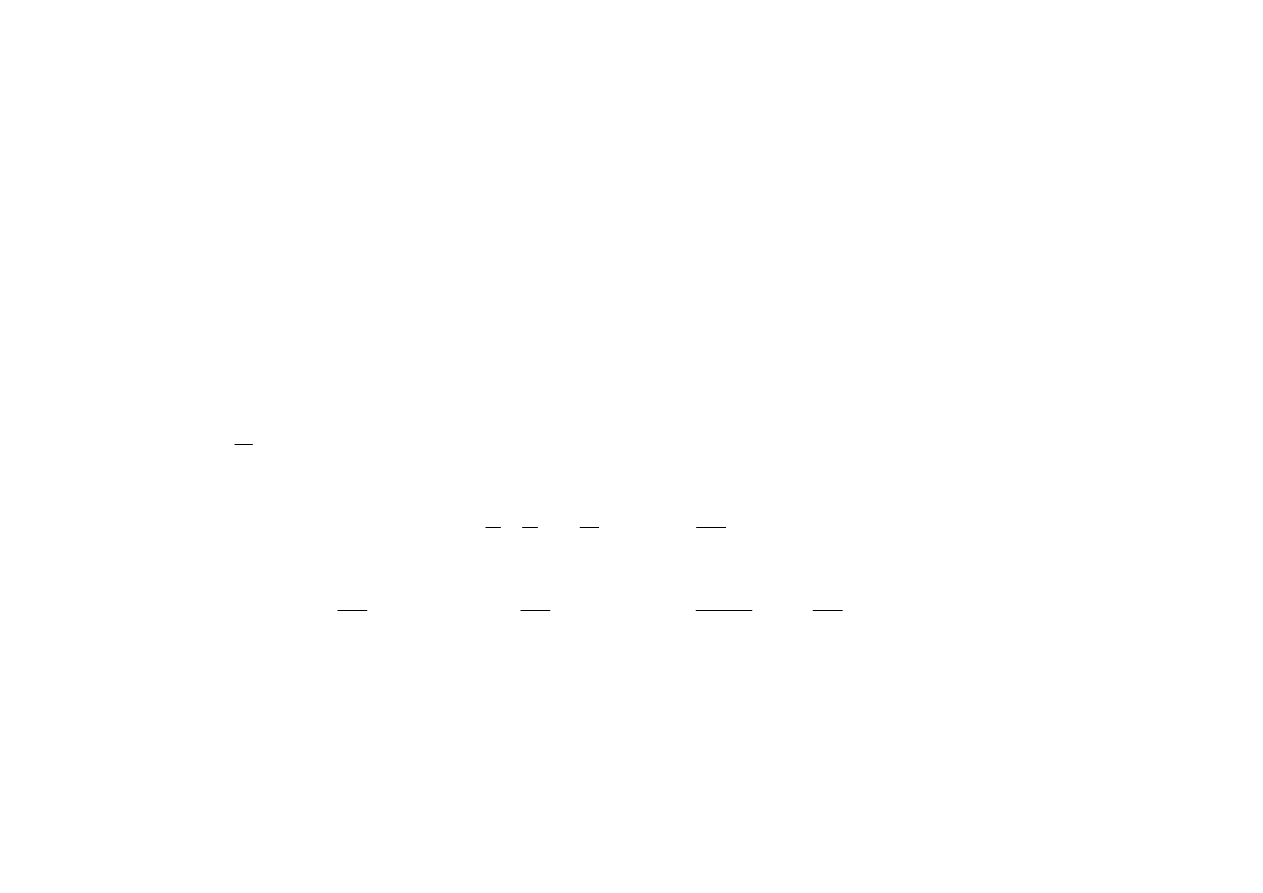
Z własności transformaty Fouriera wynika, że dla ciągu x[n] o wartościach rzeczywistych:
ω
ω
ω
j
j
j
e
jX
e
X
e
X
)
(
)
(
)
(
I
R
+
=
gdzie
i
są transformatami Fouriera odpowiednio ciągu x
)
(
ω
j
R
e
X
)
(
ω
j
I
e
X
e
[n] i x
o
[n].
ω
j
Dla przyczynowego, stabilnego ciągu o wartościach rzeczywistych
całkowicie (jednoznacznie) określa
widmo
ω
j
. Znając
ω
j
widmo sygnału
ω
j
można wyznaczyć w następujący sposób:
ω
j
)
(
R
e
X
)
(e
X
)
(
R
e
X
)
(e
X
1. Obliczyć x
e
[n] poprzez odwrotną transformatę Fouriera z
,
]
[
]
0
[
]
[
]
[
2
]
[
n
x
n
u
n
x
n
x
)
(
R
e
X
δ
−
=
2. Obliczyć x[n] z zależności
e
e
,
ω
j
3. Obliczyć
jako transformatę Fouriera ciągu x[n].
)
(e
X
Stosując twierdzenie o splocie oraz zależność x
e
[0]= x[0] widmo sygnału można wyliczyć ze wzoru:
π
]
0
[
)
(
)
(
1
)
(
)
(
x
d
e
U
e
X
e
X
j
j
R
j
−
Θ
=
∫
−
Θ
−
Θ
π
ω
ω
π
Podstawiając
∑
∞
=
−∞
=
−
+
−
=
k
k
j
j
k
e
U
2
cot
2
2
1
)
2
(
)
(
ω
π
ω
πδ
ω
i
∫
−
Θ
Θ
=
π
π
π
d
e
X
x
j
R
)
(
2
1
]
0
[
otrzymujemy:
∫
∫
∫
−
Θ
−
Θ
−
Θ
Θ
−
Θ
Θ
−
−
Θ
+
=
π
π
π
π
π
π
ω
ω
π
ω
π
π
d
e
X
d
e
X
j
d
e
X
e
X
e
X
j
R
j
R
j
R
j
R
j
)
(
2
1
2
cot
)
(
2
)
(
2
1
)
(
)
(
Porównując części rzeczywiste i urojone w powyższym wzorze ze wzorem
otrzymujemy zależność pomiędzy częścią rzeczywistą a urojoną widma sygnału rzeczywistego:
)
(
)
(
)
(
ω
ω
ω
j
I
j
R
j
e
jX
e
X
e
X
+
=
2
∫
−
Θ
Θ
Θ
−
−
=
π
π
ω
ω
π
d
e
X
e
X
j
R
j
I
2
cot
)
(
2
1
)
(
w analogiczny sposób można wyprowadzić zależność
pomiędzy częścią urojoną a rzeczywistą widma sygnału
rzeczywistego:
∫
−
Θ
Θ
Θ
−
+
=
π
π
ω
ω
π
d
e
X
x
e
X
j
I
j
R
2
cot
)
(
2
1
]
0
[
)
(
Powyższe dwa równania są dyskretną zależnością transformaty Hilberta (discrete Hilbert transform
relationships) dla części rzeczywistej i urojonej widma przyczynowego, stabilnego ciągu o wartościach
rzeczywistych. Są to całki niewłaściwe (ze względu na wartość funkcji
(
)
2
/
)
(
cot
Θ
−
ω
dla
0
=
Θ
−
ω
) i muszą
być liczone w granicy:
Θ
Θ
−
+
Θ
Θ
−
−
=
∫
∫
+
Θ
−
−
Θ
→
π
ε
ω
ε
ω
π
ε
ω
ω
ω
π
d
e
X
d
e
X
e
X
j
R
j
R
j
I
2
cot
)
(
2
cot
)
(
lim
2
1
)
(
0
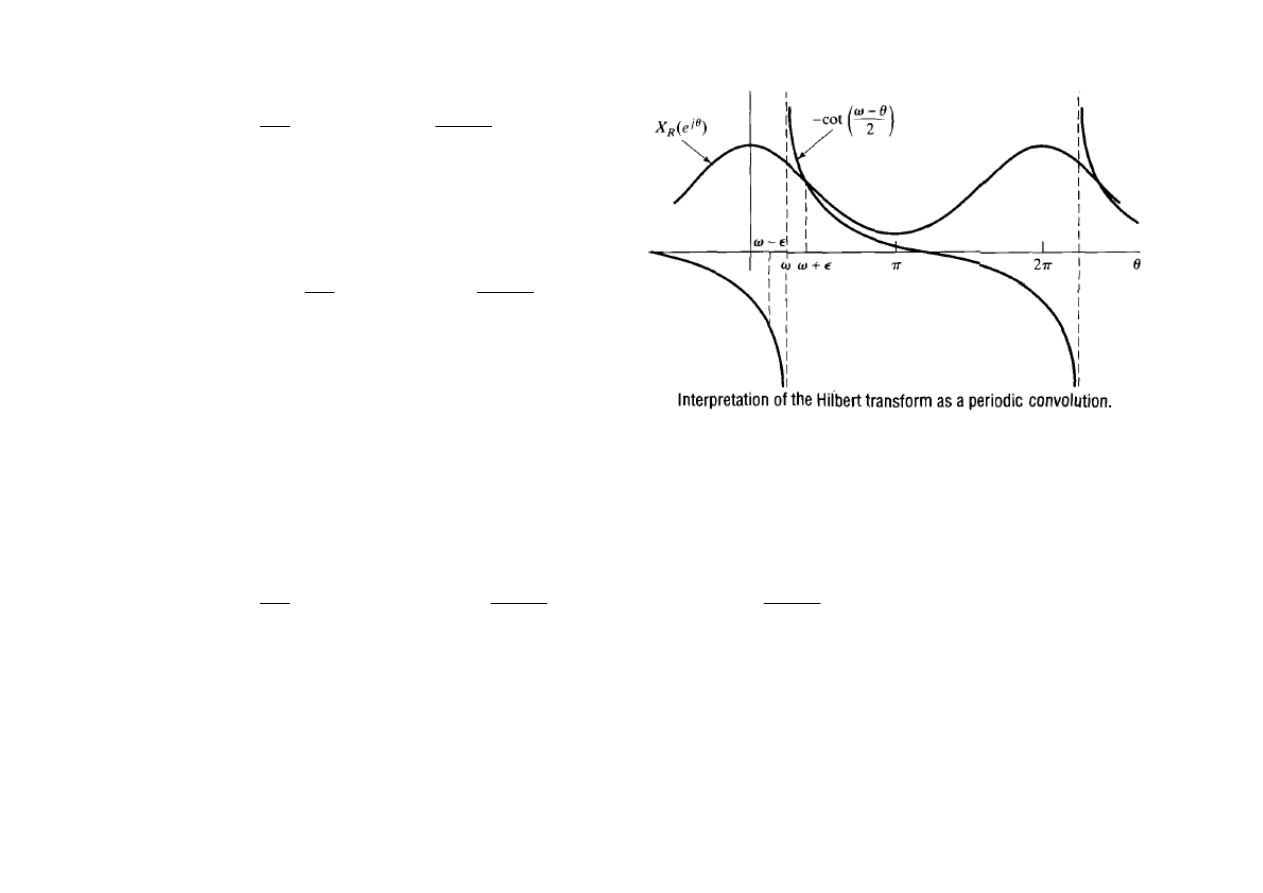
Powyższe równanie przedstawia
jako splot kołowy
)
(
ω
j
I
e
X
)
2
/
cot(
ω
−
i
(ze szczególną ostrożnością
obliczeń dla
)
(
ω
j
R
e
X
ω
=
Θ
). Analogicznie
ω
j
jest splotem kołowym
)
(
R
e
X
)
2
/
cot(
ω
i
ω
j
. Granica w całce
istnieje ponieważ funkcja
(
cot
)
(
I
e
X
)
2
/
)
(
Θ
−
ω
jest antysymetryczna dla
0
=
Θ
−
ω
.
3
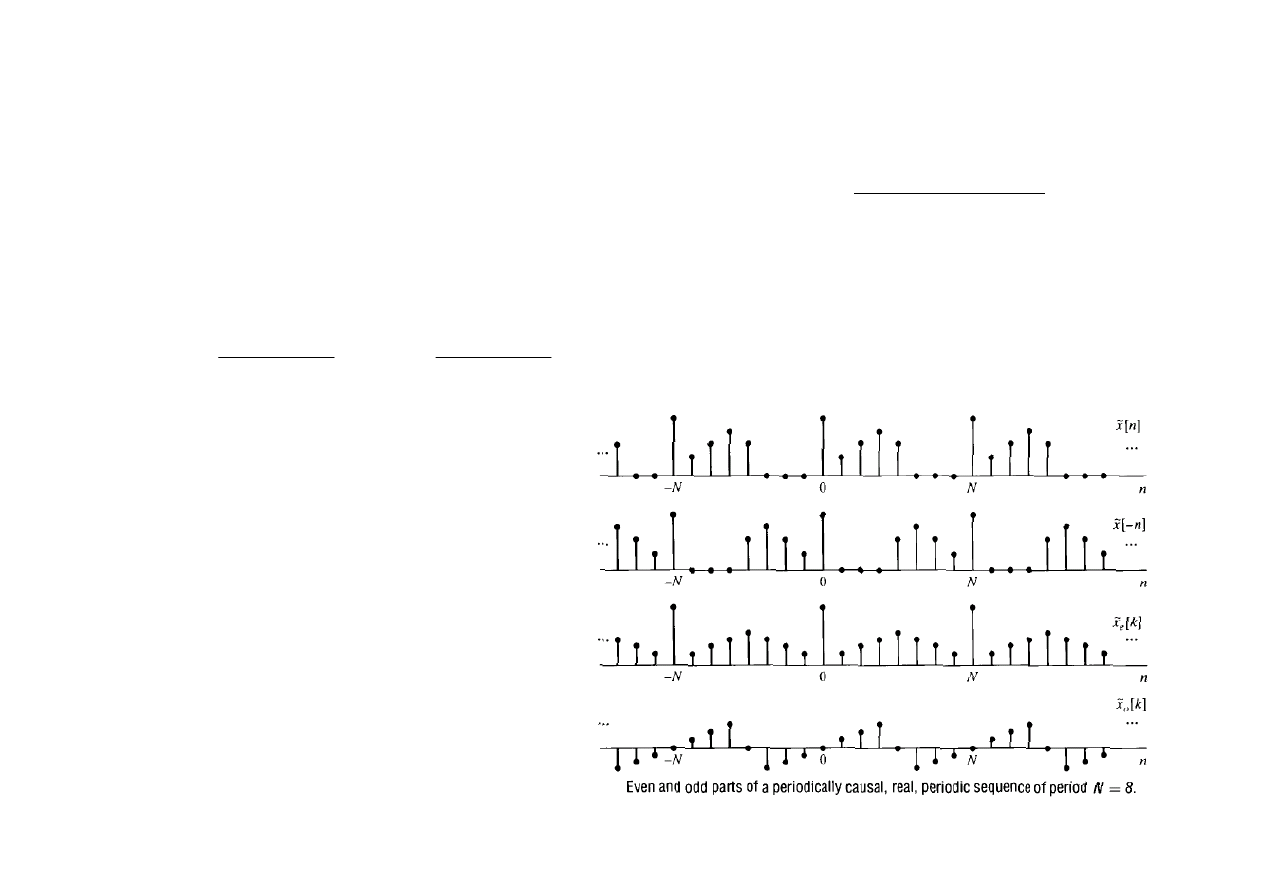
Ciągi o skończonym czasie trwania
Dla ciągów o skończonej długości reprezentację częstotliwościową można uzyskać za pomocą DFT. Przy
wyprowadzaniu zależności Hilberta należy pamiętać, że DFT jest reprezentacją ciągów okresowych.
]
[
~ n
(
[
n
x
n
(
]
[
~
=
Rozważmy ciąg okresowy
x
, którego jeden okres o długości N stanowi sygnał x[n], tj.
)
]
N
x
)
.
]
[
~ n
Ciąg
x
można przedstawić w postaci sumy składowej parzystej i nieparzystej:
)
1
,...(
1
,
0
],
[
~
]
[
~
~
−
=
+
=
N
n
n
n
]
[
x
x
n
x
o
e
gdzie:
)
1
,...(
1
,
0
,
2
]
[
~
]
[
~
]
[
~
,
2
]
[
~
]
[
~
]
[
~
−
=
−
−
=
−
+
=
N
n
n
x
n
x
n
x
n
x
n
x
n
x
o
e
Zdefiniujmy ciąg okresowo przyczynowy jako ciąg
okresowy, który w drugiej połowie okresu ma
same zera
N
n
N
n
x
<
<
=
2
/
,
0
]
[
~
. Okresowo
przyczynowe ciągi spełniają zależności:
−
+
=
=
−
=
=
1
,...,
1
)
2
/
(
,
0
2
/
,
0
],
[
~
1
)
2
/
(
,...,
2
,
1
],
[
~
2
]
[
~
N
N
n
N
n
n
x
N
n
n
x
n
x
e
e
i
−
+
=
−
=
=
1
,...,
1
)
2
/
(
],
[
~
1
)
2
/
(
,...,
2
,
1
],
[
~
2
]
[
~
0
N
N
n
n
x
N
n
n
x
n
x
o
4

Definiując ciąg okresowy
ciąg
−
+
=
−
=
=
=
1
,...,
1
)
2
/
(
,
0
1
)
2
/
(
,...,
2
,
1
,
2
2
/
,
0
,
1
]
[
~
N
N
n
N
n
N
n
n
u
N
]
[
~ n
x
można zapisać w postaci:
]
[
~
]
[
~
]
[
~
n
u
n
x
n
x
N
e
=
i
)]
2
/
(
[
~
]
2
/
[
]
[
~
]
0
[
]
[
~
]
[
~
]
[
~
N
n
N
x
n
x
n
u
n
x
n
x
N
o
−
+
+
=
δ
δ
~
gdzie
]
[n
δ
jest ciągiem impulsowym okresowym z okresem N.
~
]
[
~ n
Ciąg
]
[n
x
może być całkowicie odtworzony z
x
e
, lub może być odtworzony z
]
[
~ n
x
o
za wyjątkiem indeksów
0
=
n
i
2
/
N
=
.
n
Jeżeli
]
[
~
]
[
~
]
[
~
k
X
j
k
X
k
X
I
R
+
=
jest DFS (dyskretnym szeregiem Fouriera) ciągu
]
[
~ n
x
to część rzeczywista widma
]
[
~
k
X
R
jest DFS ciągu
]
[
~ n
x
e
, a część urojona widma
]
[
~
k
X
I
jest DFS ciągu
]
[
~ n
x
o
. Dla ciągu okresowo
przyczynowego widmo sygnału
]
[
~
k
X
jest całkowicie określone przez część rzeczywistą
]
[
~
k
X
R
i prawie
całkowicie przez część urojoną
]
[
~
k
X
I
.
~
~
Znając
]
[k
X
R
możemy wyznaczyć
]
[k
X
w następujący sposób:
1. Obliczyć
]
[
~ n
x
e
poprzez odwrotne DFS
∑
−
=
=
1
0
)
/
2
(
]
[
~
1
]
[
~
N
k
kn
N
j
R
e
e
k
X
N
n
x
π
~
2. Obliczyć
]
[
~
]
[
~
]
[
n
u
n
x
n
x
N
e
=
3. Obliczyć
]
[
~
k
X
poprzez DFS
]
[
~
]
[
~
]
[
~
]
[
~
1
0
)
/
2
(
k
X
j
k
X
e
n
x
k
X
I
R
N
n
kn
N
j
+
=
=
∑
−
=
−
π
Kroki 1-3 można wyznaczyć przez FFT.
5
Stosując twierdzenie o splocie otrzymujemy (
]
[
~
]
[
~
]
[
~
n
u
n
x
n
x
N
e
=
):
∑
−
=
−
=
+
=
1
0
]
[
~
]
[
~
1
]
[
~
]
[
~
]
[
~
N
m
N
R
I
R
m
k
U
m
X
N
k
X
j
k
X
k
X
DFS
]
[
~ n
u
N
wynosi
, definiując
otrzymujemy:
−
=
=
even
,
0
odd
),
/
cot(
2
0
,
]
[
~
k
k
N
k
j
k
N
k
U
N
π
−
=
even
,
0
odd
),
/
cot(
2
]
[
~
k
k
N
k
j
k
V
N
π
∑
−
=
−
+
=
1
0
]
[
~
]
[
~
1
]
[
~
]
[
~
N
m
N
R
R
m
k
V
m
X
N
k
X
k
X
~
~
Podstawiając powyższy wzór do
]
[
~
]
[
]
[
k
X
j
k
X
k
X
I
R
+
=
otrzymujemy zależność pomiędzy częścią rzeczywistą a
urojoną widma sygnału okresowo przyczynowego:
∑
−
=
−
=
1
0
]
[
~
]
[
~
1
]
[
~
N
m
N
R
I
m
k
V
m
X
N
k
X
j
w analogiczny sposób można wyprowadzić zależność pomiędzy częścią urojoną a rzeczywistą widma sygnału
okresowo przyczynowego:
∑
=
−
+
+
−
=
0
]
2
/
[
~
)
1
(
]
0
[
~
]
[
~
]
[
~
1
]
[
~
m
k
N
I
R
N
x
x
m
k
V
m
X
j
N
k
X
−1
N
Dla sygnału x[n] o skończonej długości N mającego własność okresowej przyczynowości (tzn. x[n]=0 dla n<0 i
n>N/2) możemy zastosować DFT i zapisać powyższe zależności w postaci:
−1
N
−1
N
−
≤
≤
−
=
∑
=
h
pozostalyc
dla
,
0
1
0
,]
[
]
[
1
]
[
0
N
k
m
k
V
m
X
N
k
jX
m
N
R
I
i
−
≤
≤
−
+
+
−
=
∑
=
h
pozostalyc
dla
,
0
1
0
],
2
/
[
)
1
(
]
0
[
]
[
]
[
1
]
[
0
m
k
N
I
R
N
k
N
x
x
m
k
V
m
jX
N
k
X
6
Analiza zależności Hilberta dla zespolonego ciągu dyskretnego
Rozważmy ciąg dyskretny
]
[
]
[
]
[
n
jx
n
x
n
x
i
r
+
=
o wartościach zespolonych. Wyprowadzimy zależność Hilberta
pomiędzy jego częścią rzeczywistą
, a urojoną
]
[n
x
w (postaci splotu) analogiczną do występującej w
widmie sygnału przyczynowego (okresowo przyczynowego).
]
[n
x
]
[n
x
r
i
Ponieważ żądamy, aby część rzeczywista
i urojona
sygnału
były powiązane transformatą
Hilberta, więc zakładamy, że widmo sygnału
ω
j
musi być jednostronne (analogia do sygnału okresowo
przyczynowego) tj.
ω
j
.
r
(
X
]
[n
x
i
]
[n
x
)
e
0
,
0
)
(
<
≤
−
=
ω
π
e
X
Sygnały ciągłe o jednostronnym widmie są nazywane sygnałami analitycznymi taką samą terminologię stosuje
się dla ciągów, (chociaż bez uzasadnienia formalnego).
]
[n
x
w powyższej postaci nazywany jest więc sygnałem
analitycznym.
ω
j
Jeżeli
i
są transformatami Fouriera ciągów
i
, to możemy zapisać:
ω
j
)
(
r
e
X
)
(
ω
j
i
e
X
]
[n
x
r
]
[n
x
i
)
(
)
(
)
(
ω
ω
i
j
r
j
e
jX
e
X
e
X
+
=
oraz
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
r
e
X
e
X
e
X
−
+
=
,
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
i
e
X
e
X
e
jX
−
−
=
)
(
ω
j
e
X
może być całkowicie odtworzony z
lub
(inaczej niż dla ciągów przyczynowych, dla
których ze składowej nieparzystej nie można odtworzyć wartości na końcach przedziałów):
)
(
ω
j
r
e
X
)
(
ω
j
i
e
X
i
<
≤
−
<
≤
=
0
,
0
0
),
(
2
)
(
ω
π
π
ω
ω
ω
j
r
j
e
X
e
X
<
≤
−
<
≤
=
0
,
0
0
),
(
2
)
(
ω
π
π
ω
ω
ω
j
i
j
e
jX
e
X
na podstawie powyższych wzorów można podać zależność pomiędzy
i
)
(
ω
j
r
e
X
)
(
ω
j
i
e
X
7
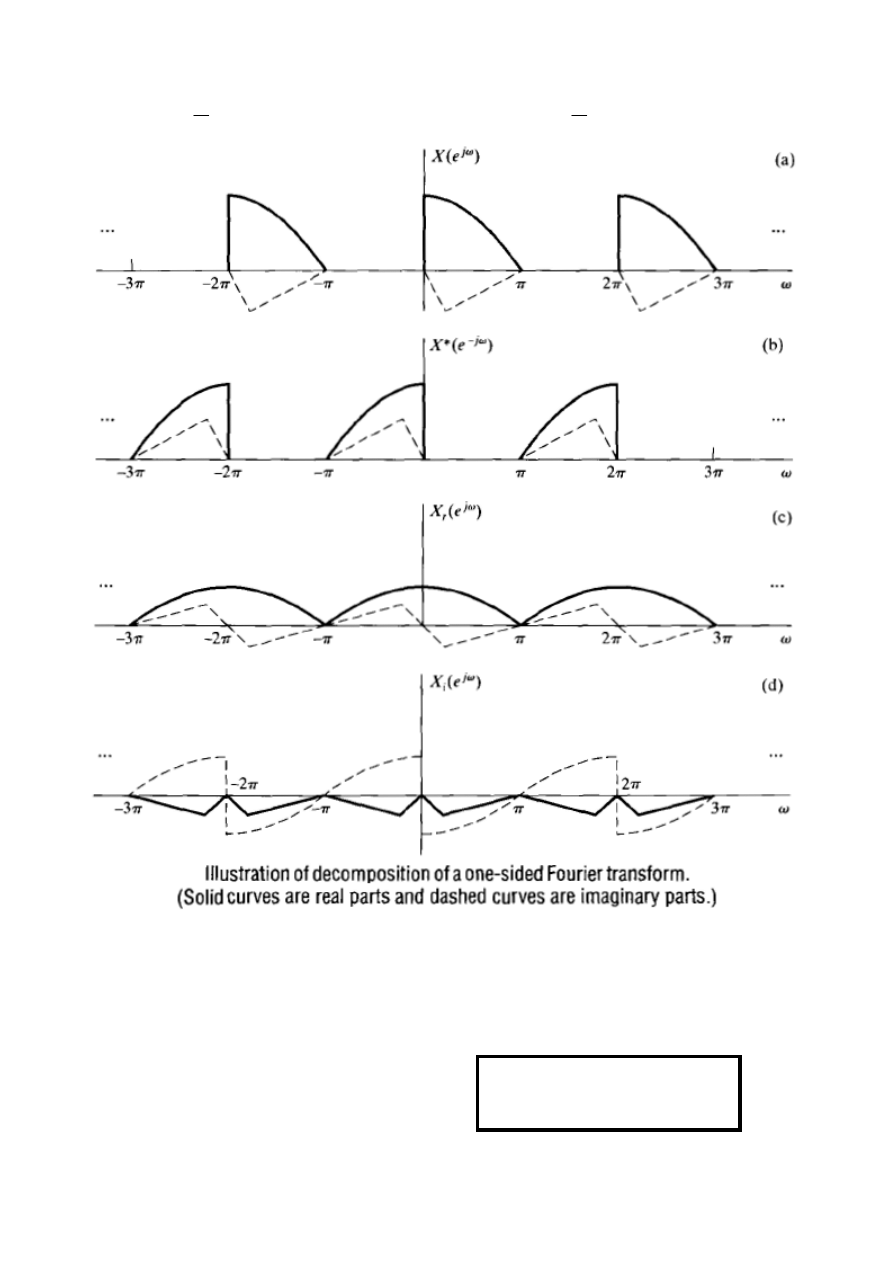
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
r
e
X
e
X
e
X
−
+
=
,
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
i
e
X
e
X
e
jX
−
−
=
<
≤
−
<
≤
−
=
0
),
(
0
),
(
)
(
ω
π
π
ω
ω
ω
ω
j
r
j
r
j
i
e
jX
e
jX
e
X
, lub
)
(
)
(
)
(
ω
ω
ω
j
r
j
j
i
e
X
e
H
e
X
=
, gdzie
<
≤
−
<
≤
−
=
0
,
0
,
)
(
ω
π
π
ω
ω
j
j
e
H
j
8
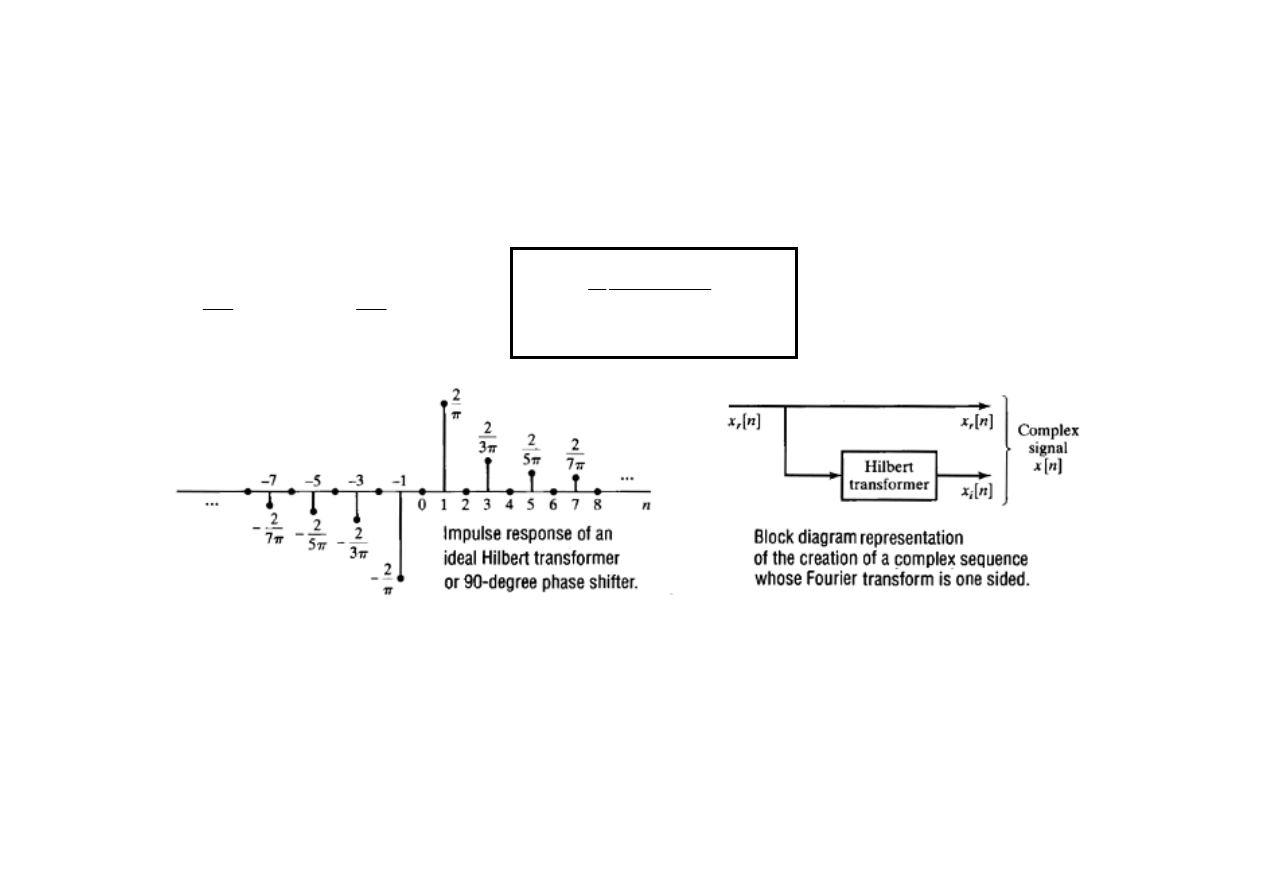
Cześć urojoną
dyskretnego sygnału analitycznego
]
[n
x
i
]
[
]
[
]
[
n
jx
n
x
n
x
i
r
+
=
=
)
(
ω
e
H
j
można wyznaczyć z części
rzeczywistej
poprzez filtrację filtrem o charakterystyce widmowej
<
≤
−
0
,
π
ω
j
.
]
[n
x
r
<
≤
−
0
,
ω
π
j
Filtr
jest nazywany idealnym 90 stopniowym przesuwnikiem fazowym, lub idealnym filtrem Hilberta.
)
(
ω
j
e
H
Odpowiedź impulsowa filtra Hilberta jest następująca:
∫
∫
−
=
−
π
ω
π
ω
ω
π
ω
π
0
0
2
1
2
1
]
[
d
je
d
je
n
h
n
j
n
j
,
=
≠
=
.
0
,
0
,
0
,
)
2
/
(
sin
2
]
[
2
n
n
n
n
n
h
π
π
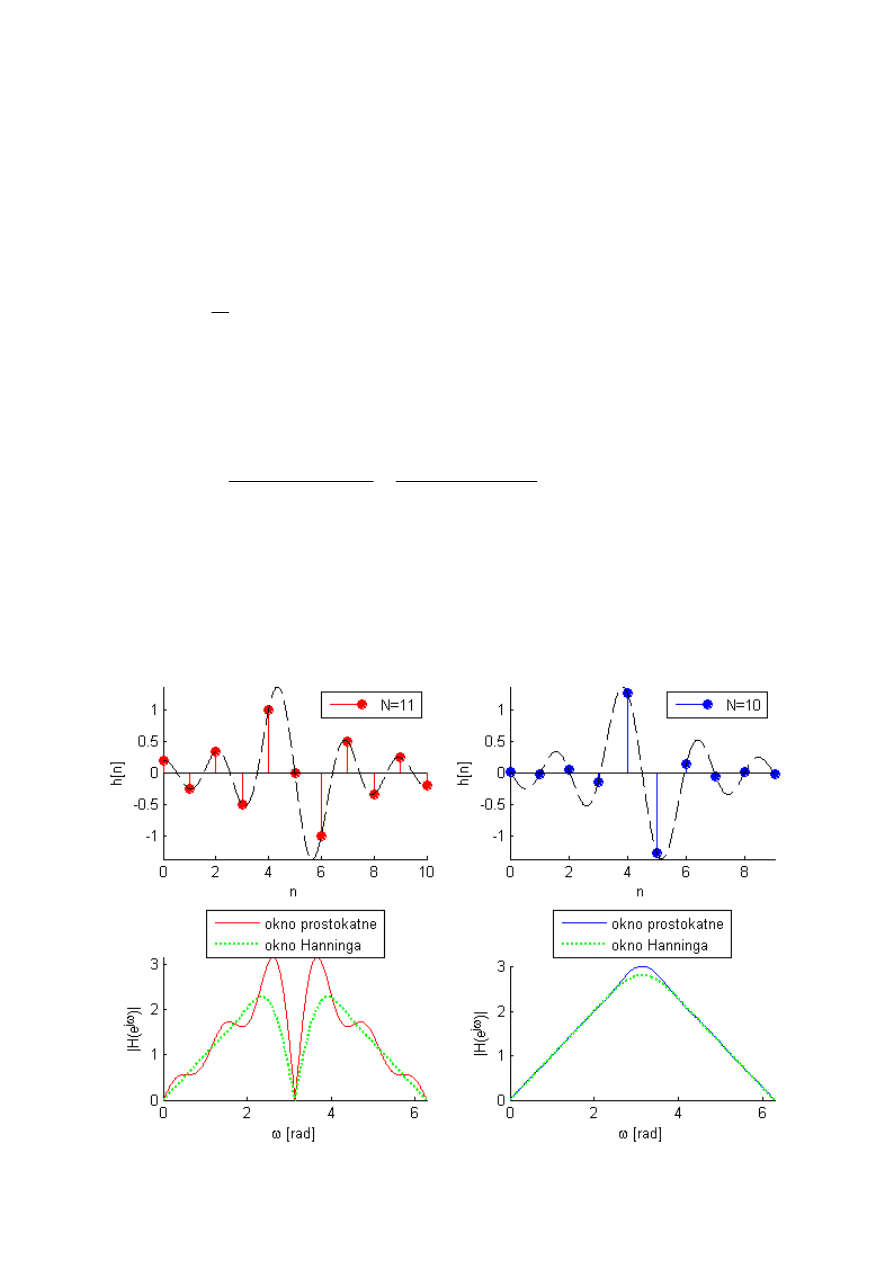
Projektowanie filtra Hilberta
Idealny filtr Hilberta (podobnie jak idealny filtr dolnoprzepustowy) jest nieprzyczynowy i ma nieskończoną
odpowiedź impulsową. Aproksymacje filtra Hilberta uzyskuje się metodą okien lub metodą Parksa-McClellana.
Dla filtrów przyczynowych opóźnienie o 90 - stopni posiada dodatkową składową liniową.
9
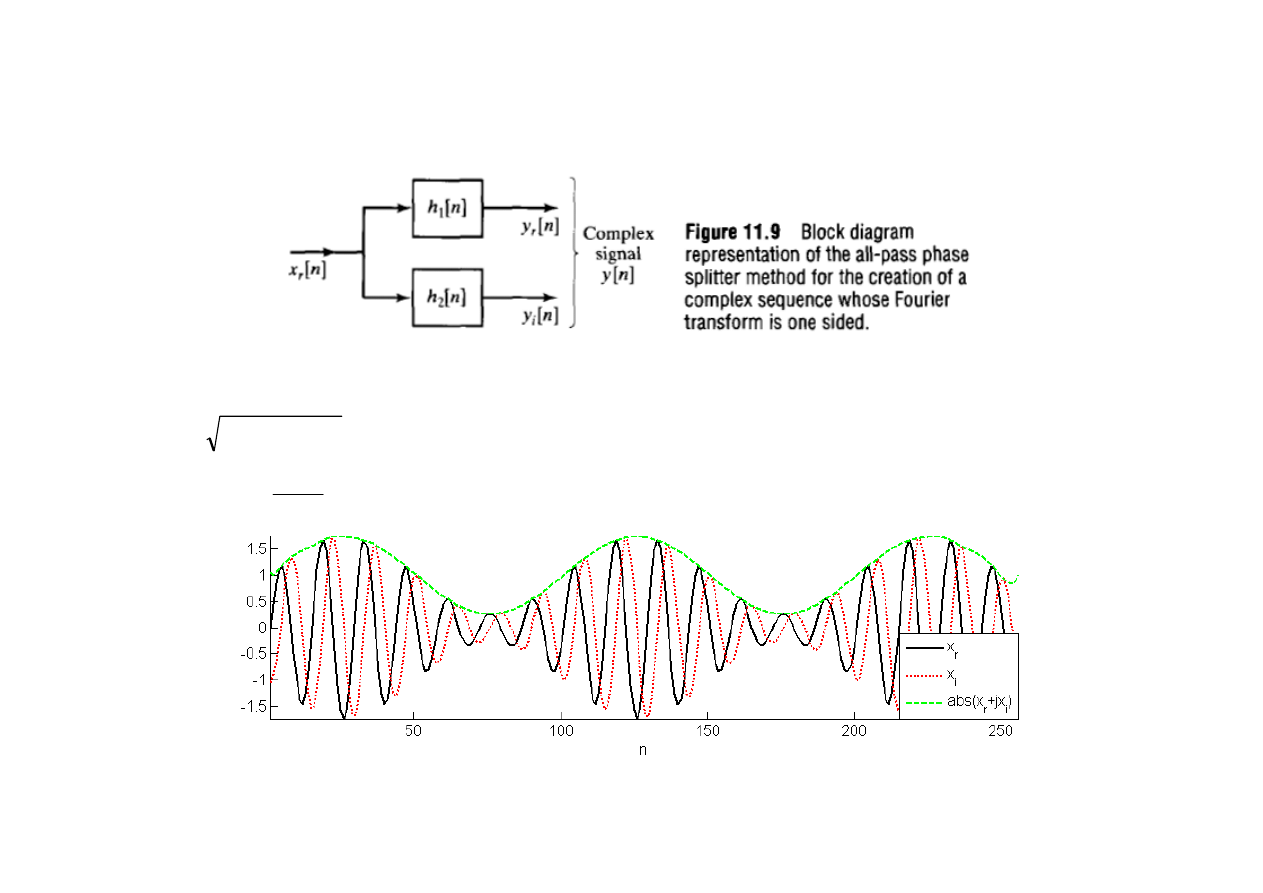
Do aproksymacji filtra Hilberta można również stosować filtry IIR w układzie phase-splitter, który składa
się z dwóch filtrów wszechprzepustowych, których charakterystyki fazowe różnią się w przybliżeniu o 90
o
w
przedziale
π
ω
<
<
|
|
0
Ciąg
]
[
]
[
]
[
n
jx
n
x
n
x
i
r
+
=
można zapisać w postaci
, gdzie:
]
[
]
[
]
[
n
j
e
n
A
n
x
ϕ
=
]
[
]
[
]
[
2
2
n
x
n
x
n
A
i
r
+
=
- obwiednia chwilowa sygnału x[n]
=
]
[
]
[
arctan
]
[
n
x
n
x
n
r
i
ϕ
- faza chwilowa sygnału x[n]
10
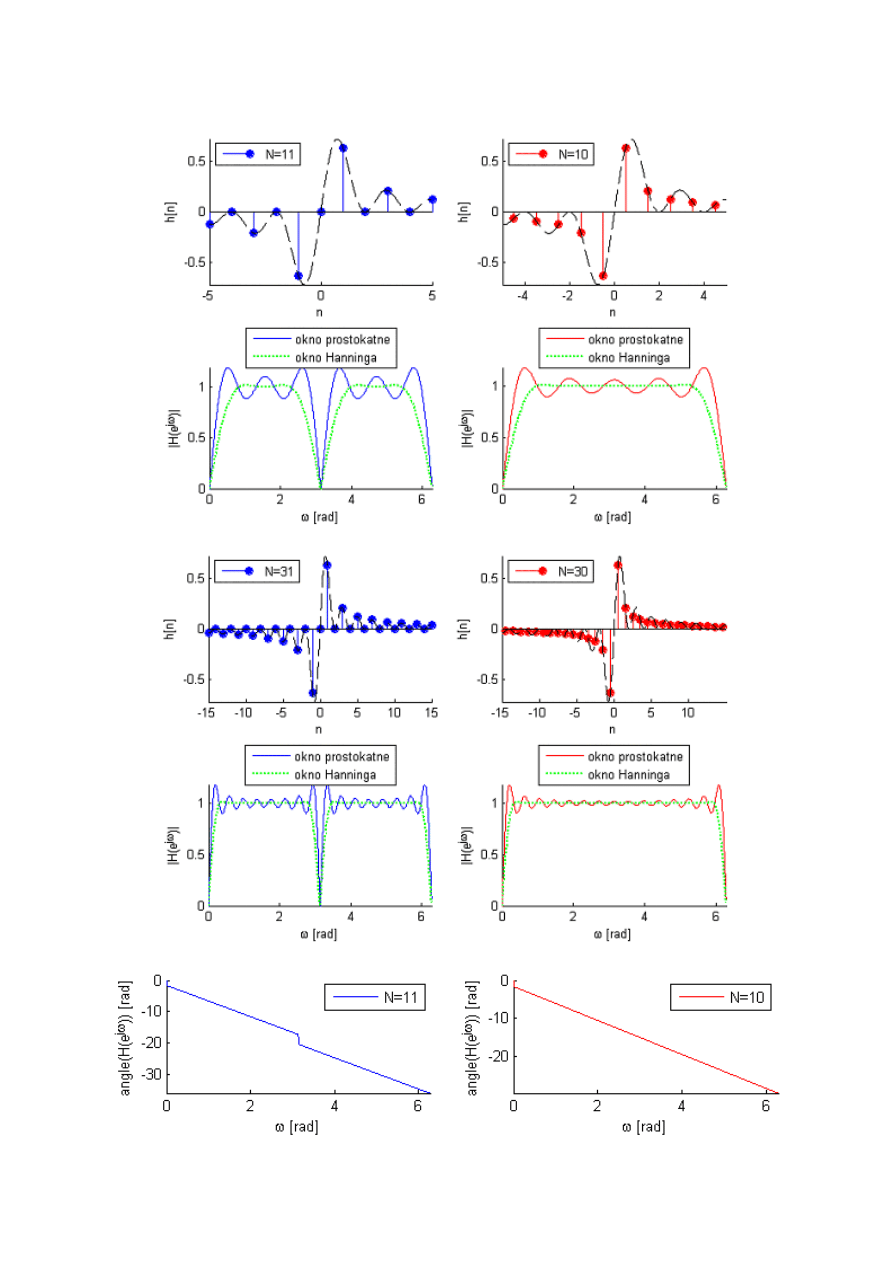
Typ
III
(
mniej liczenia
)
Typ
IV
(
lepsza aproksymacja
)
opóźnienie grupowe (N-1)/2 dla typu IV pół próbki
11
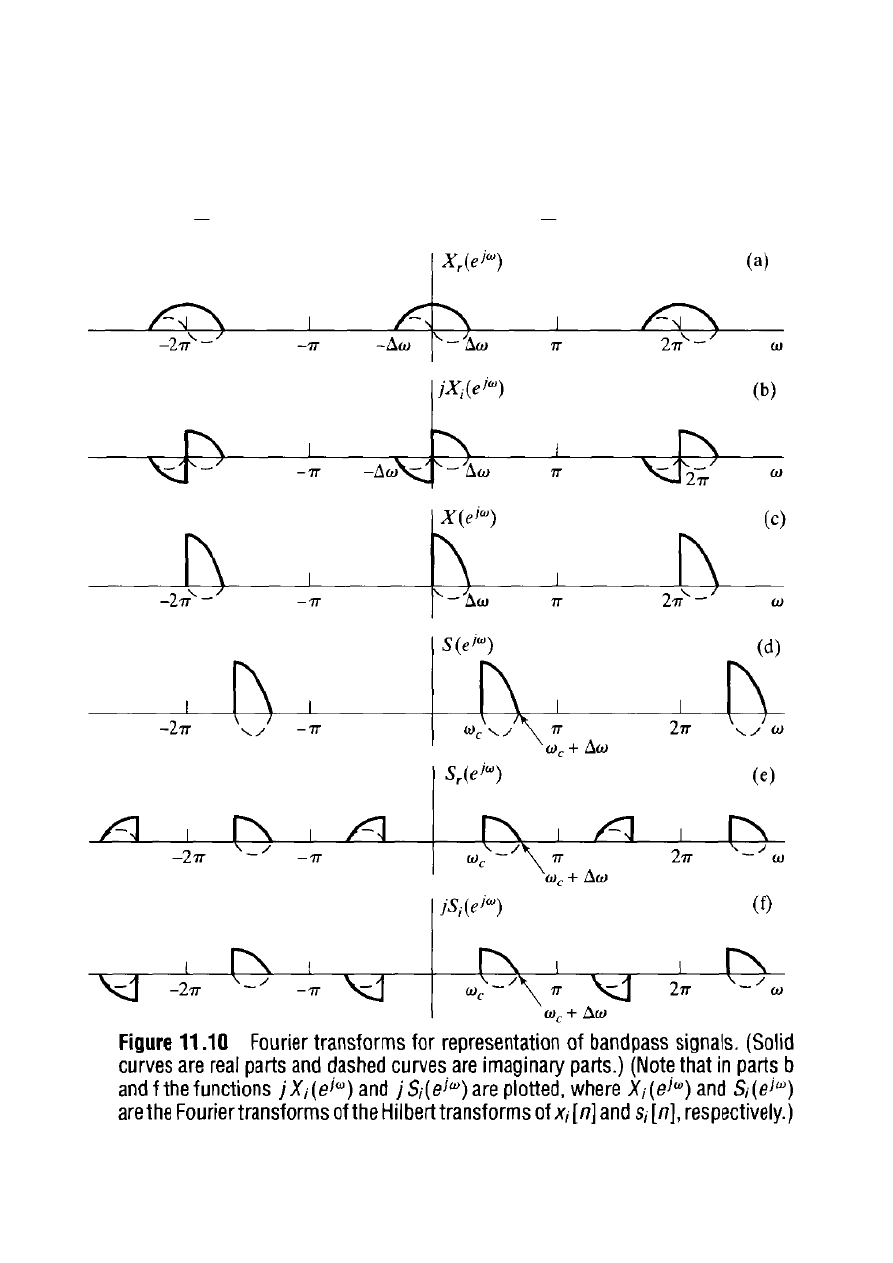
Zastosowania DSA - 1. Reprezentacja Sygnałów Pasmowych
Rozważmy sygnał analityczny
]
[
]
[
]
[
n
jx
n
x
n
x
i
r
+
=
zmodulowany sygnałem
wykładniczym
. Wówczas
]
[
]
[
n
js
n
s
i
r
+
]
[
]
[
e
n
x
n
s
n
j
c
=
=
ω
)
(
)
(
)
(
c
j
j
e
X
e
S
ω
ω
ω
−
=
i
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
r
e
S
e
S
e
S
−
+
=
oraz
[
]
)
(
)
(
2
1
)
(
*
ω
ω
ω
j
j
j
i
e
S
e
S
e
jS
−
−
=
Dla
π
ω
ω
<
∆
+
c
ciąg
jest sygnałem analitycznym.
]
[n
s
12
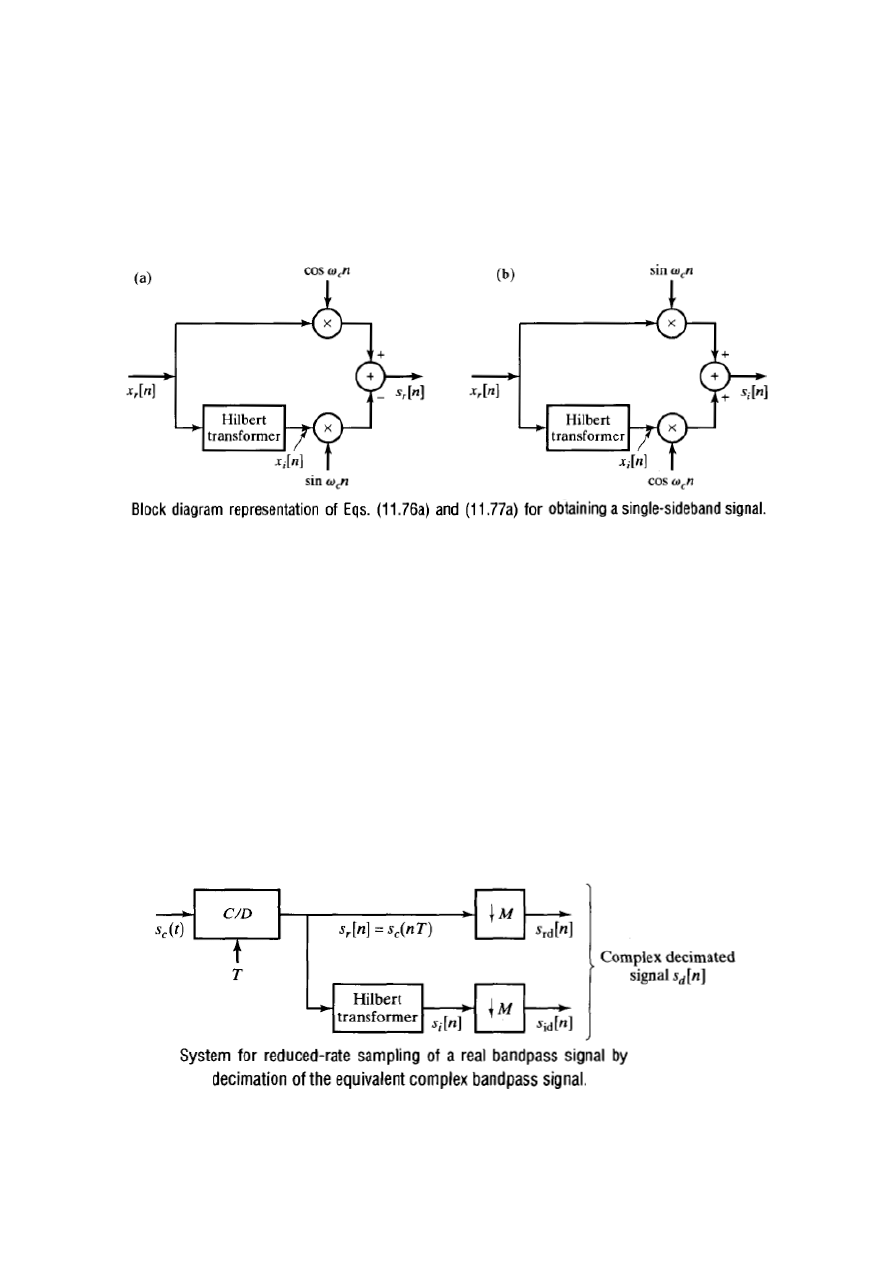
Dla ciągu
mamy:
]
[
]
[
]
[
]
[
n
js
n
s
e
n
x
n
s
i
r
n
j
c
+
=
=
ω
, skąd:
])
[
(
]
[
])
[
]
[
(
]
[
n
n
j
n
j
i
r
c
c
e
n
A
e
n
jx
n
x
n
s
ϕ
ω
ω
+
=
+
=
])
[
cos(
]
[
sin
]
[
cos
]
[
]
[
n
n
n
A
n
n
x
n
n
x
n
s
c
c
i
c
r
r
φ
ω
ω
ω
+
=
−
=
])
[
sin(
]
[
cos
]
[
sin
]
[
]
[
n
n
n
A
n
n
x
n
n
x
n
s
c
c
i
c
r
i
i
φ
ω
ω
ω
+
=
+
=
Powyższe wzory ilustrują, w jaki sposób rzeczywisty sygnał
dolnoprzepustowy można przedstawić jako sygnał pasmowy o
jednostronnym widmie.
Zastosowania DSA - 2. Próbkowanie Pasmowe
Podstawowym wymaganiem przy próbkowaniu sygnałów ciągłych jest
unikniecie aliasingu (tj. nakładania się powielonych widm). Dla sygnałów
pasmowych częstotliwość próbkowania powinna być 2 razy większa niż
szerokość pasma sygnału. Dla sygnału analitycznego można dodatkowo
wykorzystać jednostronność widma.
13
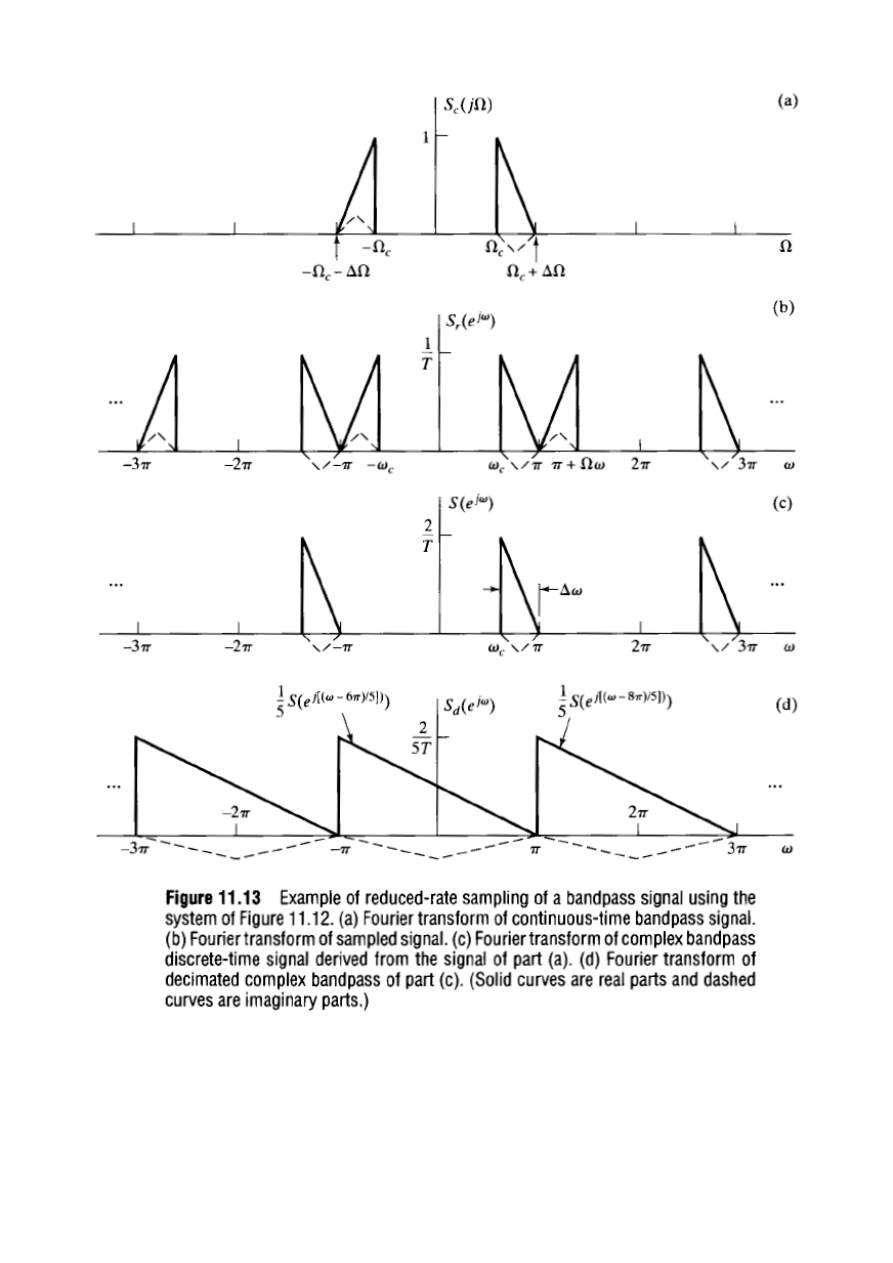
Wejściowy ciąg rzeczywisty
może zostać odtworzony z
zespolonego ciągu decymowanego
]
[n
s
r
]
[n
s
d
Sygnał
(lub zespolony ciąg
) może być następnie dalej
przetwarzany z niższą częstotliwością próbkowania.
)
(
ω
i
d
e
S
]
[n
s
d
14
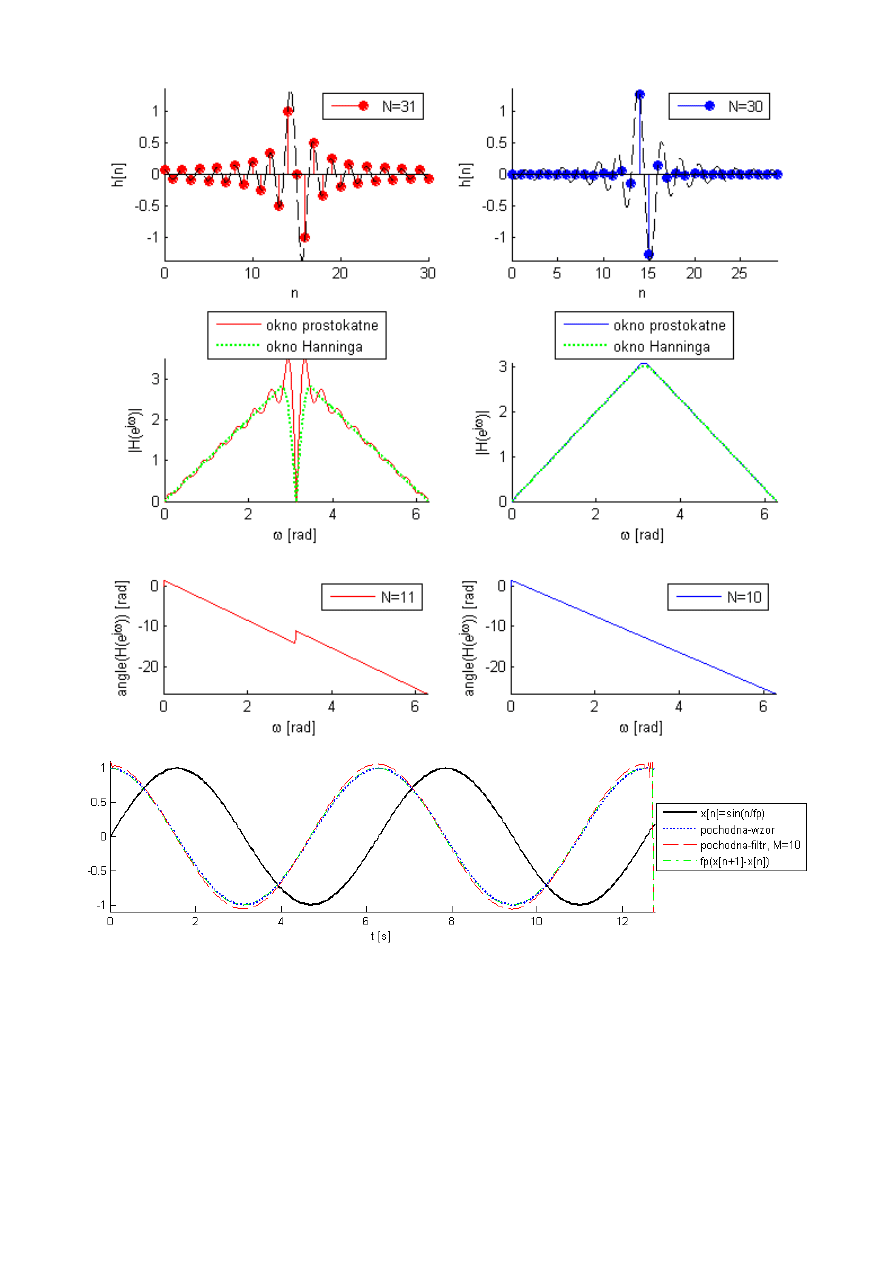
Dyskretne układy różniczkujące
Dla sygnałów ciągłych widmo pochodnej sygnału można wyznaczyć
licząc widmo sygnału, które następnie należy przemnożyć przez
.
Ω
j
Dla sygnałów dyskretnych idealny filtr różniczkujący (o liniowej
charakterystyce fazowej) definiuje się w sposób następujący:
π
ω
π
ω
ω
<
<
−
=
−
,
)
(
1
2
/
M
j
diff
e
j
T
H
Przyczynowa odpowiedź impulsowa tego filtra dla okna o długości M+1
wynosi (z pominięciem współczynnika 1/T):
M
n
M
n
M
n
M
n
M
n
n
h
diff
<
<
−
−
−
−
−
=
0
,
)
2
/
(
)
2
/
(
sin
)
2
/
(
)
2
/
(
cos
]
[
2
π
π
Filtr różniczkujący może być realizowany układem o liniowej fazie z
symetrią typu III lub typu IV.
Typ III
Typ IV (
lepsza aproksymacja
)
opóźnienie grupowe (N-1)/2 dla typu IV pół próbki
15
16
Wyszukiwarka
Podobne podstrony:
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
cw 7 Dyskretna Transformata Fouriera (DFT)
Dyskretna transformata Fouriera
Dyskretna transformata Fouriera
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
transformator hilberta (wersja bardzo skromna)
Dyskretna oraz szybka transform Nieznany
T7 Transformacja układu odniesienia
11 BIOCHEMIA horyzontalny transfer genów
Transformacje91
11Tor z transformatoramiid 13123 ppt
01Zmienne losowe dyskretneid 3335 ppt
Transformacje2
20 H16 POST TRANSFUSION COMPLICATIONS KD 1st part PL
Immunologia Transfuzjologiczna1[1]
w 5 ciagle a dyskretne
3 Rodzaje jednorodnych transformacji stosowanych w kinematy
więcej podobnych podstron