GEOMETRIA I GRAFIKA IN
ŻYNIERSKA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI
KATEDRA URZĄDZEŃ ELEKTRYCZNYCH I TECHNIKI ŚWIETLNEJ
Przykładowe zadania z rozwi
ązaniami - część 2
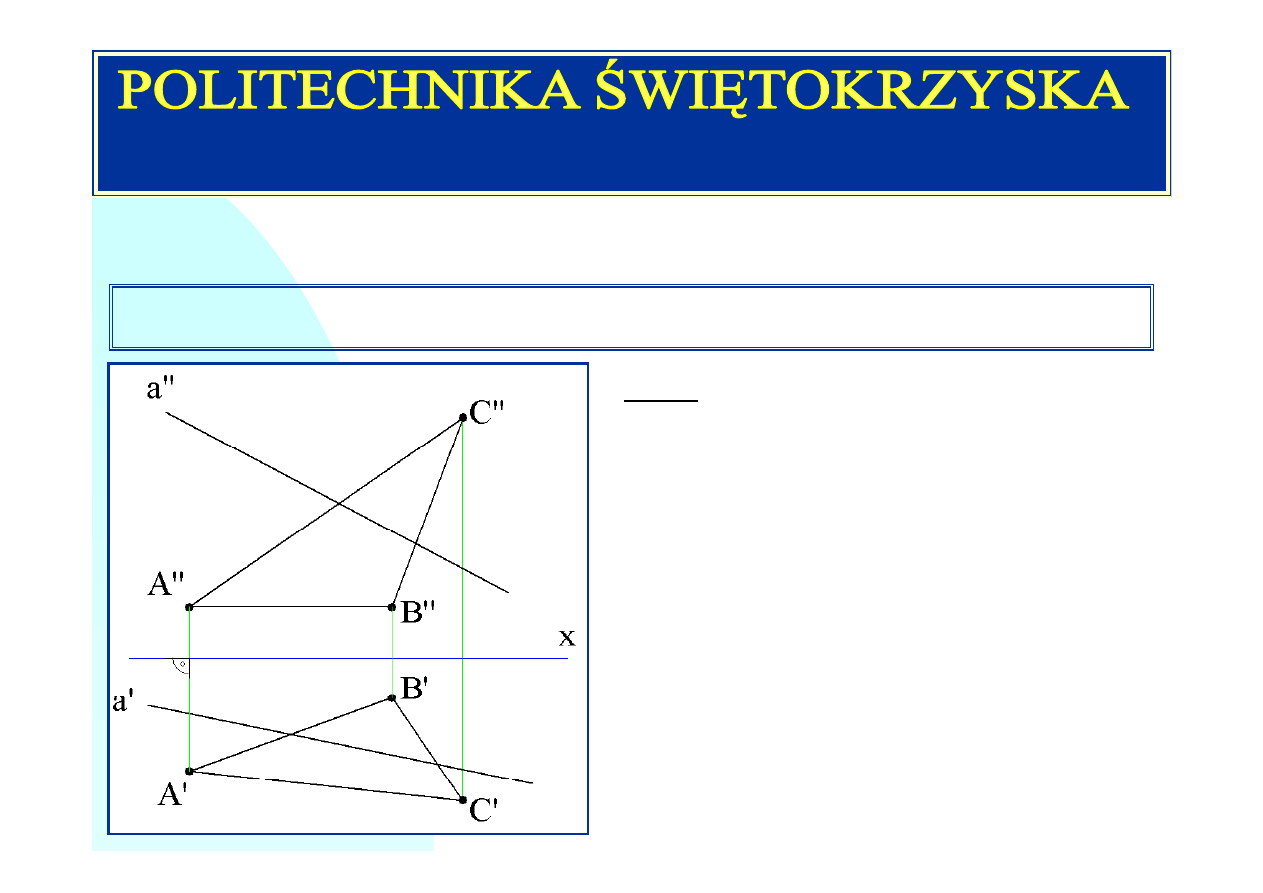
Zad. 5. Dane rzuty: poziomy i pionowy prostej
i trójkąta. Wyznaczyć rzeczywisty kąt jaki two-
rzy ta prosta z płaszczyzną trójkąta.
Należy zauważyć, że bok
AB
trójkąta
ABC
jest
równoległy do rzutni poziomej, zatem dla
uzyskania rzutu, w którym płaszczyzna trójkąta
jest prostopadła do rzutni, nie wymaga
wprowadzania obiektów pomocniczych.
Dla wyznaczenia rzeczywistego kąta pomiędzy
prostą i płaszczyzną trójkąta musimy właśnie
wprowadzić rzutnię prostopadłą do płaszczyzny
trójkąta.
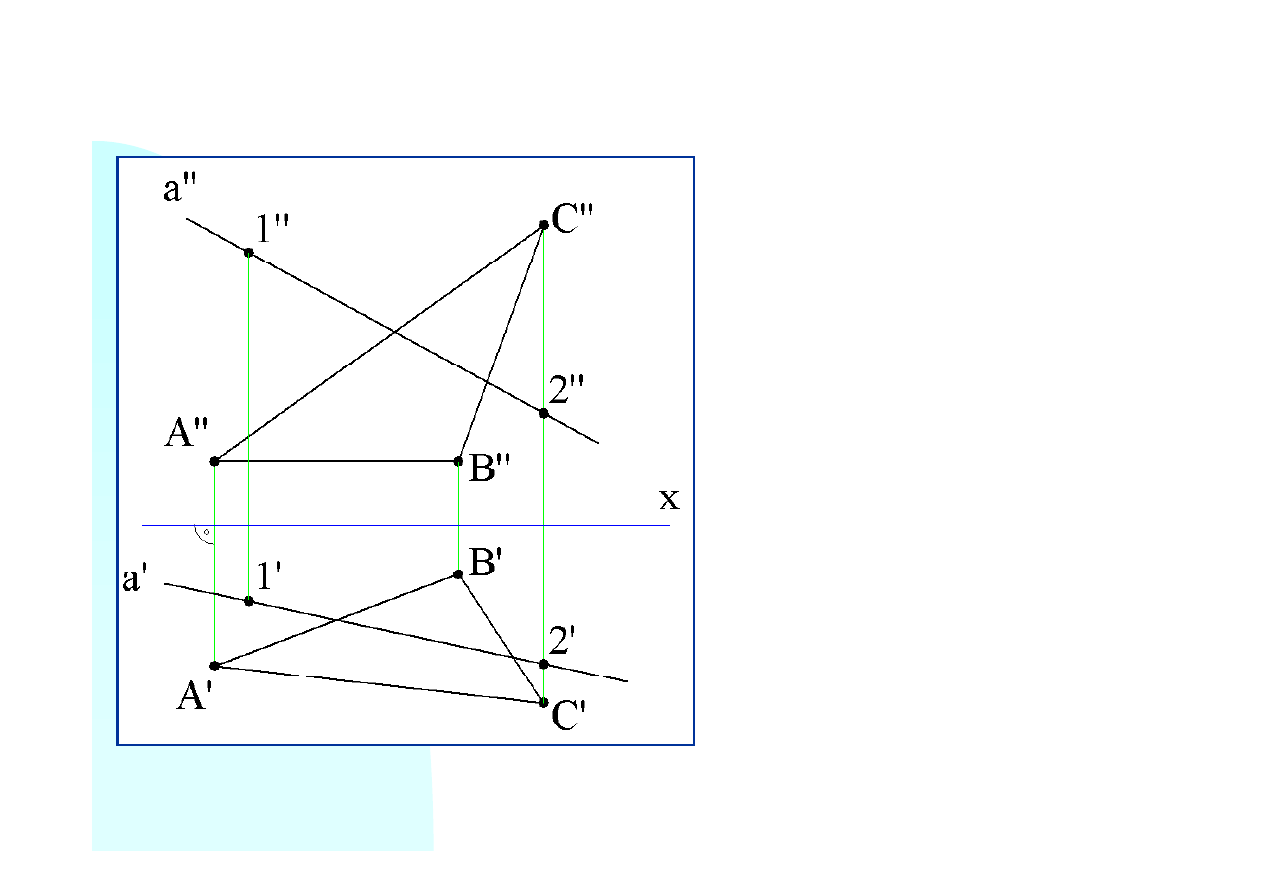
Konstrukcję należy jednak zacząć od
wybrania dowolnych dwóch punktów
leżących na prostej
a
. Na rysunku są
to punkty
1
i
2
dane rzutami
pionowymi
1’’
i
2’’
i poziomymi
1’
i
2’
. Rzuty: pionowy i poziomy tych
punktów leżą na tych samych
prostych prostopadłych do osi
x
.
Promień rzutujący punkt
2
pokrywa
się z promieniem rzutującym
wierzchołek
C
trójkąta.
Prowadzenie wspólnych prostych
rzutujących zmniejsza liczbę
elementów rysunku - jest on bardziej
przejrzysty i mniej pracochłonny -
może jednak czynić konstrukcję
mniej czytelną i wymagającą przy
tworzeniu rysunków większej uwagi.
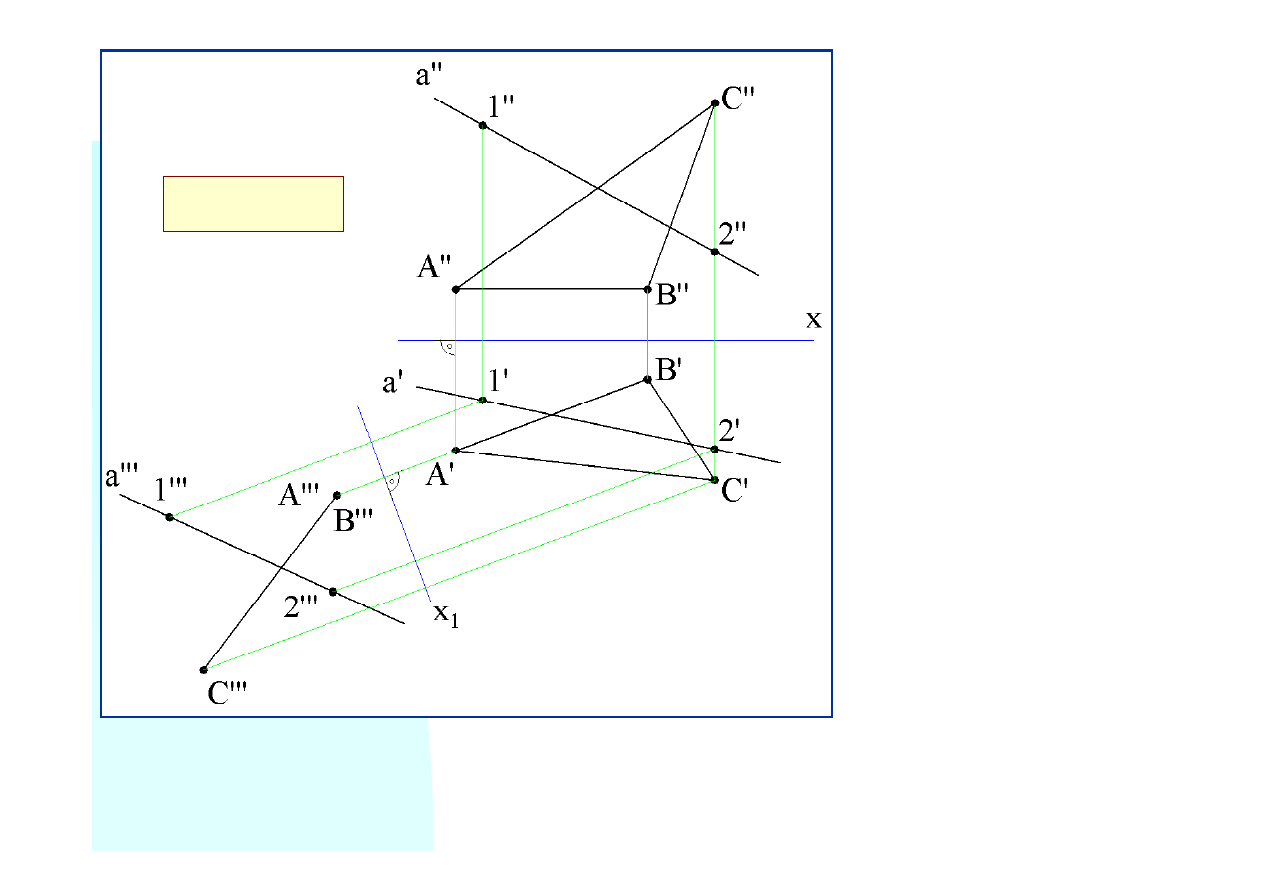
Stawiamy nową rzutnię
prostopadłą do rzutni po-
ziomej i prostopadłą do
boku
AB
trójkąta. Krawędź
przecięcia nowej rzutni z
rzutnią poziomą to oś
x
1
prostopadła do rzutu pozio-
mego boku
AB
, czyli
odcinka
A’B’
.
Rzutujemy na nową rzutnię
prostą i trójkąt prowadząc
od
rzutów
poziomych
punktów (czyli punktów
A’
,
B’
,
C’
,
1’
i
2’
) proste
rzutujące prostopadłe do
nowej osi.
Z
drugiej
strony
osi
odmierzamy dodatnie wy-
sokości
tych
punktów
(odległości punktów
A’’
,
B’’
,
C’’
,
1’’
i
2’’
od osi
x
)
znajdując położenie ich
trzecich rzutów.
W efekcie otrzymujemy taką konfigurację prostej i trójkąta na
której uwidoczniony jest rzeczywisty kąt jaki tworzy prosta
z płaszczyzną trójkąta.
x
1
⊥
A’B’
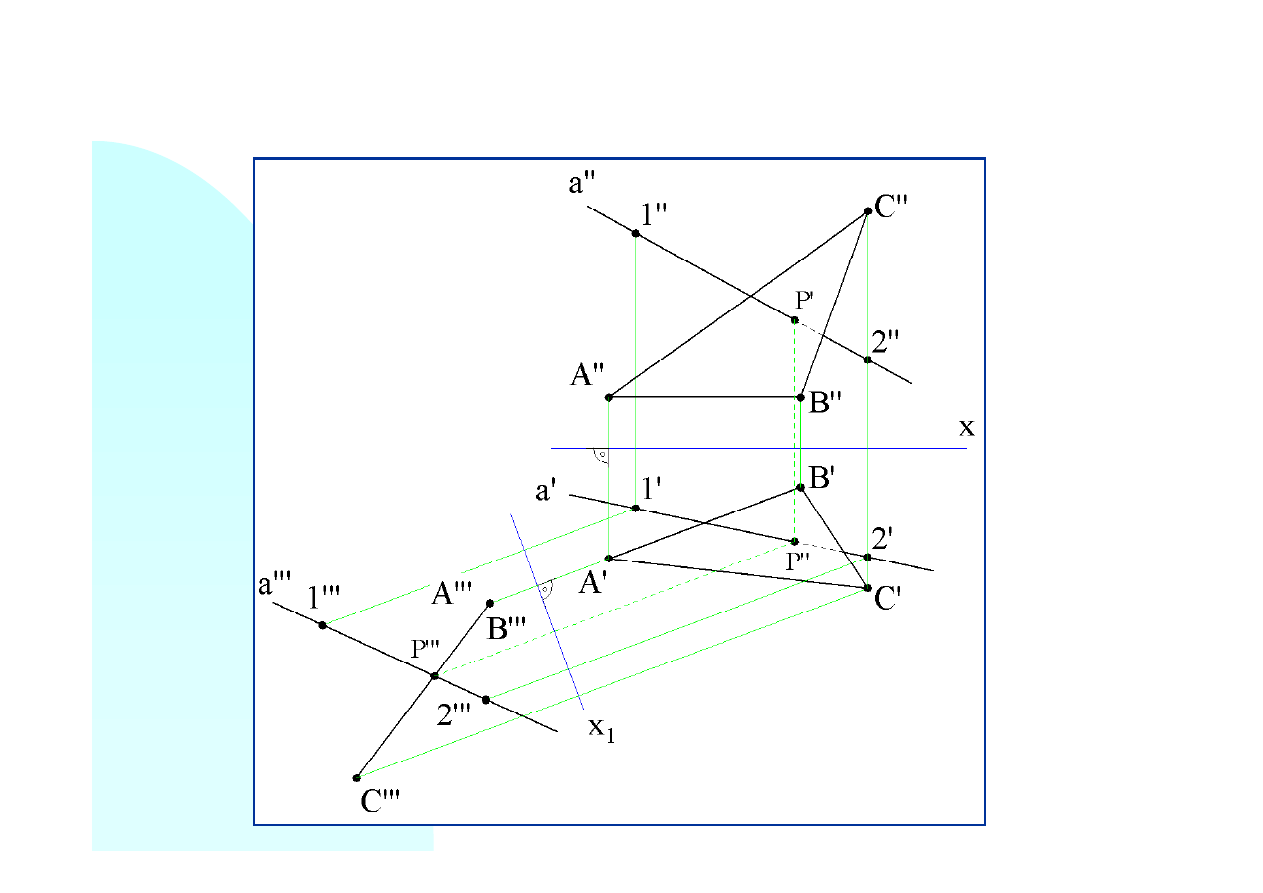
Opisaną konstrukcję można wykorzystać do wyznaczania punktu przebicia płaszczyzny przez
prostą. W tym zadaniu, sposób wyznaczenia rzutów punktu przebicia trójkąta przez prostą,
zaznaczono linią kreskową (proste rzutujące punkt
P
- punkty
P’’’
,
P’’
i
P’
).
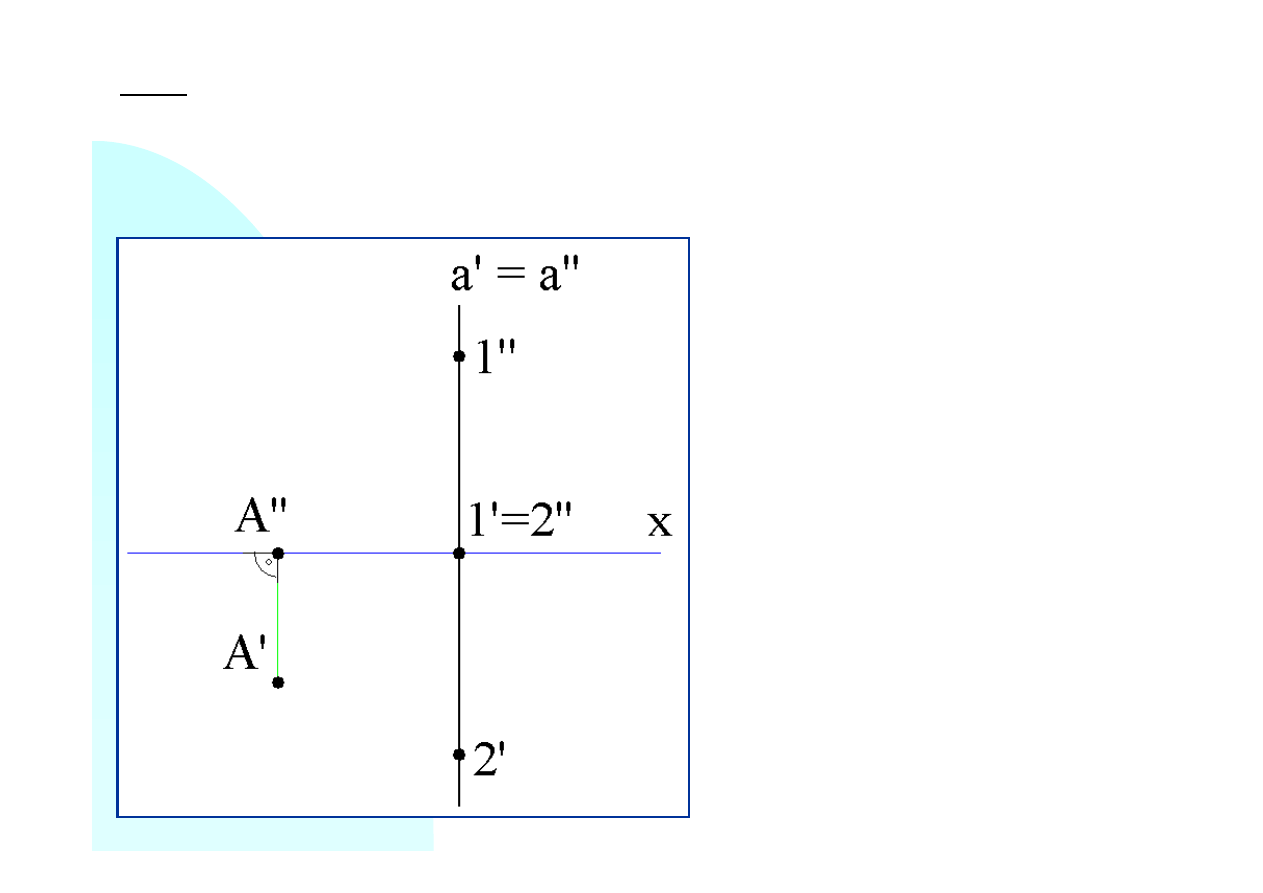
Zad.6. Dane rzuty: poziomy i pionowy prostej i punktu. Wyznaczyć rzeczywistą odległość
punktu od prostej i wykreślić rzuty poziomy i pionowy tej odległości.
Na rysunku, na prostej, zaznaczono punkty odpowiadające punktom przebicia rzutni
poziomej i pionowej przez tą prostą.
Należy także zauważyć, że punkt
A
leży na płaszczyźnie poziomej, więc
rzut poziomy punktu
A
,
A’
, jest też
punktem rzeczywistym
A
. Wynika to
z położenia
A’’
na osi
x
.
Punkt
1’’
=
1
to punkt przebicia rzutni
pionowej przez prostą
a
.
Punkt
2’ = 2
to punkt przebicia
płaszczyzny poziomej przez prostą
a
.
Dla wyznaczenia odległości należy
skorzystać z niezmiennika o rzutowa-
niu kąta prostego.
Stawiamy nową rzutnię, prostopadłą
do rzutni poziomej i równoległą do
prostej
a
. Jej krawędź przecięcia z
płaszczyzną poziomą (
x
1
) będzie
równoległa do
a’
(także do
a’’
).
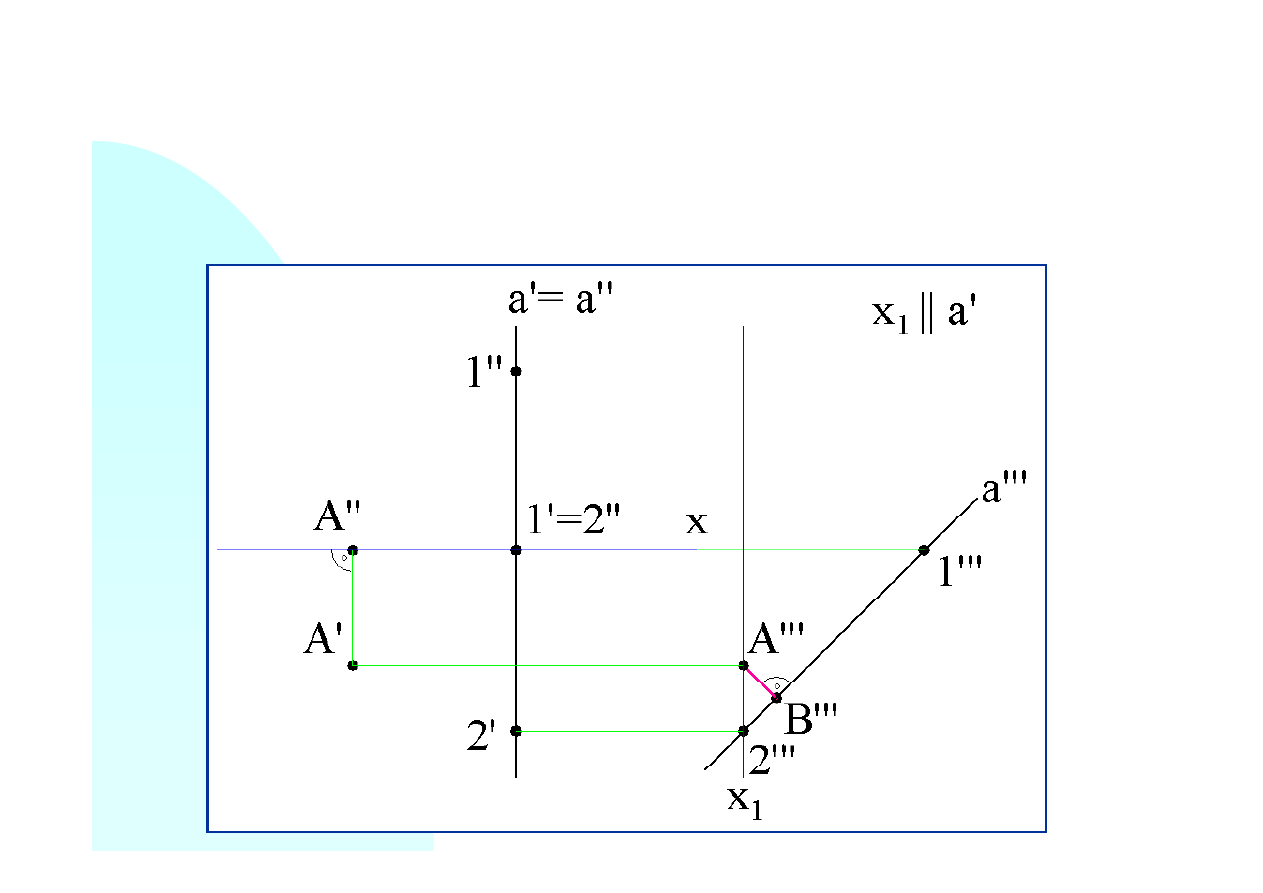
Proste rzutujące prostopadłe do nowej osi łączą rzuty poziome (
1’
,
2’
i
A’
) i rzuty trzecie (
1’’’
,
2’’’
,
A’’’
) punktów. Ponieważ wysokości punktów
2
i
A
są równe 0 (rzuty
2’’
i
A’’
leżą na osi
x
)
więc trzecie rzuty tych punktów leżą na osi
x
1
. Wysokość punktu
1
(odległość
1’’
od osi
x
)
została odmierzona na prostej rzutującej punkt
1
na trzecią rzutnię - jest więc także odległością
punktu
1’’’
od osi
x
1
. Odcinek
A’’’B’’’
, prostopadły do
a’’’
, jest trzecim rzutem odległości
punktu
A
od prostej
a
. Nie jest to jednak jeszcze odległość rzeczywista.
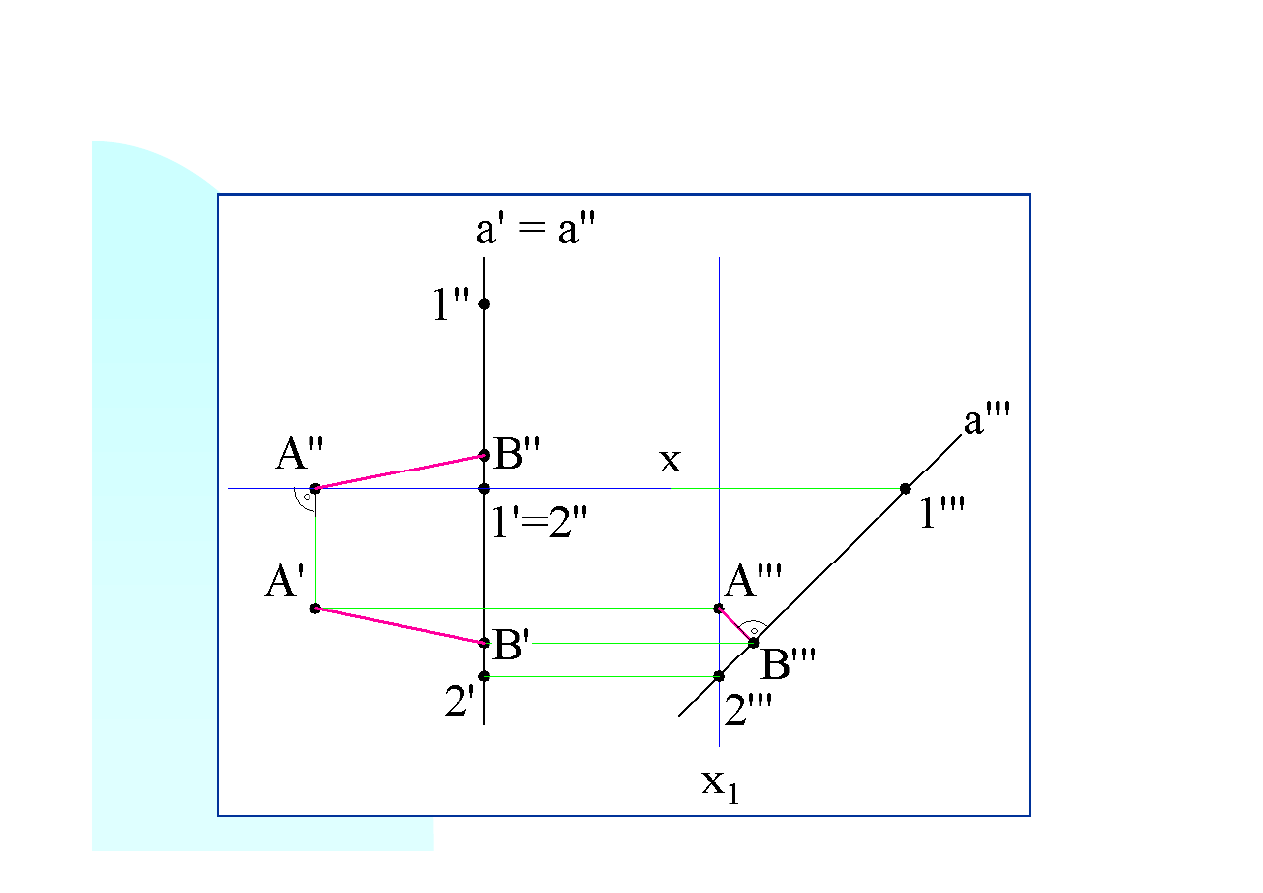
Aby wyznaczyć rzuty poziomy i pionowy tej odległości, należy zrzutować punkt
B
na rzutnię
poziomą i pionową za pomocą prostych rzutujących. Odcinek
A’B’
jest rzutem poziomym
odległości, a odcinek
A’’B’’
jej rzutem pionowym. Odległość
B’’
od osi
x
jest równa odległości
punktu
B’’’
od osi
x
1
.
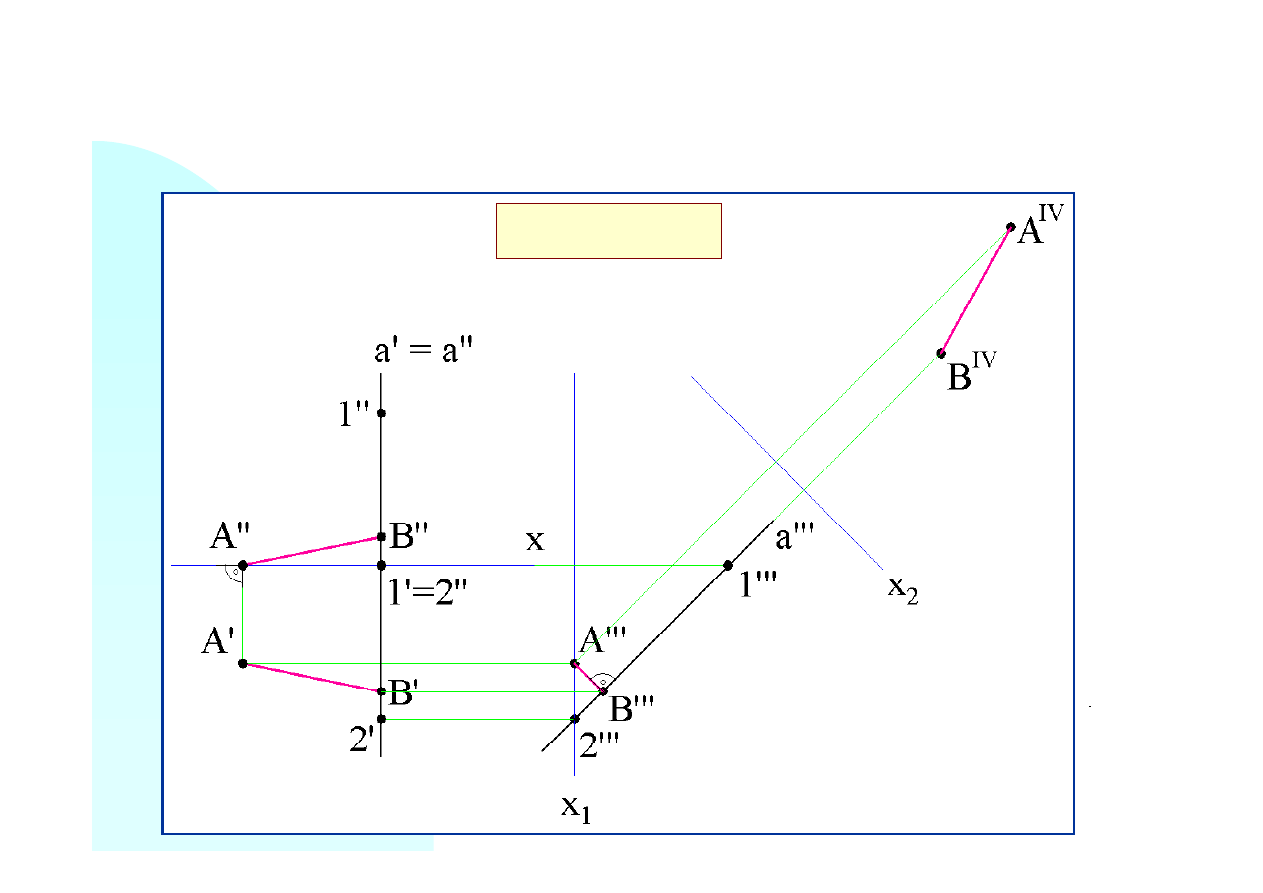
Rzeczywistą odległość otrzymamy wykonując kolejny rzut odcinka
AB
na płaszczyznę do niego
równoległą. Budujemy nową oś
x
2
równoległą do
A’’’B’’’
. Na prostych rzutujących odmierzamy
odległości rzutów poziomych
A’
i
B’
od osi
x
1
. Rzeczywistą odległość stanowi długość odcinka
A
IV
B
IV
.
x
2
|| A’’’B’’’
A’’’B’’’
⊥
a’’’|| b’’’
Zad.7. Dane rzuty: poziomy i pionowy dwóch prostych
a
i
b
. Wyznaczyć trzecią prostą
c
prostopadłą do płaszczyzny utworzonej przez proste
a
i
b
i przechodzącą przez punkt
przecięcia tych prostych. Wykreślić rzuty poziomy i pionowy prostej
c
.
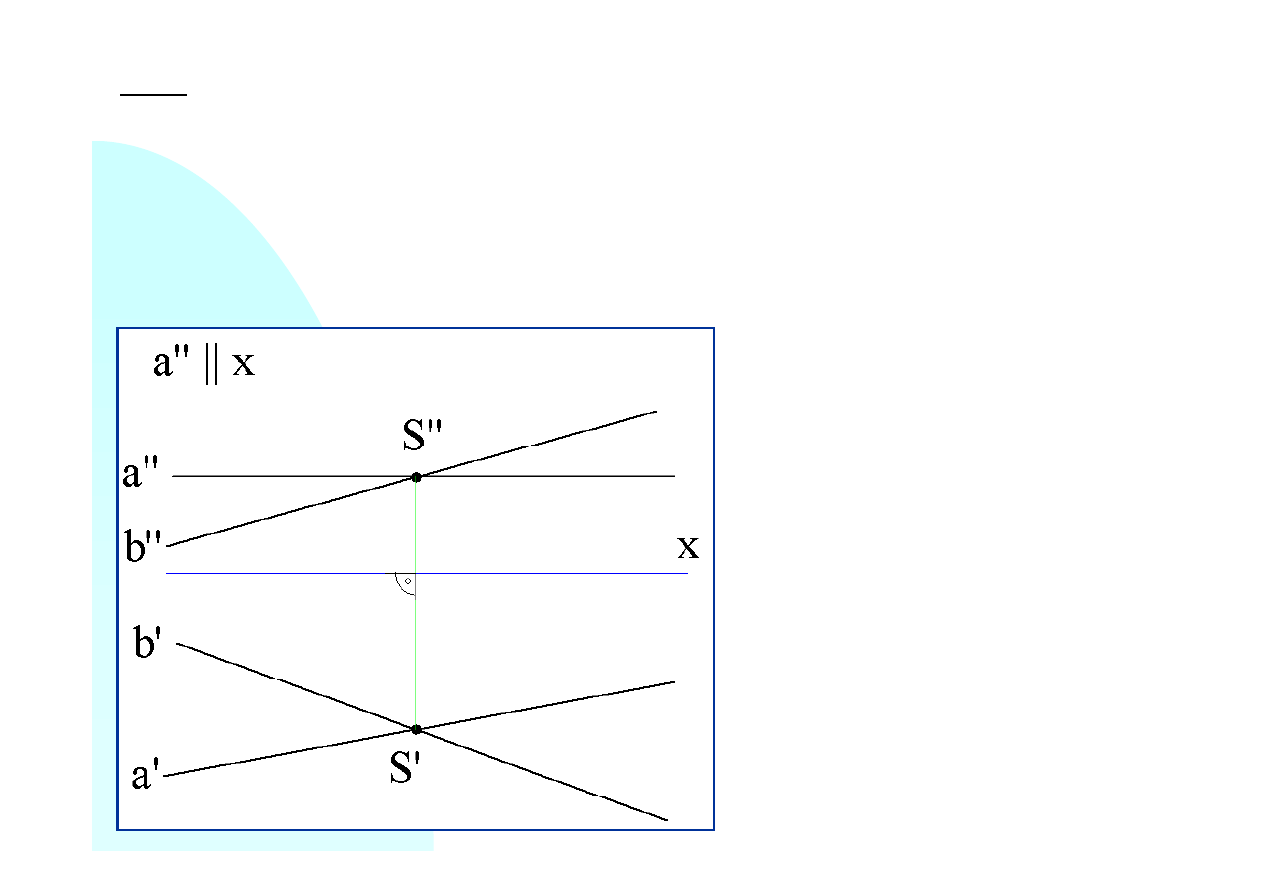
Prosta
a
zajmuje położenie szczególne. Jest równoległa do rzutni poziomej. Świadczy o tym
równoległość rzutu pionowego tej prostej
a’’
do osi
x
. Zadanie jest więc łatwiejsze - nie
musimy wprowadzać elementu pomocniczego w postaci odcinka łączącego obie proste i
równoległego do jednej z rzutni.
Aby wykonać nowy rzut prostych
należy na każdej z nich obrać po
jednym dowolnym punkcie. Drugim
punktem dla każdej z prostych
będzie punkt przecięcia
S
.
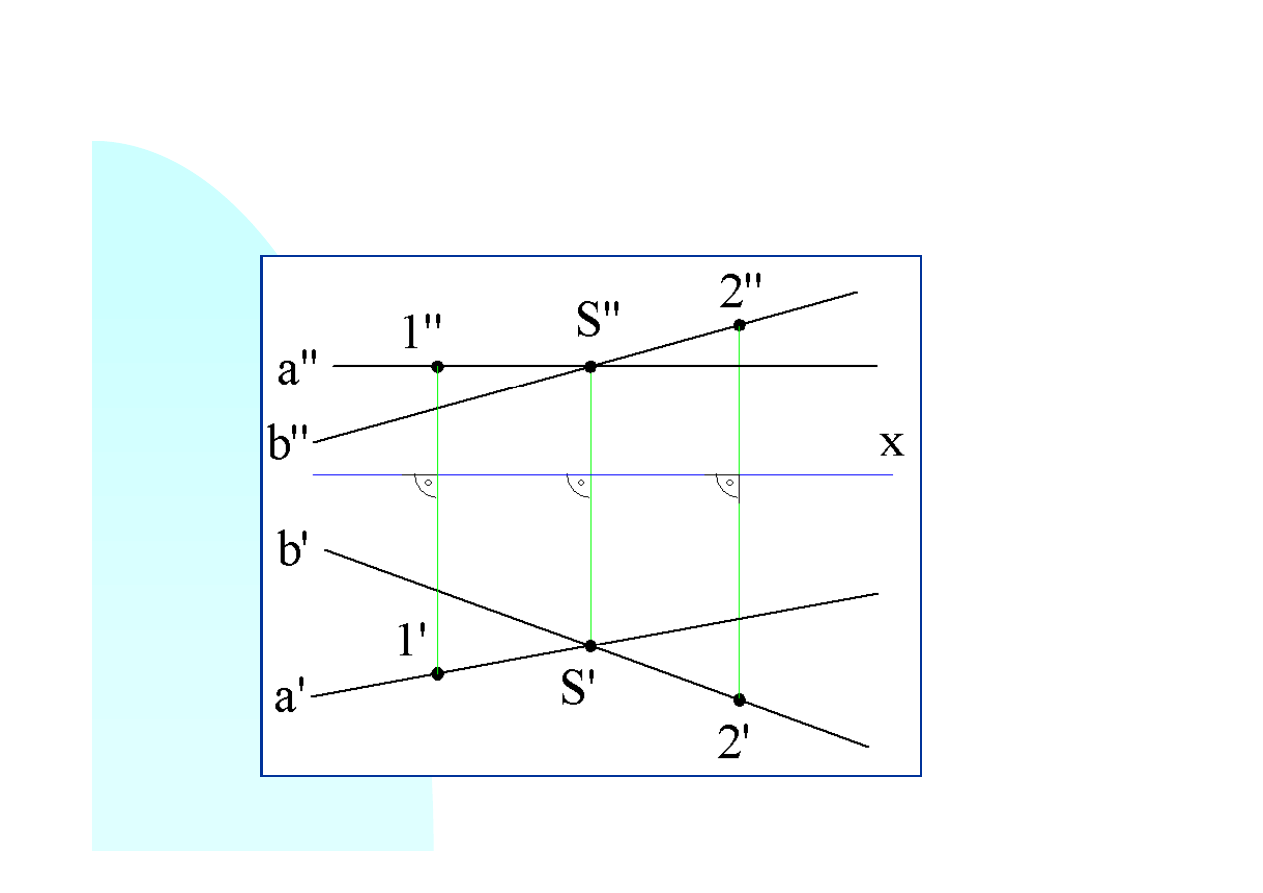
Zaznaczony punkt
1
należy do prostej
a
, a punkt
2
do prostej
b
. Rzuty tych punktów leżą na
tych samych prostych prostopadłych do osi
x
.
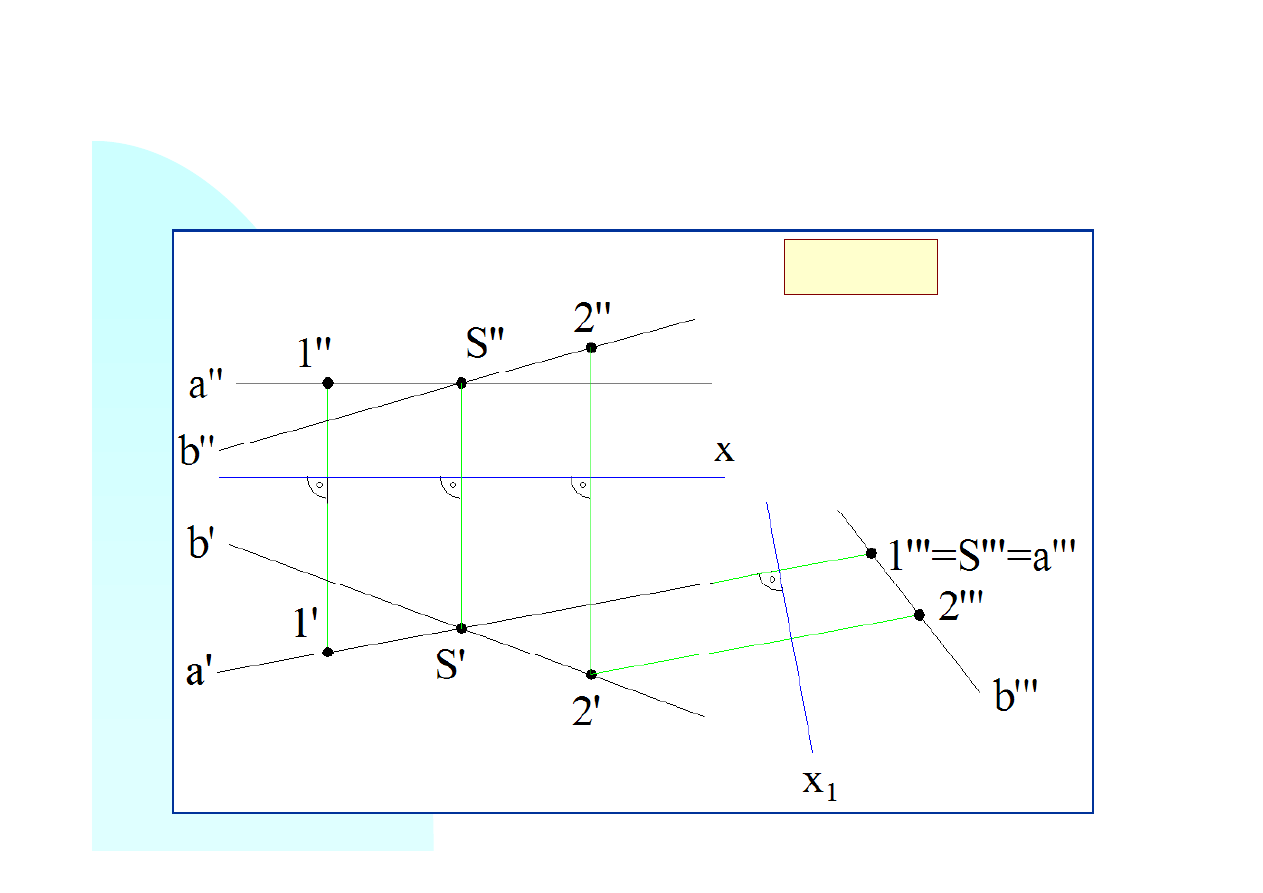
Stawiamy nową rzutnię prostopadle do rzutni poziomej i prostopadle do prostej
a
- oś
x
1
będzie
prostopadła do rzutu
a’
. Konstrukcja ta ma na celu wprowadzenie rzutni prostopadłej do
płaszczyzny określonej dwoma prostymi przecinającymi się. Położenie punktów
1’’’
,
2’’’
i
S’’’
znajdujemy po odmierzeniu od osi
x
1
wysokości tych punktów.
x
1
⊥
a’
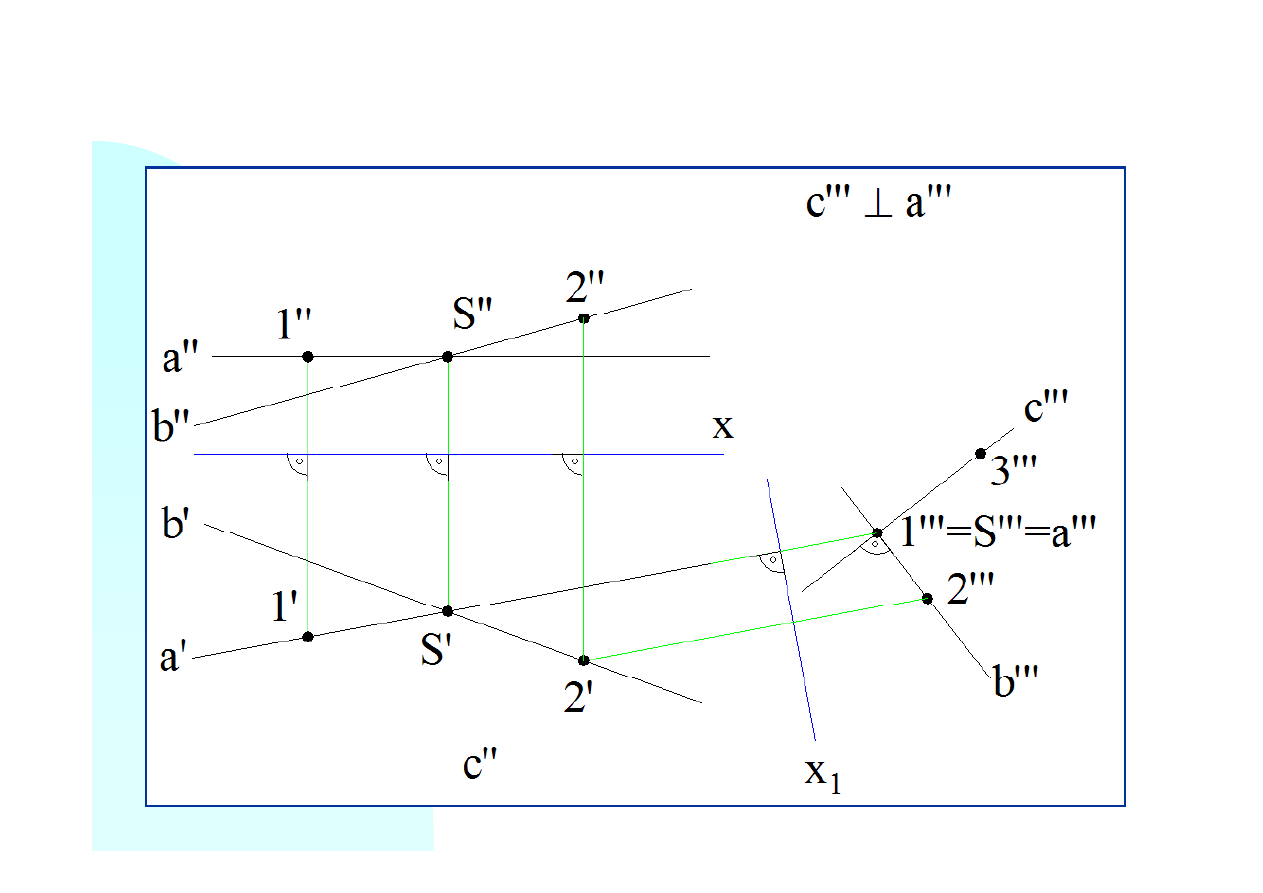
Rysujemy rzut prostej
c’’’
prostopadle do trzecich rzutów obu prostych (czyli do płaszczyzny
określonej tymi prostymi) w punkcie
S’’’
. Obieramy na prostej
c
punkt
3
(w rzucie trzecim
punkt
3’’’
). Następnie rzutujemy punkt
3
na rzutnię poziomą i pionową.
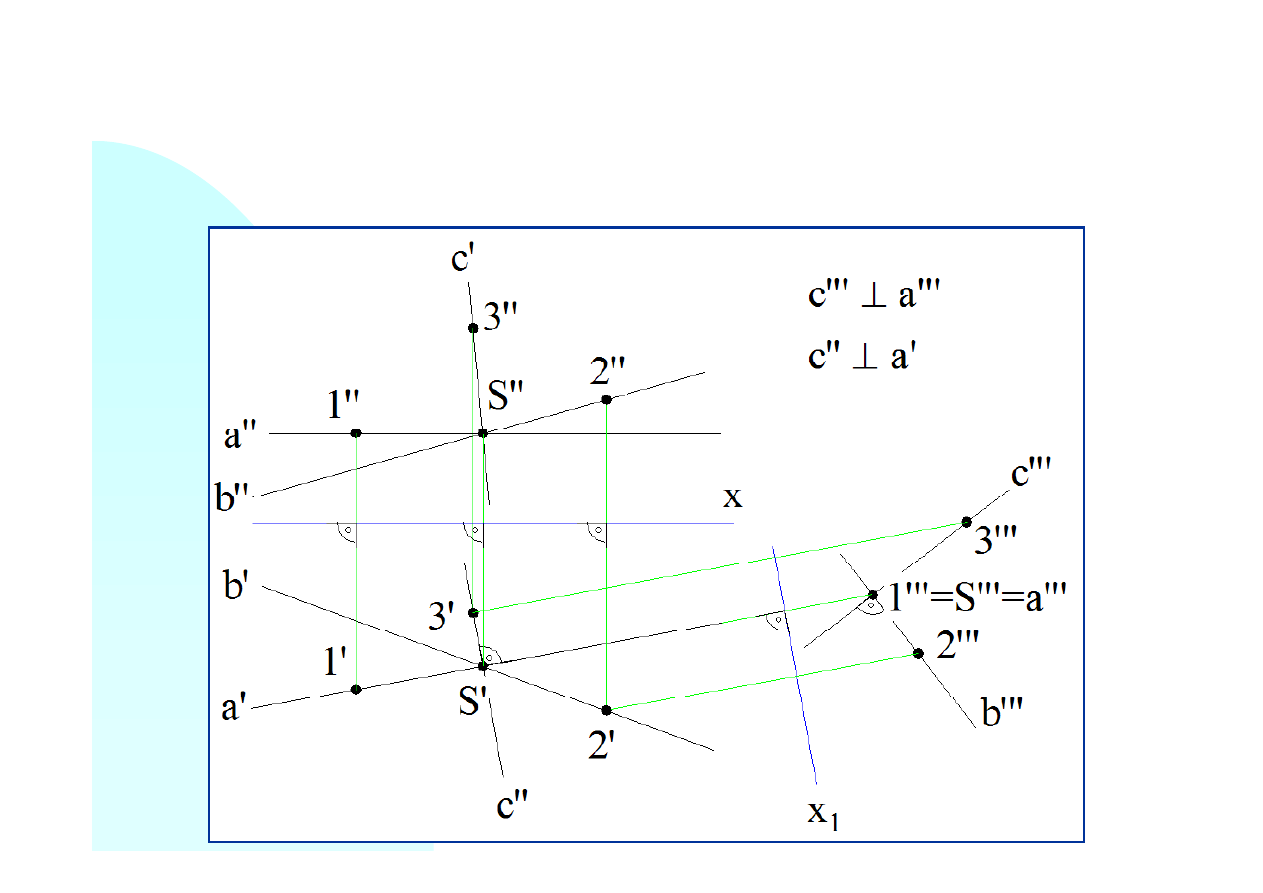
Rzut poziomy prostej
c
(
c’
) będzie prostopadły do rzutu
a’
gdyż prosta
a
jest równoległa do
rzutni poziomej. Po narysowaniu rzutu poziomego
c’
prostej
c
,
rzutujemy na nią punkt
3
.
Prowadząc od punktu
3’
prostą rzutującą prostopadłą do osi
x
, znajdujemy rzut pionowy
3’’
i możemy narysować prostą
c’’
. Odległość punktu
3’’
od osi
x
(wysokość punktu
3
) jest
równa odległości punktu
3’’’
od osi
x
1
.
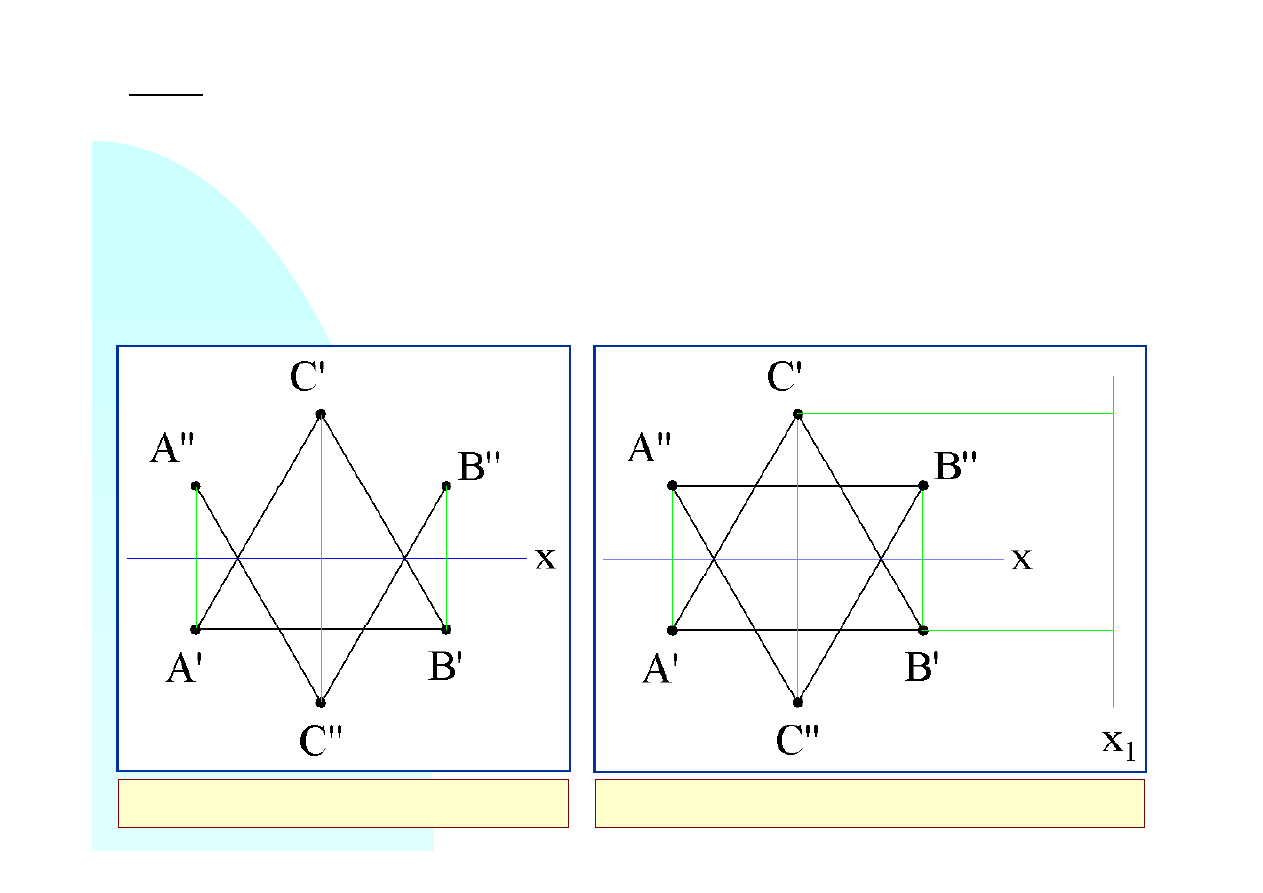
Zad.8. Wyznaczyć rzeczywisty kształt i rozmiary trójkąta
ABC
danego dwoma rzutami.
Rzeczywisty kształt i rozmiary trójkąta poznamy po zrzutowaniu go na płaszczyznę do niego
równoległą. Aby tego dokonać należy wcześniej wykonać rzut pośredni na płaszczyznę
prostopadłą do płaszczyzny trójkąta. Korzystając ze szczególnego ułożenia boku
AB
(jest on
równoległy do osi
x
czyli do obu płaszczyzn pionowej i poziomej) możemy zrzutować trójkąt
na płaszczyznę prostopadłą do boku
AB
i do płaszczyzny poziomej (i pionowej). Na rysunku
prawym tę płaszczyznę przedstawia oś
x
1
.
A’’B’’ || x, A’B’ || x
x
1
⊥
A’B’
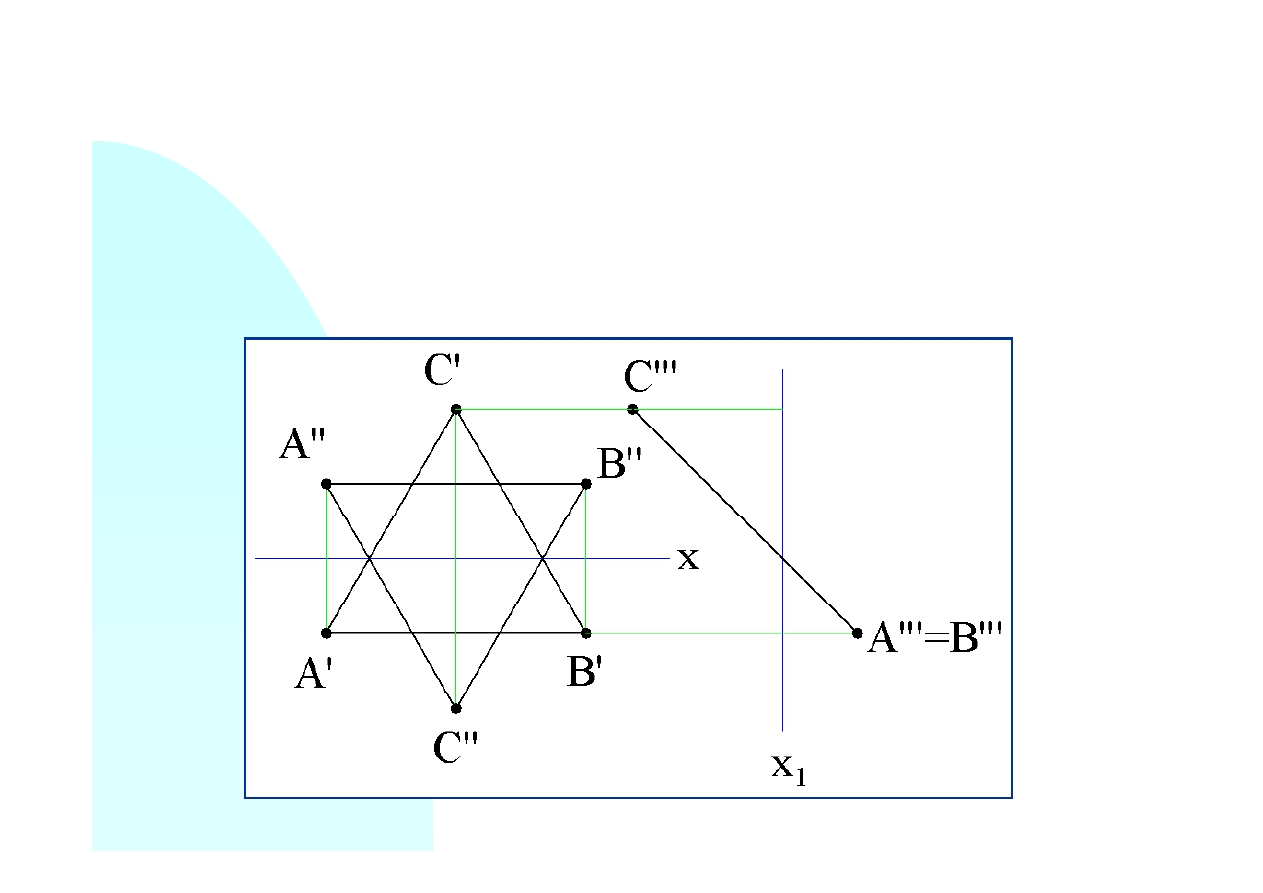
Rzutujemy trójkąt na nową płaszczyznę odmierzając wysokości (można też głębokości)
punktów
A
,
B
i
C
od osi
x
1
. Należy zauważyć, że wysokość punktu
C
jest ujemna -
odmierzamy ją z lewej strony osi
x
1
. Wysokości punktów
A
i
B
(odległości rzutów
A’’
i
B’’
od osi
x
) są dodatnie i jednakowe. Ponieważ rzuty
A’’’
i
B’’’
pokrywają się, płaszczyzna
trójkąta jest prostopadła do nowej rzutni. Jeśli zrzutujemy teraz trójkąt na płaszczyznę do
niego równoległą, otrzymamy jego rzeczywiste rozmiary i kształt. Można również dokonać
kładu płaszczyzny trójkąta na płaszczyznę poziomą.
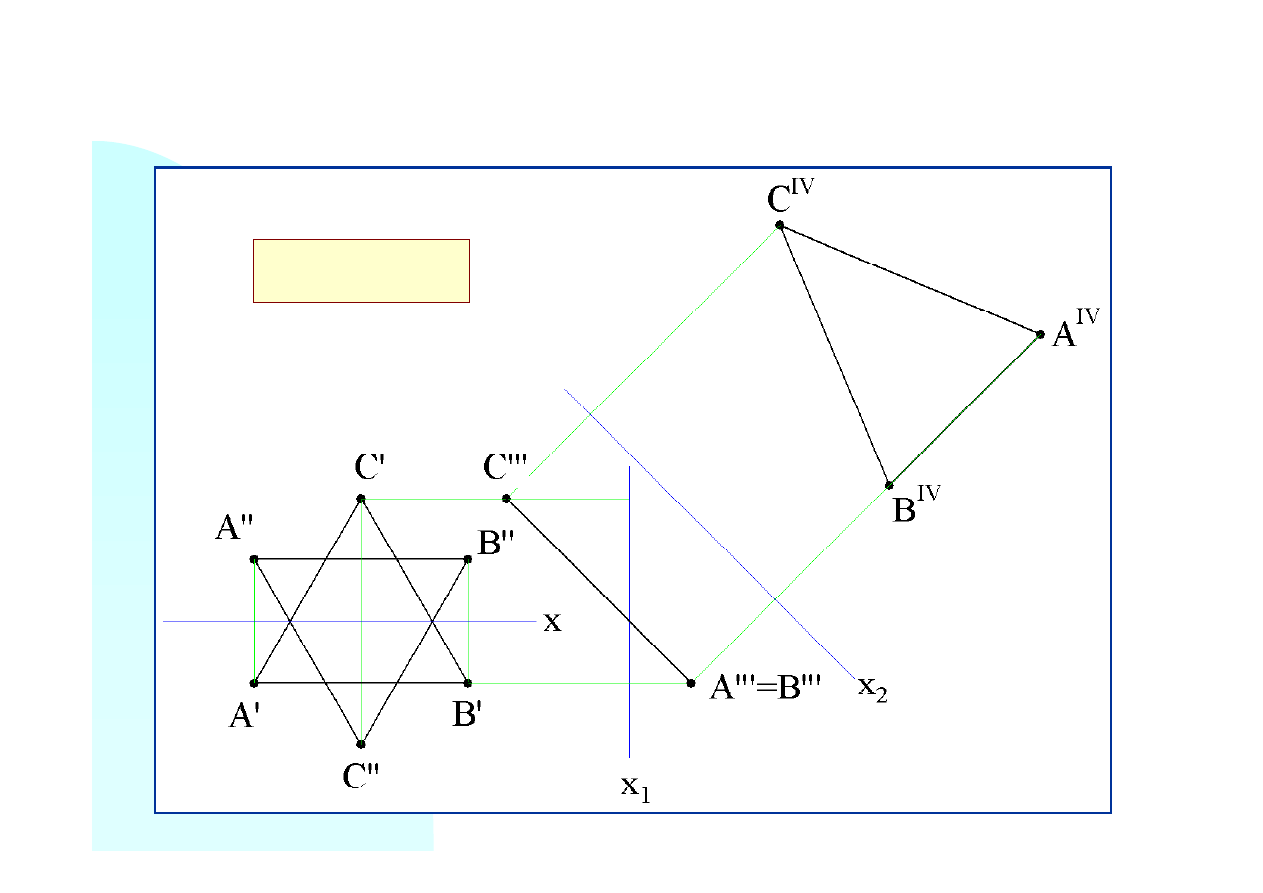
Od osi
x
2
, wzdłuż prostych rzutujących, odmierzamy odległości rzutów poziomych punktów od
osi
x
1
. Otrzymujemy czwarty rzut trójkąta odpowiadający trójkątowi rzeczywistemu. Jest to
trójkąt równoramienny.
x
2
||
A’’’C’’’
Uwagi i wnioski
1. Wykorzystując rzutnię poziomo-rzutującą (np.
ππππ
3
⊥ π
⊥ π
⊥ π
⊥ π
1111
)
i stawiając ją równolegle (lub prosto-
padle) do prostej lub odcinka, rysujemy nową oś równolegle lub (prostopadle) do rzutu poziome-
go tej prostej lub tego odcinka, np.
x
1
|| a’
. Konstruując rzut wykonujemy następujące czynności:
- prowadzimy proste rzutujące od rzutów poziomych punktów, czyli np.
1’, 2’, 3’, A’, B’
...
prostopadle do nowej osi
x
1
- na prostych rzutujących odmierzamy wysokości punktów, czyli odległości rzutów pionowych
1”, 2”, 3”, A”, B”
itd. od osi
x
. Należy pamiętać, że o tym z której strony osi
x
1
odmierzamy
odległości rzutów
1’’’, 2’’’
itd. zależy od znaku tej wysokości. Punktom, których rzuty piono-
we (z indeksem bis) leżą po różnych stronach osi
x
, przyporządkowujemy przeciwne znaki.
Nie ma przy tym znaczenia którą stronę uznamy za dodatnią a którą za ujemną.
2. Wykorzystując rzutnię pionowo-rzutującą (np.
ππππ
3
⊥ π
⊥ π
⊥ π
⊥ π
2222
)
i stawiając ją równolegle (lub prosto-
padle) do prostej lub odcinka, rysujemy nową oś równolegle lub (prostopadle) do rzutu pionowe-
go tej prostej lub tego odcinka, np.
x
1
|| a”
. Konstruując rzut wykonujemy następujące czynności:
- prowadzimy proste rzutujące od rzutów pionowych punktów, czyli np.
1”, 2”, 3”, A”, B”
...
prostopadle do nowej osi
x
1
- na prostych rzutujących odmierzamy głębokości punktów, czyli odległości rzutów poziomych
1’, 2’, 3’, A’, B’
itd. od osi
x
. Należy pamiętać, że o tym z której strony osi
x
1
odmierzamy
odległości rzutów
1’’’, 2’’’
itd. zależy od znaku tej głębokości. Punktom, których rzuty pozio-
me (z indeksem prim) leżą po różnych stronach osi
x
, przyporządkowujemy przeciwne znaki.
Nie ma przy tym znaczenia którą stronę uznamy za dodatnią a którą za ujemną.
3. Aby wyznaczyć rzeczywisty kształt i rozmiary płaskich obiektów geometrycznych, musimy
konstrukcję doprowadzić do takiego stanu, aby można było użyć rzutni równoległej do
płaszczyzny tego obiektu. Najczęściej konstrukcja sprowadza się do wykorzystania elementu
obiektu znajdującego się w położeniu szczególnym względem jednej (lub dwóch rzutni), np.
krawędź figury równoległa do rzutni poziomej lub pionowej. Jeżeli rozpatrywany obiekt nie
posiada takiego elementu to powinniśmy go dorysować. Musi się on znajdować na tej samej
płaszczyźnie co obiekt.
- Rzut pionowy prostej lub odcinka równoległy do osi
x
(np.
a” || x
,
A”B” || x
) oznacza, że ta
prosta lub ten odcinek są równoległe do rzutni poziomej. W takim przypadku wykorzystuje-
my rzutnię poziomo-rzutującą przecinającą rzutnię poziomą w krawędzi
x
1
⊥
⊥
⊥
⊥
a’
lub
x
1
⊥
⊥
⊥
⊥
A’B’
. Taka rzutnia jest wtedy prostopadła do płaszczyzny obiektu. Kolejny rzut już
może być wykonany na płaszczyznę równoległą do rozpatrywanego obiektu.
- Rzut poziomy prostej lub odcinka równoległy do osi
x
(np.
a’ || x
,
A’B’ || x
) oznacza, że ta
prosta lub ten odcinek są równoległe do rzutni pionowej. W takim przypadku wykorzystuje-
my rzutnię pionowo-rzutującą przecinającą rzutnię pionową w krawędzi
x
1
⊥
⊥
⊥
⊥
a’’
lub
x
1
⊥
⊥
⊥
⊥
A”B”
. Taka rzutnia jest wtedy prostopadła do płaszczyzny obiektu. Kolejny rzut już
może być wykonany na płaszczyznę równoległą do rozpatrywanego obiektu.
Dzi
ękuję za uwagę