GEOMETRIA I GRAFIKA IN
ŻYNIERSKA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI
KATEDRA URZĄDZEŃ ELEKTRYCZNYCH I TECHNIKI ŚWIETLNEJ
Przykładowe zadania z rozwi
ązaniami - część 1
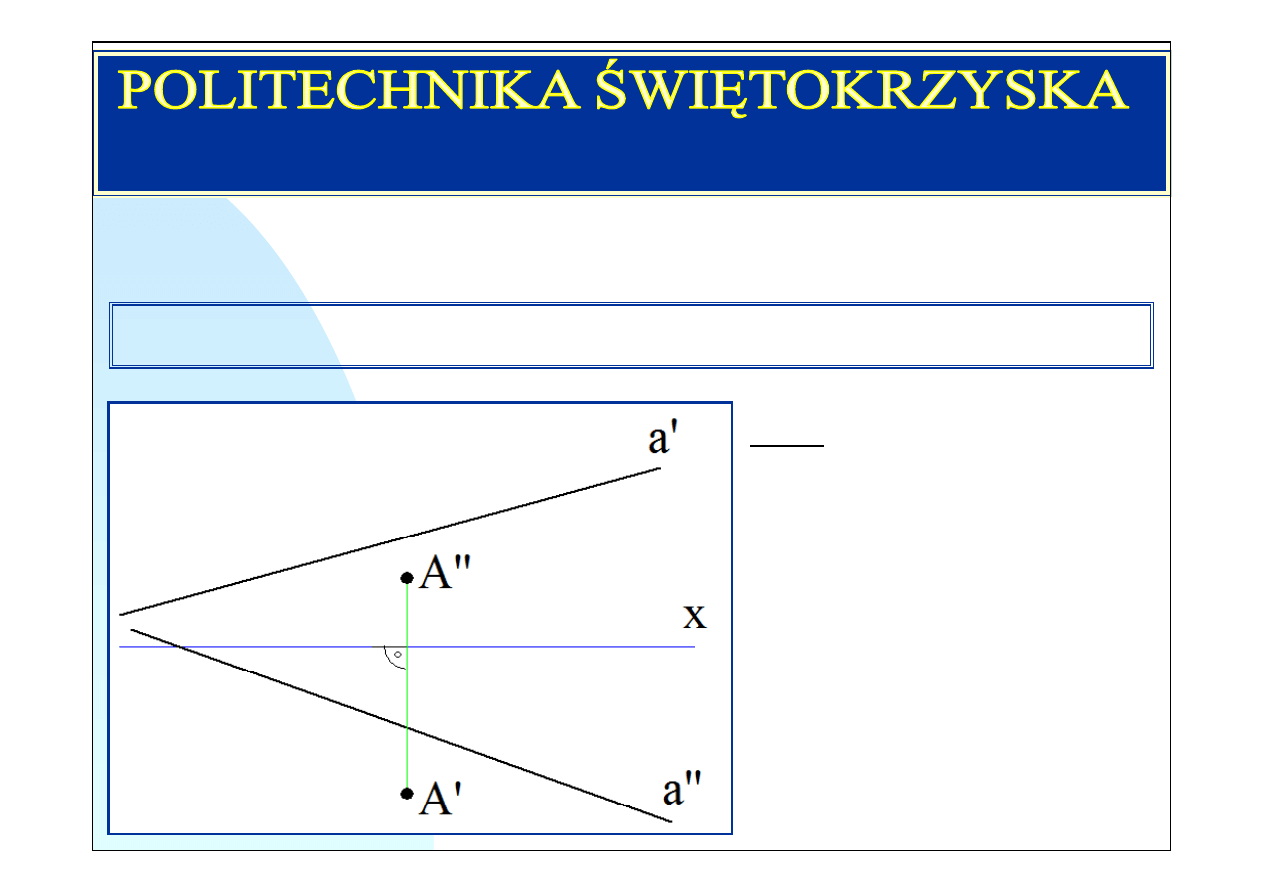
Zad. 1. Dane rzuty: poziomy i piono-
wy prostej i punktu. Wyznaczyć
rzeczywistą odległość między prostą
a
i punktem
A
. Wykreślić rzuty tej
odległości.
Należy zauważyć, że na rysunku rzut
poziomy prostej
a
leży nad osią
x
a
pionowy pod osią
x
(w większej
części). Wysokości i głębokości
punktów leżących w tych częściach
prostej będą zatem ujemne.
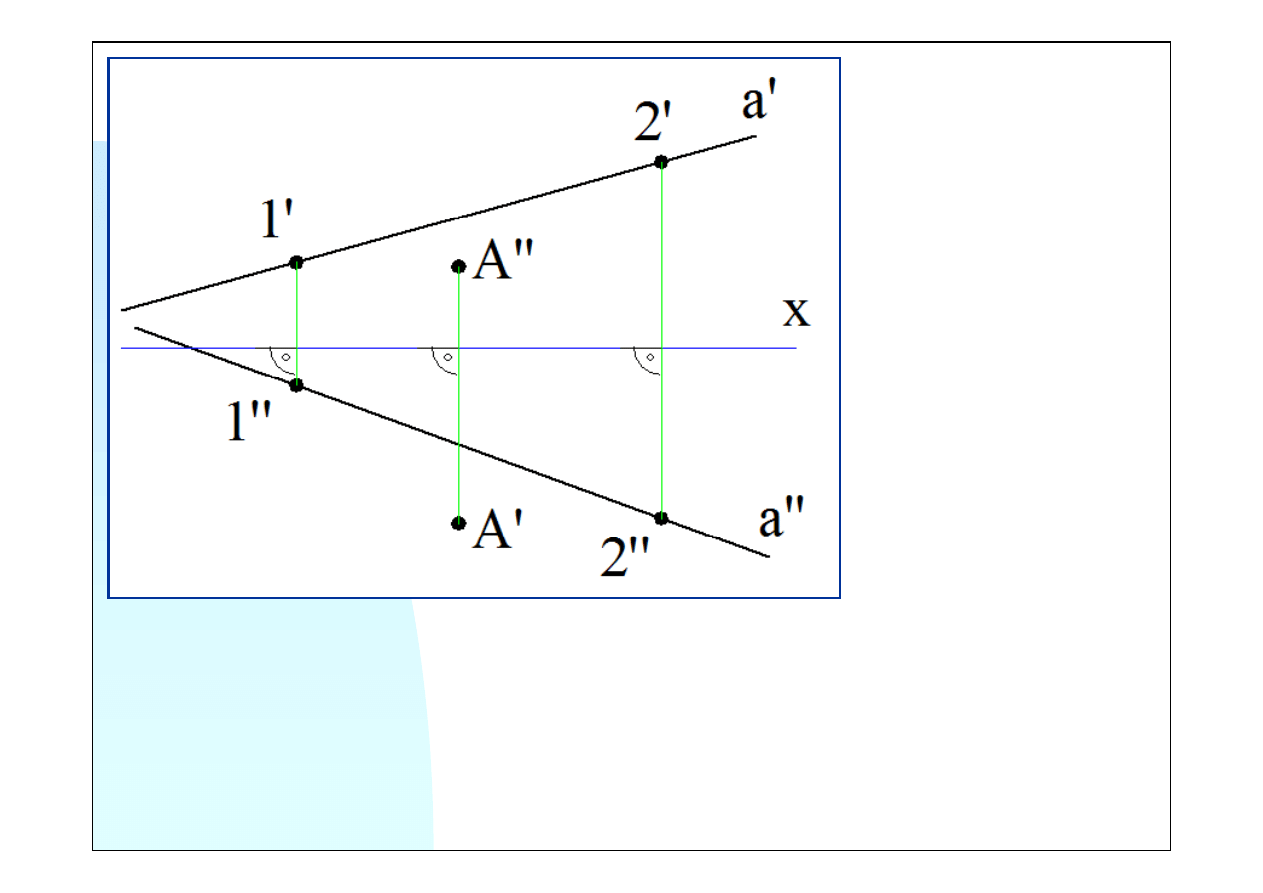
Aby wykonać kolejne rzuty
prostej, należy na tej
prostej obrać przynajmniej
dwa dowolne punkty.
Niech to będą punkty
1
i
2
.
Rzuty tych punktów muszą
leżeć na tych samych
prostych prostopadłych do
osi
x
.
Tak samo rzuty punktu
A
leżą na tej samej prostej
prostopadłej do osi.
Aby wyznaczyć odległość między punktem i prostą należy skorzystać z niezmiennika o rzuto-
waniu kąta prostego, ponieważ między odcinkiem będącym odległością punktu od prostej
i prostą, jest kąt prosty. Aby rzut kąta prostego był również kątem prostym należy zrzutować
go na rzutnię równoległą do jednego ramienia tego kąta. W naszym przypadku tym ramieniem
jest prosta, odległość musimy dopiero wyznaczyć. Dla wykonania rzutu najlepiej wykorzystać
rzutnię w postaci płaszczyzny pionowo- lub poziomo rzutującej.
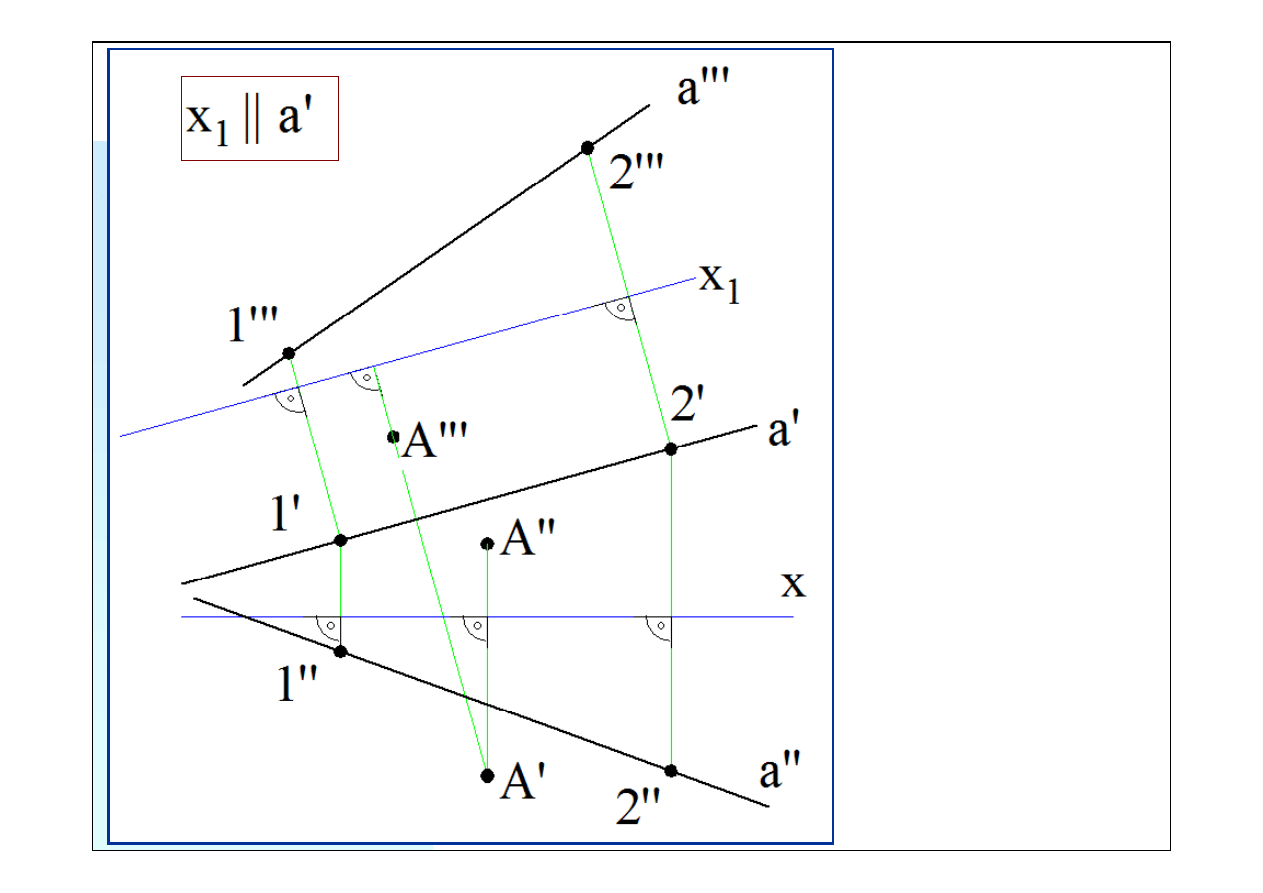
Stawiamy płaszczyznę pros-
topadłą do rzutni poziomej
i równoległą do prostej
a
(może ona również przecho-
dzić przez prostą
a
). Kra-
wędź przecięcia nowej rzutni
z rzutnią poziomą (
x
1
) będzie
równoległa do
a’
(rzutu po-
ziomego prostej
a
).
Rysujemy proste rzutujące
prostopadłe do nowej osi
x
1
od punktów z indeksem
prim. Wyznaczamy położe-
nia trzecich rzutow punktów
w odległości, od nowej osi,
równej ich wysokościom
(odległościom rzutów piono-
wych od osi
x
). Jeżeli przyj-
miemy zasadę, że dodatnie
wysokości odmierzamy w
dół a głębokości w górę, to
z punktami
1
i
2
musimy
postąpić odwrotnie. Wyso-
kości punktów
1
i
2
są ujem-
ne. Wysokość punktu
A
jest
dodatnia.
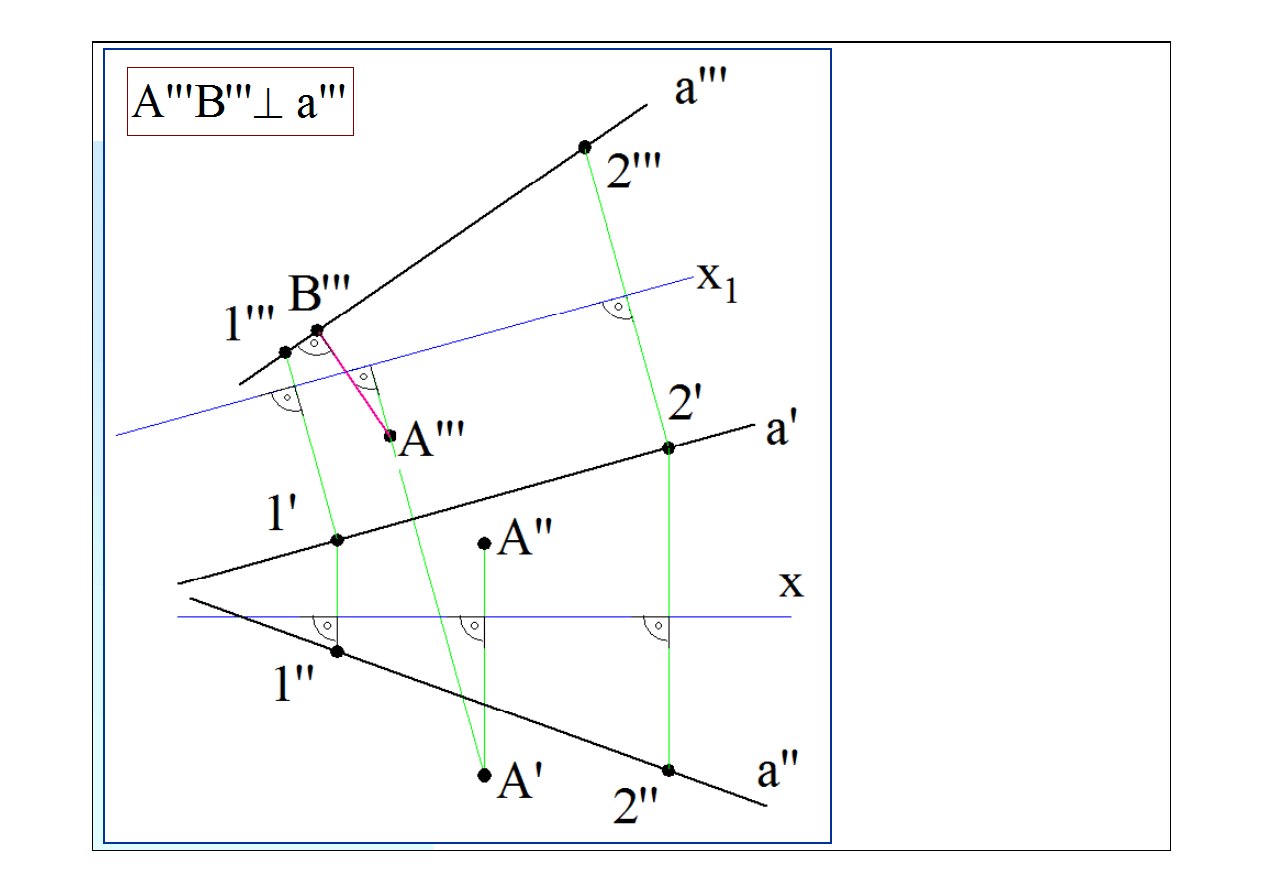
Punkty
1’’’
i
2’’’
wyzna-
czają trzeci rzut prostej
a
.
Kąt
między
odcinkiem
będącym trzecim rzutem
odległości punktu
A
od
prostej
a
a trzecim rzutem
prostej
będzie
również
kątem prostym. Rysujemy
odcinek od punktu
A’’’
prostopadle do rzutu prostej
a’’’
. Oznaczamy drugi ko-
niec tego odcinka, leżący
na prostej, przez
B’’’
.
Otrzymaliśmy rzut odleg-
łości
A’’’B’’’
który nie jest
jeszcze równy rzeczywis-
tej odległości. Aby wyz-
naczyć rzeczywistą odle-
głość należy ją zrzutować
na płaszczyznę do niej
równoległą.
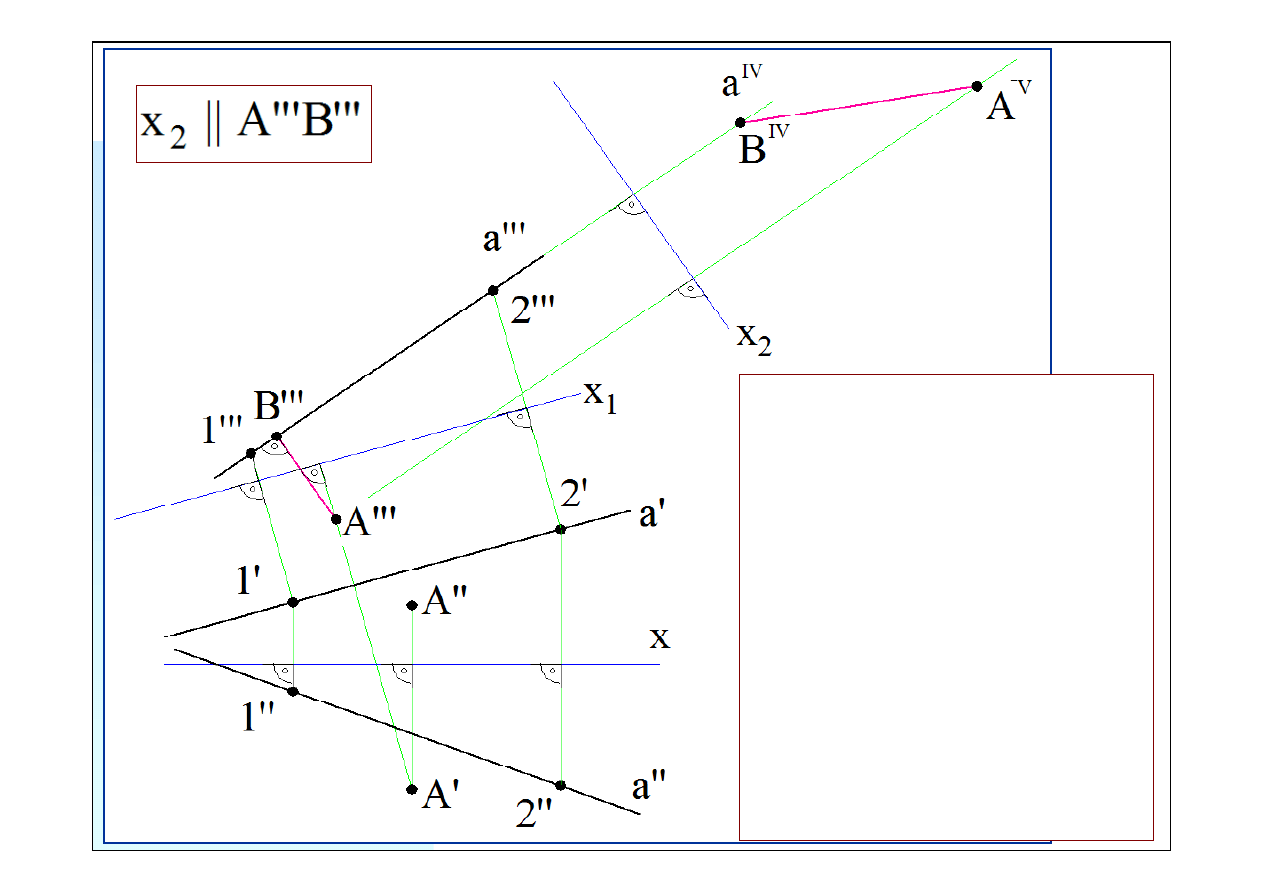
Stawiamy nową rzutnię prosto-
padłą do poprzedniej i równoległą
do odległości czyli do odcinka
A’’’B’’’
. Prowadzimy od punktów
1’’’
,
2’’’
,
A’’’
i
B’’’
proste
rzutujące prostopadłe do nowej osi
x
2
. Na prostych rzutujących odmie-
rzamy odległości rzutów pozio-
mych poszczególnych punktów od
osi
x
1
(ponieważ rzutnia pozioma i
czwarta rzutnia są prostopadłe do
rzutni trzeciej). Długość odcinka
A
IV
B
IV
jest rzeczywistą odległoś-
cią punktu
A
od prostej
a
.
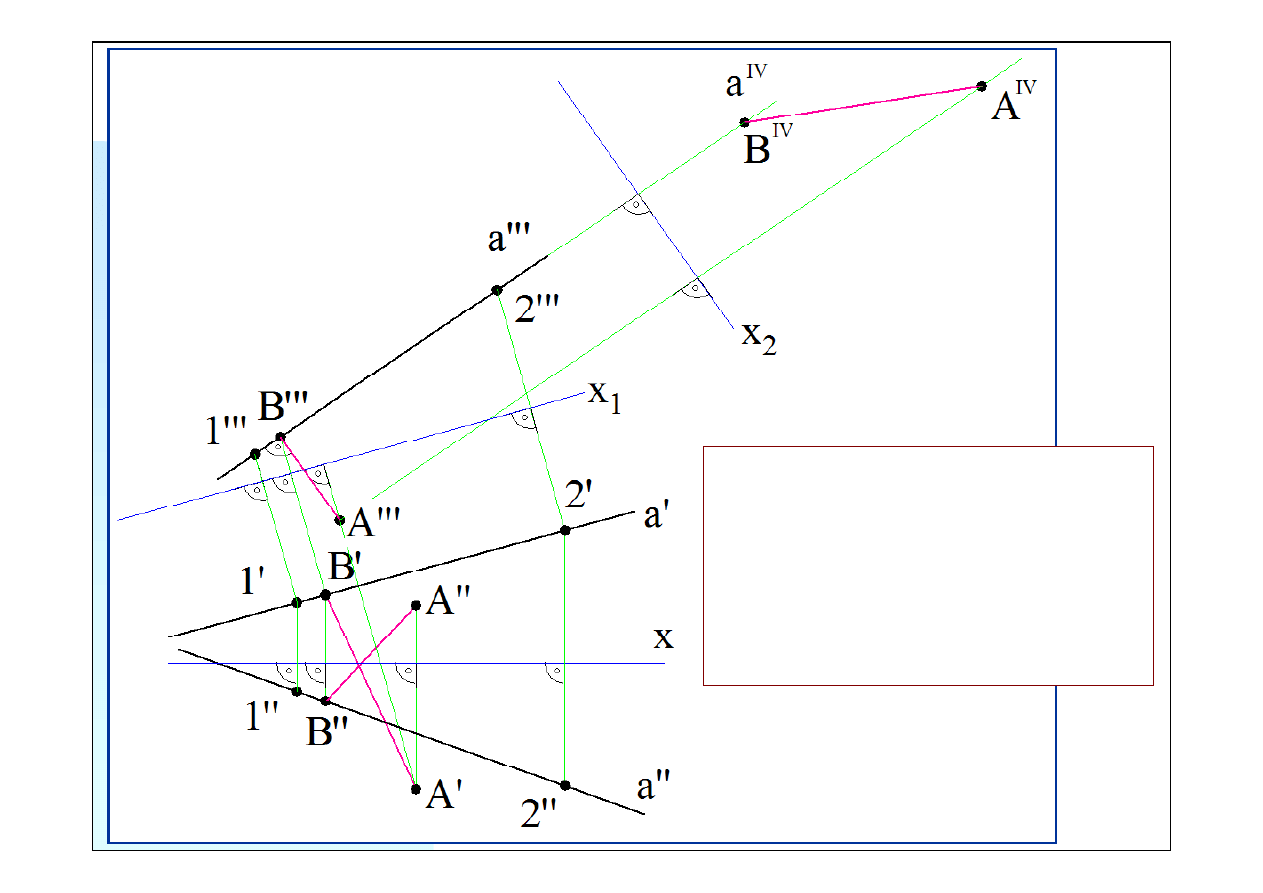
Aby wyznaczyć rzuty poziomy i pio-
nowy tej odległości, należy zrzutować
punkt
B
na rzutnię poziomą i pionową
za pomocą prostych rzutujących.
Odcinek
A’B’
jest rzutem poziomym
odległości, a odcinek
A’’B’’
jej rzutem
pionowym.
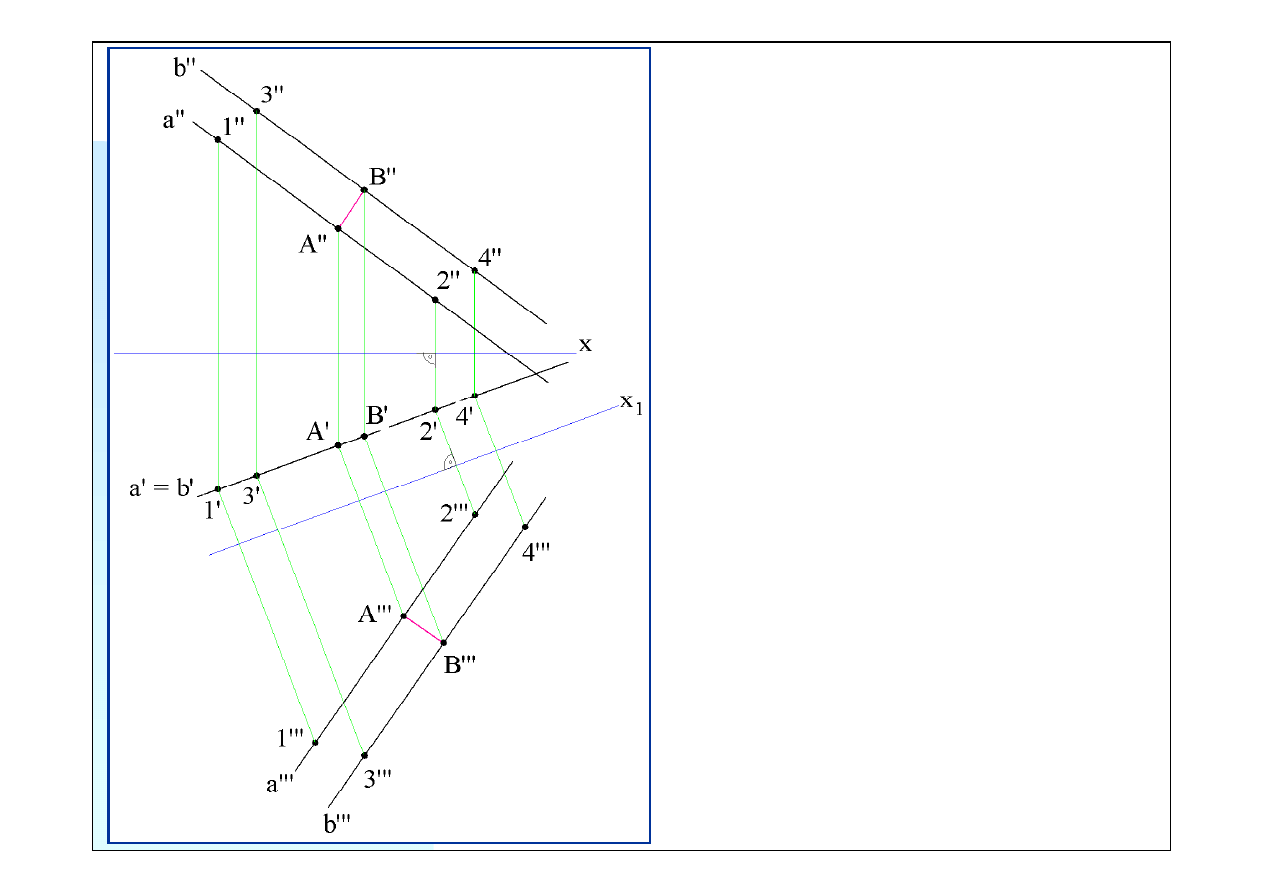
Zad. 2. Mając dane rzuty: poziomy
i pionowy dwóch prostych równo-
ległych, wyznaczyć rzeczywistą
odległość między tymi prostymi.
Wykreślić rzut poziomy i pionowy
tej odległości.
Rozwiązanie zadania zaczynamy
od wybrania dwóch dowolnych
punktów leżących na każdej z tych
prostych. Są to punkty
1
i
2
leżące
na prostej
a
i punkty
3
i
4
leżące na
prostej
b
. Rzuty pionowe i pozio-
me danego punktu leżą na jednej
prostej prostopadłej do osi
x
.
Aby wyznaczyć odległość między
prostymi należy skorzystać z niez-
miennika o rzutowaniu kąta proste-
go, ponieważ między odcinkiem
będącym odległością a prostymi
jest kąt prosty. Aby rzut kąta
prostego był również kątem pros-
tym należy zrzutować go na rzut-
nię równoległą do prostych.
Stawiamy nową rzutnię prostopadle
do rzutni poziomej i równolegle do
prostych. Krawędź przecięcia tej
rzutni z rzutnią poziomą będzie
równoległa do rzutów poziomych
tych prostych.
Dla wyznaczenia trzecich rzutów
punktów
1
,
2
,
3
i
4
, odmierzamy
wysokości tych punktów (czyli
odległości rzutów pionowych od osi
x
) na prostych rzutujących
prostopadłych do nowej osi.
Otrzymujemy trzecie rzuty prostych
rysując linie przechodzące przez
trzecie rzuty przynależnych do nich
punktów.
Dowolny odcinek
A’’’B’’’
łączący
trzecie rzuty prostych i prostopadły
do tych prostych, określa nam
odległość między prostymi
a
i
b
.
Ze względu na szczególne ułożenie
prostych - ich rzuty poziome
pokrywają się - jest to rzeczywista
odległość między prostymi.
A’’’B’’’
⊥
a’’’|| b’’’
Rzut poziomy odległości wyznaczamy
rzutując punkty
A
i
B
na rzutnię poziomą.
Prowadzimy od trzecich rzutów punktów
proste rzutujące prostopadłe do osi
x
1
. Na
rzutach poziomych prostych otrzymujemy
rzuty poziome
A’
i
B’
punktów
A
i
B
.
Odcinek
A’B’
jest rzutem poziomym
odległości.
Podobnie wyznaczamy rzuty pionowe. Od
punktów
A’
i
B’
prowadzimy proste
rzutujące prostopadłe do osi
x
. Znajdujemy
punkty
A’’
i
B’’
i rysujemy rzut pionowy
odległości
A’’B’’
.
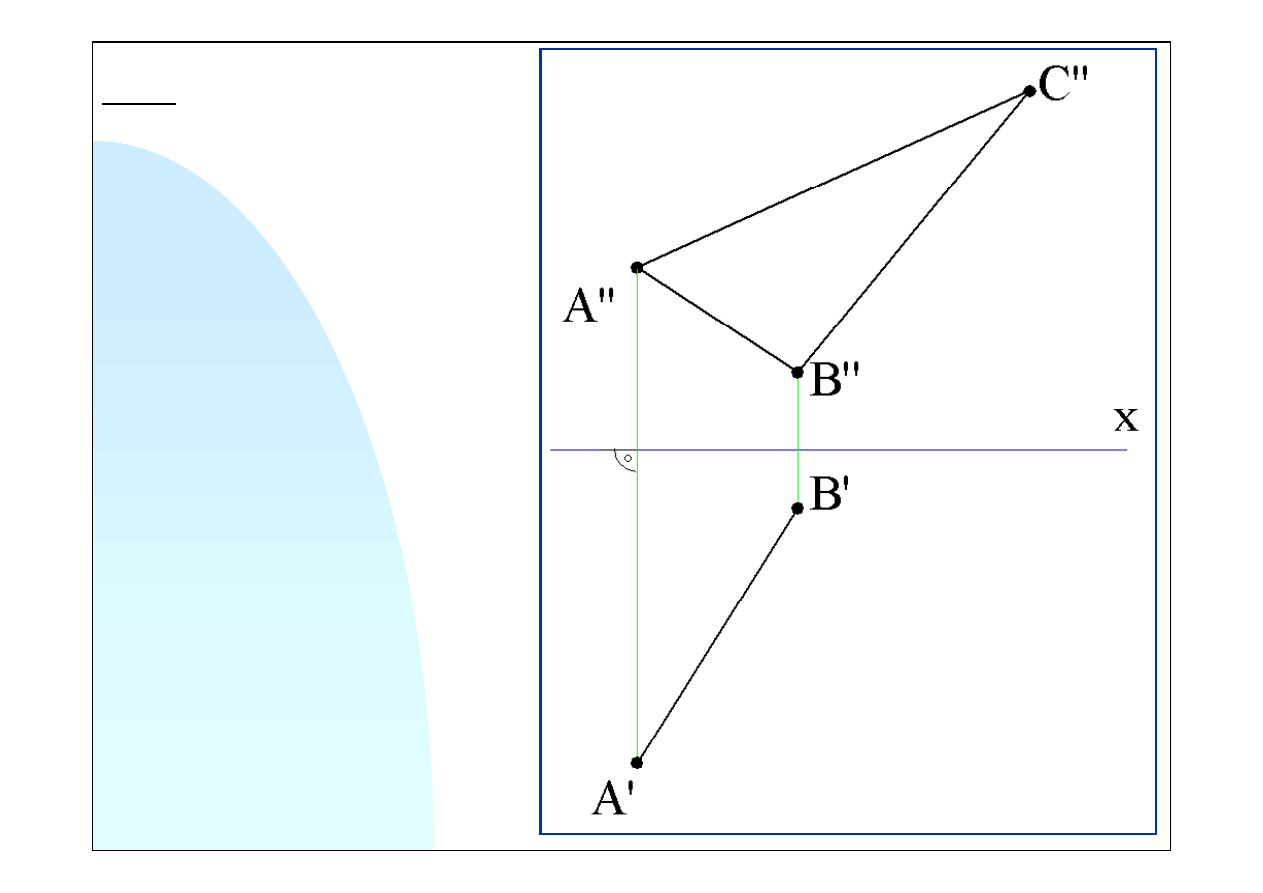
Zad.3. Wyznaczyć rzut poziomy
trójkąta
ABC
wiedząc, że kąt przy
wierzchołku
A
tego trójkąta jest
kątem prostym.
Mamy dany rzut pionowy trójkąta i
rzuty poziome dwóch wierzchołków
A
i
B
. Zadanie będzie rozwiązane
jeżeli znajdziemy położenie rzutu
poziomego wierzchołka
C
.
Punkty
C’
i
C’’
będą leżały na tej
samej prostej prostopadłej do osi
x
.
Aby wyznaczyć odległość rzutu
C’
od osi
x
(głębokość punktu
C
)
musimy skorzystać z niezmiennika o
rzutowaniu kąta prostego.
Rzutujemy trójkąt
ABC
na
płaszczyznę równoległą do boku
AC
(lub
AB
) i prostopadłą do rzutni
pionowej - jednego z ramion kąta
prostego.
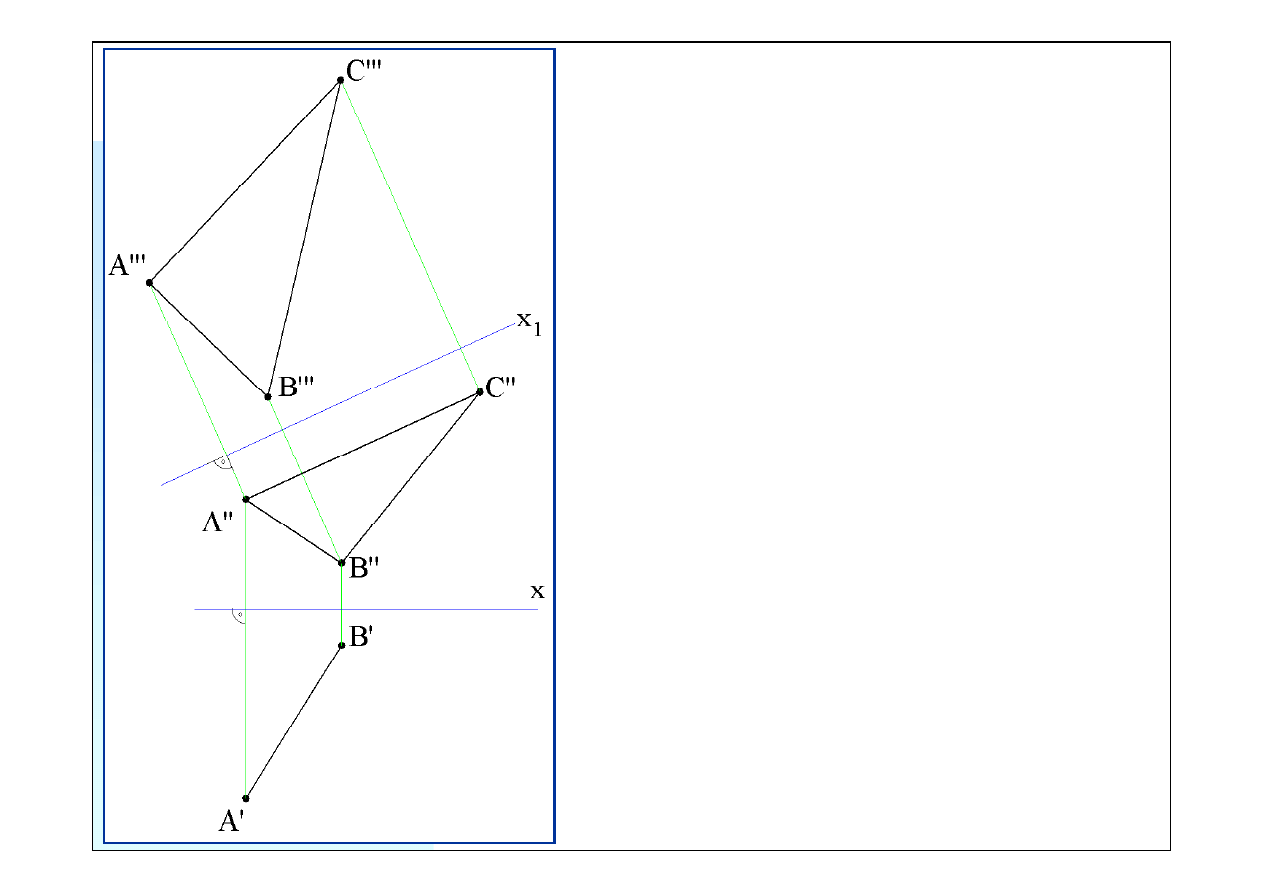
Rysujemy nową oś
x
1
równolegle do rzutu piono-
wego boku
AC
trójkąta. Rzuty pionowe i trzecie
rzuty punktów
A
,
B
i
C
leżeć będą na tych samych
prostych prostopadłych do osi
x
1
. Położenia rzutów
A’’’
i
B’’’
znajdujemy odmierzając od osi
x
1
w górę,
głębokości punktów A i B, czyli odległości rzutów
poziomych
A’
i
B’
od osi
x
.
Na trzecim rzucie trójkąta
ABC
kąt przy wierzchołku
A’’’
jest kątem prostym - rzutnia trzecia jest równo-
legła do jednego ramienia kąta prostego. Rysujemy
prostą prostopadłą do
A’’’B’’’
w punkcie
A’’’
.
W miejscu przecięcia tej prostej z prostą rzutującą
punkt
C
, znajdujemy położenie wierzchołka
C’’’
trzeciego rzutu trójkąta.
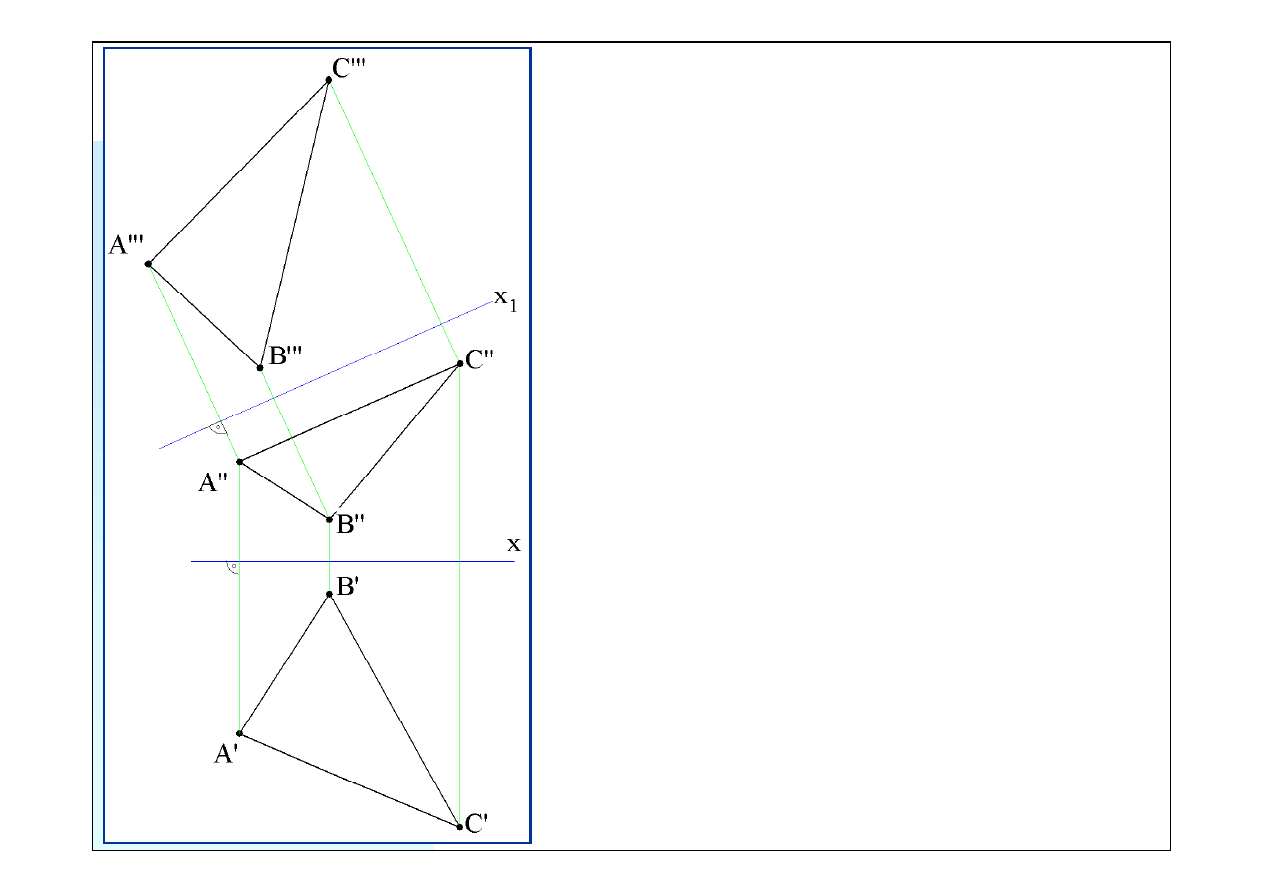
Położenie rzutu poziomego
C’
wierzchołka
C
znajdujemy odmierzając głębokość punktu C
(odległość
C’
od osi
x
) równą odległości rzutu
C’’’
od osi
x
1
.
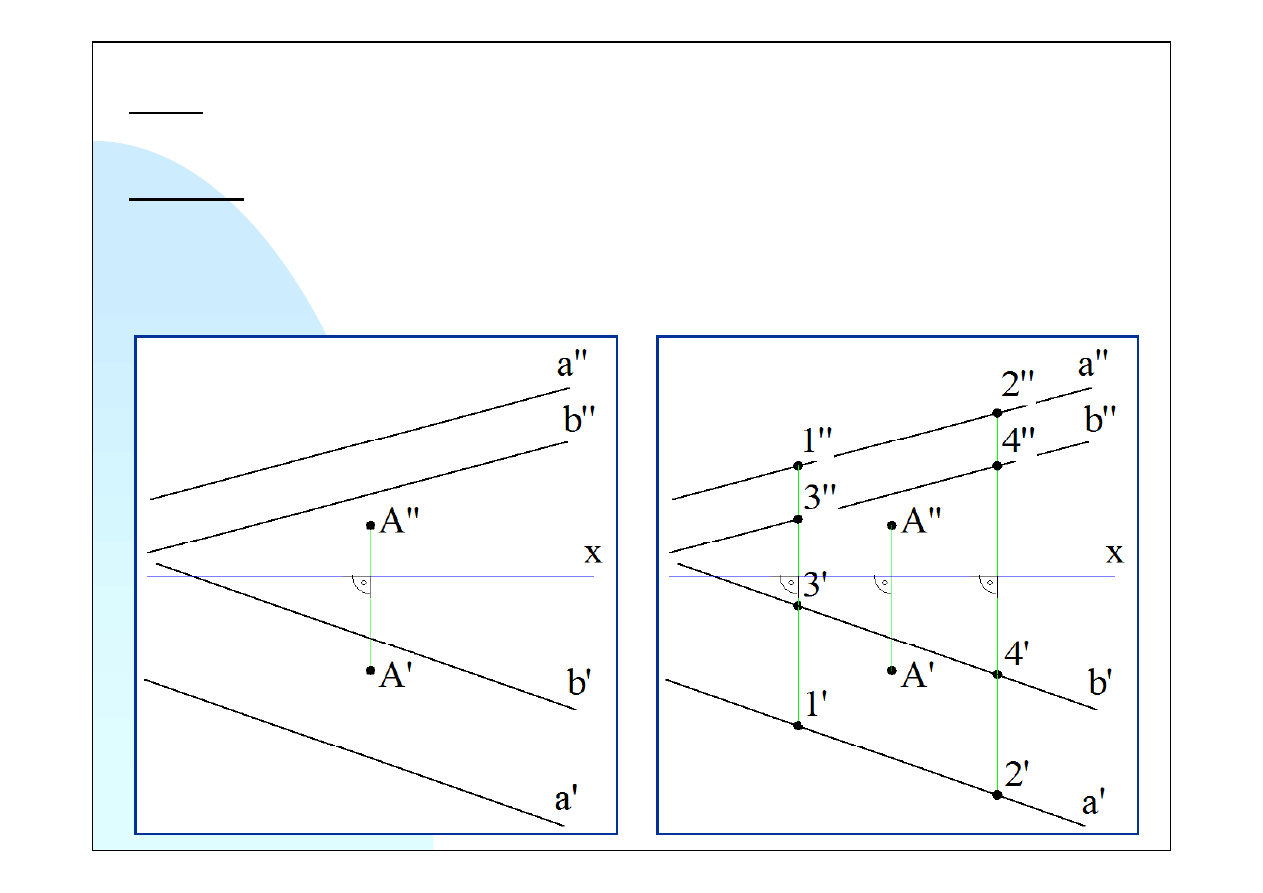
Zad.4. Wyznaczyć rzeczywistą odległość punktu od płaszczyzny określonej dwoma prostymi
równoległymi. Wykreślić rzuty tej odległości.
Sposób 1
W celu wykonania kolejnych rzutów prostych, należy na każdej z nich obrać dwa punkty.
Proste rzutujące prostopadłe do osi
x
łączą rzuty pionowe i poziome obranych punktów
(rysunek z prawej).
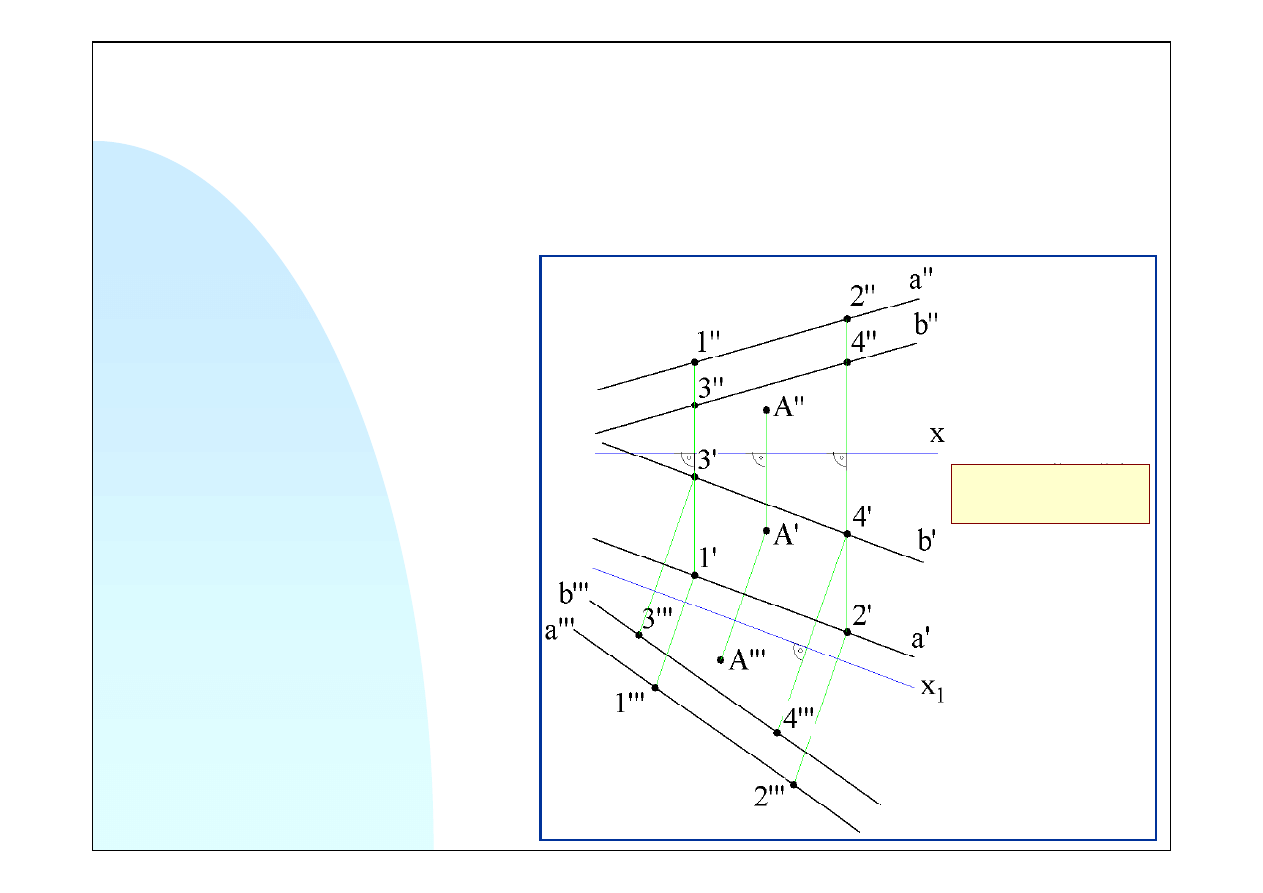
Odległość tworzy z płaszczyzną określoną prostymi równoległymi kąt prosty. Aby narysować
odcinek stanowiący rzeczywistą odległość punktu od tej płaszczyzny, należy wykonać rzut tej
płaszczyzny na rzutnię do niej prostopadłą. Aby móc taką rzutnię postawić należy najpierw
dokonać rzutu prostych na płaszczyznę do nich równoległą. Na rysunku poniżej, stawiamy nową
rzutnię równoległą do prostych i prostopadłą do rzutni poziomej.
Rzuty poziome i trzecie rzuty
punktów leżą na tych samych prostych
prostopadłych do osi
x
1
. Odległości
trzecich rzutów od osi
x
1
są równe ich
wysokościom, czyli odległościom
rzutów pionowych od osi
x
.
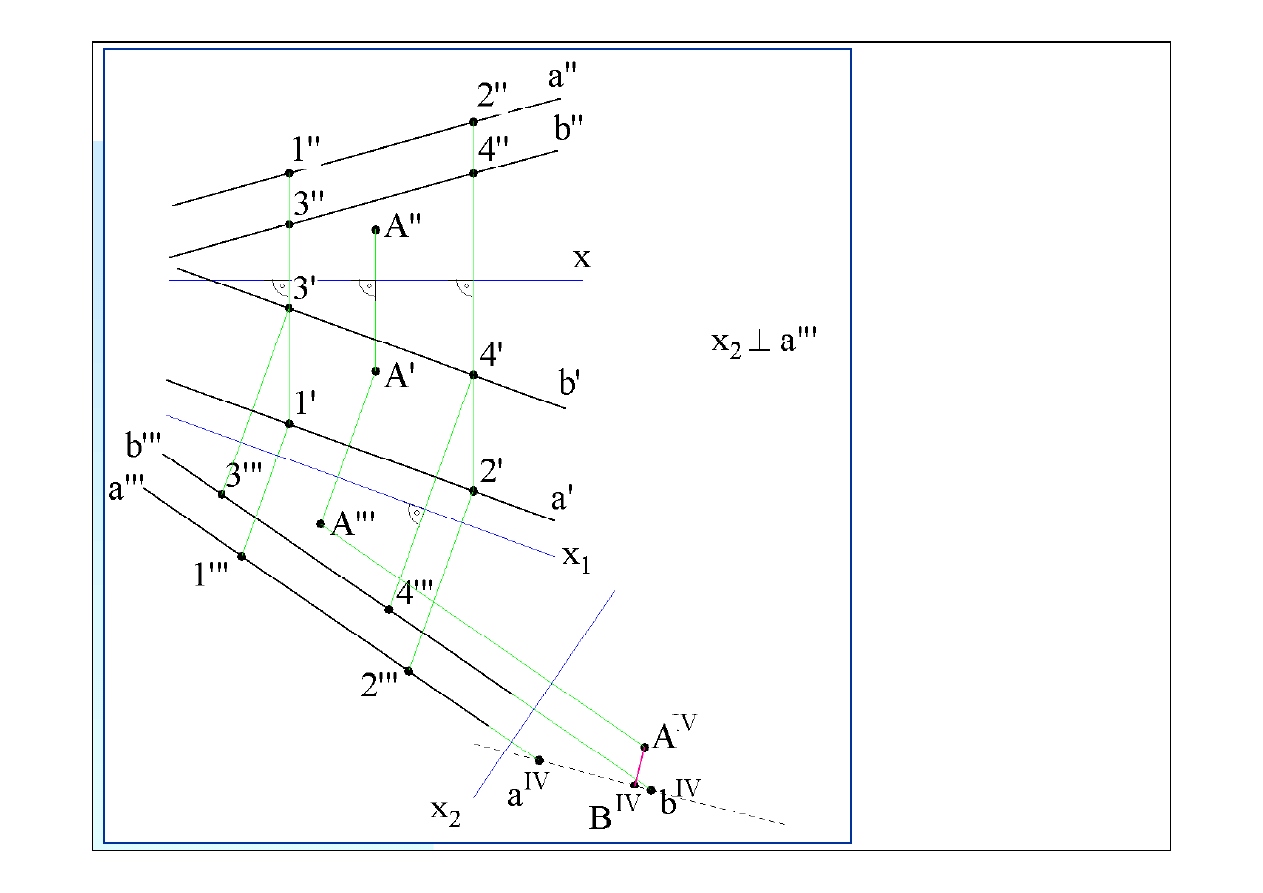
Trzeci rzut odległości będzie prosto-
padły do trzecich rzutów prostych, ale
nie znamy jeszcze położenia końca
tego odcinka leżącego na płaszczyźnie
określonej przez te proste. Musimy
więc wykonać kolejny rzut prostych i
punktu na płaszczyznę prostopadłą do
prostych i prostopadłą do rzutni
trzeciej.
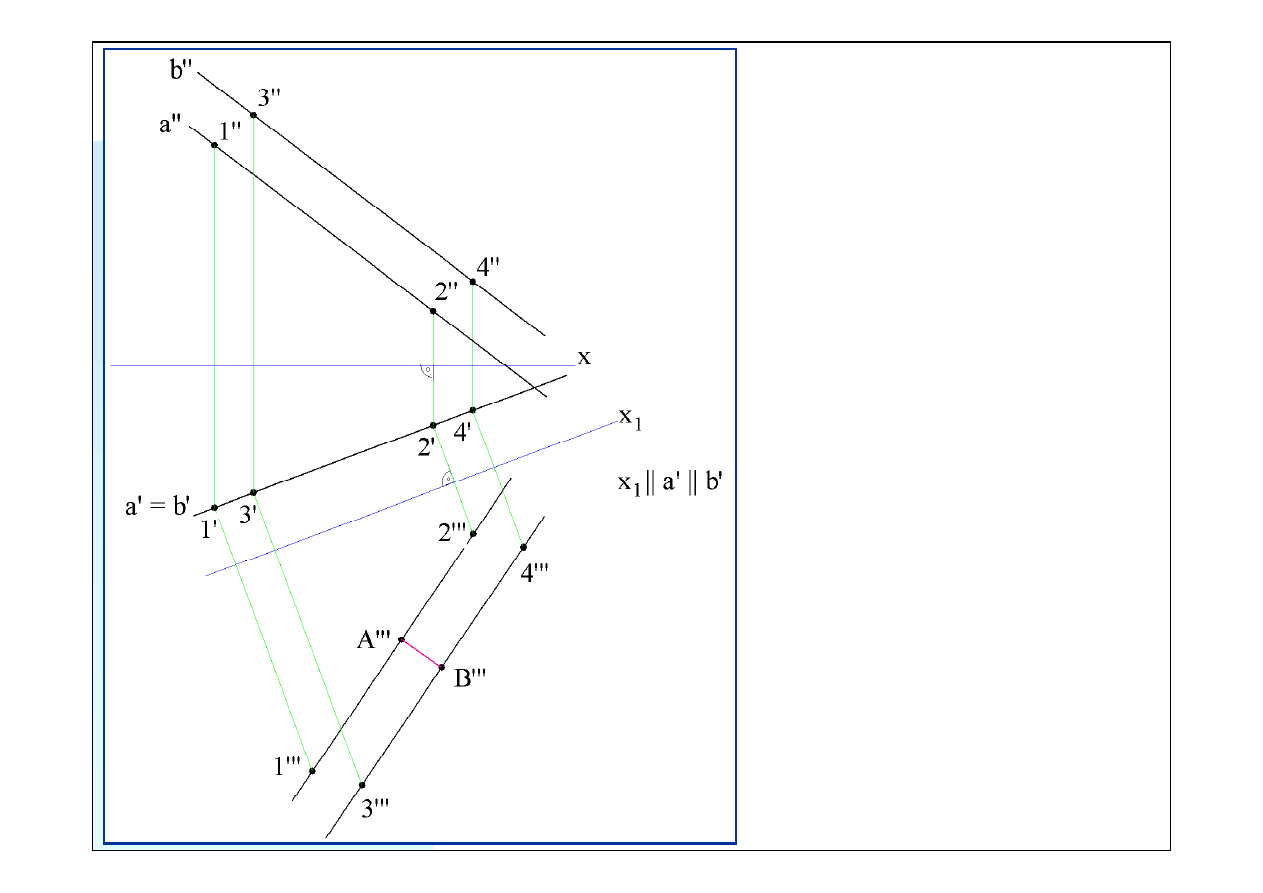
x
1
|| a’ || b’
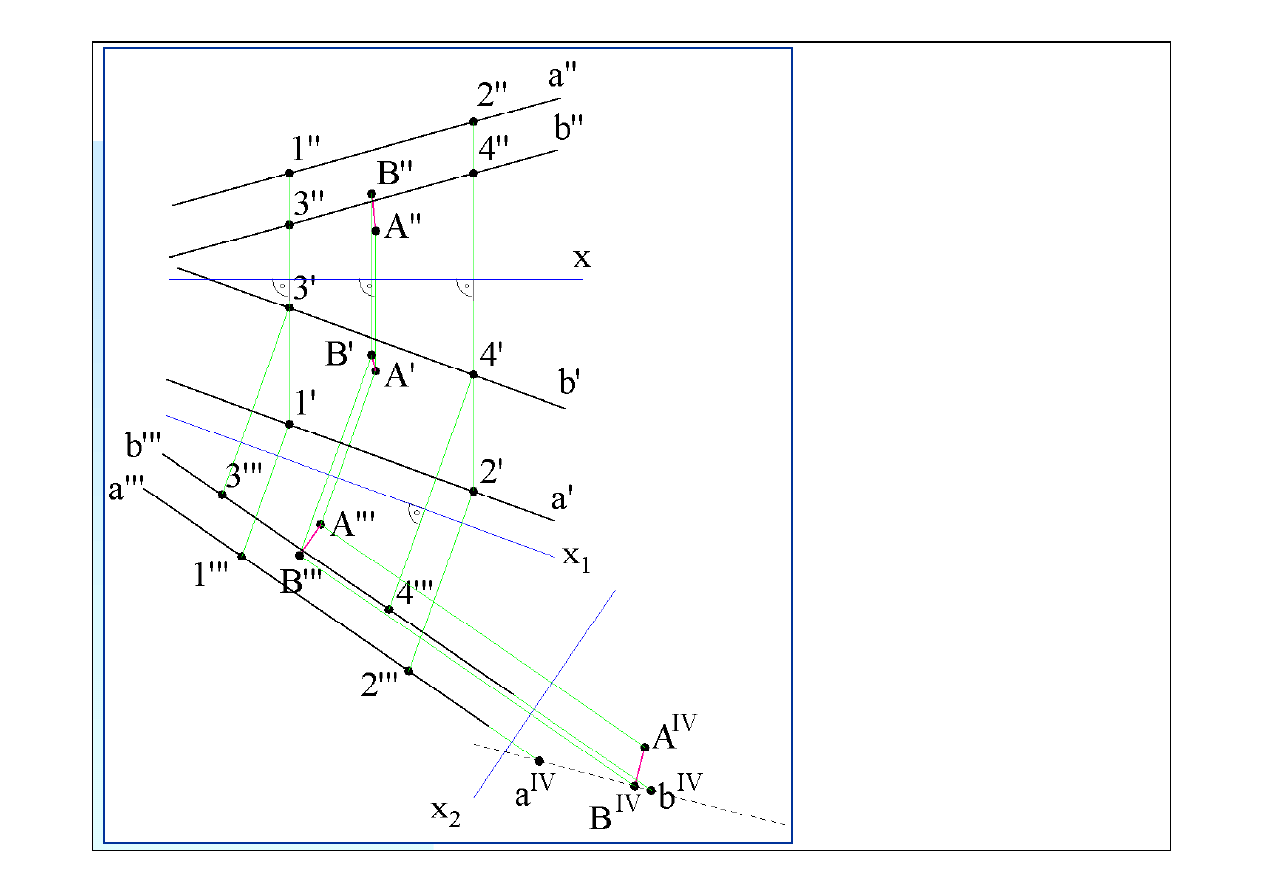
Odcinek
A
IV
B
IV
jest
czwartym rzutem szukanej
odległości i jego długość
odpowiada rzeczywistej
odległości. Odległości
czwartych rzutów punk-
tów od osi
x
2
są równe
odległościom rzutów
poziomych tych punktów
(
1’
,
2’
, ...) od osi
x
1
.
Płaszczyzna, którą tworzą
proste równoległe, została
zaznaczona linią
kreskową.
Rzuty czwarte prostych są
punktami bo proste te są
prostopadłe do rzutni.
Aby zakończyć zadanie
należy jeszcze wyznaczyć
rzuty odległości, czyli
znaleźć rzuty
B’’’
,
B’
i
B’’
.
Położenie punktu
B’’’
tworzy
punkt przecięcia prostej rzutu-
jącej (od punktu
B
IV
) i prostej
prostopadłej do prostych
a’’’
i
b’’’
poprowadzonej od punktu
A’’’
.
Odległość punktu
B’
od osi
x
1
jest równa odległości punktu
B
IV
od osi
x
2
, a odległość punktu
B’’
od osi
x
jest równa odległości
B’’’
od osi
x
1
.
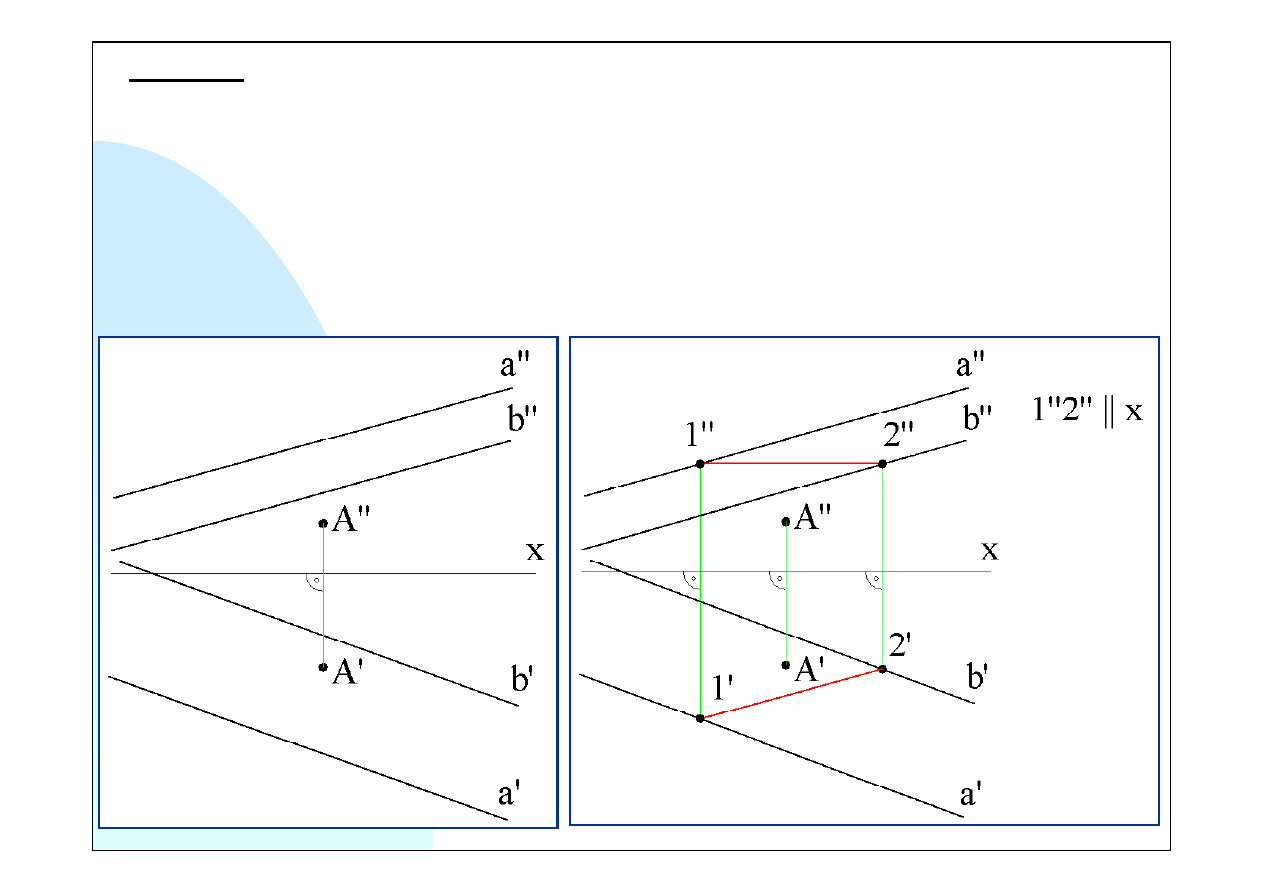
Sposób 2
Sposób drugi polega na uzyskaniu rzutu płaszczyzny (określonej prostymi równoległymi) na
rzutnię do niej prostopadłą która niekoniecznie musi być prostopadła także do tych prostych.
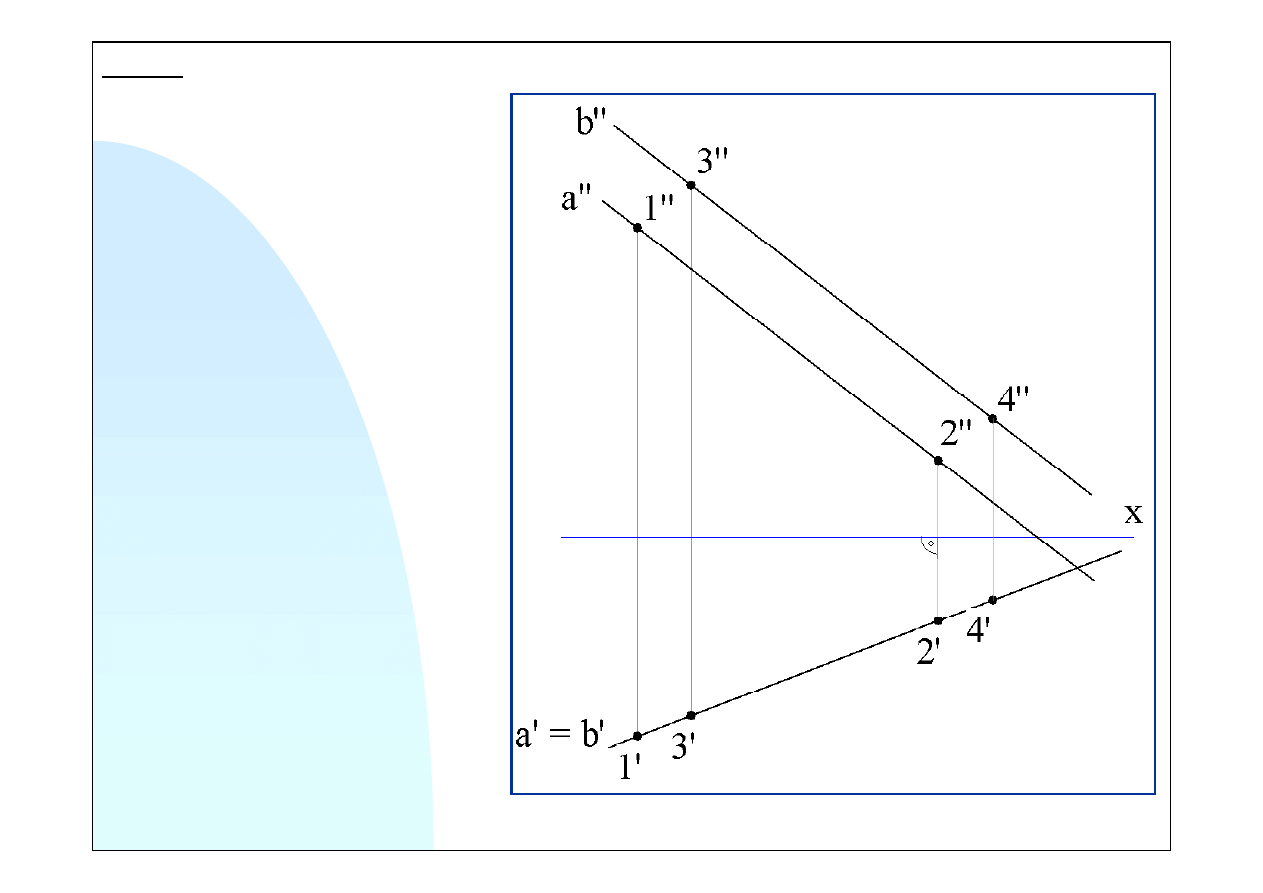
Wykorzystamy pomocniczy element w postaci odcinka równoległego do płaszczyzny poziomej
(jego rzut pionowy jest równoległy do osi
x
) i należącego do płaszczyzny określonej danymi
prostymi równoległymi. Końce
1
i
2
tego odcinka leżą na tych prostych. Na rysunku po prawej
pokazano rzut pionowy i poziomy tego odcinka.
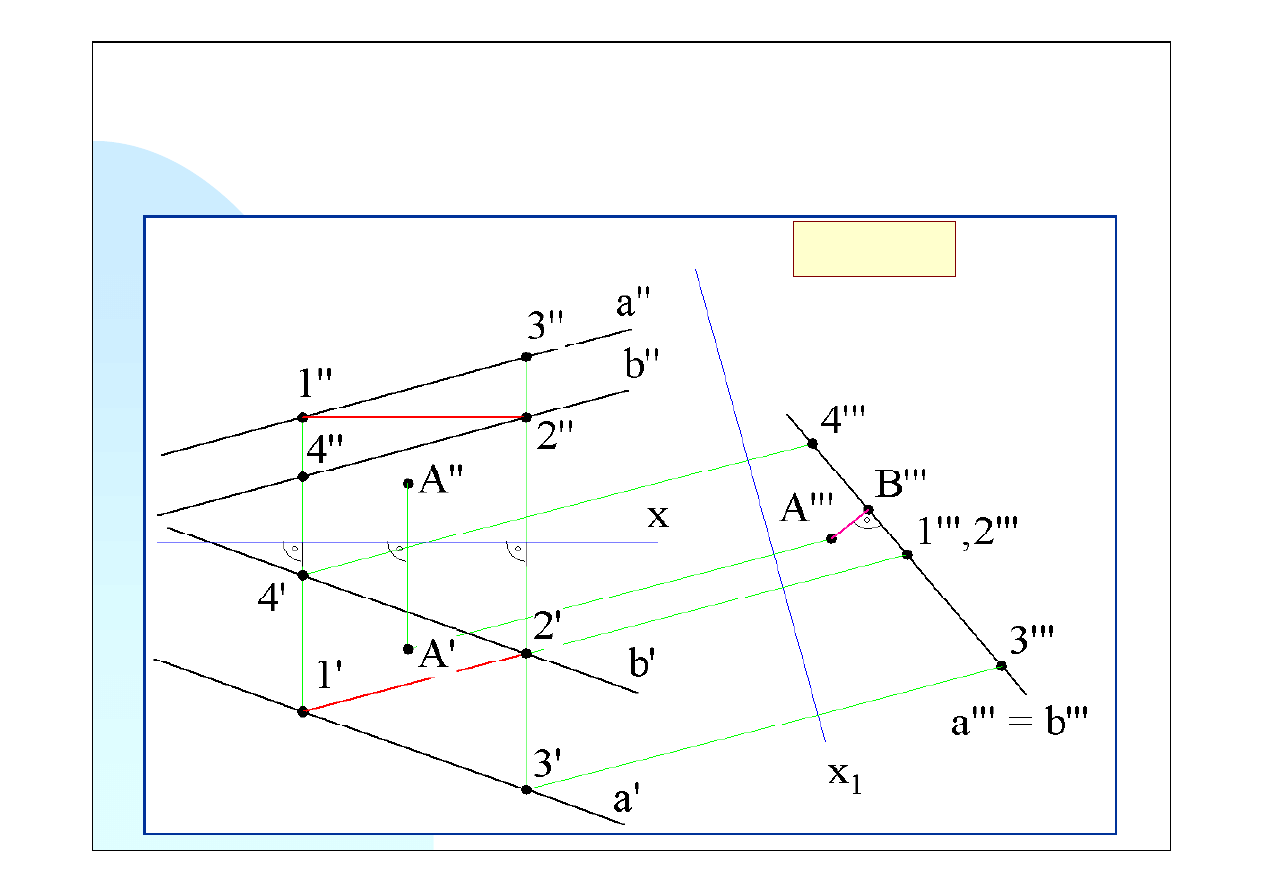
Rzutujemy punkt i proste na płaszczyznę prostopadłą do rzutni poziomej i prostopadłą do
odcinka (
x
1
prostopadłe do
1’2’
). Trzecie rzuty otrzymujemy przez odmierzenie wysokości
rzutowanych punktów (czyli odległości rzutów pionowych od osi
x
) na prostych rzutujących od
osi
x
1
. Płaszczyzna określona prostymi równoległymi jest prostopadła do rzutni trzeciej, zatem
odległość będzie określona odcinkiem
A’’’B’’’
prostopadłym do trzecich rzutów prostych.
x
1
⊥
1’2’
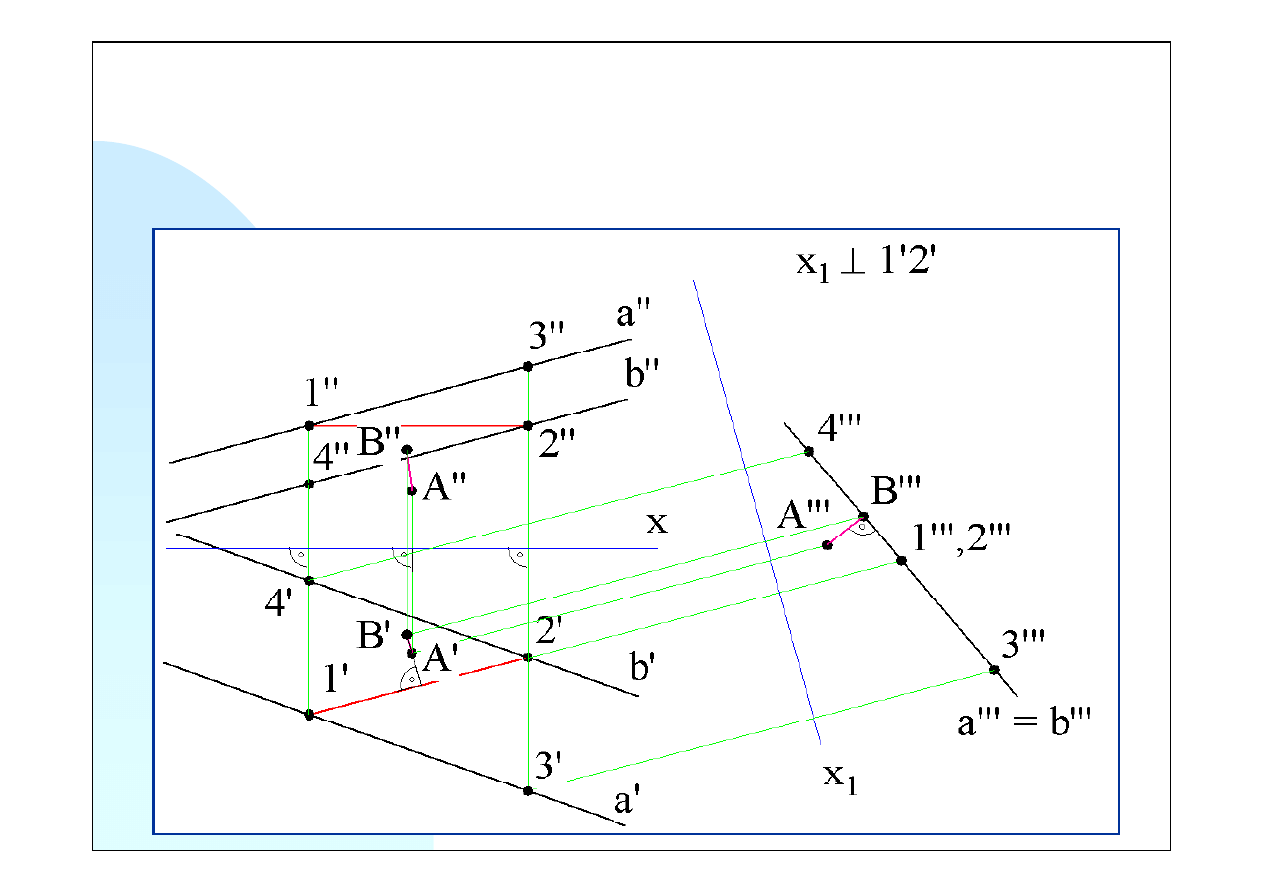
Rzut poziomy punktu
B
(
B’
) znajduje się w punkcie przecięcia prostej rzutującej prostopadłej
do osi
x
1
prowadzącej od punktu
B’’’
i prostej poprowadzonej prostopadle do odcinka
1’2’
i
przechodzącej przez punkt
A’
. Punkt
B’’
(rzut pionowy punktu
B
) wyznaczamy odmierzając od
osi
x
, na promieniu rzutującym prostopadłym do osi
x
, odległość równą odległości punktu
B’’’
od osi
x
1
.
Dzi
ękuję za uwagę
Wyszukiwarka
Podobne podstrony:
GiGi 2013 zadania 1
GiGi 2013 zadania 4
GiGi 2013 zadania 2
GiGi 2013 zadania 3
GiGi 2013 zadania 1
GiGi 2013 zadania 4
GiGi 2013 zadania 4
GiGi 2013 zadania 2
RP2-2013 Zadania na druga kartkowke
drgania 2013 zadania cz2
Kolokwium nr 3 - 121N - 24042014 - 2013 - zadanie, astronawigacja, astro, Przykładowe kolokwia z ast
drgania 2013 zadania z ćwiczeń
3. 16.12.2013, Zadania lekcji:
Cwiczenie 12 2013 zadania
drgania 2013 zadania
drgania 2013 zadania cz2
CHiF zadania 06 2013
więcej podobnych podstron