
1
LOKALNA ANALIZA
CZĘSTOTLIWOŚCIOWA SYGNAŁÓW
Spis treści
1. Definicja
2. Okna
3. Transformacja Gabora
2
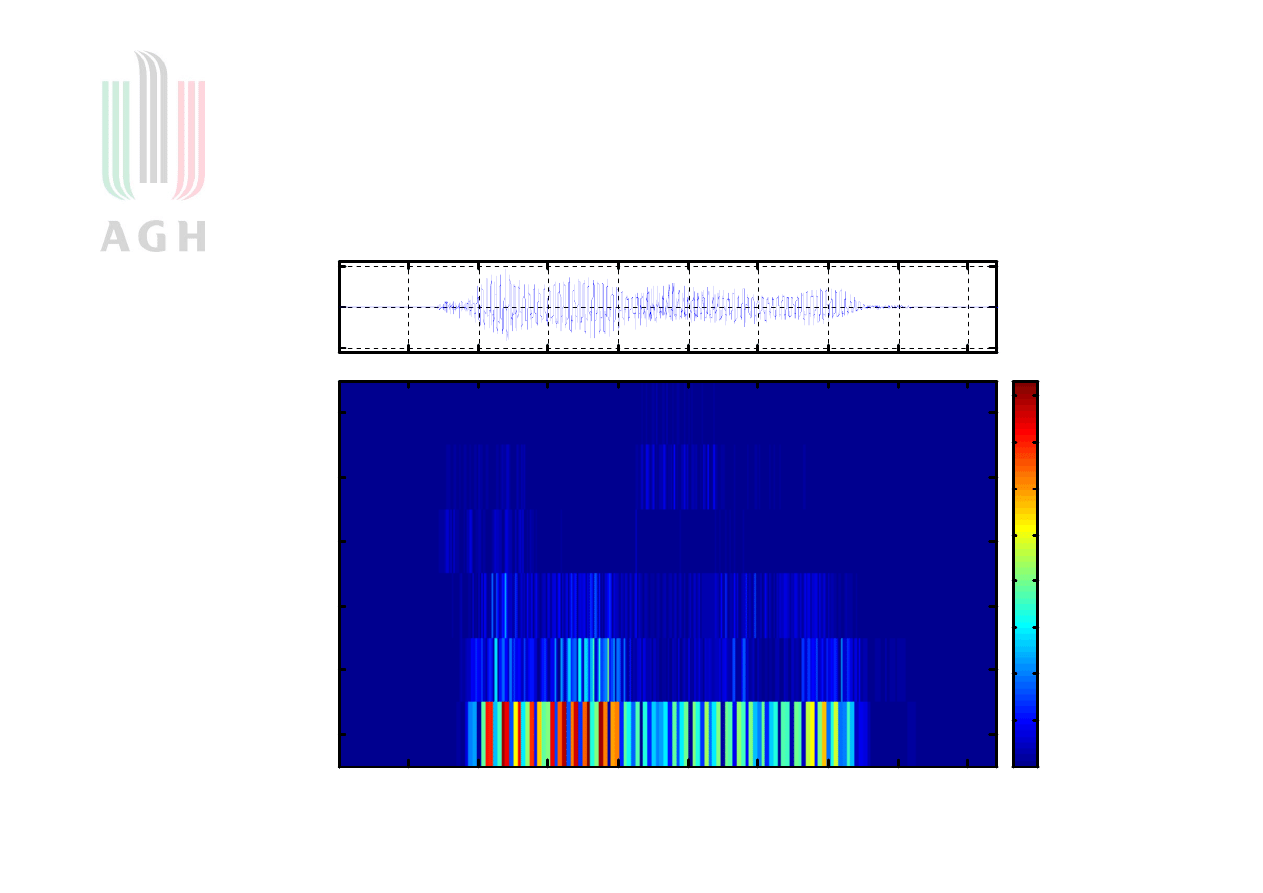
Analiza czasowo-częstotliwościowa
sygnału mowy
0
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 0 0
7 0 0
8 0 0
9 0 0
- 1 . 0
0 . 0
1 . 0
an d rze j_01_35_m.wav
Am
p
li
tu
d
a
Cz as [m s ]
DW
T
0
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 0 0
7 0 0
8 0 0
9 0 0
D 1
D 2
D 3
D 4
D 5
D 6
0 . 0
0 . 5
1 . 0
1 . 5
2 . 0
2 . 5
3 . 0
3 . 5
4 . 0
3
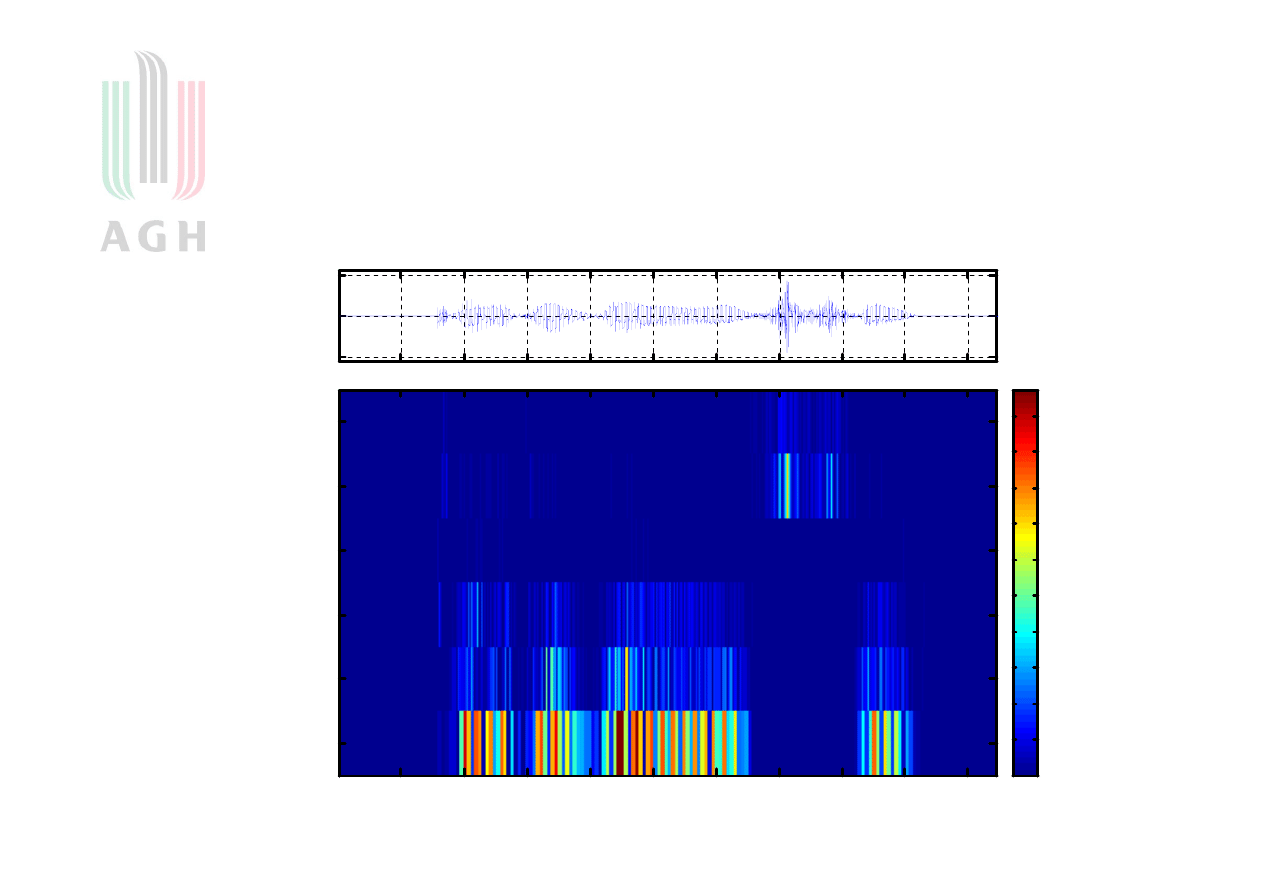
Kolejny przykład sygnału mowy
0
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 0 0
7 0 0
8 0 0
9 0 0
1 0 0 0
- 1 . 0
0 . 0
1 . 0
c ze rwie ñ s zy_01_35_m.wav
Am
p
li
tu
d
a
Cz as [m s ]
DW
T
0
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 0 0
7 0 0
8 0 0
9 0 0
1 0 0 0
D 1
D 2
D 3
D 4
D 5
D 6
0 . 0
0 . 2
0 . 4
0 . 6
0 . 8
1 . 0
1 . 2
1 . 4
1 . 6
1 . 8
2 . 0
4
Krótkoczasowa transformacja Fouriera
( )
t
t
t
1
1
0
1
dla
dla
Ang.
short-time Fourier transform
b
b
t
f
j
t
f
j
w
dt
e
t
s
dt
e
b
t
t
s
f
b
s
1
1
2
2
)
(
)
(
)
(
)
,
(
ˆ
Widmo
czasowo-częstotliwościowe
można obliczyć posługując się wzorem

5
Porównanie transformaty Fouriera z ....
Załóżmy, że
s t
f t
( ) cos(
)
2
0
Jak wiemy uogólniona transformata Fouriera tego sygnału ma postać
( )
.
(
)
,
(
)
s f
f
f
f
f
0 5
0 5
0
0
Obliczmy teraz jego krótkotrwałą transformatę Fouriera
ograniczoną do przedziału .
[ , ]
4 4

6
.... krótkoczasową transformatą Fouriera
Odpowiada to znalezieniu widma sygnału
s t
t
f t
w
( )
/
cos(
)
4
2
0
czyli
( )
cos(
) ( / )
cos(
)
s
f
f t
t
e
dt
f t e
dt
w
j f t
j f t
2
4
2
0
2
0
2
4
4
Posługując się wzorem na transformatę sygnału zmodulowanego
otrzymujemy
( )
sin
(
)
(
)
sin
(
)
(
)
s
f
f
f
f
f
f
f
f
f
w
8
8
8
8
0
0
0
0
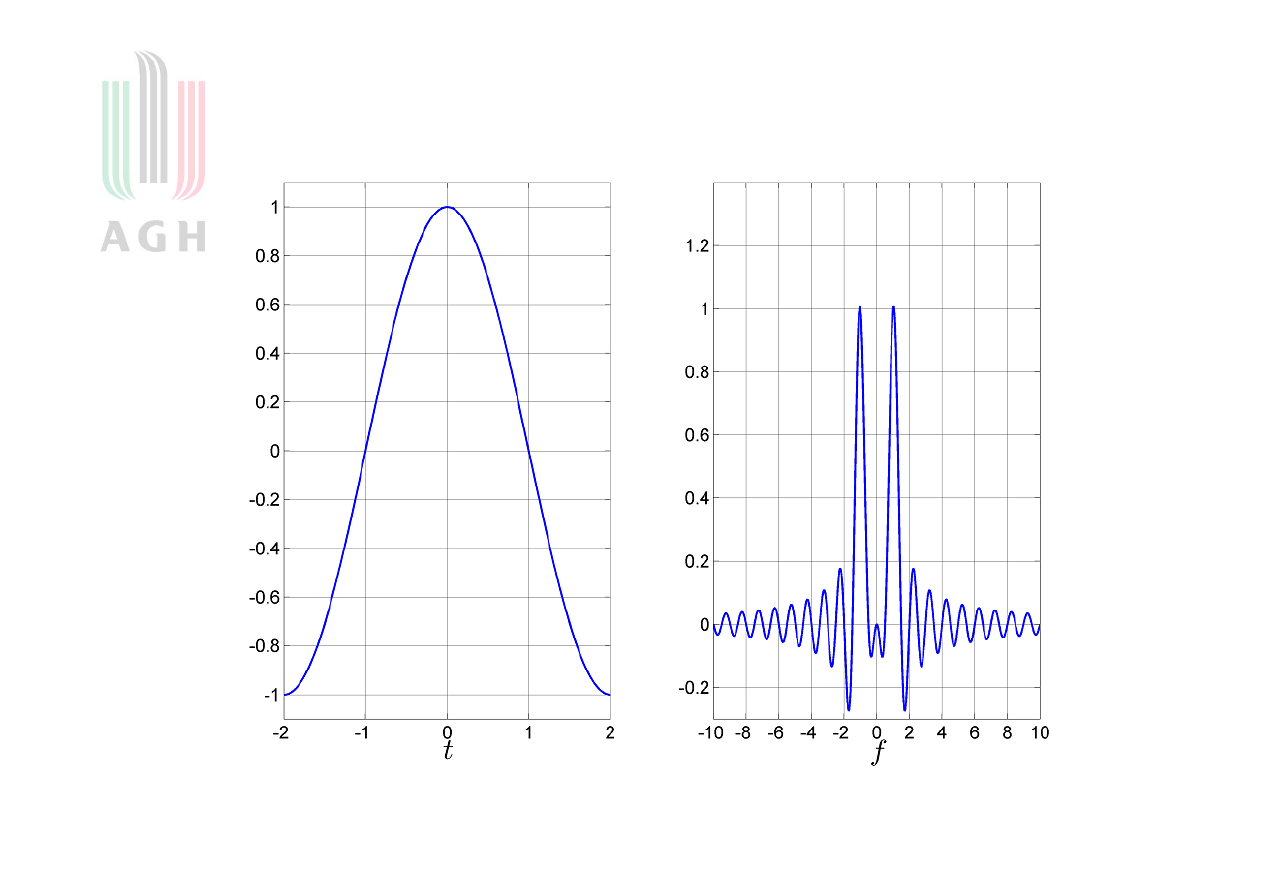
7
Ilustracja przykładu
Sygnał s(t)
Jego transformata

8
Widmo okna
( )
( )
w f
w t e
dt
j f t
2
dla
t
T
w
2T
w
jest nazywane rozmiarem okna
0
)
(
t
w
Okno z nośnikiem zwartym
9
Środek i szerokość okna
Środek okna
c
w
t w t dt
w
1
2
2
( )
Szerokość okna
w
w
w
t
c
w t dt
2
2
2
1
2
( )
gdzie norma jest obliczana w przestrzeni
L
2
( )
2
2
)
(
w
t
w
odpowiada gęstości prawdopodobieństwa

10
Normalizacja okna
Okno
powinno być
znormalizowane
w
w f df
( )
( )
0
1
w
c
f
j
w
e
f
w
c
t
w
2
)
(
ˆ
)
(
w c
w f e
df
w
j f c
w
( )
( )
2
1
gdzie
c
w
jest
środkiem okna.
w t
( )
Po przesunięciu
czyli okno też będzie znormalizowane bo

11
Widmo sygnału wyciętego przez okno
Sygnał
pomnożony przez okno
posiada widmo
s t
s t w t
w
( )
( ) ( )
dg
g
w
g
f
s
dt
e
t
w
t
s
f
s
t
f
j
w
)
(
ˆ
)
(
ˆ
)
(
)
(
)
(
ˆ
*
2
dt
e
b
t
w
t
s
b
f
s
t
f
j
w
2
)
(
)
(
)
,
(
ˆ
w t
( )
)
(t
s
)
(
ˆ
*
f
w
gdzie
oznacza funkcję sprzężoną do widma
)
(
ˆ f
w
dt
e
t
s
f
s
t
f
j
w
w
2
)
(
)
(
ˆ
12
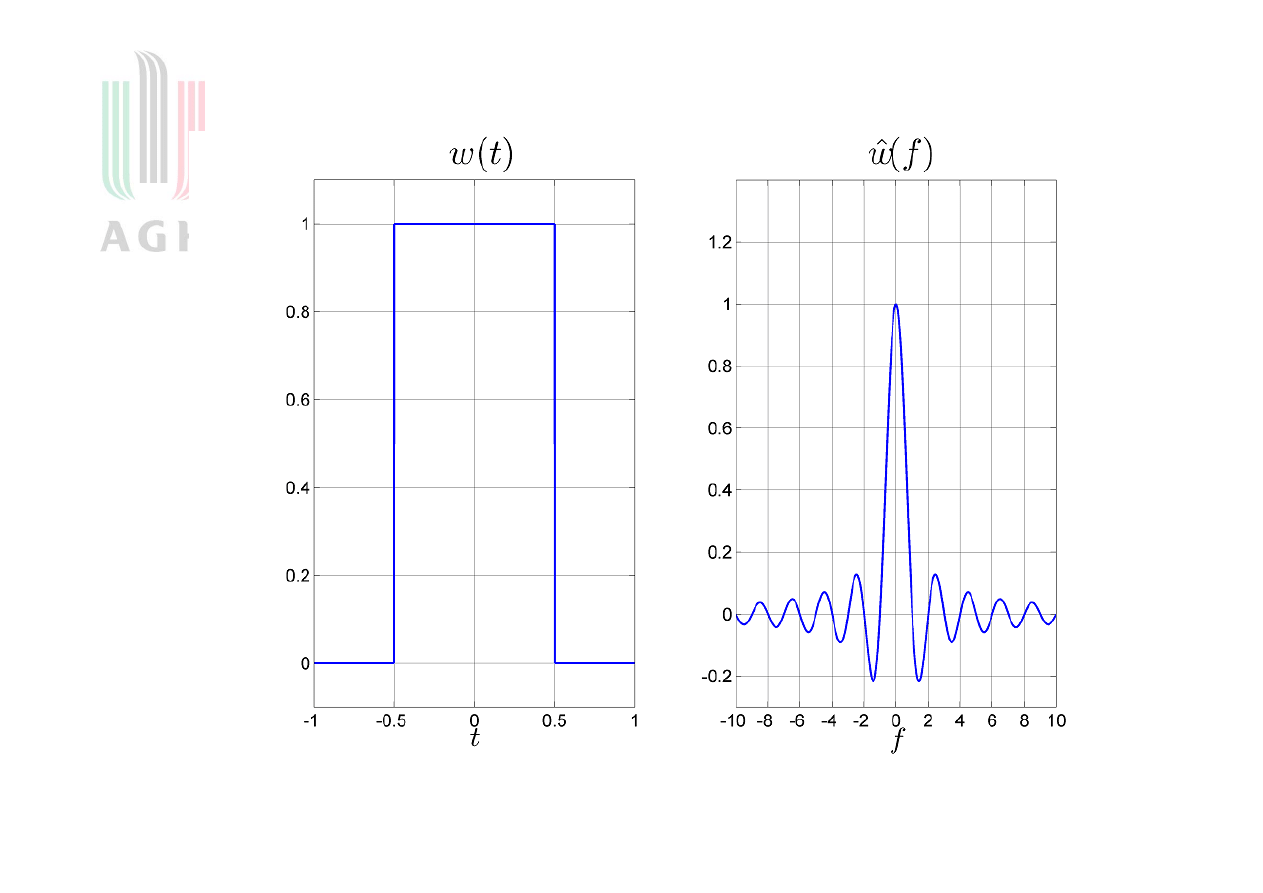
Okno prostokątne (rysunek)
13
Okno prostokątne
w t
t
T
t
T
( )
1
0
dla
dla
w
dt
T
T
T
2
2
środek okna znajduje się w zerze
c
T
t dt
w
T
T
1
2
0
a szerokość okna zgodnie z przyjętą definicją wynosi
w
T
T
T
t dt
T
2
2
2
3
2
1
2
czyli jest różna od
.
2T
Widmo częstotliwościowe tego okna ma postać
( )
sin(
)
w f
f T
f
2
14
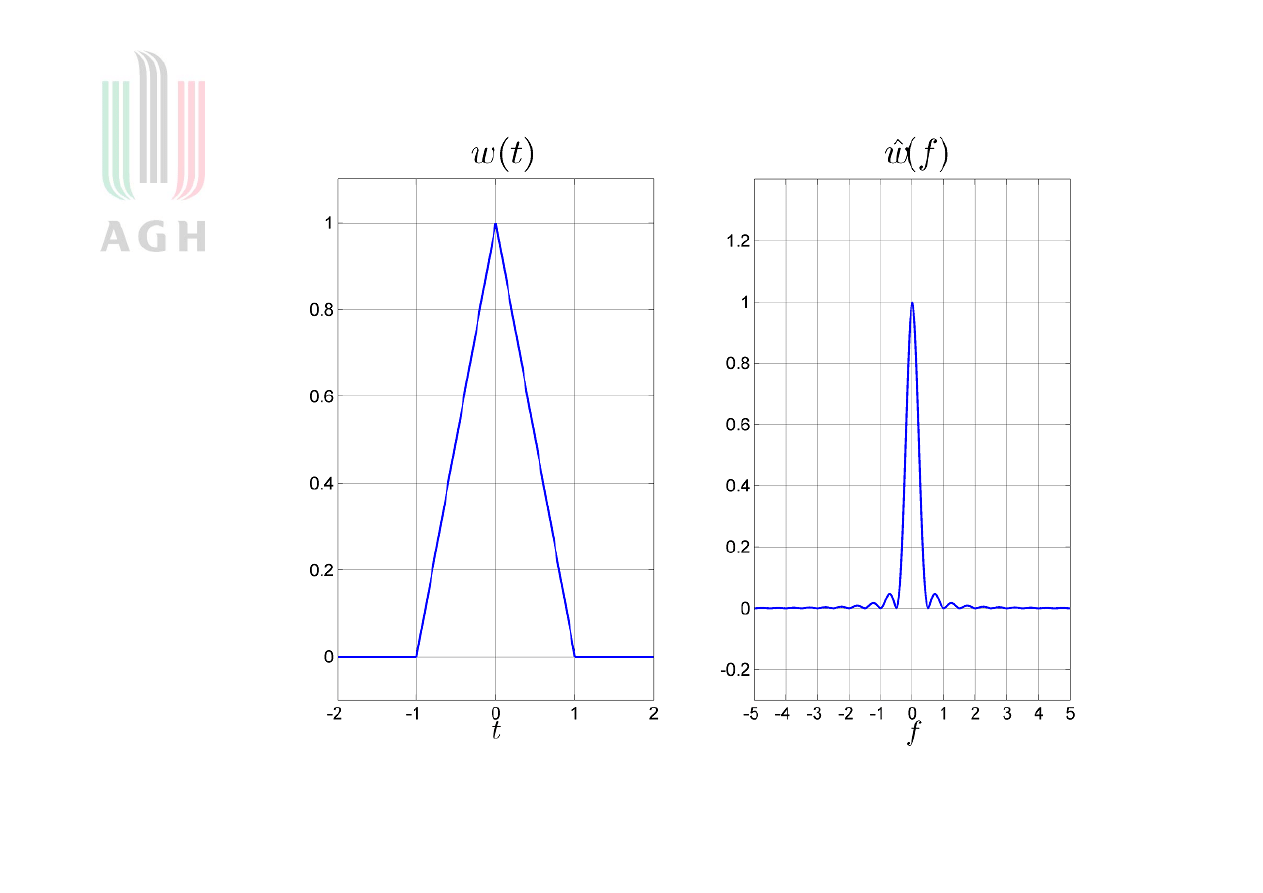
Okno Bartletta (rysunek)
15
Okno Bartletta zwane trójkątnym
środek tego okna również znajduje się w zerze, co można łatwo
policzyć
c
T
t
t
T
dt
t
t
T
dt
w
T
T
3
2
1
1
0
2
0
2
0
Szerokość okna wynosi
w
T
T
T
t
t
T
dt
t
t
T
dt
T
6
1
1
2
5
2
2
2
2
0
0
a widmo częstotliwościowe
( )
sin (
)
w f
f T
T f
2
2
2
w t
t
T
t
T
t
T
( )
1
0
dla
dla
w
t
T
dt
t
T
dt
T
T
T
2
2
2
0
0
1
1
2
3
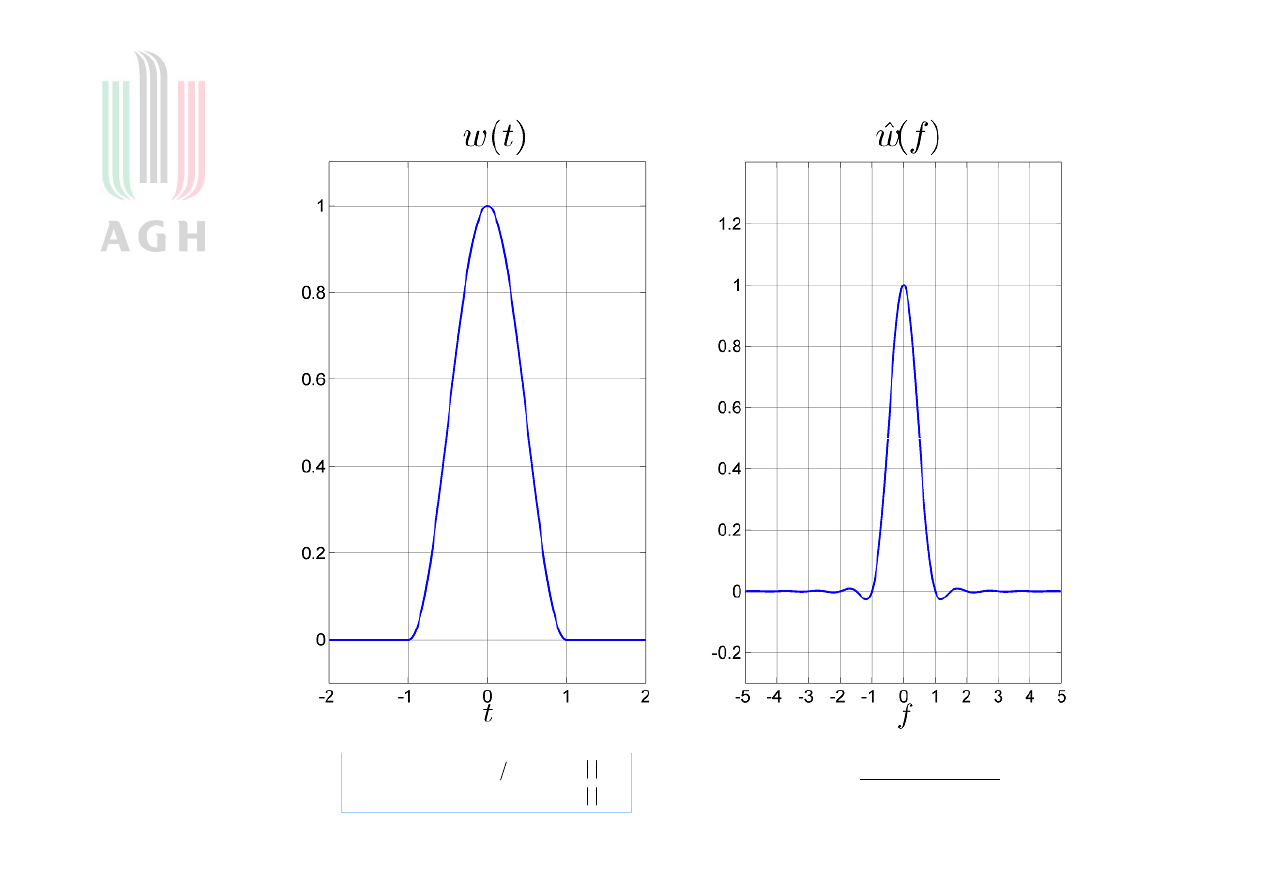
16
Okno Hanna (rysunek)
w t
t T
t
T
t
T
( )
,
cos(
)
0 5 1
0
dla
dla
( )
sin(
)
(
)
w f
f T
T f
f
2
2 1 4
2
2
17
Okno Hanna
w t
t T
t
T
t
T
( )
,
cos(
)
0 5 1
0
dla
dla
w
t
T
dt
T
T
T
2
2
1
4
1
3
4
cos
bo
cos ( )
sin(
)
2
1
2
1
4
2
at dt
t
a
at
Widmo częstotliwościowe ma postać
( )
sin(
)
(
)
w f
f T
T f
f
2
2 1 4
2
2
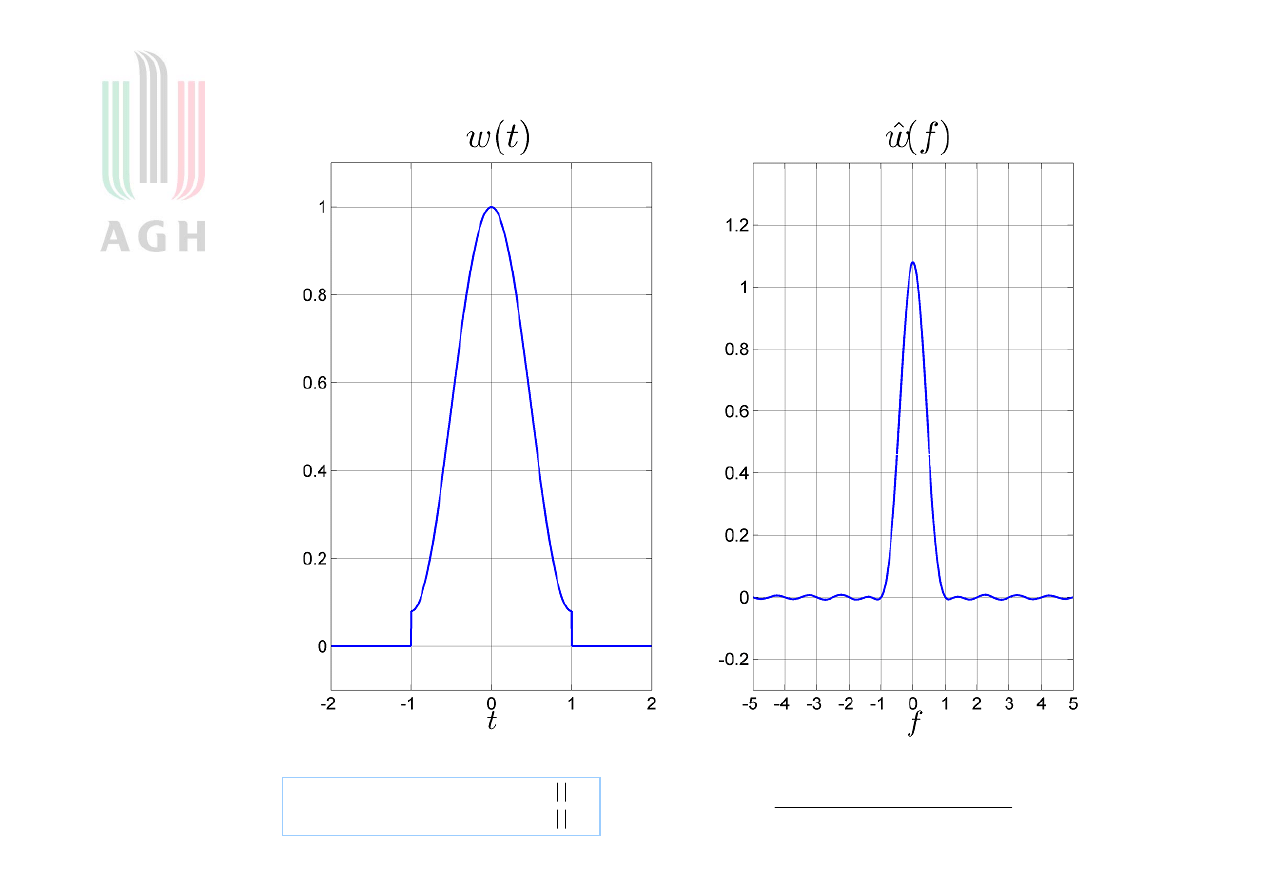
18
Okno Hamminga
w t
t T
t
T
t
T
( )
,
,
cos(
/ )
0 54 0 46
0
dla
dla
( )
( ,
,
)sin(
)
(
)
w f
T f
T f
f
T f
1 08 0 64
2
2
1 4
2
2
2
2
19
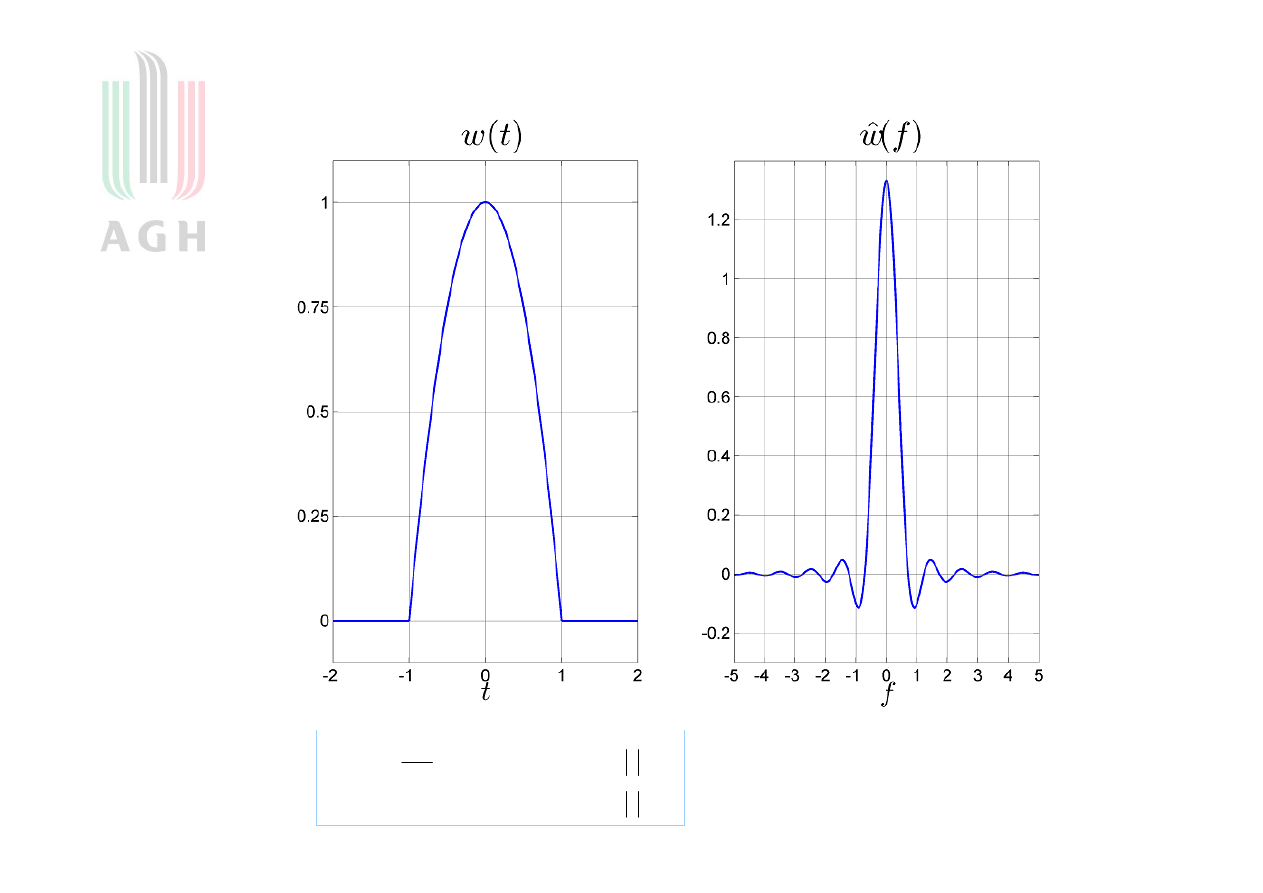
Okno paraboliczne
w t
T
t T
t
T
t
T
( )
/
3
4
1
0
2
dla
dla
20
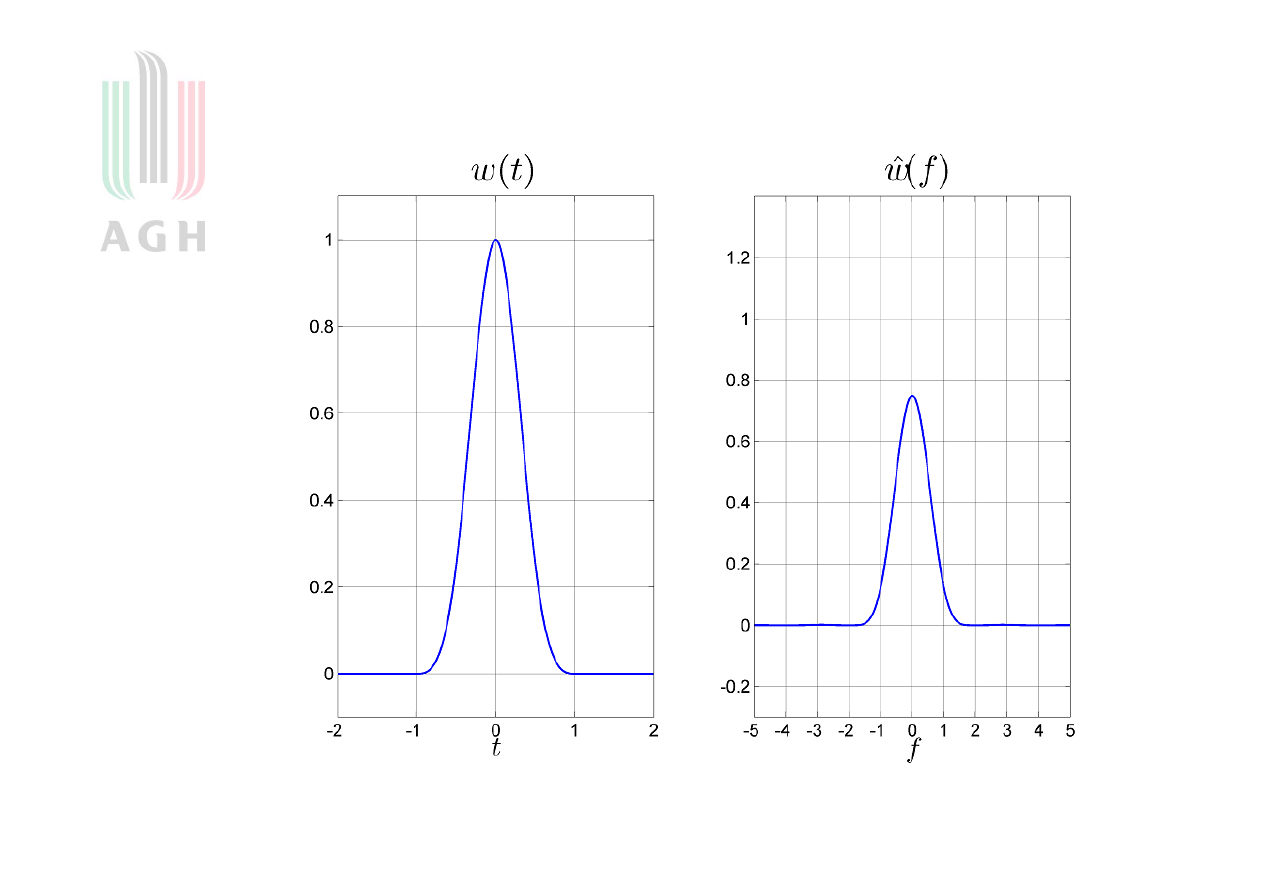
Okno Parzena (rysunek)
jest zbudowane z wielomianów trzeciego stopnia

21
Okno Parzena
ma charakterystykę częstotliwościową
2
/
sin
12
)
(
ˆ
4
4
3
4
f
T
f
T
f
w
rok 1961
T
t
T
t
T
T
t
T
t
T
t
T
t
t
w
dla
0
2
/
dla
/
1
2
2
/
dla
/
6
/
6
1
)
(
3
3
3
2
2
22
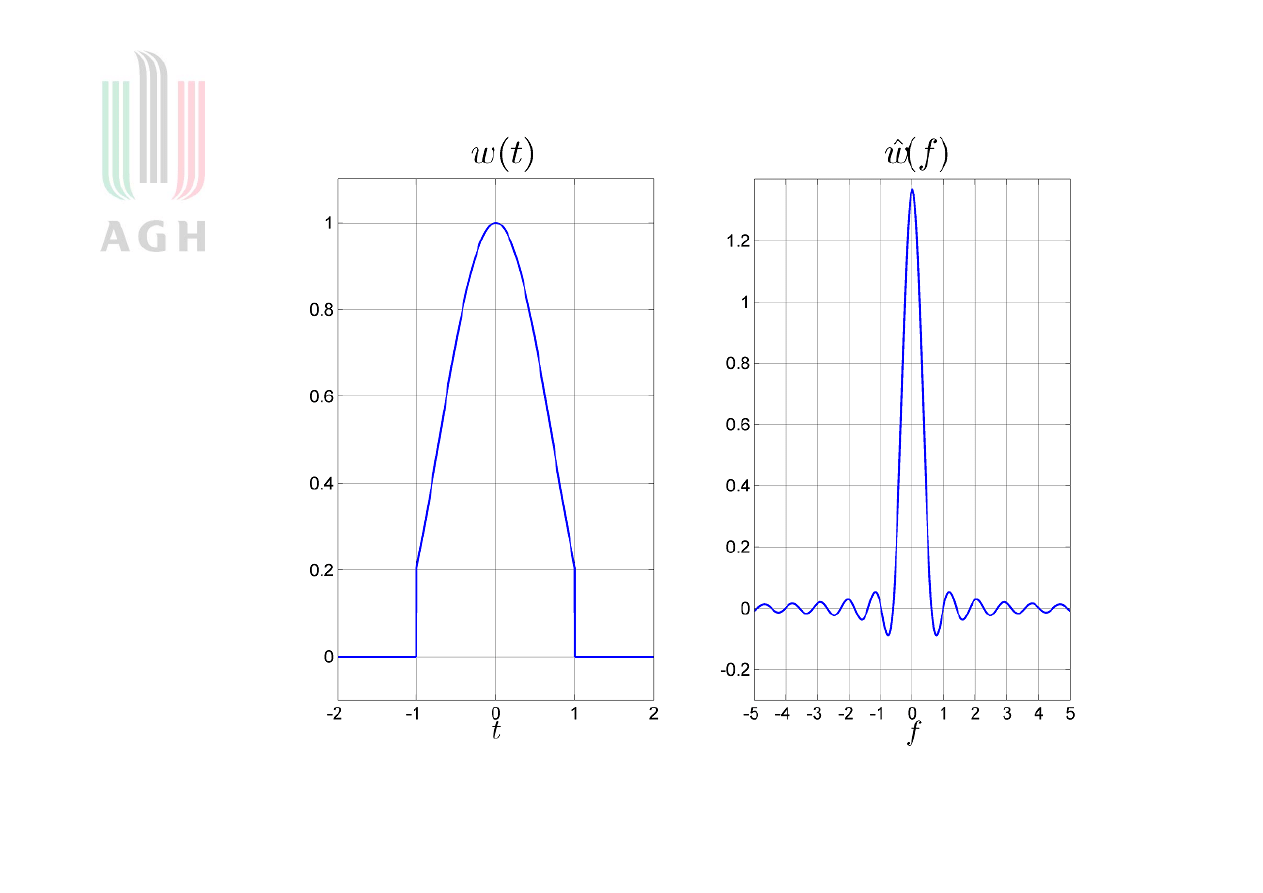
Okno Kaisera (rysunek), β=3

23
Okno Kaisera
2
)
(
0
0
T
t
I
I
t
w
2
1
2
1
T
t
gdzie
1
2
0
2
!
1
1
k
k
k
I
jest funkcją Bessela rzędu zerowego

24
Okno Gaussa
w t
e
t
( )
1
2
2
4
a widmo częstotliwościowe
( )
w f
e
f
4
2
2
w
a
a
w
t w t dt
a
2
2
2
2
0 5
( )
,
Jego szerokość wynosi
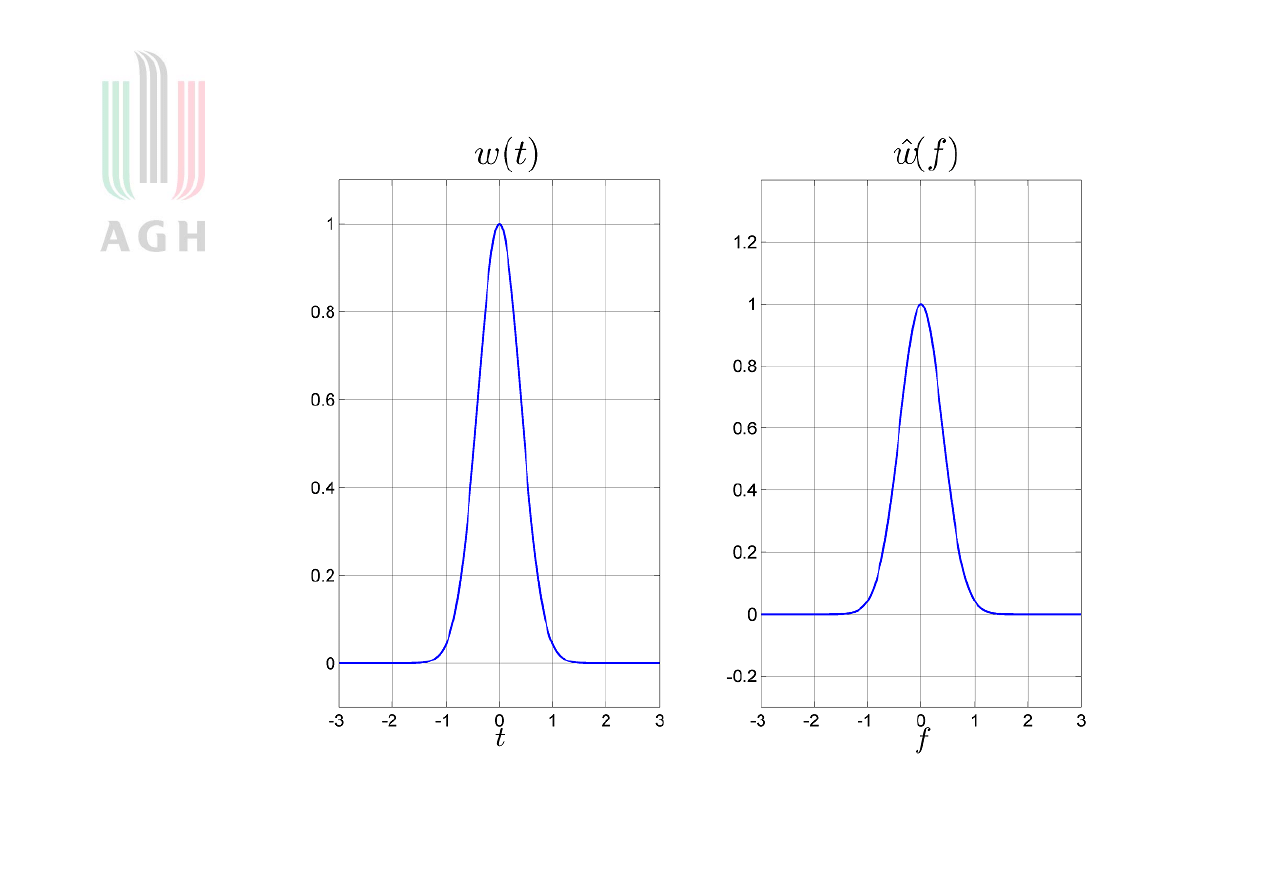
25
Okno Gaussa (rysunek)

26
Przykład
Dany jest sygnał
s t
f t
( ) cos(
)
2
0
który ma widmo
)
(
)
(
5
,
0
)
(
ˆ
0
0
f
f
f
f
f
s
Jakie jest widmo po wymnożeniu sygnału przez wybrane okno ?
)
(
ˆ
)
(
ˆ
2
1
)
(
ˆ
0
0
f
f
w
f
f
w
f
s
w
Odpowiedź jest prosta. Postać widma lokalnego
zależy od widma okna i częstotliwości analizowanego sygnału.
27
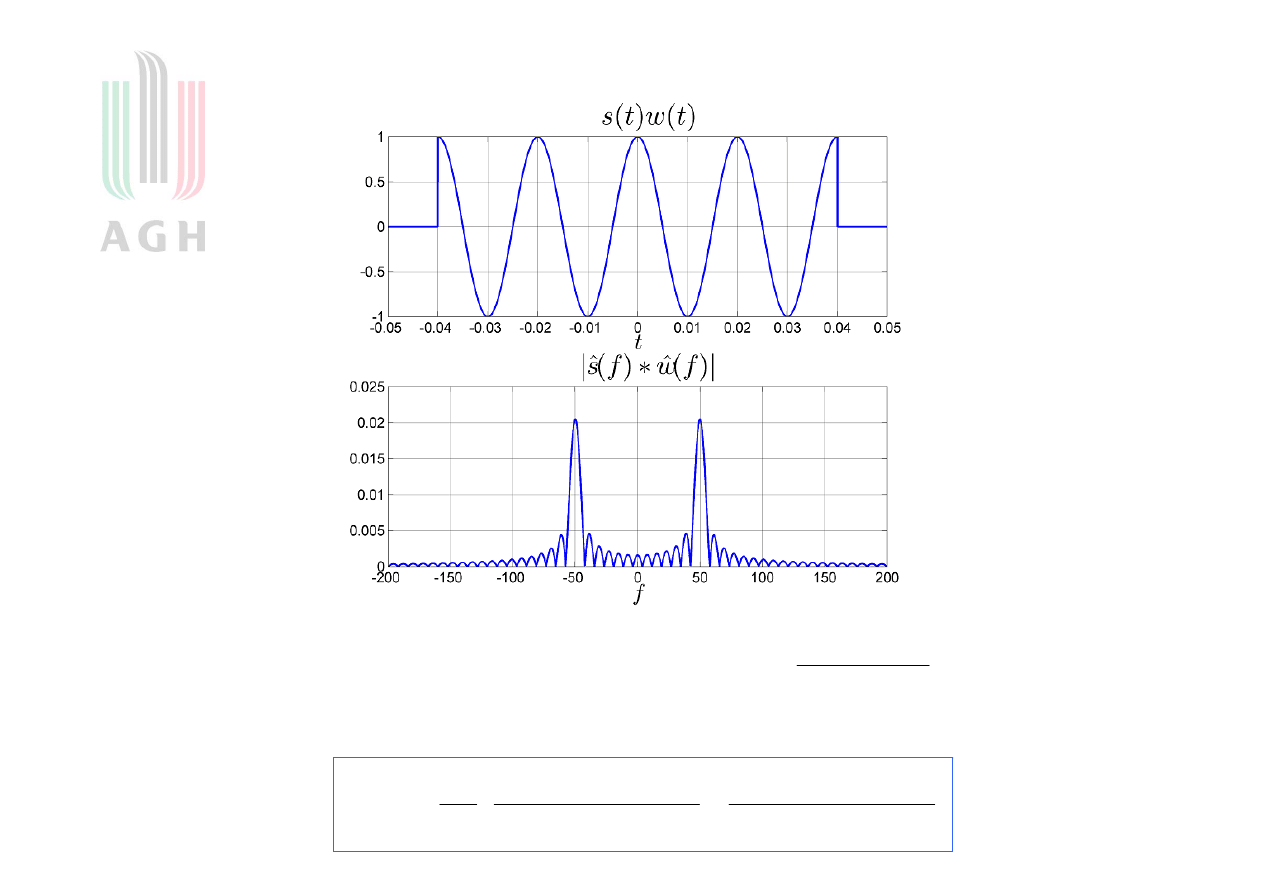
Przykład z oknem prostokątnym
( )
,
(
)
(
)
sin(
)
s
f
f
f
f
f
T
d
w
T
T
0 5
2
0
0
)
(
)
(
2
sin
)
(
)
(
2
sin
2
1
)
(
ˆ
0
0
0
0
f
f
f
f
T
f
f
f
f
T
f
s
w
Bo widmo iloczynu dwóch sygnałów jest równe splotowi ich widm, czyli
28
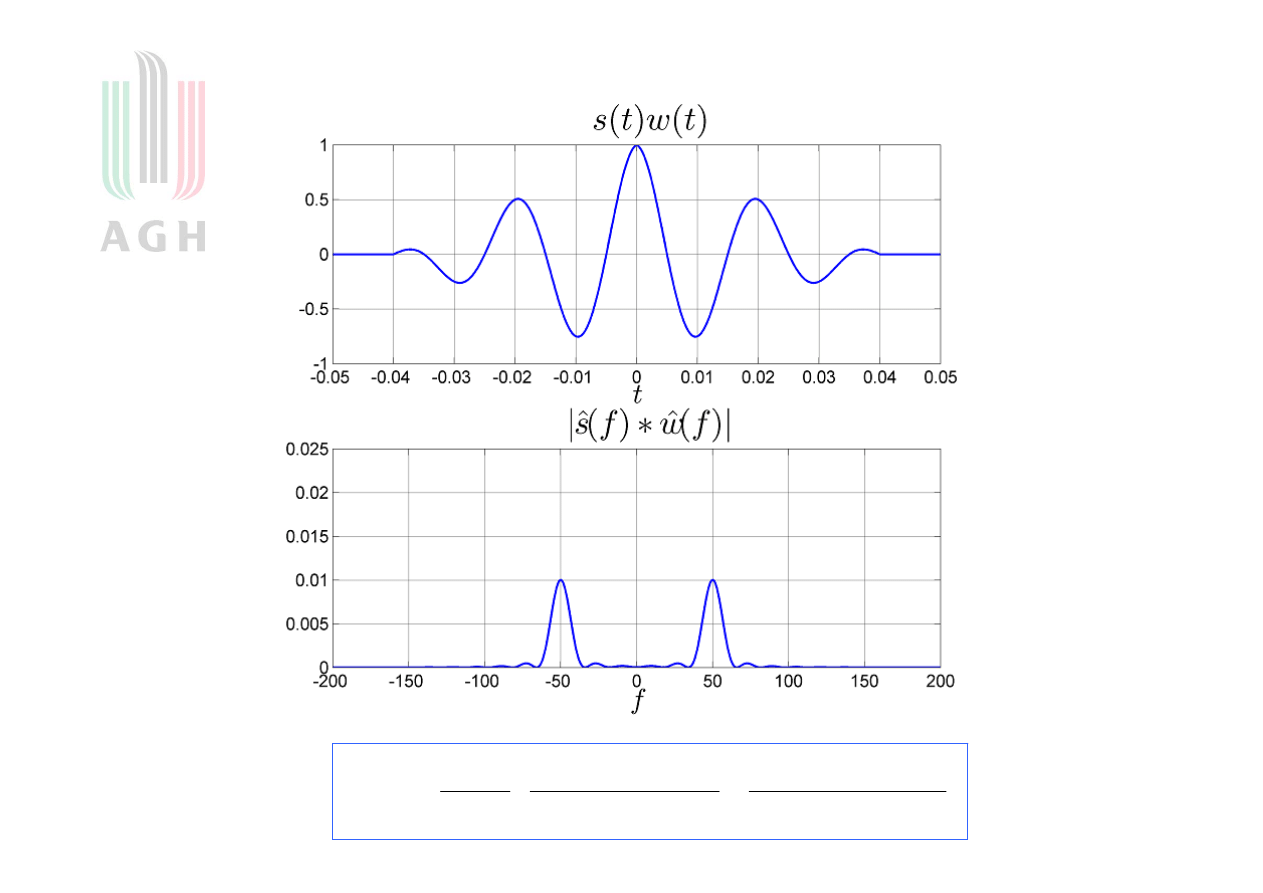
Przykład z oknem Bartletta
2
0
0
2
2
0
0
2
2
)
f
+
(f
)
f
+
T(f
sin
+
)
f
-
(f
)
f
-
T(f
sin
T
2
1
)
(
ˆ
f
s
w
29
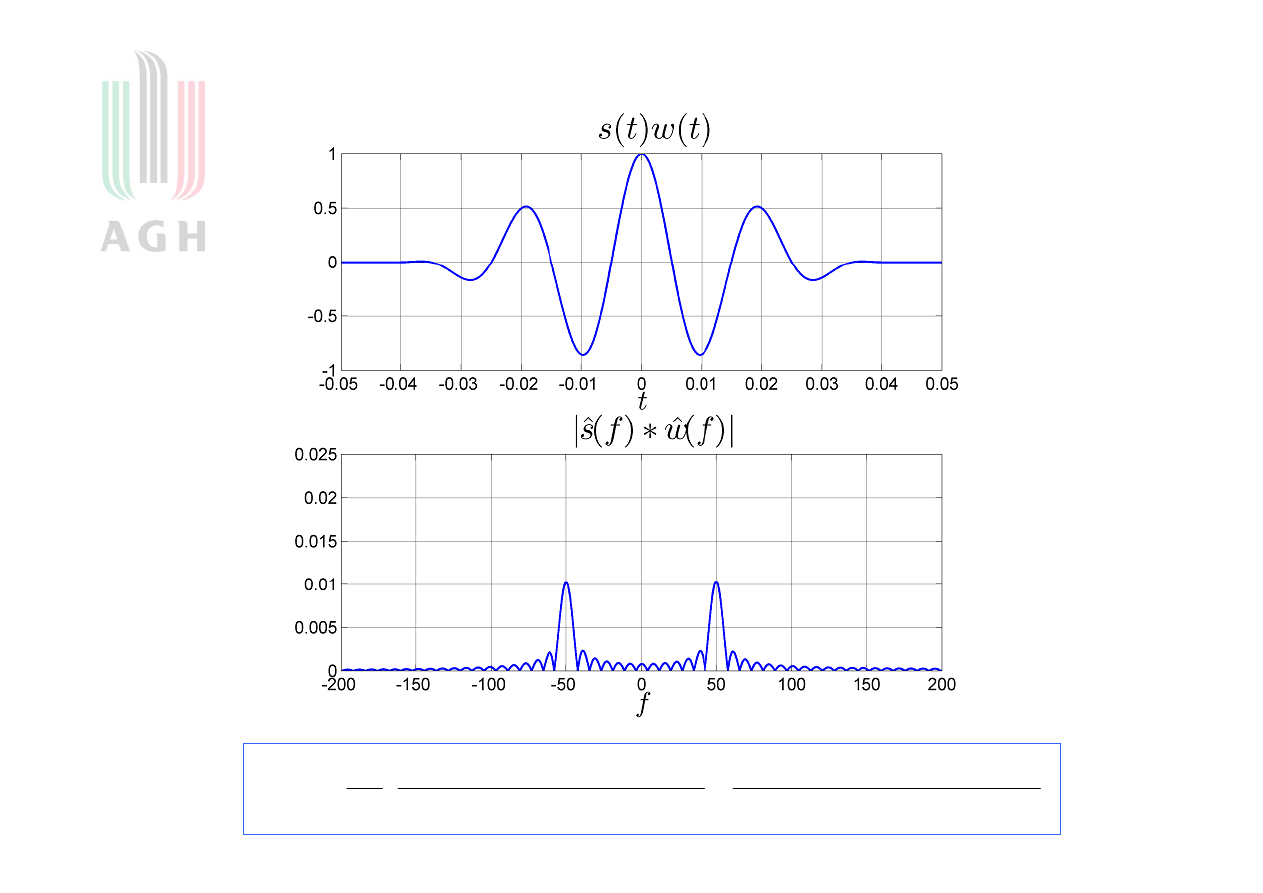
Przykład z oknem Hanna
]
)
(
4
1
)[
(
)
(
2
sin
]
)
(
4
1
)[
(
)
(
2
sin
4
1
)
(
ˆ
2
0
2
0
0
2
0
2
0
0
f
f
T
f
f
f
f
T
f
f
T
f
f
f
f
T
f
s
w
30
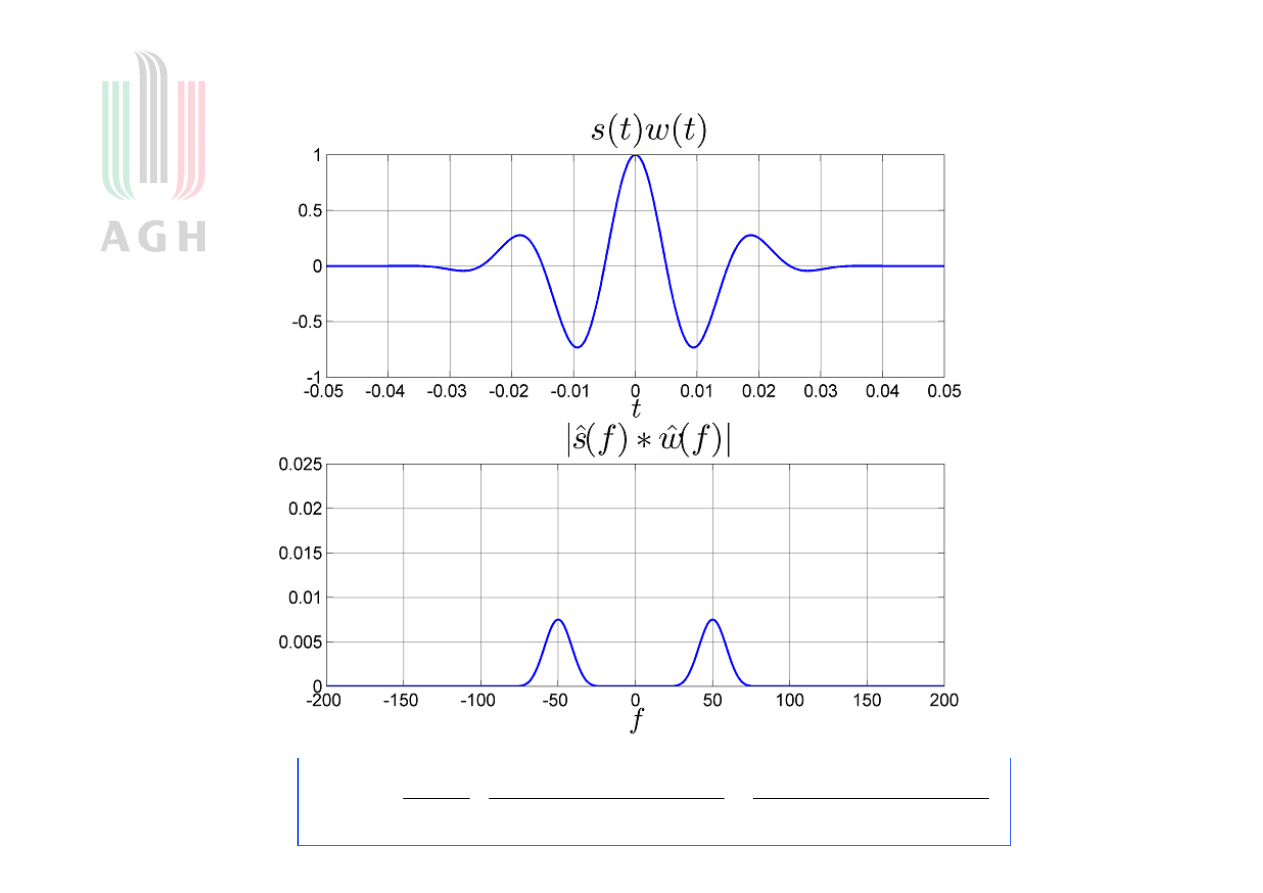
Przykład z oknem Parzena
4
0
0
4
4
0
0
4
3
4
)
(
)
(
5
,
0
sin
)
(
)
(
5
,
0
sin
6
)
(
ˆ
f
f
f
f
T
f
f
f
f
T
T
f
s
w
31
Transformacja Gabora
opiera się na funkcji Gaussa
( , , )
( )
(
)
s f a b
s t w t
b e
dt
a
j f t
2
w t
b db
a
(
)
1
)
(
ˆ
)
,
,
(
ˆ
f
s
db
b
a
f
s
a b
t b
a
j f t
f t
a
e
,
(
)
( , )
1
2
2
4
2
( , , )
( )
( , )
,
s f a b
s t
f t dt
a b
Transformację Gabora można zatem zapisać w postaci
gdzie
w t
a
e
a
t
a
( )
1
2
2
4
i jest zdefiniowana następująco
Posiada własności
Wyszukiwarka
Podobne podstrony:
Podatki i oplaty lokalne id 365 Nieznany
Istota rozwoju lokalnego id 220 Nieznany
Prasa lokalna id 385188 Nieznany
Podatki i oplaty lokalne id 365 Nieznany
Istota rozwoju lokalnego id 220 Nieznany
AKTYWIZACJA I ROZWOJ LOKALNY id Nieznany (2)
Ksiazki sieci Sieci Lokalne id Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
więcej podobnych podstron