Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-1 

Wykład 12 

12. Ruch obrotowy 

12.1 

Wstęp 

Mówiąc o środku masy wspominaliśmy o ruchu obrotowym oraz o toczeniu się ciał. 

Dużym ułatwieniem w analizie układów cząstek jest możliwość rozpatrywania oddziel-
nego  ruchu  postępowego  i  ruchu  obrotowego.  Aby  wprowadzić  to  uproszczenie  zdefi-
niujemy dwie nowe wielkości: 

moment pędu

 i 

moment siły

. Zasada zachowania momen-

tu pędu jest równie istotna jak zasada zachowania pędu i zasada zachowania energii. 

12.2 

Kinematyka ruchu obrotowego 

Musi w pierwszym kroku wypracować ujęcie matematyczne dla ruchu obrotowego. 

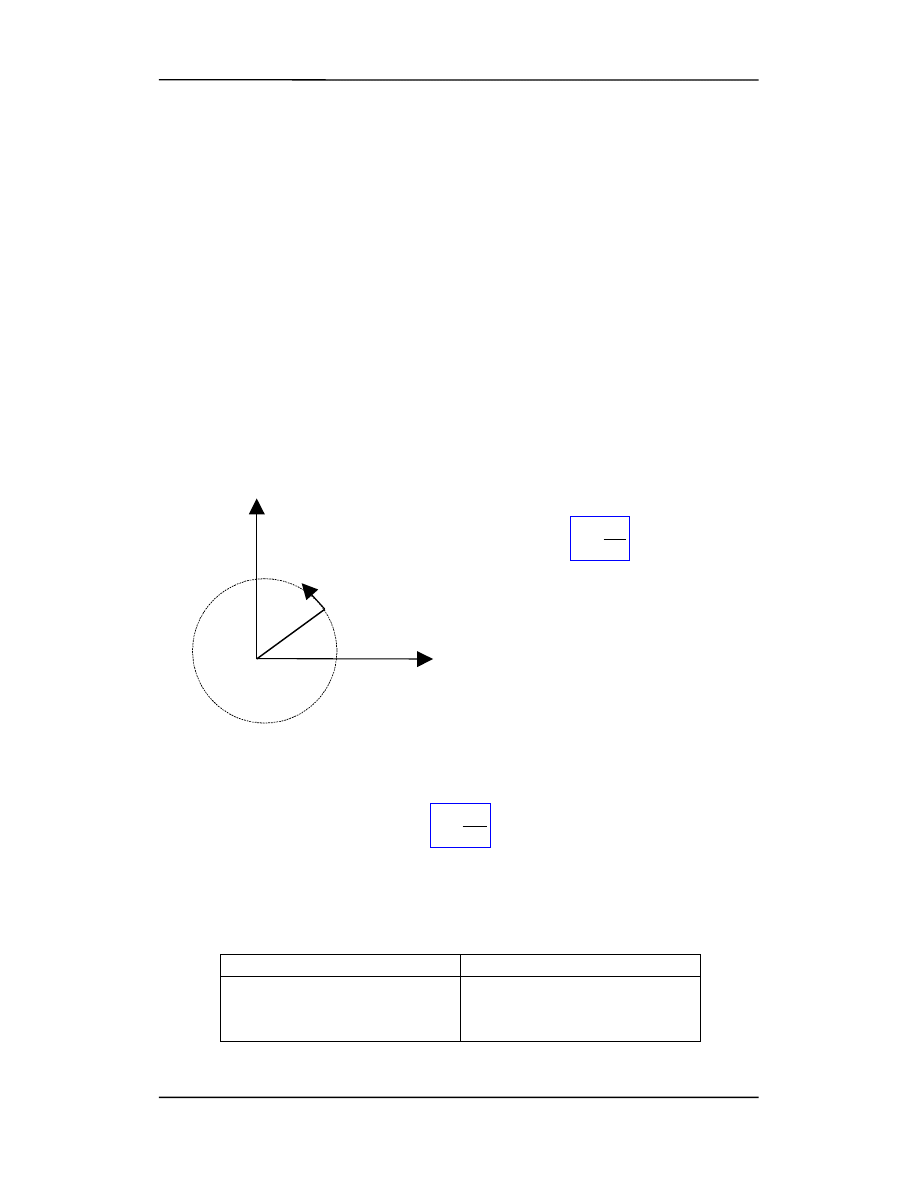
Dla  ruchu  obrotowego  wielkością  analogiczną  do  przesunięcia  jest 

przesunięcie  kąto-

we 

θ. Kąt θ określa położenie punktu względem układu odniesienia. Dla ruchu po okrę-

gu,  z definicji  miary  łukowej  kąta 

θ = S/R. (w radianach). Kątową analogią prędkości 

v = dx/dt jest 

prędkość kątowa

 

ω. 

 

 

t

d

d

θ

ω

=

 

(12.1) 

 
Dla ruchu po okręgu v

 = 

ω R. 

W  przypadku  ruchu  jednostajnego  po  okrę-
gu 

ω jest nazywane 

częstością kątową

 i jest 

związana z częstotliwością f relacją 
 

ω = 2

π

f 

 

Podobnie jak przyspieszenie liniowe a = dv/dt zostało zdefiniowane przyspieszenie ką-
towe 

α. 

 

 

t

d

d

ω

α

=

 

(12.2) 

 
Dla ruchu po okręgu związek pomiędzy a i 

α jest analogiczny do związku pomiędzy v 

i 

ω tzn. a = αR. Możemy teraz np. podać opis ruchu obrotowego ze stałym przyspiesze-

niem 

α poprzez analogię do ruchu postępowego jednostajnie zmiennego. 

 

Ruch postępowy 

Ruch obrotowy 

a = const 
v

 = v

0

 + at 

s = s

0

 + v

0

t + (1/2)at

2

 

α = const 

ω = ω

0

 + 

αt 

θ =θ

0

 + 

ω

0

t + (1/2)

αt

2

 

θ

R

S

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-2 

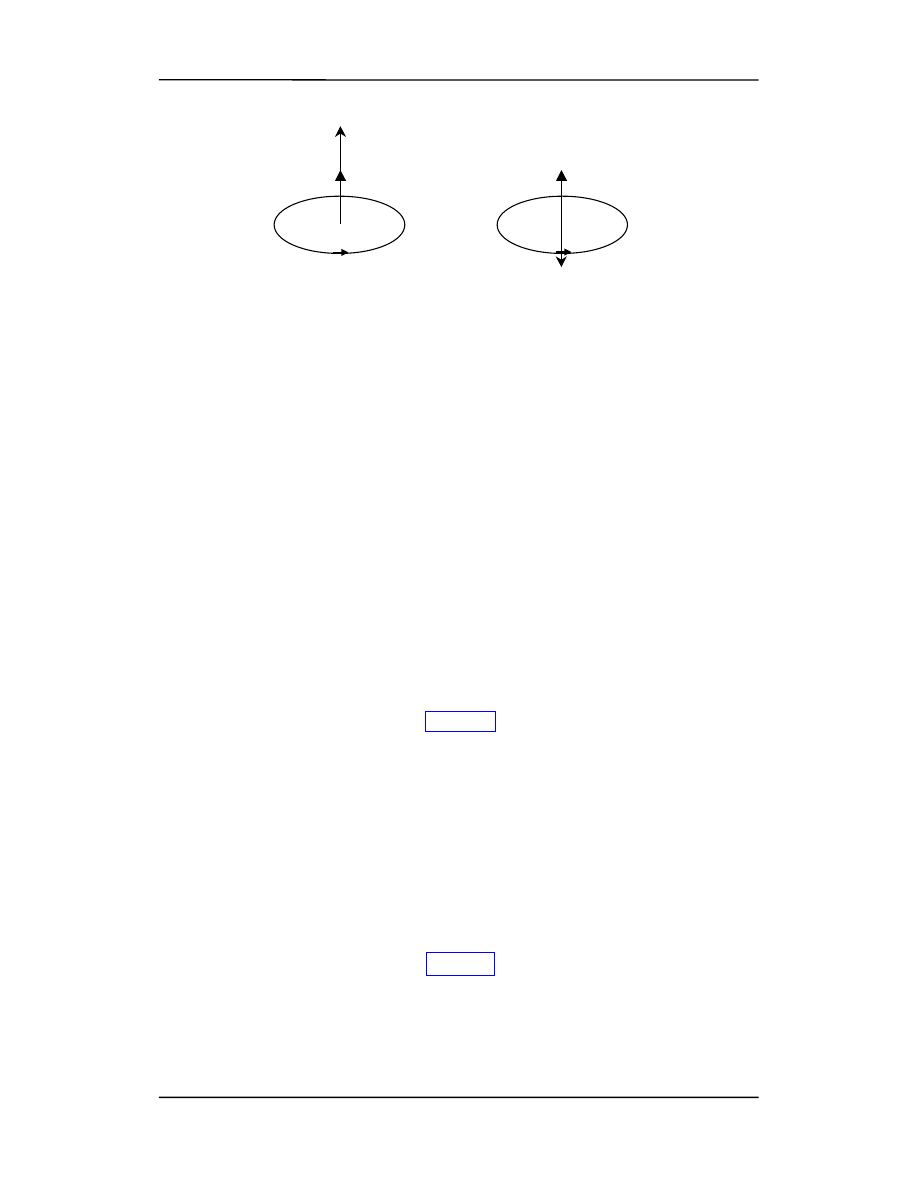
Kierunek i zwrot wektorów prędkości kątowej 

ω i przyspieszenia kątowego α

 

w ruchu 

obrotowym są pokazane na rysunku poniżej. 

12.3 

Dynamika ruchu obrotowego 

12.3.1  Moment siły 

W  ruchu  postępowym  siłę  wiążemy  z  liniowym  przyspieszeniem  ciała.  Jaką  wiel-

kość będziemy wiązać z przyspieszeniem kątowym? 
Nie  może  być  to  tylko  siła  bo  jak  pokazuje  doświadczenie  np.  z  otwieraniem  drzwi 
przyspieszenie  kątowe  zależy  od  tego  gdzie  i  pod  jakim  kątem  jest  przyłożona siła. W 
szczególności siła przyłożona w miejscu zawiasów zarówno wzdłuż jak i prostopadle do 
nich  nie  wytwarza  żadnego  przyspieszenia.  Natomiast  siła  przyłożona  do  drzwi  na  ich 
zewnętrznej krawędzi i pod kątem prostym nadaje im maksymalne przyspieszenie. 
Dla ruchu obrotowego odpowiednikiem siły w ruchu postępowym jest 

moment siły

 (tzw. 

moment obrotowy) 

τ. 

Jeżeli siła F działa na cząstkę to moment siły jest definiowany jako 
 
 

F

r

τ

×

=

 

(12.3) 

 
gdzie wektor r reprezentuje położenie cząstki względem wybranego inercjalnego układu 
odniesienia. Moment siły jest wielkością wektorową, której wartość bezwzględna wyno-
si: 

τ = rFsinθ  (iloczyn  wektorowy).  Wielkość  r  nazywamy  ramieniem  siły  (widać,  że 

bierzemy albo r

⊥

 albo F

⊥

). 

12.3.2  Moment pędu 

Zdefiniujmy teraz wielkość, która w ruchu obrotowym odgrywa rolę analogiczną do 

pędu. Wielkość L będziemy nazywać 

momentem pędu

 i definiujemy ją 

 
 

p

r

L

×

=

 

(12.4) 

 
gdzie p jest pędem cząstki, a r reprezentuje położenie cząstki względem wybranego in-
ercjalnego układu odniesienia. Wartość L wynosi rpsin

θ i analogicznie do momentu siły 

wielkość rsin

θ nazywamy ramieniem pędu. 

ω

α

ω

α

ruch przyspieszony

ruch opóźniony

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-3 

Istnieje bezpośrednia zależność pomiędzy momentem siły i momentem pędu. Zacznijmy 
od  znanej  zależności,  że  siła  F  =  dp/dt  (dla  pojedynczej  cząstki).  Mnożąc  wektorowo 
obie strony przez r otrzymujemy 
 

t

d

d p

r

F

r

×

=

×

 

 

F

r

×

jest momentem siły 

τ więc 

 

 

t

d

d p

r

τ

×

=

 

(12.5) 

 
Teraz  przechodzimy  do  równania  na  moment  pędu  L  =  r

×

p  i  różniczkujemy  je  obu-

stronnie względem czasu, otrzymując 
 

t

t

t

t

d

d

d

d

d

)

d(

d

d

p

r

p

r

p

r

L

×

+

×

=

×

=

 

 
ponieważ dr/dt = 

v więc 

 

t

m

t

d

d

)

(

d

d

p

r

L

×

+

×

=

v

v

 

 
Wiemy, że 

v

v

m

×

 = 0 (z definicji iloczynu wektorowego), więc 

 

 

t

t

d

d

d

d

p

r

L

×

=

 

(12.6) 

 
Porównanie równań (12.5) i (12.6) prowadzi do wniosku, że 
 

 

t

d

d L

τ

=

 

(12.7) 

 
Widzimy, że wypadkowy moment siły działający na cząstkę jest równy prędkości zmian 
momentu pędu tej cząstki. 

12.3.3  Zachowanie momentu pędu 

Dla układu n cząstek możemy zsumować równanie (12.7) po wszystkich cząstkach 

 

 

t

t

wypadkowy

i

i

i

i

d

d

d

d

L

L

τ

=













=

∑

∑

 

(12.8) 

 
Zauważmy,  że  jeżeli  na  układ  nie  działa  zewnętrzny  moment  siły  (lub  suma  =  0)  to 
moment pędu układu pozostaje stały. 
 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-4 

.

const

0

d

d

=

⇒

=

wypadkowy

wypadkowy

t

L

L

 

 

Przykład 1 

Osoba stoi na stoliku obrotowym i w obu rękach trzyma hantle, mając rozłożone ra-

miona. Popychamy ją, tak aby obracała się z częstotliwością f

1

 = 0.5 obrotów na sekun-

dę. Wtedy osoba zgina ramiona, przyciągając hantle do tułowia. Jaka jest częstotliwość 
jej obrotów? Załóżmy, że hantle początkowo znajdujące się 80 cm od osi obrotu, zostają 
ściągnięte do odległości 10 cm od osi. Masa hantli jest taka, że obracająca się osoba ma 
taki sam moment pędu jak hantle w odległości 80 cm od osi obrotu. 
Początkowo moment pędu hantli wynosi 
 

L

h1

 = R

1

mv

1

 = R

1

m(

ω

1

R

1

) = m

ω

1

(R

1

)

2

 

 
gdzie m jest masą pary hantli. Moment pędu układu osoba-hantle wynosi więc 
 

L

1

 = L

o1

 + m

ω

1

(R

1

)

2

 

 
Ponieważ L

o1

 = L

h1

 więc L

o1

 = m

ω

1

(R

1

)

2

. 

Dla hantli w odległości R

2

 moment pędu układu wynosi 

 

L

2

 = L

o2

 + m

ω

2

(R

2

)

2

 

 
Stosując zasadę zachowania pędu otrzymujemy 
 

L

1

 = L

2

 

czyli: 

L

o1

 + m

ω

1

(R

1

)

2

 = L

o2

 + m

ω

2

(R

2

)

2

 

 
Pamiętając, że L

o2

 = L

o1

ω

2

/

ω

1

 ponieważ L 

∼

 

ω rozwiązujemy to równanie względem ω

2

  

 

2

2

2

1

2

1

1

2

2

R

R

R

+

=

ω

ω

 

 

ω

2

 = 1.97 

ω

1

 

 
Prędkość obrotów rośnie dwukrotnie. 

 

Przykład 2 

 

Rower  jedzie  ze  stałą  prędkością  gdy  siła 

działająca  pomiędzy  nawierzchnią  i  kołem  F

2

  =  4 

N.  Z jaką  siłą  F

1

  łańcuch  musi  ciągnąć zębatkę je-

żeli stosunek R

2

/R

1

 = 10? 

Ponieważ prędkość kątowa jest stała więc dL/dt = 0 
i co za tym idzie 

R

1

R

2

F

1

F

2

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-5 

τ

wypadkowy

 = (

τ

1

 - 

τ

2

) = 0 

czyli 

τ

1

 = 

τ

2

 

Stąd 

R

1

F

1

 = R

2

F

2

 

więc 

F

1

 = (R

2

/R

1

)F

2

 = 40N 

 

12.4 

Ciała sztywne i moment bezwładności 

Większość  mas  w  przyrodzie  to  nie  cząstki  tylko  rozciągłe  ciała  stałe,  które  mogą 

wykonywać  zarówno  ruch  postępowy  jak  i  obrotowy.  Przez  ciała  stałe,  sztywne,  rozu-
miemy ciała, w których odległość między dwoma wybranymi elementami pozostaje sta-
ła. 
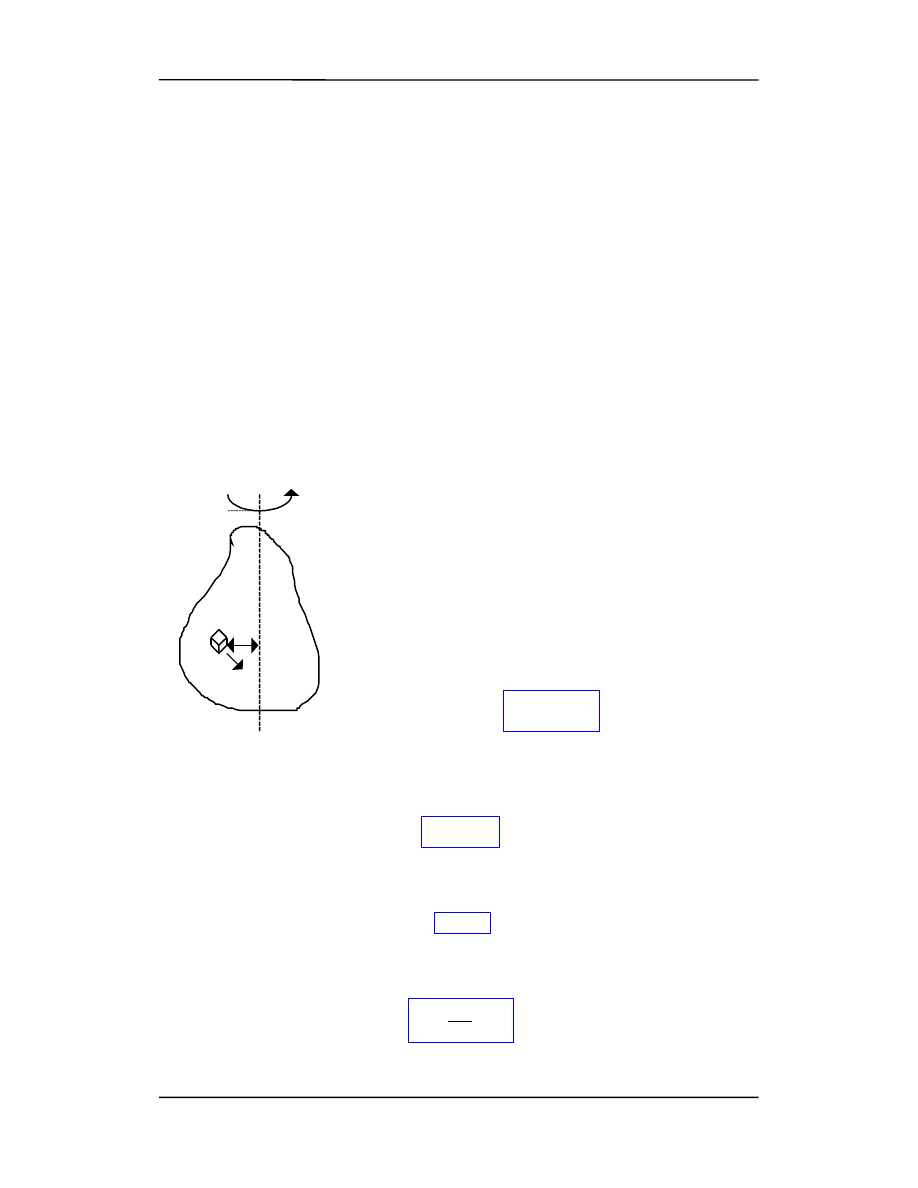
Przeanalizujmy  ruch  takiej  bryły  obracającej  się  ze  stałą  prędkością  kątowa 

ω  wokół 

stałej osi w układzie środka masy (rysunek). Zauważmy, że różne części ciała mają róż-
ną prędkość liniową v chociaż tą samą kątową 

ω. Dla potrzeb opisu ciało możemy po-

dzielić  na  elementy  o  masie 

∆

m

i

  odległe  od  osi  obrotu  o  r

i

. 

Wtedy  prędkość  takiego  elementu  wynosi v

i

  =  r

i

ω. Wartość 

momentu pędu L tego ciała można obliczyć 
 

ω

ω













∆

=

∆

=

∆

=

∑

∑

∑

i

i

i

i

i

i

i

i

i

i

i

m

r

r

m

r

m

r

L

2

)

(

v

 

 
Wielkość  w  nawiasie  nazywamy 

momentem  bezwładności

  I, 

który definiujemy jako 
 

∑

∆

=

i

m

r

I

i

i

2

 

 

 
a dla ciągłego rozkładu masy mamy 
 

 

∫

=

m

r

I

d

2

 

(12.9) 

 
Zwróćmy uwagę, że I zależy od osi obrotu. Możemy teraz zapisać moment pędu 
 
 

 L = I

ω  

(12.10) 

 
a ponieważ 

τ = dL/dt więc 

 

 

α

ω

τ

I

t

I

=

=

d

d

 

(12.11) 

 
 

∆

m

i

r

i

v

i

ω

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-6 

Energia kinetyczna w układzie środka masy 
 

2

2

2

2

2

1

)

(

2

1

2

1

ω

ω

∑

∑

∑













∆

=

∆

=

∆

=

i

i

i

i

i

i

i

i

i

k

r

m

r

m

m

E

v

 

więc 

 

2

2

1 ω

I

E

k

=

 

(12.12) 

 
Zestawmy teraz obliczone wielkości z ich odpowiednikami dla ruchu postępowego. 
 

Ruch postępowy 

Ruch obrotowy 

p = mv 
F = ma 
E

k

 = (1/2) mv

2

 

L= I

ω  

τ = Iα  
E

k

 = (1/2)I

ω

2

 

 

Teraz  widzimy,  że  moment  bezwładności  I  jest  analogiczną  wielkością  do  masy  m  w 
ruchu  postępowym.  Chociaż  masa  ciała  nie  zależy  od  jego  położenia  to  moment  bez-
władności zależy od osi, wokół której obraca się ciało. Momenty bezwładności niektó-
rych ciał są podane w tabeli. 
 

Ciało 

I 

Obręcz, pierścień względem osi 

⊥

 przez środek 

Krążek, walec względem osi 

⊥

 przez środek 

Pręt wokół osi 

⊥

 przez środek 

Pręt wokół osi 

⊥

 przez koniec 

Pełna kula wokół osi przez środek 
Czasza kulista wokół osi przez środek 

mR

2

 

mR

2

/2 

ml

2

/12 

ml

2

/3 

2mR

2

/5 

2mR

2

/3 

 

Często  do  obliczania  momentu  bezwładności  wygodnie  jest  posłużyć  się  twierdze-

niem Steinera. Podaje ono zależność pomiędzy momentem bezwładności I ciała wzglę-
dem danej osi, a momentem bezwładności I

śr.m.

 tego ciała względem osi przechodzącej 

przez jego środek masy i równoległej do danej. 
 
 

 I = I

śr.m.

 + md

2

  

(12.13) 

 
gdzie m jest masą ciała, a d odległością pomiędzy osiami. 

12.5 

Ruch postępowo-obrotowy ciała sztywnego 

Rozpatrywaliśmy  ruch  obrotowy  ciała  względem  osi  nieruchomych.  Jednakże  gdy 

ciało się toczy to wykonuje zarówno ruch postępowy, jak i obrotowy. Dlatego też tocze-
nie możemy traktować jako złożenie ruchu postępowego i obrotowego tak jak pokazano 
to na rysunku poniżej dla toczącego się walca. 

W ruchu postępowym, rysunek (a), wszystkie punkty poruszają się z takimi samymi 

prędkościami,  natomiast  w  ruchu  obrotowym,  rysunek  (b),  przeciwległe  punkty  po-

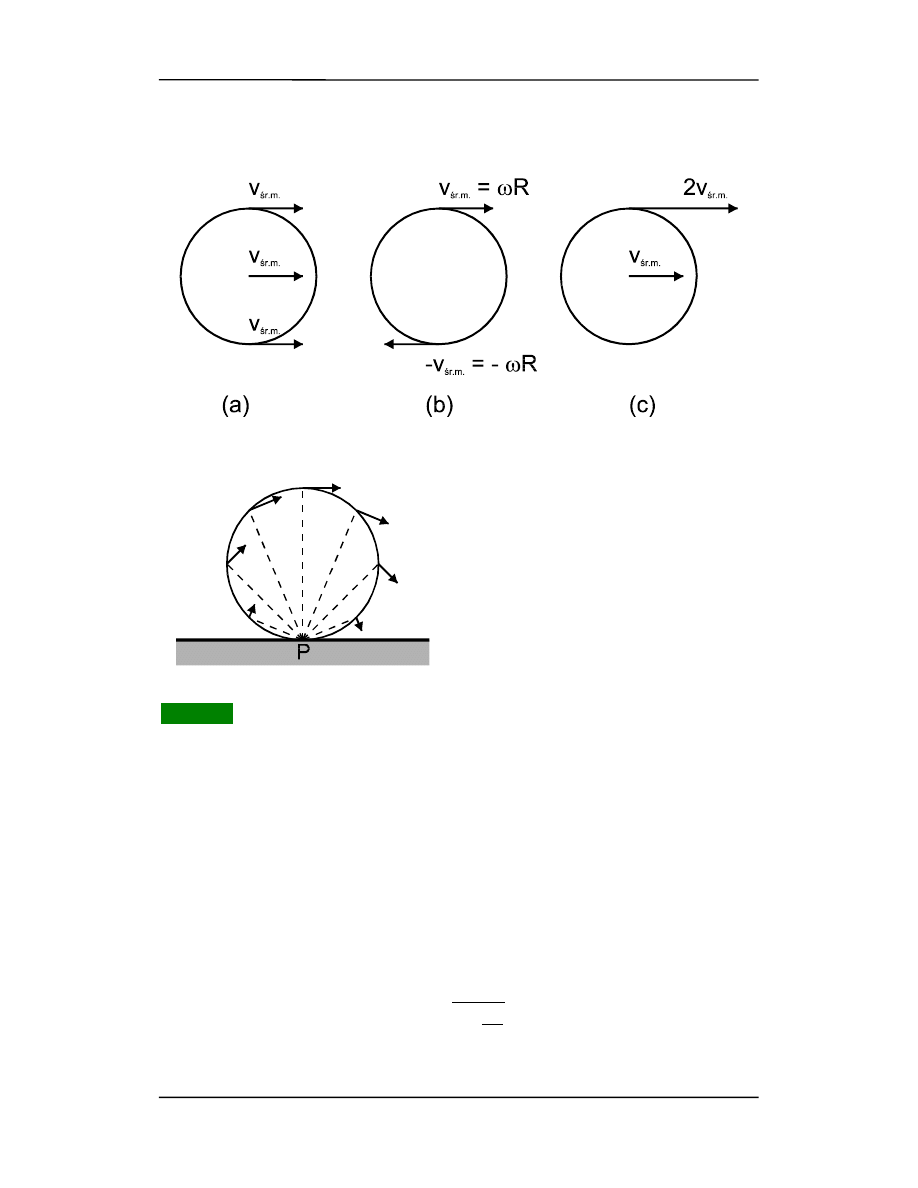
Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-7 

ruszają  się z przeciwnymi prędkościami, a środek jest nieruchomy. Na rysunku (c) po-
kazano wynik złożenia (sumowania) odpowiednich wektorów z rysunków (a) i (b). 

Zwróćmy uwagę, że podstawa walca (punkt P styczności z podłożem na rysunku obok) 

w każdej chwili spoczywa (v = 0). Natomiast 
prędkość liniowa każdego innego punktu jest 
w  każdej  chwili  prostopadła  do  linii  łączącej 
ten  punkt  z  podstawą  P  i  proporcjonalna  do 
odległości  tego  punktu  od  P.  Oznacza  to,  że 
walec 

obraca się wokół punktu P

. Oznacza to, 

że  możemy  toczenie  opisywać  również  jako 
"czysty"  ruch  obrotowy  ale  względem  osi 
przechodzącej  przez  punkt  P  styczności 
z powierzchnią, po której toczy się ciało. 
 

Przykład 3 

Krążek i kula o masach m i promieniach R staczają się po równi pochyłej o wysokości h 
Obliczyć ich prędkości u dołu równi. 
Z zasady zachowania energii 
 

mgh = (1/2)mv

2

 + (1/2)I

ω

2

 

 
Ponieważ 

ω = v/R więc 

 

mgh = (1/2)mv

2

 + (1/2)I(v/R)

2

 

 
Przekształcając 
 

2

2

2

R

I

m

mgh

+

=

v

 

Dla krążka I = mR

2

/2 więc 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-8 

gh

3

4

=

v

 

 
podczas gdy dla kuli I = 2mR

2

/5 więc 

gh

7

10

=

v

 

 
Zauważmy,  że  odpowiedź  nie  zależy  od  masy  i  promienia  ale 

zależy  tylko  od  kształtu

. 

Gdyby te ciała zsuwały się to 

gh

2

=

v

 dla obu brył. 

Ten sam przykład możemy rozwiązać traktując toczenie wyłącznie jako ruch obrotowy 
ale wtedy musimy skorzystać z twierdzenia Steinera, żeby obliczyć moment bezwładno-
ści względem osi przechodzącej przez punkt styczności z powierzchnią. 

12.6 

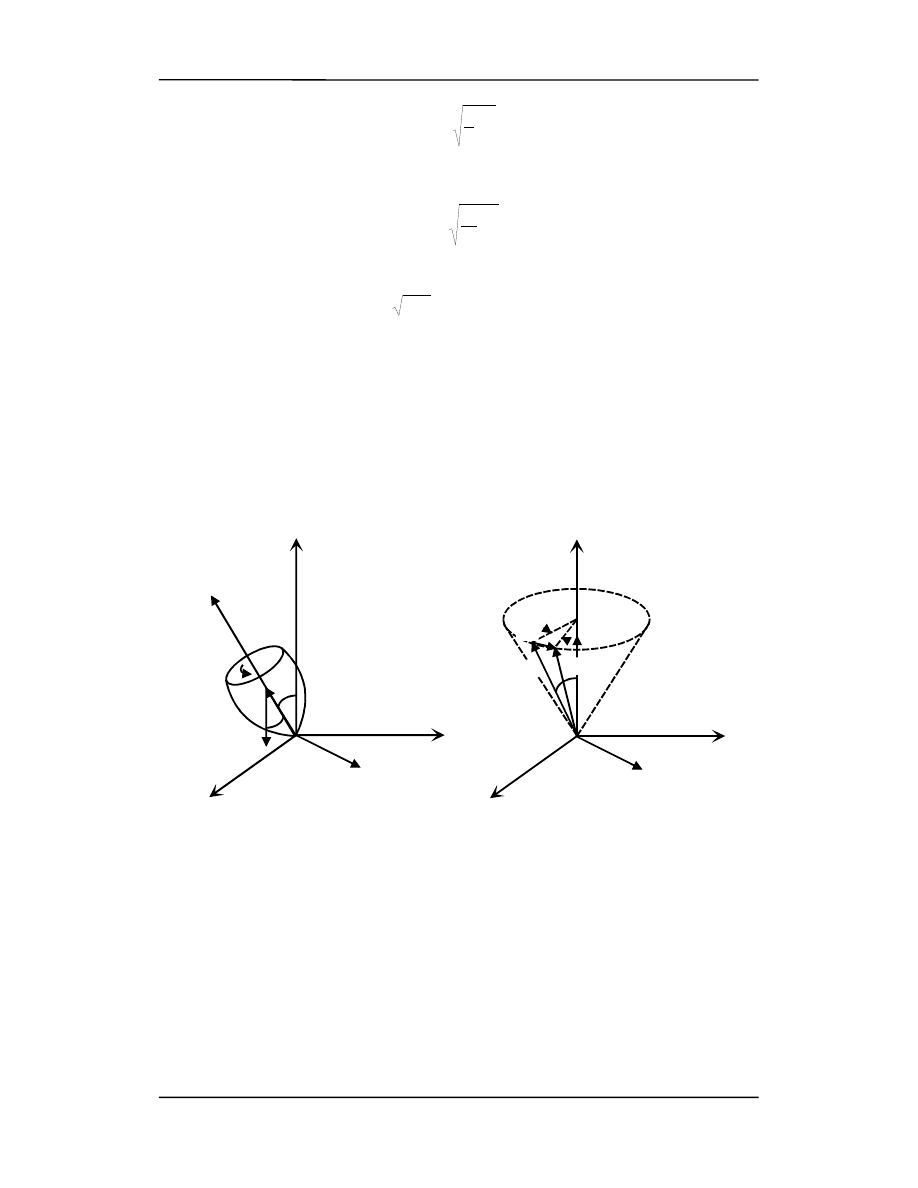
Ruch precesyjny (bąk) 

Inny przykładem ruchu obrotowego, w którym oś obrotu nie jest nieruchomą w iner-

cjalnym układzie odniesienia jest bąk wirujący dookoła pewnej osi symetrii. Punkt pod-
parcia  bąka  znajduje  się  w  początku  inercjalnego  układu  odniesienia. Z doświadczenia 
wiemy, że oś wirującego bąka porusza się dookoła osi pionowej, zakreślając powierzch-

nię stożka. Taki ruch nazywamy 

precesją

. 

W  sytuacji  przedstawionej  na  rysunku  poniżej  bąk  ma  prędkość  kątową 

ω 

dookoła 

swej osi

. Ma również moment pędu L względem tej osi, która tworzy kąt 

θ z osią pio-

nową. 
Na bąk działają dwie siły: siła w punkcie podparcia działa w górę i siła ciężkości przy-
łożona do środka masy działa w dół. Siła reakcji działająca w górę ma zerowy moment 
bo  ma  zerowe  ramię  (względem  punktu  podparcia).  Ciężar  mg  wytwarza  jednak  mo-
ment siły względem punktu podparcia: 
 

τ = r

×

F = r

×

mg 

L

mg

r

θ

θ

τ

x

y

z

y

z

x

τ

L+

∆

L

L

∆

L

∆ϕ

ω

p

θ

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

12-9 

gdzie r określa położenie środka masy. Z iloczynu wektorowego wynika, że 

τ jest pro-

stopadłe do r i do mg.  
Zauważmy, że 

τ, L i r wirują dokoła osi pionowej z częstością precesji ω

p

. 

Obliczymy teraz kątową precesję 

ω

p

. 

 

t

p

∆

∆

=

ϕ

ω

 

 
Ponieważ 

∆

L << L, to mamy  

 

∆

ϕ 

≅

 

∆

L/Lsin

θ 

 
Z równania (12.5) wynika, że 

∆

L = 

τ

∆

t 

więc 

∆

ϕ 

≅

 

τ

∆

t/Lsin

θ 

Otrzymujemy więc 
 
 

 

ω

p

 = 

∆

ϕ/

∆

t = 

τ/Lsinθ  

(12.14) 

 
Moment siły jest równy 
 

τ = rmg sin(180°-θ) = rmg sinθ 

 
więc ostatecznie 
 
 

 

ω

p

 = rmg/L  

(12.15) 

 
Zwróćmy uwagę, że 

prędkość precesji nie zależy od kąta 

θ

 i jest odwrotnie proporcjo-

nalna do wartości momentu pędu. 
Równanie  (12.14)  można  zapisać  w  postaci  wektorowej.  Najpierw  przepisujemy  je  do 
postaci 
 

τ = ω

p

L sin

θ 

 
Widać,  że  po  prawej  stronie  równania  otrzymaliśmy  wartość  iloczynu  wektorowego 
ω

p

×

L. Tak  więc  ostatecznie  wyrażenie  wiążące  prędkość kątową precesji z momentem 

siły i momentem pędu ma postać 
 
 

L

ω

τ

×

=

p

 

(12.16) 

 
Zjawisko  precesji  momentu  magnetycznego  (spinu)  jest  podstawą  różnych  technik  do-
świadczalnych (NMR, EPR), które znalazły szerokie zastosowanie w badaniach, techni-
ce i medycynie.