1

Funkcja wymierna. Ułamki proste

Definicja

Funkcję wymierną

P (x)

Q(x)

, gdzie funkcje

P (x)

i

Q(x)

są wielomianami, nazywamy:

• ułamkiem właściwym, jeżeli

st.P (x) < st.Q(x)

,

• ułamkiem niewłaściwym, jeżeli

st.P (x) > st.Q(x)

.

Definicja

(Ułamków prostych)

• Funkcję wymierną postaci:

A

(ax + b)

n

,

gdzie

A, a, b

są stałymi rzeczywistymi a

n = 1, 2, . . .

, nazywamy

ułamkiem prostym pierwszego rodzaju.

2

• Funkcję wymierną postaci:

Ax + B

(ax

2

+ bx + c)

n

,

gdzie

A, B, a, b, c

są stałymi rzeczywistymi,

n = 1, 2, . . .

a

ax

2

+ bx + c

jest trójmianem nierozkładalnym

(∆ < 0)

,

nazywamy ułamkiem prostym drugiego rodzaju.

Twierdzenie Każdą funkcję wymierną będącą ułamkiem właściwym

można przedstawić w postaci skończonej sumy ułamków prostych

pierwszego lub drugiego rodzaju.

3

Przykład Rozłóż funkcję wymierną na ułamki proste, nie obliczając

odpowiednich stałych:

•

f (x) =

1

x

3

(x − 4)

•

f (x) =

2x − 5

(x + 4)

2

(x − 2) (x

2

+ 1)

•

f (x) =

3x

2

+ 2

x (3x + 2)

2

(x

2

+ 8) (x

2

+ x + 1)

2

4

Całkowanie ułamków prostych

• Ułamek prosty pierwszego rodzaju -

n = 1

Z

1

ax + b

dx =

1

a

ln | ax + b | + C

• Ułamek prosty pierwszego rodzaju -

n = 2, 3, . . .

Z

1

(ax + b)

n

dx =

1

a

(ax + b)

−n+1

−n + 1

+ C

5

• Ułamek prosty drugiego rodzaju -

n = 1

i

A = 0

Z

1

ax

2

+ bx + c

dx

Trójmian kwadratowy sprowadzamy do postaci kanonicznej a na-

stępnie, stosując odpowiednie podstawienie, całkę powyższą sprowa-

dzamy do całki

Z

1

1 + t

2

dt

Przykład

Z

1

x

2

− 2x + 5

dx

6

• Ułamek prosty drugiego rodzaju -

n = 1

i

A 6= 0

Z

Ax + B

ax

2

+ bx + c

dx

Całkę taką zapisujemy jako sumę, z odpowiednimi stałymi, całek

Z

2ax + b

ax

2

+ bx + c

dx

i

Z

1

ax

2

+ bx + c

dx

a następnie znanymi już metodami obliczmy je.

Przykład

Z

3x + 6

x

2

− 6x + 18

dx

7

Całkowanie funcji wymiernych

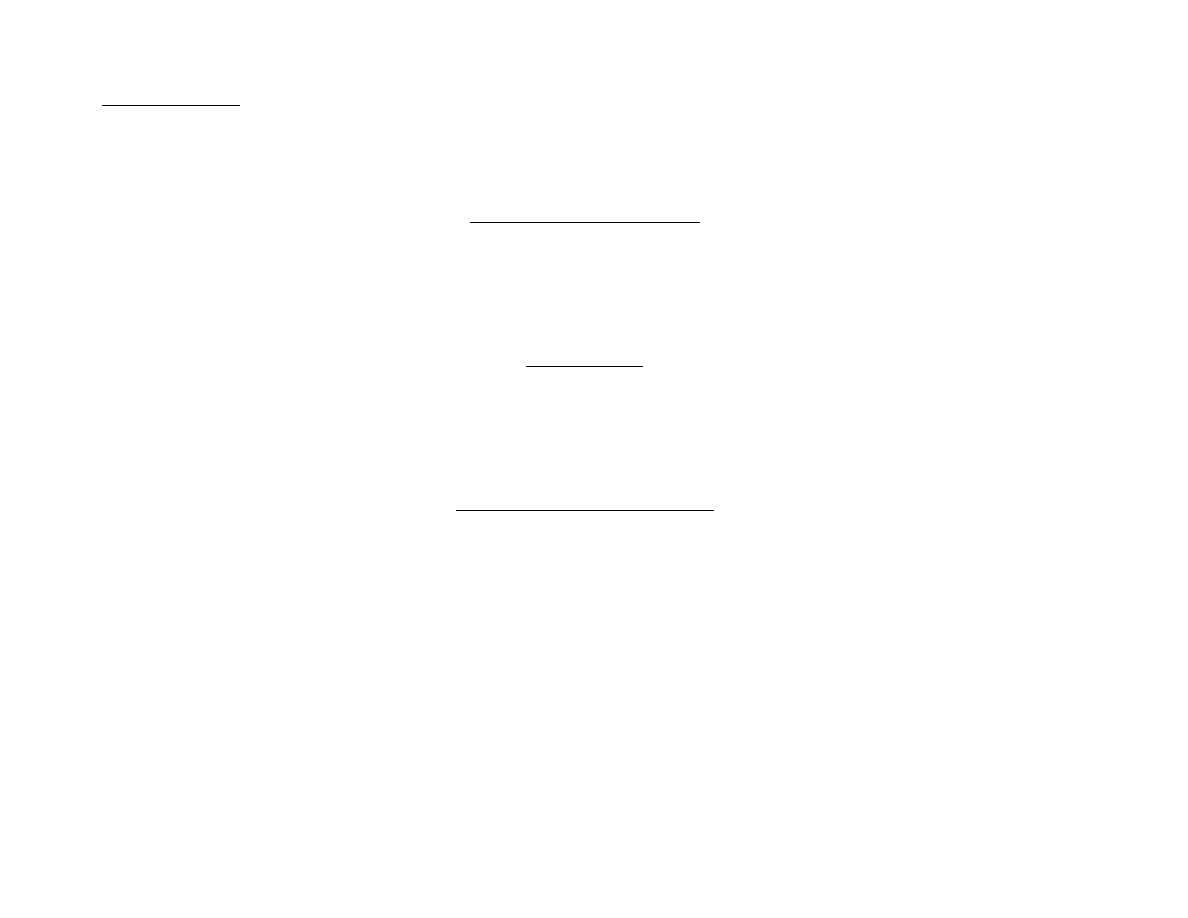
8

Przykład

Z

3x

2

− 13x + 18

x

3

− 6x

2

+ 9x

dx

Z

2x + 4

x

3

+ 4x

dx

Z

x

3

+ 2x

2

− x + 1

x

2

− 1

dx

9

Całkowanie funcji niewymiernych

Z

R










x ,

n

v
u
u
u
u
u
u
t

ax + b

cx + d










dx

ad − bc 6= 0

Podstawienie:

ax + b

cx + d

= t

n

Przykład

Z

x

2

3

3

√

x + 2

dx

10

Uwaga

Jeżeli funkcja podcałkowa jest funkcją wymierną zmiennej

x

i potęg wyrażenia

ax + b

cx + d

o wykładnikach postaci

m

n

, to wykonujemy podstawienie

ax + b

cx + d

= t

N , przy czym

N

jest wspólnym mianownikiem ułam-

ków

m

n

.

Przykład

Z

1

3

√

x +

√

x

dx

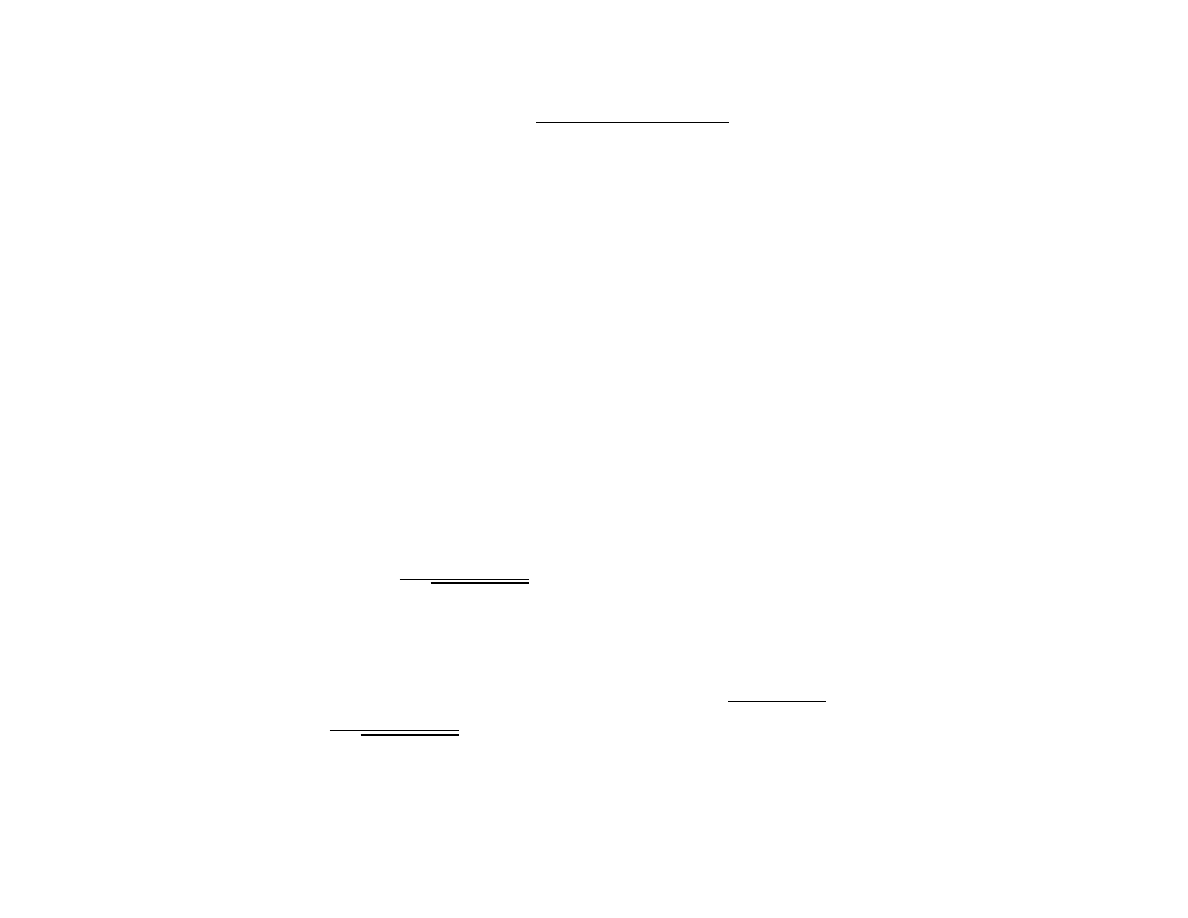
11

Z

R






x ,

s

ax

2

+ bx + c






dx

∆ = b

2

− 4ac 6= 0

• Wykorzystywane wzory:

Z

1

√

1 − x

2

dx = arcsin x + C

Z

1

√

x

2

± 1

dx = ln | x +

s

x

2

± 1 | + C

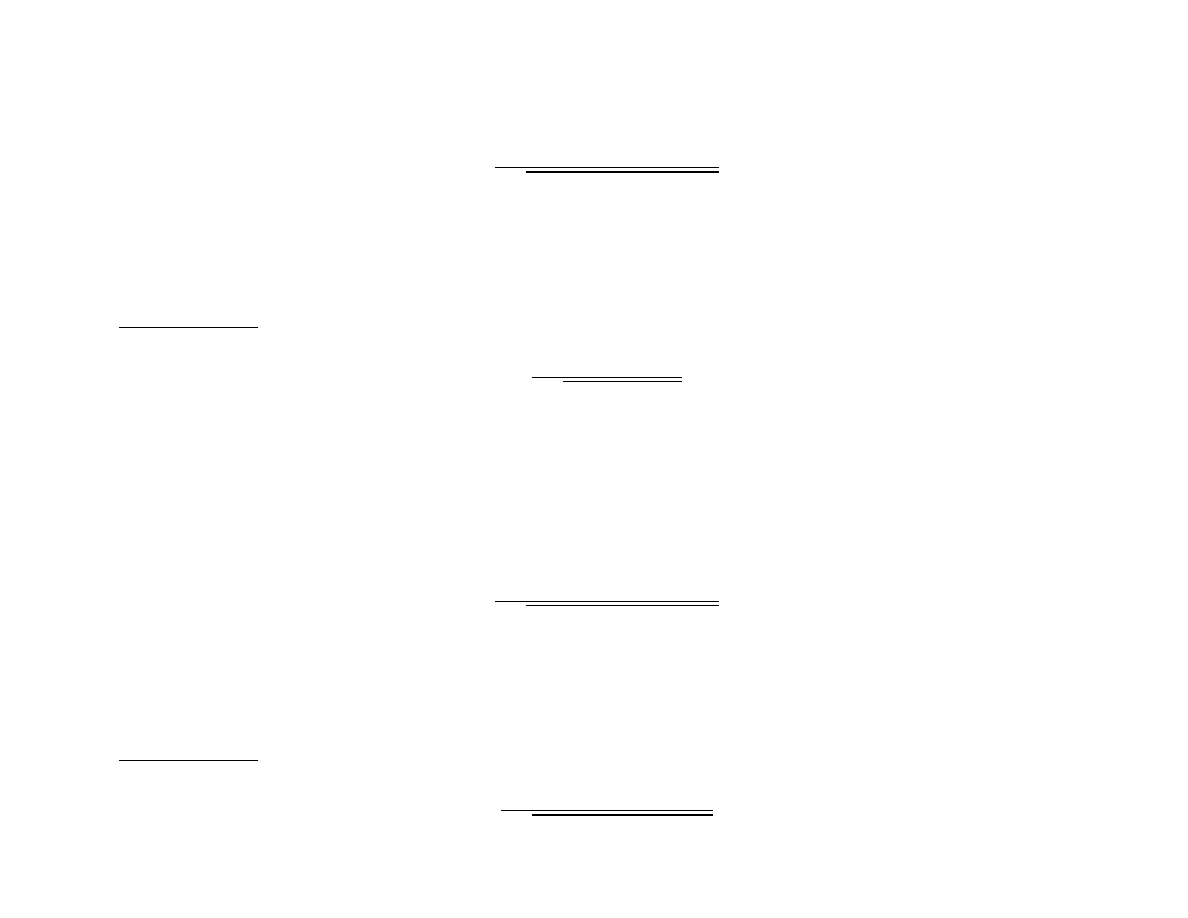
12

• Obliczanie całki postaci:

Z

1

√

ax

2

+ bx + c

dx

Przykład

Z

1

√

x

2

− 4x

dx

• Obliczanie całki postaci:

Z

Ax + B

√

ax

2

+ bx + c

dx

Przykład

Z

4x + 1

√

8 − 2x − x

2

dx

13

Przykład

Z

s

x

2

+ 1 dx

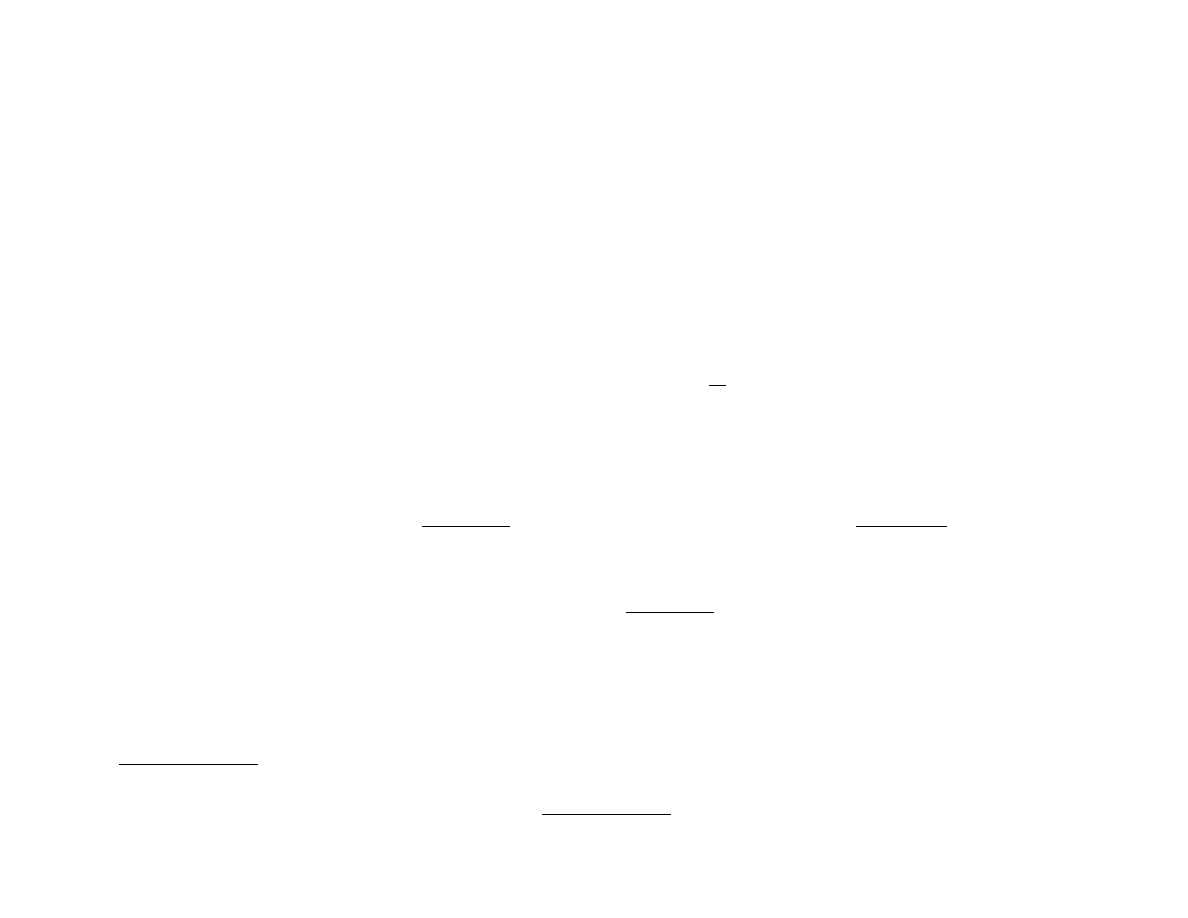
14

Całkowanie funcji trygonometrycznych

Z

R ( sin x , cos x ) dx

• Podstawienie ”uniwersalne”:

t = tg

x

2

sin x =

2t

1 + t

2

cos x =

1 − t

2

1 + t

2

dx =

2 dt

1 + t

2

Przykład

Z

1

1 + sin x

dx

15

• Podstawienie:

t = sin x

(można je skutecznie zastosować,

gdy funkcja wymierna

R(u, v)

jest nieparzysta ze względu na

v = cos x

)

Przykład

Z

cos

5

x dx

• Podstawienie:

t = cos x

(można je skutecznie zastosować,

gdy funkcja wymierna

R(u, v)

jest nieparzysta ze względu na

u = sin x

)

Przykład

Z

1

sin

3

x

dx

16

• Podstawienie:

t = tg x

sin

2

x =

t

2

1 + t

2

sin x cos x =

t

1 + t

2

cos

2

x =

1

1 + t

2

dx =

dt

1 + t

2

(można

je

skutecznie

zastosować,

gdy

funkcja

wymierna

R(sin x, cos x) = R

∗

(sin

2

x, cos

2

x, sin x cos x)

)

Przykład

Z

1

1 + 2 cos

2

x

dx

Z

tg

4

x dx