1
Całka nieoznaczona
Definicja Założmy, że funkcja
f
jest funkcją rzeczywistą określoną
na pewnym przedziale. Każdą funkcję
F
, która spełnia w tym
przedziale warunek
F
0
(x) = f (x),
nazywamy funkcją pierwotną do funkcji
f
.
Przykład
Wyznacz funkcję pierwotną do funkcji
f (x) = cos x.
Ile różnych funkcji pierwotnych do funkcji
f
potrafisz wskazać?
2
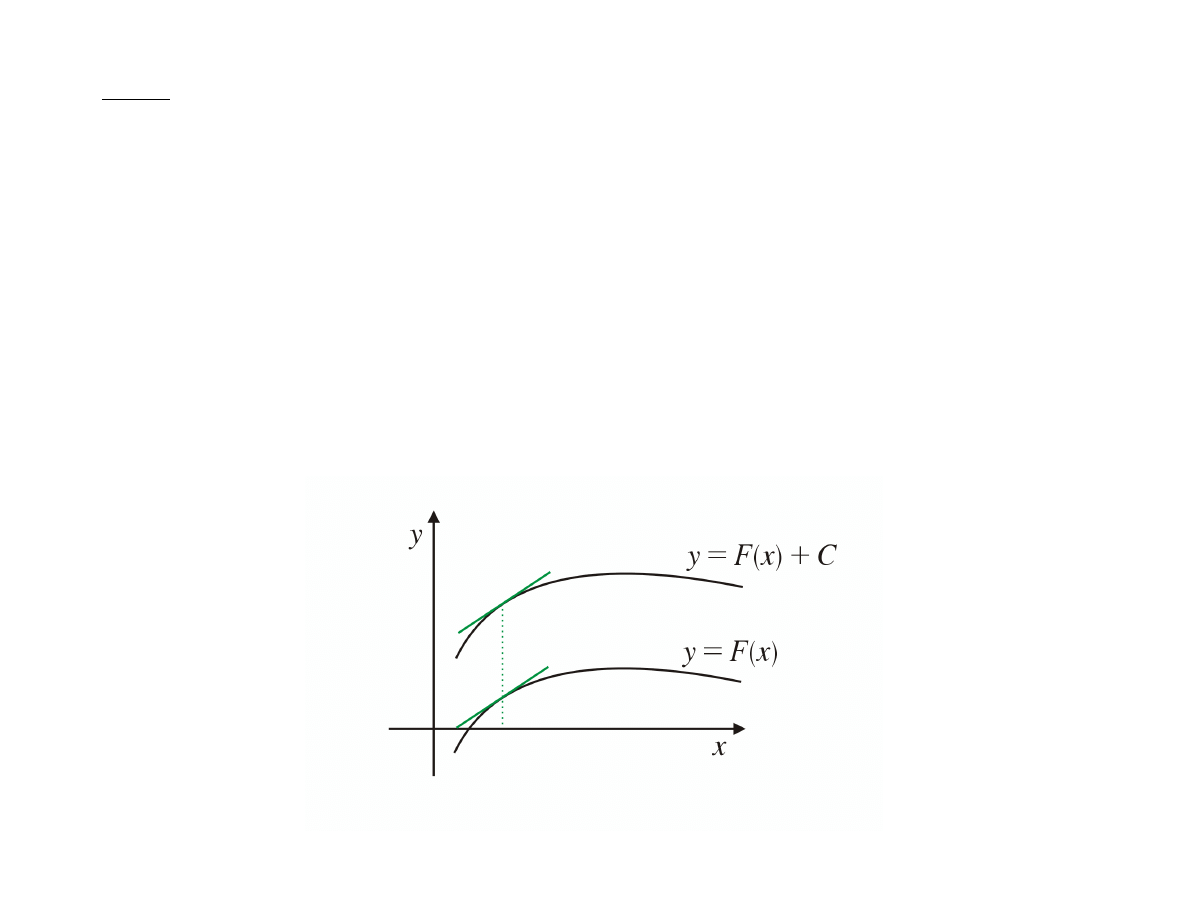
Fakt
• Jeżeli
F
jest funkcją pierwotną funkcji
f
w pewnym przedziale,
to dla dowolnej stałej
C ∈ R
funkcja
F + C
jest funkcją
pierwotną funkcji
f
.
• Zbiór wszystkich funkcji pierwotnych funkcji
f
, określonej w
pewnym przedziale, jest złożony z funkcji
Φ = F + C
, gdzie
C ∈ R
a
F
jest jakąkolwiek funkcją pierwotną funkcji
f
.
3
Definicja
(Całki nieoznaczonej)
Jeżeli
F
jest funkcją pierwotną funkcji
f
w pewnym przedziale, to
zbiór wszystkich funkcji pierotnych nazywamy całką nieoznaczoną
funkcji
f
i oznaczamy symbolem
Z
f (x) dx.
Zatem
Z
f (x) dx = F (x) + C ,
gdzie
C ∈ R
a
F
jest jakąkolwiek funkcją pierwotną funkcji
f
.
Funkcję
f
nazywamy funkcją podcałkową, a
f (x) dx
wyrażeniem
podcałkowym.
Twierdzenie
Każda funkcja ciągła w pewnym przedziałe jest
całkowalna w tym przedziale (istnieje całka nieoznaczona tej funkcji).
4
Własności Całki nieoznaczonej
Załóżmy, że funkcje
f
i
g
są ciągłe w pewnym przedziale.
Wówczas
•
Z
f (x) dx
0
= f (x) ,
•
Z
f
0
(x) dx = f (x) + C ,
•
Z
a · f (x) dx = a ·
Z
f (x) dx ,
a ∈ R,
•
Z
f (x) + g(x)
!
dx =
Z
f (x) dx +
Z
g(x) dx.
5
Całki nieoznaczone podstawowych funkcji elementarnych
Z
0 dx = C
Z
a dx = ax + C
Z
x
α
dx =
x
α+1
α + 1
+ C
α 6= −1
Z
1
x
dx = ln |x| + C
Z
e
x
dx = e
x
+ C
Z
a
x
dx =
a
x
ln a
+ C
6
Z
sin x dx = − cos x + C
Z
cos x dx = sin x + C
Z
1
cos
2
x
dx = tg x + C
Z
1
sin
2
x
dx = −ctg x + C
Z
1
1 + x
2
dx = arctg x + C
Z
1
√
1 − x
2
dx = arcsin x + C
7
Przykłady
Z
−3x
4
+ 2x
3
− 5x
2
+ 1
x
3
dx
Z
(2x
2
− 3)
√
x dx
Z
( 5 cos x + 3 sin x) dx
Z
ctg
2
x dx
Z
3e
x
−
4
1 + x
2
−
1
√
1 − x
2
dx
8
Całkowanie przez podstawianie
Twierdzenie
Jeżeli
F
jest funkcją pierwotną funkcji
f
, to
Z
f ( ϕ(x) ) ϕ
0
(x) dx = F ( ϕ(x) ) + C,
gdzie o funkcjach
f, ϕ
i
ϕ
0
zakładamy, że są ciągłe i funkcja
t = ϕ(x)
jest odwracalna.
Zatem dla
t = ϕ(x)
mamy
Z
f ( ϕ(x) ) ϕ
0
(x) dx =
Z
f ( t ) dt = F ( t ) + C = F ( ϕ(x) ) + C.
Przykład
Oblicz całki:
9
a)
Z
sin ax dx
b)
Z
cos ax dx
c)
Z
f
0
(x)
f (x)
dx
d)
Z
tg x dx
e)
Z
x
1 + x
2
dx
f )
Z
(ax + b)
n
dx
g)
Z
sin
2
x dx
h)
Z
1
x ln x
dx
i)
Z
e
cos x
sin x dx
j)
Z
x
3
s
4 − x
4
dx
k)
Z
arcsin x
√
1 − x
2
dx
l)
Z
e
2x
1 + e
4x
dx
10
Całkowanie przez części
Twierdzenie
Załóżmy, że funkcje
f
i
g
są różniczkowalne w
pewnym przedziale. Wówczas
Z
f (x) · g
0
(x) dx = f (x) · g(x) −
Z
f
0
(x) · g(x) dx.
Przykład
Oblicz całki:
a)
Z
x e
−x
dx
b)
Z
x
2
cos 2x dx
c)
Z
ln x dx
d)
Z
arctg x dx
e)
Z
5x + 1
sin
2
x
dx
f )
Z
e
ax
sin bx dx
g)
Z
e
ax
cos bx dx