Sprzężenie zwrotne w układach liniowych i nieliniowych

Postać ogólna układu sterowania wygląda następująco:

(1)

{

̇

, gdzie

Przy zadanym sterowaniu u(t) powyższe równanie daje zależny od czasu układ dynamiczny:

̇ ( ) .

Ważną klasę układów sterowania są tak zwane układy afiniczne:

(2)

{

̇ ∑

Są one ważne ze względu na to, że wiele układów spotykanych w praktyce ma właśnie takie równania
(układy pochodzące z mechaniki Lagrange’owskiej), a także dlatego, że są one przybliżeniem układu
(1).

Składnik f(x) w równaniu (2) nazywamy dryfem, ponieważ opisuje on ruch układu przy zerowych
sterowaniach.

Przyjmując f(x) = Ax, g(x)=B oraz h(x) = Cx otrzymujemy liniowy układ sterowania:

{

̇

Wśród układów sterowanie można wyróżnić układ otwarty, czyli taki, w którym sygnał wejściowy nie
zależy od aktualnej wartości sygnału wyjściowego, ponieważ nie występuje sprzężenie zwrotne, a
wynika jedynie z wewnętrznego stanu obiektu (przebieg sygnału następuje tylko w jednym kierunku,
od wejścia do wyjścia. Innymi słowy w układzie nie ma połączenia między wyjściem a wejściem
układu) oraz układ zamknięty, w którym przebieg sygnału następuje w dwóch kierunkach. Od wejścia
do wyjścia przebiega sygnał realizujący wzajemne oddziaływanie elementów, natomiast od wyjścia
do wejścia przebiega sygnał sprzężenia zwrotnego.

Układ zamknięty z ujemnym sprzężeniem zwrotnym zwany też układem regulacji, jest pewnym dalej
idącym usprawnieniem w porównaniu do sterowania w układzie otwartym lub sterowania w układzie
ze sprzężeniem w przód. W praktyce na układ sterowania (sterowany obiekt i sterownik) oddziałują
zakłócenia zewnętrzne ponadto sam obiekt sterowany wykazuje pewną zmienność (przez co
ewentualny jego opis albo model nie jest zwykle dokładny). Dlatego też aby poprawić skuteczność
sterowania w takich warunkach wprowadza się do układu sprzężenie. Pewną poprawę sterowania
(czasami wystarczającą) daje już sprzężenie w przód ale znacznie lepsze efekty przynosi zastosowanie
sprzężenia zwrotnego (najczęściej jest to sprzężenie zwrotne ujemne).

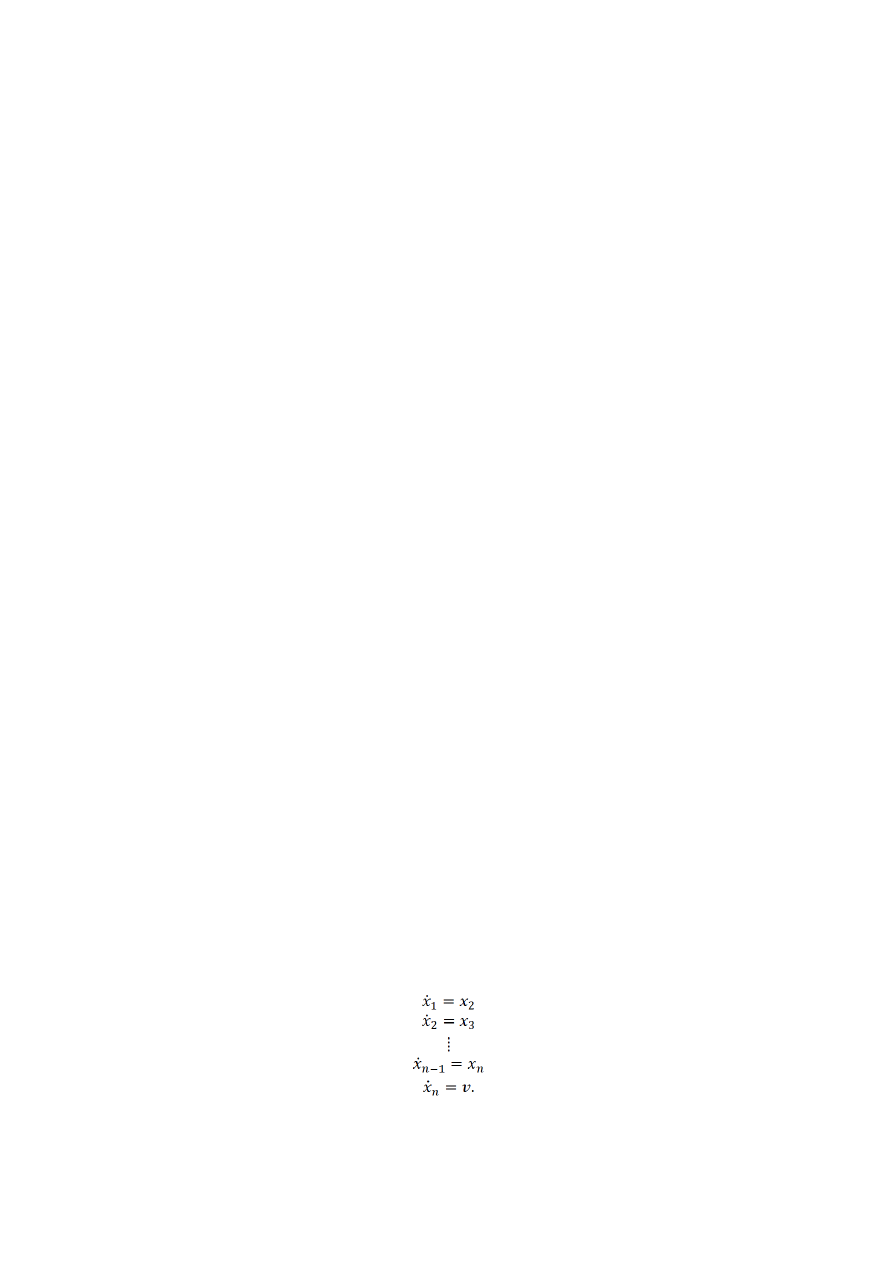
Zamknięta ujemna pętlą sprzężenia zwrotnego, ma właściwości stabilizujące i linearyzujące. Układ
zamknięty, w porównaniu do układu otwartego, jest mniej czuły na zmiany wzmocnienia statycznego
w układzie, powodując zmniejszenie uchybów statycznych (jeśli występują), jednak zbyt duża wartość
współczynnika wzmocnienia, może spowodować niestabilność układów wyższych rzędów. Poprawia
parametry jakościowe odpowiedzi skokowej układu automatyki oraz lepiej sprawdza się w przypadku
tłumienia nieznanych zakłóceń, których pojawienie się powoduje zmianę błędu regulacji, co skutkuje
powstaniem odpowiedniego sygnału sterującego.

Układy sterowania można też podzielić ze względu na inne kryterium na wspomniane już układy
liniowe, które można opisać za pomocą równań liniowych algebraicznych, różniczkowych,
różnicowych lub całkowych (układy liniowe spełniają zasadę superpozycji) oraz na układy nieliniowe,
czyli takie, które zawierają przynajmniej jeden element nieliniowy. W praktyce każdy układ jest
nieliniowy, lecz w przybliżeniu zakłada się jego liniowość lub linearyzuje się jego nieliniową
charakterystykę. Robi się to zwłaszcza gdy działanie procesu ogranicza się do niewielkiego obszaru
wokół pewnego punktu pracy.

Znana jest metoda linearyzacji układu poprzez sprzężenie zwrotne. Układ sterowania



nazywamy

linearyzowalnym przez sprzężenie zwrotne wtedy i tylko wtedy, gdy



jest równoważne poprzez

sprzężenie zwrotne układowi



̇ .





⇔

̇

)

( ( ) ( ) ( ))

̇ ̇ ( )

( ) ( )

Linaeryzowalności poprzez sprzężenie zwrotne dotyczy twierdzenie Jakubczyka-Respondka:

Załóżmy, że f(0)=0 oraz ze układ



̇ jest sterowalny.





⇔

̇

1.

2.

3. [

]

Kolejnym zastosowaniem sprzężenia zwrotnego znajdujemy, gdy chcemy sprowadzić układ do
postaci kanonicznej Brunovsky’ego, czyli postaci kontrolowalności dla liniowych układów
sterowania. Postać ta jest następująca:

Postać ta ma wiele zastosowań. Zastosowanie, które poznaliśmy dotyczy postaci układu przy
linearyzacji i odsprzęganiu wejściowo-wyjściowym.

Równania układów sterowania o dwóch niezależnych sterowaniach mogą być również zapisane w
postaci łańcuchowej:

Istnieją różne algorytmy (np. Sordalena czy Astolfiego), które wymagają podania układu właśnie w
taki sposób. Jedną z metod przekształcania układów do postaci łańcuchowej jest właśnie sprzężenie
zwrotne.