Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 2
W2 - 1
Liniowe zadanie aproksymacji średniokwadratowej
funkcja przybliżana
,
)
x
(
f
siatka węzłów
m
i
(
f
∑
=0
)
x
(
f
f
,
m
,...,
i
,
x
i
i
i
=
= 0
m
,...,
i
dane: punkty węzłowe
(
Instytut Automatyki Politechniki
)
f
,
x
i
i
0
=
m
,...,
i
w
i
0
0
współczynniki wagowe
m
i
∑
=
=
>
n
,...,
i
funkcje
bazowe
(
i
0
=
ϕ
Ł
)
x
funkcja aproksymująca
ódzkiej - Metody Numeryczne wyk
∑
=
=
n
i
i
*
c
)
x
(
f
0
ϕ
i
min
)
x
(
f
(
i
*
−
0
i
)
x
(
w
)
f
i
i
→
2
szukane stałe
c
takie by
ład 2
W2 - 2
Jeżeli
to funkcje
nazywamy
ortogonalnymi.
dla dowolnych funkcji
przy danej siatce
węzłów i wsp. wagowych
i
i
i
w
)
x
(
g
)
x
:
g
,
f
=
Notacja:
),
(
g
),
(
f
⋅
⋅
0
=
g
,
f
),
(
g
),
(
f
⋅
⋅
Jeżeli
dla
j
i
i
to funkcje
układem (rodziną) funkcji
ortogonalnych.
0
=
j
i
f
,
f
≠
0
≠
i
i
f
,
f
,...
,
i
),
(
f
i
2
1
=
⋅
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 2
W2 - 3
Twierdzenie
Jeżeli funkcje bazowe są liniowo niezależne to liniowe
zadanie aproksymacji średniokwadratowej ma jedyne
rozwiązanie. Rozwiązanie to spełnia układ równań
normalnych;
=
n
n
n
n
n
n
n
n
f
f
f
c
c
c
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
,
,
,
,
,
,
,
,
,
,
,
,
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
0
L
M
L
L
L
L
L
L
L
Jeżeli funkcje bazowe są rodziną funkcji ortogonalnych to
rozwiązanie upraszcza się do:
n
,...,
i
,
,
,
f
c
i
i
i
i
0
=
=
ϕ
ϕ
ϕ
Instytut Automatyki Politechniki
i
,
i
0
=
1
1
=
,
m
x
m
,...,
i 0
=
Ł
ład 2
ódzkiej - Metody Numeryczne wyk
1
W2 - 4
n
,...,
x
)
x
(
i
=
ϕ
Przykład
0
0
=
=
m
x
,
...
,
x
,
w
i
1
n
el. max. mac. odwr.
1 0.9
2 12.5
3 375
4 9
874
5 252
828
6
8 771 904
7 3.9133e+008
n
el. max. mac. odwr.
8 1.9908e+010
9 1.4199e+012
10 2.4218e+014
=
, m=10
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 2
W2 - 5
Wielomiany Czebyszewa
,...
,
n
,
x
)
x
cos
arc
n
cos(
)
x
(
T
n
1
0
1
1
=
≤
≤
−
=
,...
,
n
)
x
(
T
)
x
(
xT
)
x
(
T
,
x
)
x
(
T
)
x
(
T
n
n
n
2
1
2
1
1
1
1
0
=
−
=
=
=
−
+
Współczynnik wiodący wielomianu
T
n
)
x
(
T
)
(
)
x
(
T
n
n
n
1
−
=
−
jest równy
2
n-1
dla n=1,2,.
)
x
(
Wielomian
T
n 1
+
ma n+1 zer
)
x
(
,....
,
,
)
n
(
n
,
n
,...,
,
k
0
1
0
=
=
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wyk
(
T
),...,
x
(
T
),
x
(
n
1
0
1
=
i
)
x
(
n 1
+
=
=
≠
=
≠
=
1
2
1
0
n
n
T
,
T
j
i
0
0
j
i
dla
j
i
dla
j
i
dla
)
k
(
cos
x
k
1
1
2
1
2
+
+
=
π
ład 2
W2 - 6
Układ wielomianów
T
jest
ortogonalny względem wag
w
i węzłów
, które są
zerami wielomianu
T
:
+
+
)
x
i
x
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 2
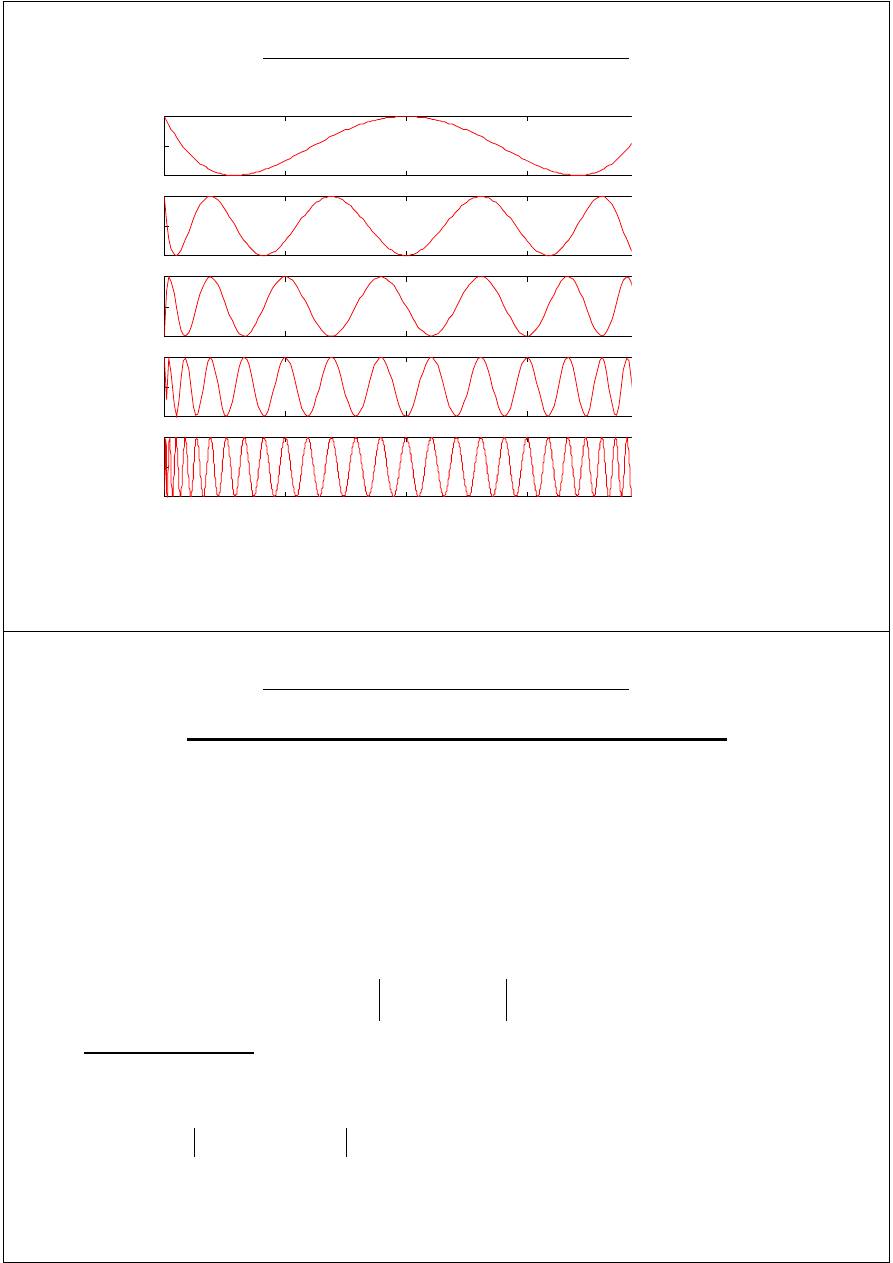
W2 - 7
-1
-0.5
0
0.5
-1
0
1
T4
(x
)
-1
-0.5
0
0.5
-1
0
1
T
10(
x)
-1
-0.5
0
0.5
-1
0
1
-1
-0.5
0
0.5
-1
0
1
T3
0
(x
)
-1
-0.5
0
0.5
-1
0
1
T6
0
(x
)
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 2
W2 - 8
Zadanie wielomianowej aproksymacji jednostajnej
x
i
i
i
i
funkcja przybliżana
,
)
x
m
,...,
0
,
x
i
*
x
(
f
ax
i
(
f
siatka węzłów
)
x
(
f
f
,
i
,
=
=
m
,...,
i
dane: punkty węzłowe
(
funkcja aproksymująca
ma być
wielomianem stopnia co najwyżej n
szukane stałe
a
takie by
m
Tw. Weierstrassa
)
f
i
0
=
∑
=
=
n
i
i
i
x
a
)
0
min
f
)
x
(
f
i
i
*
→
−
Jeżeli funkcja f(x) jest ciągła w skończonym przedziale
[
, to dla
każdego
ε
istnieje wielomian
stopnia n, taki że dla każdego
,
[ ]
b
,
a
x
∈
]
b
,
a
0
>
ε
<
−
)
x
(
P
)
x
(
f
n
)
x
(
P
n