Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
118
53
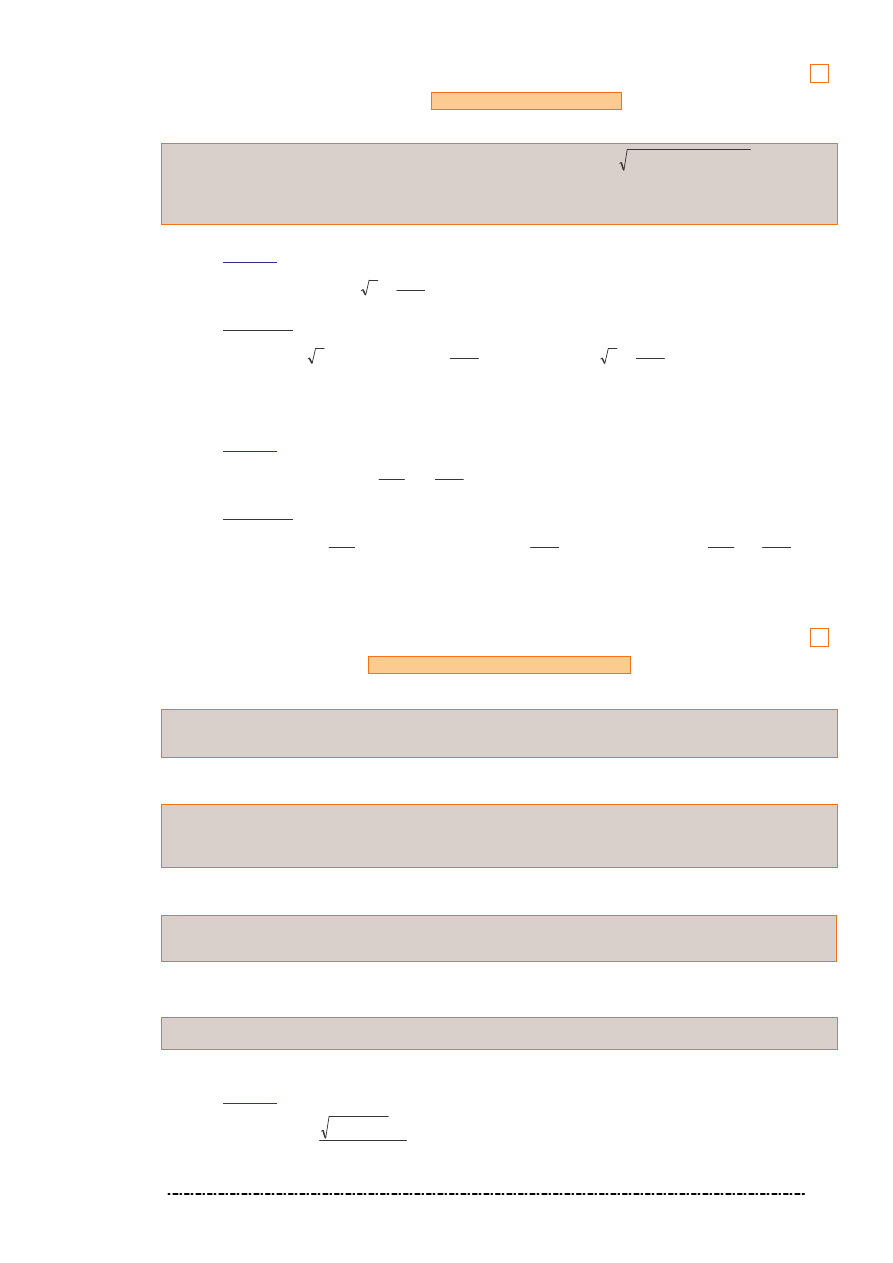
Granica ci gu punktów
Ci g punktów
)
(
n
P ,
)
;
(
n
n
n
y
x
P
=
, jest zbie ny do punktu
)
;
(
0
0
0
y
x
P
=
, gdy
0
)
(
)
(
lim
2
0
2
0
=
−
+
−
∞
→
y
y
x
x
n
n
n
. Zatem
)
,
(
)
,
(
lim
lim
0
0
0
y
x
P
y
x
P
n
n
n
n
n
=
=
=
∞
→
∞
→
⇔ (
0
lim
x
x
n
n
=
∞
→
i
0
lim
y
y
n
n
=
∞
→
)
Zadanie 1.
Obliczy granic ci gu
)
2
1
ln
,
(
)
,
(
+
+
=
n
n
n
y
x
n
n
n
.
Rozwi zanie
Poniewa
1
lim
lim
=
=
∞
→
∞
→
n
n
n
n
n
x
,
0
1
ln
2
1
ln
lim
lim
=
=
+
+
=
∞
→
∞
→
n
n
y
n
n
n
, wi c ci g
)
2
1
ln
,
(
+
+
n
n
n
n
jest zbie ny i jego granic
jest punkt
)
0
,
1
(
.
Zadanie 2.
Obliczy granic ci gu
)
2
cos
,
1
(sin
)
,
(
+
π
+
π
=
n
n
y
x
n
n
.
Rozwi zanie
Poniewa
0
0
sin
1
sin
lim
lim
=
=
+
π
=
∞
→
∞
→
n
x
n
n
n
,
1
0
cos
2
cos
lim
lim
=
=
+
π
=
∞
→
∞
→
n
y
n
n
n
, wi c ci g
)
2
cos
,
1
(sin
+
π
+
π
n
n
jest
zbie ny i jego granic jest punkt
)
1
,
0
(
.
54
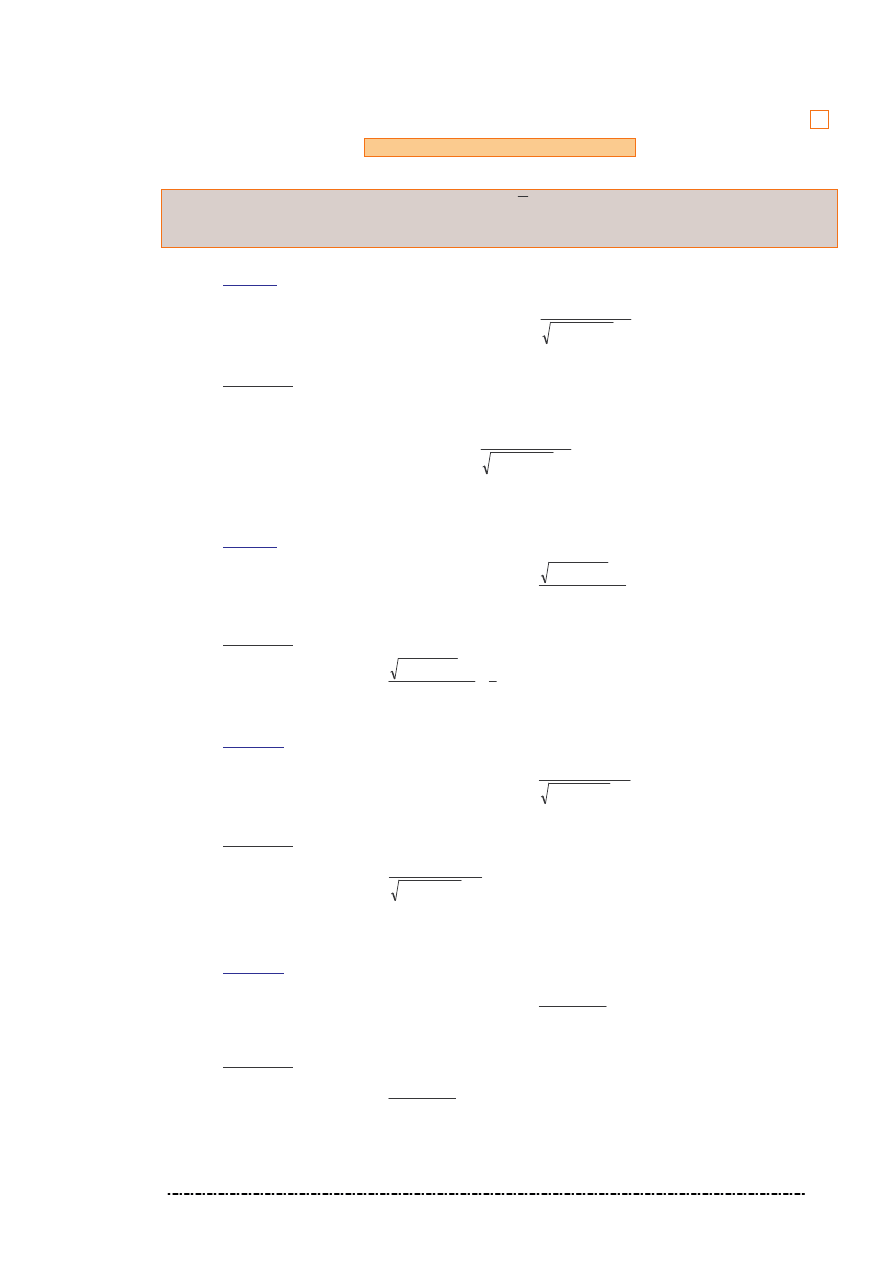
Granica funkcji dwu zmiennych
g
y
x
f
y
x
y
x
=
→
)
,
(
lim
)
,
(
)
,
(
0
0
⇔ dla ka dego ci gu Heinego
)
,
(
n
n
y
x
dla punktu
)
,
(
0
0
y
x
i zbioru
f
D ci g
(
)
)
,
(
n
n
y
x
f
jest
zbie ny do g.
Definicja granicy cz
ciowej:
Liczba g jest granic cz ciow funkcji f w punkcie
)
,
(
0
0
y
x
⇔ istnieje ci g Heinego
)
,
(
n
n
y
x
dla punktu
)
,
(
0
0
y
x
i
zbioru
f
D taki, e ci g
(
)
)
(
n
x
f
jest zbie ny do g.
F
AKT
.
Je li g jest granic funkcji f w punkcie
)
,
(
0
0
y
x
skupienia dziedziny funkcji, to wszystkie granice cz ciowe funkcji f w
punkcie
)
,
(
0
0
y
x
s równe liczbie g.
F
AKT
.
Je li funkcja f ma dwie ró ne granice cz ciowe w punkcie
)
,
(
0
0
y
x
, to funkcja f nie ma granicy w tym punkcie.
Zadanie 3.
Obliczy granic
2
2
2
2
)
0
,
0
(
)
,
(
1
1
lim
y
x
y
x
y
x
+
−
+
+
→
.

Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
119
Rozwi zanie
Wyra enie w liczniku przekształcamy w oparciu o wzór
b
a
b
a
b
a
+
−
=
−
2
2
.
=
+
+
+
+
+
+
+
−
+
+
=
+
−
+
+
→
→
)
1
1
)(
(
)
1
1
)(
1
1
(
lim
1
1
lim
2
2
2
2
2
2
2
2
)
0
,
0
(
)
,
(
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
2
1
2
2
)
0
,
0
(
)
,
(
2
2
2
2
2
2
)
0
,
0
(
)
,
(
1
1
1
lim
)
1
1
)(
(
lim
=
+
+
+
=
+
+
+
+
+
=
→
→
y
x
y
x
y
x
y
x
y
x
y
x
.
Zadanie 4.
Obliczy granic
y
x
y
x
y
x
−
−
→
3
3
)
1
,
1
(
)
,
(
lim
.
Rozwi zanie
3
)
(
lim
)
)(
(
lim
lim
2
2
)
1
,
1
(
)
,
(
2
2
)
1
,
1
(
)
,
(
3
3
)
1
,
1
(
)
,
(
=
+
+
=
−
+
+
−
=
−
−
→
→
→
y
xy
x
y
x
y
xy
x
y
x
y
x
y
x
y
x
y
x
y
x
Zadanie 5.
Obliczy granic
xy
y
x
y
x
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
+
→
.
Rozwi zanie
Korzystaj c z twierdzenia o trzech funkcjach poka emy, e
0
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
xy
y
x
y
x
.
Dla ka dego punktu
f
D
y
x
∈
)
,
(
słuszne s nierówno ci
2
2
2
2
2
2
1
cos
)
(
)
(
y
x
xy
y
x
y
x
+
≤
+
≤
+
−
.
Poniewa
0
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
−
−
→
y
x
y
x
,
0
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
y
x
y
x
, wi c
0
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
xy
y
x
y
x
.
Zadanie 6.
Obliczy granic
2
4
lim
2
2
2
2
)
0
,
0
(
)
,
(
−
−
−
+
→
y
x
y
x
y
x
.
Zadanie 7.
Obliczy granic
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
−
+
→
.
Rozwi zanie
Poka emy, e granica ta nie istnieje. W tym celu rozpatrujemy dwa ci gi
)
0
,
1
(
)
,
(
n
y
x
n
n
=
′
′
,
)
1
,
0
(
)
,
(
n
y
x
n
n
=
′′
′′
zbie ne
do punktu
)
0
,
0
(
oraz odpowiadaj ce im ci gi warto ci funkcji:
2
2
2
2
)
0
,
0
(
)
,
(
)
(
)
(
)
(
)
(
lim
n
n
n
n
y
x
y
x
y
x
n
n
′
−
′
′
+
′
→
′
′
1
0
1
0
1
lim
2
2
=
−
+
=
∞
→
n
n
n
,
2
2
2
2
)
0
,
0
(
)
,
(
)
(
)
(
)
(
)
(
lim
n
n
n
n
y
x
y
x
y
x
n
n
′′
−
′′
′′
+
′′
→
′′
′′
1
1
0
1
0
lim
2
2
−
=
−
+
=
∞
→
n
n
n
.
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
120
Otrzymali my ró ne granice cz ciowe, zatem rozwa ana granica nie istnieje.
55
Ci gło
funkcji dwu zmiennych
Funkcja f jest okre lona w otoczeniu
)
,
(
0
0
y
x
U
punktu
f
y
x
D
∈
)
,
(
0
0
(a tym samym i w punkcie
)
,
(
0
0
y
x
). Wówczas
funkcja f jest ci gła w punkcie
)
,
(
0
0
y
x
wtedy i tylko wtedy, gdy
)
,
(
)
,
(
lim
0
0
)
,
(
)
,
(
0
0
y
x
f
y
x
f
y
x
y
x
=
→
.
Zadanie 8.
Czy mo na dobra warto A tak, by była ci gła funkcja
=
≠
−
+
+
+
=
).
0
,
0
(
)
,
(
),
0
,
0
(
)
,
(
1
1
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
dla
dla
Rozwi zanie
Skorzystamy z definicji ci gło ci funkcji w punkcie. Funkcja
f
jest ci gła dla
2
1
1
lim
2
2
2
2
)
0
,
0
(
)
,
(
=
−
+
+
+
=
→
y
x
y
x
A
y
x
.
Granica taka została obliczona w zadaniu 3.
Zadanie 9.
Czy mo na dobra warto A tak, by była ci gła funkcja
=
≠
+
−
+
+
=
).
0
,
0
(
)
,
(
),
0
,
0
(
)
,
(
1
1
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
dla
dla
Rozwi zanie
Funkcja
f
jest ci gła dla
2
1
2
2
2
2
)
0
,
0
(
)
,
(
1
1
lim
=
+
−
+
+
=
→
y
x
y
x
A
y
x
.
Zadanie 10.
Czy mo na dobra warto A tak, by była ci gła funkcja
=
≠
−
−
−
+
=
).
0
,
0
(
)
,
(
),
0
,
0
(
)
,
(
2
4
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
dla
dla
Rozwi zanie
Funkcja
f
jest ci gła dla
4
2
4
lim
2
2
2
2
)
0
,
0
(
)
,
(
−
=
−
−
−
+
=
→
y
x
y
x
A
y
x
.
Zadanie 11.
Czy mo na dobra warto A tak, by była ci gła funkcja
=
≠
+
+
=
).
0
,
0
(
)
,
(
),
0
,
0
(
)
,
(
)
sin(
)
,
(
2
2
3
3
y
x
A
y
x
y
x
y
x
y
x
f
dla
dla
Rozwi zanie
Funkcja
f
jest ci gła dla
0
)
sin(
lim
2
2
3
3
)
0
,
0
(
)
,
(
=
+
+
=
→
y
x
y
x
A
y
x
.
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
121
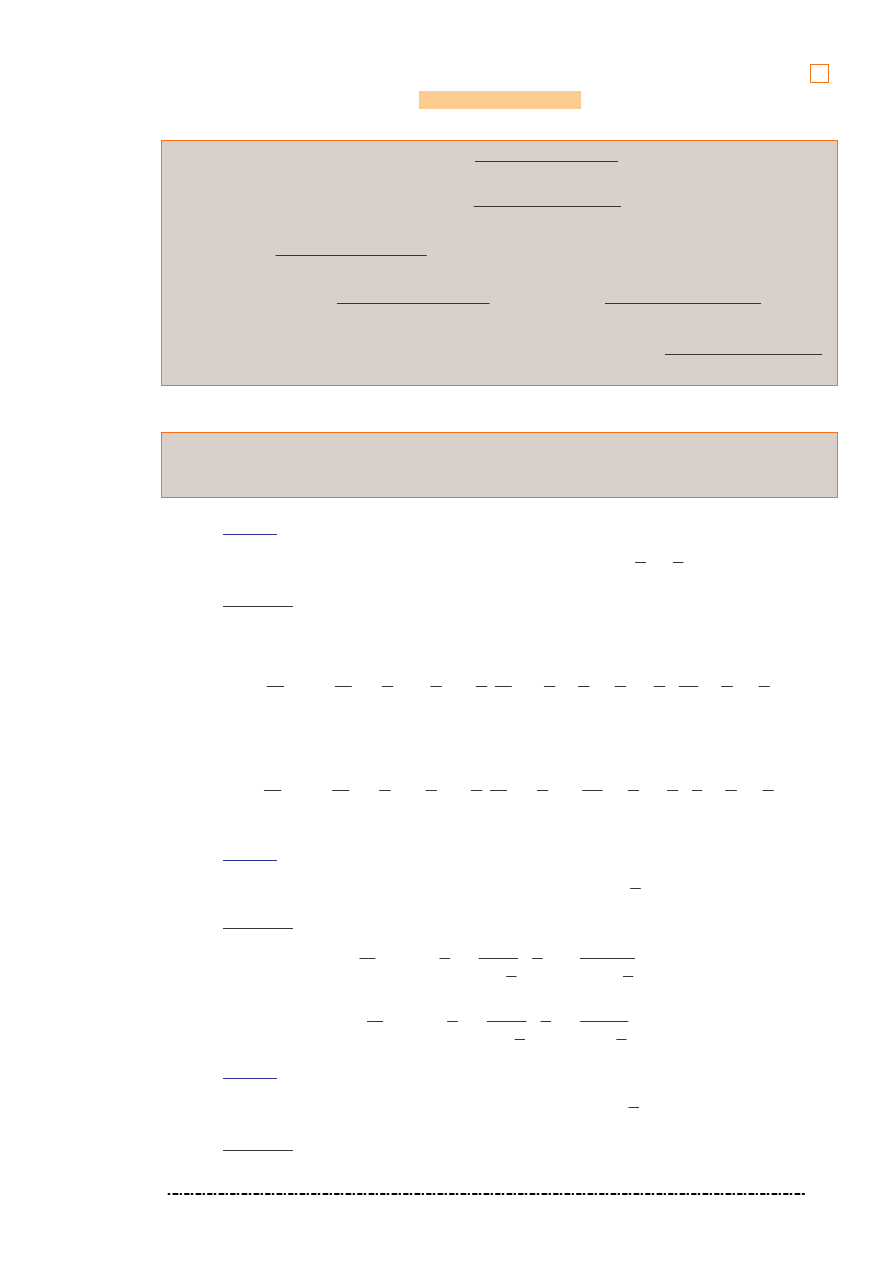
56
Pochodne cz stkowe
x
y
x
f
y
x
x
f
y
x
f
x
x
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
,
y
y
x
f
y
y
x
f
y
x
f
y
y
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
,
x
y
x
f
y
x
x
f
y
x
f
x
x
x
xx
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
,
x
y
x
f
y
x
x
f
y
x
f
y
y
x
xy
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
,
y
y
x
f
y
y
x
f
y
x
f
x
x
y
yx
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
,
y
y
x
f
y
y
x
f
y
x
f
y
y
y
yy
∆
−
∆
+
=
→
∆
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
.
Twierdzenie (Schwarza o pochodnych mieszanych)
Niech funkcja f b dzie okre lona na otoczeniu punktu
)
,
(
0
0
0
y
x
P
=
. Ponadto niech pochodne cz stkowe
xy
f
,
yx
f
istniej na otoczeniu punktu
)
,
(
0
0
0
y
x
P
=
i b d ci głe w punkcie
)
,
(
0
0
0
y
x
P
=
. Wówczas
)
(
)
(
0
0
P
f
P
f
yx
xy
=
.
Zadanie 1.
Obliczy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
x
y
y
x
y
x
f
cos
sin
)
,
(
⋅
=
.
Rozwi zanie
Zastosujemy wzór na pochodn iloczynu funkcji. Pochodn cz stkow wzgl dem x liczymy tak jak zwykł pochodn
funkcji jednej zmiennej x, przy czym zmienn y traktujemy jako stały parametr.
x
y
y
x
x
y
x
y
y
x
y
x
y
x
y
x
x
y
y
x
x
y
x
x
f
sin
sin
cos
cos
1
cos
sin
cos
sin
)
,
(
2
⋅
−
⋅
=
∂
∂
⋅
+
⋅
∂
∂
=
∂
∂
;
Pochodn cz stkow wzgl dem y liczymy tak jak zwykł pochodn funkcji jednej zmiennej y, przy czym zmienn x
traktujemy jako stały parametr.
x
y
y
x
x
x
y
y
x
y
x
x
y
y
y
x
x
y
y
x
y
y
x
y
f
sin
sin
1
cos
cos
cos
sin
cos
sin
)
,
(
2
⋅
−
⋅
−
=
∂
∂
⋅
+
⋅
∂
∂
=
∂
∂
.
Zadanie 2.
Obliczy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
x
y
y
x
f
tg
=
)
,
(
.
Rozwi zanie
x
y
x
y
x
y
x
y
x
y
y
x
x
f
x
x
2
2
2
cos
cos
1
)
,
(
−
=
⋅
=
=
∂
∂
tg
;
x
y
x
x
y
x
y
x
y
y
x
y
f
y
y
2
2
cos
1
cos
1
)
,
(
=
⋅
=
=
∂
∂
tg
.
Zadanie 3.
Oblicz pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
y
x
y
x
f
tg
ln
)
,
(
=
.
Rozwi zanie
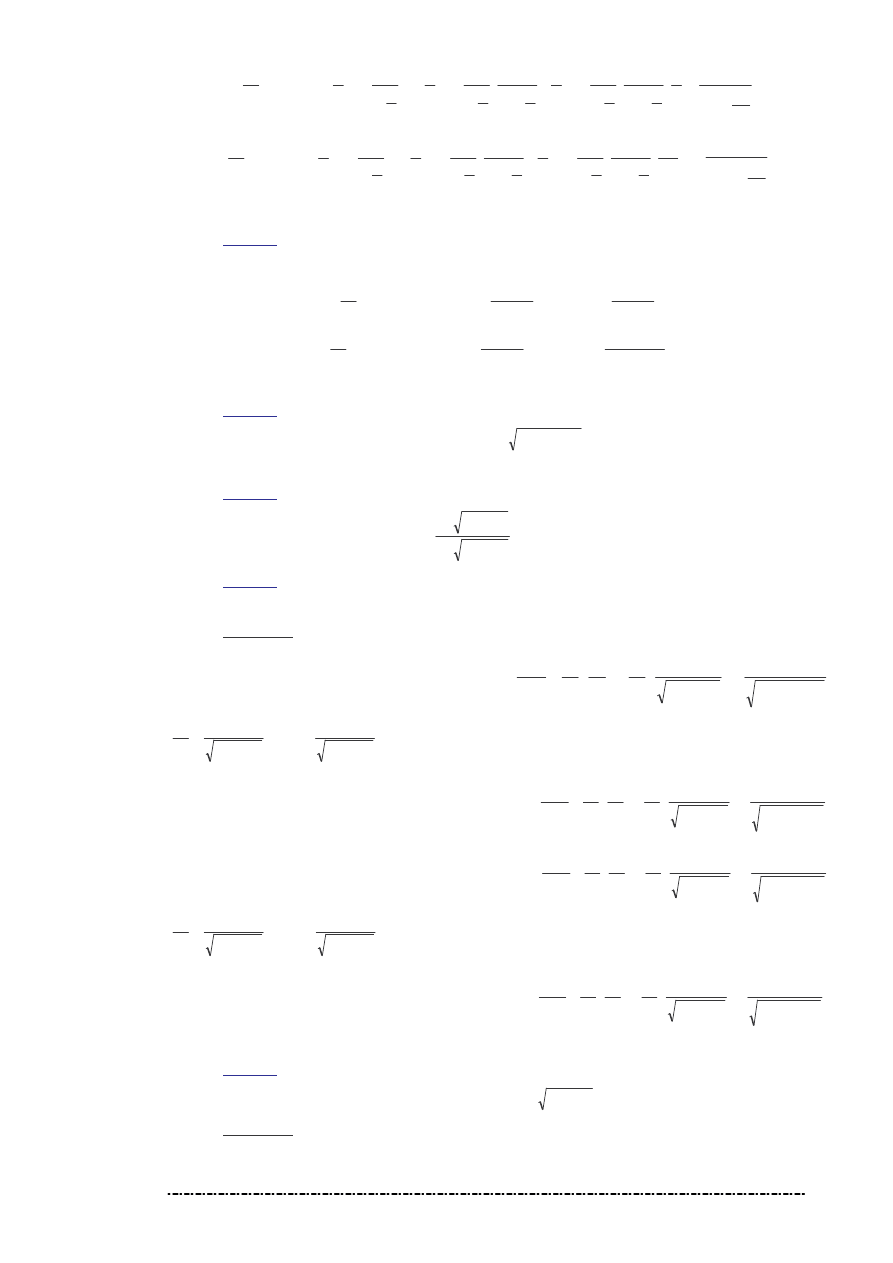
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
122
=
⋅
⋅
=
⋅
⋅
=
⋅
=
=
∂
∂
y
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
x
f
x
x
x
1
cos
1
1
cos
1
1
1
)
,
(
2
2
tg
tg
tg
tg
lntg
y
x
y
2
sin
2
;
=
−
⋅
⋅
=
⋅
⋅
=
⋅
=
=
∂
∂
2
2
2
cos
1
1
cos
1
1
1
)
,
(
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
f
y
y
y
tg
tg
tg
tg
lntg
y
x
y
x
2
sin
2
2
−
.
Zadanie 4.
Oblicz pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
)
ln
ln(
)
,
(
y
x
y
x
f
+
=
.
(
)
y
x
y
x
y
x
y
x
y
x
x
f
x
x
ln
1
)
ln
(
ln
1
)
ln
ln(
)
,
(
+
=
+
⋅
+
=
+
=
∂
∂
;
(
)
=
+
⋅
+
=
+
=
∂
∂
y
y
y
x
y
x
y
x
y
x
y
f
)
ln
(
ln
1
)
ln
ln(
)
,
(
)
ln
(
1
y
x
y
+
.
Zadanie 5.
Oblicz pochodne cz stkowe funkcji
2
2
9
)
3
2
(
)
,
(
y
x
x
y
x
f
−
−
+
−
= arcsin
.
Zadanie 6.
Oblicz pochodne cz stkowe funkcji
2
2
2
2
1
1
ln
)
,
(
y
x
y
x
y
x
f
+
+
+
−
=
.
Zadanie 7.
Oblicz pochodne cz stkowe drugiego rz du funkcji
)
(
)
,
(
xy
y
x
f
arcsin
=
.
Rozwi zanie
(
)
3
2
3
2
2
2
)
(
1
)
(
1
xy
xy
xy
y
x
x
f
x
x
f
−
=
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
2
2
)
(
1
)
(
)
(
1
1
xy
y
xy
xy
x
f
x
−
=
⋅
−
=
∂
∂
;
(
)
3
2
2
2
)
(
1
1
)
(
1
xy
xy
y
y
x
f
y
x
y
f
−
=
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
(
)
3
2
2
2
)
(
1
1
)
(
1
xy
xy
x
x
y
f
x
y
x
f
−
=
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
2
2
)
(
1
)
(
)
(
1
1
xy
x
xy
xy
y
f
y
−
=
⋅
−
=
∂
∂
(
)
3
2
3
2
2
2
)
(
1
)
(
1
xy
y
x
xy
x
y
y
f
y
y
f
−
=
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
.
Zadanie 8.
Oblicz pochodne cz stkowe drugiego rz du funkcji
)
ln(
)
,
(
2
2
y
x
x
y
x
f
+
+
=
.
Rozwi zanie
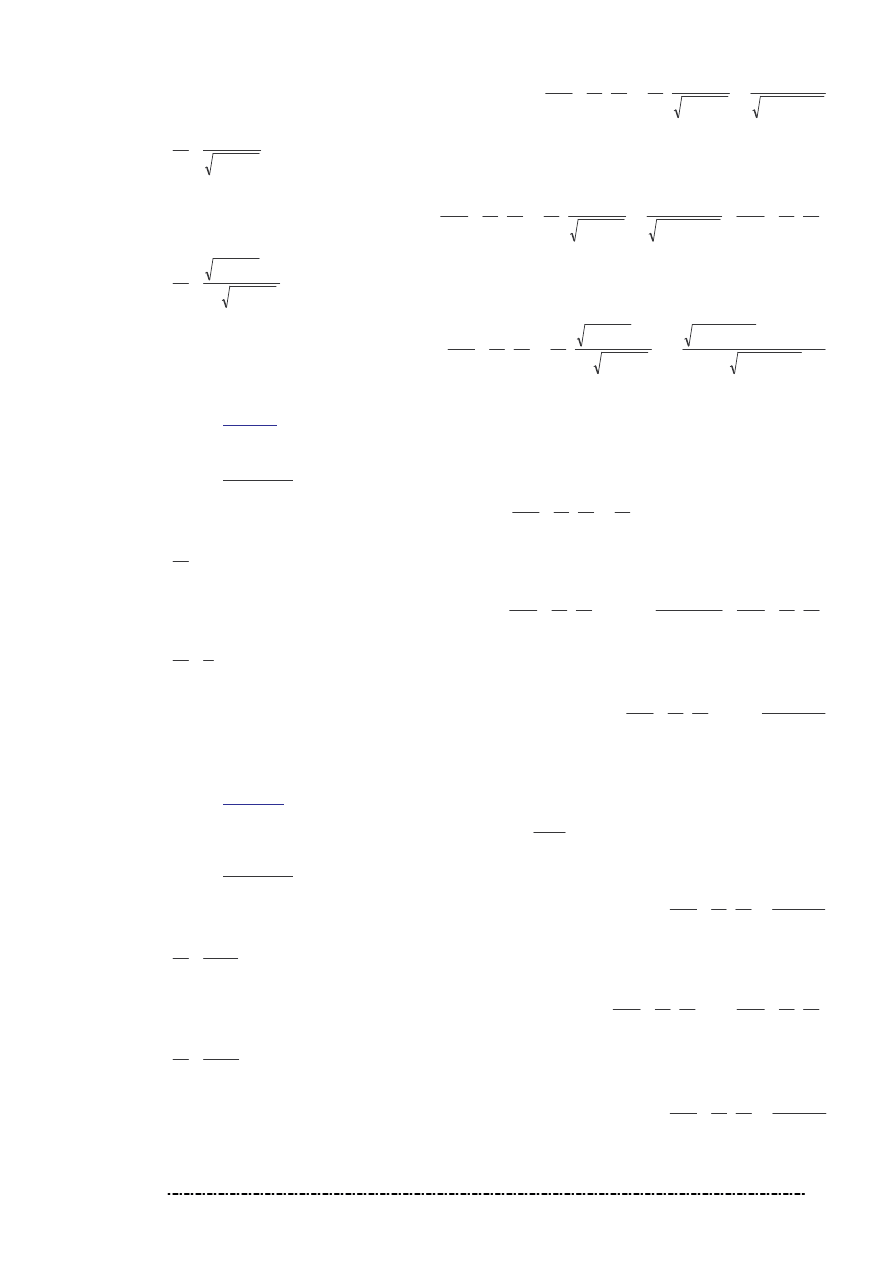
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
123
3
2
2
2
2
2
2
)
(
1
y
x
x
y
x
x
x
f
x
x
f
+
−
=
+
∂
∂
=
∂
∂
∂
∂
=
∂
∂
2
2
1
y
x
x
f
+
=
∂
∂
;
∂
∂
∂
∂
=
∂
∂
∂
=
+
−
=
+
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
y
f
x
y
x
f
y
x
y
y
x
y
x
f
y
x
y
f
2
3
2
2
2
2
2
)
(
1
2
2
2
2
y
x
y
x
y
x
y
f
+
⋅
−
+
=
∂
∂
3
2
2
2
2
3
3
2
2
2
2
2
2
2
2
)
(
2
)
(
y
x
y
xy
x
y
x
y
x
y
x
y
x
y
y
f
y
y
f
+
⋅
−
−
+
−
=
+
⋅
−
+
∂
∂
=
∂
∂
∂
∂
=
∂
∂
Zadanie 9.
Oblicz pochodne cz stkowe drugiego rz du funkcji
x
y
y
x
f
ln
)
,
(
=
.
Rozwi zanie
(
)
)
ln
(ln
ln
2
2
ln
1
ln
2
2
y
y
x
y
x
x
x
f
x
x
f
y
y
−
=
⋅
∂
∂
=
∂
∂
∂
∂
=
∂
∂
−
−
y
x
x
f
y
ln
1
ln
⋅
=
∂
∂
−
;
∂
∂
∂
∂
=
∂
∂
∂
=
+
⋅
⋅
=
∂
∂
∂
∂
=
∂
∂
∂
−
y
f
x
y
x
f
y
y
x
x
x
f
y
x
y
f
y
2
1
ln
2
1
ln
ln
x
x
y
y
f
y
ln
1
ln
⋅
⋅
=
∂
∂
2
2
ln
2
2
ln
ln
y
x
x
x
y
f
y
y
f
y
−
⋅
=
∂
∂
∂
∂
=
∂
∂
Zadanie 10.
Oblicz pochodne cz stkowe drugiego rz du funkcji
xy
y
x
y
x
f
−
+
=
1
)
,
(
tg
arc
.
Rozwi zanie
2
2
2
2
)
1
(
2
+
−
=
∂
∂
∂
∂
=
∂
∂
x
x
x
f
x
x
f
1
1
2
+
=
∂
∂
x
x
f
∂
∂
∂
∂
=
∂
∂
∂
=
=
∂
∂
∂
∂
=
∂
∂
∂
y
f
x
y
x
f
x
f
y
x
y
f
2
2
0
1
1
2
+
=
∂
∂
y
y
f
2
2
2
2
)
1
(
2
+
−
=
∂
∂
∂
∂
=
∂
∂
y
y
y
f
y
y
f

Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
124
Zadanie 11.
Dana jest funkcja
≠
=
=
.
0
1
,
0
0
)
,
(
xy
xy
y
x
f
dla
dla
Czy funkcja f jest ci gła w punkcie O(0,0)? Obliczy
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
.
Rozwi zanie
Funkcja nie jest ci gła w punkcie O(0,0), gdy nie ma granicy w tym punkcie. Aby to uzasadni wystarczy wzi dwa
ci gi punktów zbie ne do punktu O(0,0), dla których odpowiadaj ce im ci gi warto ci funkcji b d miały ró ne granice.
Dla ci gów
)
0
,
1
(
)
,
(
n
y
x
n
n
=
′
′
,
)
1
,
1
(
)
,
(
n
n
y
x
n
n
=
′′
′′
mamy
0
)
,
(
lim
)
0
,
0
(
)
,
(
=
′
′
→
′
′
n
n
y
x
y
x
f
n
n
,
1
)
,
(
lim
)
0
,
0
(
)
,
(
=
′′
′′
→
′′
′′
y
x
f
n
y
x
n
n
.
Otrzymali my ró ne granice, zatem granica funkcji w punkcie O(0,0) nie istnieje.
Pochodne cz stkowe
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
b dziemy wylicza na podstawie definicji.
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
.
Z tego przykładu wynika, e nawet nieci głe w punkcie funkcje mog mie obie pochodne cz stkowe w tym punkcie.
Zadanie 12.
Dla funkcji
xy
y
x
f
=
)
,
(
obliczy
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
.
Rozwi zanie
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
.
Zadanie 13.
Dla funkcji
2
2
)
,
(
y
x
y
x
f
+
=
obliczy
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
.
Rozwi zanie
x
x
x
x
x
f
x
f
f
x
x
x
x
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
|
|
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
0
nie istnieje,
y
y
y
y
y
f
y
f
f
y
y
y
y
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
|
|
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
0
nie istnieje.
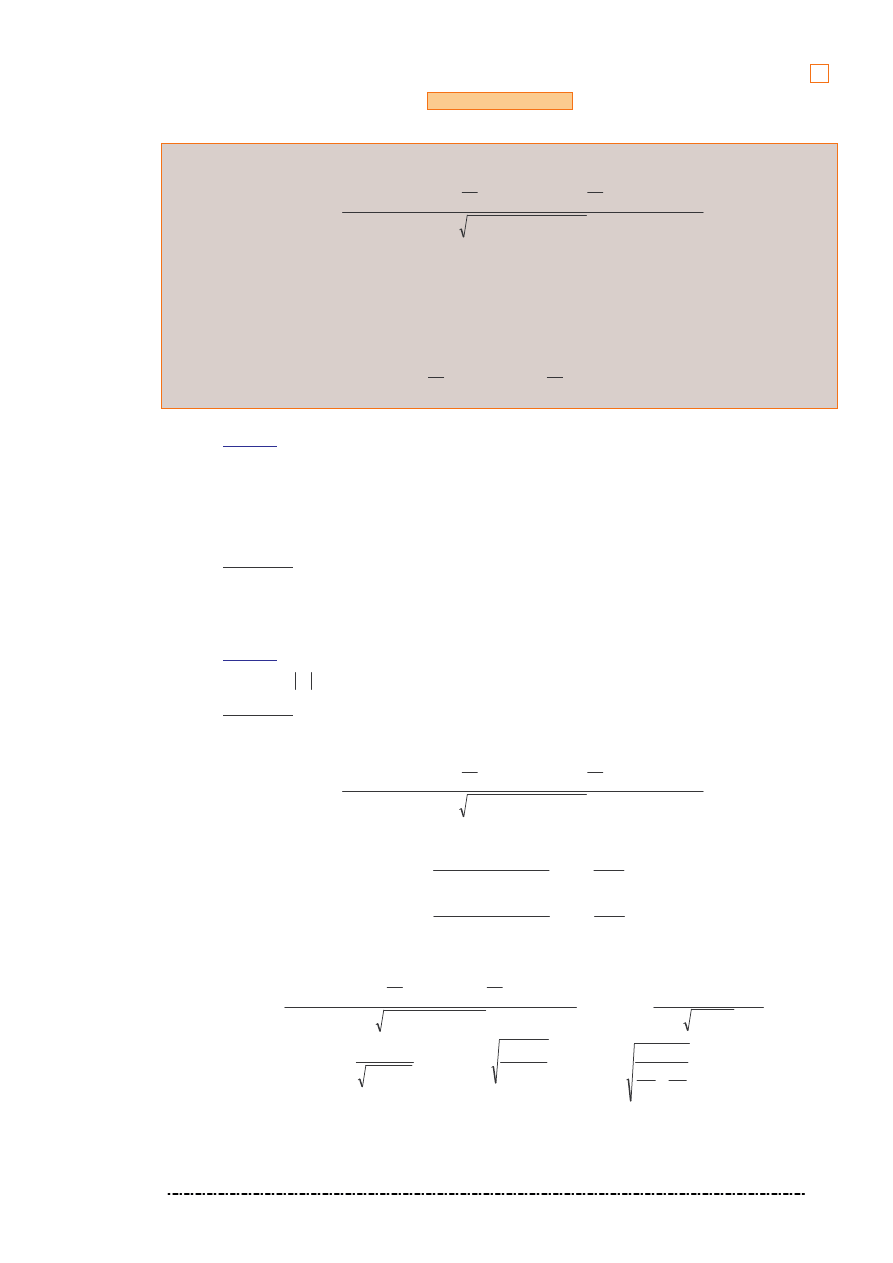
Zadanie 14.
Dla funkcji
3
3
3
)
,
(
y
x
y
x
f
+
=
obliczy
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
.
Rozwi zanie
1
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
3
3
0
0
=
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
x
x
x
x
x
f
x
f
f
x
x
x
x
,
1
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
3
3
0
0
=
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
y
y
y
y
y
f
y
f
f
y
y
y
y
.
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
125
57
Ró niczkowalno
Funkcja jest ró niczkowalna w punkcie
)
,
(
0
0
y
x
wtedy i tylko wtedy, gdy
0
)
(
)
(
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
lim
2
0
2
0
0
0
0
0
0
0
0
0
)
,
(
)
,
(
0
0
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
y
y
x
x
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
y
x
f
y
x
y
x
.
Ró niczkowalno funkcji f w punkcie
)
,
(
0
0
y
x
oznacza, e istnieje niepionowa płaszczyzna styczna do wykresu tej
funkcji w punkcie
)
)
,
(
,
,
(
0
0
0
0
y
x
f
y
x
Równanie płaszczyzny stycznej w punkcie
)
)
,
(
,
,
(
0
0
0
0
y
x
f
y
x
do wykresu funkcji ró niczkowalnej
)
,
( y
x
f
z
=
ma
posta
)
(
)
,
(
)
(
)
,
(
)
,
(
0
0
0
0
0
0
0
0
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
z
−
⋅
∂
∂
+
−
⋅
∂
∂
=
−
Zadanie 1.
Funkcja
≠
=
=
.
0
1
,
0
0
)
,
(
xy
xy
y
x
f
dla
dla
ma pochodne cz stkowe w punkcie O(0,0). Czy jest ró niczkowalna w punkcie O(0,0)?
Rozwi zanie
Funkcja nie jest ci gła w punkcie O(0,0) (gdy nie ma granicy w tym punkcie), zatem nie spełnia warunku koniecznego
ró niczkowalno ci.
Zadanie 2.
Czy funkcja
xy
y
x
f
=
)
,
(
jest ró niczkowalna w punkcie O(0,0)?
Rozwi zanie
Przypominamy, e na mocy definicji, funkcja jest ró niczkowalna w punkcie
)
,
(
0
0
y
x
wtedy i tylko wtedy, gdy
0
)
(
)
(
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
lim
2
0
2
0
0
0
0
0
0
0
0
0
)
,
(
)
,
(
0
0
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
y
y
x
x
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
y
x
f
y
x
y
x
.
Poniewa
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
,
wi c
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
=
+
⋅
−
⋅
−
−
→
2
2
)
0
,
0
(
)
,
(
0
0
0
|
|
lim
y
x
y
x
xy
y
x
2
2
)
0
,
0
(
)
,
(
|
|
lim
y
x
xy
y
x
+
=
→
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
+
=
→
0
1
1
1
lim
2
2
)
0
,
0
(
)
,
(
=
+
=
→
x
y
y
x
.
Dlatego funkcja jest ró niczkowalna w punkcie O(0,0). Macierz Jacobiego funkcji f w punkcie O(0,0) jest
[
]
[ ]
0
0
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
=
=
′
y
x
f
f
f
.
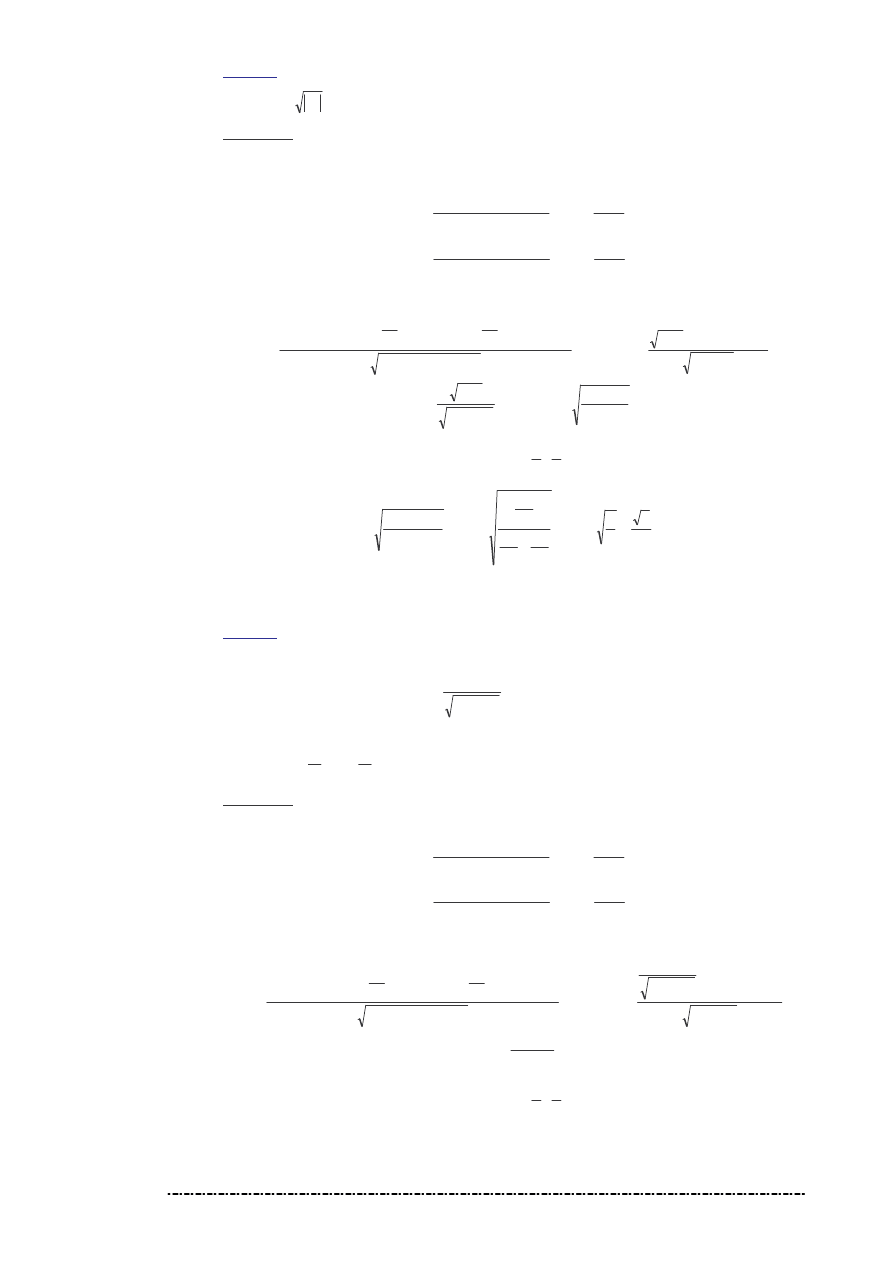
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
126
Zadanie 3.
Czy funkcja
xy
y
x
f
=
)
,
(
jest ró niczkowalna w punkcie O(0,0)?
Rozwi zanie
Skorzystamy z definicji funkcji ró niczkowalnej w punkcie O(0,0).
Poniewa
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
,
wi c
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
=
+
⋅
−
⋅
−
−
→
2
2
)
0
,
0
(
)
,
(
0
0
0
|
|
lim
y
x
y
x
xy
y
x
2
2
)
0
,
0
(
)
,
(
|
|
lim
y
x
xy
y
x
+
=
→
2
2
)
0
,
0
(
)
,
(
lim
y
x
xy
y
x
+
=
→
.
Poka emy, e ostatnia granica nie jest równa 0. Niech
)
1
,
1
(
)
,
(
n
n
y
x
n
n
=
. Wówczas
2
2
2
1
lim
1
1
1
lim
lim
2
2
2
2
2
=
=
+
=
+
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
y
x
y
x
.
Dlatego funkcja nie jest ró niczkowalna w punkcie O(0,0).
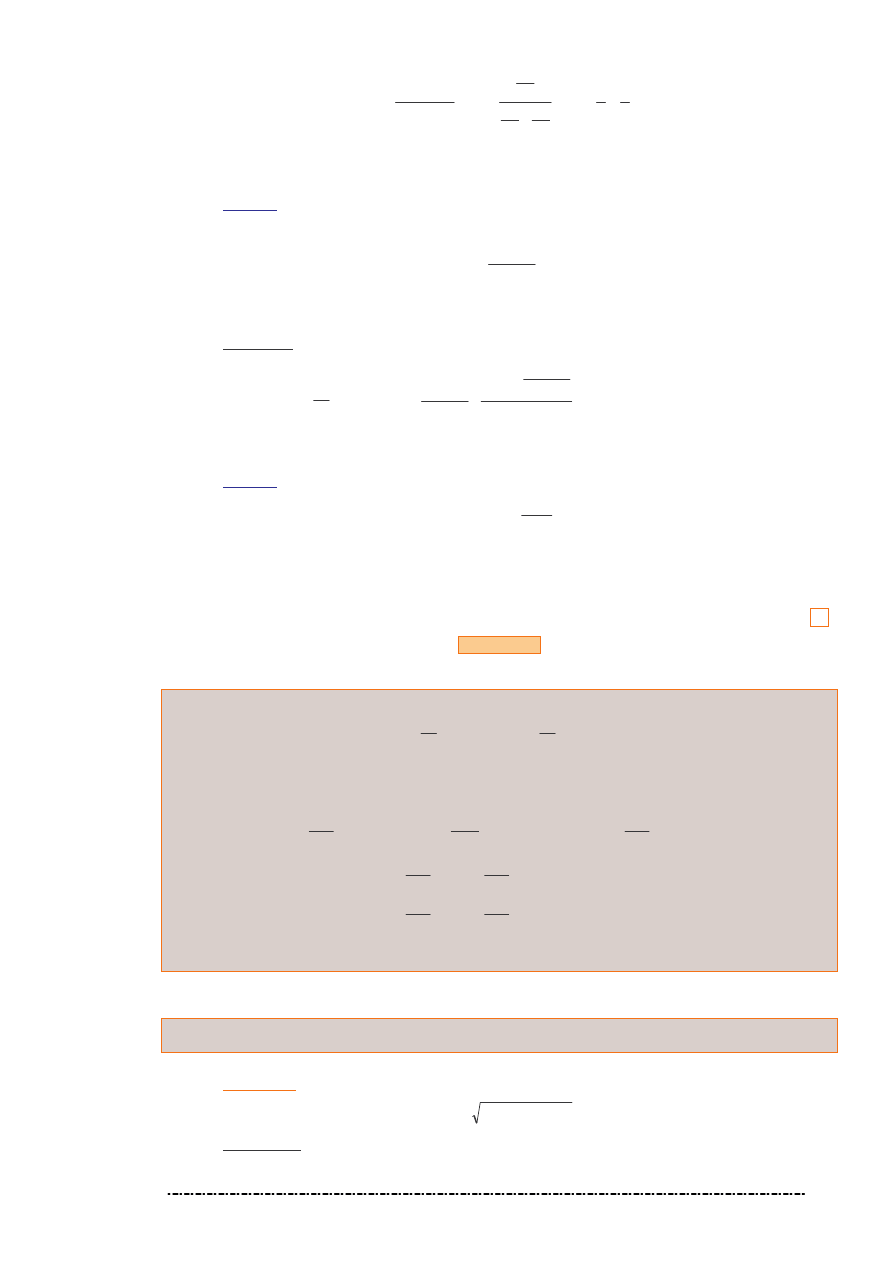
Zadanie 4.
Sprawdzi , e funkcja
=
≠
+
=
),
0
,
0
(
)
,
(
0
),
0
,
0
(
)
,
(
)
,
(
2
2
y
x
y
x
y
x
xy
y
x
f
dla
dla
ma pochodne cz stkowe
)
0
,
0
(
x
f
∂
∂
,
)
0
,
0
(
y
f
∂
∂
, ale nie jest ró niczkowalna w punkcie (0,0).
Rozwi zanie
Mamy
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
.
Dlatego
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
=
+
⋅
−
⋅
−
−
+
→
2
2
2
2
)
0
,
0
(
)
,
(
0
0
0
lim
y
x
y
x
y
x
xy
y
x
2
2
)
0
,
0
(
)
,
(
lim
y
x
xy
y
x
+
=
→
.
Poka emy, e ostatnia granica nie jest równa 0. Niech
)
1
,
1
(
)
,
(
n
n
y
x
n
n
=
. Wówczas
Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
127
2
1
2
1
lim
1
1
1
lim
lim
2
2
2
2
2
=
=
+
=
+
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
y
x
y
x
.
Dlatego funkcja nie jest ró niczkowalna w punkcie O(0,0).
Zadanie 5.
Sprawdzi , e funkcja
=
≠
+
⋅
+
=
),
0
,
0
(
)
,
(
0
),
0
,
0
(
)
,
(
1
sin
)
(
)
,
(
2
2
2
2
y
x
y
x
y
x
y
x
y
x
f
dla
dla
ma nieci głe pochodne cz stkowe w punkcie O(0,0). Sprawd to! Jest jednak w tym punkcie ró niczkowalna.
Rozwi zanie
=
≠
+
+
⋅
−
+
⋅
=
∂
∂
),
0
,
0
(
)
,
(
0
),
0
,
0
(
)
,
(
1
cos
2
1
sin
2
)
,
(
2
2
2
2
2
2
y
x
y
x
y
x
y
x
x
y
x
x
y
x
x
f
dla
dla
Zadanie 6.
Czy jest ró niczkowalna w punkcie O(0,0) funkcja
=
≠
=
+
−
).
0
,
0
(
)
,
(
0
),
0
,
0
(
)
,
(
)
,
(
2
2
1
y
x
y
x
e
y
x
f
y
x
dla
dla
58
Ró niczka
Wyra enie
)
(
)
,
(
)
(
)
,
(
)
,
(
0
0
0
0
0
0
0
0
y
y
y
x
y
f
x
x
y
x
x
f
y
x
df
−
⋅
∂
∂
+
−
⋅
∂
∂
=
nazywa si
ró niczk pierwszego rz du (cz ci liniow przyrostu warto ci funkcji)
.
Wyra enie
[
]
−
−
⋅
∂
∂
∂
∂
∂
∂
∂
∂
⋅
−
−
=
=
−
⋅
∂
∂
+
−
−
⋅
∂
∂
∂
+
−
⋅
∂
∂
=
0
0
0
0
2
2
0
0
2
2
0
0
2
2
0
0
2
2
0
0
2
0
0
0
2
2
0
0
0
0
2
2
0
0
0
2
2
0
0
)
,
(
)
,
(
)
,
(
)
,
(
)
(
)
,
(
)
)(
(
)
,
(
2
)
(
)
,
(
)
,
(
y
y
x
x
y
x
y
f
y
x
y
f
y
x
y
f
y
x
x
f
y
y
x
x
y
y
y
x
y
f
y
y
x
x
y
x
y
x
f
x
x
y
x
x
f
y
x
df
nazywa si
ró niczk drugiego rz du
.
Zastosowanie ró niczki do oblicze przybli onych.
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
0
0
0
0
0
0
0
0
y
y
y
x
f
x
x
y
x
f
y
x
f
y
x
f
y
x
−
⋅
+
−
⋅
+
≈
Zadanie 1.
Za pomoc ró niczki oblicz przybli on warto liczby
2
2
)
02
,
2
(
)
01
,
1
(
+
.
Rozwi zanie
Wykorzystamy wzór

Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
128
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
0
0
0
0
0
0
0
0
y
y
y
x
f
x
x
y
x
f
y
x
f
y
x
f
y
x
−
⋅
+
−
⋅
+
≈
.
W zadaniu mamy
2
2
)
,
(
y
x
y
x
f
+
=
,
01
,
1
=
x
,
1
0
=
x
,
02
,
2
=
y
,
2
0
=
y
. St d
=
−
⋅
+
+
−
⋅
+
+
+
≈
+
=
=
=
=
)
2
02
,
2
(
)
1
01
,
1
(
4
1
)
02
,
2
(
)
01
,
1
(
2
;
1
2
2
2
;
1
2
2
2
2
y
x
y
x
y
x
y
y
x
x
2,258429.
Zadanie 2.
Za pomoc ró niczki oblicz przybli on warto liczby
4
3
)
996
,
0
(
)
02
,
1
(
⋅
.
Rozwi zanie
W zadaniu mamy
4
3
)
,
(
y
x
y
x
f
=
,
02
,
1
=
x
,
1
0
=
x
,
996
,
0
=
y
,
1
0
=
y
. St d
=
−
⋅
+
−
⋅
+
≈
=
=
=
=
)
1
996
,
0
(
3
)
1
02
,
1
(
3
1
)
996
,
0
(
)
02
,
1
(
1
;
1
4
2
1
;
1
4
2
4
3
y
x
y
x
y
x
y
x
1,048.
Zadanie 3.
Obliczy , jaki popełniamy maksymalny bł d bezwzgl dny oraz wzgl dny przy obliczaniu obj to ci prostopadło cianu o
kraw dziach wyznaczonych z podan dokładno ci :
1
,
0
1
,
4
±
=
x
,
1
,
0
2
,
3
±
=
y
,
2
,
0
4
,
8
±
=
z
.
Wskazówka. Obj to prostopadło cianu liczymy ze wzoru
xyz
V
=
.
Rozwi zanie
Wykorzystamy wzór
0
0
0
z
z
V
y
y
V
x
x
V
V
z
y
x
−
⋅
′
+
−
⋅
′
+
−
⋅
′
≤
∆
.
Mamy
=
−
+
−
+
−
≤
∆
0
0
0
z
z
xy
y
y
xz
x
x
yz
V
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
624
,
2
444
,
3
688
,
2
2
,
0
2
,
3
1
,
4
1
,
0
4
,
8
1
,
4
1
,
0
4
,
8
2
,
3
8,756,
0794497
,
0
208
,
110
756
,
8
4
,
8
2
,
3
1
,
4
786
,
8
=
=
⋅
⋅
=
∆
=
δ
V
V
V
(8%)
Zadanie 4.
Znale maksymalny bł d bezwzgl dny i wzgl dny powstały przy obliczaniu obj to ci sto ka, je li promie podstawy
wynosi
02
,
0
0
,
3
±
=
r
, wysoko sto ka
1
,
0
2
,
2
±
=
h
oraz
14
,
3
=
π
.
Wskazówka. Obj to sto ka liczymy ze wzoru
h
r
V
2
3
1
π
=
, gdzie r jest długo ci promienia podstawy, za h jest
wysoko ci sto ka.
Zadanie 5.
Znale maksymalny bł d bezwzgl dny i wzgl dny powstały przy obliczaniu długo ci przek tnej prostok ta, je li
długo ci jego boków wynosz
4
,
0
0
,
8
±
=
a
,
1
,
0
0
,
6
±
=
b
.
Wskazówka. Zastosowa twierdzenie Pitagorasa.
59
Pochodna kierunkowa
Definicja.
Pochodn kierunkow funkcji f w punkcie
)
,
(
0
0
y
x
w kierunku wersora
]
,
[
y
x
v
v
=
v
okre la si wzorem
t
y
x
f
v
t
y
v
t
x
f
y
x
v
f
y
x
t
)
,
(
)
,
(
lim
)
,
(
0
0
0
0
0
0
0
−
⋅
+
⋅
+
=
∂
∂
+
→

Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
129
Definicja.
Gradientem funkcji f punkcie
)
,
(
0
0
y
x
nazywa si wektor
]
)
,
(
),
,
(
[
)
,
(
0
0
0
0
0
0
y
x
f
y
x
f
y
x
f
y
x
=
grad
Wzór do obliczania pochodnej kierunkowej.
v
•
=
∂
∂
)
,
(
)
,
(
0
0
0
0
y
x
f
y
x
v
f
grad
Zadanie 1.
Obliczy pochodn kierunkow funkcji
1
2
)
,
(
4
4
+
+
+
=
xy
y
x
y
x
f
w punkcie
)
2
,
1
(
i kierunku
[ ]
2
1
2
3
;
−
=
v
.
Rozwi zanie
Znajdujemy macierz pochodnej funkcji (gradient) we wskazanym punkcie
[
]
=
′
′
=
)
2
,
1
(
)
2
,
1
(
)
2
,
1
(
y
x
f
f
f
grad
+
+
=
=
=
=
2
;
1
3
2
;
1
3
2
4
2
4
y
x
y
x
x
y
y
x
[
]
34
8
=
,
a nast pnie
[
]
[
]
17
3
4
34
8
)
2
,
1
(
)
2
,
1
(
2
1
2
3
−
=
−
•
=
•
=
∂
∂
v
v
f
f
grad
.
Zadanie 2.
Obliczy pochodn kierunkow funkcji
)
ln(
)
,
(
2
2
y
x
y
x
f
+
=
w punkcie
)
1
,
1
(
i kierunku wektora dwusiecznej
pierwszej wiartki.
Zadanie 3.
Obliczy pochodn kierunkow funkcji
2
2
3
2
)
,
(
y
x
y
x
f
−
=
w punkcie
)
0
,
1
(
i kierunku wektora tworz cego k t 120
° z
osi odci tych.
Zadanie 4.
Obliczy pochodn kierunkow funkcji
|
|
2
|
|
)
,
(
y
x
y
x
f
+
=
w punkcie (0,0) i kierunku
[ ]
2
2
2
2
;
=
v
.
Zadanie 5.
Obliczy pochodn kierunkow funkcji
3
)
,
(
xy
y
x
f
=
w punkcie
)
0
,
1
(
i kierunku wektora.
[ ]
2
1
2
3
;
=
v
.
Zadanie 6.
Wykaza , e funkcja
3
3
3
)
,
(
y
x
y
x
f
+
=
ma pochodn w punkcie O(0,0) w dowolnym kierunku. Czy jest
ró niczkowalna w tym punkcie?
Zadanie 7.
Wykaza , e funkcja
2
2
)
,
(
y
x
y
x
f
+
=
ma pochodn w punkcie O(0,0) w dowolnym kierunku. Czy jest
ró niczkowalna w tym punkcie?
Zadanie 8.
Wykaza , e funkcja
=
≠
+
=
),
0
,
0
(
)
,
(
0
),
0
,
0
(
)
,
(
)
,
(
2
6
3
y
x
y
x
y
x
y
x
y
x
f
dla
dla
ma pochodn w punkcie O(0,0) w dowolnym kierunku. Nie jest ró niczkowalna w tym punkcie, gdy nie jest nawet
ci gła w tym punkcie.
Wsk.
)
1
,
1
(
)
,
(
3
n
n
y
x
n
n
=

Stanisław Kowalski,
Wykłady z matematyki –
Funkcje dwu zmiennych
– wykład 12.
130
Wyszukiwarka
Podobne podstrony:
wykład 3 funkcje wielu zmiennych
12 IChiP Funkcje wielu zmiennych, materiały
wykład, RACHUNEK ROZNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 63, 1)
funkcje dwóch zmiennych wykład
Wykłady z Matematyki, Wykłady - Rachunek Różniczkowy Funkcji Wielu Zmiennych, Dr Adam Ćmiel
Funkcje wielu zmiennych, Studia Budownictwo UZ, 1 semestr, Matematyka, Wyklady matematyka
Sem 1. Wykład, Rachunek Całkowy Funkcji Jednej Zmiennej cz.2
Konspekt wykładu r różniczkowy funkcji jednej zmiennej(1)
12. Definicja pochodnej funkcji jednej zmiennej w punkcie i przykład jej interpretacji, Studia, Seme
12 Twierdzenie Taylora dla funkcji wielu zmiennych (2)
12 Wypukłość Badanie funkcji jednej zmiennej
4 6 Różniczki funkcji dwóch zmiennych
więcej podobnych podstron