TWIERDZENIE TAYLORA

DLA FUNKCJI WIELU ZMIENNYCH

Twierdzenie Taylora

(

z resztą Lagrange'a

)

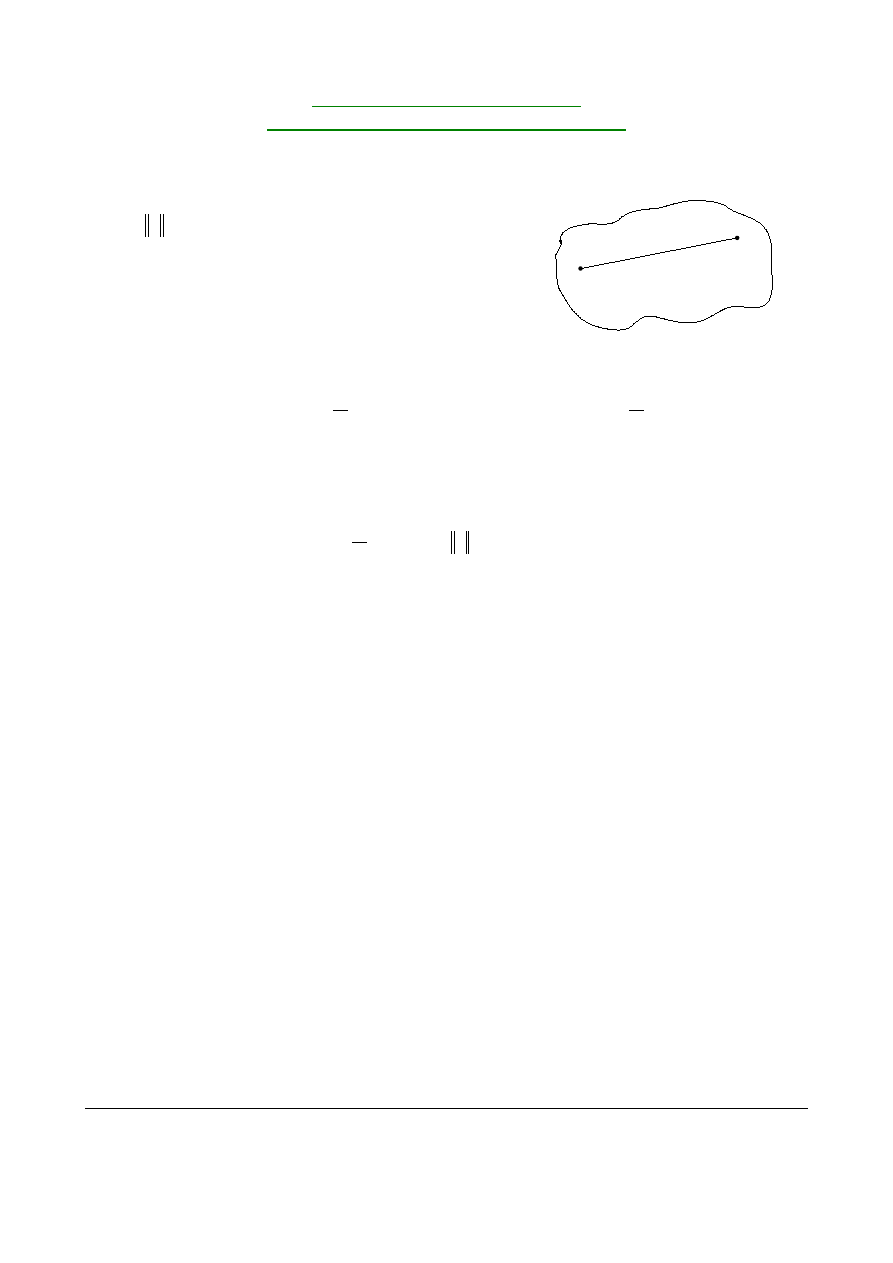
Zał: - przestrzeń unormowana nad R,

, tzn. f - k-krotnie różniczkowalna w U,

Teza:

Powyższy wzór można zapisać w następującej postaci:

Wzór Taylora z resztą Peano

opracował Marcin Uszko

1

x

x+h

U

R







U

f

X

U

X

:

Top

)

,

(





.

,

odcinek

)

(

U

h

x

x

U

D

f

k







)

(

!

1

)

(

gdzie

,

)

(

)

(

!

1

)

(

:

)

,

(

1

0

h

f

d

k

c

R

c

R

h

f

d

j

h

x

f

h

x

x

c

k

c

k

c

punkcie

w

policzona

k

rzedu

reszta

k

k

j

j

x



























 











k

j

k

j

x

h

o

h

f

d

j

h

x

f

0

)

(

!

1

)

(