BADANIE FUNKCJI.

1. Określić przedziały monotoniczności dla funkcji.

(a)

x

x

x

x

f

3

5

)

(

(b)

2

4

)

(

x

x

x

f

(c)

4

8

2

3

)

(

x

x

x

f

(d)

2

3

2

)

(

x

x

x

f

(e)

4

4

1

2

2

1

)

(

x

x

x

f

(f)

x

e

x

x

f

1

)

(

(g)

2

8

)

(

x

x

x

f

(h)

2

2

)

(

x

x

x

f

2. Określić ekstrema funkcji

(a)

2

3

4

18

8

3

)

(

x

x

x

x

f

(b)

8

24

15

2

)

(

2

3

x

x

x

x

f

(c)

6

5

)

(

2

4

x

x

x

f

(d)

x

x

x

x

f

10

5

)

(

3

5

(e)

x

x

x

f

1

4

)

(

3. Określić kształt wykresu (wklęsłość, wypukłość, punkty przegięcia)

(a)

x

x

x

x

f

4

24

)

(

2

4

(b)

2

3

1

)

(

x

x

x

f

(c)

x

x

x

x

f

4

30

)

(

3

5

(d)

2

4

5

)

(

x

x

x

f

(e)

x

x

x

f

2

5

)

(

(f)

x

x

x

x

x

f

8

120

25

2

)

(

2

4

6

4. Określić asymptoty dla funkcji.

(a)

x

x

x

f

2

1

4

1

)

(

(b)

1

2

2

2

3

)

(

x

x

x

x

f

(c)

2

)

3

(

5

2

)

(

x

x

x

f

(d)

x

x

x

f

1

1

)

(

(e)

3

4

2

)

(

x

x

x

f

(f)

x

e

x

f

2

)

(

(g)

2

1

)

(

x

e

x

f

(h)

1

)

(

2

x

x

f

5. Znaleźć najmniejszą i największą wartość funkcji w przedziale domkniętym.

(a)

x

x

x

f

2

)

(

dla

9

,

0

x

(b)

x

x

x

f

ln

)

(

2

dla

e

x

e

,

1

(c)

x

x

x

f

ln

)

(

dla

3

,

1 e

x

(d)

x

e

x

x

f

2

)

(

dla

1

,

2

x

(e)

x

x

x

f

2

cos

sin

2

)

(

dla

2

,

0

x

6. Zbadać funkcję i narysować wykres.

(a)

x

xe

x

f

)

(

(b)

x

x

x

f

ln

)

(

(c)

2

3

2

)

(

x

x

x

f

(d)

2

)

(

x

xe

x

f

(e)

x

xe

x

f

1

)

(

(f)

4

12

2

2

)

(

x

x

f

(g)

x

e

x

x

f

2

)

(

Odpowiedzi.

1.(a)

1

3

5

)

(

'

2

4

x

x

x

f

, rośnie dla

R

x

(b)

)

2

(

2

)

(

'

x

x

f

, rośnie dla

2

x

, maleje dla

2

x

(c)

2

2

)

4

(

)

4

(

2

)

2

(

)

(

'

x

x

x

x

x

f

, rośnie dla

4

x

,

2

0

x

,

2

x

;

maleje dla

2

4

x

,

0

2

x

(d)

2

)

2

(

)

3

)(

1

(

)

(

'

x

x

x

x

f

, rośnie dla

1

x

,

3

x

; maleje dla

2

1

x

,

3

2

x

(e)

)

2

)(

2

(

)

(

'

x

x

x

x

f

, rośnie dla

2

x

,

2

0

x

; maleje dla

0

2

x

,

2

x

(f)

x

e

x

f

1

)

(

'

, rośnie dla

0

x

, maleje dla

0

x

(g)

2

8

)

2

)(

2

(

2

)

(

'

x

x

x

x

f

, rośnie dla

2

2

x

; maleje dla

2

2

2

x

,

2

2

2

x

(h)

2

2

1

)

(

'

x

x

x

x

f

, rośnie dla

0

x

, maleje dla

2

x

2.(a)

)

1

)(

3

(

12

)

(

'

x

x

x

x

f

, minimum dla

3

x

,

1

x

, maksimum dla

0

x

(b)

)

4

)(

1

(

6

)

(

'

x

x

x

f

, minimum dla

4

x

, maksimum dla

1

x

(c)

)

)(

(

4

)

(

'

2

5

2

5

x

x

x

x

f

, minimum dla

2

5

x

,

2

5

x

, maksimum dla

0

x

(d)

)

2

)(

2

)(

1

)(

1

(

5

)

(

'

x

x

x

x

x

f

, minimum dla

1

x

,

2

x

,

maksimum dla

2

x

,

1

x

(e)

2

2

1

2

1

)

)(

(

4

)

(

'

x

x

x

x

f

, minimum dla

2

1

x

, maksimum dla

2

1

x

3.(a)

)

2

)(

2

(

12

)

(

'

'

x

x

x

f

, wklęsła:

2

x

,

2

x

, wypukła:

2

2

x

, p.p.

2

x

(b)

4

)

1

(

)

1

)(

1

)(

3

(

2

2

2

)

(

'

'

x

x

x

x

x

x

f

, wklęsła:

`

1

x

,

1

0

x

,wypukła:

0

1

x

,

1

x

,

p.p.

0

x

(c)

)

3

)(

3

(

20

)

(

'

'

x

x

x

x

f

, wklęsła:

3

x

,

3

0

x

,wypukła:

0

3

x

,

3

x

,

p.p.

3

x

,

0

x

(d)

)

5

6

(

2

)

(

'

'

2

x

x

f

, wklęsła:

R

x

(e)

3

4

)

(

''

x

x

f

, wklęsła:

0

x

, wypukła:

0

x

, p.p. brak

(f)

)

2

)(

2

)(

1

)(

1

(

60

)

(

'

'

x

x

x

x

x

f

, wklęsła:

2

x

,

1

1

x

,

2

x

,

wypukła:

1

2

x

,

2

1

x

, p.p.

2

x

,

1

x

4.(a)

2

1

x

,

2

y

(b)

2

x

y

(c)

3

x

,

x

y

2

(d)

1

x

, prawostronna

(e)

3

2

x

,

x

y

(f)

2

y

, lewostronna

(g)

2

x

, prawostronna;

1

y

(h)

x

y

, lewostronna;

x

y

, prawostronna

5.(a)

1

)

1

(

f

,

3

)

9

(

f

(b)

e

e

f

2

1

1

)

(

,

2

)

(

e

e

f

(c)

0

)

1

(

f

,

e

e

f

2

)

(

2

(d)

2

4

)

2

(

e

f

,

0

)

0

(

f

(e)

2

3

6

5

6

)

(

)

(

f

f

,

3

)

2

3

(

f

6. Rysunki na odwrocie.

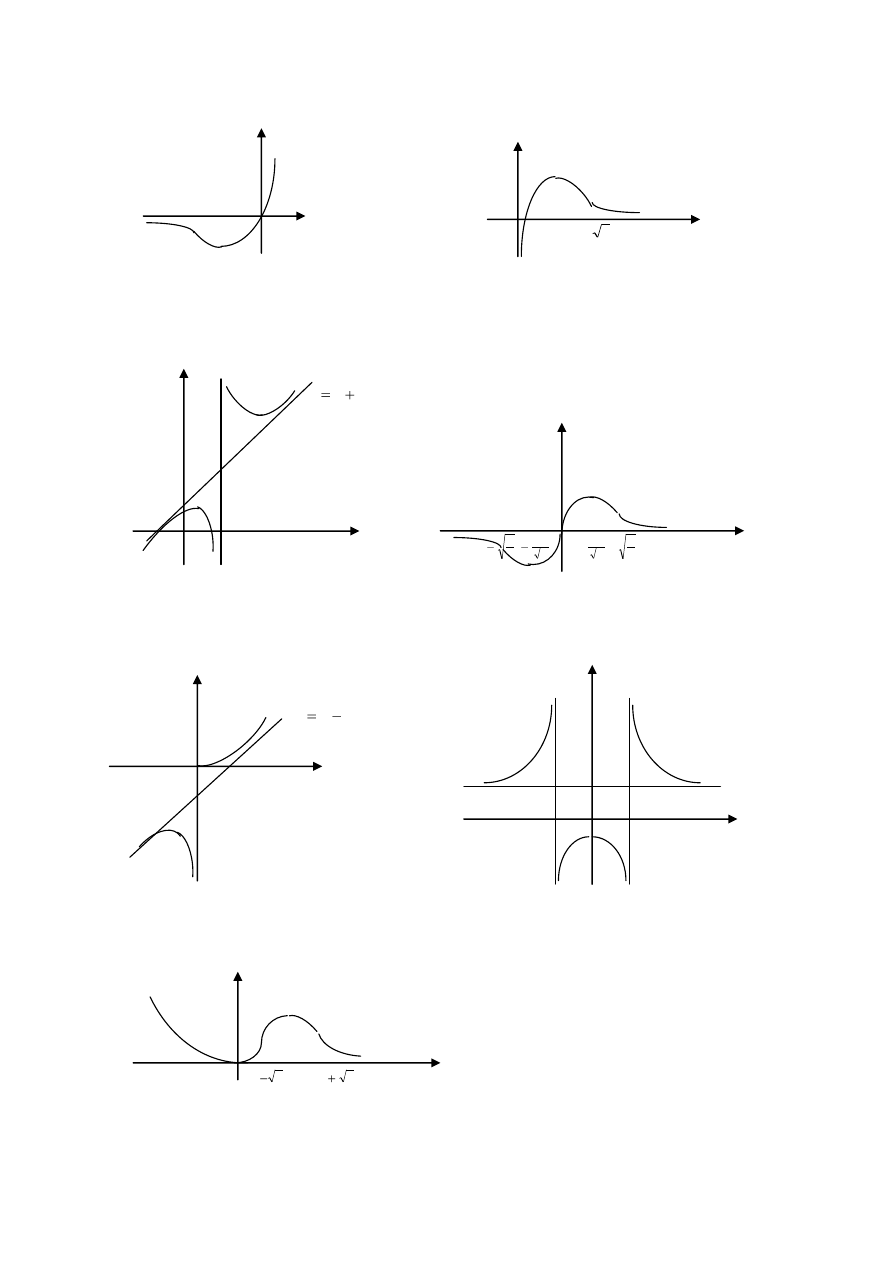
Zadanie 6.

-

-2 -1

e

e

e

(a)

(b)

2

x

y

1 2

3

2

3

2

1

2

1

2

3

(c)

(d)

1

x

y

-1

2

2

-1

(e)

(f)

2

2

2

2

2

(g)