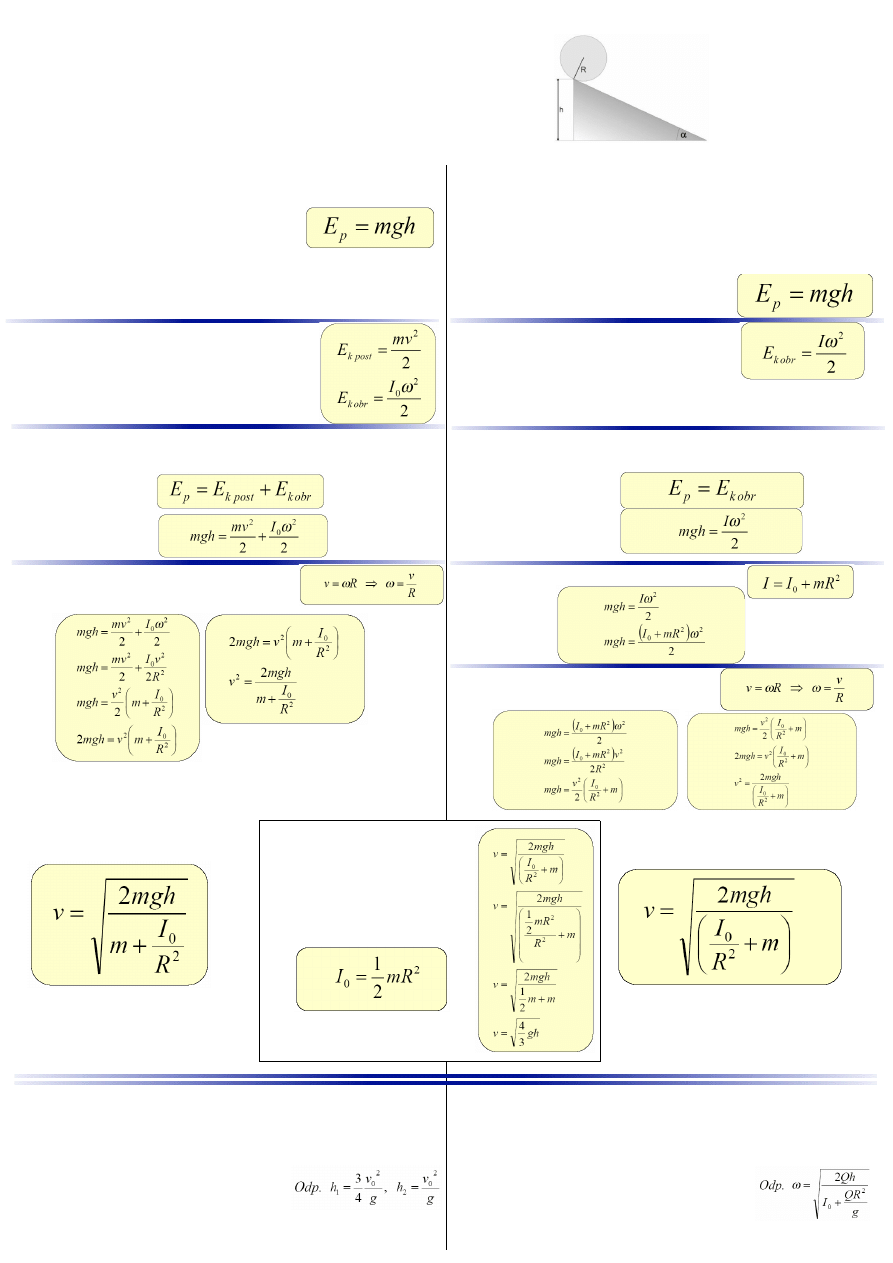
Zastosowanie zasady zachowania energii w ruchu obrotowym.

Oblicz prędkość środka masy walca o masie m i 

promieniu R toczącego się bez poślizgu po równi 

pochyłej.

Pierwsza metoda rozwiązania:

1. Walec w najwyższym położeniu na równi ma 

względem umownego poziomu 
zero energię potencjalną 
grawitacji równą :

2. W trakcie ruchu wzdłuż równi 

energia 

potencjalna 

zamieniana jest na energię 

kinetyczną ruchu postępowego i energię 
kinetyczną ruchu obrotowego walca.

3. Jeśli nie uwzględnimy oporów ruchu, to spełniona jest

zasada zachowania energii mechanicznej 

i u podstawy

równi:

czyli

4. Ponieważ ruch odbywa się bez
 

poślizgu, więc

czyli

Zadanie 1:

Walec o promieniu R i masie m i rura cienkościenna
o promieniu R i masie m wtaczają się bez poślizgu
z jednakową prędkością początkową 
v0 ruchu postępowego na równię 
pochyłą o kącie nachylenia a. Na 
jakie wysokości h1 i h2 wtoczą się walec i rura?

Druga metoda rozwiązania:
Nie rozpatrujemy ruchu walca jako złożenia ruchu 

postępowego i obrotowego tylko jako obrót względem 

chwilowej osi obrotu.

1. Walec w najwyższym położeniu na równi ma względem
umownego poziomu zero energię 
potencjalną grawitacji równą :

2. W trakcie ruchu wzdłuż równi 

energia potencjalna 

zamieniana jest na 

energię kinetyczną ruchu obrotowego 
walca względem chwilowej osi obrotu.

3. Jeśli nie uwzględnimy oporów ruchu, to spełniona jest

zasada zachowania energii mechanicznej 

i u podstawy

równi:

czyli

4. Korzystają c z twierdzenia Steinera:

4. Ponieważ ruch odbywa się bez 

poślizgu, więc

czyli

Zadanie 2:

Walec o promieniu R i momencie bezwładności I0
osadzony na osi pokrywającej się z jego osią symetrii
rozpędzany jest za pomocą nawiniętego 
sznura , na którym zawieszono cię żar Q. 
Oblicz prędkość kątową walca w chwili, 
gdy cię żar przebędzie drogę h.

W obu metodach 
rozwiązania 

podstawiamy 

wyrażenie określają ce 
moment bezwładności walca