związek energii potencjalnej z siłami pola

Znając postać energii potencjalnej, tj. funkcję E_p = E_p(x,y,z) można określić siłę działającą na ciało w każdym punkcie pola.

Otrzymaliśmy poprzednio

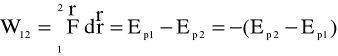
skąd wynika, że dla pracy elementarnej zachodzi

co można zapisać inaczej

gdzie
przedstawia zmianę energii potencjalnej wywołaną działaniem tylko składowej F_x ; podobnie dla pozostałych współrzędnych y oraz z.

Oznacza to, że zachodzą relacje

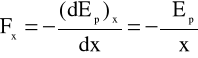
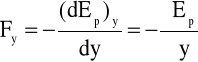
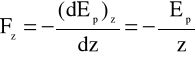
gdzie np.
nosi nazwę pochodnej cząstkowej i odpowiada szybkości zmian energii potencjalnej przy zmianie dx, podczas gdy przyjmujemy, że równocześnie dy = 0 oraz dz = 0.

Możemy więc zapisać siłę

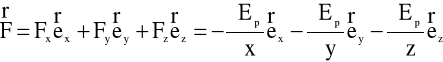
Ogólnie - wektor, o składowych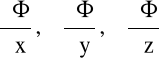
; gdzie
jest funkcją skalarną współrzędnych x, y, z nazywamy gradientem funkcji
i przyjęto oznaczać go
lub
albo
.

Ostatecznie więc

Siła zachowawcza jest równa ujemnemu gradientowi energii potencjalnej.

energia kinetyczna ruchu obrotowego bryły sztywnej

Dla elementarnej masy dm bryły sztywnej obracającej się wokół osi

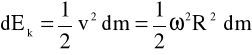
gdzie R jest odległością elementu o masie dm od osi obrotu.

Dla bryły sztywnej - energia kinetyczna

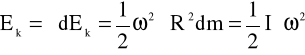
praca momentu sił zewnętrznych

Jeśli na bryłę działają siły zewnętrzne, to ich praca dW powoduje zmianę energii kinetycznej dE_k , zatem

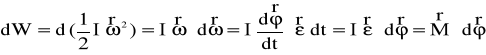
Praca w ruchu obrotowym, wykonana przez moment sił zewnętrznych, w skończonym przedziale kątowym, wyraża się więc wzorem

który jest analogiczny do zapisu pracy w ruchu postępowym.