1

00512 Mechanika nieba D – part 2

TEORIA

00512

Mechanika nieba D

Część 2

Pole grawitacyjne.

Praca w polu grawitacyjnym.

Energia potencjalna w polu centralnym.

Potencjał grawitacyjny.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 8
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Maj

ROK 2008

Dane osobowe właściciela arkusza

2

00512 Mechanika nieba D – part 2

TEORIA

Temat: 61

Pole grawitacyjne.

1.

Oddziaływanie grawitacyjne między punktami materialnymi wykorzystamy do bliższego omówie-
nia własności tzw. pola grawitacyjnego.

2.

Niech w idealnie pustej przestrzeni znajdzie się cząstka A: zgodnie z tym założeniem, nie działa na
nią żadna siła. Wpuszczamy teraz do tej przestrzeni cząstkę B. Nastąpi teraz, zgodnie z prawem
ciążenia powszechnego, oddziaływanie cząstki A na cząstkę B (i odwrotnie - zgodnie z kolei z III
zasadą dynamiki). Można to zjawisko opisać inaczej: obecność cząstki A w rozpatrywanej prze-
strzeni wpłynęła na właściwości tego obszaru, a mianowicie wytworzyła pole grawitacyjne obja-
wiające się tym, że dowolny punkt materialny (np. cząstka B) umieszczony w tej przestrzeni pod-
lega działaniu pewnej siły (grawitacyjnej) i zyskuje pewną energię (potencjalną). W tym ujęciu nie
ma bezpośrednio działania między cząstkami A i B, lecz istnieje pewien pośrednik, którym jest wy-
tworzone pole: cząstka A wytwarza w swym otoczeniu pole, które z kolei działa na cząstkę B.

3.

Zatem: pole grawitacyjne to obszar, w którym występują oddziaływania grawitacyjne Jest ono
polem wektorowym, gdyż działające w każdym jego punkcie siły mają określony kierunek, zwrot i
wartość.

4.

Tor, po którym porusza się masa próbna w polu grawitacyjnym pod działaniem sil przyciągania
nosi nazwę linii pola. Liniom tym przypisuje się zwrot odpowiadający zwrotowi ruchu masy prób-
nej, a więc np. ku środkowi kuli ziemskiej (gdy stanowi ona rozpatrywane źródło pola).

5.

Charakteryzująca pole grawitacyjne siła przyciągania

(1) F

G

M m

r

=

⋅

2

,

której podlega w danym punkcie masa m, zależy od wielkości tej masy. Dlatego lepiej określa pole
grawitacyjne charakterystyczna dla każdego jego punktu wielkość niezależna od masy m znajdują-
cego się w nim ciała, zwana natężeniem pola.
Miarą natężenia pola grawitacyjnego jest stosunek siły przyciągania F działającej na ciało w da-
nym jego punkcie do masy m tego ciała

(2)

γ

=

F

m

Natężenie

r

γ

pola grawitacyjnego jest wektorem mającym kierunek i zwrot zgodny z kierunkiem i

zwrotem siły przyciągania działającej na ciało w danym punkcie pola

(3)

r

r

γ

=

F

m

6.

Jak widać ze wzoru (3) natężenie pola grawitacyjnego w danym punkcie pola jest równe liczbowo
przyspieszeniu, jakiego doznaje w tymże punkcie ciało pod działaniem sił przyciągania.

7.

Wstawiając do wzoru (2) równanie (1) otrzymamy

(4)

γ

= ⋅

G M

r

2

,

zatem: wartość natężenia pola grawitacyjnego w danym jego punkcie maleje proporcjonalnie do
kwadratu odległości tego punktu od źródła pola.

3

00512 Mechanika nieba D – part 2

TEORIA

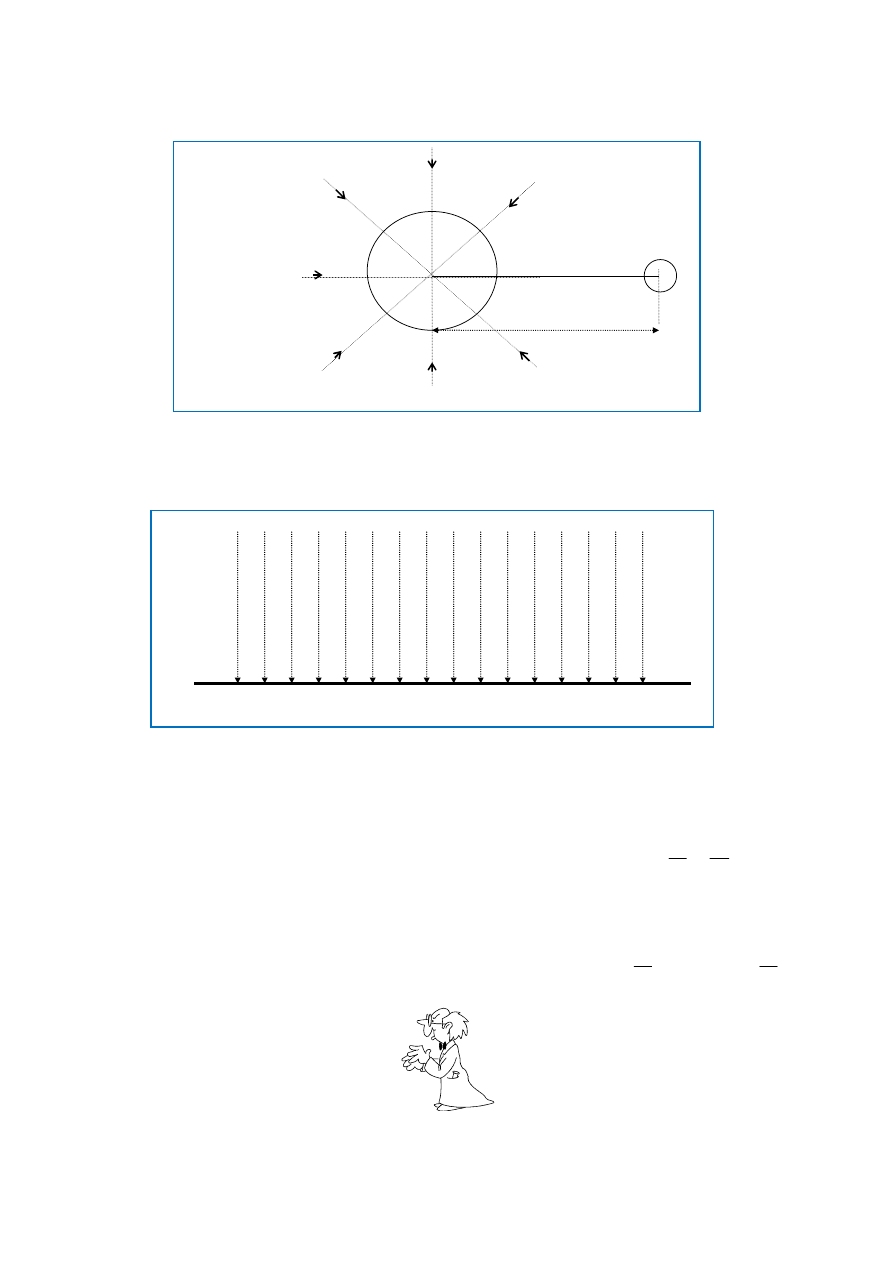
Graficznie przedstawia się ten fakt zmniejszając gęstość linii pola

M m

r

Rys. 1 Pole grawitacyjne centralne.

8.

Dla niewielkich wysokości i niewielkiego obszaru powierzchni Ziemi można z dużym przybliże-
niem przyjąć, że linie pola grawitacyjnego są wzajemnie równoległe, a jego natężenie jest we
wszystkich punktach pola stałe i liczbowo równe wartości miejscowego przyspieszenia ziemskiego
g. Pole takie nazywa się polem jednorodnym.

Rys. 2 Pole grawitacyjne jednorodne.


Zadanie: 1

Masa Księżyca wynosi

7 4 10

22

,

⋅

kg

, zaś jego promień 1720 km. Obliczyć natężenie pola grawitacyj-

nego na powierzchni Księżyca oraz jego stosunek do natężenia pola grawitacyjnego na powierzchni
Ziemi.

(Odp.

γ

γ
γ

k

k

z

m

s

=

=

1 67

0 17

2

,

,

,

)

Zadanie: 2
Jaką wartość ma przyspieszenie ziemskie na wysokości a) 1 km, b) 32 km od powierzchni Ziemi ?

(Odp.

a g

m

s

b g

m

s

a

b

)

,

,

)

,

=

=

9 8

9 71

2

2

)

4

00512 Mechanika nieba D – part 2

TEORIA

Temat: 62 Praca w polu grawitacyjnym jednorodnym i centralnym.

1.

Już wcześniej zwróciliśmy uwagę na zachowawczy charakter siły ciężkości, co sprowadzi-
liśmy do wniosków:

⇒

praca wykonywana przez siłę ciężkości (lub siłę zewnętrzną, która ją równoważy) nie
zależy od kształtu drogi, po której ciało się przesuwa, lecz od położenia początkowego
i końcowego tego ciała, czyli

⇒

praca wykonana przez siłę ciężkości po drodze zamkniętej jest zawsze równa zeru.

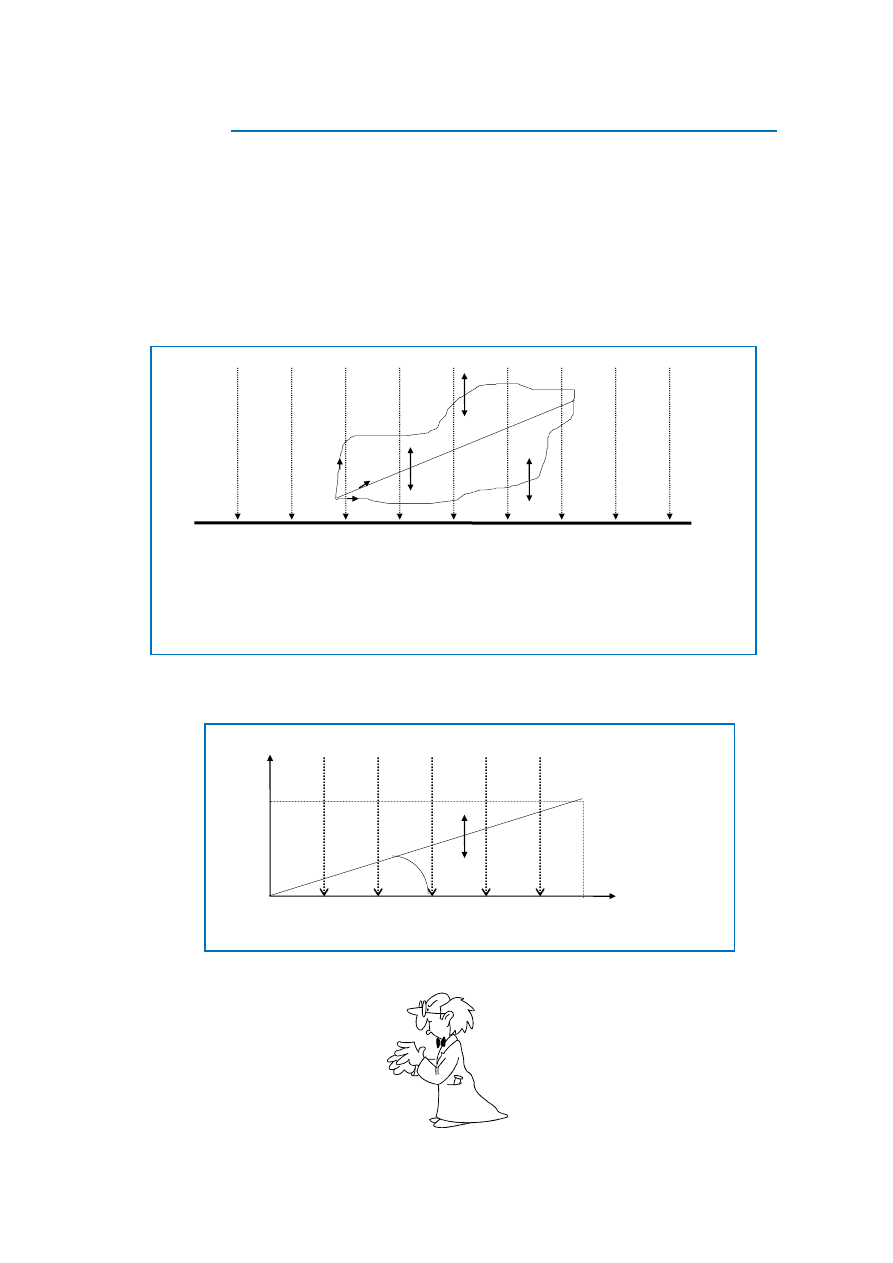
Teraz, gdy znamy pojęcie pola, stwierdzamy, że pole grawitacyjne jednorodne jest polem
zachowawczym. (rys. 1)

r

F

z

r

F

g

r

F

z

r

F

z

r

F

g

r

F

g

Rys. 1
Przesuwanie masy próbnej w polu grawitacyjnym jednorodnym po różnych dro-
gach, ale z zachowaniem początkowego i końcowego położenia daje w sumie wy-

konanie tej samej pracy..(

r

F

g

- siła ciężkości,

r

F

z

- siła zewnętrzna)

(1) W

F r

F r

F

h

m g h

g

= ⋅ = ⋅ ⋅

=

⋅ = ⋅ ⋅

r r

cos

α

(rys. 2)

Y

h

r

F

z

r

F

g

α

0 r X

Rys. 2

5

00512 Mechanika nieba D – part 2

TEORIA

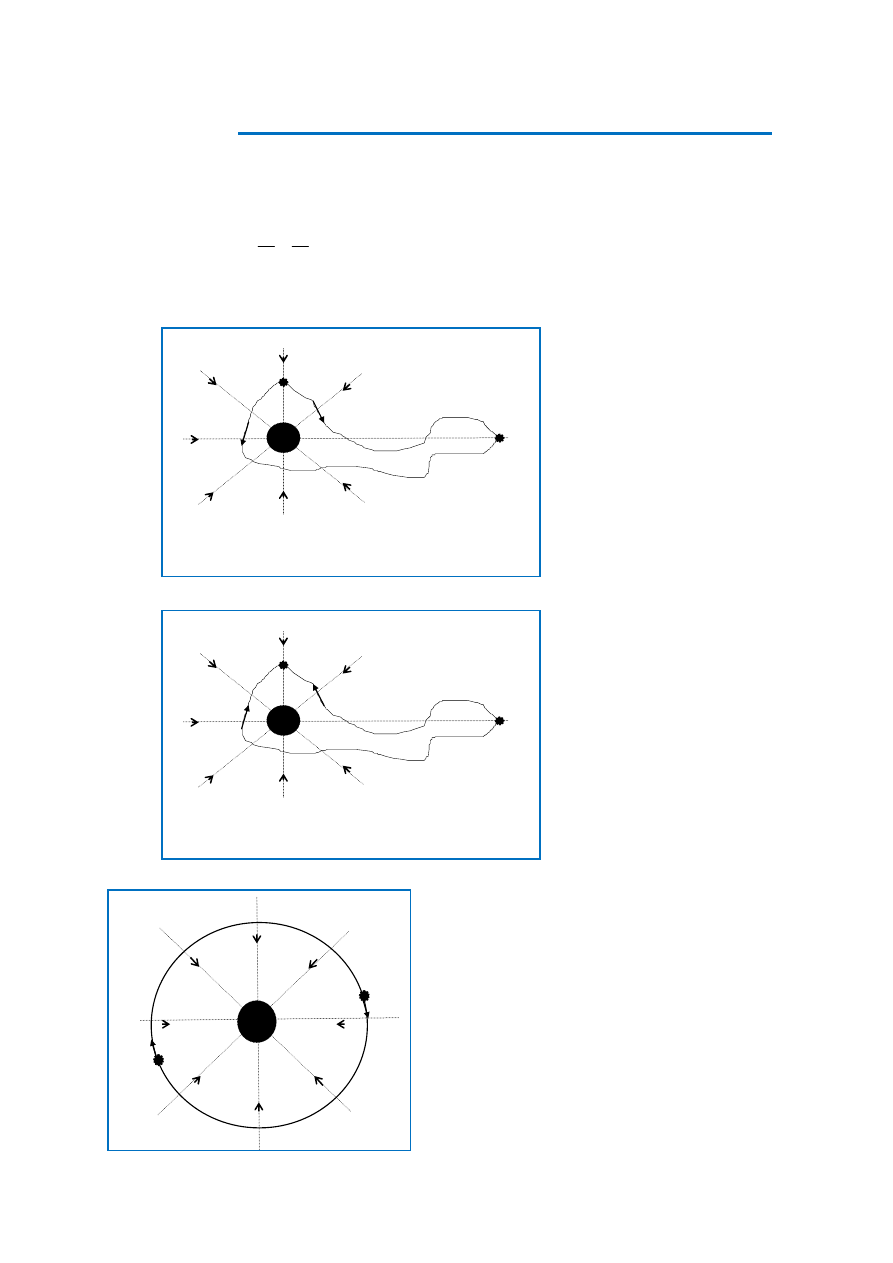
2.

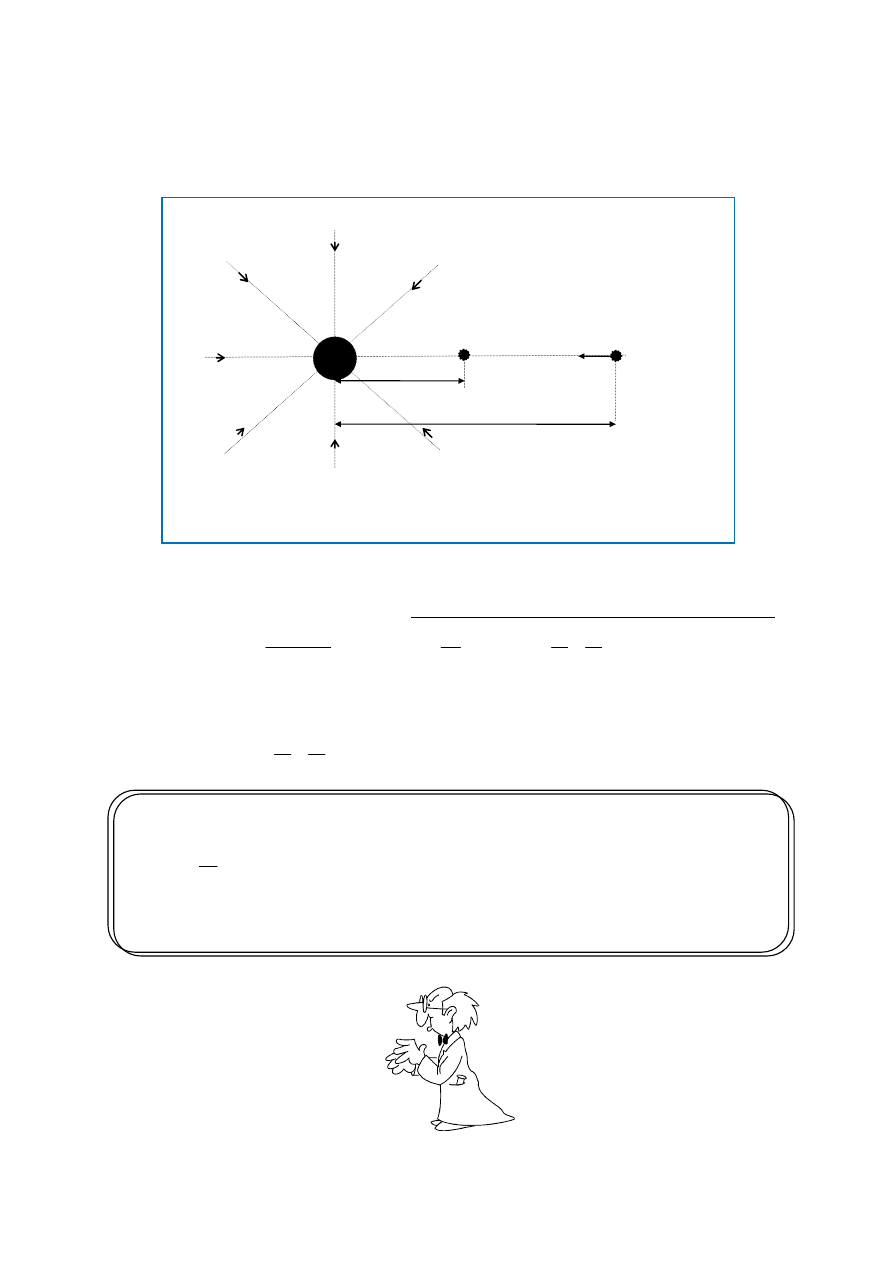
Jednakże nie każde pole grawitacyjne jest jednorodne. Rozpatrując ruch niewielkiego ciała
niebieskiego w pobliżu jakiejś planety (np. Ziemi) możemy uważać, iż ciało to jest pod
wpływem pola grawitacyjnego centralnego (rys. 3)

B A
M m

r

B

r

A

Rys. 3
Obliczanie pracy wykonanej przez siłę ciężkości (lub siłę zewnętrzną przy przesu-
waniu masy próbnej z jednego do drugiego punktu w polu grawitacyjnym central-
nym.

*Proste rachunki prowadzą do wniosku, że i takie pole jest zachowawcze. Uogólniając
nasze badania, możemy stwierdzić, że każe pole grawitacyjne jest polem zachowawczym.

(2) W

Fdr

G M m

r

dr

G M m

dr

r

G M m

r

r

r

r

r

r

r

r

A

B

A

B

A

B

A

B

=

=

⋅

⋅

= ⋅

⋅

= ⋅

⋅

−











∫

∫

∫

r r

2

2

1

1

Wzór (2) opisuje pracę wykonaną przez siłę zewnętrzną

r

F

z

, natomiast analogicznie moż-

na znaleźć wzór określający pracę siły grawitacji:

(3)

W

G M m

r

r

B

A

= ⋅

⋅ ⋅

−











1

1

Zadanie:

Wyznaczyć okres obrotu T Księżyca dokoła Ziemi wiedząc, że przyspieszenie ziemskie na biegunie wynosi

g

0

=









2

83

,

9

s

m

, promień Ziemi R = 6370[km], odległość między Księżycem a Ziemią wynosi h =

3 84 10

8

,

⋅

[m].

(Odp. 27,4 doby)

6

00512 Mechanika nieba D – part 2

TEORIA

Temat: 63 Energia potencjalna ciała w polu grawitacyjnym.

1.

Za miarę zmiany energii potencjalnej w polu grawitacyjnym przyjmujemy pracę siły ze-
wnętrznej równoważącej w każdym punkcie siłę grawitacji. W przypadku pola centralne-
go, mamy

(1)

∆

E

GMm

r

r

p

A

B

=

−











1

1

2.

*Zmiany energii potencjalnej ciała możemy rozpatrywać w przypadkach, gdy

a)

ciała oddala się od źródła pola (rys. 1)

m A

B
M m

Rys. 1

b)

ciało zbliża się do źródła pola (rys. 2)

m B

A
M m

Rys. 2

c) ciało nie zmienia odległości względem źródła pola (rys. 3)

m

M

m

Rys. 3

Mamy tu do czynienia z przyro-
stem energii potencjalnej

∆

E

p

>

0

Mamy tu do czynienia z ubyt-
kiem energii potencjalnej

∆

E

p

<

0

Energia potencjalna nie ulega zmianie

∆

E

p

= 0

Ciało porusza się po powierzchni ekwipo-
tencjalnej (powierzchni kuli o promieniu r
na której panuje ta sama wartość potencjału
grawitacyjnego)

7

00512 Mechanika nieba D – part 2

TEORIA

3.

W każdym polu zachowawczym zmiana energii potencjalnej ciała przy zmianie jego poło-
ż

enia między danymi punktami pola jest określona jednoznacznie, bo zależy tylko od po-

łożenia tych punktów.

4.

*Obliczamy teraz energię potencjalną ciała w danym punkcie pola, czyli analizujemy pracę
siły zewnętrznej przesuwania ciała z danego punktu pola do nieskończoności (lub inaczej:
punkt B przeniesiony został do nieskończoności, punkt A znajduje się w analizowanym
polu)

(2) E

E

E

GMm

r

r

B

A

pot

r

A

B

B

−

=

=

−











→∞

∆

lim

1

1

Zwykle umawiamy się, że energia potencjalna w nieskończoności jest równa zeru (w
przypadku badania pól centralnych), czyli E

B

= 0, wtedy mamy

0

1

0

−

=

→

E

GMm

r

bowiem

r

A

A

B

,

Ostatecznie:
Wzór i jego interpretacja – obowiązkowe!

E

G M m

r

p

A

= − ⋅

⋅

5.

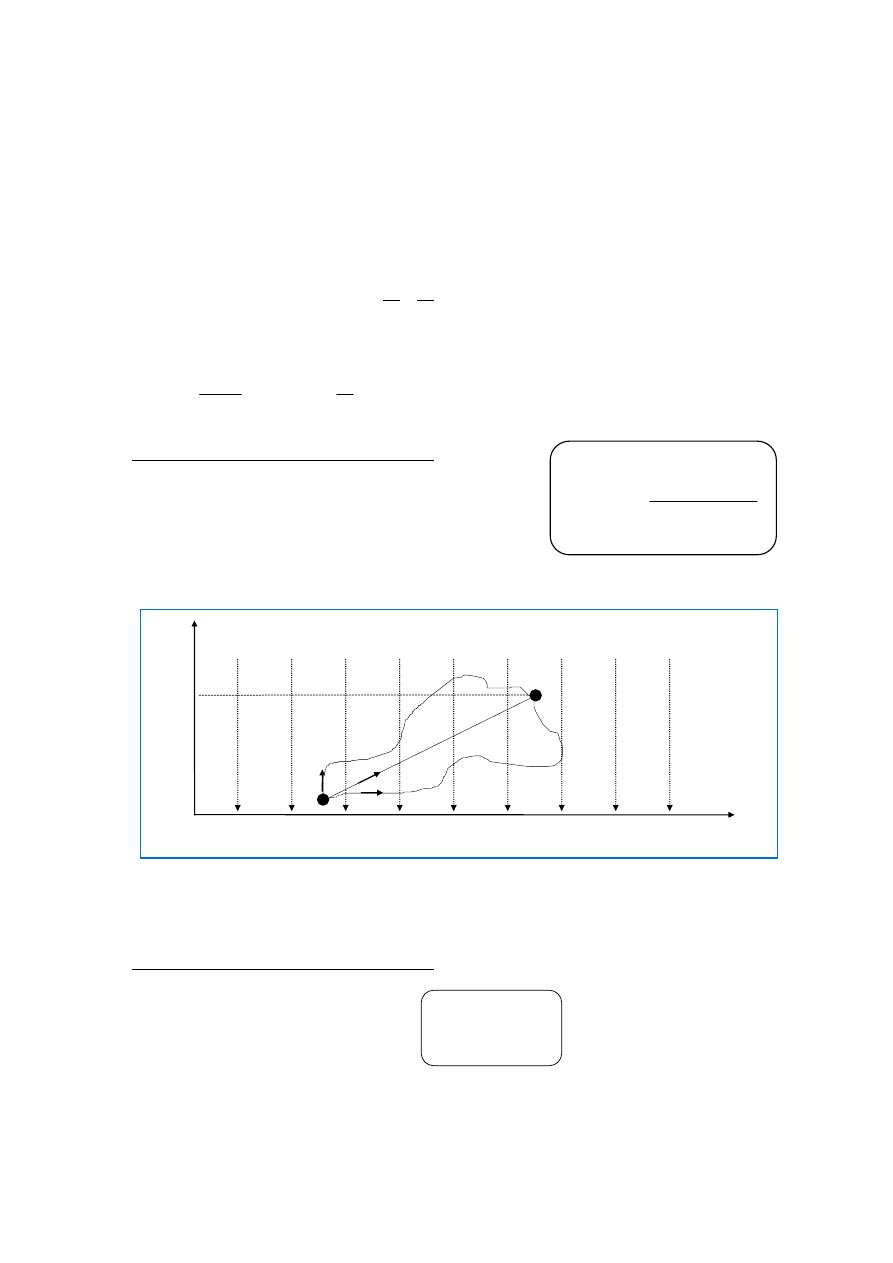
*Energia potencjalna w danym punkcie pola grawitacyjnego jednorodnego może być obli-
czona następująco:

y

B
h m

m A

x

Rys. 4

Teraz wygodnie jest przyjąć energię potencjalną ciał leżących na osi X (rys. 4) za równą
zeru (czyli E

A

= 0). Wtedy

∆

E

E

E

E

F h

m g h

pot

B

A

B

g

=

−

=

− =

⋅ = ⋅ ⋅

0

,

czyli:
Wzór i jego interpretacja – obowiązkowe!

( )

4

E

m g h

p

= ⋅ ⋅

(3)

8

00512 Mechanika nieba D – part 2

TEORIA

Temat: 64

Potencjał pola grawitacyjnego.

1.

Energia potencjalna nie charakteryzuje pola grawitacyjnego, bowiem dla różnych mas
przybiera różne wartości.

2.

Wielkością charakteryzującą pole grawitacyjne jest skalarna wielkość fizyczna zwana po-
tencjałem grawitacyjnym V:

(1) V

E

m

p

=

Zatem:

Potencjałem w określonym punkcie pola grawitacyjnego nazywamy stosunek

energii potencjalnej, jaką ma umieszczone w tym punkcie ciało, do masy tego ciała.

Jednostką potencjału grawitacyjnego w układzie SI jest

(2)

[ ]

V

J

kg

N m

kg

m

s

=

=

⋅ =













2

2

3.

Korzystając ze wzoru (1) możemy określić potencjał grawitacyjny w przypadku pola cen-
tralnego (rys. 1)

(3) V

G M m

r m

G M

r

= − ⋅

⋅

⋅

= − ⋅

4.

W przypadku pola jednorodnego otrzymujemy:

(4) V

m g h

m

g h

= ⋅ ⋅ = ⋅

5.

Ostatecznie wnioskujemy:

Pole grawitacyjne możemy opisać podając rozkład natężenia pola lub rozkład potencjału,
bowiem obie wymienione wielkości fizyczne nie zależą od masy umieszczanej w polu gra-
witacyjnym, lecz wyłącznie od własności pola.
Możemy stosować opis wektorowy (za pomocą natężenia grawitacyjnego) lub skalarny (za
pomocą potencjału grawitacyjnego) pola w zależności od potrzeby.

Rys. 1 Graficzny obraz zależności (3)

Rys. 2 Graficzny obraz zależności (4)

r

r

V

V