1

00513 Mechanika nieba D – part 3

TEORIA

00513

Mechanika nieba D

Część 3

Satelity Ziemi.

I i II prędkość kosmiczna

Stan przeciążenia i nieważkości

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 6
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

śyczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Wrzesień

ROK 2008

Dane osobowe właściciela arkusza

2

00513 Mechanika nieba D – part 3

TEORIA

Temat: 65

Satelity Ziemi.

1.

Stałym pytaniem tych, którzy nie zajmowali się nigdy studiowaniem fizyki jest „co powo-
duje, że satelity Ziemi nie spadają ?” Czy rakieta, której silnik przestał działać, nie powin-
na spadać ku środkowi Ziemi z przyspieszeniem ziemskim g, tak jak inne przedmioty w
pobliżu powierzchni Ziemi ? Odpowiemy: Tak, nisko lecące satelity Ziemi na orbicie ma-

ją przyspieszenie 9,8

m

s

2

, skierowane do środka Ziemi. Gdyby nie miały takiego przyspie-

szenia, odleciałyby w przestrzeń po stycznej do Ziemi. Każde ciało poruszające się po

obwodzie koła ma automatycznie przyspieszenie

v

r

2

. Jeśli jest to orbita kołowa wokół

Ziemi, to siłą, która nadaje to przyspieszenie jest siła ciężkości. Mamy więc

(1)

g

v

R

c

Z

=

2

, gdzie v

c

jest krytyczną prędkością orbitalną, a R

Z

- promieniem Ziemi

Rozwiązujemy równanie (1) względem v

c

(2) v

g R

m

s

m

km

s

c

Z

=

⋅

=

⋅

⋅

=

9 8

6 37 10

7 9

2

6

,

,

,

Jest to minimalna prędkość potrzebna, aby umieścić ciało na orbicie. Okres T, czyli czas
pełnego obiegu równa się obwodowi Ziemi podzielonemu przez v

c

(3)

T

R

v

km

km

s

Z

c

=

⋅

=

=

2

4000

7 9

84

π

,

min.

Ten wynik zgadza się ze znanym okresem orbitowania wielu nisko latających satelitów
Ziemi od Sputnika I zaczynając.
Isaac Newton był pierwszym, który zrobił pierwsze tego typu obliczenie (przed ok. 300
laty)
Osiągnięcie dokładnie v

c

nie jest konieczne do wejścia na orbitę. Przypuśćmy, że v jest o

10 % większe od v

c

. Przyspieszenie w pobliżu powierzchni Ziemi musi być g, mamy więc

(4)

g

v

R

czyli

R

v

g

=

=

2

2

,

, gdzie R - początkowy promień krzywizny orbity.

W tym przykładzie

v

v

g R

c

Z

= ⋅ = ⋅

⋅

11

11

,

,

. Wstawmy ten rezultat do równania (4):

(5)

(

)

R

g R

g

R

Z

Z

=

⋅

⋅

=

⋅

11

1 21

2

,

,

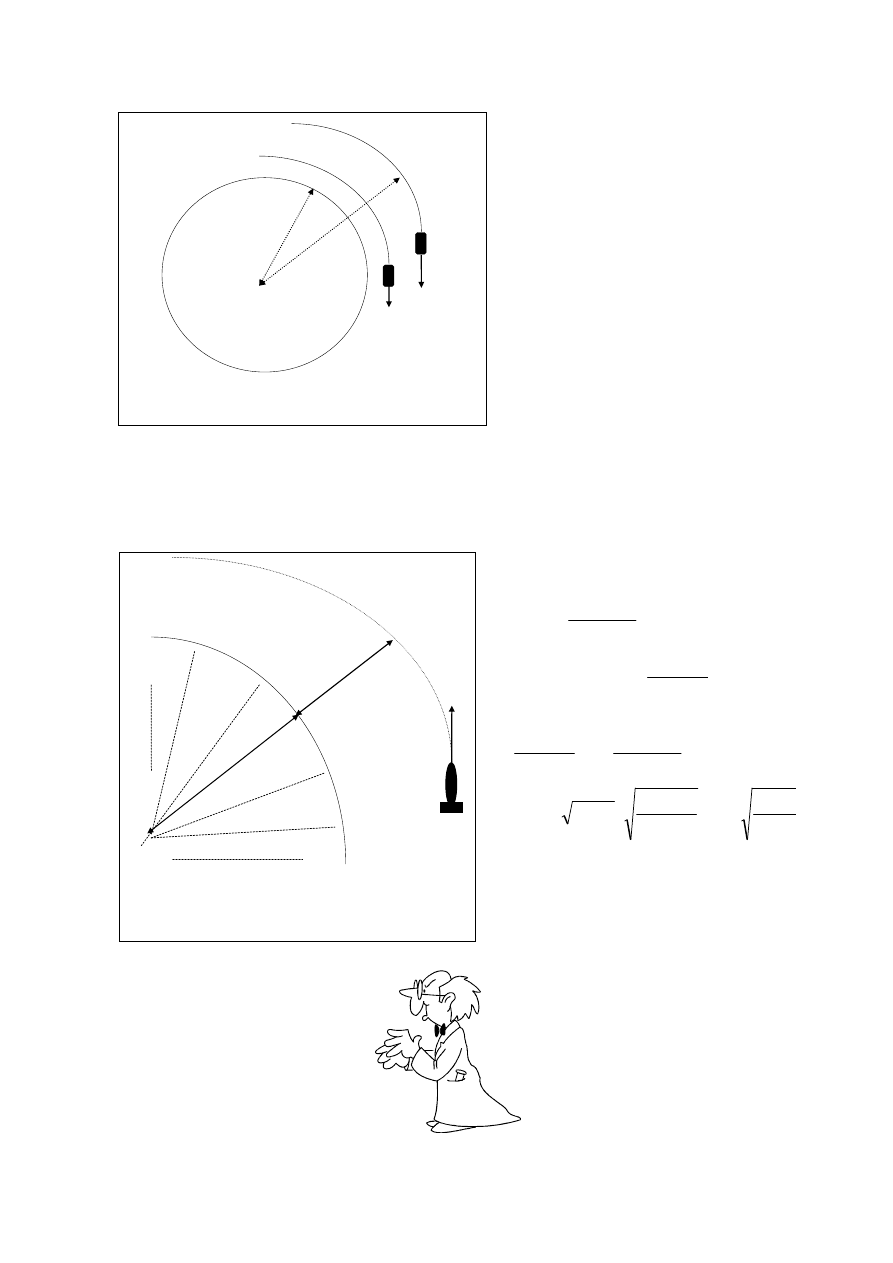
(rys. 1)

Widzimy, że promień początkowy orbity jest o 21 % większy od promienia satelity nisko
lecącego po orbicie kołowej.

3

00513 Mechanika nieba D – part 3

TEORIA

R

Z

1,21 R

Z

1,1 V

c

V

c

Rys. 1


2.

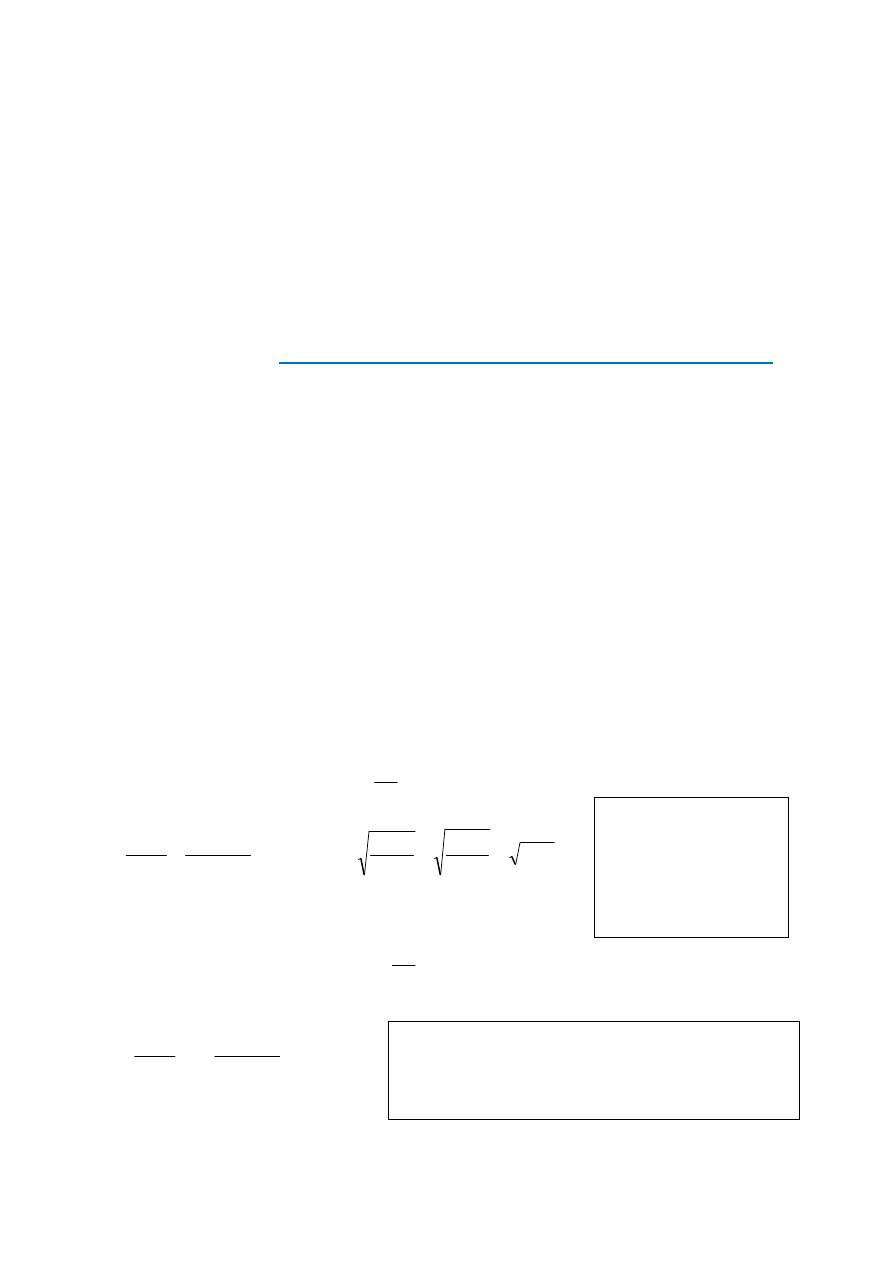
Gdy satelita na orbicie kołowej znajduje się na znacznej wysokości h powyżej powierzchni
Ziemi, musimy wtedy wziąć pod uwagę fakt doświadczalny, że przyspieszenie grawitacyj-
ne zależy odwrotnie proporcjonalnie do kwadratu odległości od środka Ziemi (rys. 2).
Przyspieszenie grawitacyjne w odległości

R

h

Z

+

jest

ZIEMIA

h

r

v

R

Z

Rys. 2

Taki pocisk początkowo będzie
oddalał się od Ziemi. Po pewnym
czasie jego prędkość będzie miała
składową skierowaną od środka
Ziemi. Siła grawitacji przeciwsta-
wia się tej składowej ruchu i w
konsekwencji v zmniejsza się do
tego stopnia, że pocisk zacznie
„spadać” ku Ziemi. Dokładnie, tor
będzie biegł po elipsie z jednym
ognisk w środku Ziemi.

(6)

(

)

g

g

R

R

h

Z

Z

1

2

2

= ⋅

+

Przyrównując g

1

do

(

)

v

R

h

Z

2

+

otrzymu-

jemy:

(7)

(

)

(

)

v

R

h

g

R

R

h

Z

Z

Z

2

2

2

+

= ⋅

+

(8)

(

)

(

v

g

g R

R

R

h

v

R

R

Z

Z

Z

c

Z

Z

= ⋅

⋅

⋅

+

= ⋅

+

Widzimy, że prędkość jest mniejsza od
prędkości krytycznej.

4

00513 Mechanika nieba D – part 3

TEORIA

3.

Gdy pojazd kosmiczny chce przejść z wyższej orbity kołowej na niższą, musi uruchomić
silniki rakietowe zwrócone w kierunku ruchu (siła przeciwstawiająca się ruchowi). W cza-
sie, gdy czynne są silniki wsteczne, pojazd kosmiczny nabiera prędkości jednocześnie
„spadając” powoli ku Ziemi. Gdyby taki silnik wsteczny uruchomić na masce samochodu,
spowodowałby on zmniejszenie prędkości samochodu, jednak według równania (8) pręd-
kość musi rosnąć, gdy h maleje - co wydaje się niezgodne ze zdrowym rozsądkiem. Takie
manewry można symulować używając komputera z odpowiednim wyświetlaczem. Zabawa
w gwiezdne wojny kryje pułapki dla nowicjusza. Jeśli będzie on postępować zgodnie ze
swoimi naturalnymi odruchami, pojazd kosmiczny będzie robić coś przeciwnego niż gracz
zamierzał.

Temat: 66

Loty kosmiczne. I i II prędkość kosmiczna.

1.

Loty między planetarne są najlepszą metodą poznawania najbliższych planet. Udane loty
kosmiczne bezzałogowe, ale z aparaturą naukową odbyły się na planety Wenus i Mars.

2.

Orbity rakiet międzyplanetarnych są bardzo złożone. Rakieta po przekroczeniu tzw. II
prędkości kosmicznej znajduje się głównie pod wpływem przyciągania grawitacyjnego
wywieranego przez Ziemię, dopiero w odległości około 900 000 km zaczyna przeważać
wpływ przyciągania przez Słońce i dlatego odległość ta jest przyjmowana jako granica
strefy oddziaływania grawitacyjnego Ziemi. Dalszy lot rakiety podlega tym prawom, które
rządzą ruchami planet.

3.

Pierwszym obiektem, który osiągnął II prędkość kosmiczną była radziecka stacja „Łuna 1”
wypuszczona 2 stycznia 1959 roku.

4.

Pierwszym człowiekiem, który znalazł się w przestrzeni kosmicznej był Jurij Gagarin; było
to 12 kwietnia 1961 roku. Lot kosmiczny statku „Wostok” trwał 108 minut. Warto tu jed-
nak zaznaczyć, że fakt ten jest aktualnie kontrowersyjny. W niektórych środowiskach
uważa się, że w rzeczywistości Gagarin nie opuścił Ziemi, lot był bezzałogowy, a kampa-
nia reklamowa była związana z chęcią wygrania przez ZSRR specyficznego (i prestiżowe-
go) wyścigu z USA o to, który z tych krajów pierwszy wyśle człowieka w kosmos.

5.

Prędkości kosmiczne.

⇒

I prędkość kosmiczna v

km

s

I

=

7 9

,

: po uzyskaniu tej prędkości ciało wyrzucone z Ziemi

staje się jego sztucznym satelitą.

m v

R

G M m

R

czyli

v

G M

R

g R

R

g R

I

⋅

= ⋅ ⋅

=

⋅

=

⋅

=

⋅

2

2

2

,

gdzie: m - masa satelity, M - masa Ziemi, R - promień Ziemi,

⇒

II prędkość kosmiczna v

km

s

II

=

11 2

,

: prędkość, po uzyskaniu której ciało uwalnia się z

wpływu grawitacyjnego Ziemi (skąd nazwa - prędkość ucieczki)

m v

G M m

R

⋅ + − ⋅ ⋅











=

2

2

0

Równanie wynika z fak-
tu, iż siła grawitacji pełni
rolę siły dośrodkowej
zmuszając

satelitę

do

ruchu po orbicie kołowej

.

Całkowita energia mechaniczna ciała wyrzuconego z
Ziemi z II prędkością kosmiczną jest podczas jego ruchu
stała i równa zeru (dlaczego ?)

5

00513 Mechanika nieba D – part 3

TEORIA

⇒

III prędkość kosmiczna v

km

s

III

=

16 7

,

: prędkość, po uzyskaniu której ciało może opu-

ś

cić Układ Słoneczny,

⇒

IV prędkość kosmiczna: v

km

s

IV

≥

130

: prędkość, po uzyskaniu której ciało może opu-

ś

cić Galaktykę.

Temat: 67

Stan przeciążenia i nieważkości.

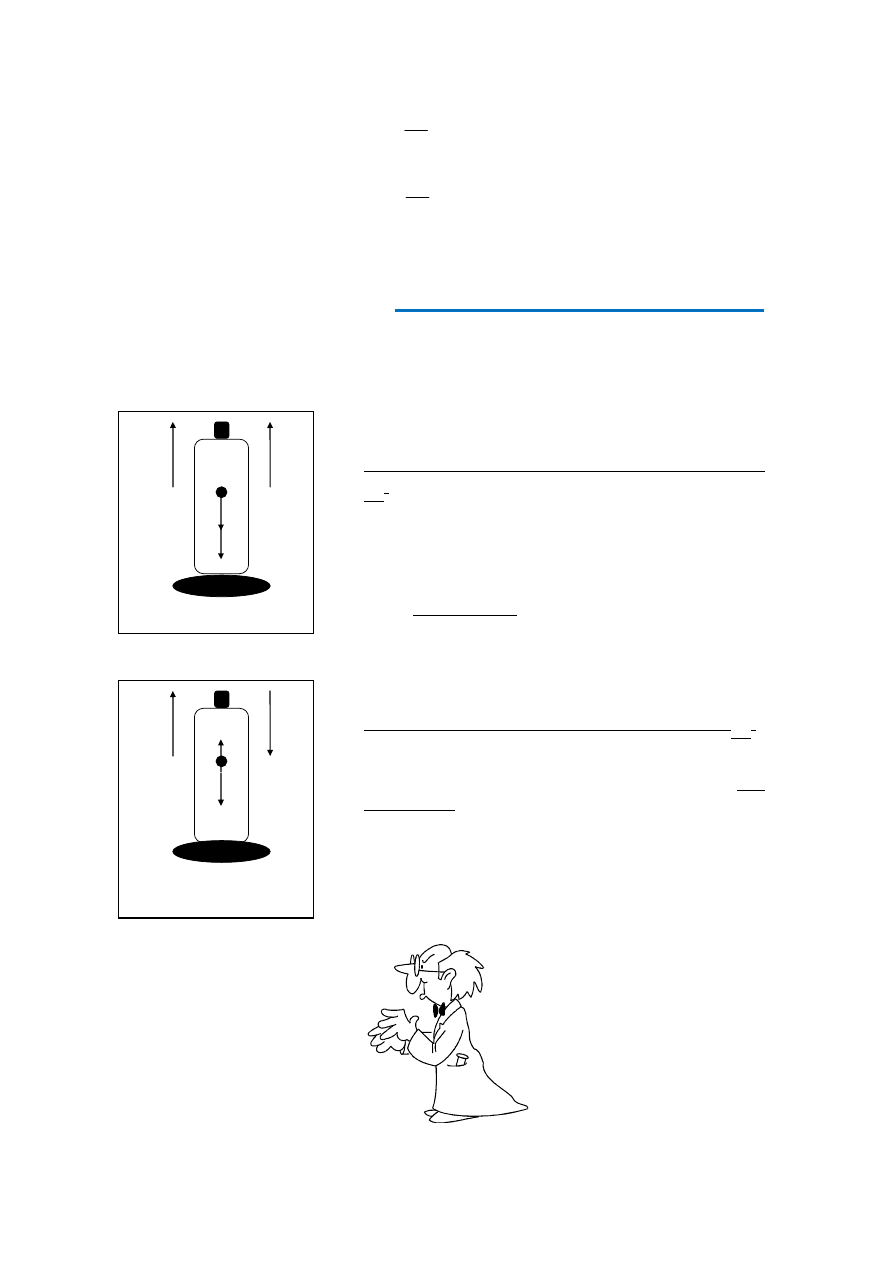
1.

Rakieta oddala się od powierzchni Ziemi. Jakie siły działają na kosmonautę? Dla prostoty
rozważań układ odniesienia zwiążemy z rakietą (układ nieinercjalny).

r

v

r

a

r

r

F

g

r

F

b

Rys. 1

2.

Rakieta nadal porusza się do góry, lecz zaczyna hamować :

r

v

r

a

r

r

F

b

r

F

g

Rys. 2

Rakieta przemieszcza się „do góry” z przyspieszeniem

r

a

r

:

r

r

r

F

F

F

g

b

=

+

, gdzie: F - siła działająca na kosmonautę,

F

g

- siła grawitacji, F

b

siła bezwładności ( zdefiniowa-

na jako F

b

= - ma

r

). Siła działająca na kosmonautę

jest większa od jego ciężaru (F

>

F

g

). Stan ten nazy-

wamy przeciążeniem.

Rakieta przemieszcza się „do góry” z opóźnieniem

r

a

r

:

r

r

r

F

F

F

g

b

=

−

Siła działająca na kosmonautę jest mniej-

sza od jego ciężaru (F

<

F

g

). Stan ten nazywamy nie-

dociążeniem.

6

00513 Mechanika nieba D – part 3

TEORIA

3.

Po wyhamowaniu (w pewnej odległości od powierzchni Ziemi) - rakieta wraca znowu do
miejsca startu.

r

v

r

a

r

r

F

b

r

F

g

Rys. 3


4.

W celu wylądowania rakieta zaczyna hamować.

r

v

r

a

r

r

F

g

r

F

b

Rys. 4

5.

W szczególnym przypadku, gdy rakieta porusza się bez napędu (np. niczym satelita po
orbicie okołoziemskiej), czyli pozostaje pod działaniem tylko siły grawitacji, wtedy

r

F

g

= 0

Stan taki nazywamy nieważkością.

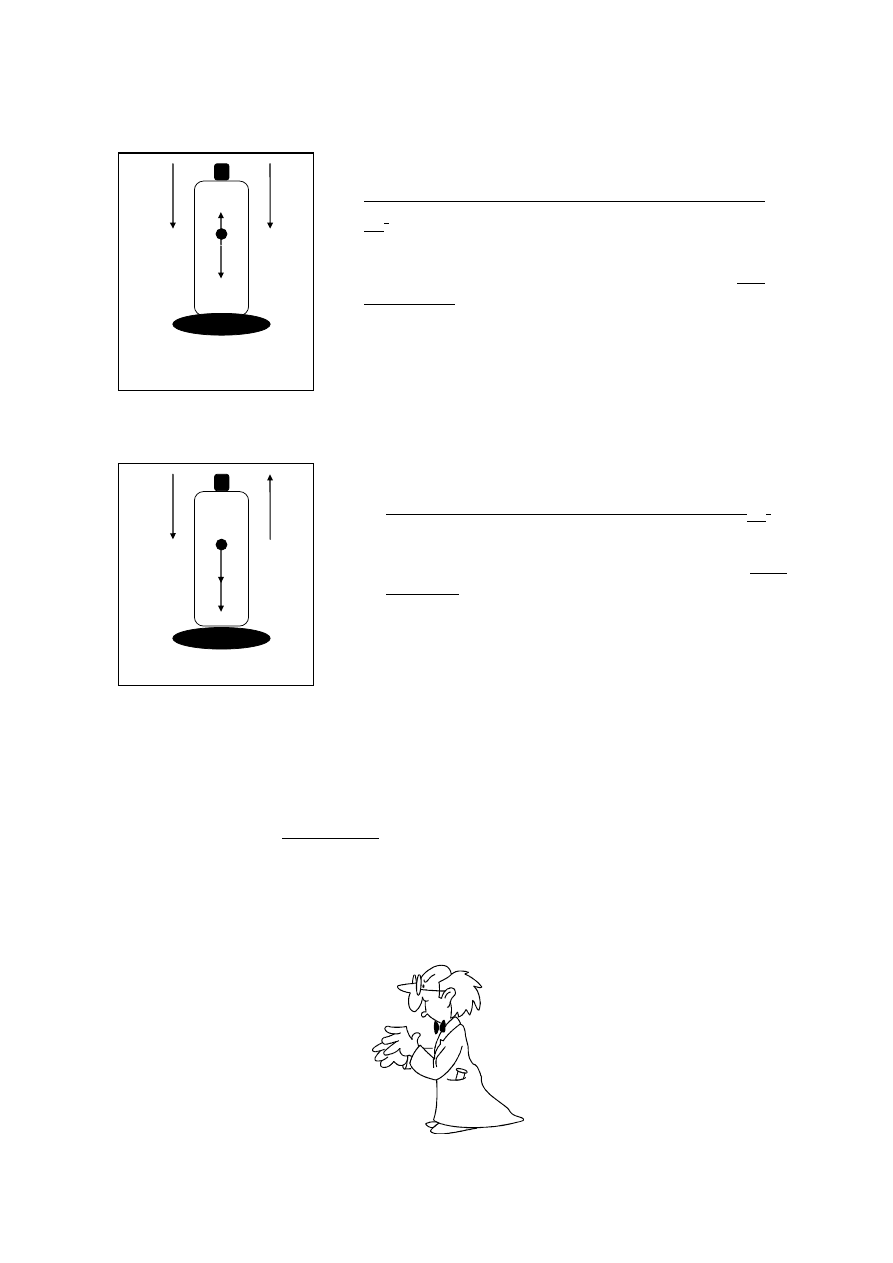
6.

Identyczna sytuacja ma miejsce w przypadku windy poruszającej się w górę i w dół, jedy-
nie przyspieszenia wind są znacznie mniejsze niż rakiet.

Rakieta przemieszcza się „w dół” z przyspieszeniem

r

a

r

:

r

r

r

F

F

F

g

b

=

−

Siła działająca na kosmonautę jest mniej-

sza od jego ciężaru (F

<

F

g

). Stan ten nazywamy nie-

dociążeniem.

Rakieta przemieszcza się „w dół” z opóźnieniem

r

a

r

:

r

r

r

F

F

F

g

b

=

+

, Siła działająca na kosmonautę jest więk-

sza od jego ciężaru (F

>

F

g

). Stan ten nazywamy prze-

ciążeniem.