MECHANIKA NIEBA

WYKŁAD 2

12.03.2008 r

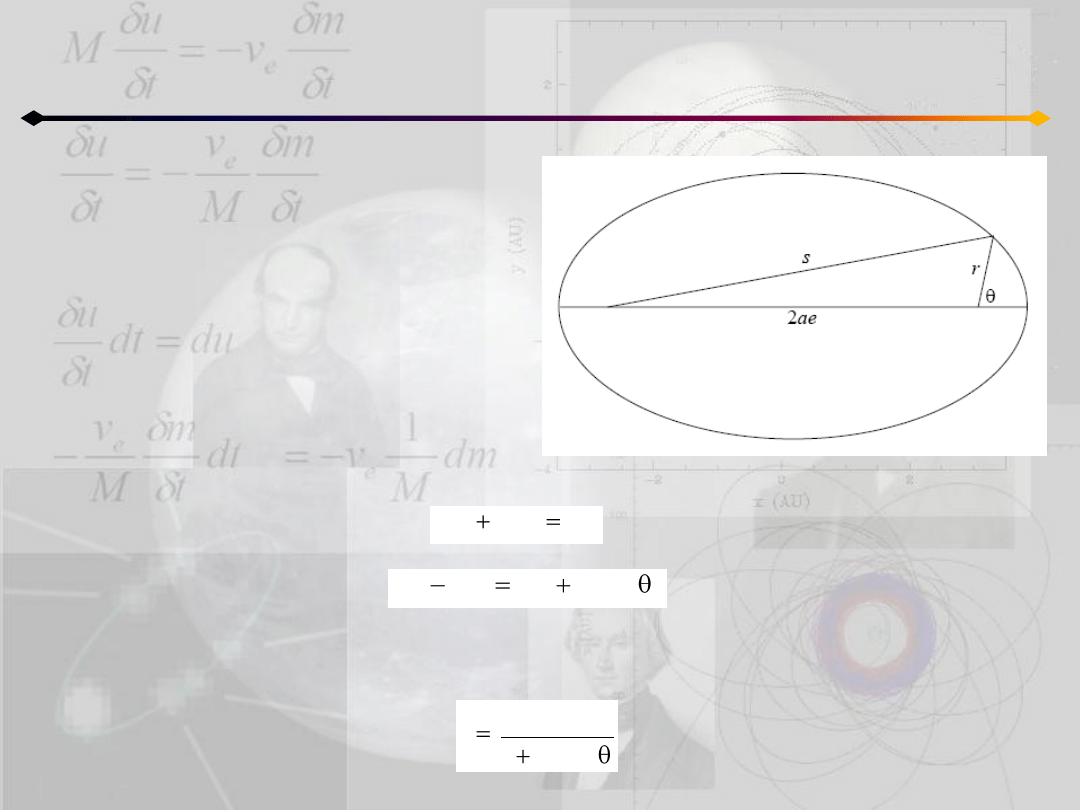
Krzywe stożkowe. Elipsa

Równanie biegunowe

P

F

2

F

1

F

2

leży w punkcie początkowym

układu (biegunie), a duża półoś
pokrywa się z linią początkową
(osią biegunową, θ=0

o

)

θ nie jest tym samym kątem co
wprowadzony wcześniej ν !

Korzystając z definicji elipsy:

można otrzymad:

lewa strona to wprowadzony wcześniej parametr elipsy p. Ostatecznie r-nie biegunowe
elipsy przyjmuje postad:

a

2

P

F

P

F

2

1

)

cos

e

1

(

r

)

e

1

(

a

2

cos

e

1

p

r

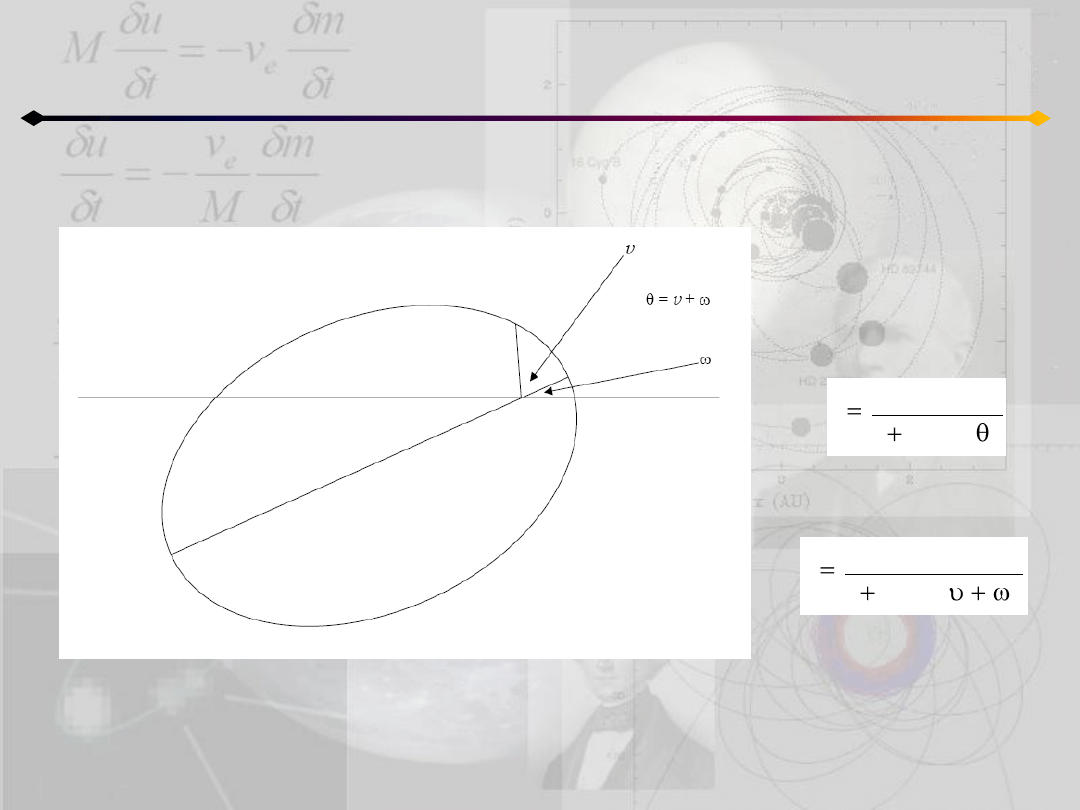
Krzywe stożkowe. Elipsa

Równanie biegunowe

Jeśli wielka półoś jest
nachylona pod kątem ω
do linii początkowej (osi
biegunowej) to:

czyli:

Różnica między θ oraz ν
jest oczywista

)

cos(

e

1

p

r

)

cos(

e

1

p

r

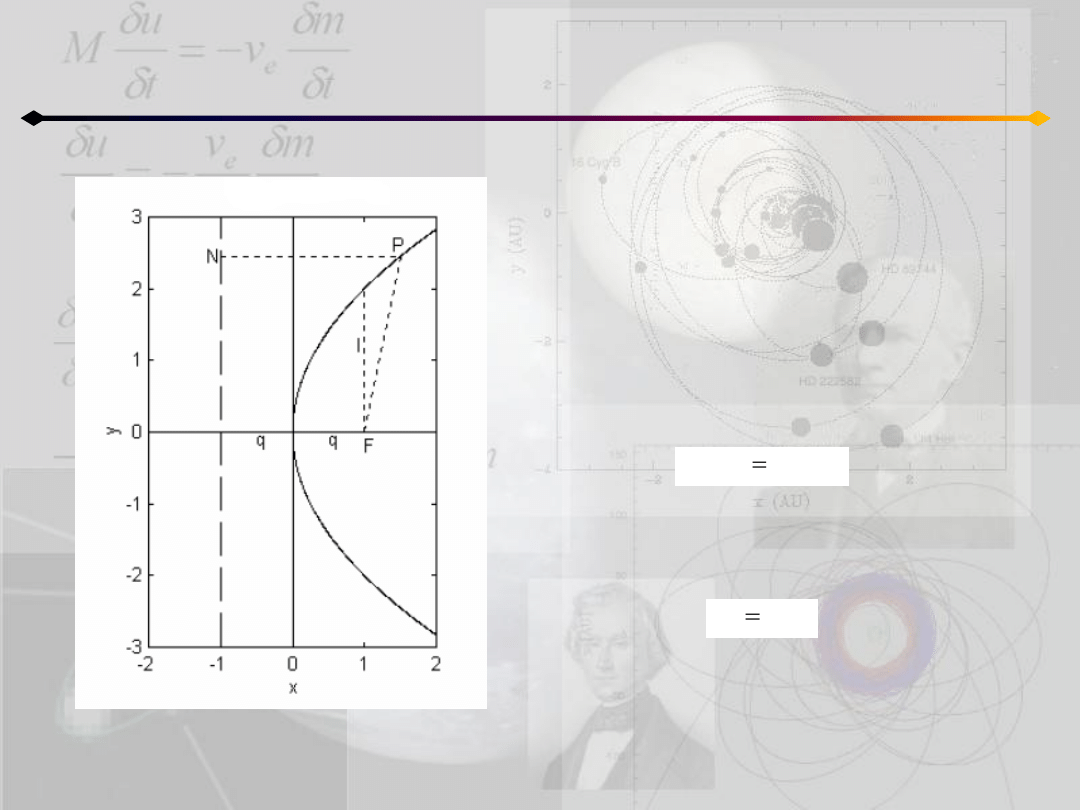
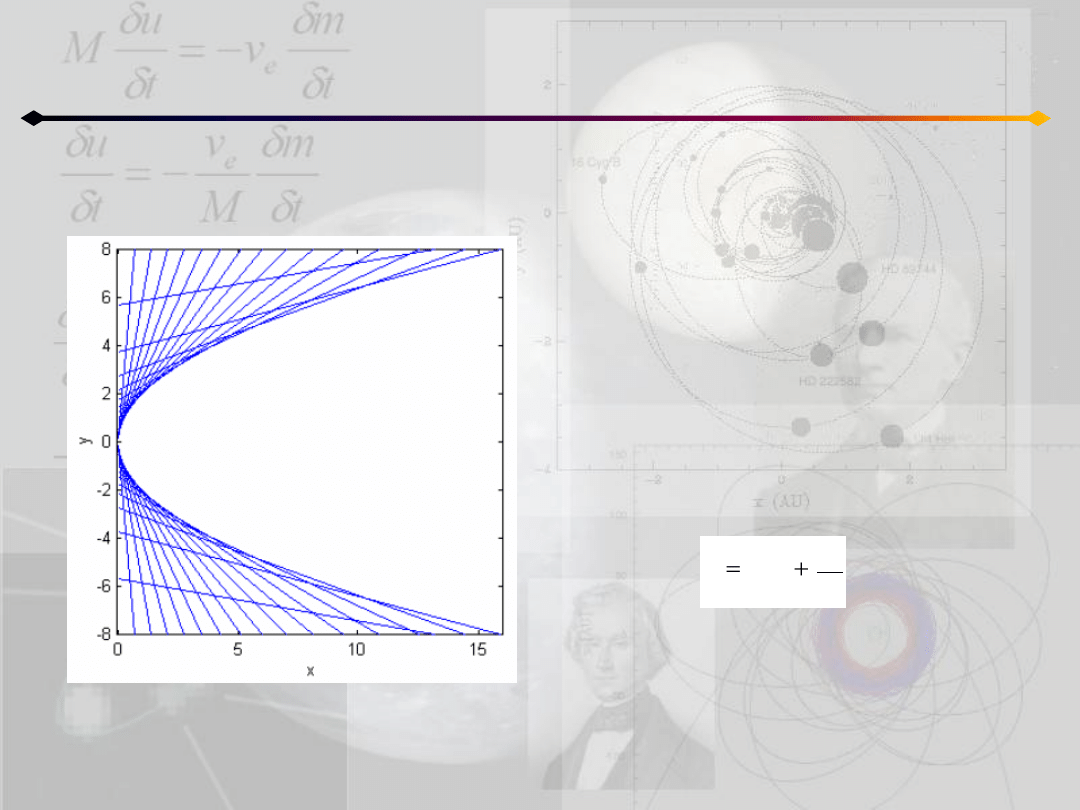
Krzywe stożkowe. Parabola

Parabola jest krzywą jaką zakreśla punkt
poruszający się tak, że jego odległośd od
tworzącej (NP) jest równa odległości od
ogniska (PF).

Jeśli N=(-q,0), F(q,0) to z definicji paraboli
otrzymamy:

Po kilku przekształceniach dostajemy r-nie
paraboli:

2

2

)

PN

(

)

PF

(

qx

4

y

2

p

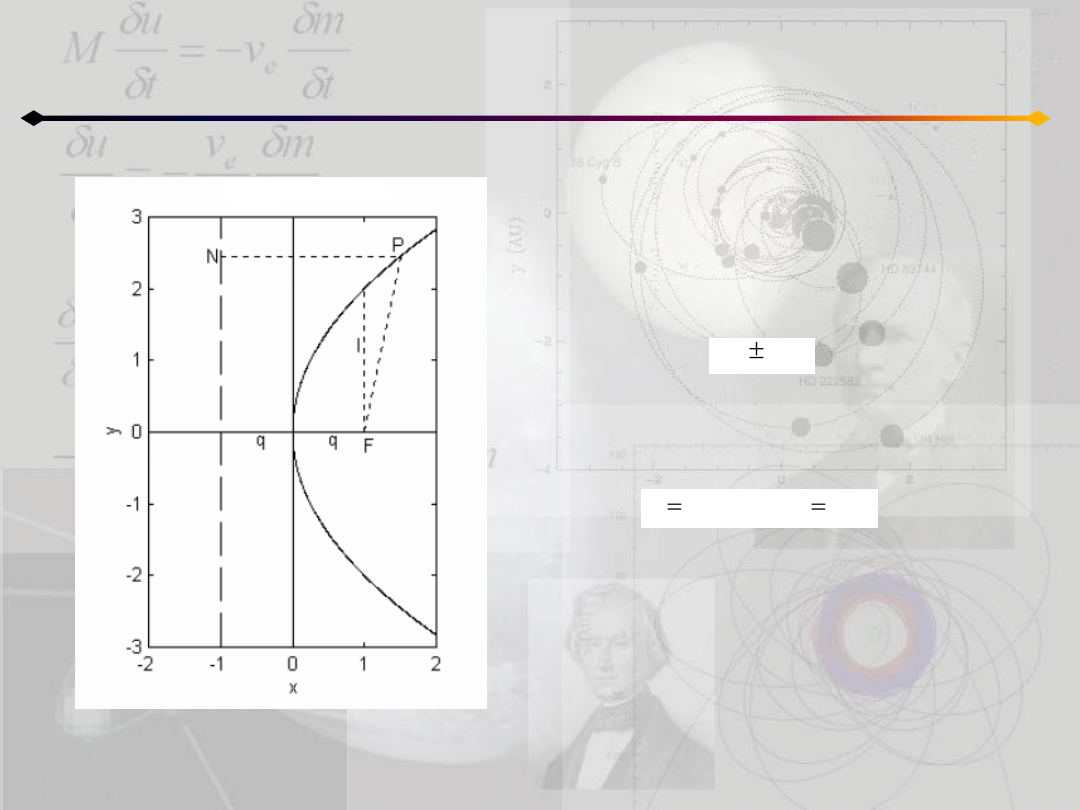
Krzywe stożkowe. Parabola

Linia równoległa do tworzącej i przechodząca
przez ognisko to parametr paraboli p. Przecina
on parabolę w dwóch punktach:

Stąd możemy otrzymad równania
parametryczne paraboli:

Wniosek:

Ciało, które porusza się ze stałą
prędkością w jednym kierunku i ze
stałym przyspieszeniem w drugim
kierunku – porusza się po paraboli.

p

)

q

2

,

q

(

qt

2

y

qt

x

2

Krzywe stożkowe. Parabola

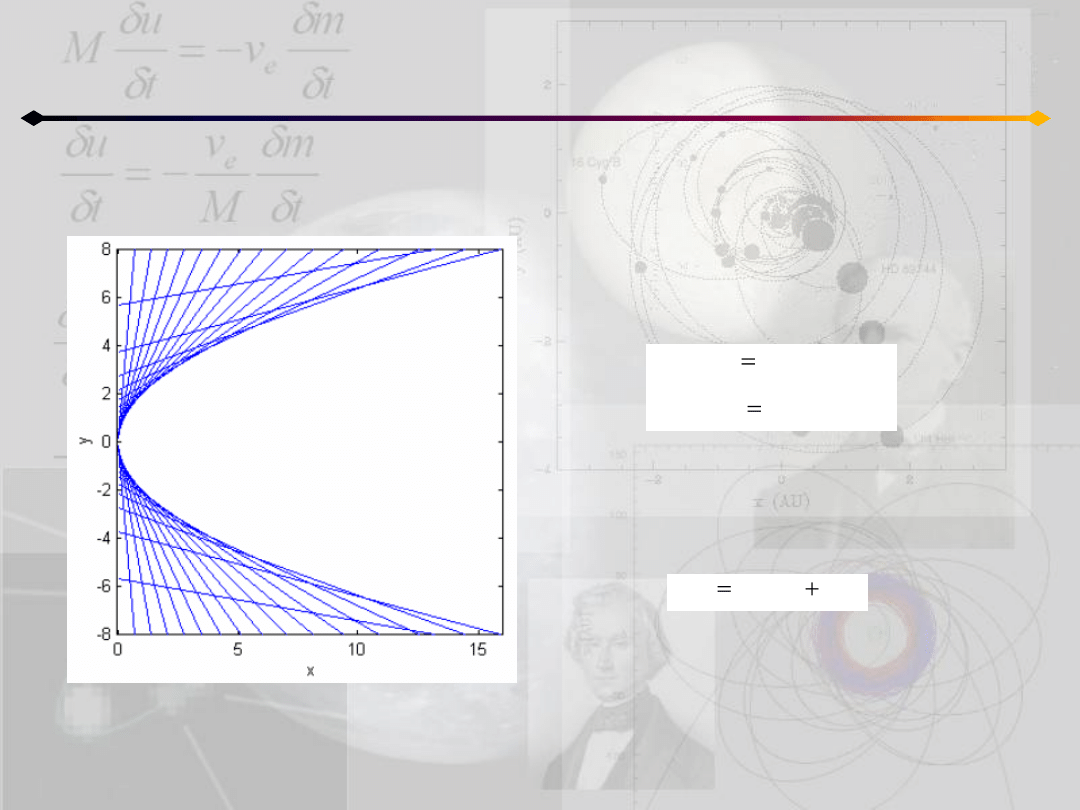
Styczne do paraboli

Postępujemy podobnie jak w przypadku
elipsy.

Wychodząc od równania na punkty wspólne
prostej i paraboli, szukamy przypadku z
jednym rozwiązaniem (punkt styczności).

Styczna (przy zadanym współczynniku
kierunkowym, m) do paraboli :

m

q

mx

y

Krzywe stożkowe. Parabola

Styczne do paraboli

Styczną w punkcie znajdujemy także
analogicznie jak w przypadku elipsy.

Wybieramy dwa dowolne punkty:

Wyznaczając prostą między nimi i
przechodząc do granicy t

2

-t

1

->0

otrzymujemy:

)

qt

2

,

qt

(

)

y

,

x

(

)

qt

2

,

qt

(

)

y

,

x

(

2

2

2

2

2

1

2

1

1

1

)

x

x

(

q

2

y

y

1

1

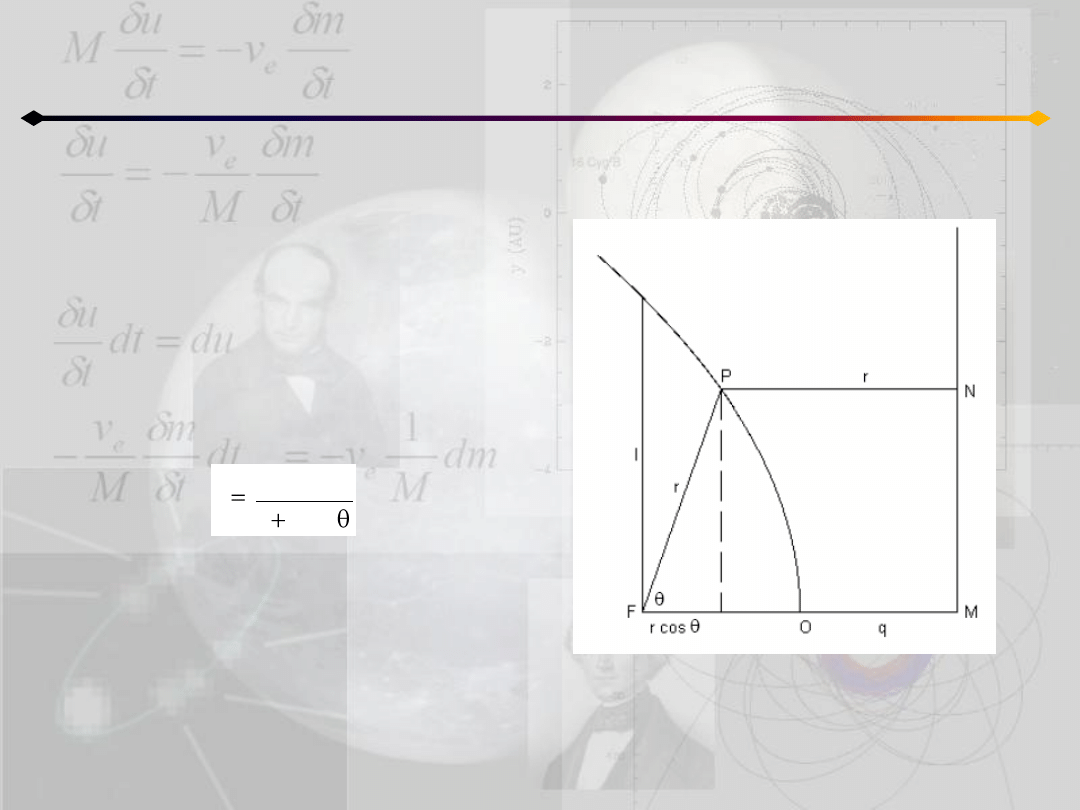
Krzywe stożkowe. Parabola

Równanie biegunowe

Z definicji: FP=PN=r a także FO=OM=q

FM=2q=p oraz rcosθ+r=2q=p

ostatecznie:

cos

1

p

r

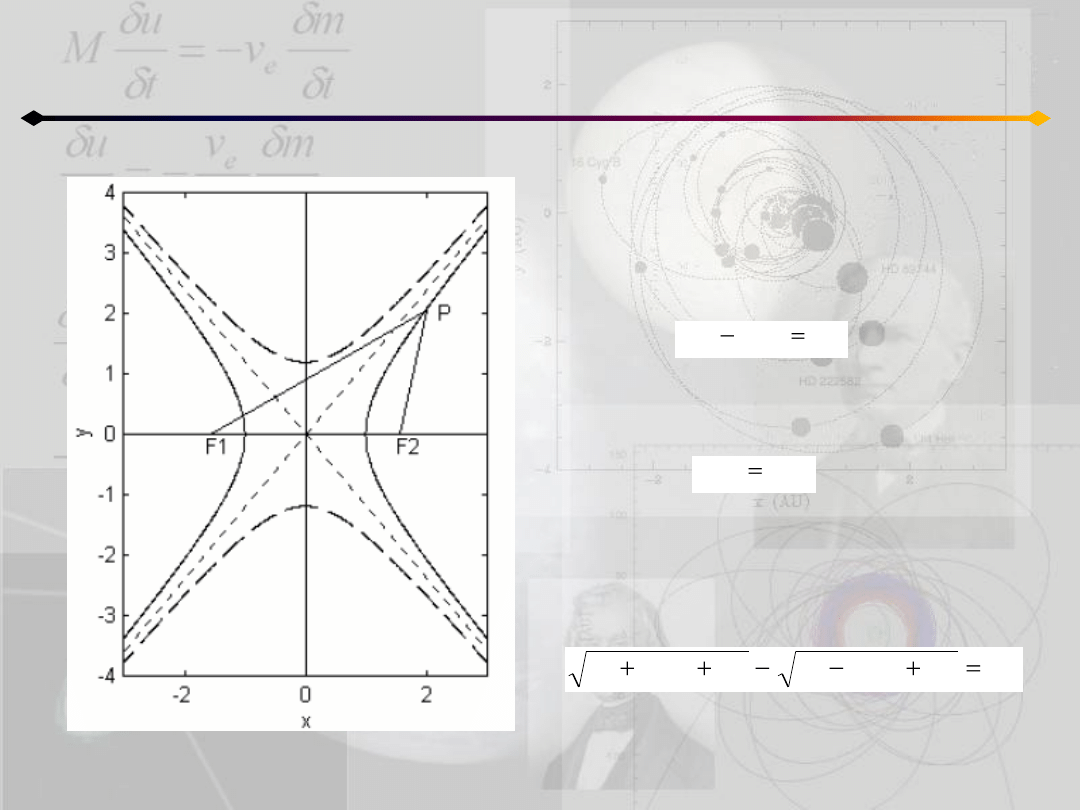
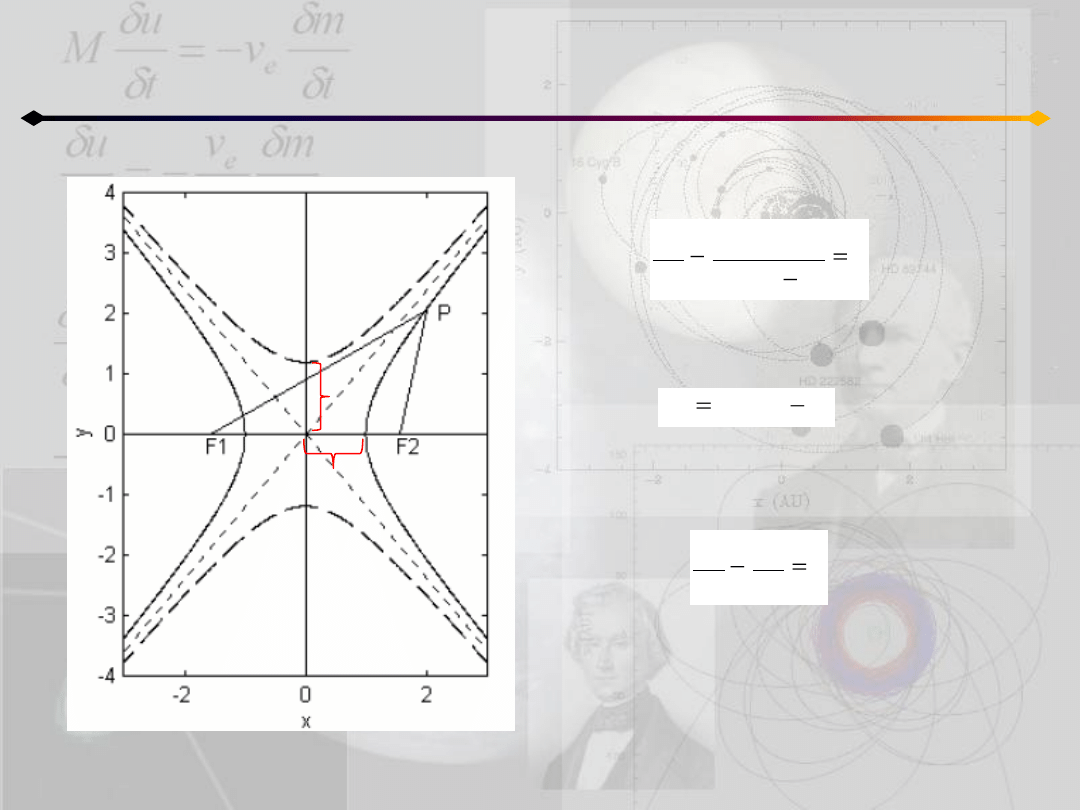
Krzywe stożkowe. Hiperbola

Hiperbola to linia, po której porusza się punkt
tak, że różnica jego odległości od ognisk jest
stała:

Odległośd między ogniskami:

gdzie e jest mimośrodem hiperboli.

Z definicji hiperboli:

a

2

P

F

P

F

2

1

ae

2

F

F

2

1

a

2

y

)

ae

x

(

y

)

ae

x

(

2

2

2

2

Krzywe stożkowe. Hiperbola

1

)

1

e

(

a

y

a

x

2

2

2

2

2

otrzymujemy:

po uwzględnieniu:

dostajemy ostatecznie:

)

1

e

(

a

b

2

2

2

1

b

y

a

x

2

2

2

2

b

a

asymptoty:

co można zapisad jako:

Krzywe stożkowe. Hiperbola

hiperbola sprzężona:

1

b

y

a

x

2

2

2

2

b

a

0

b

y

a

x

2

2

2

2

a

bx

y

Krzywe stożkowe. Hiperbola

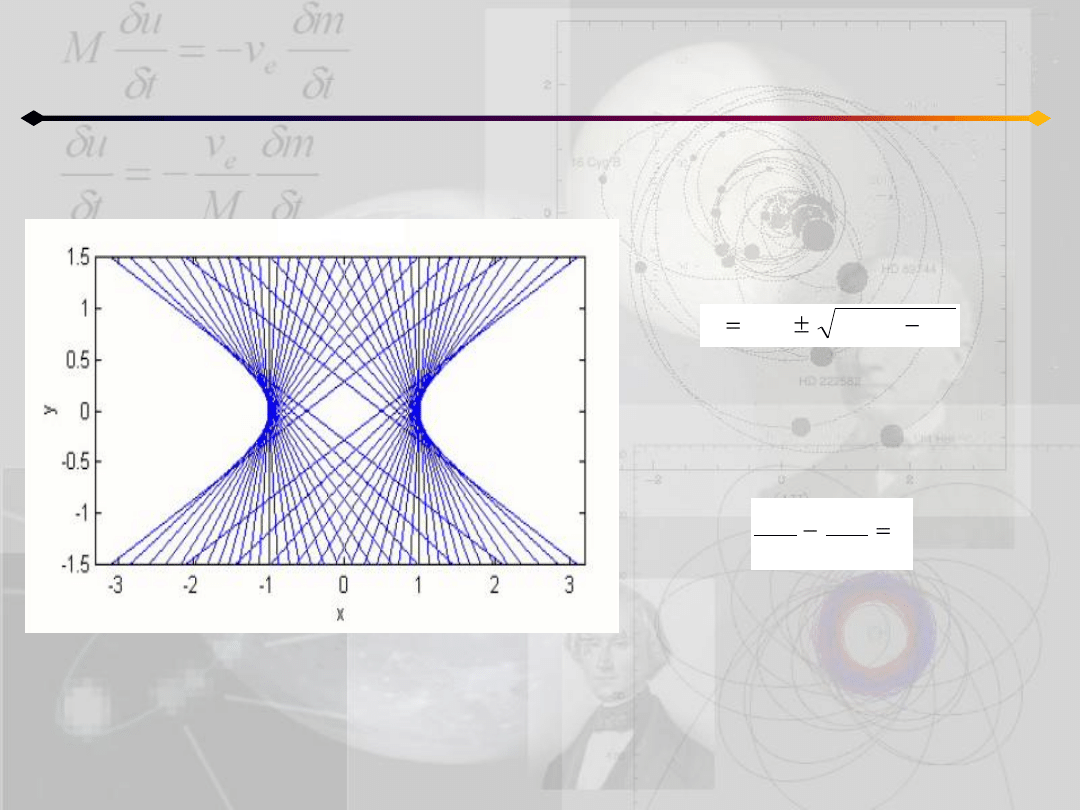
Parametr zderzenia

Poruszająca się szybko cząstka pod
wpływem siły ~ 1/r

2

zakreśla

hiperbolę.

Odległośd K

2

F

2

w jakiej cząstka

minęłaby F

2

w przypadku braku siły

jest nazywana parametrem
zderzenia.

Parametr zderzenia jest równy b
(z r-nia hiperboli).

Krzywe stożkowe. Hiperbola

Styczne do hiperboli

Wyznaczamy je identycznie jak
w przypadku elipsy (dwiczenia):

dla stycznej o zadanym
współczynniku kierunkowym
oraz:

dla stycznej w punkcie (x

1

,y

1

):

1

b

y

y

a

x

x

2

1

2

1

2

2

2

b

m

a

mx

y

Krzywe stożkowe. Hiperbola

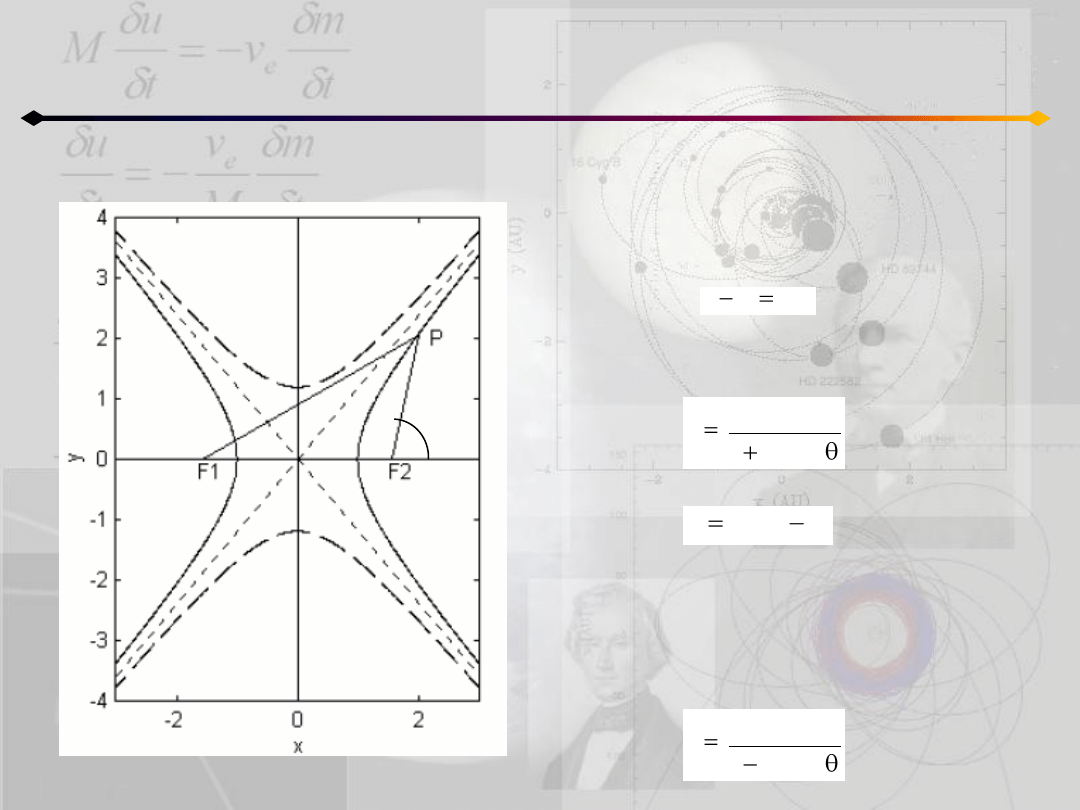
Równanie biegunowe

r

s

Postępujemy podobnie jak w przypadku
elipsy. Z definicji:

Stosując wzór cosinusów do trójkąta F

1

F

2

P

i łącząc z powyższym dostajemy:

gdzie:

jest parametrem hiperboli

a

2

r

s

θ

cos

e

1

p

r

)

1

e

(

a

p

2

cos

e

1

p

r

Dla drugiej hiperboli postępujemy podobnie
i otrzymujemy:

Krzywe stożkowe.

Równanie biegunowe

Można zauważyd, że krzywa każdego
typu ma podobne równanie biegunowe:

cos

e

1

p

r

Odpowiednie krzywe różnią się tylko
wartością mimośrodu, e:

elipsa

e<1

parabola

e=1

hiperbola

e>1

P

F

2

F

1

Równanie:

przedstawia elipsę, której wielka
półoś leży na osi 0X, a środek
znajduje się w początku układu
współrzędnych

Krzywe stożkowe. Ogólna postad

1

b

y

a

x

2

2

2

2

Co się stanie w przypadku odsunięcia elipsy od początku układu współrzędnych
i skręcenia wielkiej półosi względem osi układu?

Krzywe stożkowe. Ogólna postad

Przesunięcie środka do punktu
(p,q) powoduje zmianę
współrzędnych do (x-p,y-q).

Nachylenie osi wielkiej pod
kątem θ do osi 0X powoduje,
że:

x -> xcosθ +ysinθ
y -> -xsinθ +ycosθ

Uwzględniając to w równaniu elipsy otrzymamy równanie zawierające czynniki
x

2

,y

2

,xy,x,y oraz stałą. Podobnie będzie w przypadku hiperboli i paraboli.

0

c

fy

2

gx

2

by

hxy

2

ax

2

2

W takim razie, każdą krzywą stożkową można przedstawid za pomocą równania:

Czy takie równanie zawsze przedstawia parabolę, hiperbolę lub elipsę?

Krzywe stożkowe. Ogólna postad

0

4

x

4

y

4

xy

4

x

2

2

2

Otóż, nie zawsze. Np.:

Jest spełnione tylko przez jeden punkt.

Potrzebny jest niezmiennik ogólnego równania, który pozwoli określid postad
rozwiązao

Krzywe stożkowe. Ogólna postad

0

c

fy

2

gx

2

by

hxy

2

ax

2

2

Niezmiennikiem tego równania jest wyznacznik:

gdzie:

c

c

f

f

g

g

f

f

b

b

h

h

g

g

h

h

a

a

c

f

g

f

g

b

h

h

a

ch

fg

h

h

ab

c

bg

hf

g

g

ca

b

af

gh

f

f

bc

a

2

2

2

Krzywe stożkowe. Ogólna postad

Współrzędne środka dowolnej krzywej stożkowej:

a kąt jaki tworzy wielka półoś z osią 0X:

Wartości współczynników równania i niezmienników pozwalają
jednoznacznie określid z jakim przypadkiem mamy do czynienia:

c

f

;

c

g

b

a

h

2

2

tg

punkt

dwie nierównoległe
linie proste

prosta

dwie proste
równoległe

dwie proste
prostopadłe

dwie proste
nieprostopadłe i
nierównoległe

Krzywe stożkowe. Ogólna postad

tu zaczynamy

następna strona

Krzywe stożkowe. Ogólna postad

parabola

nic

okrąg

elipsa

w pozostałych

i

hiperbola prostokątna

hiperbola
(nieprostokątna)

Weźmy równanie:

pięd punktów potrzeba i wystarcza,
aby jednoznacznie dopasowad do nich
krzywą stożkową.

Jeżeli przynajmniej trzy z nich leżą na jednej
prostej to dostajemy krzywą stożkową
niewłaściwą

Najprostszy sposób polega na podstawieniu
do niego współrzędnych kolejnych punktów
i rozwiązanie otrzymanego układu równao
w celu uzyskania współczynników.

Krzywe stożkowe. Ogólna postad

0

c

fy

2

gx

2

by

hxy

2

ax

2

2

A(1,8), B(4,9), C(5,2), D(7,6), E(8,4)

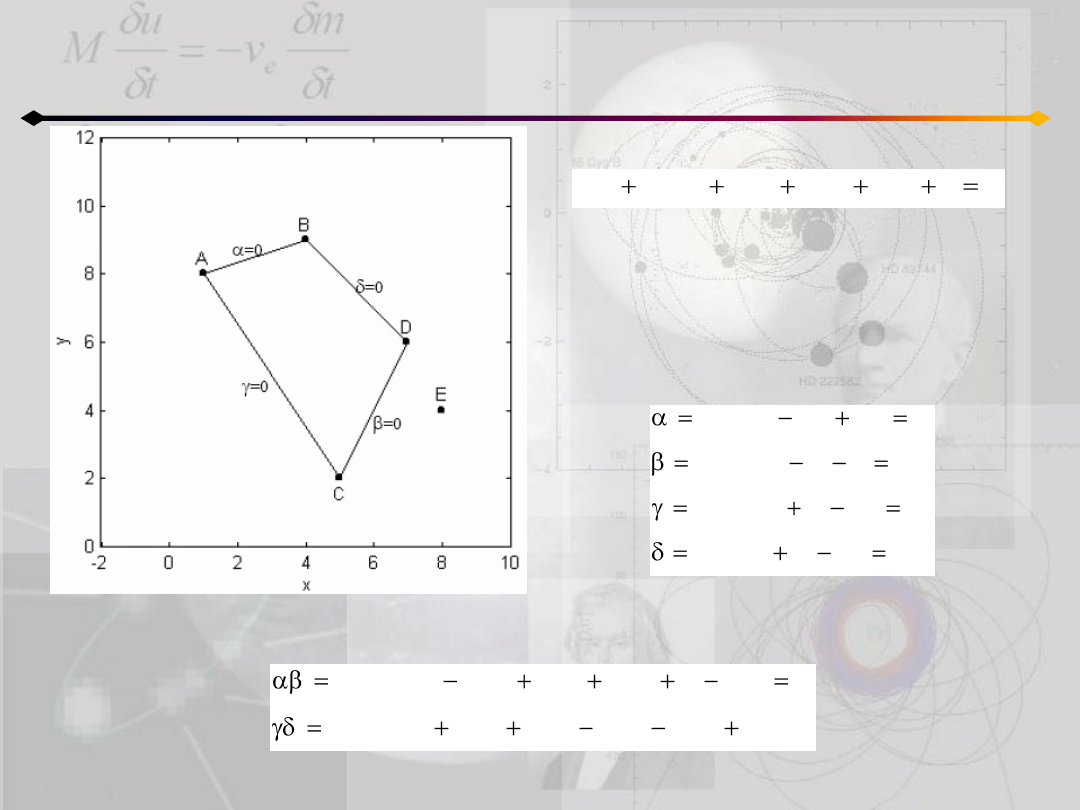
Krzywe stożkowe. Ogólna postad

0

c

fy

2

gx

2

by

hxy

2

ax

2

2

Można to zrobid nieco inaczej (w prostszy
sposób?)

Piszemy równania prostych α=0, β=0,
γ=0 i δ=0:

0

13

y

x

:

0

0

19

y

x

3

:

0

0

8

y

x

2

:

0

0

23

y

3

x

:

0

Wtedy r-nie αβ=0 opisuje proste AB i CD, natomiast γδ=0 zawiera pozostałe dwie proste:

247

y

45

x

58

y

2

xy

5

x

3

:

0

0

184

y

x

38

y

3

xy

7

x

2

:

0

2

2

2

2

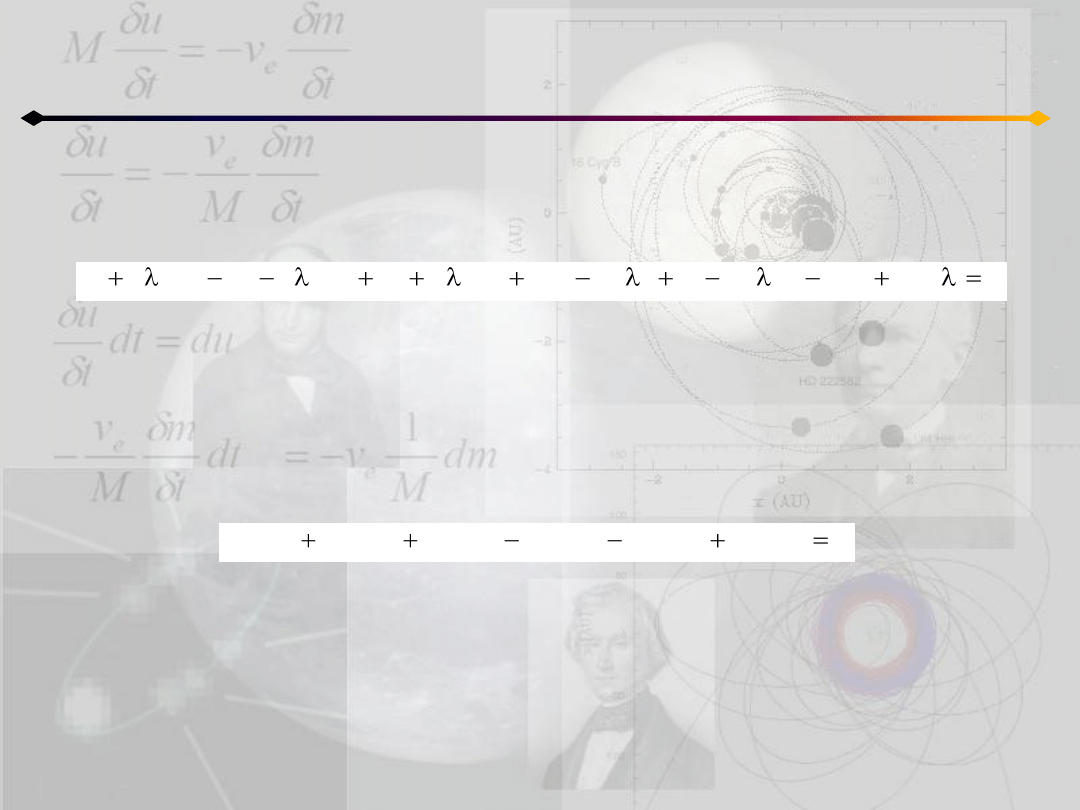
Otrzymujemy λ=76/13 i ostatecznie szukane równanie krzywej stożkowej
przechodzącej przez zadane pięd punktów:

Mając współczynniki równania możemy określid (z tabeli krzywych stożkowych), że
otrzymaliśmy elipsę, której środek znajduje się w punkcie (4.619, 5.425) nachylonej
do osi OX po kątem 128

o

51’

Krzywe stożkowe. Ogólna postad

Ostatecznie, równanie opisujące całą rodzinę krzywych stożkowych przechodzących
przez A, B, C, D przyjmuje postad αβ+λγδ =0 (gdzie λ jest stałą):

0

247

184

y

)

45

1

(

)

58

38

(

y

)

2

3

(

xy

)

5

7

(

x

)

3

2

(

2

2

0

32760

y

6814

x

7828

y

382

xy

578

x

508

2

2

Podstawiając x=8, y=4 wyznaczamy takie λ, dla którego dana krzywa stożkowa
przechodzi przez punkt E.

Pole grawitacyjne i potencjał

Prawo powszechnego ciążenia

Każda cząstka we Wszechświecie działa
na każdą inną cząstkę z siłą, która jest
wprost proporcjonalna do iloczynu mas
tych cząstek i odwrotnie proporcjonalna
do kwadratu ich odległości:

gdzie G jest uniwersalną (obowiązuje
wszędzie(?) we Wszechświecie) stałą
(niezmienną w czasie) grawitacji równą:

2

2

1

r

m

m

G

F

2

3

8

2

3

11

s

g

cm

10

s

kg

m

10

7259

,

6

Natężenie pola grawitacyjnego
pochodzącego od masy M:

czyli iloraz siły grawitacyjnej działającej
na ciało próbne m i jego masy.

Pole grawitacyjne i potencjał

Natężenie pola grawitacyjnego

m

F

2

r

M

G

M

m

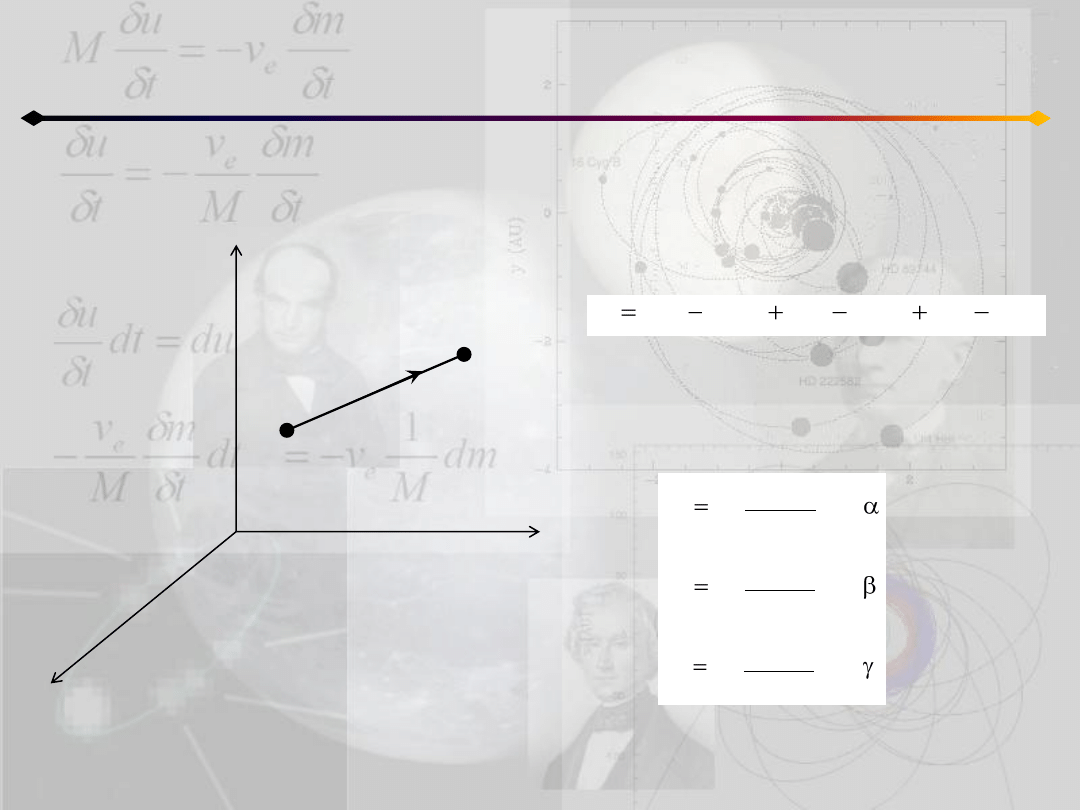
Pole grawitacyjne i potencjał

Dwa punkty materialne

z

y

x

0

P(x

0

,y

0

,z

0

)

Q(x

1

,y

1

,z

1

)

r



Dane są dwa punkty P i Q o masach
równych m

0

i m

1

odległych o r:

Załóżmy, że P jest przyciągany przez Q,
wtedy składowe siły:

2

0

1

2

0

1

2

0

1

2

)

z

z

(

)

y

y

(

)

x

x

(

r

cos

r

m

m

G

F

cos

r

m

m

G

F

cos

r

m

m

G

F

2

1

0

z

2

1

0

y

2

1

0

x

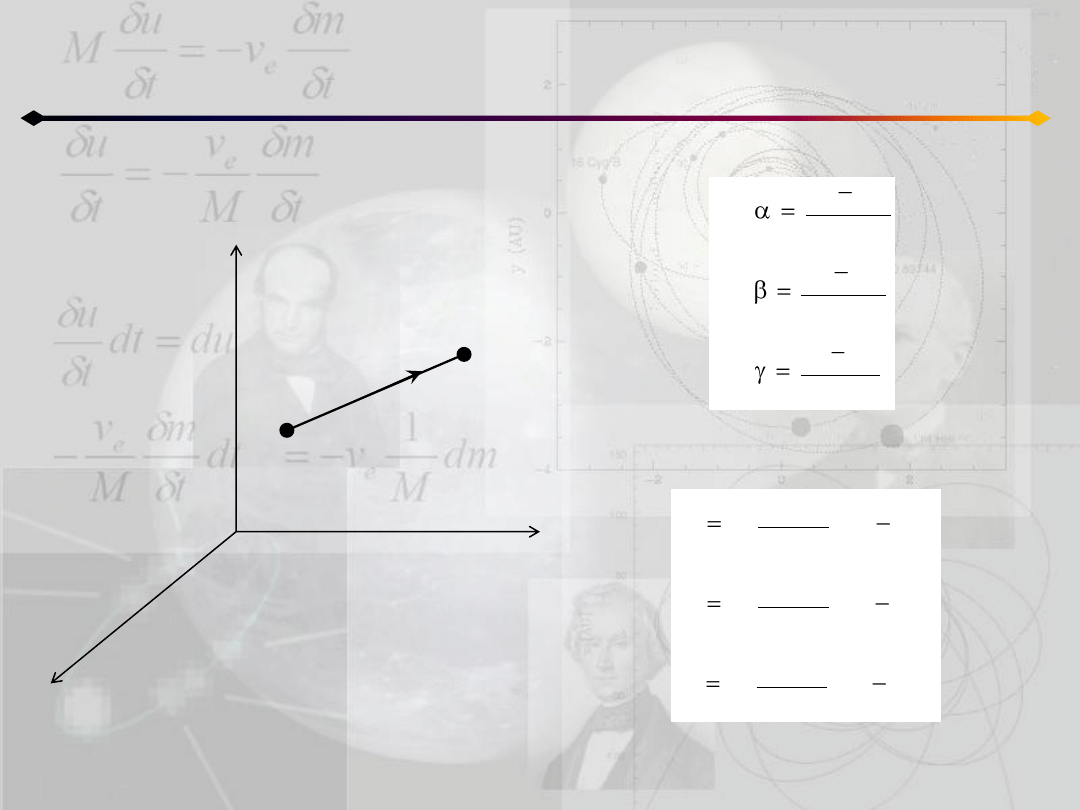
r

z

z

cos

r

y

y

cos

r

x

x

cos

0

1

0

1

0

1

Pole grawitacyjne i potencjał

Dwa punkty materialne

z

y

x

0

P(x

0

,y

0

,z

0

)

Q(x

1

,y

1

,z

1

)

r



)

z

z

(

r

m

m

G

F

)

y

y

(

r

m

m

G

F

)

x

x

(

r

m

m

G

F

0

1

3

1

0

z

0

1

3

1

0

y

0

1

3

1

0

x

Odpowiednie cosinusy kierunkowe
są równe:

a więc:

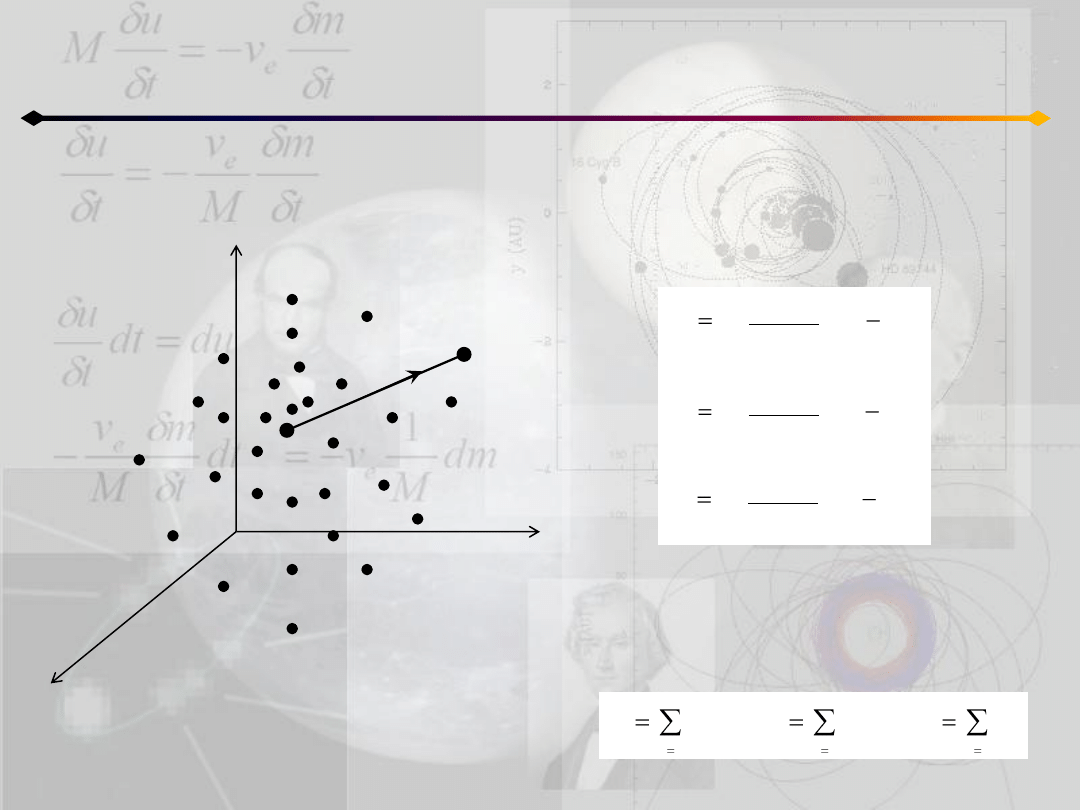
Siła przyciągania punktu P przez
dowolny punkt Q

i

:

dodając odpowiednie składowe do siebie
otrzymamy składowe całkowitej siły
działającej na P:

Pole grawitacyjne i potencjał

n punktów

)

z

z

(

r

m

m

G

F

)

y

y

(

r

m

m

G

F

)

x

x

(

r

m

m

G

F

0

i

3

i

i

0

zi

0

i

3

i

i

0

y i

0

i

3

i

0

xi

i

z

y

x

0

P(x

0

,y

0

,z

0

)

Q

i

(x

i

,y

i

,z

i

)

i

r



n

1

i

zi

z

n

1

i

yi

y

n

1

i

xi

x

F

F

;

F

F

;

F

F

Ostatecznie:

Pole grawitacyjne i potencjał

n punktów

n

1

i

0

i

3

i

0

z

n

1

i

0

i

3

i

0

y

n

1

i

0

i

3

i

0

x

)

z

z

(

r

m

Gm

F

)

y

y

(

r

m

Gm

F

)

x

x

(

r

m

Gm

F

i

i

i

z

y

x

0

P(x

0

,y

0

,z

0

)

Q

i

(x

i

,y

i

,z

i

)

i

r



W mechanice nieba zazwyczaj mamy do
czynienia z ciałami o symetrycznym
rozkładzie masy co pozwala uprościd
problem wyznaczania siły działającej od
układu punktów.

Pole grawitacyjne i potencjał

n punktów

copyright: http://www.robgendlerastropics.com/

copyright: Hubble Heritage Team

W obiektach nieregularnych, odległości
(zwykle) między poszczególnymi centrami
grawitacji są na tyle duże, że można
zaniedbad wpływ innych obiektów niż
najbliższe.

Pole grawitacyjne i potencjał

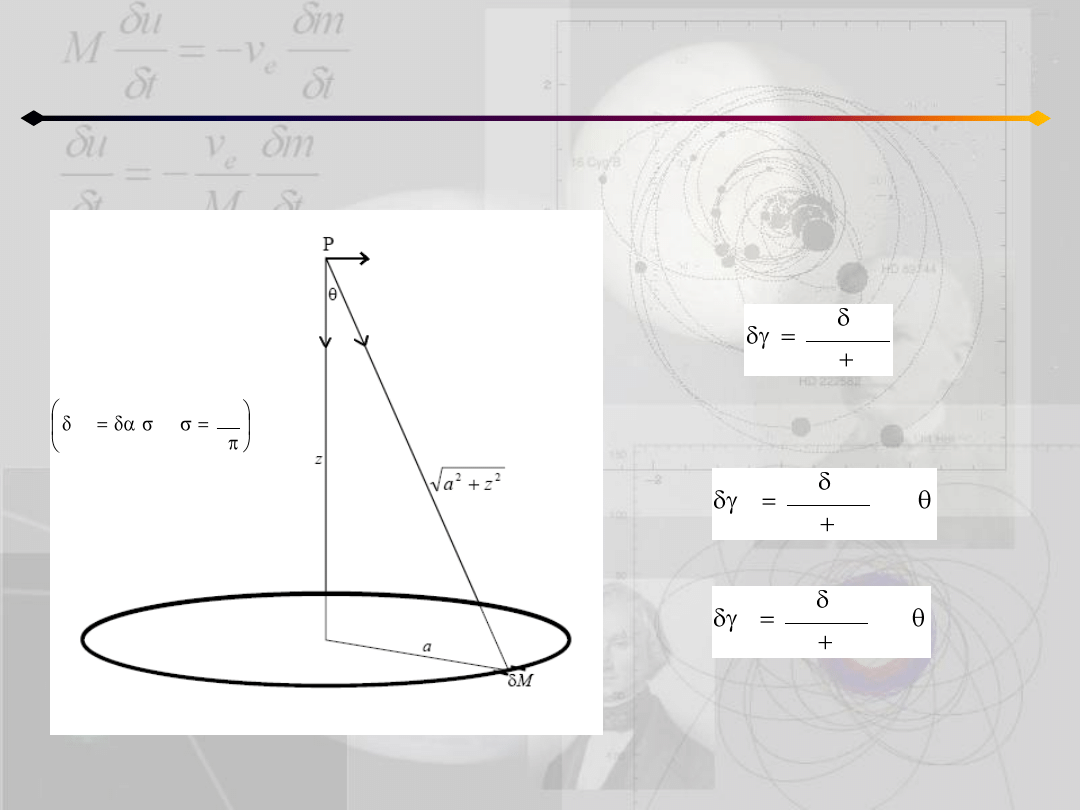
Pole na osi pierścienia

δγ

r

δγ

o

δγ

Wkład od elementu masy δM do
całego natężenia:

który można rozłożyd na składowe:

2

2

z

a

M

G

cos

z

a

M

G

2

2

o

sin

z

a

M

G

2

2

r

2

M

;

M

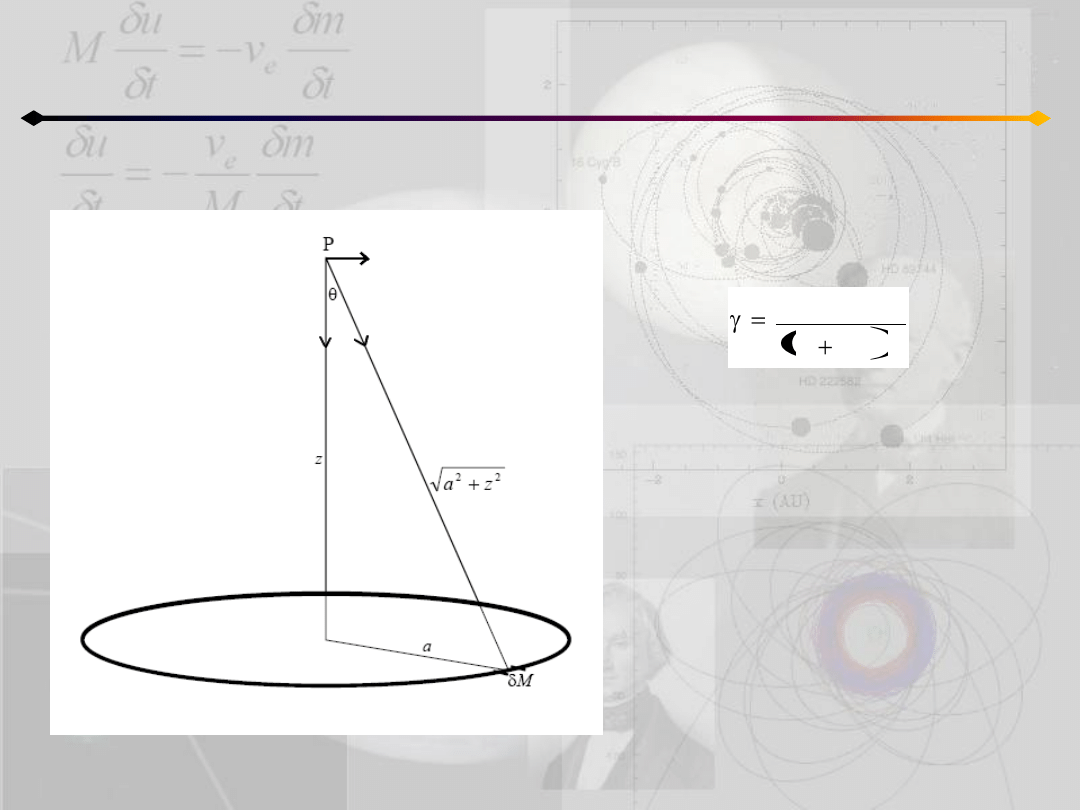
Pole grawitacyjne i potencjał

Pole na osi pierścienia

2

/

3

2

2

z

a

GMz

δγ

r

δγ

o

δγ

Całkując po wszystkich przyczynkach
otrzymujemy:

natężenie skierowane do środka
pierścienia.

Powyższa funkcja zeruje się w środku
pierścienia i w nieskooczoności
osiągając po drodze maksimum
(dwiczenia).

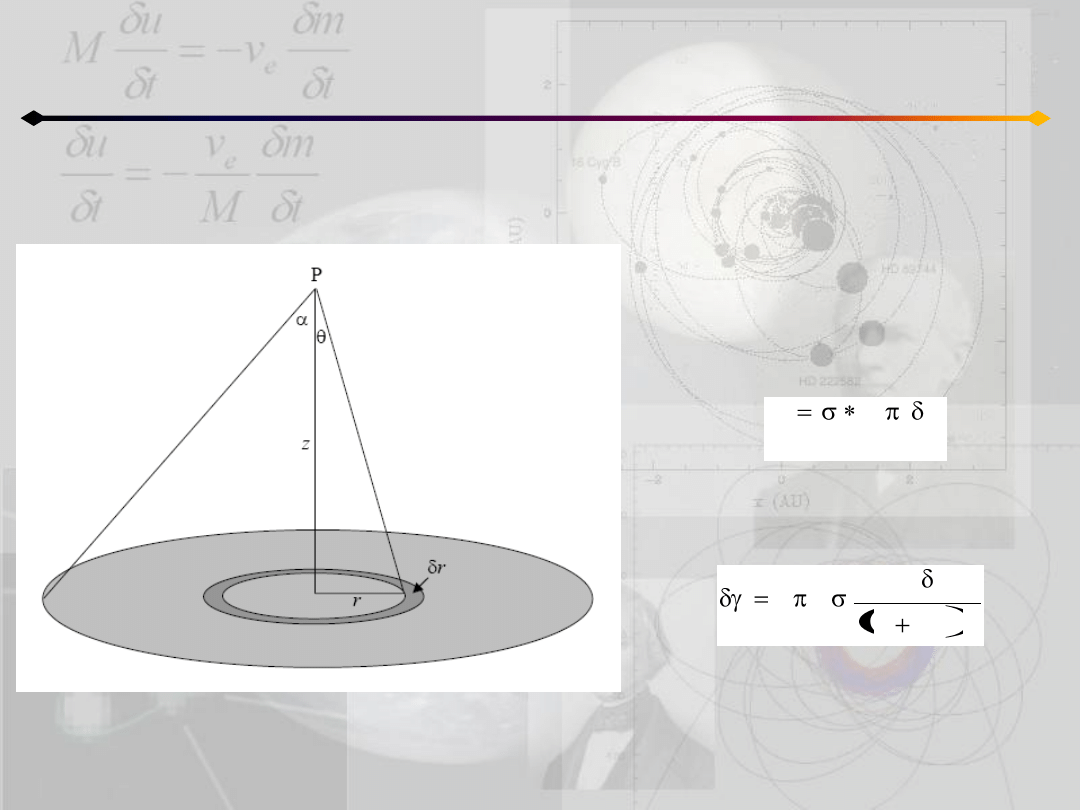
Pole grawitacyjne i potencjał

Pole na osi jednorodnego dysku

Punkt P leży na osi dysku o gęstości
powierzchniowej σ, w odległości z
od środka.

Masa elementarnego pierścienia:

jego wkład do całkowitego natężenia:







ia

powierzchn

r

r

2

m

2

/

3

2

2

r

z

r

r

z

G

2

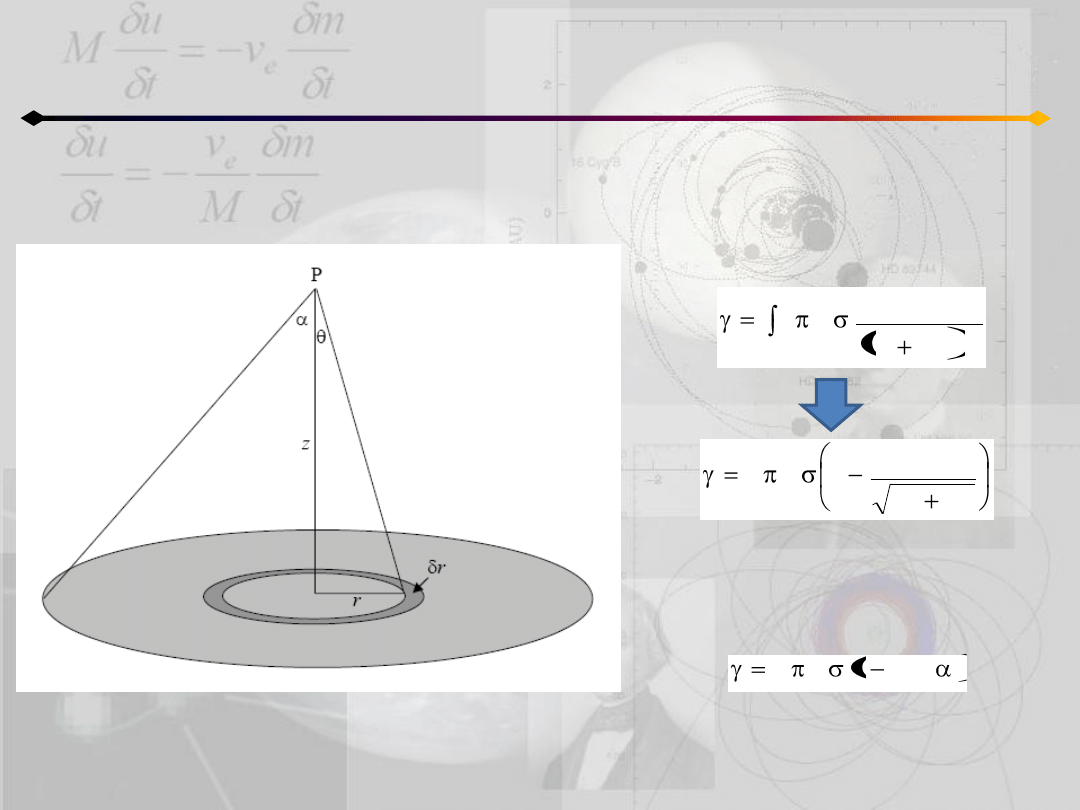
Sumaryczne natężenie znajdujemy
licząc całkę:

Pole grawitacyjne i potencjał

Pole na osi jednorodnego dysku

2

2

a

z

z

1

G

2

a

0

2

/

3

2

2

r

z

dr

r

z

G

2

cos

1

G

2

Możemy wyrazid tę zależnośd w
funkcji kąta α:

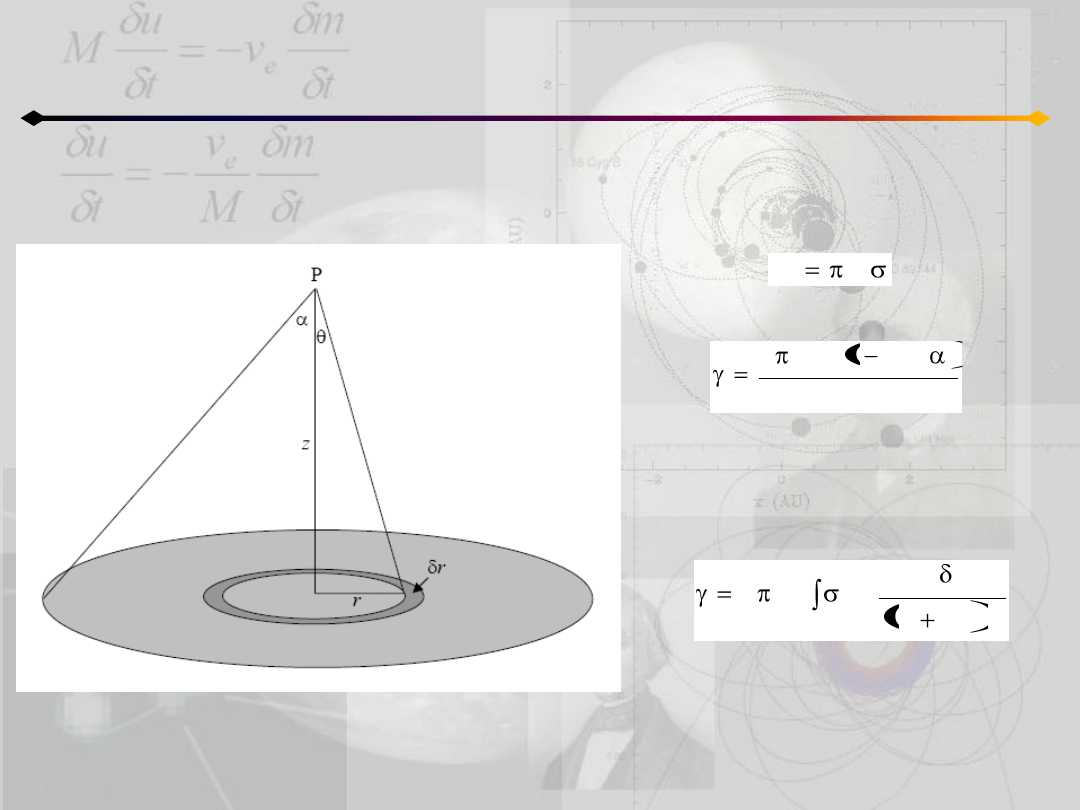
Jeśli masa całego dysku wynosi:

to:

Pole grawitacyjne i potencjał

Pole na osi jednorodnego dysku

2

a

cos

1

GM

2

2

a

M

a

0

2

/

3

2

2

r

z

r

r

)

r

(

Gz

2

W ogólnym przypadku gęstośd
zależy od r i wtedy natężenie pola
grawitacyjnego:

Pole grawitacyjne i potencjał

Pole na osi dowolnego dysku

Zakładając różne postaci rozkładu gęstości
można przybliżad natężenia pola
grawitacyjnego pochodzącego od
rzeczywistych obiektów
(dwiczenia)

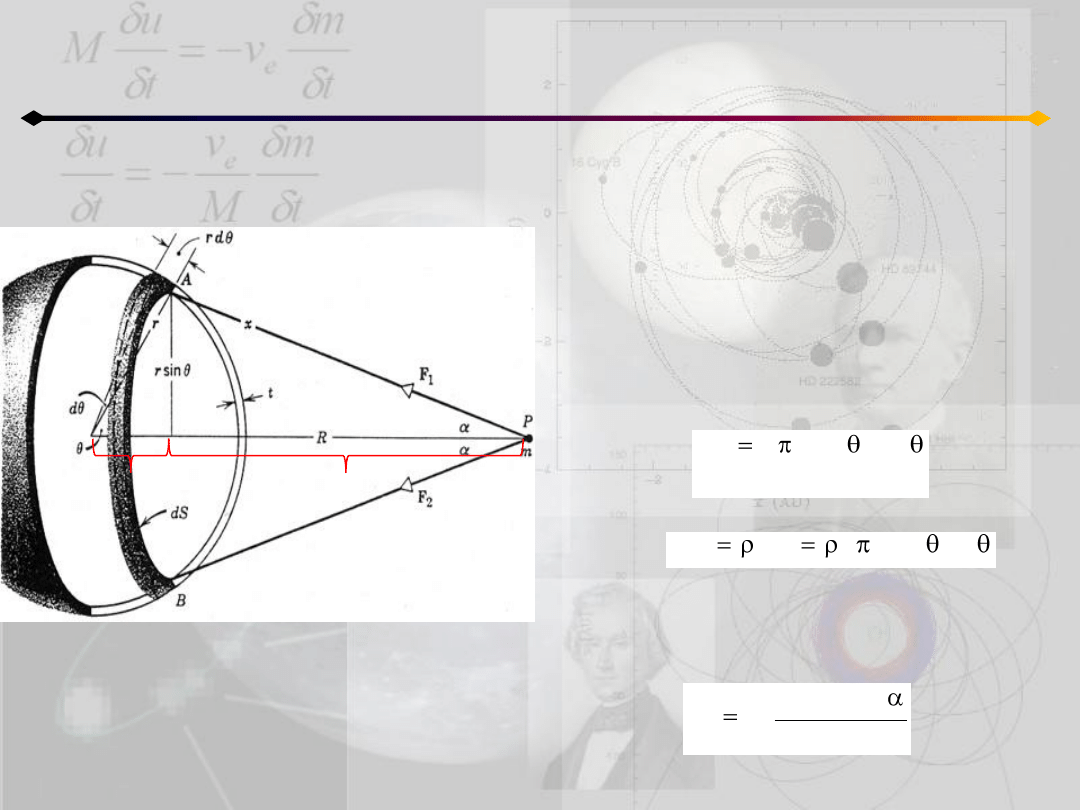
Pole grawitacyjne i potencjał

Pole na zewnątrz sfery

copyright: Resnick, Halliday

rcosθ

xcosα

Zał.:
- sfera ma masę M rozłożoną równomiernie
na całej powierzchni
- grubośd t jest mała w porównaniu z
promieniem r

Rozpatrujemy cienki pasek o szerokości rdθ:

objętośd

masa

Wykorzystując uzyskane wcześniej wyrażenie
dla pierścienia możemy zapisad:

 

.

szer

.

gr

obwód

rd

t

sin

r

2

dV









rd

t

sin

r

2

dV

dM

2

x

cos

dMm

G

dF

Pole grawitacyjne i potencjał

Pole na zewnątrz sfery

copyright: Resnick, Halliday

rcosθ

xcosα

Po uwzględnieniu wyrażenia na dM:

z rys.:

oraz z tw. cosinusów:

Łącząc te trzy czynniki dostajemy:

cos

x

d

sin

mr

Gt

2

dF

2

2

x

cos

r

R

cos

cos

Rr

2

r

R

x

2

2

2

/

3

2

2

2

cos

Rr

2

r

R

)

cos

r

R

(

d

sin

mr

Gt

2

dF

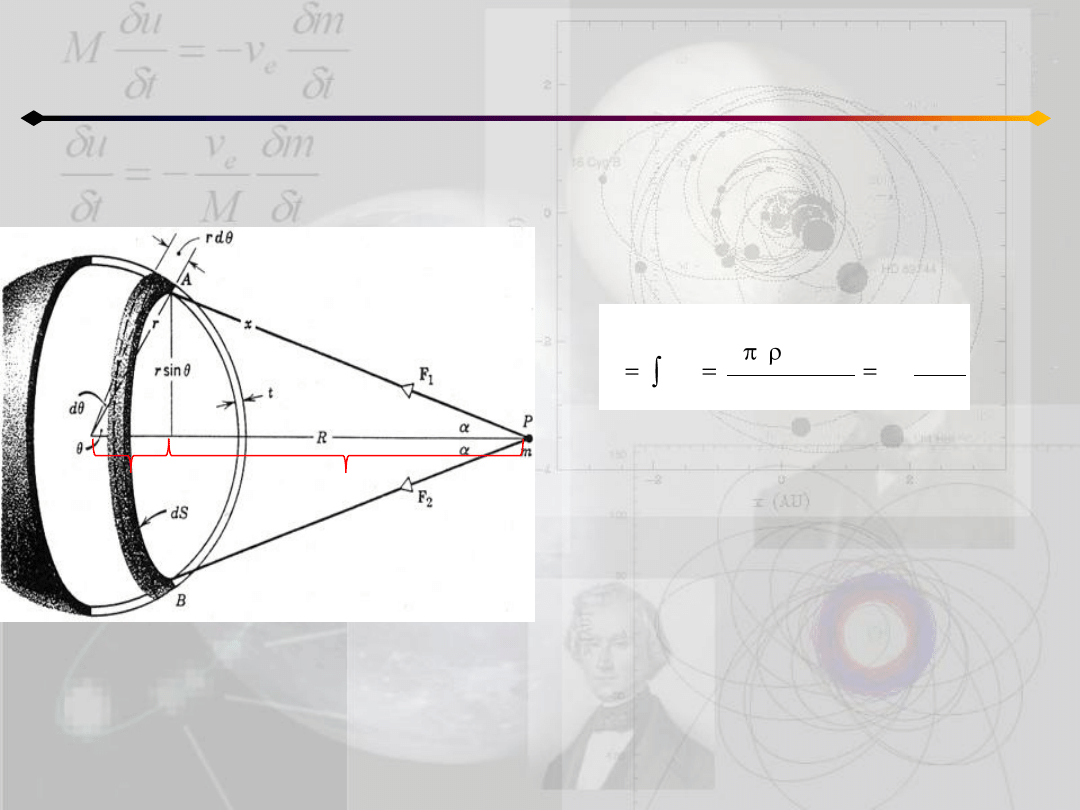
Pole grawitacyjne i potencjał

Pole na zewnątrz sfery

copyright: Resnick, Halliday

rcosθ

xcosα

Siłę pochodzącą od całej sfery wyznaczamy
licząc całkę:

To oznacza, że pole grawitacyjne na
zewnątrz sfery jest takie jakby cała masa
była skupiona w punkcie.

Identyczny wynik otrzymujemy dla kuli
(całkujemy cienkie sfery od 0 do R)

2

2

sfery

masa

2

R

Mm

G

R

Gm

r

t

4

dF

F







Pole grawitacyjne i potencjał

Pole wewnątrz sfery

copyright: Resnick, Halliday

Podobnie postępujemy w przypadku
gdy punkt materialny umieścimy
wewnątrz kuli.

Wyrażenie na dF jest identyczne. Zmianie
ulegają granice całkowania.

W wyniku otrzymujemy, że:

Oczywiście to jest prawda tylko w
przypadku gdy nie ma innych mas (sfera
nie tworzy „ekranu grawitacyjnego”!)

0

F