MECHANIKA NIEBA

WYKŁAD 12

28.05.2008 r

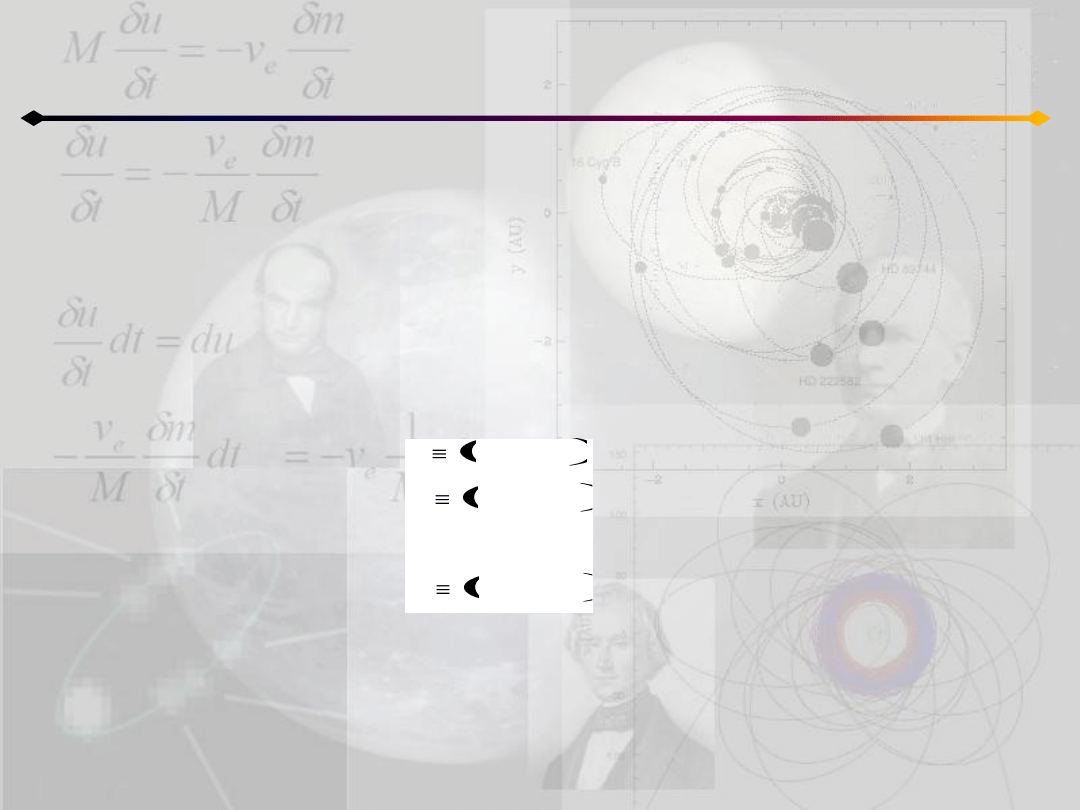
Formalizm Lagrange’a

Formalizm Lagrange’a polega na opisywaniu układów dynamicznych za pomocą:

1. współrzędnych i prędkości uogólnionych
2. funkcji Lagrange’a
3. równao ruchu Lagrange’a drugiego rodzaju

Układ n punktów materialnych jest opisany, w dowolnym momencie czasu,
3n współrzędnymi:

W miejsce tych współrzędnych wprowadzamy współrzędne uogólnione q, które
mogą byd dowolnymi funkcjami r i mogą zależed jawnie od czasu.

Równania Lagrange’a

n

n

n

n

2

2

2

2

1

1

1

1

z

,

y

,

x

r

z

,

y

,

x

r

z

,

y

,

x

r









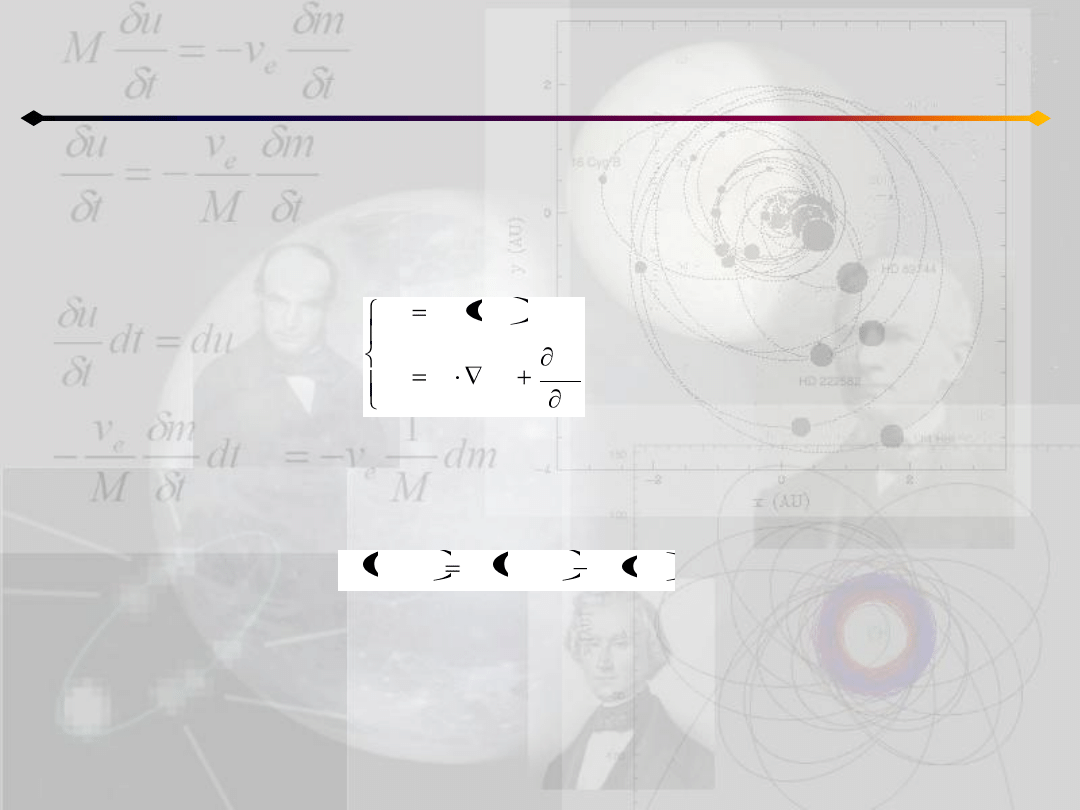
Formalizm Lagrange’a

Równania Lagrange’a

Prędkości uogólnione uzyskujemy różniczkując po czasie współrzędne uogólnione, w
efekcie mamy:

gdzie i=1,2,…,N (N jest liczbą stopni swobody)

Funkcja Lagrange’a (lagranżjan, potencjał kinetyczny) jest definiowana następująco:

Znając potencjał kinetyczny układu o N stopniach swobody możemy otrzymad równania
Lagrange’a drugiego rodzaju.

t

q

q

r

q

t

,

r

q

q

i

i

i

i

i







t

,

q

V

t

,

q

,

q

T

t

,

q

,

q

L











Formalizm Lagrange’a

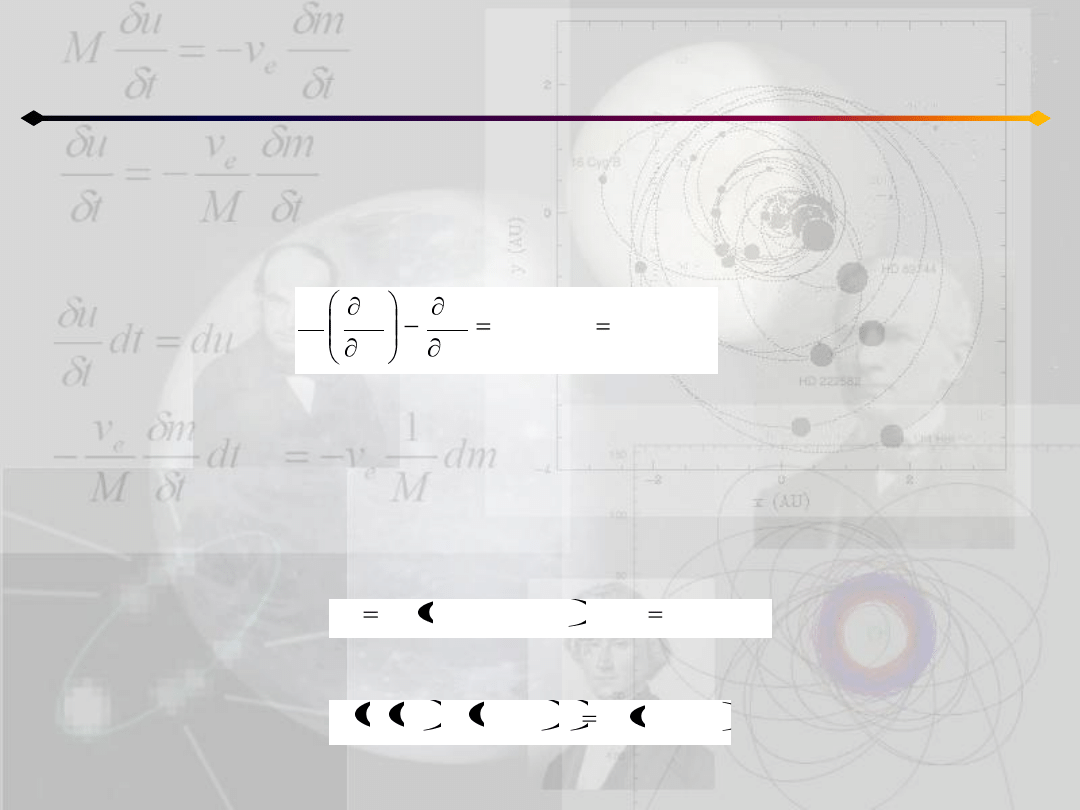
Równania Lagrange’a

Równania Lagrange’a drugiego rodzaju:

tworzą układ równao rzędu 2N.

Równania Lagrange’a nie ulegają zmianie podczas transformacji zmiennych uogólnionych
(czyli zmianie układu odniesienia).

Zdefiniujmy transformację do N nowych zmiennych y

1

,y

2

,…,y

N

:

wtedy potencjał kinetyczny:

N

,...,

2

,

1

i

,

0

q

L

q

L

dt

d

i

i



N

,...,

2

,

1

i

y

,...,

y

,

y

q

q

N

2

1

i

i

t

,

y

,

y

L

~

t

,

y

,

y

q

,

y

q

L

i

i

j

j

i

j

i







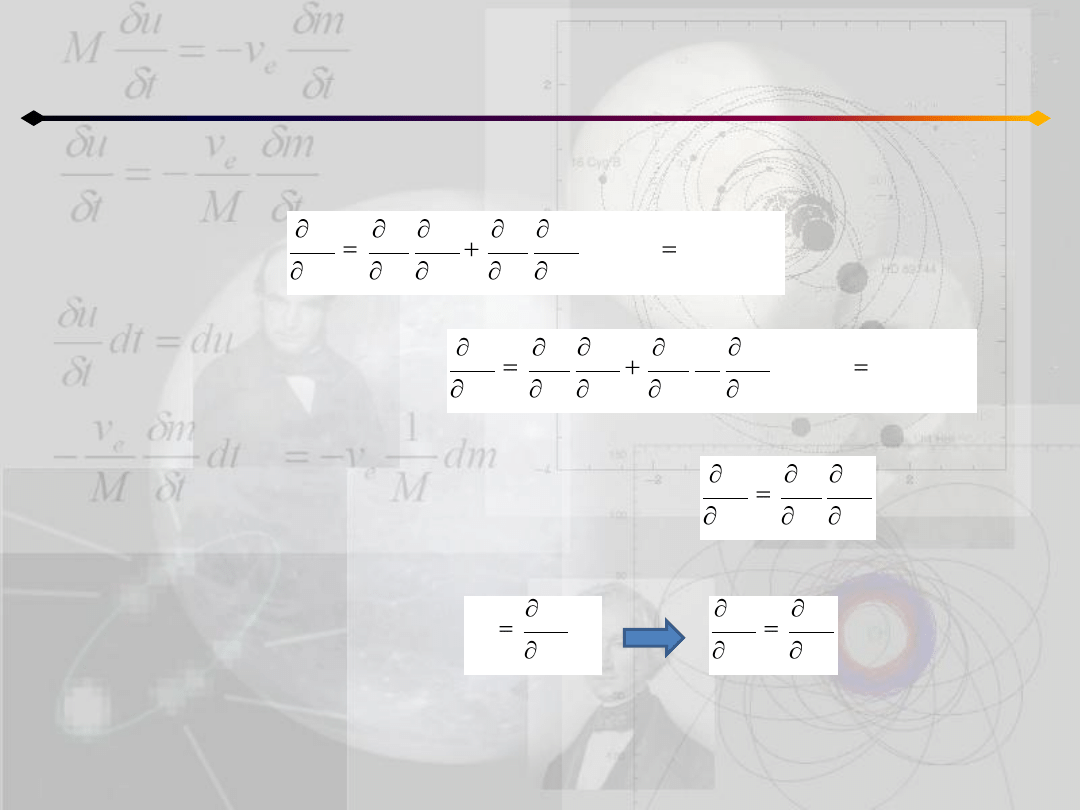
Formalizm Lagrange’a

Równania Lagrange’a

Poza tym:

co można przepisad w postaci:

Ponieważ q

i

nie zależą od pochodnych y

k

, więc mamy:

Oprócz tego należy pamiętad, że:

N

,...,

2

,

1

k

y

q

q

L

y

q

q

L

y

L

~

k

i

i

k

i

i

k





N

,...,

2

,

1

k

y

q

dt

d

q

L

y

q

q

L

y

L

~

k

i

i

k

i

i

k



k

i

i

k

y

q

q

L

y

L

~









k

k

i

i

y

y

q

q





k

i

k

i

y

q

y

q





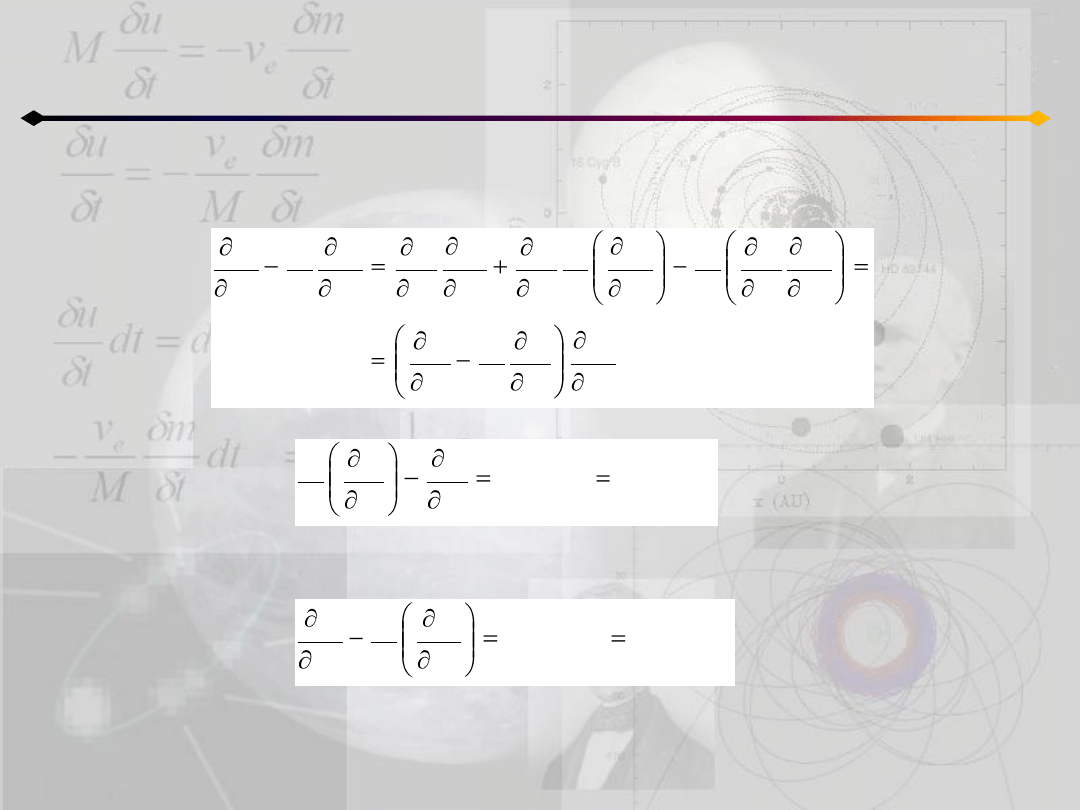
Formalizm Lagrange’a

Równania Lagrange’a

Uwzględniając te zależności w równaniu Lagrange’a drugiego rodzaju dostajemy:

ponieważ:

więc mamy również:

Co oznacza, że równania Lagrange’a nie ulegają zmianie przy zmianie układu
współrzędnych

k

i

i

i

k

i

i

k

i

i

k

i

i

k

k

y

q

q

L

dt

d

q

L

y

q

q

L

dt

d

y

q

dt

d

q

L

y

q

q

L

y

L

~

dt

d

y

L

~









N

,...,

2

,

1

i

,

0

q

L

q

L

dt

d

i

i



N

,...,

2

,

1

k

,

0

y

L

~

dt

d

y

L

~

k

k



Formalizm Lagrange’a

Cząstka w potencjale radialnym

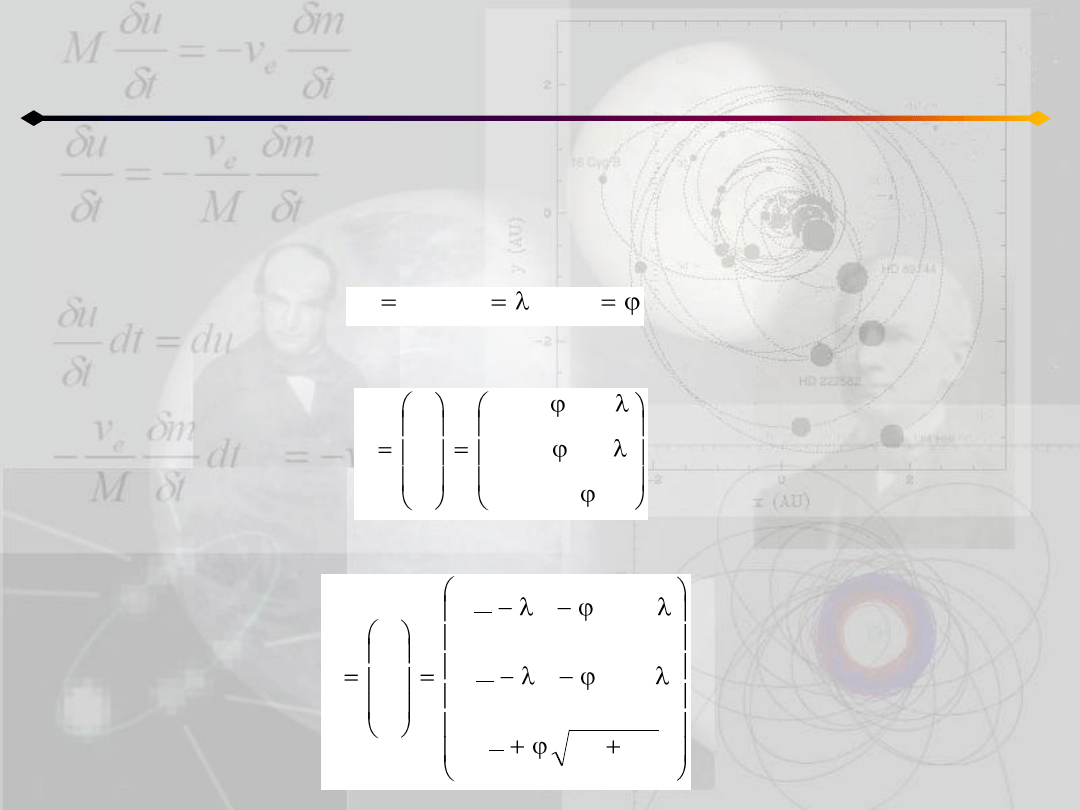
Potencjał posiadający symetrię sferyczną ma ogólną postad V=V(r). Wprowadźmy
współrzędne biegunowe:

Transformacji między układami dokonujemy poprzez:

różniczkując po czasie

3

2

1

q

,

q

,

r

q

sin

r

sin

cos

r

cos

cos

r

z

y

x

r



2

2

y

x

r

z

r

sin

z

x

r

y

r

cos

z

y

r

x

r

z

y

x

r

























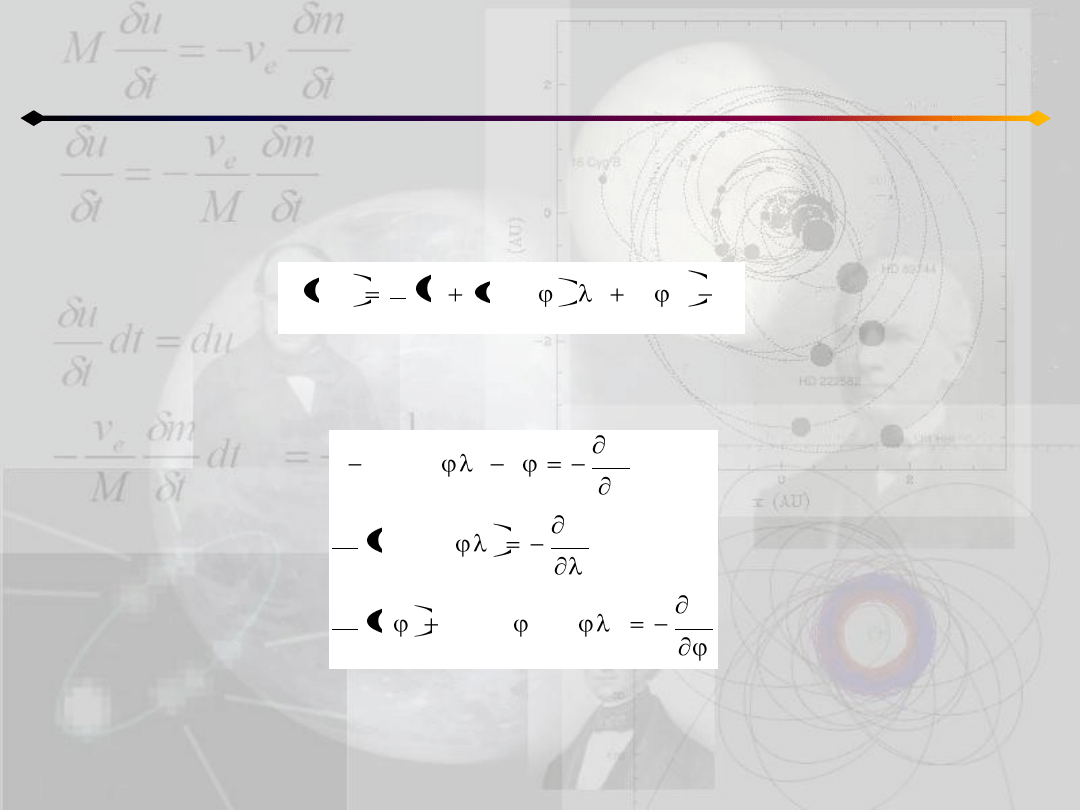
Formalizm Lagrange’a

Cząstka w potencjale radialnym

Funkcja Lagrange’a na jednostkę masy (dla dowolnego potencjału)

Korzystając z niej możemy napisad równania ruchu cząstki:

V

r

cos

r

r

2

1

q

,

q

L

2

2

2

2

2











V

cos

sin

r

r

dt

d

V

cos

r

dt

d

r

V

r

cos

r

r

2

2

2

2

2

2

2















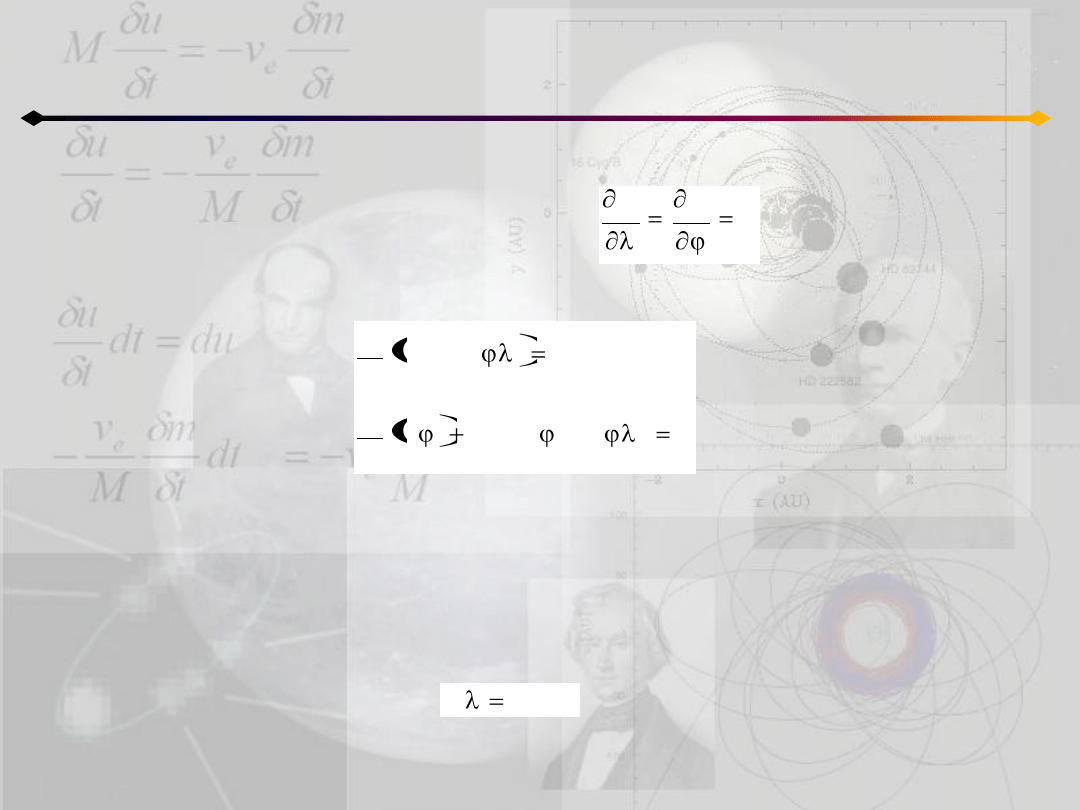
Formalizm Lagrange’a

Cząstka w potencjale radialnym

W przypadku potencjału radialnego mamy:

Wtedy dwa ostatnie równania ruchu przyjmują postad:

Oznacza to, że dla potencjału o symetrii sferycznej:

1. Wszystkie orbity są krzywymi płaskimi – zawsze istnieje rozwiązanie trywialne

φ=0, dφ/dt=0, które otrzymamy przez odpowiedni wybór płaszczyzny odniesienia

2. Każde zagadnienie posiada całkę pól:

0

V

V

0

cos

sin

r

r

dt

d

0

cos

r

dt

d

2

2

2

2

2







const

r

2



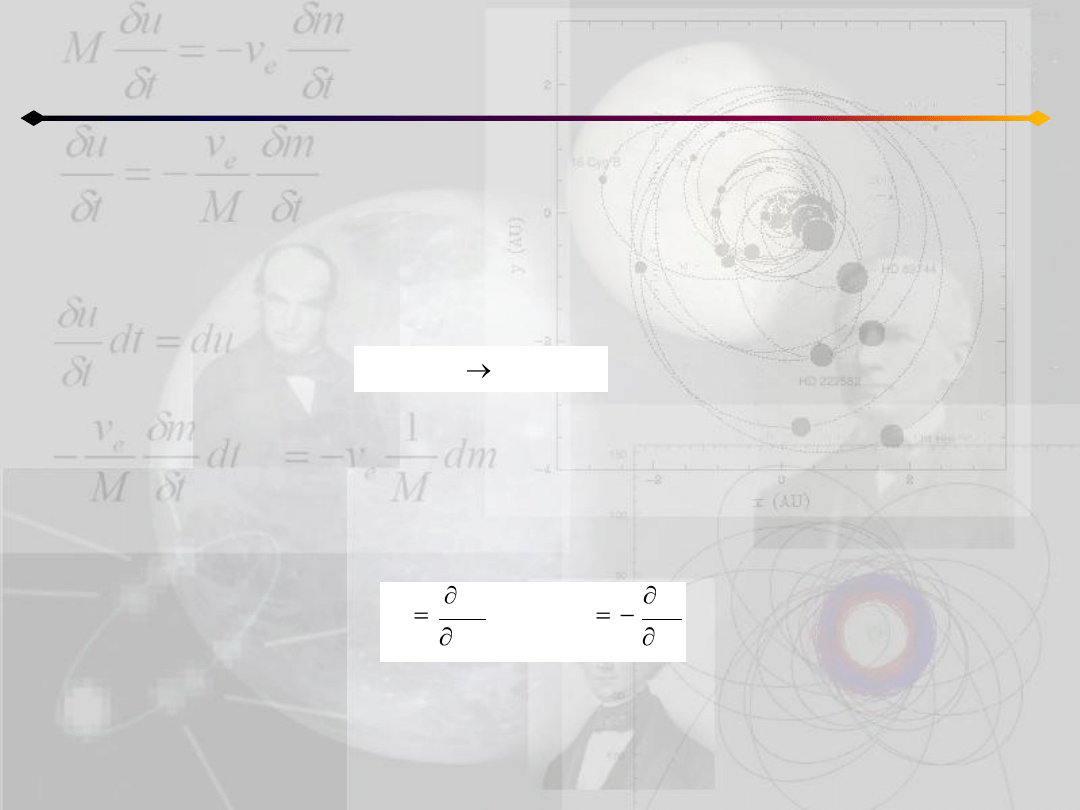
Formalizm kanoniczny

Równania Hamiltona

Mamy układ o M stopniach swobody , który jest opisany przez M współrzędnych
uogólnionych q

i

. Układ posiada funkcję Lagrange’a.

Transformacja Legendre’a

współrzędnym i prędkościom uogólnionym przypisuje położenia i pędy uogólnione,
natomiast funkcji Lagrange’a przypisuje nową funkcję – funkcję Hamiltona (hamiltonian)

Możemy przekształcid układ N równao drugiego rzędu (równania Lagrange)
w 2N równao pierwszego rzędu (równania kanoniczne Hamiltona):

}

H

,

Q

,

q

{

}

L

,

q

,

q

{

i









i

i

i

i

q

H

Q

,

Q

H

q





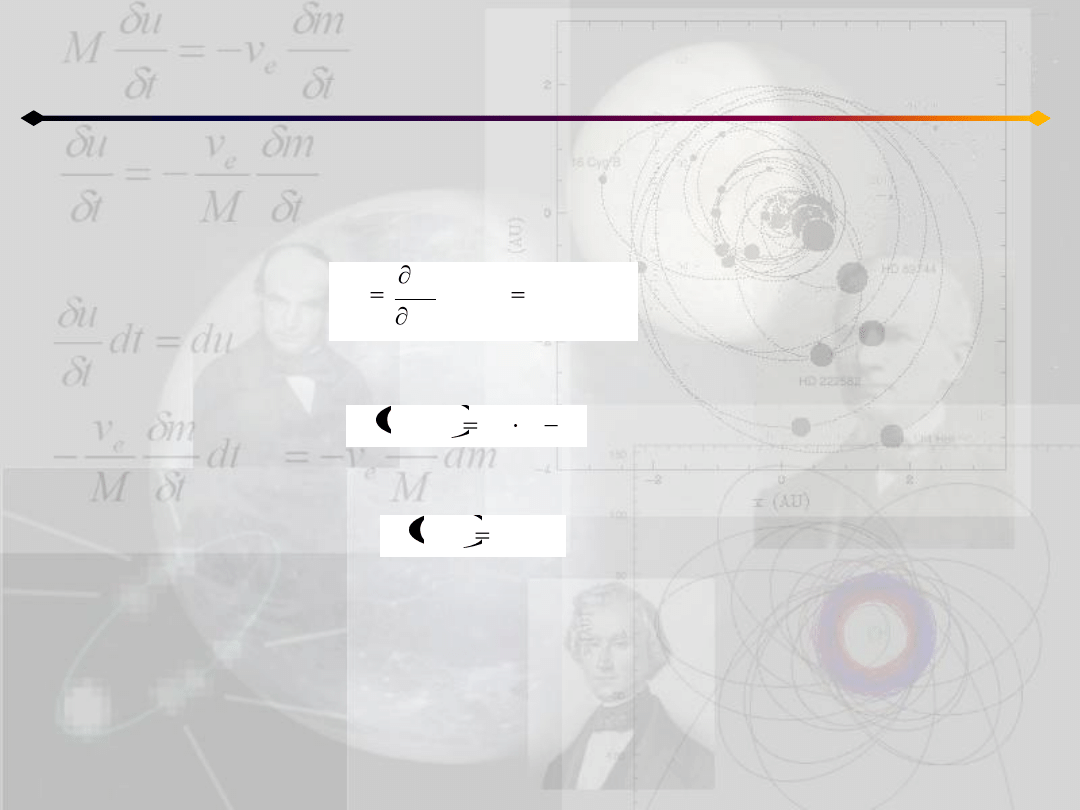
Formalizm kanoniczny

Równania Hamiltona

Hamiltonian:

jeżeli nie zależy jawnie od czasu to jest całką ruchu:

Poza tym hamiltonian określa całkowitą energię układu jeżeli:

1. transformacja z wektorów r do współrzędnych uogólnionych nie zależy jawnie od czasu
2. potencjał V(r) nie zależy jawnie od czasu

L

q

Q

t

,

Q

,

q

H









const

Q

,

q

H





M

,...,

2

,

1

i

,

q

L

Q

i

i



Pędy uogólnione:

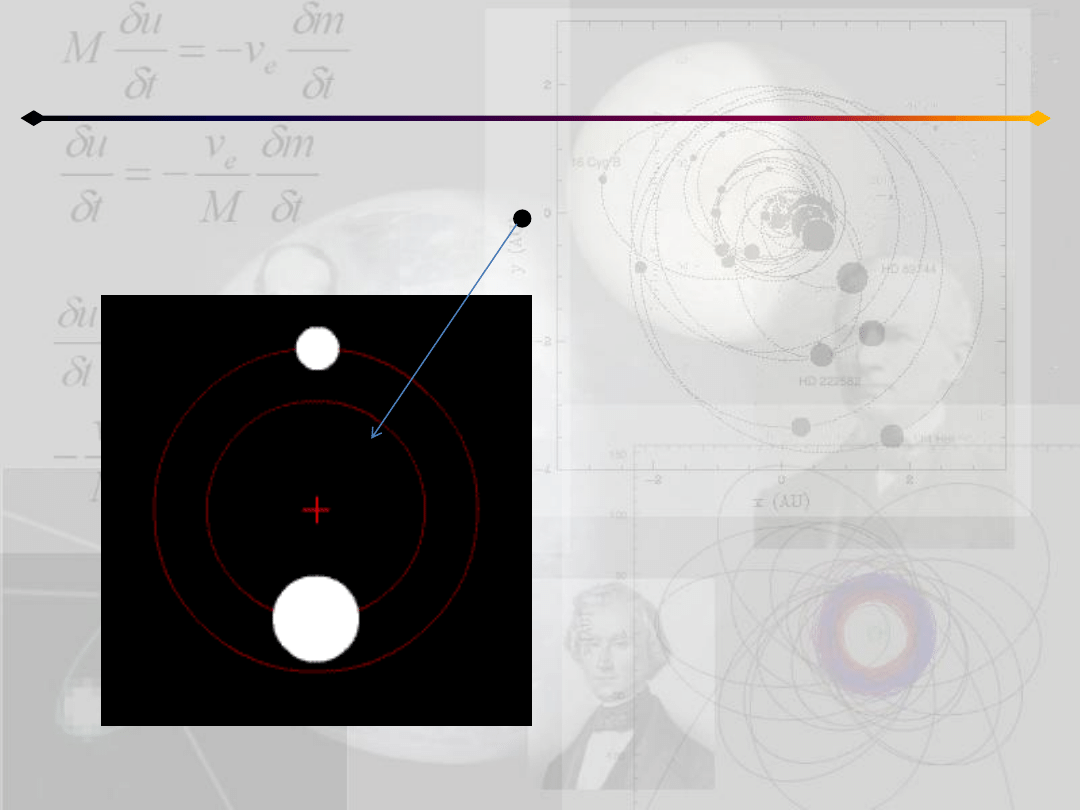
Ograniczone zagadnienie 3 ciał

Równania ruchu

W polu grawitacyjnym dwóch mas
porusza się cząstka o zaniedbywalnie
małej masie

Zakładamy, że obie masy poruszają
się po orbitach kołowych wokół
barycentrum

Masa cząstki jest tak mała, że nie
wywiera żadnej siły na obie masy

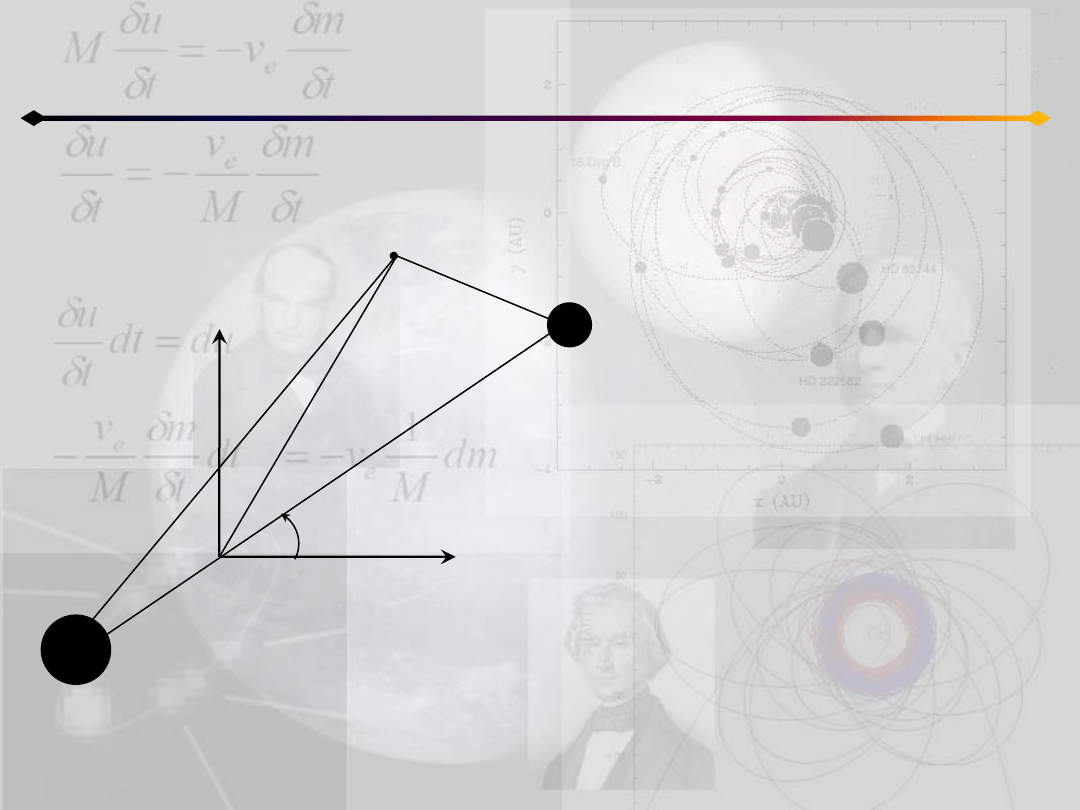
Ograniczone zagadnienie 3 ciał

Równania ruchu

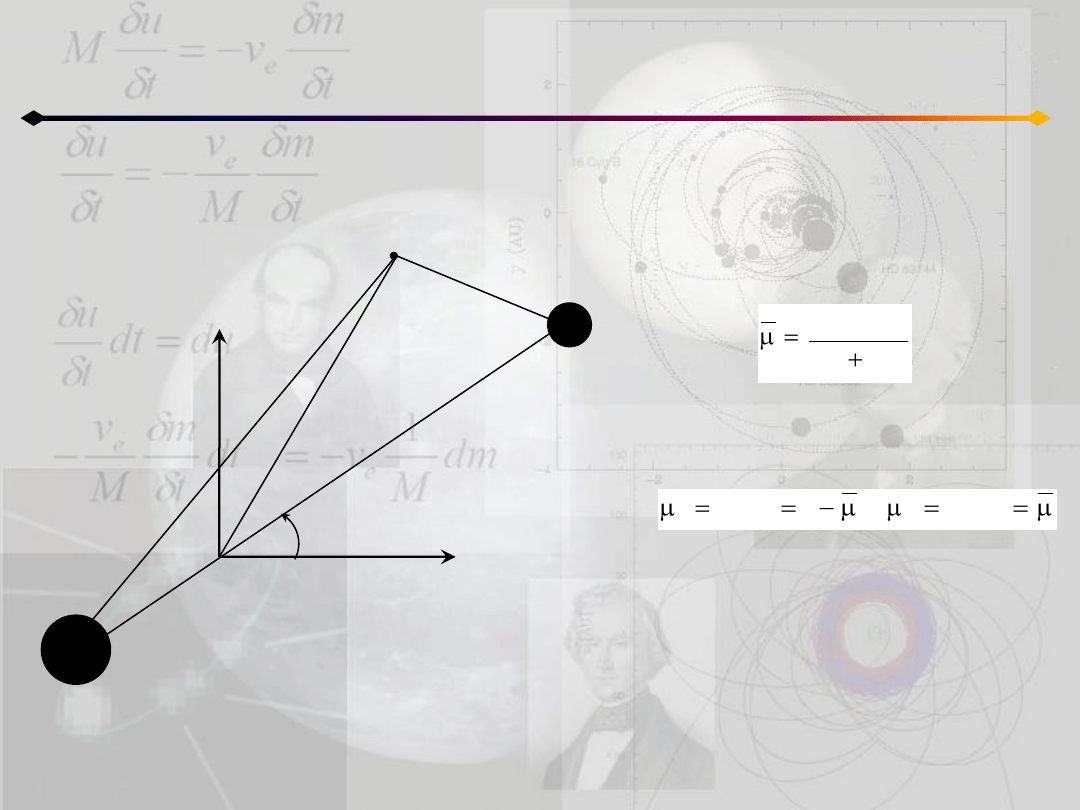
Nieruchomy układ współrzędnych
(ξ,η,ζ) jest zaczepiony w barycentrum
układu

Oś ξ pokrywa się z kierunkiem m

1

m

2

w chwili t

0

Ruch obu mas odbywa się w
płaszczyźnie ξ-η. Oś ζ jest prostopadła
do niej i zgodna ze zwrotem wektora
momentu pędu

Obie masy są stale w tej samej
odległości od siebie i poruszają się ze
stałą prędkością wokół siebie i środka
masy.

nt

ξ

η

μ

2

μ

1

r

1

r

r

2

O

(ξ

2

,η

2

,ζ

2

)

(ξ

1

,η

1

,ζ

1

)

Ograniczone zagadnienie 3 ciał

Równania ruchu

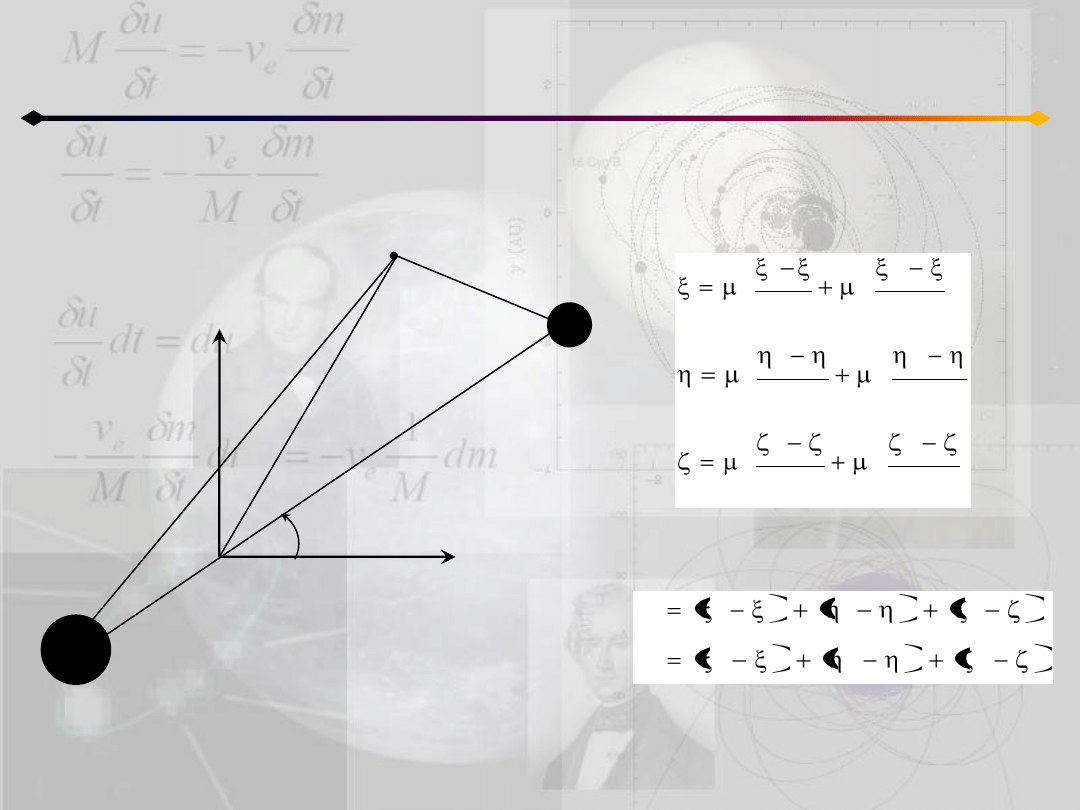
Jednostki dobieramy tak aby
μ=G(m

1

+m

2

)=1. Jeśli dodatkowo

założymy, że m

1

>m

2

to:

wtedy w obranym układzie jednostek
masy ciał są równe:

Jednostkę odległości dobieramy tak
aby odległośd miedzy masami była
równa 1

Wtedy wspólny ruch średni, n, obu
mas jest również równy 1

2

1

2

m

m

m

2

2

1

1

Gm

1

Gm

nt

ξ

η

μ

2

μ

1

r

1

r

r

2

O

(ξ

2

,η

2

,ζ

2

)

(ξ

1

,η

1

,ζ

1

)

Ograniczone zagadnienie 3 ciał

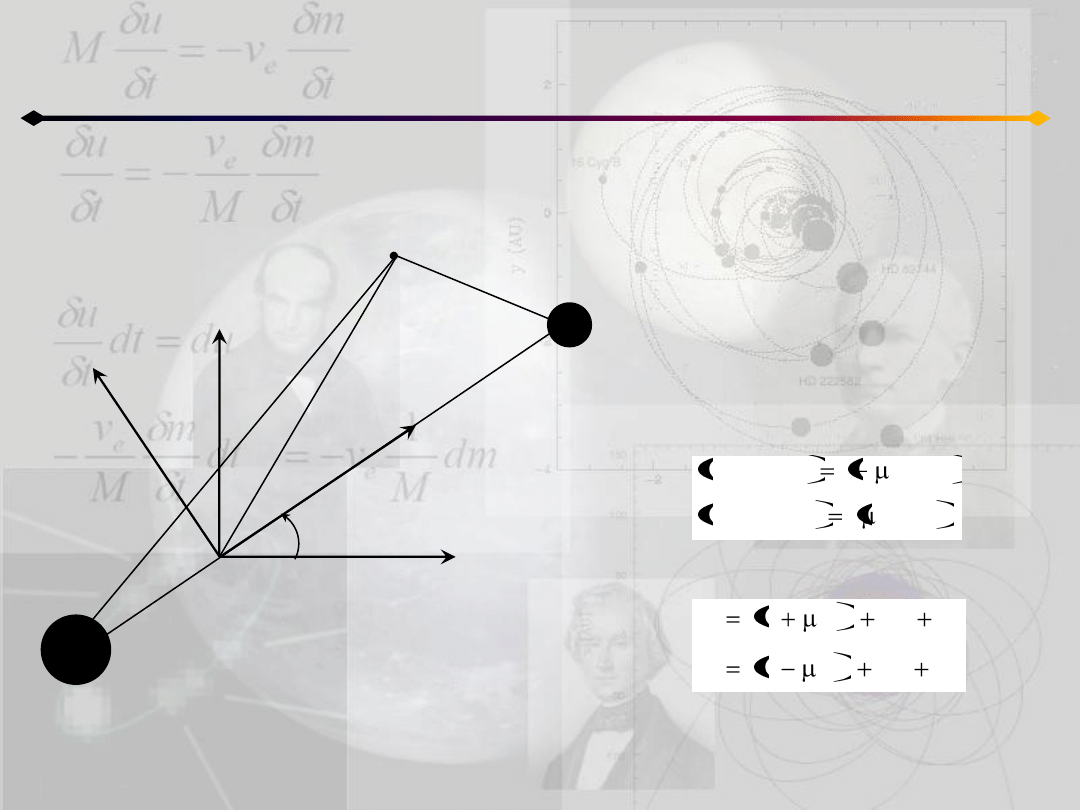
Równania ruchu

Równania ruchu cząstki:

gdzie:

3

2

2

2

3

1

1

1

3

2

2

2

3

1

1

1

3

2

2

2

3

1

1

1

r

r

r

r

r

r













2

2

2

2

2

2

2

2

2

1

2

1

2

1

2

1

r

r

nt

ξ

η

μ

2

μ

1

r

1

r

r

2

O

(ξ

2

,η

2

,ζ

2

)

(ξ

1

,η

1

,ζ

1

)

(12.1)

Ograniczone zagadnienie 3 ciał

Równania ruchu

nt

ξ

η

x

μ

2

μ

1

y

r

1

r

r

2

O

(ξ

2

,η

2

,ζ

2

)

(ξ

1

,η

1

,ζ

1

)

Obie masy poruszają się po kołowych
orbitach z jednakowym ruchem średnim

Z tego powodu ruch cząstki jest
wygodnie opisywad w układzie (x,y,z)
rotującym ze stałą prędkością

Kierunek osi x jest dobrany tak, aby
obie masy leżały zawsze na niej, tzn.:

wtedy:

gdzie (x,y,z) są współrzędnymi cząstki
w układzie rotującym

0

,

0

,

z

,

y

,

x

0

,

0

,

z

,

y

,

x

1

2

2

2

2

1

1

1

2

2

2

1

2

2

2

2

2

2

2

1

z

y

x

r

z

y

x

r

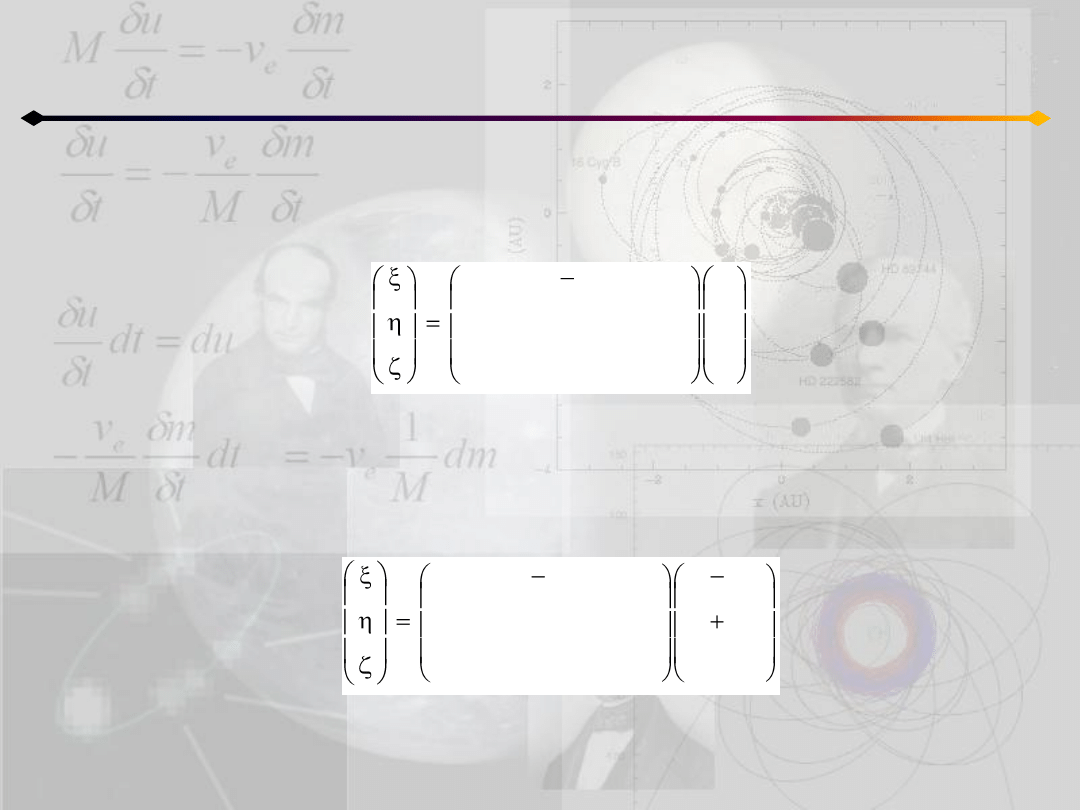
Ograniczone zagadnienie 3 ciał

Równania ruchu

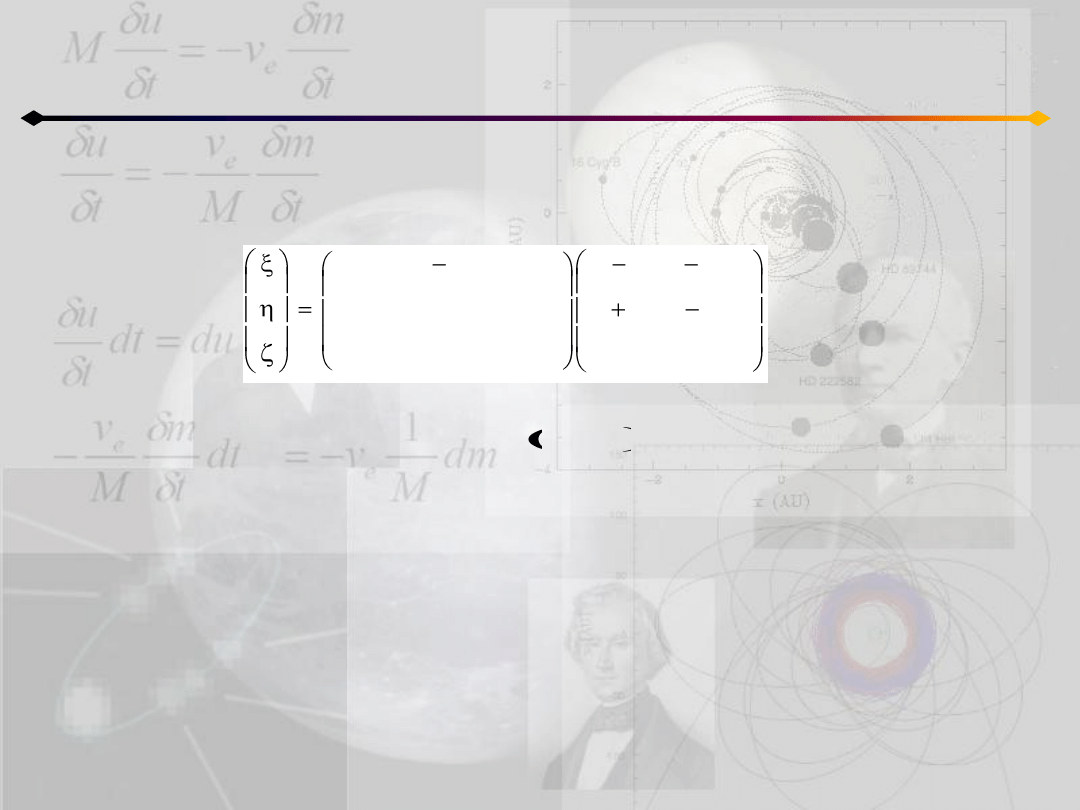
Współrzędne (x,y,z) można wyrazid w układzie nieruchomym poprzez zwykły obrót:

w tym i następnych równaniach n będzie obecne (pomimo tego, że wybraliśmy n=1) dla
podkreślenia tego, że wszystkie czynniki w równaniach ruchu są przyspieszeniami

Różniczkujemy powyższą równośd:

z

y

x

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

z

nx

y

ny

x

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos













(12.2)

(12.3)

Ograniczone zagadnienie 3 ciał

Równania ruchu

Różniczkujemy ponownie:

Przejście do rotującego układu odniesienia powoduje pojawienie się czynników
związanych z przyspieszeniem Coriolisa

oraz przyspieszeniem

odśrodkowym (n

2

x,n

2

y).

Otrzymane wyrażenia na współrzędne ξ, η, ζ oraz ich drugie pochodne można
użyd do wyrażenia równao ruchu za pomocą współrzędnych x,y,z związanych z
rotującym układem współrzędnych

z

y

n

x

n

2

y

x

n

y

n

2

x

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

2

2





























y

n

2

,

x

n

2





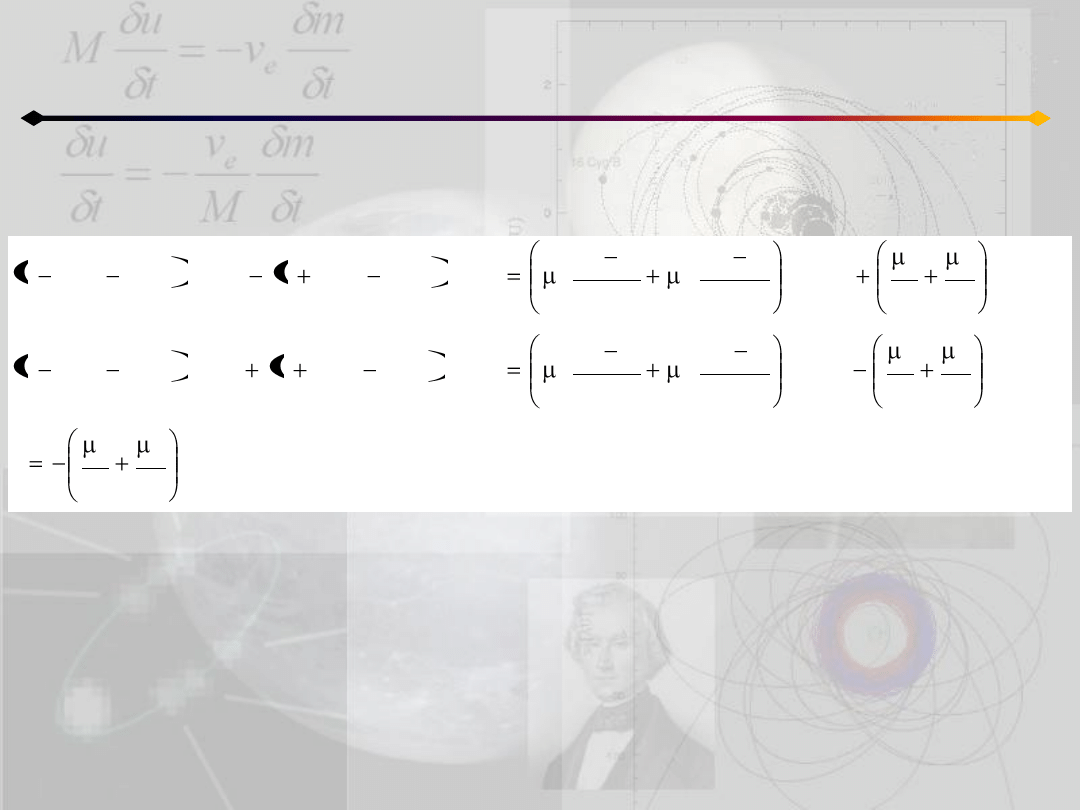
Ograniczone zagadnienie 3 ciał

Równania ruchu

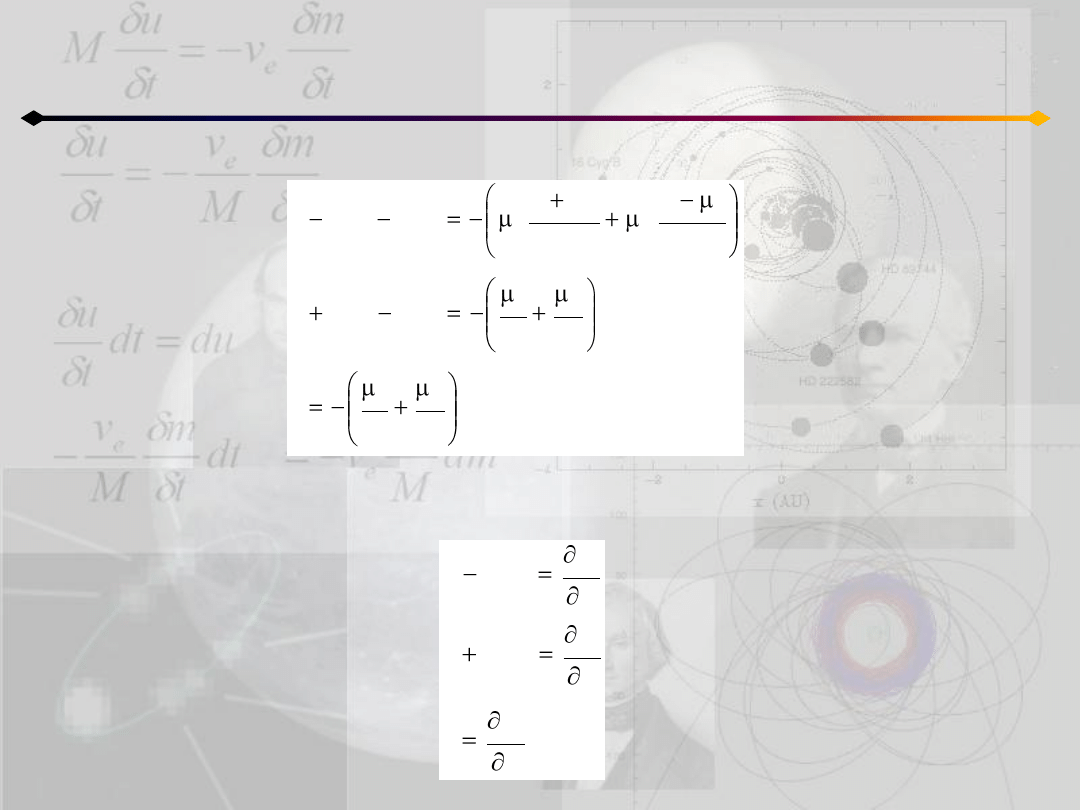
Otrzymujemy:

Pomnożymy pierwsze z równao przez cos nt, a drugie przez sin nt i dodamy do siebie, a
następnie pierwsze przez –sin nt i drugie przez cos nt i dodamy do siebie. W efekcie
dostajemy:

z

r

r

z

nt

cos

y

r

r

nt

sin

r

x

x

r

x

x

nt

cos

y

n

x

n

2

y

nt

sin

x

n

y

n

2

x

nt

sin

y

r

r

nt

cos

r

x

x

r

x

x

nt

sin

y

n

x

n

2

y

nt

cos

x

n

y

n

2

x

3

2

2

3

1

1

3

2

2

3

1

1

3

2

2

2

3

1

1

1

2

2

3

2

2

3

1

1

3

2

2

2

3

1

1

1

2

2





























Ograniczone zagadnienie 3 ciał

Równania ruchu

z

r

r

z

y

r

r

y

n

x

n

2

y

r

x

r

x

x

x

n

y

n

2

x

3

2

2

3

1

1

3

2

2

3

1

1

2

3

2

1

2

3

1

2

1

2

















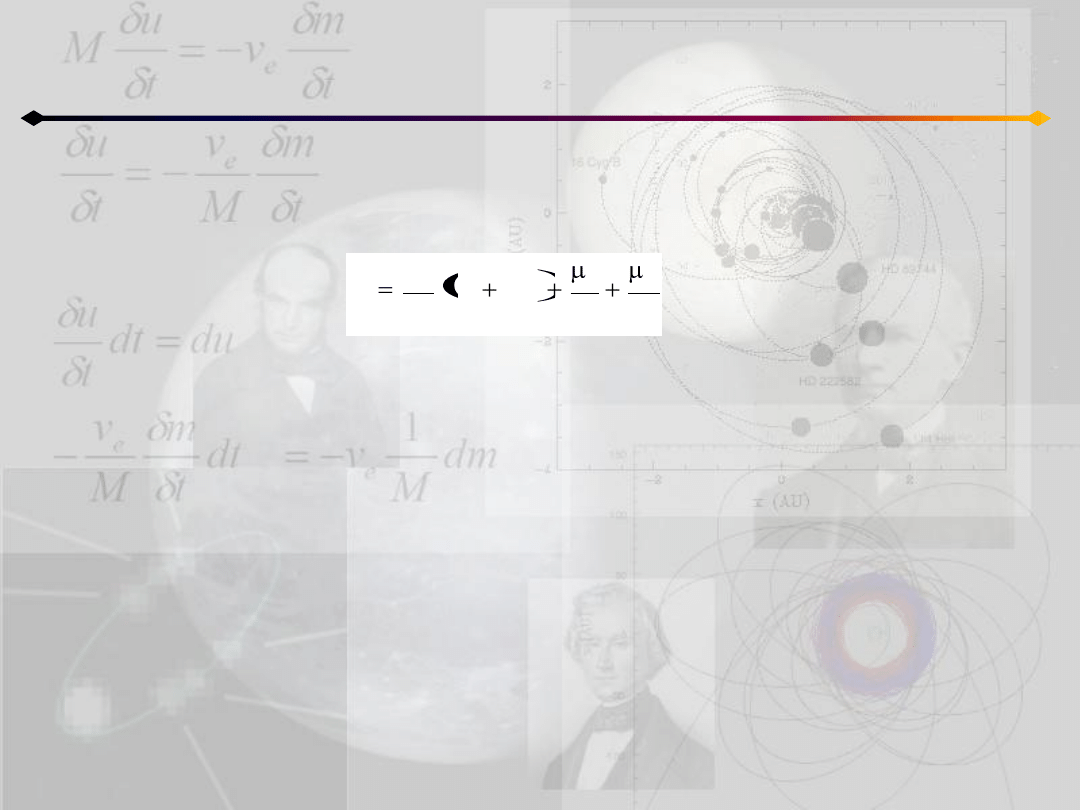
Powyższe przyspieszenia można wyrazid jako gradient skalarnej funkcji U=U(x,y,z)

z

U

z

y

U

x

n

2

y

x

U

y

n

2

x

















(12.4)

Ograniczone zagadnienie 3 ciał

Równania ruchu

gdzie:

w powyższym równaniu x

2

+y

2

jest potencjałem odśrodkowym a czynniki 1/r

1

i 1/r

2

odpowiadają potencjałowi grawitacyjnemu. Pochodne cząstkowe tych czynników
dają wkład do siły odśrodkowej i grawitacyjnej.

Funkcja U nie jest prawdziwym potencjałem, ale funkcją skalarną, z której można
wyznaczyd niektóre (nie wszystkie) przyspieszenia jakich doznaje cząstka w układzie
rotującym. Taka funkcja U jest „pseudo potencjałem”.

2

2

1

1

2

2

2

r

r

y

x

2

n

U

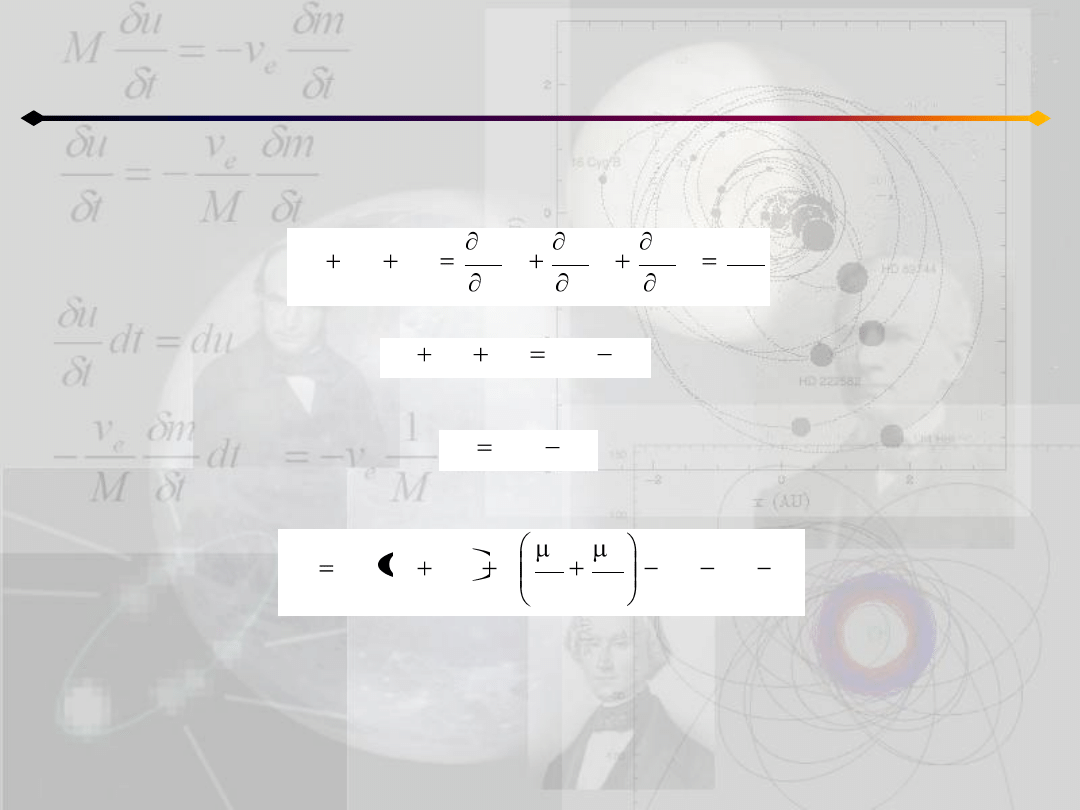
Ograniczone zagadnienie 3 ciał

Całka Jacobiego

Mnożąc równania 12.4 kolejno przez pierwsze pochodne x,y,z i dodając do siebie
dostajemy:

Po scałkowaniu:

gdzie C

J

jest stałą całkowania. Lewa strona jest kwadratem prędkości w układzie

rotującym, stąd:

wykorzystując otrzymane wcześniej wyrażenie na potencjał:

C

J

jest tzw. całką Jacobiego. Jest to jedyna znana całka ruchu w ograniczonym

zagadnieniu 3 ciał.

To nie jest całka energii! – w ograniczonym zagadnieniu trzech ciał energia i całkowity
moment pędu nie są zachowane

dt

dU

z

z

U

y

y

U

x

x

U

z

z

y

y

x

x

























J

2

2

2

C

U

2

z

y

x







J

2

C

U

2

v

2

2

2

2

2

1

1

2

2

2

J

z

y

x

r

r

2

y

x

n

C







Ograniczone zagadnienie 3 ciał

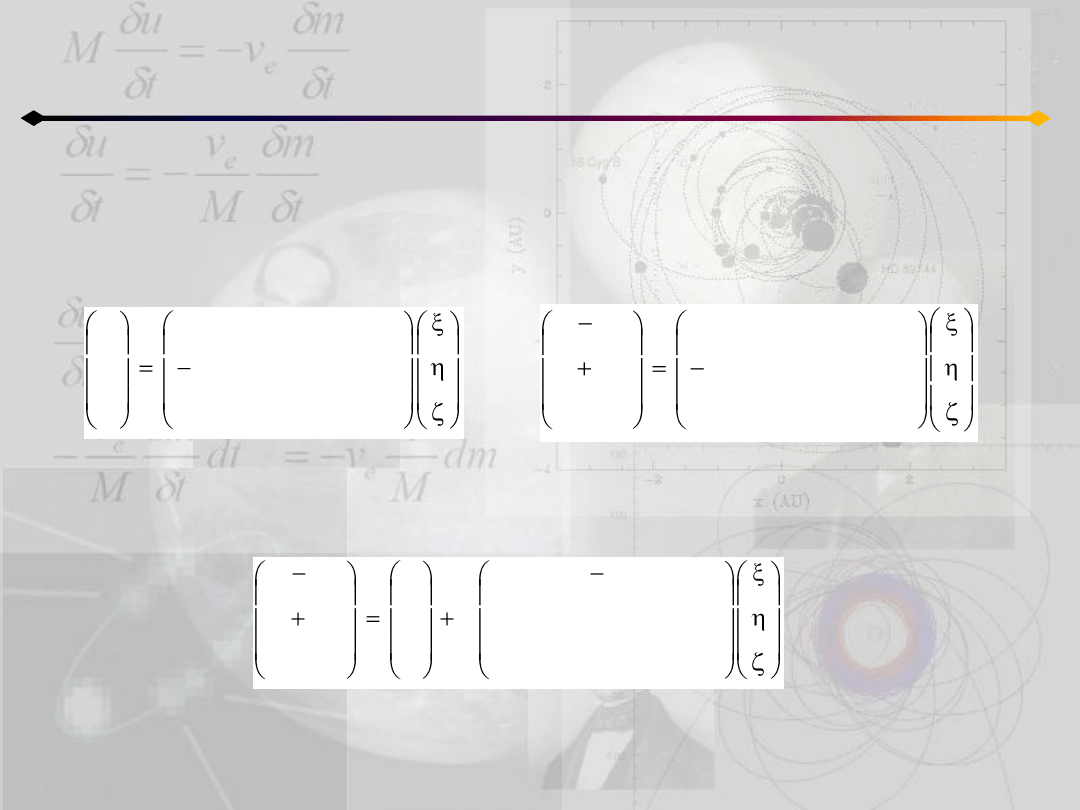
Całka Jacobiego

C

J

można wyrazid również we współrzędnych układu nieruchomego. W tym celu możemy

wykorzystad uzyskane wcześniej wyrażenia (12.2, 12.3) na przejście między układem
nieruchomym i obracającym się:

Drugie z wyrażeo można zapisad nieco inaczej:

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

z

y

x













1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

z

nx

y

ny

x

0

0

0

0

nt

sin

nt

cos

0

nt

cos

nt

sin

n

z

y

x

z

nx

y

ny

x













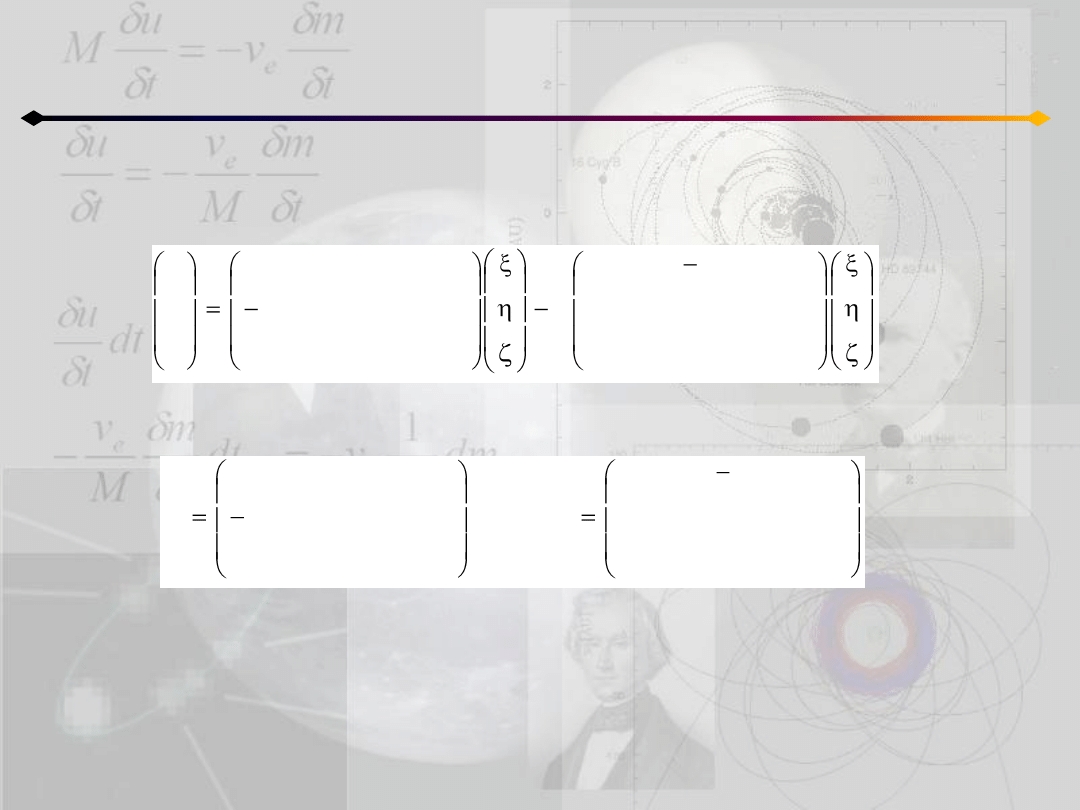
Ograniczone zagadnienie 3 ciał

Całka Jacobiego

Porównując oba wyrażenia:

Wprowadzamy oznaczenia:

Możemy z 12.5 otrzymad:

0

0

0

0

nt

sin

nt

cos

0

nt

cos

nt

sin

n

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

z

y

x













0

0

0

0

nt

sin

nt

cos

0

nt

cos

nt

sin

B

1

0

0

0

nt

cos

nt

sin

0

nt

sin

nt

cos

A





(12.5)

Ograniczone zagadnienie 3 ciał

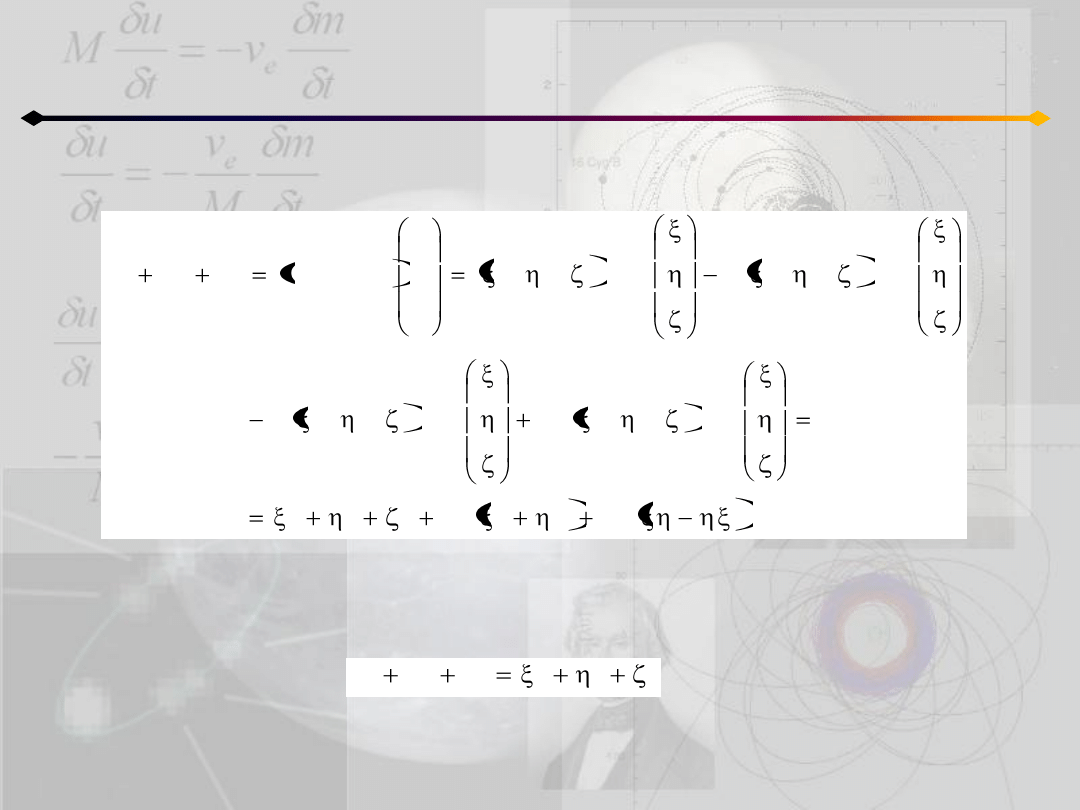
Całka Jacobiego





































































n

2

n

B

B

n

A

B

n

B

A

n

A

A

z

y

x

z

y

x

z

y

x

2

2

2

2

2

2

T

2

T

T

T

2

2

2

Macierze A i B są ortogonalne więc macierze odwrotne są po prostu macierzami
transponowanymi. Ponieważ obrót nie zmienia odległości więc:

2

2

2

2

2

2

z

y

x

Ograniczone zagadnienie 3 ciał

Całka Jacobiego

W takim razie całka Jacobiego wyrażona we współrzędnych układu nieruchomego:

co można przepisad w postaci:

Lewa strona tego równania jest całkowitą energią na jednostkę masy cząstki. Ponieważ
iloczyn momentu pędu i ruchu średniego nie jest stały, więc jasnym jest dlaczego
całkowita energia nie jest zachowana w ograniczonym zagadnieniu trzech ciał.

Całka Jacobiego nie przydaje się do uzyskania dokładnego rozwiązania ograniczonego
zagadnienia trzech ciał, ale może byd użyta do wyznaczenia obszarów wzbronionych
dla ruchu cząstki.

2

2

2

2

2

1

1

J

n

2

r

r

2

C











n

,

0

,

0

n

;

C

2

1

n

c

r

r

2

1

J

2

2

1

1

2

2

2













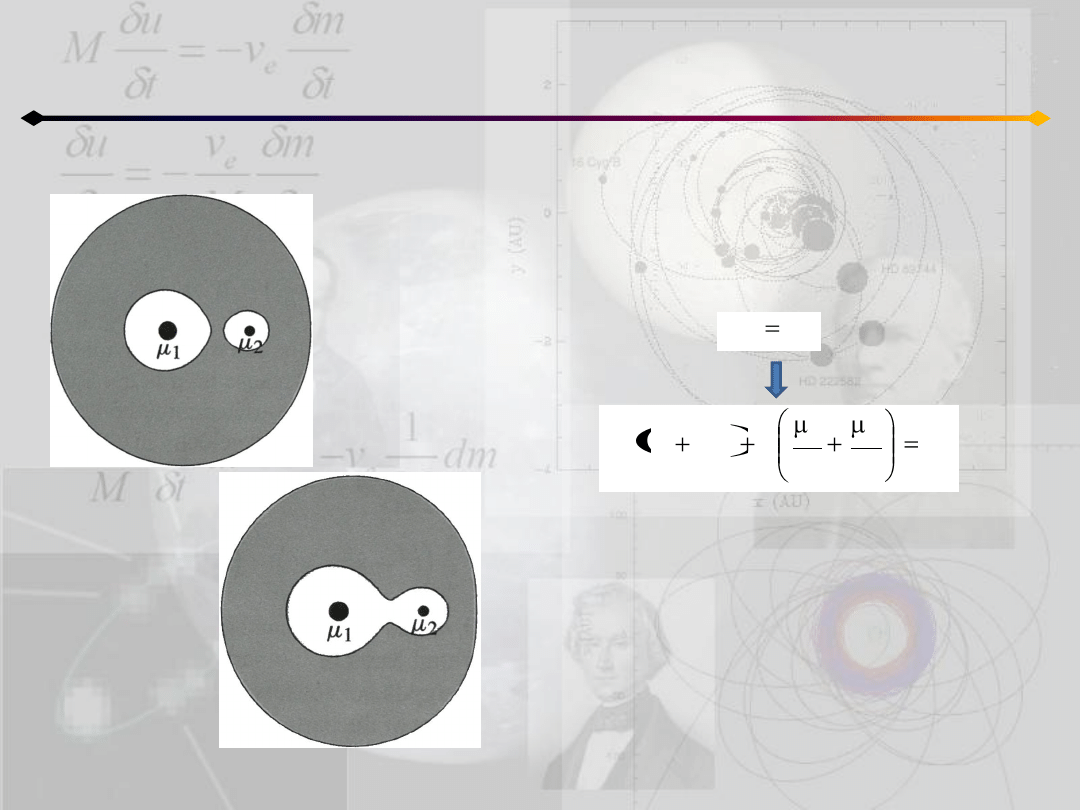
Użytecznośd całki Jacobiego jest dobrze
widoczna przy analizie miejsc, w których
prędkośd cząstki jest równa 0. Mamy wtedy:

Powyższe równanie definiuje powierzchnie dla
danej wartości C

J

– powierzchnie zerowej

prędkości.

Są one przydatne przy określaniu warunków
brzegowych dla ruchu cząstki

Ograniczone zagadnienie 3 ciał

Całka Jacobiego

J

C

U

2

J

2

2

1

1

2

2

2

C

r

r

2

y

x

n

C

J

=3.9

C

J

=3.7

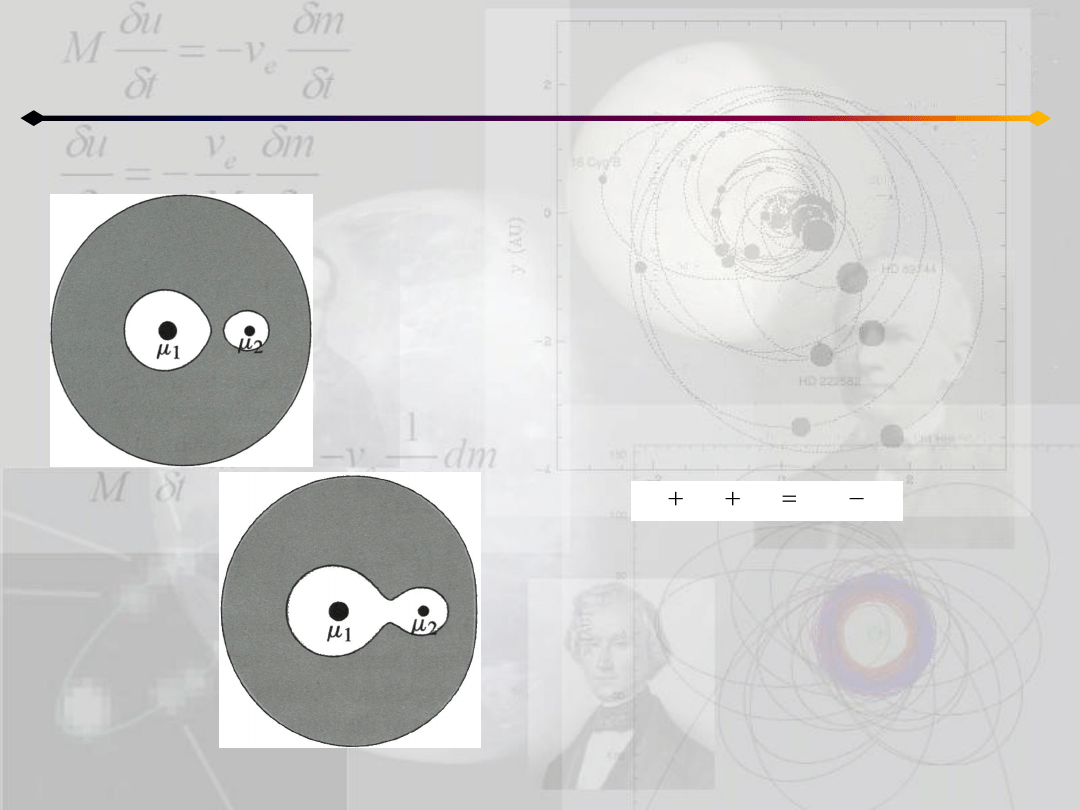
Dla ułatwienia ograniczymy się do płaszczyzny
x-y.

W takim wypadku przecięcia powierzchni
zerowej prędkości z płaszczyzną x-y dają
krzywe zerowej prędkości (rysunek).

Z równania:

widad, że zawsze musi byd 2U>=C

J

, bo w

przeciwnym razie prędkośd ma wartośd
zespoloną. Stąd równanie 12.7 definiuje
obszary, w których ruch jest dozwolony.

Ograniczone zagadnienie 3 ciał

Całka Jacobiego

J

2

2

2

C

U

2

z

y

x







(12.7)

C

J

=3.9

C

J

=3.7

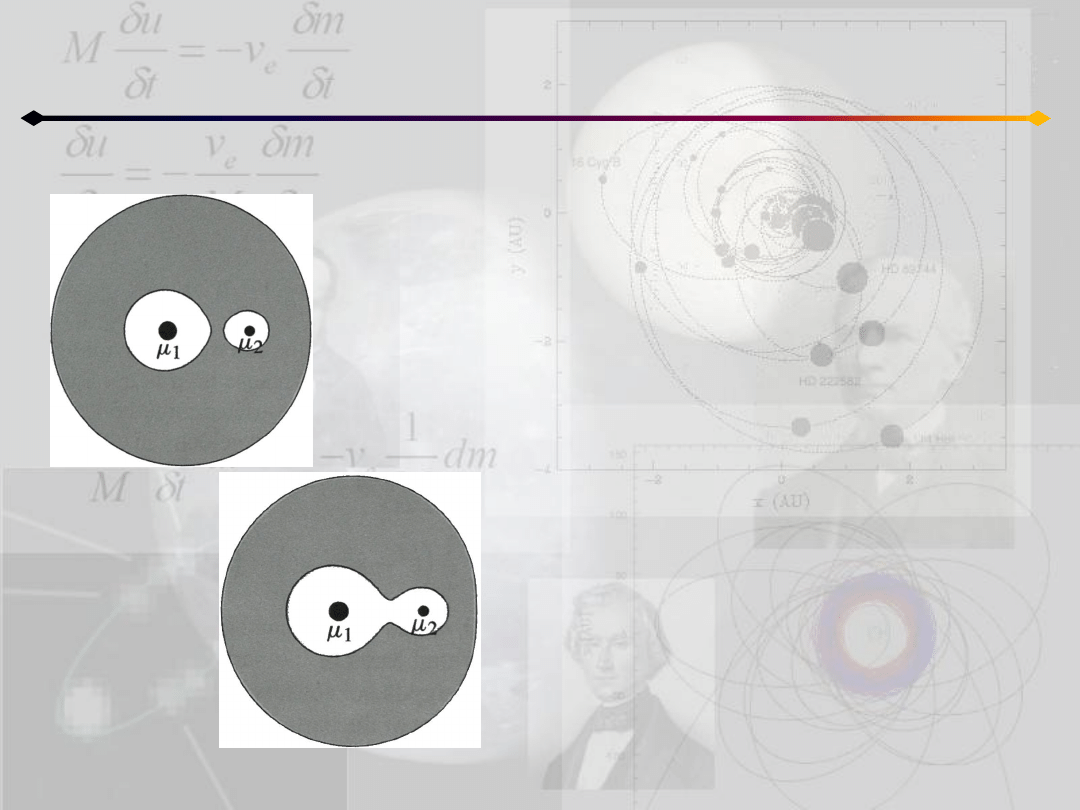
Obszary szare są zakazane dla ruchu cząstki

Weźmy przypadek C

J

=3.9.

Wynika stąd, że jeżeli cząstka znajduje się w
dozwolonym obszarze wokół μ

1

to nie może

nigdy krążyd wokół μ

2

, a także nie może uciec z

układu ponieważ nie może poruszad się przez
obszar wzbroniony.

To jest podstawa teorii stabilnych orbit Hilla

Należy jednak pamiętad, że powyższe wnioski
dotyczą przypadku gdy dwie masy poruszają
po kołowych orbitach wokół barycentrum, a
trzecia masa nie działa na nie siłą grawitacyjną

Ograniczone zagadnienie 3 ciał

Całka Jacobiego

C

J

=3.9

C

J

=3.7

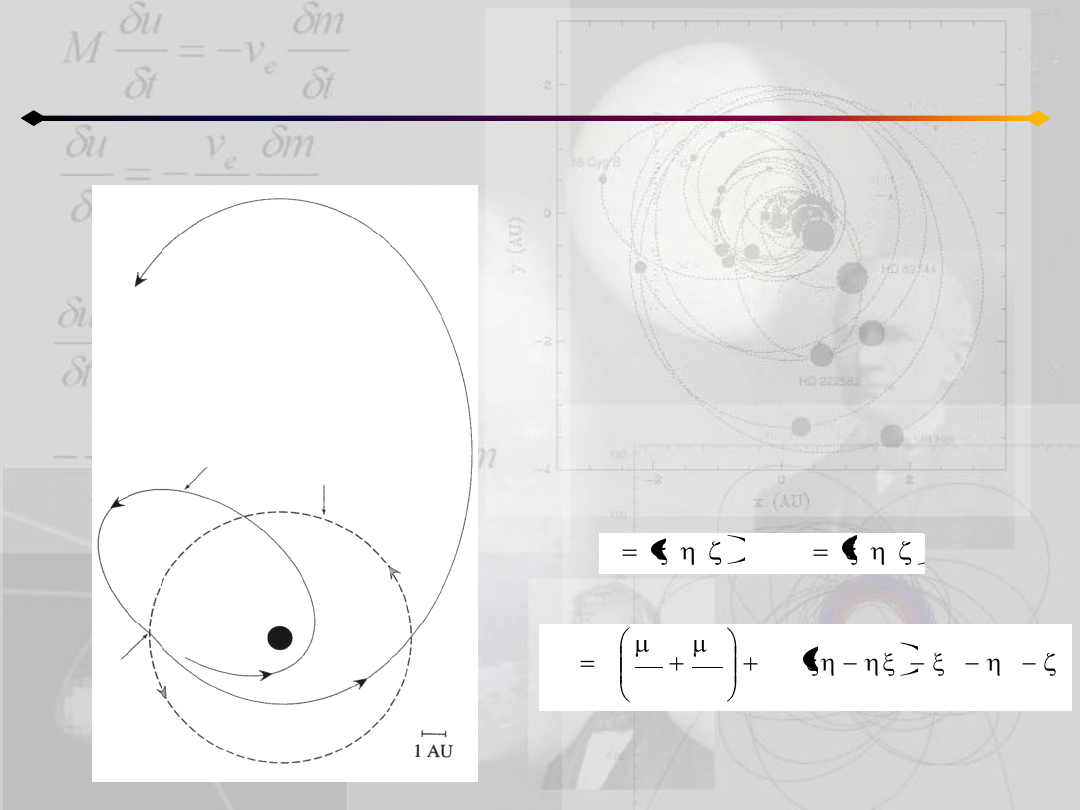
Ograniczone zagadnienie 3 ciał

Kryterium Tisseranda

bliskie
przejście

orbita
komety

orbita
Jowisza

Słooce

Kometa porusza się początkowo po orbicie
o elementach a, e, I

Po bliskim przejściu w pobliżu Jowisza orbita
ulega zmianie, a nowe parametry to: a’, e’, I’

Całka Jacobiego (która pozostaje stała
podczas zbliżenia) może byd wykorzystana do
uzyskania związku między tymi elementami

Położenie i prędkośd komety w układzie
nieruchomym:

Całka Jacobiego w tym układzie:

gdzie r

1

i r

2

są odpowiednio odległością komety

od Słooca i Jowisza











,

,

r

,

,

r

2

2

2

2

2

1

1

J

n

2

r

r

2

C











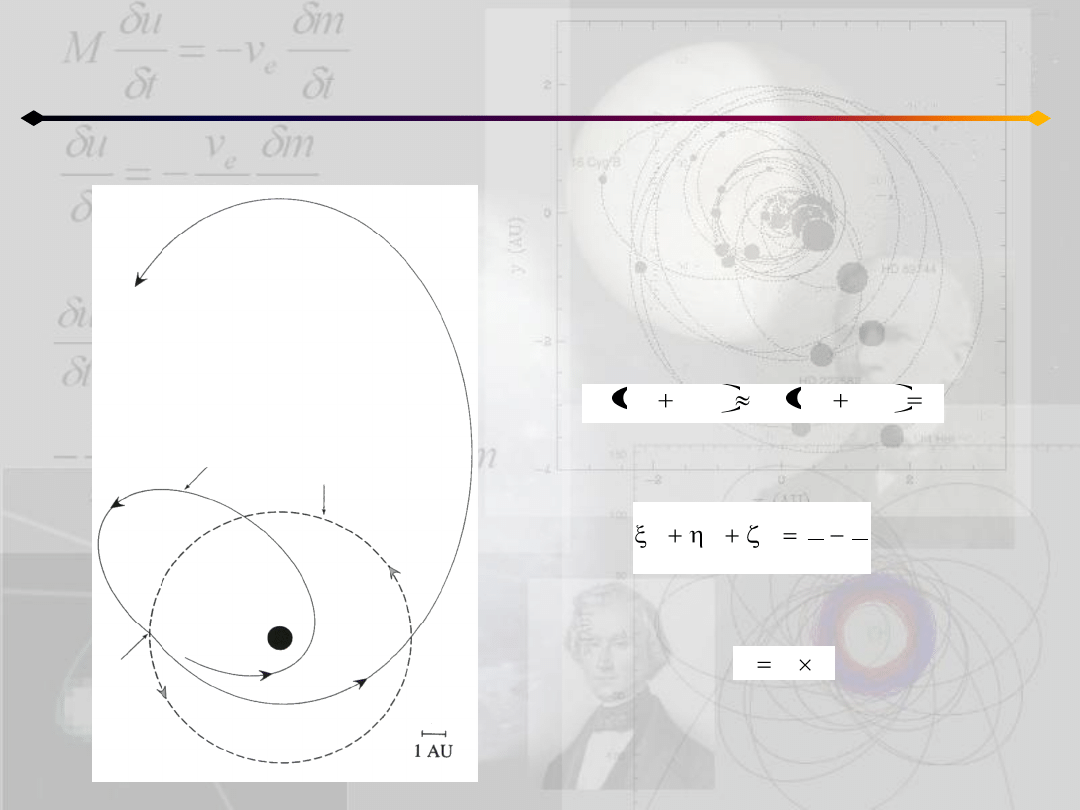
Ograniczone zagadnienie 3 ciał

Kryterium Tisseranda

bliskie
przejście

orbita
komety

orbita
Jowisza

Słooce

Wybieramy układ jednostek, w którym wielka
półoś i ruch średni Jowisza są jednostkowe

Ponieważ masy Jowisza i komety są dużo
mniejsze od masy Słooca:

Całka energii dla układu dwóch ciał
kometa-Słooce:

całkowity moment pędu (kometa-Słooce) na
jednostkę masy:

1

m

m

G

m

m

G

J

S

k

S

a

1

r

2

2

2

2







r

r

c







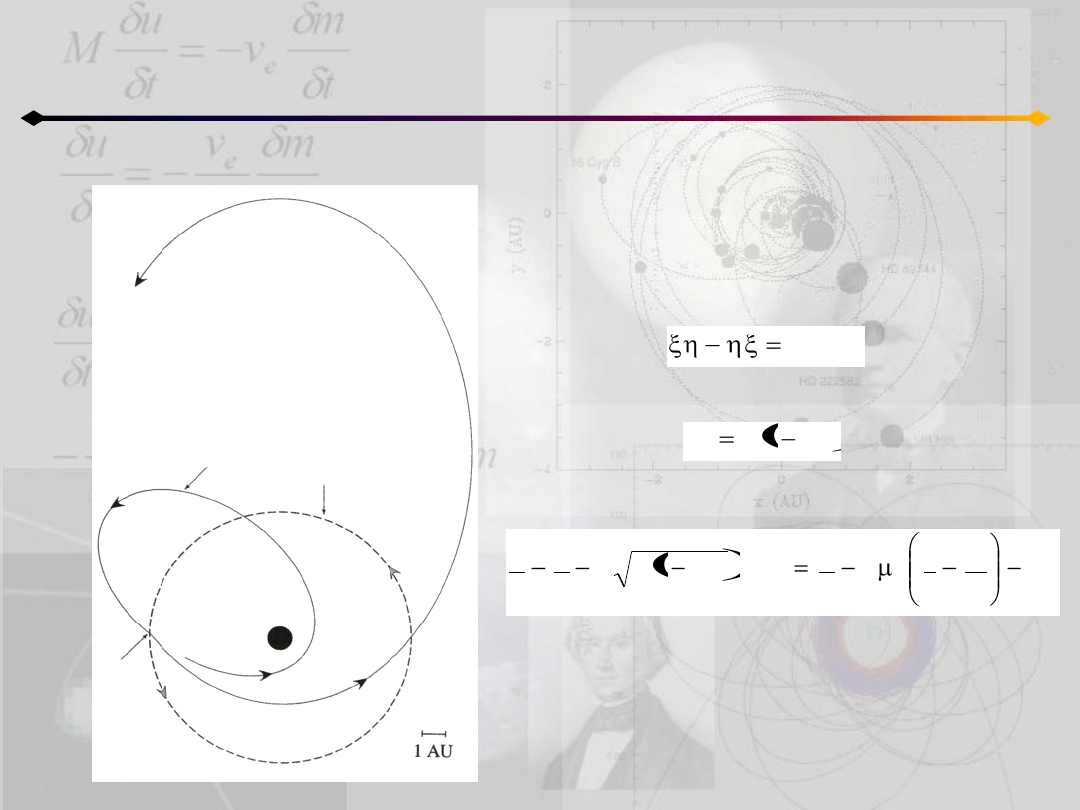
Ograniczone zagadnienie 3 ciał

Kryterium Tisseranda

bliskie
przejście

orbita
komety

orbita
Jowisza

Słooce

Jeśli I jest nachyleniem orbity komety względem
płaszczyzny orbity Jowisza, to składowa ξ-owa
wektora momentu pędu:

gdzie w naszym układzie jednostek mamy:

Ostatecznie całka Jacobiego przyjmuje postad:

I

cos

c





2

2

e

1

a

c

J

2

2

2

C

r

1

r

1

2

r

2

I

cos

e

1

a

2

a

1

r

2

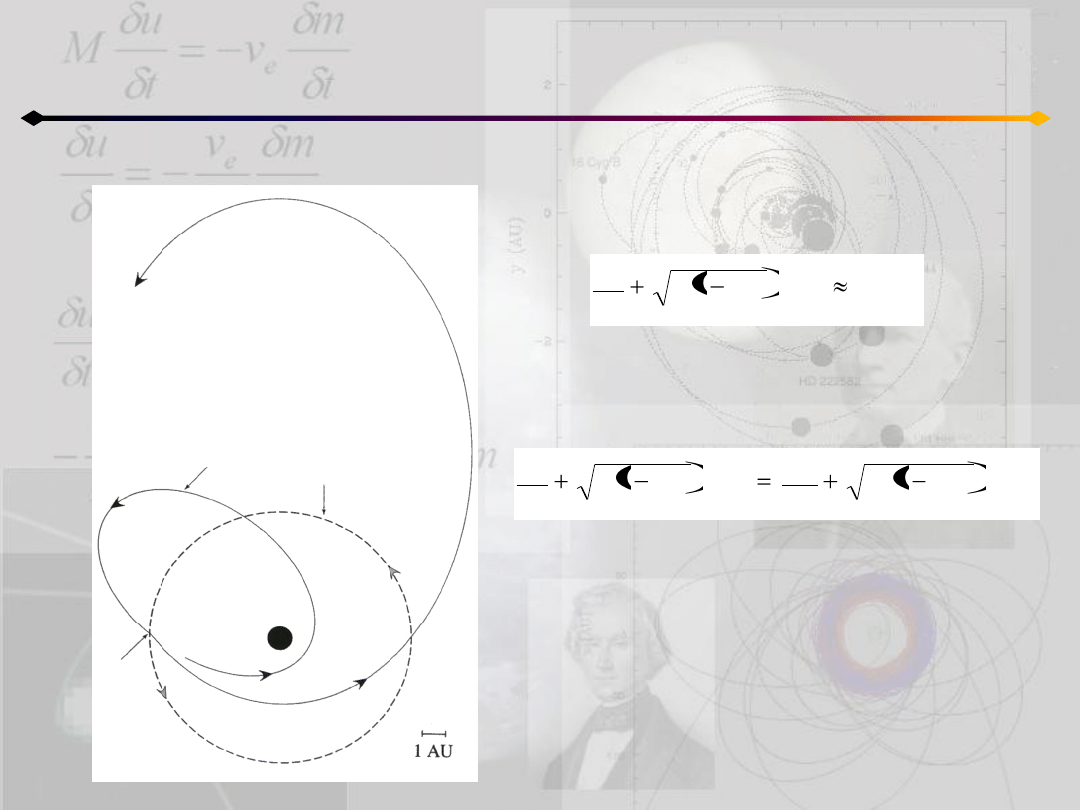
Ograniczone zagadnienie 3 ciał

Kryterium Tisseranda

bliskie
przejście

orbita
komety

orbita
Jowisza

Słooce

Jeśli założymy, że kometa znajduje się
stosunkowo daleko od Jowisza (1/r

2

jest zawsze

małe) i pominiemy wyrażenia z μ

2

, to kryterium:

W takim razie zależnośd między elementami
orbitalnymi komety przed i po „spotkaniu” z
Jowiszem:

Ta zależnośd jest zwana kryterium Tisseranda.

Może byd użyte do określenia, czy odkryta
kometa jest obiektem znanym wcześniej, którego
elementy orbitalne uległy zmianie po przejściu
w pobliżu planety

const

I

cos

e

1

a

a

2

1

2

'

I

cos

'

e

1

'

a

'

a

2

1

I

cos

e

1

a

a

2

1

2

2

Ograniczone zagadnienie 3 ciał

Kryterium Tisseranda

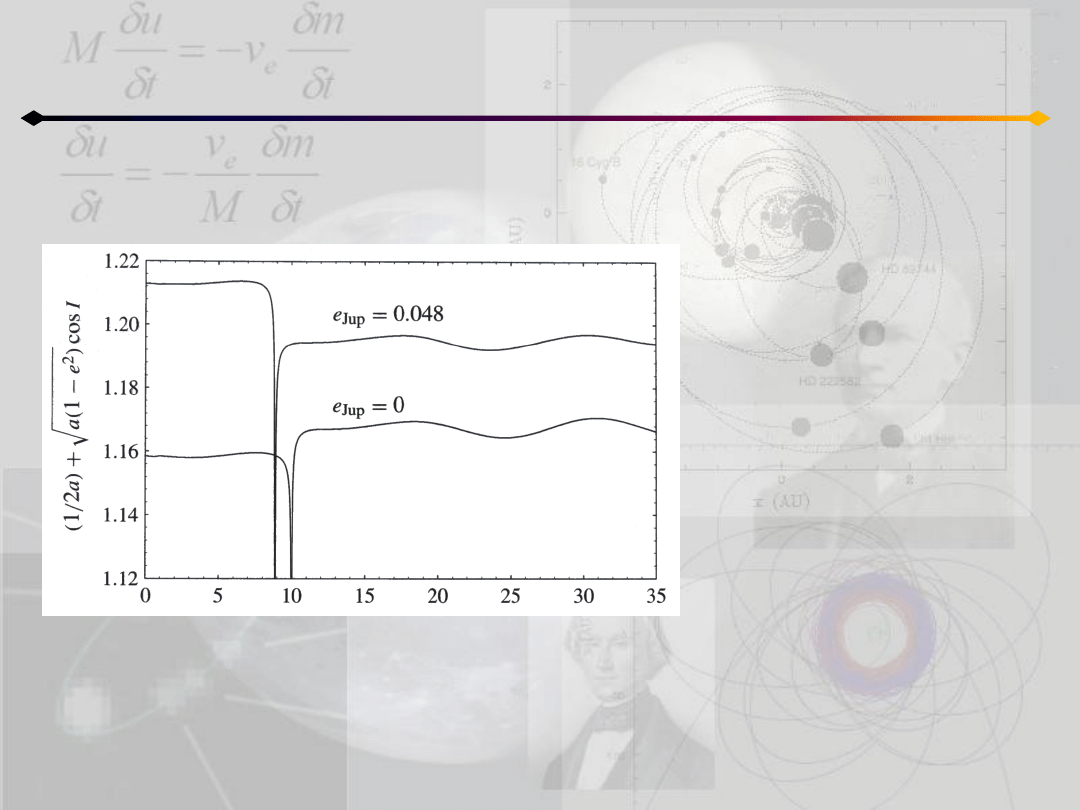
Przykład.

Początkowe parametry orbity
komety:
a=4.81 AU
e=0.763
I=7.47

o

Po przejściu w pobliżu Jowisza:
a’=10.8 AU
e’=0.731
I’=21.4

o

Murray,Dermott 1999

czas (lata)

Zmiana stałej Tisseranda dla dwóch wyznaczeo orbity komety przy założeniu kołowej i
eliptycznej orbity Jowisza.
Można zauważyd, że stała zmienia się bardzo niewiele w obu przypadkach, a więc może
byd traktowana jako stała nawet w przypadku bardziej rzeczywistego przybliżenia orbity
Jowisza

Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

F

1

F

2

F

P

a

b

c

O

Pozycje dwóch mas m

1

i m

2

poruszających

po kołowych orbitach wokół wspólnego środka
masy pozostają niezmienne w układzie rotującym
wokół barycentrum ze stałą prędkością.

Punkty równowagi – miejsca, w których cząstka p
poruszająca się z pewną prędkością w układzie
nieruchomym będzie stacjonarna w układzie
rotującym

Należy pamiętad, że w takim punkcie cząstka
nadal podlega działaniu kilku sił i w układzie
nieruchomym porusza się po orbicie keplerowskiej

Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

F

1

F

2

F

P

a

b

c

O

Niech wektory a,b,c oznaczają odpowiednio
położenia masy m

1

, barycentrum i m

2

względem punktu P

F

1

i F

2

– siły (na jednostkę masy) działające na

cząstkę P skierowane do mas m

1

i m

2

Jeśli P znajduje się w stałym położeniu w układzie
rotującym to znajduje się w stałej odległości b od
barycentrum, które jest jedynym punktem stałym
w układzie nieruchomym.

P podlega działaniu siły odśrodkowej, która jest
równoważona przez:

2

1

F

F

F







Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

F

1

F

2

F

P

a

b

c

O

Położenie barycentrum:

Po pomnożeniu wektorowo przez F

1

+F

2

:

Ponieważ kąt między F

1

i c jest równy minus

kąt między F

2

i a, więc możemy napisad

powyższe równanie w postaci skalarnej:

2

1

2

1

m

m

c

m

a

m

b







c

b

m

b

a

m

2

1









0

a

F

m

c

F

m

2

1

1

2









a

F

m

c

F

m

2

1

1

2

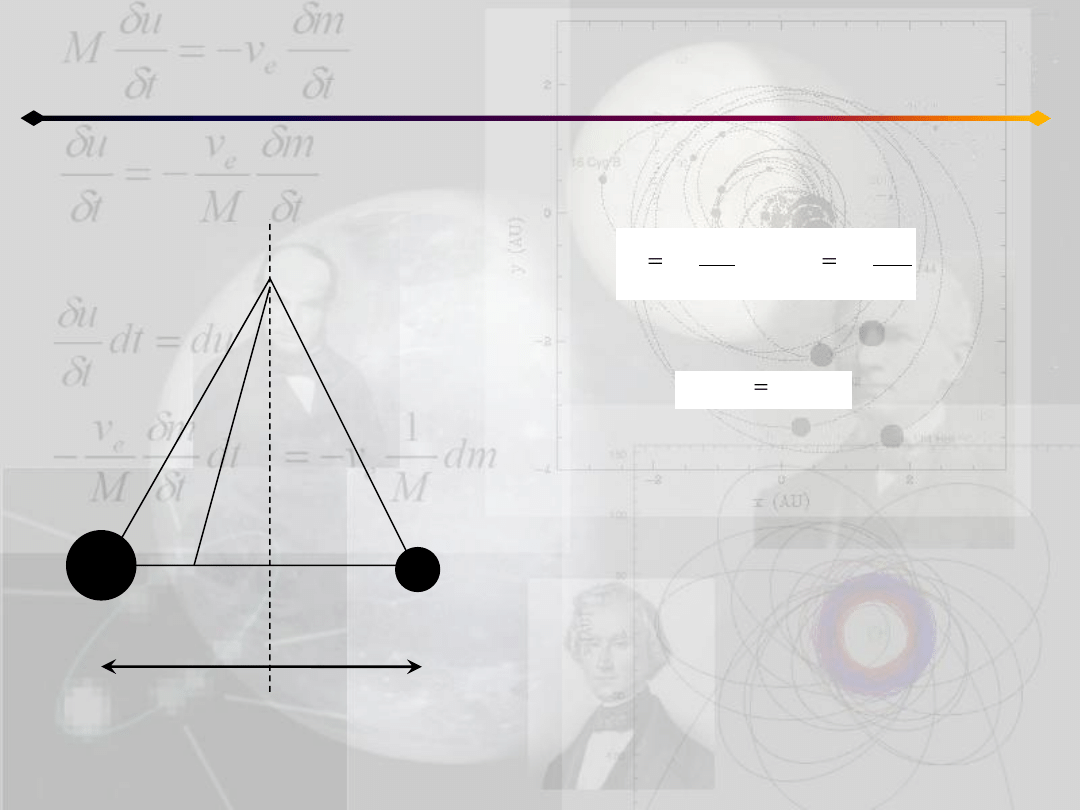
Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

W przypadku sił grawitacyjnych:

co w połączeniu z równaniem:

daje: a=c – trójkąt utworzony przez cząstkę
i obie masy jest równoramienny

W takim razie wszystkie punkty P, dla których
F przechodzi przez barycentrum są położone
na linii prostopadłej do linii łączącej masy
m1 i m2.

2

2

2

2

1

1

c

m

G

F

,

a

m

G

F

a

F

m

c

F

m

2

1

1

2

m

1

m

2

P

a

b

a

O

d

α

α

β

γ

g

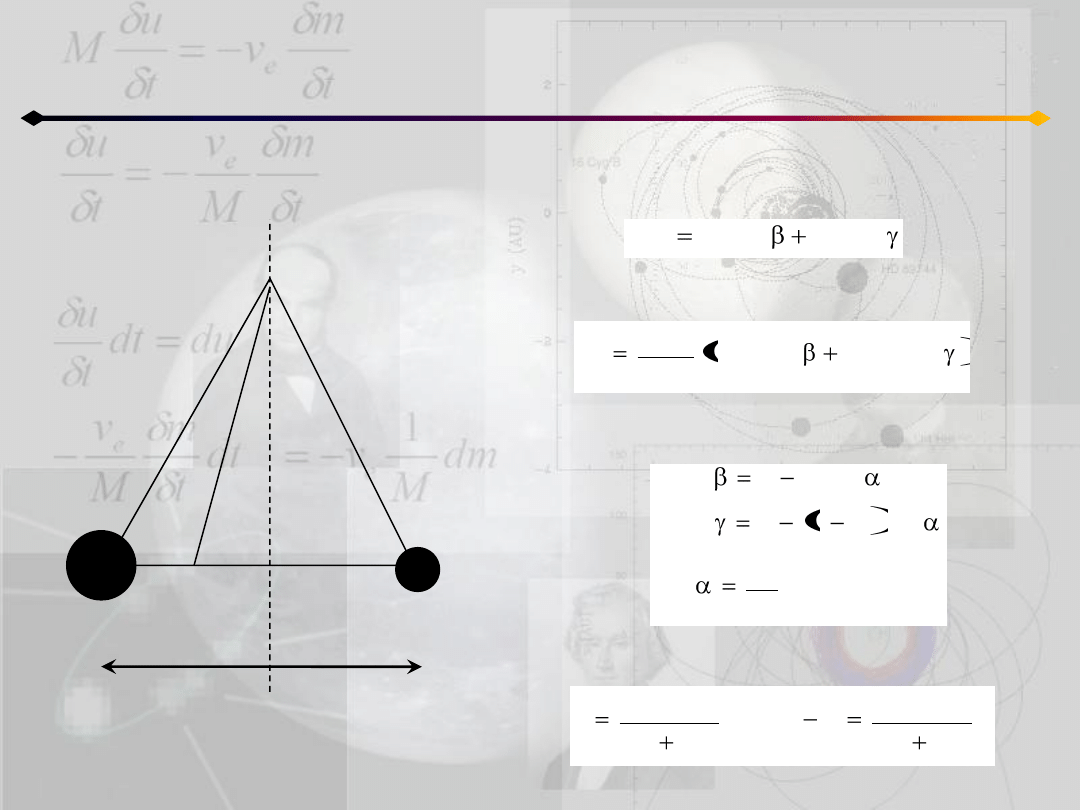
Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

P

a

b

a

O

Siła odśrodkowa równoważy siłę skierowaną
do barycentrum, stąd:

co dla sił grawitacyjnych daje:

z trójkątów utworzonych przez punkty O, P i
obie masy mamy:

a z definicji środka masy:

d

α

α

β

γ

cos

F

cos

F

b

n

2

1

2

cos

b

m

cos

b

m

b

a

G

n

2

1

2

2

2

a

2

d

cos

cos

g

d

a

cos

b

cos

g

a

cos

b

d

m

m

m

g

d

d

m

m

m

g

2

1

1

2

1

2

g

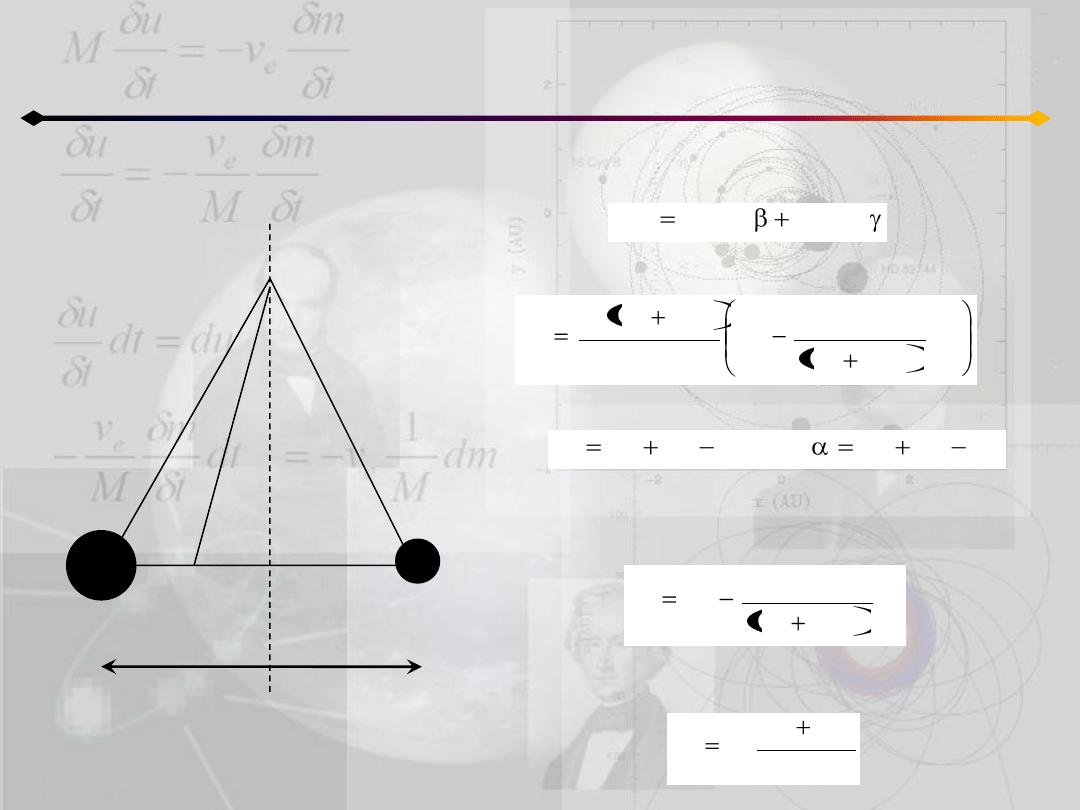
Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

P

a

b

a

O

Wykorzystując te zależności możemy równanie:

zapisad w postaci:

(12.6)

z tw. cosinusów:

Podstawiając w powyższym wyrażenia na g
wynikające z definicji środka masy dostajemy:

co w połączeniu z 12.6 daje:

d

α

α

β

γ

cos

F

cos

F

b

n

2

1

2

2

2

2

1

2

1

2

2

3

2

1

2

d

m

m

m

m

a

b

a

m

m

G

n

gd

g

a

cos

ag

2

g

a

b

2

2

2

2

2

2

2

2

1

2

1

2

2

d

m

m

m

m

a

b

3

2

1

2

a

m

m

G

n

g

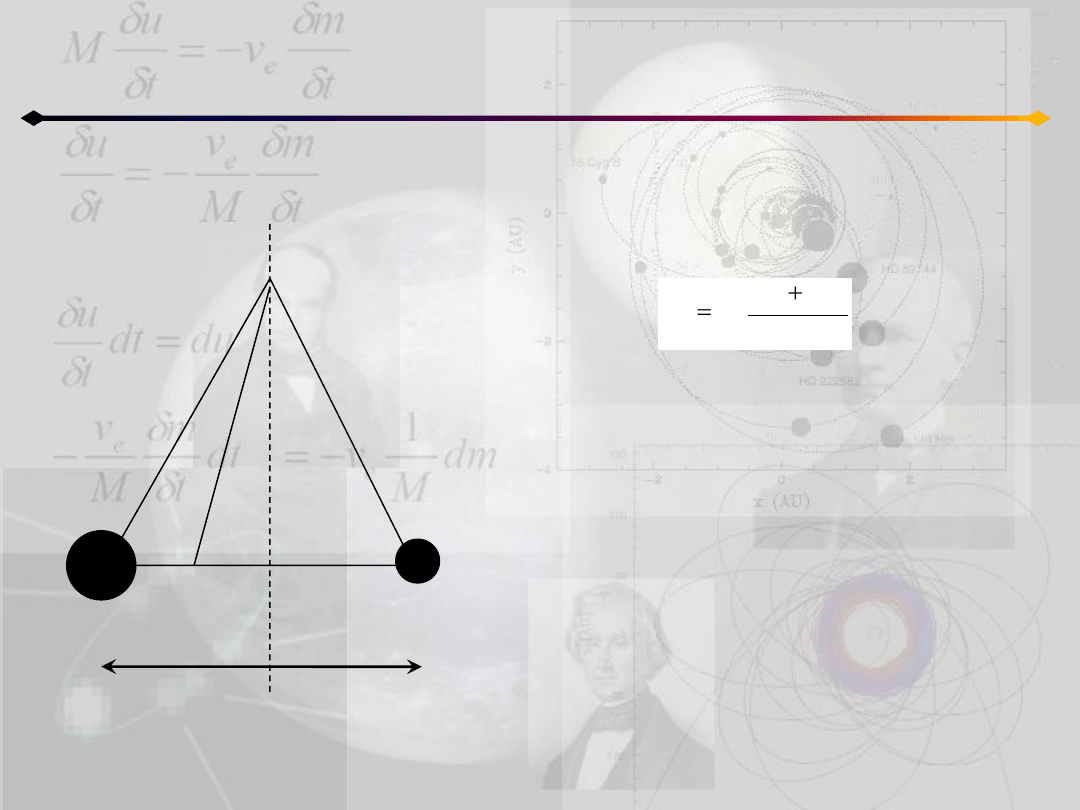
Ograniczone zagadnienie 3 ciał

Punkty równowagi Lagrange’a

m

1

m

2

P

a

b

a

O

Oprócz tego układ odniesienia rotuje w układzie
nieruchomym z prędkością kątową n więc:

czyli a=d

d

α

α

β

γ

3

2

1

2

d

m

m

G

n

g