MECHANIKA NIEBA

WYKŁAD 5

02.04.2008 r

E

r

Zagadnienie dwóch ciał

I prawo Keplera

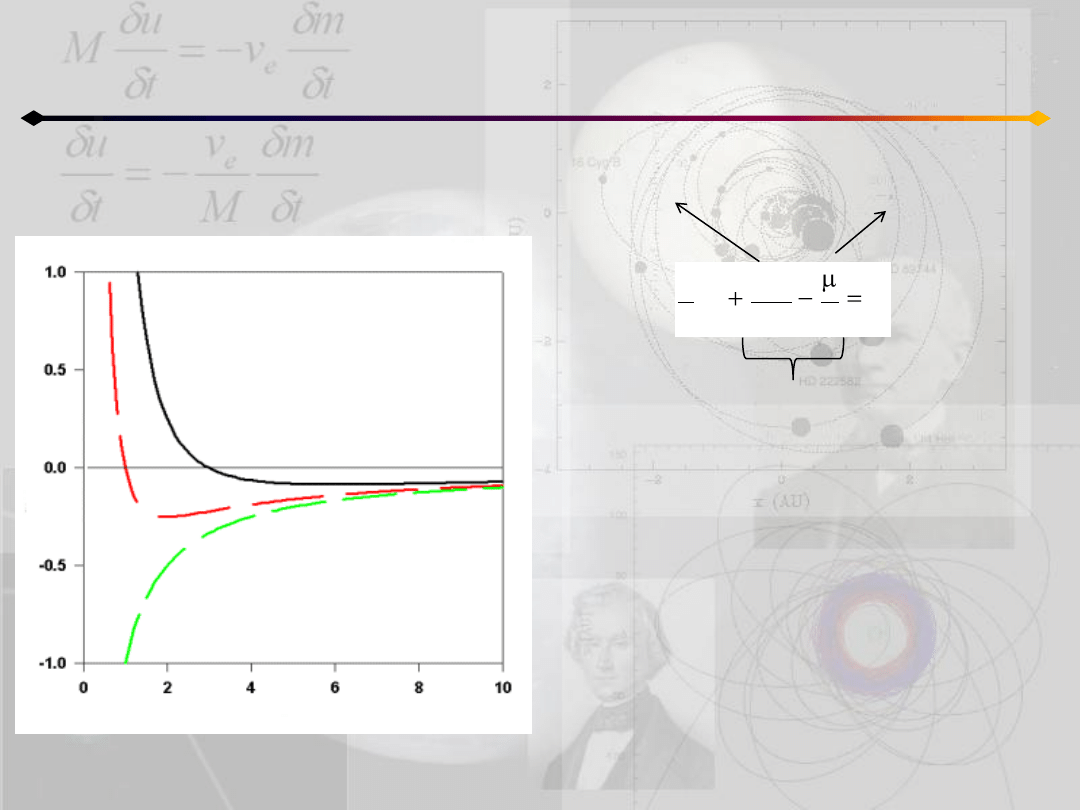
Potencjał efektywny

Potencjał efektywny w łatwy sposób tłumaczy
kształty orbit:

kołowa – minimum energii planety
eliptyczna – planeta zmienia odległośd między

dwoma skrajnymi wartościami

paraboliczna – zerowa energia (ciało nadlatuje

z nieskooczonosci)

hiperboliczna– energia większa od 0

h

r

r

2

c

r

2

1

2

2

2



czynnik związany z
działaniem siły
odśrodkowej

energia potencjalna

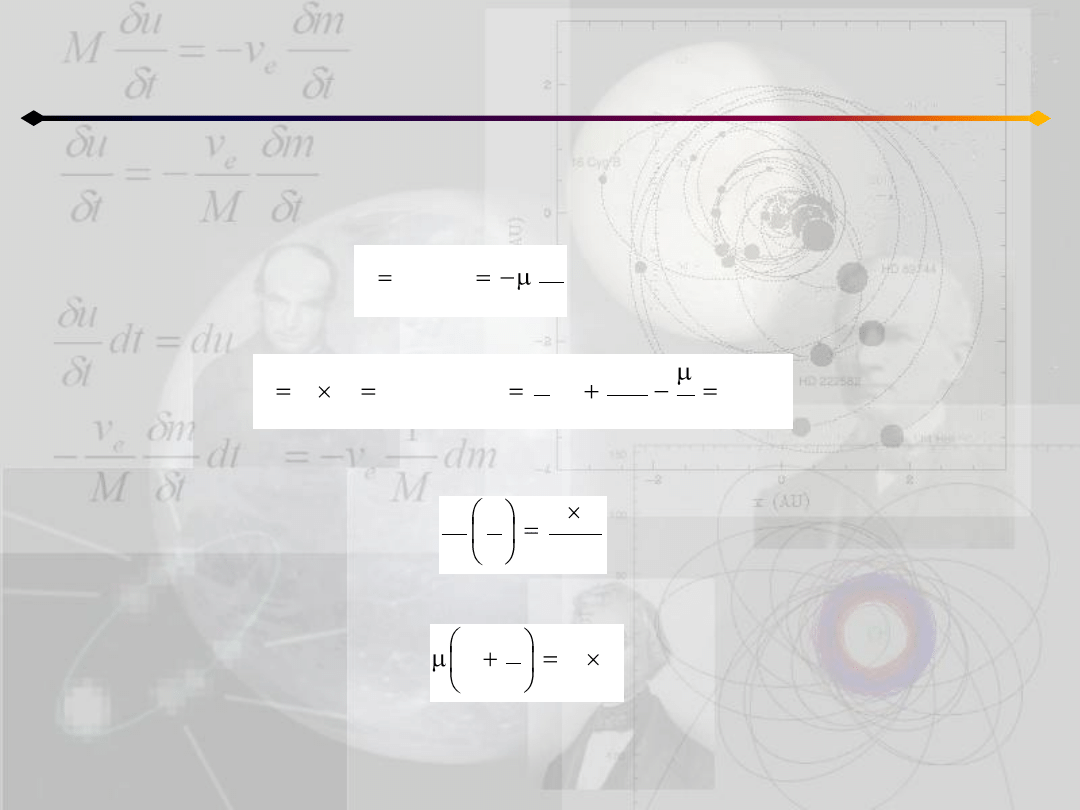
Zagadnienie dwóch ciał

I prawo Keplera

Wródmy do równao:

z pierwszymi całkami:

3

r

r

v

;

v

r









const

r

r

2

c

r

2

1

h

;

const

v

r

c

2

2

2









Korzystając z nich i całkując równanie:

otrzymujemy:

3

r

r

c

r

r

dt

d







c

v

r

r

e









Zagadnienie dwóch ciał

I prawo Keplera

c

v

r

r

e









e jest stałym wektorem (Laplace-Runge-Lenz wektor).

1. c=0(ruch prostoliniowy), wtedy , wektor e leży na linii ruchu a

jego długośd jest równa 1.

e

r

r





(5.1)

2. c≠0 , skąd dostajemy, że . To oznacza, że e leży w

płaszczyźnie ruchu.

0

c

r





0

c

e





Możemy rozróżnid dwa przypadki:

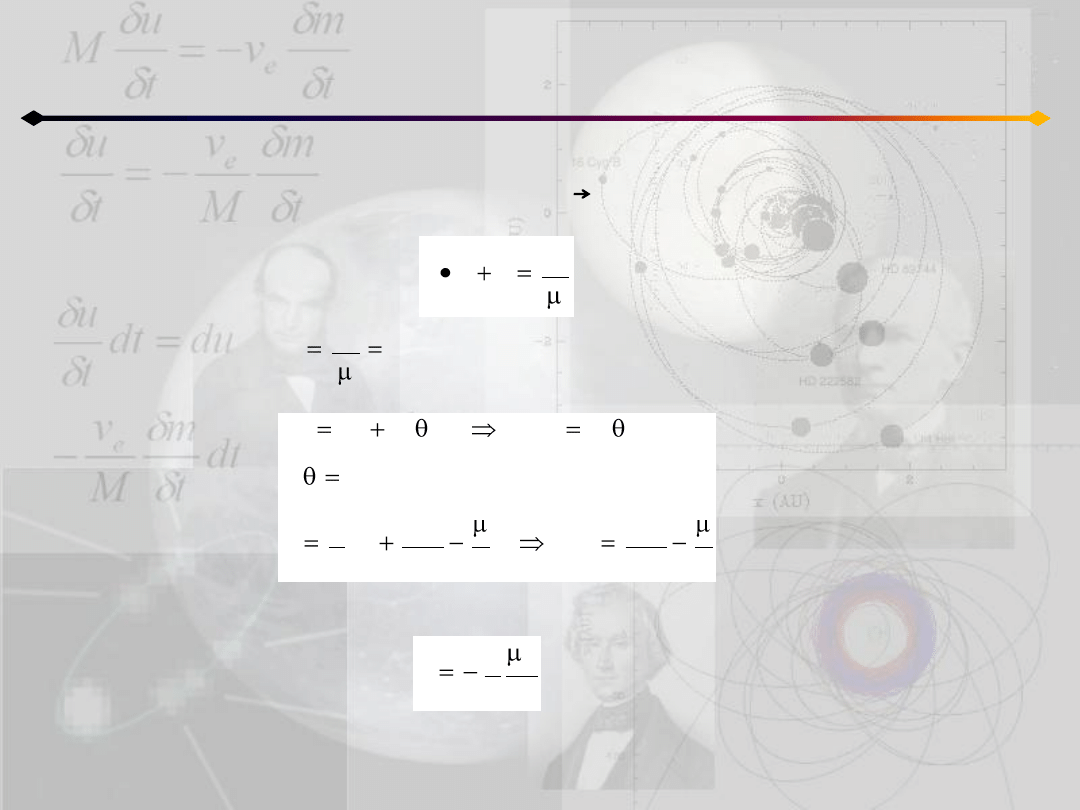
Zagadnienie dwóch ciał

I prawo Keplera

2. c≠0 c.d., mnożymy (5.1) skalarnie przez r i otrzymujemy:

2

c

r

r

e





Dla e=0 mamy , a więc ruch po okręgu, dla którego:

const

c

r

2

r

r

2

c

h

r

r

2

c

r

2

1

h

c

r

r

v

r

r

v

2

2

2

2

2

2

2

2

2

2

2

2

2











Przekształcając ten układ dostajemy:

2

2

c

2

1

h

co oznacza, że dla e=0 mamy ruch po okręgu z ujemną energią.

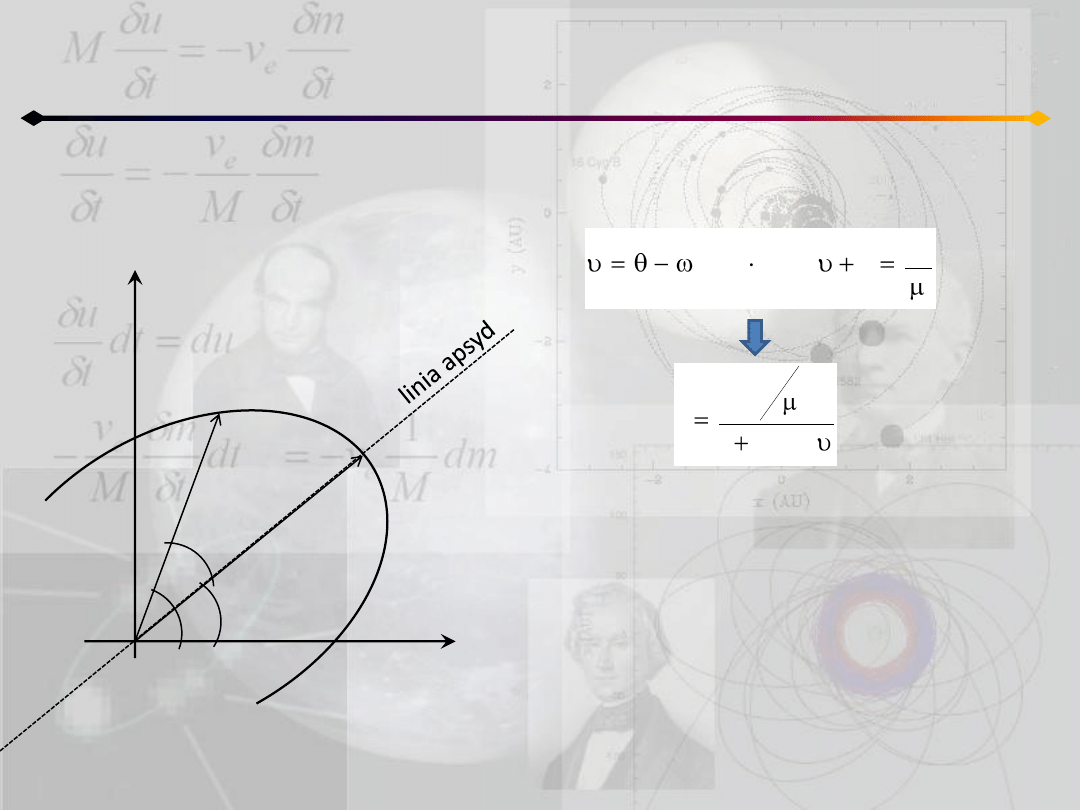
Zagadnienie dwóch ciał

I prawo Keplera

Dla e≠0 wprowadźmy do równania (5.1)
kąty υ i ω:

2

c

r

cos

r

e

;

cos

e

1

c

r

2

Otrzymujemy równanie orbity, które jest
równaniem biegunowym krzywej stożkowej

e ma długośd równą mimośrodowi, a jego
koniec leży w perycentrum

υ – anomalia prawdziwa

0

Q

P

θ

υ

ω

e



r



(5.2)

Dotąd znaleźliśmy dla układu równao:

dwa wektory i jeden skalar będące stałymi ruchu, a więc siedem stałych.
To oznacza, że nie mogą one byd niezależne. Istnieją między nimi dwie
zależności.

Zagadnienie dwóch ciał

Podsumowanie

3

r

r

v

;

v

r









Pierwsza: oznacza, że e i c są do siebie prostopadłe.

0

c

e





Drugą zależnośd uzyskamy przekształcając równanie:

c

v

r

r

e









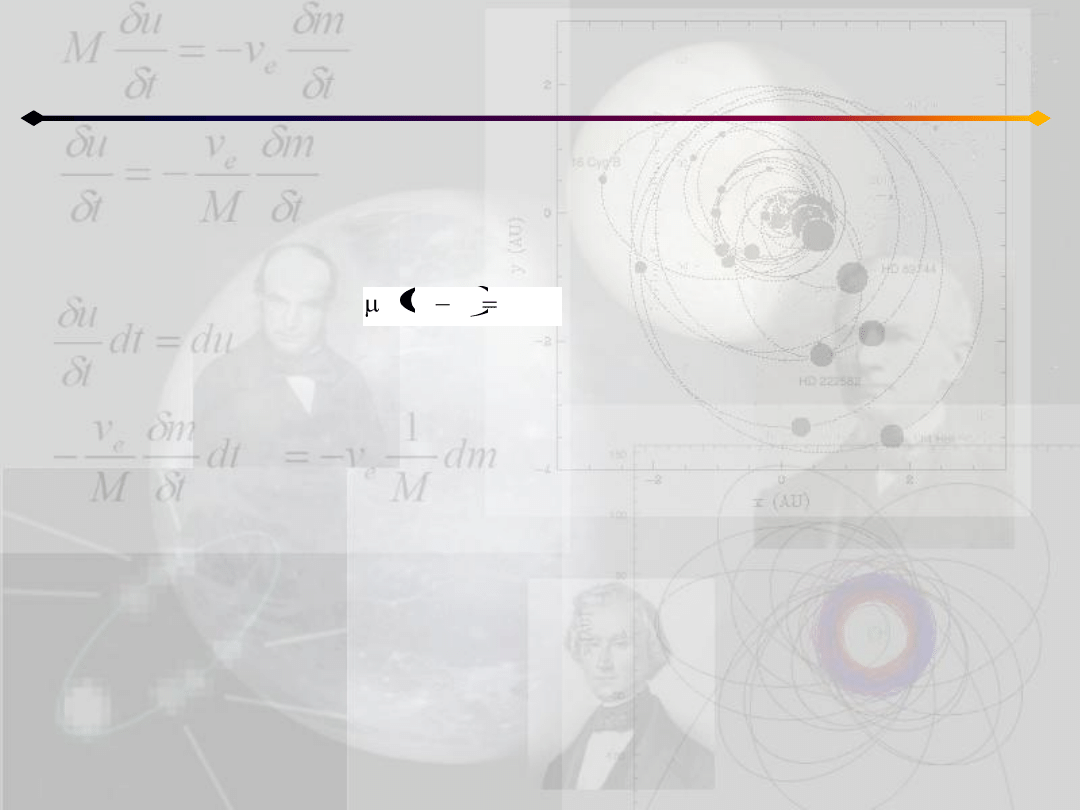
Zagadnienie dwóch ciał

Podsumowanie

otrzymujemy:

co oznacza, że znaleźliśmy tylko pięd niezależnych stałych.

2

2

2

hc

2

1

e

Powyższe równanie wskazuje, że:

- dla e<1 (ruch eliptyczny) mamy h<0
- dla e=1 (ruch paraboliczny) mamy h=0
- dla e>1 (ruch hiperboliczny) mamy h>0
- wcześniej zostało pokazane, że dla e=0 (orbita kołowa) mamy h=h

min

(5.3)

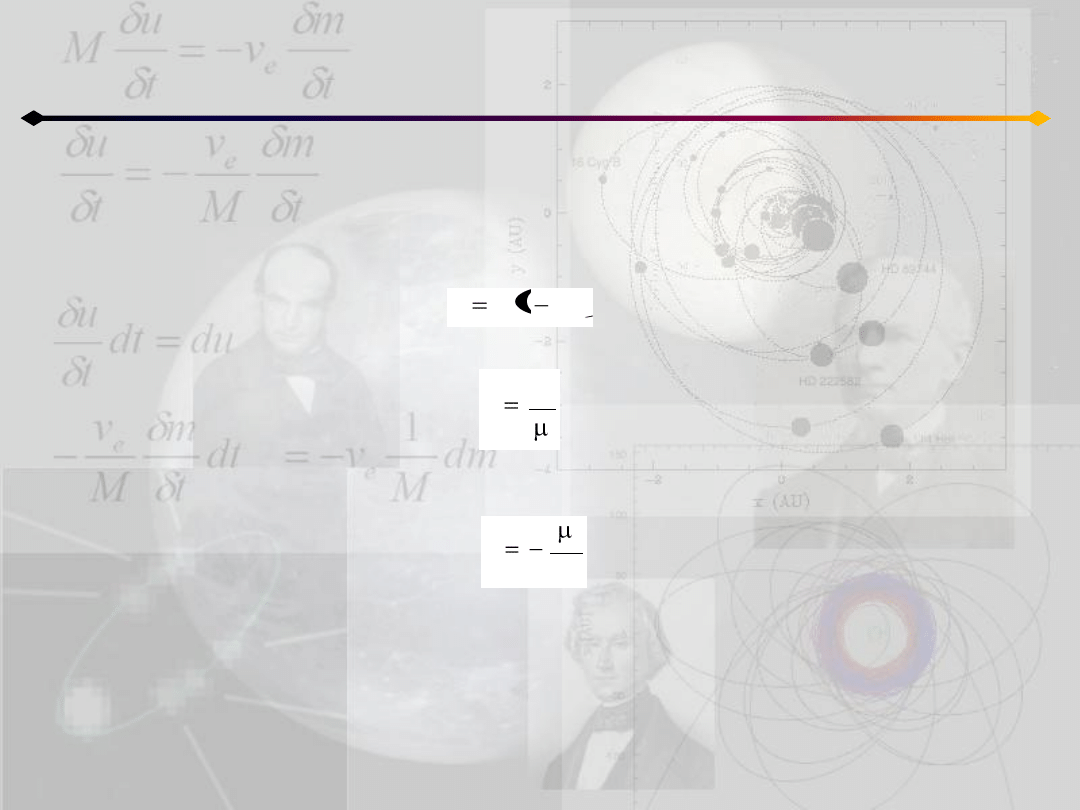
Zagadnienie dwóch ciał

III prawo Keplera

Parametr elipsy (z definicji) jest równy:

w naszym przypadku (r-nie 5.2):

porównując prawe strony i uwzględniając w (5.3) otrzymujemy:

2

e

1

a

p

2

c

p

h

2

a

to znaczy, że rozmiar wielkiej półosi zależy od całkowitej energii układu

Zagadnienie dwóch ciał

III prawo Keplera

r

r+δr

δS

Wródmy do prędkości polowej:

ponieważ:

więc:

d

r

2

1

dS

2



2

r

c

c

2

1

dt

dS

korzystając z uzyskanego wcześniej związku
między c i a mamy:

2

e

1

a

2

1

dt

dS

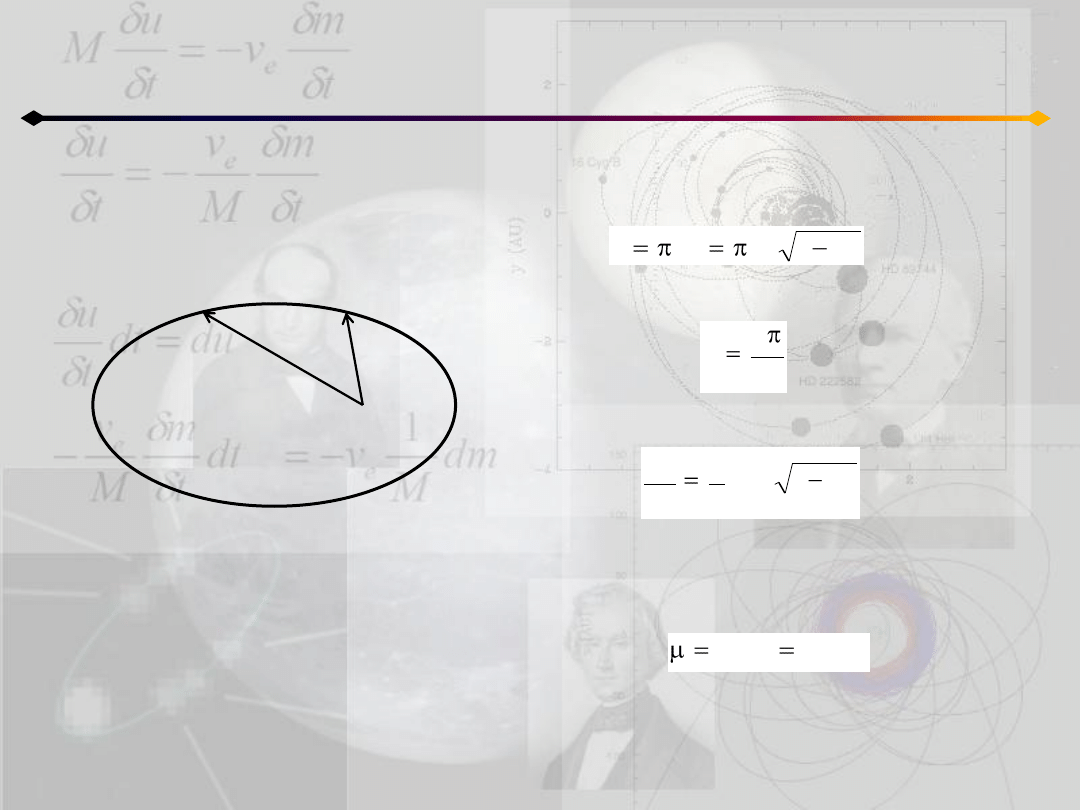
Zagadnienie dwóch ciał

III prawo Keplera

r

r+δr

δS

Z drugiej strony, pole elipsy:

Wprowadźmy okres obiegu P i ruch średni n:

wtedy:

2

2

e

1

a

ab

S

P

2

n

2

2

e

1

na

2

1

dt

dS

Porównując oba otrzymane wyrażenia na
prędkośd polową dostajemy:

const

a

n

3

2

czyli trzecie prawo Keplera

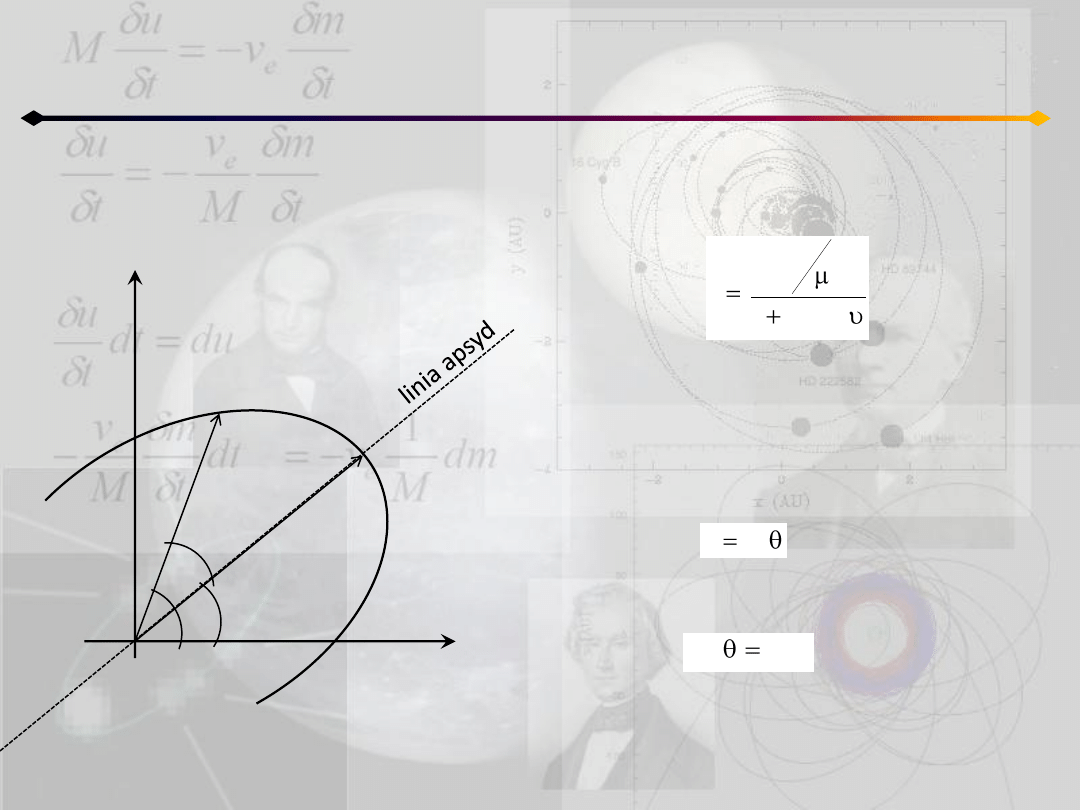
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

cos

e

1

c

r

2

0

Q

P

θ

υ

ω

e



r



Otrzymane wcześniej równanie orbity:

można wyznaczyd używając metody
zaproponowanej przez J. Bineta.

Korzystając z:

możemy napisad:



2

r

c

dt

c

d

r

2

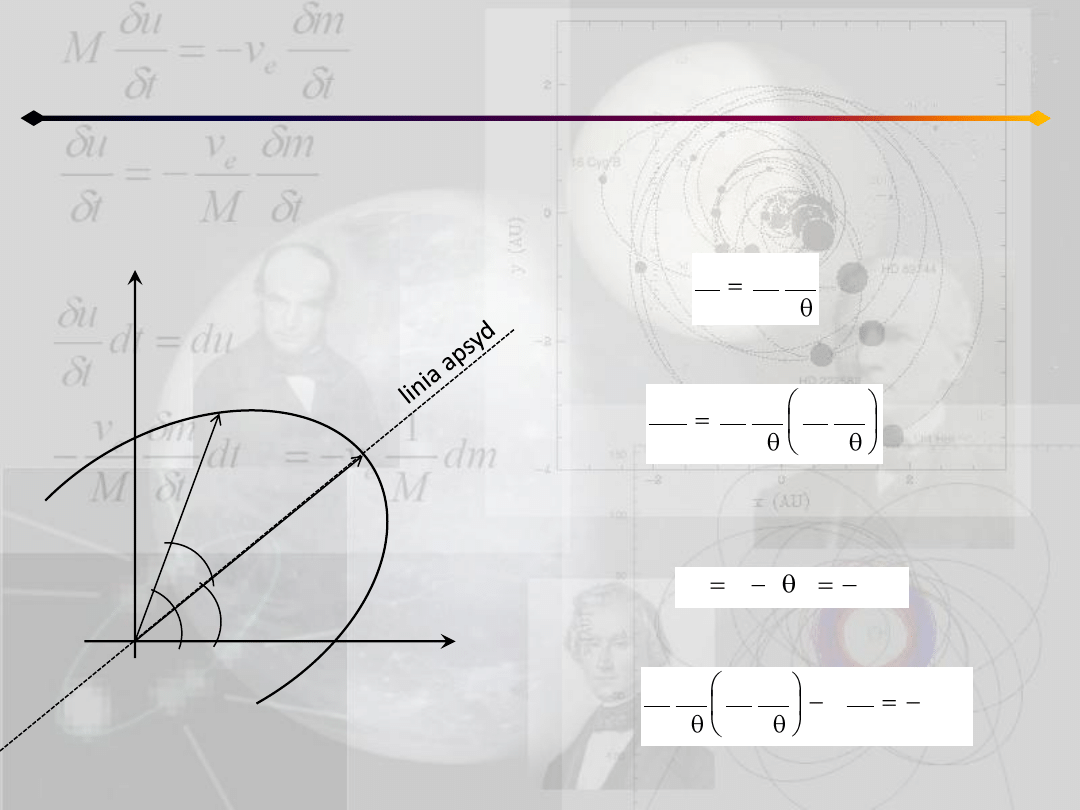
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

0

Q

P

θ

υ

ω

e



r



a następnie:

oraz:

d

d

r

c

dt

d

2

d

d

r

c

d

d

r

c

dt

d

2

2

2

2

W ruchu środkowym działa tylko składowa
radialna przyspieszenia:

co można zapisad w postaci:

)

r

(

f

r

r

a

2

r







)

r

(

f

r

c

r

d

dr

r

c

d

d

r

c

4

2

2

2

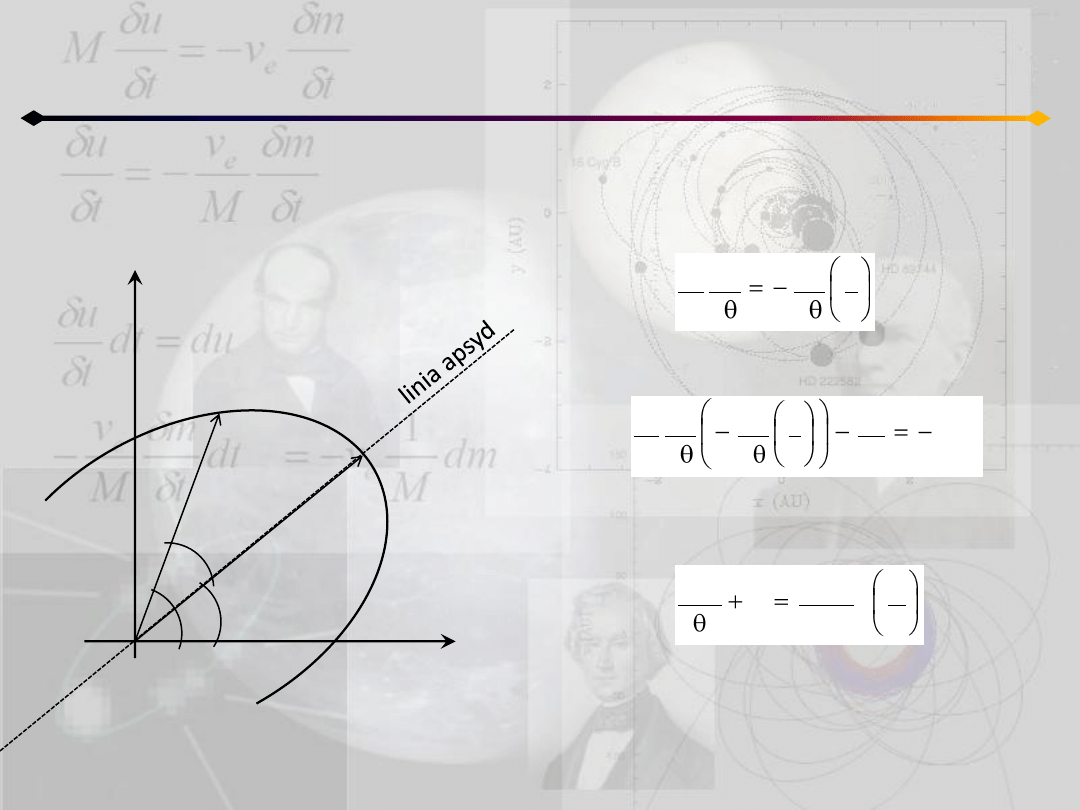
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

0

Q

P

θ

υ

ω

e



r



a następnie uwzględniając:

zapisad jako:

r

1

d

d

d

dr

r

1

2

)

r

(

f

r

c

r

1

d

d

d

d

r

c

3

2

2

Jeśli podstawimy u=1/r to otrzymamy wzór
Bineta:

czyli równanie różniczkowe orbity.

u

1

f

u

c

1

u

d

u

d

2

2

2

2

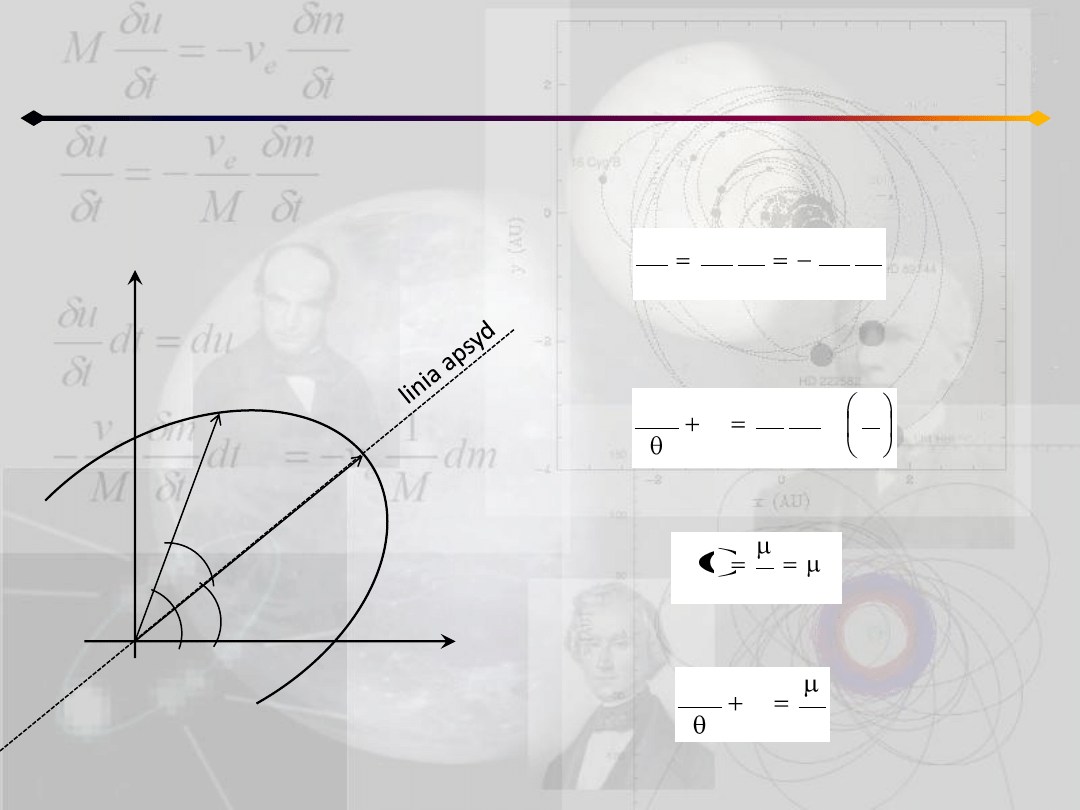
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

0

Q

P

θ

υ

ω

e



r



Uwzględniając:

we wzorze Bineta możemy go przekształcid
do postaci:

u

1

f

du

d

c

1

u

d

u

d

1

2

2

2

dr

d

u

1

dr

d

du

dr

du

d

2

Wprowadzając potencjał newtonowski

dostajemy ostatecznie:

u

r

r

f

1

2

2

2

c

u

d

u

d

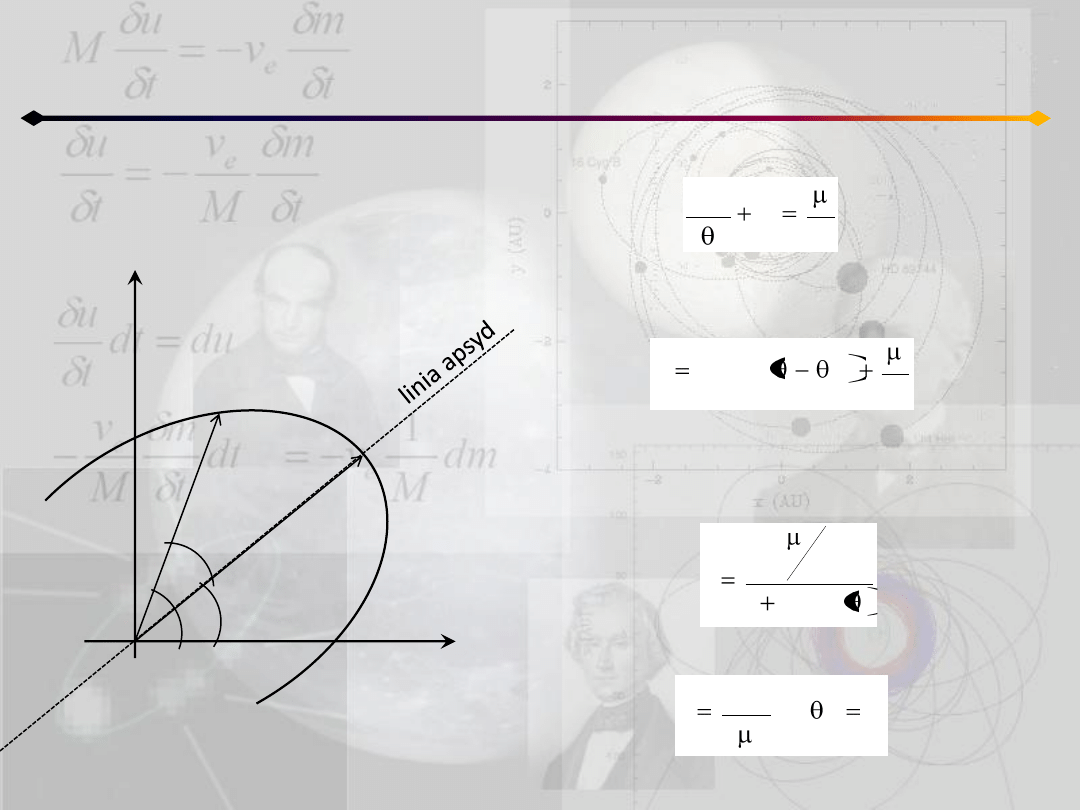
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

0

Q

P

θ

υ

ω

e



r



2

2

2

c

u

d

u

d

przekształcając to równanie dostajemy
równanie krzywej stożkowej we
współrzędnych biegunowych:

gdzie:

2

0

c

cos

A

u

cos

e

1

c

r

2

0

;

Ac

e

0

2

Rozwiązaniem tego równania jest:

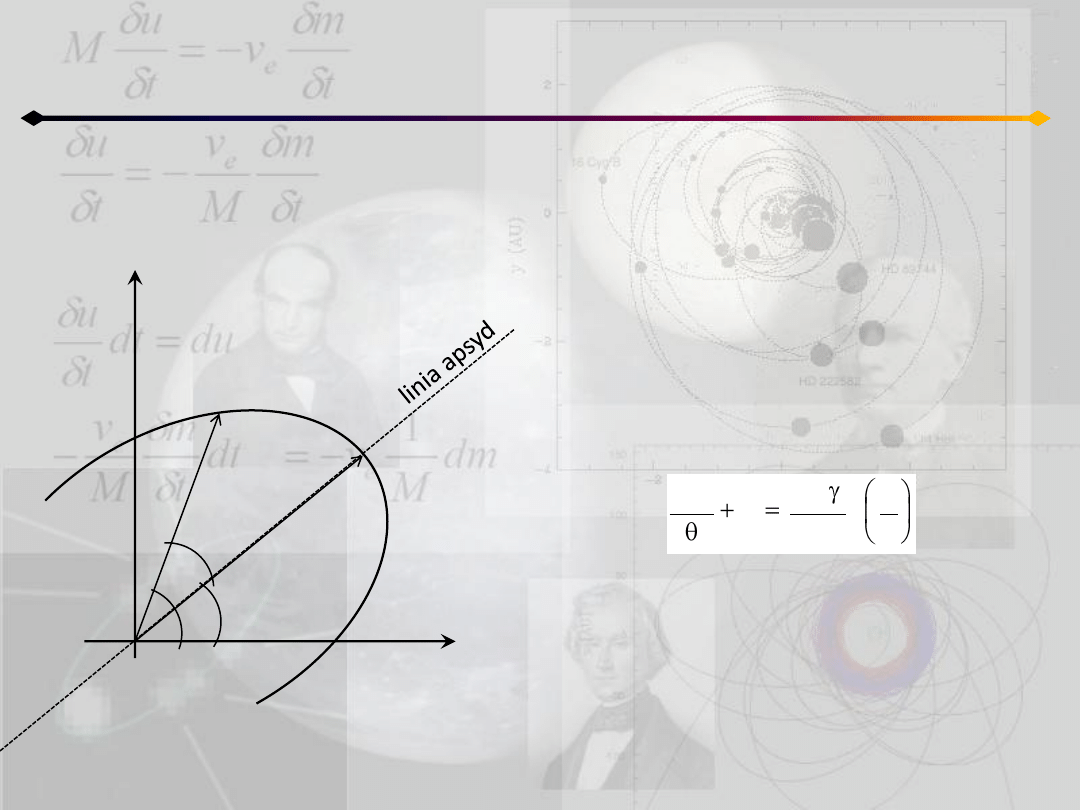
Zagadnienie dwóch ciał

Równanie orbity – metoda Bineta

0

Q

P

θ

υ

ω

e



r



Równanie Bineta pozwala ze znanej
postaci siły środkowej wyznaczyd
orbitę.

Istotną własnością tego równania jest
to, że ma taką samą postad w przypadku
relatywistycznym:

Francisc D. Aaron 2005, Rom. Journ. Phys.,
Vol. 50, Nos. 5-6, 615

u

1

f

u

c

m

u

d

u

d

2

2

0

2

2

Położenie punktu na orbicie

Anomalia mimośrodowa

O

Jak było pokazane wcześniej, wektory c i e
definiują jednoznacznie orbitę. Możemy ją
wyznaczyd mając dane warunki początkowe
r

0

i v

0

.

Nie jesteśmy jednak w stanie podad jawnej
postaci funkcji r=r(t), a więc nie potrafimy
określid położenia punktu na orbicie.

Potrzebujemy do tego ostatnią, brakującą
stałą ruchu.

Aby to uzyskad dokonamy zamiany
zmiennych t=t(E), gdzie E jest anomalią
mimośrodową.

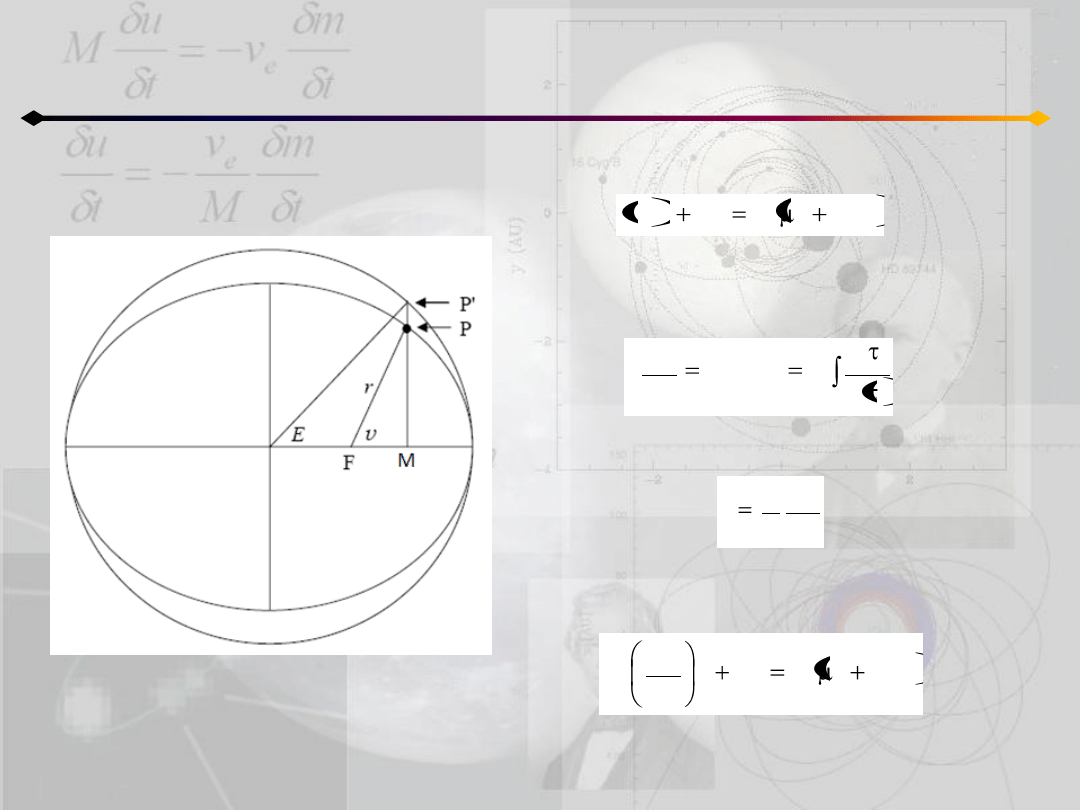
Położenie punktu na orbicie

Anomalia mimośrodowa

O

Z całki energii dostajemy:

h

r

r

2

c

r

r

2

2

2



(5.4)

Wprowadźmy nową zmienną w następujący
sposób:

gdzie k i T są stałymi. Ponadto:

t

T

r

d

k

E

;

k

dt

dE

r

dE

dr

r

k

r

Uwzględniając to w (5.4) dostajemy:

h

r

r

2

c

dE

dr

k

2

2

2

2

(5.5)

Rozpatrzymy dwa przypadki h=0 oraz h≠0

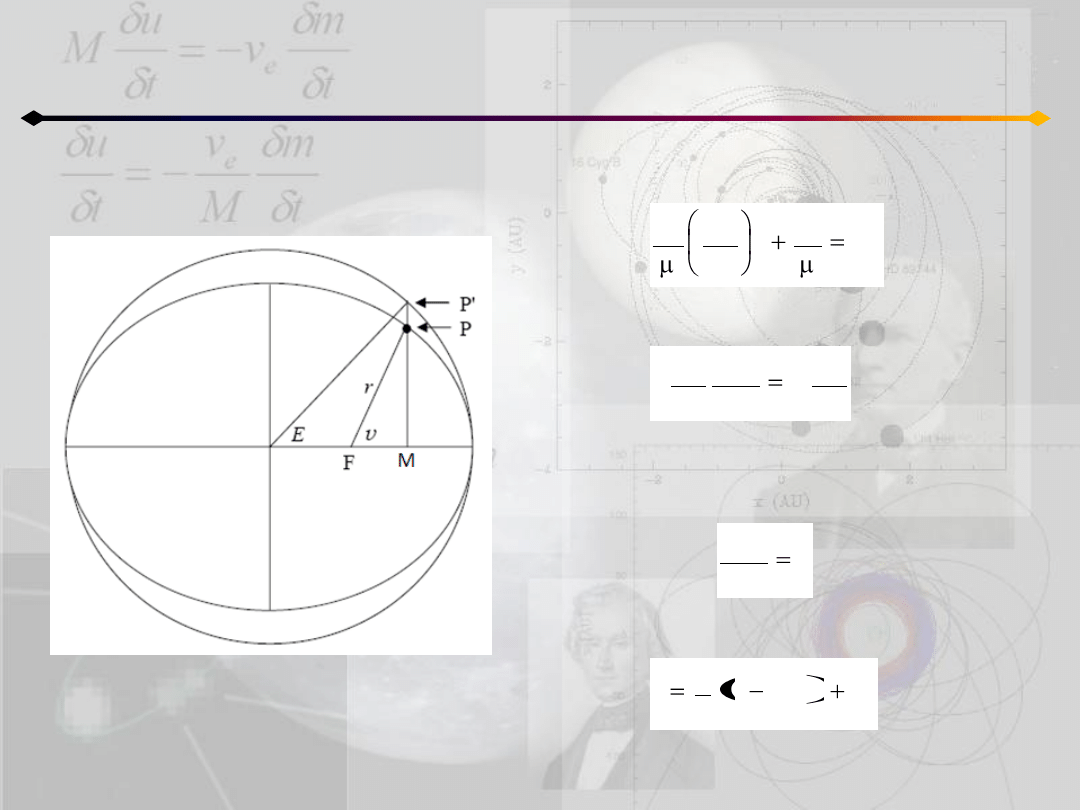
Położenie punktu na orbicie

h=0

O

W tym przypadku równanie (5.5):

wybieramy k

2

=μ i różniczkujemy:

r

2

c

dE

dr

k

2

2

2

dE

dr

2

dE

r

d

dE

dr

2

2

2

ponieważ r nie może byd stałe więc powyższe
równanie upraszcza się do:

1

dE

r

d

2

2

całkując otrzymujemy:

A

E

E

2

1

r

2

0

(5.6)

Położenie punktu na orbicie

h=0

O

Aby wyznaczyd A zakładamy E

0

=0 i

podstawiamy do (5.6) co daje:

2

c

2

1

A

więc:

2

2

c

E

2

1

r

z definicji E:

całkując i uwzględniając wyrażenie na r
mamy:

dE

r

dt

k

E

2

c

E

6

1

T

t

2

3

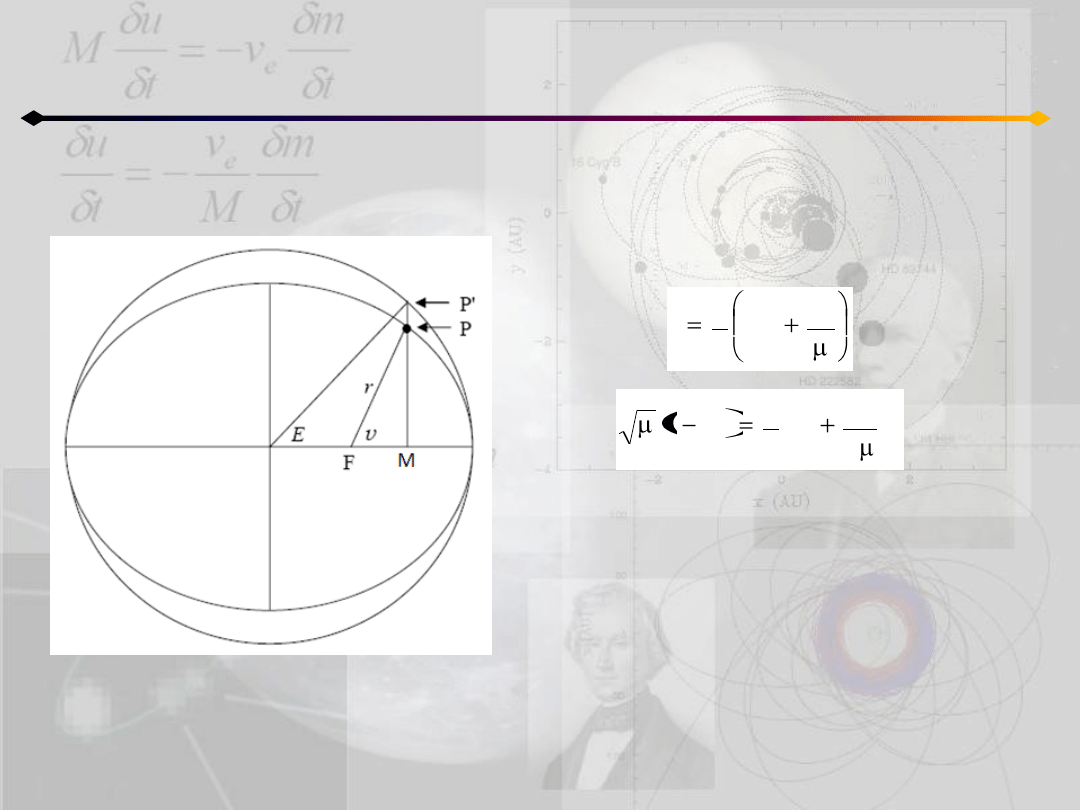
Położenie punktu na orbicie

h=0

O

Otrzymaliśmy:

w drugim z tych równao t jest funkcją E.
Rozwiązując je dostaniemy E=E(t) musimy
jednak rozpatrywad dwa przypadki c=0 i c≠0

E

2

c

E

6

1

T

t

2

3

2

2

c

E

2

1

r

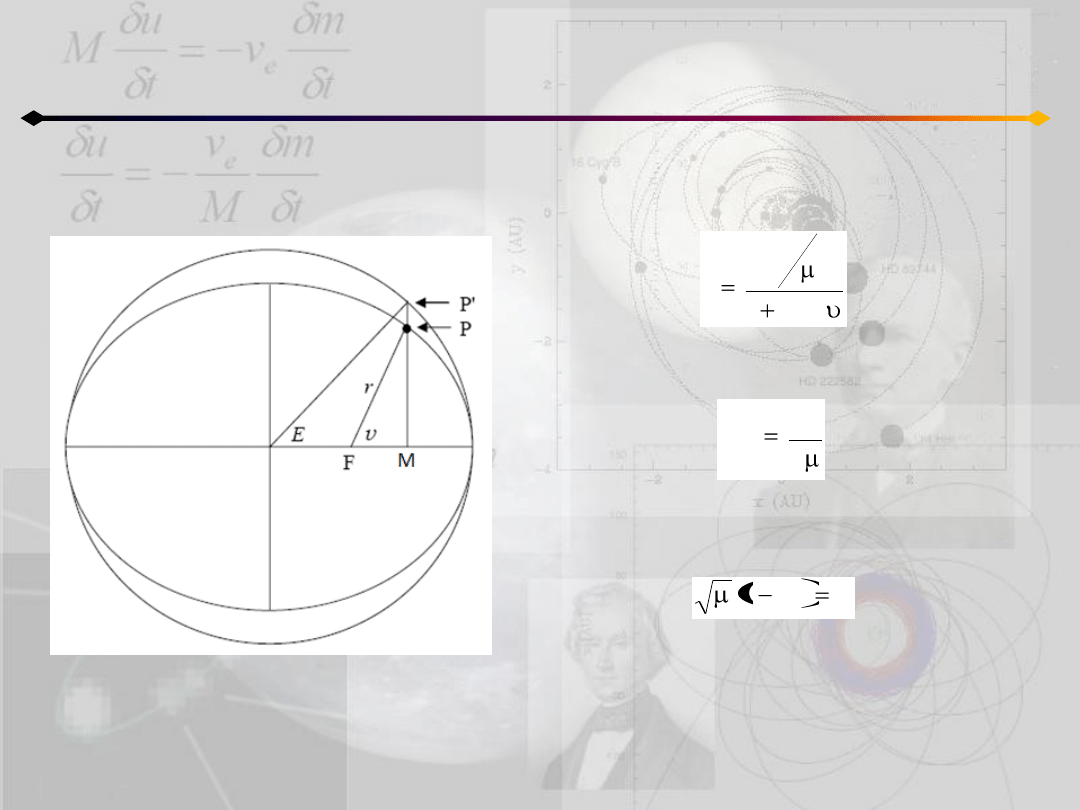
Położenie punktu na orbicie

h=0, c≠0

O

Ponieważ h=0 więc e=1 i orbita jest parabolą:

r ma wartośd minimalną dla υ=0:

cos

1

c

r

2

2

c

r

2

min

Gdy r=r

min

to jednocześnie E=0, stąd:

a więc t=T – czas przejścia przez perycentrum

0

T

t

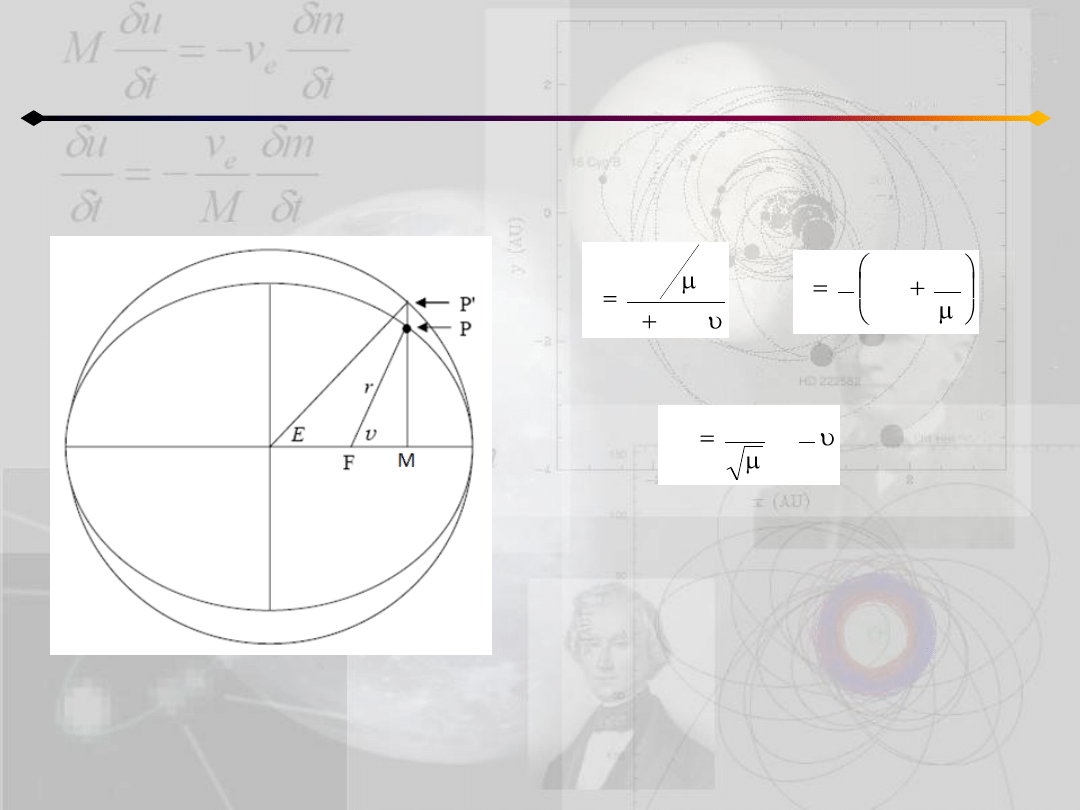
Położenie punktu na orbicie

h=0, c≠0

O

Z porównania równao:

dostajemy:

cos

1

c

r

2

2

2

c

E

2

1

r

2

1

tg

c

E

2

To pozwala na przejście od anomalii
prawdziwej do mimośrodowej.

Anomalię prawdziwą można łatwo
wyznaczyd z tzw. tablic Barkera jeśli tylko
znamy t-T oraz c

2

/2μ.

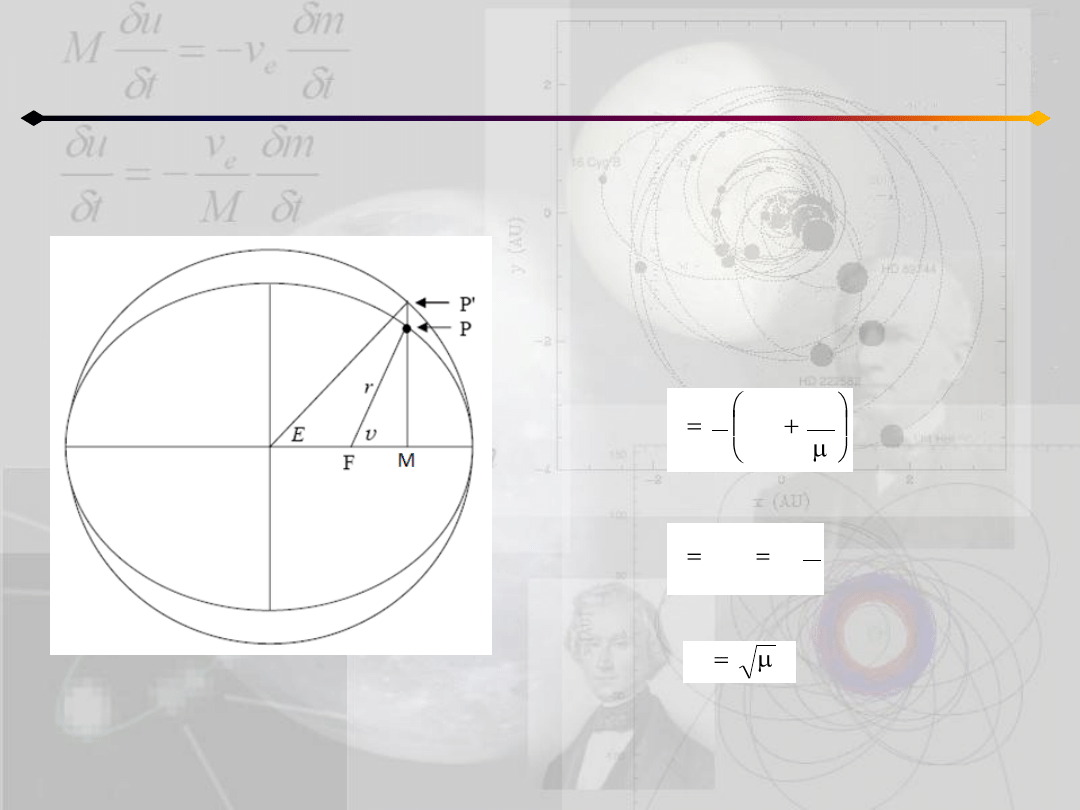
Położenie punktu na orbicie

h=0, c≠0

O

Aby wyznaczyd położenie z anomalii
mimośrodowej należy postępowad w
następujący sposób:

1. na moment czasu t=0 mamy r

0

i v

0

2. różniczkujemy r-nie

w wyniku czego otrzymujemy:

wtedy:

2

2

c

E

2

1

r

r

k

E

E

E

r





E

r

r

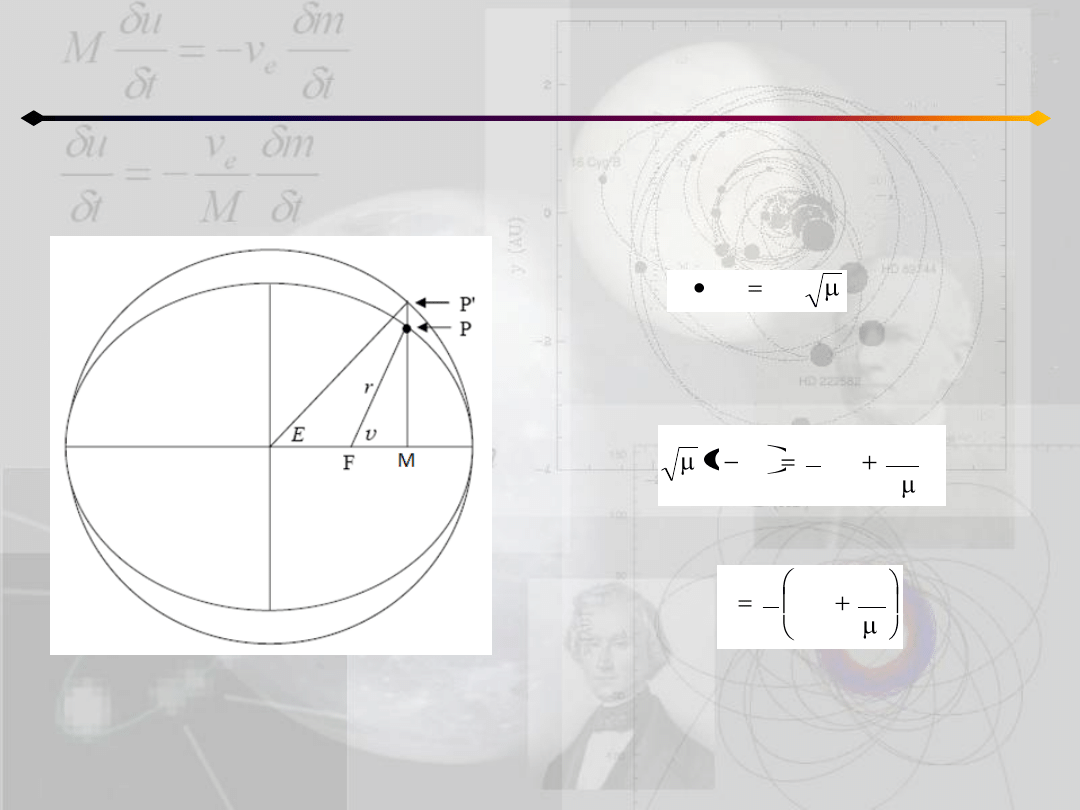
4. Podstawiając T do równania:

dostajemy E(t), a z równania:

mamy r(t).

Położenie punktu na orbicie

h=0, c≠0

O

3. Używając tego do wartości początkowych

mamy:

co pozwala otrzymad T.

0

0

0

E

v

r





E

2

c

E

6

1

T

t

2

3

2

2

c

E

2

1

r

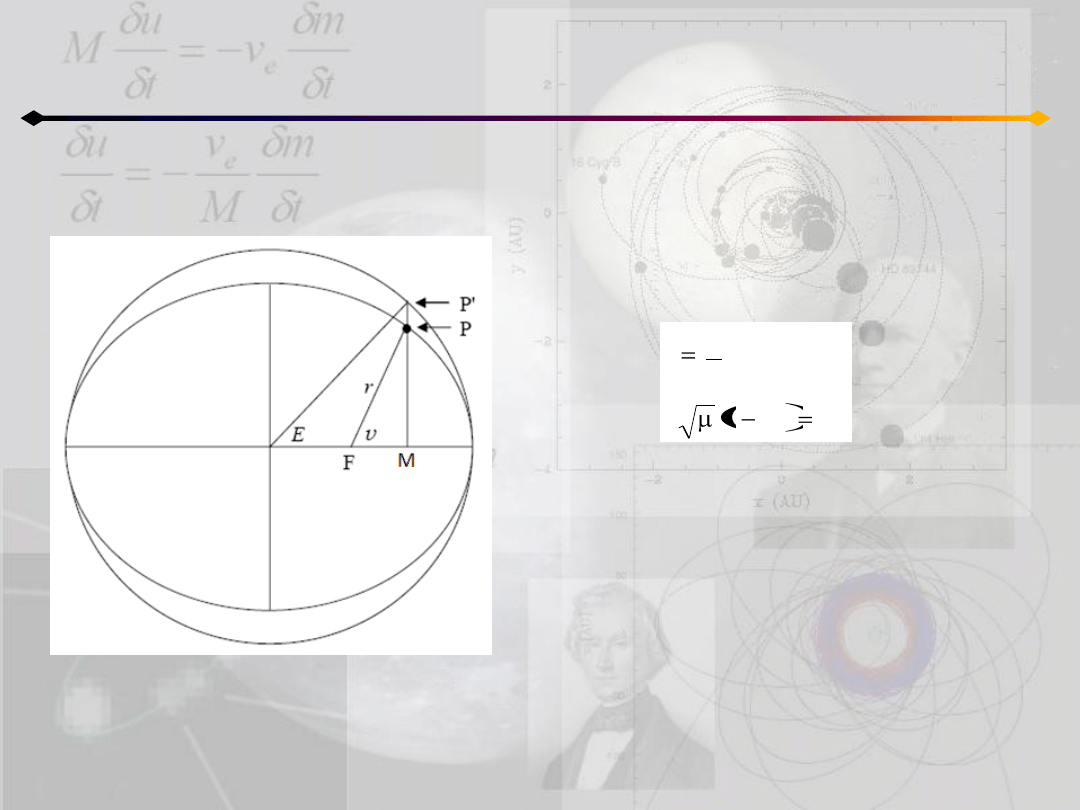
Położenie punktu na orbicie

h=0, c=0

O

W tym przypadku:

i dla t=T następuje kolizja w centrum siły

3

2

E

T

t

6

E

2

1

r

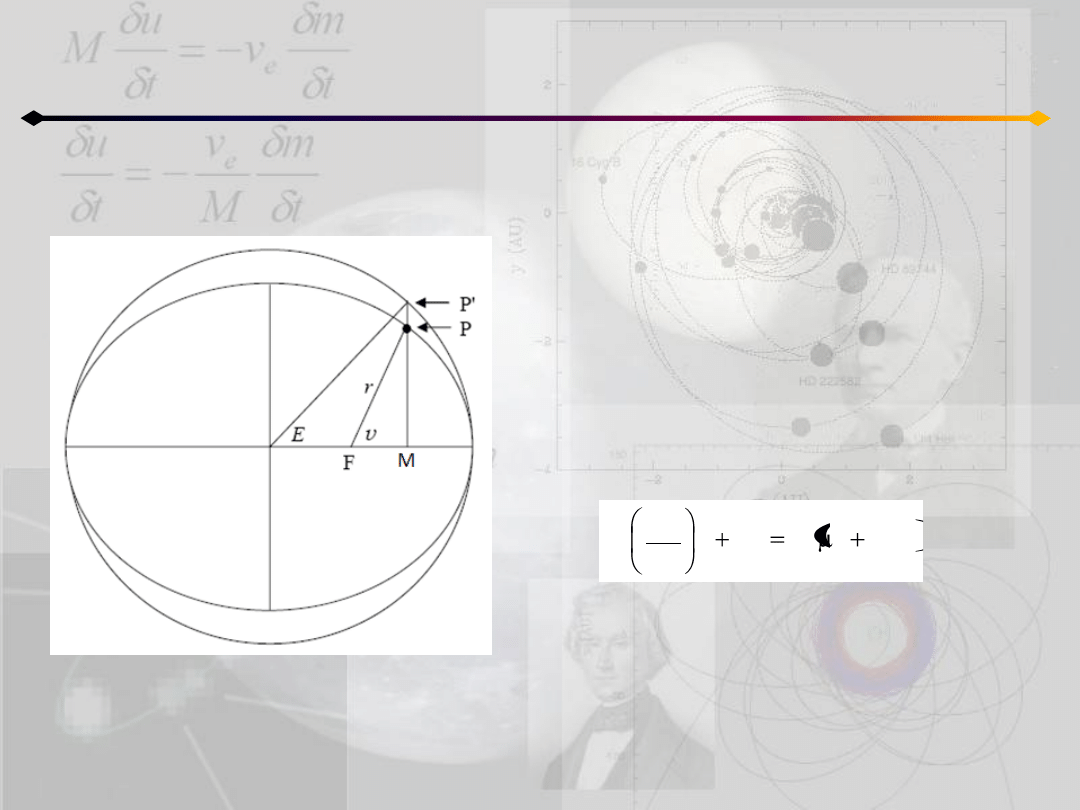
Położenie punktu na orbicie

h≠0

O

W tym wypadku mamy trzy możliwe rodzaje
ruchu:

a) liniowy – c=0
b) hiperboliczny – c≠0, h>0
c) eliptyczny – c≠0, h<0

Rozpatrzmy równanie (5.5):

h

r

r

2

c

dE

dr

k

2

2

2

2