1

00502 Kinematyka D

TEORIA

00502

Podstawy kinematyki D

Część 2

Iloczyn wektorowy i skalarny.

Wektorowy opis ruchu. Względność ruchu.

Prędkość w ruchu prostoliniowym.

Instrukcja dla zdającego

1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 8
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Kwiecień

ROK 2008

Dane osobowe właściciela arkusza

2

00502 Kinematyka D

TEORIA

Temat: 5

Iloczyn skalarny i iloczyn wektorowy.

1.

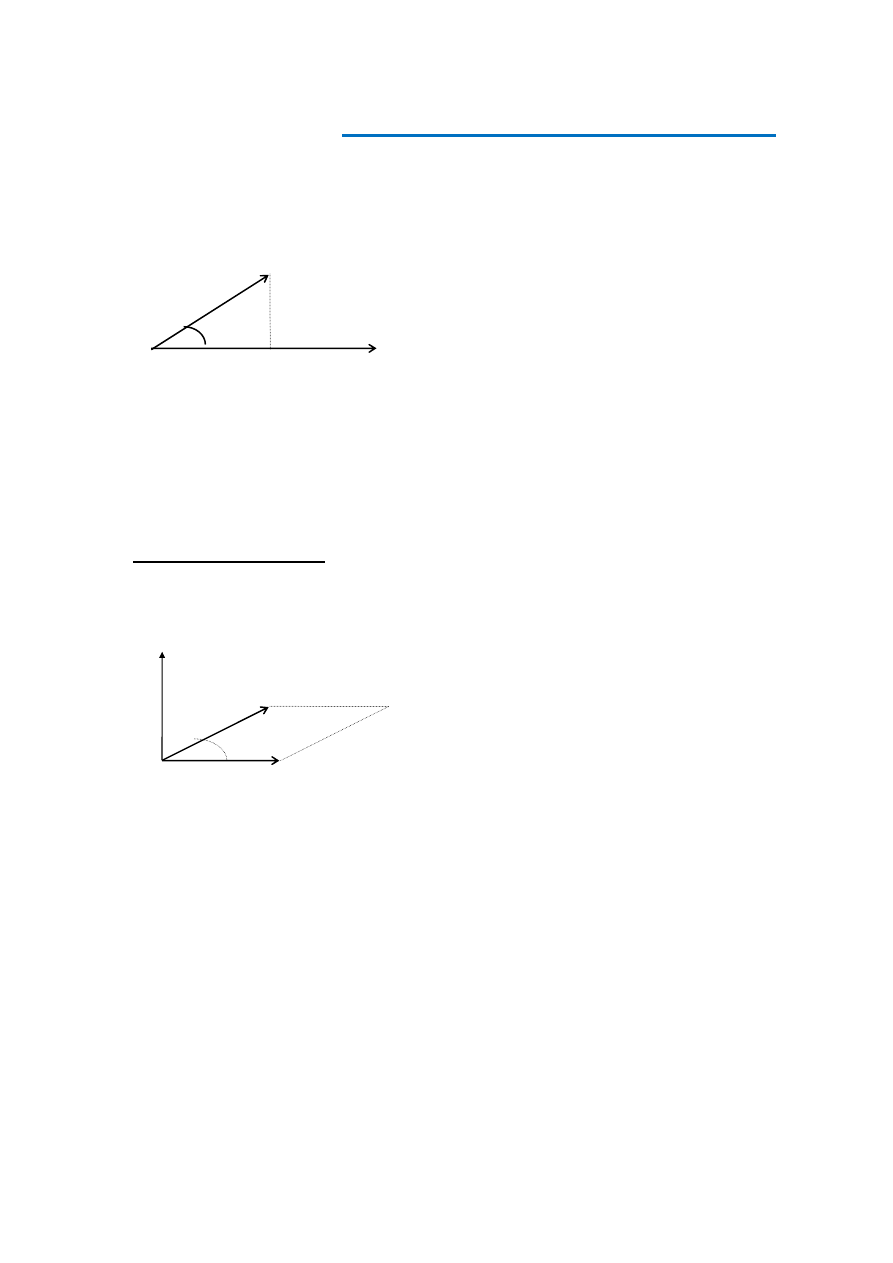
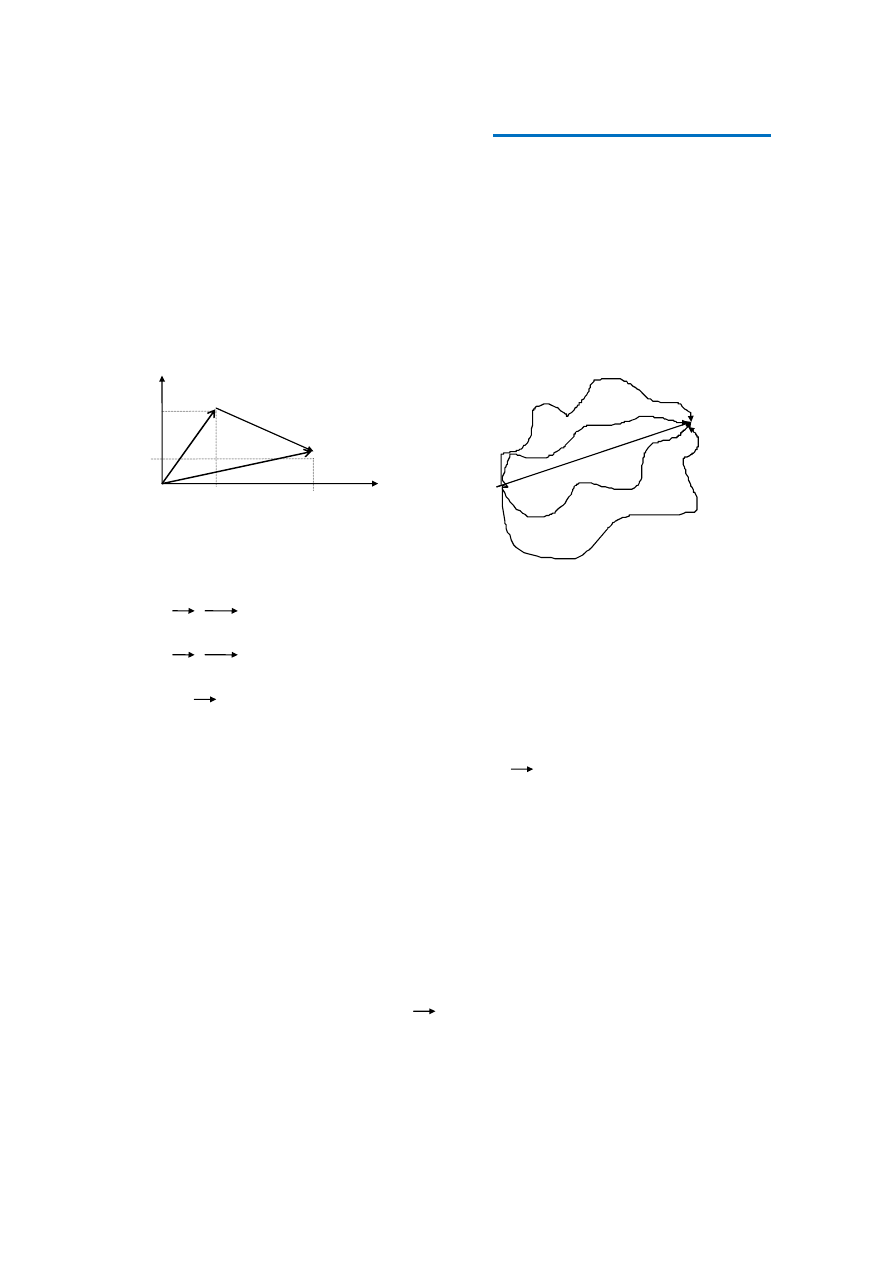
Iloczyn skalarny

r r

a b

⋅

jest iloczynem jednego wektora przez rzut drugiego

wektora na kierunek pierwszego wektora (rys. 1).

r

b

(1)

r r

a b

a b

⋅ = ⋅

cos

α

α

r

a

Rys. 1

Wynikiem iloczynu skalarnego jest wielkość skalarna o wartości określonej
wzorem (1). Z mnożeniem skalarnym wektorów mamy do czynienia w fizyce
np. przy definicji pracy mechanicznej.

2.

Iloczyn wektorowy. W wyniku mnożenia wektorowego dwóch wektorów,
co zapisujemy

r

a

x

r

b

,

otrzymujemy nowy wektor

r

c

prostopadły do wektorów

r

a

i

r

b

o zwrocie określonym m. in. przez regułę korkociągu i o wartości

zgodnej ze wzorem (2).

r

c

r

b

(2)

c

a b

= ⋅ ⋅

sin

α

α

r

a

3.

Wektory jednostkowe*.

Wektor prędkości może być określany przez podanie jego trzech składo-
wych
(

v v v

x

y

z

,

,

). Używamy wówczas takiej symboliki:

(3)

r

r

r

r

v

i v

jv

kv

x

y

z

=

+

+

We wzorze (3)

r r r

i j k

, ,

są zdefiniowane jako wektory jednostkowe (wersory)

wzdłuż osi odpowiednio x, y, z. Analityczny sposób przedstawiania wektorów
za pomocą wersorów jest bardzo wygodny, gdyż upraszcza bardzo wiele działań
na wektorach i umożliwia łatwe przedstawianie wzoru w postaci wektorowej:

3

00502 Kinematyka D

TEORIA

(4)

F

G

M m

r

r

=

⋅

2

$

Suplement:

Przydatne wzory wynikające z twierdzenia Pitagorasa i twierdzenia kosinusów:

a)

c

a

b

=

+

2

2

, gdzie c jest przeciwprostokątną trójkąta prostokątnego o przyprostokąt-

nych równych a i b,

b)

c

a

b

ab

=

+ +

⋅

2

2

2

cos

α

, gdzie c jest przekątną równoległoboku utworzonego przez

wektory o długościach a i b spięte pod kątem

α

.

Temat: 6

Ruch i jego względność.

1.

Mechanika jest nauką, która bada i wyjaśnia ruchy ciał oraz warunki i przyczyny, na skutek
których ciała poruszają się lub pozostają w spoczynku.

Mechanika

statyka kinematyka dynamika

Statyka - nauka o zjawiskach równowagi sił.
Kinematyka - nauka badająca ruchy ciał niezależnie od ich przyczyn.
Dynamika - nauka badająca ruchy ciał w zależności od występujących sił.

2.

Ruchem mechanicznym nazywamy zmianę, w miarę upływu czasu, wzajemnego położenia
ciał w przestrzeni lub jednych ich części względem innych.

3.

Podstawowymi pojęciami nie tylko w fizyce, lecz także we wszystkich naukach przyrodni-
czych, są pojęcia przestrzeni i czasu. Nonsensem jest pojęcie „pustej przestrzeni” i „czyste-
go” czasu nie związanych z materią w ruchu. Związek między tymi dwoma formami istnienia
materii i zależności tych form od ruchu materii wyjaśniła w dużym stopniu teoria względno-
ś

ci.

4.

Ruch jest pojęciem względnym: badane ciało może być względem jednych ciał w spoczynku
i równocześnie względem innych w ruchu. Jego opis zależy od wyboru układu odniesienia
(położenia obserwatora) .

Przykład

: Człowiek w windzie, która się wznosi, jest w spoczynku względem windy,

natomiast porusza się po linii prostej względem domu, w którym jest zain-
stalowana winda.

4

00502 Kinematyka D

TEORIA

5.

Ruch ciała opisujemy w ten sposób, że podajemy położenie tego ciała w każdej chwili wzglę-
dem jakiegoś innego ciała (lub zbioru ciał względem siebie nieruchomych). Z ciałem lub zbio-
rem ciał, względem których opisujemy ruch, wiążemy zwykle w kinematyce jakiś układ
współrzędnych, najczęściej jest to układ współrzędnych prostokątnych

6.

Układ współrzędnych związany z ciałem (lub zbiorem ciał), względem którego opisuje-
my ruch innych ciał, nazywamy układem odniesienia

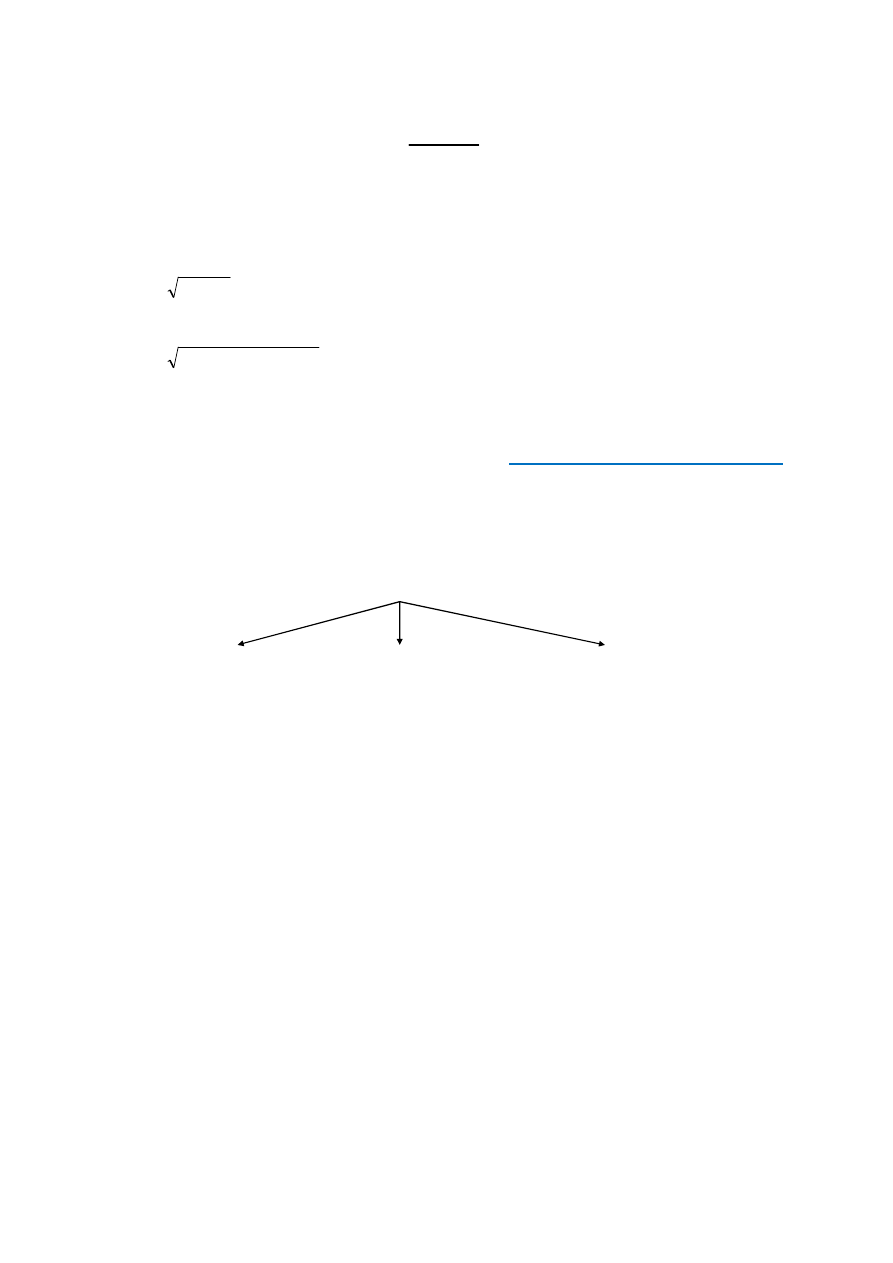
7. Układ współrzędnych prostokątnych (płaski) przedstawia rys. 1:


y

y

p

•

P(x

p

,y

p

)

Rys. 1
0 x

p

x

8.

Opisując zjawiska posługujemy się zwykle pewnymi abstrakcyjnymi modelami, gdyż uzysku-
jemy przez to większą prostotę opisu. Jednym z takich modeli jest punkt materialny

Punktem materialnym nazywamy ciało, którego rozmiary są małe w porównaniu z
pokonywanymi przez nie odległościami.

9.

Podczas swojego ruchu punkt materialny przemieszcza się do coraz to dalszych punktów
przestrzeni. Zbiór tych punktów stanowi tor ruchu, który może być linią prostą lub krzywą.

10.

W zależności od kształtu toru możemy rozróżnić:

Ruch


prostoliniowy krzywoliniowy



Ruch krzywoliniowy może być płaski lub przestrzenny. Przykładem ruchu płaskiego jest ruch po
elipsie, po okręgu itp., przykładem ruchu przestrzennego (trójwymiarowego) - ruch po linii śru-
bowej.
Długość odcinka toru zakreślonego przez punkt materialny stanowi drogę.

5

00502 Kinematyka D

TEORIA

Temat: 7

Wektorowy opis ruchu.

1.

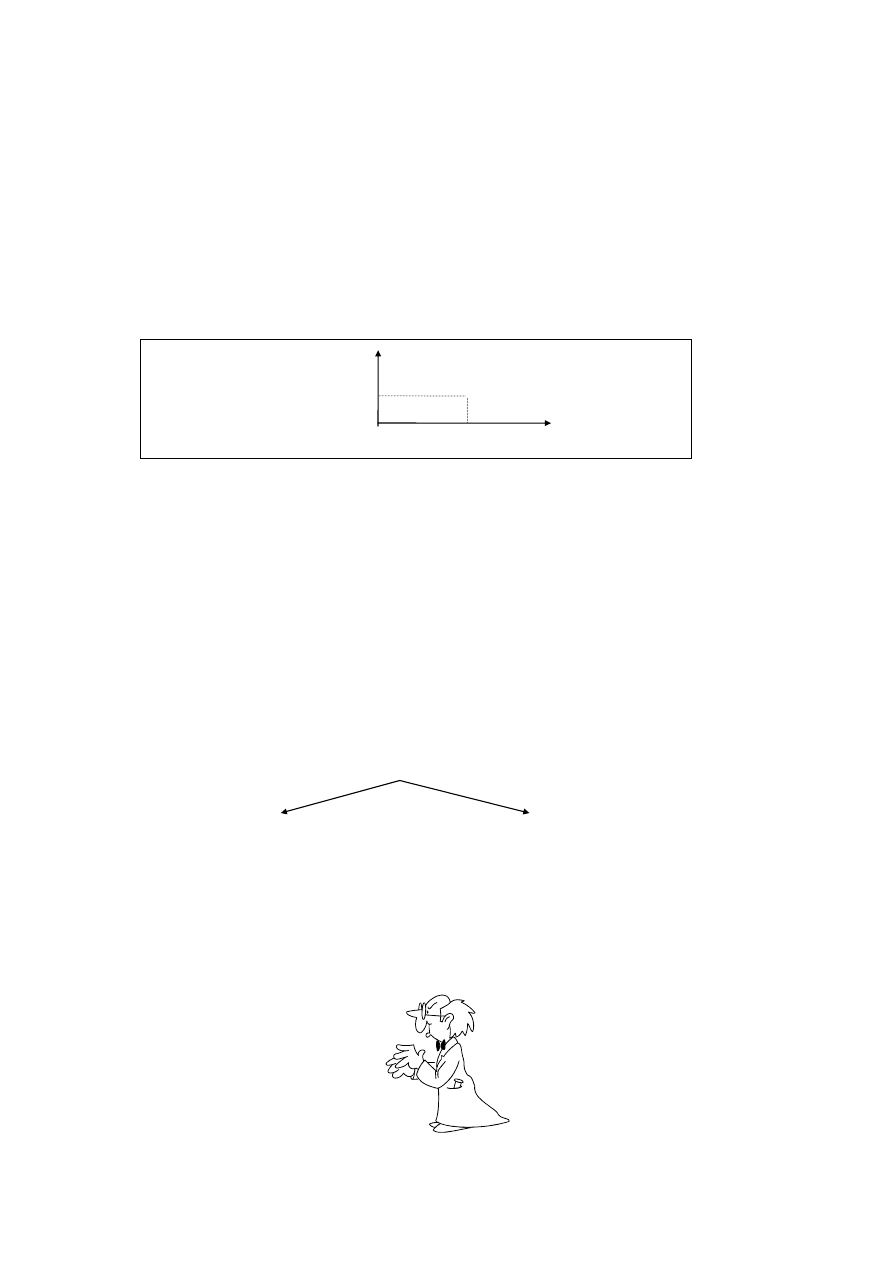
Położenie punktu materialnego względem układu odniesienia jest opisane poprzez poda-
nie co najwyżej trzech współrzędnych tego punktu. Fakt ten wyraża właśnie podstawową
zaletę punktu materialnego jako modelu ciała.

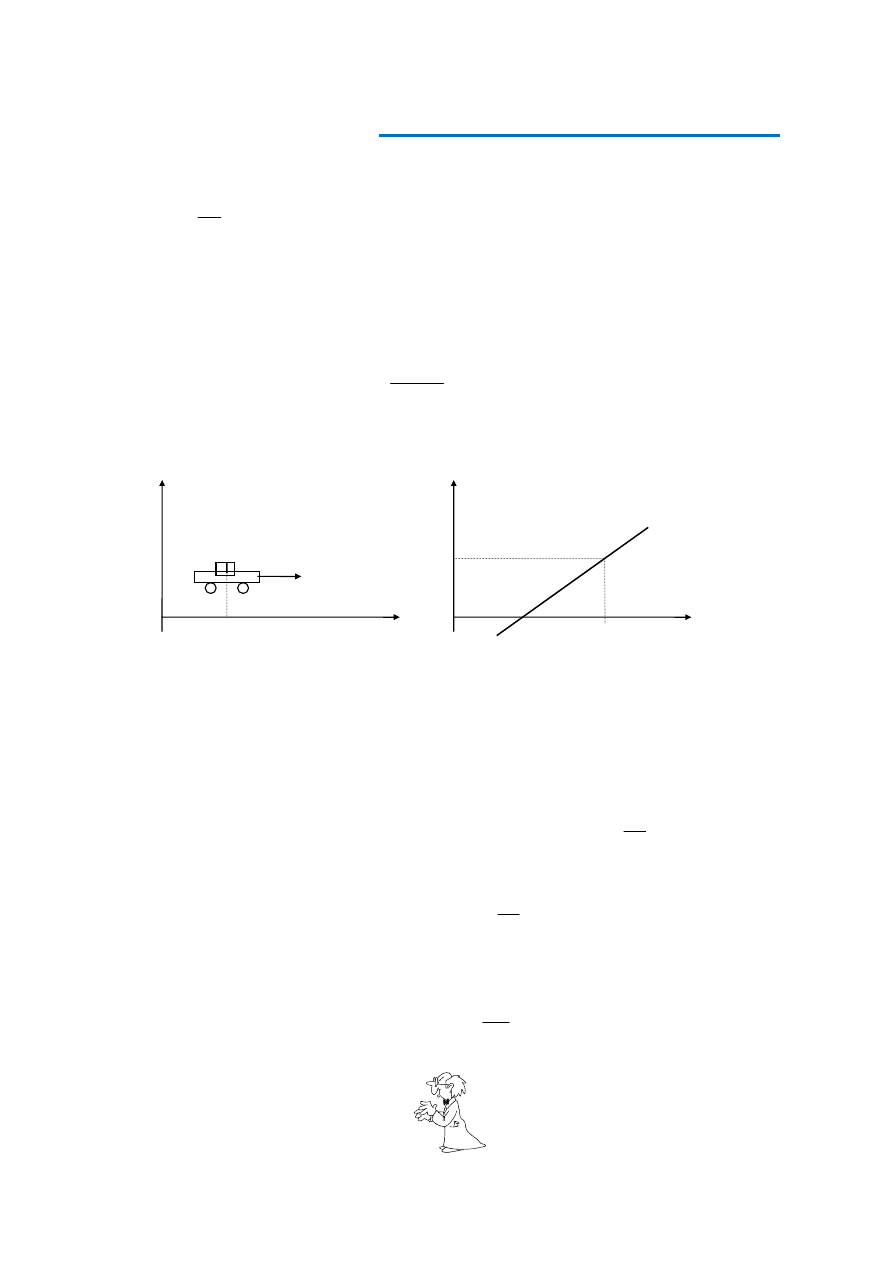
2.

Aby zaobserwować ruch, musimy zatem wybrać układ odniesienia oraz stwierdzić zmianę
położenia poruszającego się punktu materialnego względem tego układu. Zmiana położe-
nia oznacza, że w momencie rozpoczęcia obserwacji (chwila t

o

) punkt znajdował się w

położeniu A (rys.1), a w momencie jej zakończenia (chwila t) - w punkcie B.

y
A s

1

y

1

∆

r

r

r

r

0

s

2

r

r

∆

r

r

s

3

0 x

1

x

2

x

s

4

Rys. 1 Rys. 2

Na rysunku 1 mamy:

Wektor r

o

= OA nazywany wektorem położenia początkowego,

Wektor r = OB nazywany wektorem położenia końcowego,

3.

Wektor

∆

r zwany przesunięciem (przemieszczeniem), określa zmianę położenia punktu

materialnego w danym układzie, która zaszła w czasie

∆

t = t - t

0

, a więc nie tylko odle-

głość od punktu B do punktu A, ale również kierunek, w którym przesunął się dany punkt
materialny w czasie

∆

t i zwrot. Początek wektora

∆

r leży w punkcie A, a koniec w punk-

cie B.

4.

Przesunięcie (przemieszczenie) dodaje się również wektorowo stosując np. regułę równo-
ległoboku, czy też wieloboku sił.

5.

Przesunięcie świadczy o ruchu i określa jego wektorowy charakter, ale nie opisuje tego
ruchu (rys.2).

6.

Tylko w ruchu prostoliniowym można przyjąć równość drogi, którą się zawsze mierzy
wzdłuż toru

, i wartości wektora przesunięcia:

∆∆∆∆

s = 





∆∆∆∆

r





7.

W ruchach krzywoliniowych trzeba dokonać bardziej złożonej operacji, która bywa
analizowana na zajęciach z matematyki.

6

00502 Kinematyka D

TEORIA

Temat: 8 Prędkość w ruchu prostoliniowym.

1.

W naszym wieku - w dobie samochodów - prędkość jest pojęciem, które poznajemy już w dzie-
ciństwie. Prędkościomierz samochodu wskazuje wielkość chwilowej prędkości. w kilometrach na

godzinę (

km

h

) Prędkość jest zmianą odległości w jednostce czasu.

2.

Prędkość stała. Jeśli samochód porusza się ze stałą prędkością v, to odległość jaką przebywa w
czasie t jest x = vt. Jeżeli w czasie t

0

znajdował się w punkcie x

0

, to

(1)

x - x

0

= v(t - t

0

), czyli

(2)

v

x

x

t

t

=

−
−

0

0

(stała prędkość)

Zależność między x i t przedstawia rysunek 1a i 1 b:

y x

x

0

0 x

0

x 0

t

0

t

Rys. 1 a

Rys. 1 b

Wielkość v może być dodatnia lub ujemna, jej znak wskazuje kierunek ruchu. Jeśli prędkość v jest
ujemna, to ruch odbywa się w stronę malejących x.

3.

Prędkość chwilowa. Jeżeli samochód zwalnia albo przyspiesza, to wskazania szybkościomierza
nie zgadzają się ze wzorem (2), chyba że użyjemy bardzo małych wartości x - x

0

. Takie bardzo

małe wartości x - x

0

oznaczać będziemy przez

∆

x, a bardzo małe odstępy czasu, w których samo-

chód przebył drogę

∆

x, jako

∆

t. Wtedy prędkość chwilowa jest granicą

∆

∆

x

t

, gdy

∆

t dąży do ze-

ra.

(3)

v

x

t

t

=

→

∆

∆

∆

0

lim

Właśnie tak dokładnie definiuje się w rachunku różniczkowym pierwszą pochodną x względem czasu t co zapisujemy:

(4)

dt

dx

v

=

7

00502 Kinematyka D

TEORIA

Nachylenie krzywej przedstawiającej zależność x od t jest prędkością chwilową. Interpretację geometryczną prędkości

chwilowej przedstawia rysunek 2.

x

Krzywa na rys. 2 ma nachylenie

x

1

(5)

v

x

x

t

t

tg

=

−
−

=

2

1

2

1

α

x

2

które w granicy, gdy t

2

zbliża się do t

1

jest

0 t

1

t

2

t

nachyleniem krzywej.

Rys. 2 Wykres przedstawia zależność położenia x od czasu t w dowolnym ruchu.

4.

Prędkość średnią określamy zgodnie ze wzorem (6):

(6)

v

x

x

t

ś

r

=

−

0

W kinematyce przyjmuje się, że termin prędkość średnia oznacza prędkość średnią względem czasu (uśrednioną po cza-
sie). Zatem prędkość średnia nie zawsze oznacza średnią matematyczną

Zadania:

1.

Korzystając ze wzoru (6) wykaż, że ciało, które w czasach t

1

i t

2

przebyło jednakowe drogi wynoszące za każdym razem

s, poruszało się z prędkością średnią, zgodną ze wzorem (7).

(7)

2

1

2

1

2

v

v

v

v

v

úr

+

⋅

=

,

v

1 i

v

2

to prędkości ciała odpowiednio w chwilach t

1

i t

2.

2.

Kiedy prędkość średnią możemy policzyć jako średnią matematyczną, czyli:

(8)

v

v

v

ś

r

=

+

1

2

2

.

Koniec

8

00502 Kinematyka D

TEORIA

Notatki: