











Kinematyka: opis ruchu
Fizyka I (B+C)
Wykład IV:
• Ruch jednostajnie przyspieszony
• Ruch harmoniczny
• Ruch po okr ęgu















Klasyfikacja ruchów
Ze wzgl ędu na tor wybrane przypadki szczególne
• prostoliniowy, odbywający si ę wzdłuż lini prostej Zawsze możemy tak wybra ć układ współrz ędnych aby y(t) = z(t) = 0 ⇒ ~
r(t) = ~ix · x(t)
• płaski, odbywający si ę w ustalonej płaszczyźnie z(t) = 0 ⇒ ~
r(t) = ~ix · x(t) + ~iy · y(t)
• po okr ęgu
Ze wzgl ędu na przyspieszenie
• jednostajny ⇒ wartość pr ędkości pozostaje stała: |~
V | = const
• jednostajnie przyspieszony ⇒ przyspieszenie jest stałe: ~a = const A.F. Żarnecki
Wykład IV
1














Ruch jednostajnie przyspieszony
Prostoliniowy
Pr ędkość jest liniową funkcją czasu: t
Z
V
= V0 +
a dt = V0 + a · (t − t0)
t0
Położenie jest kwadratową funkcją czasu: t
t
Z
Z
x = x0 +
V dt = x0 +
[V0 + a · (t − t0)] dt
t0
t0
1
= x0 + V0 · (t − t0) +
a · (t − t0)2
2
Drogi w kolejnych odcinkach czasu mają si ę do siebie jak kolejne liczby nieparzyste: x1 : x2 : x3 : ... = 1 : 3 : 5 : 7 : ...
A.F. Żarnecki
Wykład IV
2













Ruch jednostajnie przyspieszony
W ogólnym przypadku ruch jednostajnie przyspieszony nie jest prostoliniowy.
~
V
= ~
V0 + ~a · (t − t0)
1
~
r = ~
r0 + ~
V0 · (t − t0) +
~a · (t − t0)2
2
Ruch b ędzie si ę odbywał w płaszczyźnie przechodzącej przez ~
r0
i wyznaczonej przez kierunki wektorów ~
V0 i ~a.
Możemy wybrać układ współrz ędnych tak aby:
~ix ⊥ ~a
~iy || ~a
⇒ ruch jednostajny (X) ⊕ ruch jednostajnie przyspieszony (Y) ⊕ spoczynek (Z): ax = 0
Vx = Vx,0 = const
x = x0 + Vx,0 · (t − t0)
a
1
y
= a
Vy = Vy,0 + a t
y = y0 + Vy,0 · (t − t0) +
a · (t − t0)2
a
2
z
= 0
Vz = 0
z = 0
A.F. Żarnecki
Wykład IV
3













Ruch jednostajnie przyspieszony
Ruch w polu grawitacyjnym
Ruch ciala w jednorodnym polu grawitacyjnym: y
~a = ~g = (0, −g, 0)
V0
g
Θ
(wygodny wybór układu współrz ędnych) h
Pole grawitacyjne Ziemi możemy przyją ć za jednorodne, jeśli badamy ruch na odległo ściach |∆~
r| RZ
Rodzaje ruchu:
x
• spadek swobodny: V0 = 0 (ruch prostoliniowy)
• rzut pionowy: θ = ±π/2 (ruch prostoliniowy)
• rzut poziomy: θ = 0
• rzut ukośny: θ 6= 0, π/2, ...
A.F. Żarnecki
Wykład IV
4














Ruch jednostajnie przyspieszony
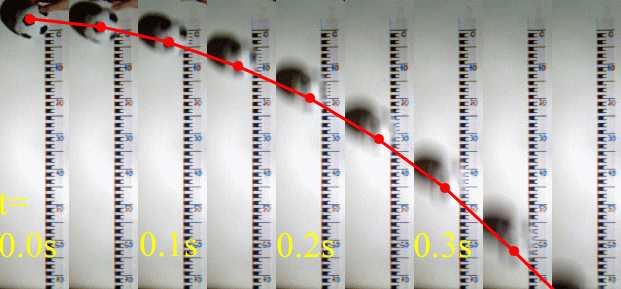
Spadek swobodny
y
g
x
Położenie zależy kwadratowo od czasu: g
y = h −
· t2
y(0) = h, Vy(0) = 0
2
A.F. Żarnecki
Wykład IV
5













Ruch jednostajnie przyspieszony
Spadek swobodny
Wyniki “domowych” pomiarów:
][m 0
y
g = 9.7 ± 0.7 m/s2
-0.2
-0.4
-0.6
0
0.1
0.2
0.3
t [s]
A.F. Żarnecki
Wykład IV
6

















Ruch jednostajnie przyspieszony
Ruch w polu grawitacyjnym
y
V
Niezależność ruchów:
t
0
0 = 0, x0 = 0, y0 = h
h
Θ
x = Vx,0 · t = V0 cos θ · t
⇒ ruch w poziomie zależy tylko od Vx,0
g
y = h + V
l
x
y,0 · t −
· t2
2 g
= h + V0 sin θ · t −
· t2
2
⇒ ruch w pionie zależy tylko od Vy,0
r
Rzut poziomy θ = 0 ⇒ V
2h
y,0 ⇒ czas spadania nie zale ży od V0: t =
g
(1)
(2)
(1)
(2)
Dwa ciała o tym samym Vx,0 = Vx,0 ⇒ taki sam ruch w poziomie: x (t) = x (t) A.F. Żarnecki
Wykład IV
7

















Ruch jednostajnie przyspieszony
Ruch w polu grawitacyjnym
y
V0
h
Θ
l
x
g
Tor w rzucie ukośnym: ⇒ y = h + x · tan θ − x2 ·
⇒ parabola
2V 2
0 cos2 θ2
V 2
π
Zasi ęg dla h=0 ⇒ l =
0 sin(2θ) ⇒ największy zasięg dla θ =
(45◦)
g
4
A.F. Żarnecki
Wykład IV
8














Ruch harmoniczny
Szczególny przykład ruchu drgającego: x
x = A · sin(ωt + φ)
1
0.5
Parametry
0
1
2
t
• amplituda A
-0.5
•
-1
cz ęstość kołowa ω2π
okres drga ń T = ω
• faza początkowa φ
dx
Pr ędkość: V =
= ω A · cos(ωt + φ)
dt
dV
Przyspieszenie: a =
= −ω2 A · sin(ωt + φ) = −ω2 · x
dt
A.F. Żarnecki
Wykład IV
9













Ruch harmoniczny
Równanie oscylatora harmonicznego:
d2x = −ω2 x
dt2
d2~r = −ω2 ~r
dt2
Równanie oscylatora dobrze opisuje zachowanie wielu układów fizycznych:
• ci ężarek na spr ężynie
• wahadło matematyczne (dla małych wychyle ń)
• kamerton, struna, itp...
A.F. Żarnecki
Wykład IV
10















Równiania rózniczkowe
Równanie oscylatora harmonicznego jest przykładem równania różniczkowego Nasza wiedza nt. ruchu ciała przedstawiana jest cz ęsto w postaci równan różniczkowych (równa ń ruchu). Aby znaleź ć opis ruchu ciała trzeba te równania rozwiąza ć.
Równania rz ędu pierwszego
Postać ogólna:
Jeśli potrafimy rozdzieli ć zmienne
F (x, y, y0) = 0
dy
y0 =
= f (x) · g(y)
dx
Najłatwiej rozwiąza ć problemy, które dają to rozwiązanie równania sprowadza si ę do si ę sprowadzić do postaci rozwikłanej całkowania:
wzgl ędem pochodnej:
Z
dy
Z
=
f (x) dx + C
y0 = f (x, y)
g(y)
lub (postać równoważna):
a(x, y) dx + b(x, y) dy = 0
A.F. Żarnecki
Wykład IV
11




















Równiania rózniczkowe
Przykład
Równanie liniowe
(w y i y0)
Rozpad promieniotwórczy.
Ogólna postać dla rz ędu pierwszego: Liczba rozpadów w jednostce czasu jest dy
proporcjonalna do liczby atomów izotopu:
+ P (x) · y = Q(x)
dx
dN = −αN α > 0
dt
• rozwiązujemy równanie jednorodne:
rozpady oznaczają zmniejszanie si ę
dv
liczby atomów izotopu
+ P (x) · v = 0
dx
Rozwiązanie:
Z
dN
Z
=
−α dt + C
• podstawiając do wyj ściowego równania N
y = u · v dostajemy
ln N = −αt + C
du
R P (x)dx
= C · Q(x) e
N (t) = N0 e−αt
dx
gdzie N0 ≡ N(0) = eC
A.F. Żarnecki
Wykład IV
12


























Równiania rózniczkowe
d2x
Równanie oscylatora harmonicznego
= − ω2 x
dt2
Jest równaniem rz ędu drugiego.
Ale
Nast ępnie możemy wróci ć do zależności od eliminując czas możemy sprowadzi ć je do czasu:
równania rz ędu pierwszego:
dx
q
= ± ω
a2 − x2
d2x
dv
dv dx
dv
dt
=
=
·
=
· v
Z
dx
Z
dt2
dt
dx dt
dx
⇒
= ± ω
dt
q
dv
a2 − x2
⇒
v
= −ω2 x
dx
x
⇒
arcsin
= ± ωt + C
które możemy wycałkowa ć:
a
Z
Z
v dv = −ω2
x dx
⇒
x = a sin(ωt + C)
v = a ω cos(ωt + C)
q
⇒
v = ± ω
a2 − x2
A.F. Żarnecki
Wykład IV
13
















Ruch po okr ęgu
Położenie ciała może by ć opisane
Y
V
jedną zmienną:
• kąt w płaszczyźnie XY - φ
s
r
φ
• długość łuku okr ęgu - s = r · φ
X
Pr ędkość:
ds
dφ
V
=
= r
= r ω
dt
dt
pr ędkość kątowa ω = dφ
dt
dω
d2φ
Przyspieszenie kątowe: α =
=
dt
dt2
Ruch jednostajny po okr ęgu: α = 0
⇒
ω = const
⇒
V = const
ale ~
V 6= const
⇒
~a 6= 0 !?
A.F. Żarnecki
Wykład IV
14


















Ruch po okr ęgu
Pr ędkość w zapisie wektorowym:
Z
~
ω
V = ~
ω × ~r
Y
Przyspieszenie:
r
φ
d~
V
d~
ω
d~
r
V
~a =
=
× ~
r + ~
ω ×
s
dt
dt
dt
X
=
~
α × ~
r + ~
ω × ~
V
=
~
at
+
~
an
Oprócz przyspieszenia stycznego ~
at ↑ ~
V , opisującego zmian ę | ~
V |,
jest też przyspieszenie normalne ~
an, odpowiedzialne za zmian ę kierunku ~
V w czasie.
~
an = ~ω × (~ω × ~r) = −ω2 · ~r
A × (B × C) = (A · C) · B − (A · B) · C
przyspieszenie do środkowe
A.F. Żarnecki
Wykład IV
15















Ruch po okr ęgu
Ruch jednostajny po okr ęgu ⇔ przyspieszenie styczne:
~
at = 0
⇒
~a = ~
an = −ω2 · ~r
Y
V
Ruch jednostajny po okr ęgu jest złożeniem dwóch niezależnych ruchów harmionicznych:
s
r
π
φ
x = r · cos(ω · t) = r · sin(ω · t +
)
X
2
y = r · sin(ω · t)
Ruch po okr ęgu
⇐⇒
różnica faz ∆φ = ±π
2
Ciekawostka:
Ruch harmoniczny można przedstawi ć jako złożenie dwóch ruchów po okr ęgu...
A.F. Żarnecki
Wykład IV
16
Wyszukiwarka
Podobne podstrony:
Kinematyka opis ruchu
Fizyka wykład 3 Kinematyka ruchu obrotowego, Geodezja i Kartografia, Fizyka
00502 Kinematyka D part 2 2008 teoria opis ruchu, prędkość w ruchu prostoliniowym(1)
19 Pojecie i opis ruchu falowego (2)
Fizyka 1 3 opis ruchu pochodne
FW2a opis ruchu 07
Opis ruchu
mega sciaga na egzamin, sciaga harmon, Kinematyczne równanie ruchu to pewna zależność (bądź układ za
Fizyka 1 3 opis ruchu pochodne
Rajfura A, Statystyka Wyklad 01 OPIS STATYSTYCZNY krotki
FM2 opis ruchu
Wykład Diag 5 Energochłonność ruchu
05 Opis ruchu & Rownanie energi Nieznany (2)
Pełny klasyczny i kwantowy opis ruchu w wirującej pułapce harmonicznej
FM2 opis ruchu
więcej podobnych podstron
















