1

Pojęcie i opis ruchu falowego. Podstawowe zjawiska towarzyszące rozchodzeniu
się fal

Falą mechaniczną nazywamy zjawisko rozchodzenia się zaburzeń ośrodka. Źródłem fali jest ciało

drgające.

Ośrodek sprężysty ma tę właściwość, ze siłom, które usiłują spowodować jego odkształcenie,

przeciwstawia siły sprężyste, które po usunięciu sił odkształcających usuwają odkształcenie. Wytrącenie
zespołu cząsteczek takiego ośrodka z położenia równowagi powoduje ich drganie wokół tego położenia,
przy czym wskutek jego właściwości sprężystych zaburzenie przenosi się z jednej warstwy ośrodka na
następną, wprawiając ją w ruch drgający o takim samym okresie drgań. Takie właśnie przenoszenie drgań
nazywamy ruchem falowym lub krótko falą.

Fale mechaniczne (ze względu na wymiar) dzielimy na:

•

fale liniowe (jednowymiarowe) - np. na gumowym wężu,

•

fale powierzchniowe (dwuwymiarowe) - np. na wodzie,

•

fale przestrzenne (trójwymiarowe) - np. dźwięk w powietrzu.

W zależności od kierunku drgań cząsteczek ośrodka w stosunku do kierunku rozchodzenia się fali
rozróżnia się fale poprzeczne i fale podłużne.
Fala poprzeczna to taka fala, której cząsteczki ośrodka drgają w kierunku prostopadłym do kierunku
rozchodzenia się fali.
Prędkość fali poprzecznej w płynach lub cienkich, długich prętach wynosi:

- współczynnik ściśliwości płynu; moduł sztywności ciała stałego
- gęstość ośrodka

Fala podłużna jest to fala, której cząsteczki ośrodka drgają w kierunku zgodnym z kierunkiem
rozchodzenia się fali.
Ponieważ rozchodzenie się fal podłużnych jest związane z okresowymi zmianami gęstości ośrodka, fale
te mogą się rozchodzić we wszystkich ośrodkach wykazujących sprężystość objętości, a więc zarówno w
ciałach stałych, cieczach jak i w gazach.

Prędkość fali podłużnej w płynach lub cienkich, długich prętach wynosi:

- moduł Younga

- gęstość ośrodka

Ze względu na czoło fali fale dzielą się na płaskie i kuliste. Jeżeli drgania rozchodzą się w jednym
kierunku, to powierzchnie fali są płaszczyznami i mówimy o fali płaskiej. Jeżeli zaś fala wywołana przez
punktowe źródło drgań rozchodzi się w ośrodku jednorodnym, to prędkość jej jest jednakowa we
wszystkich kierunkach i powierzchnia fali ma postać kuli. Mówimy wtedy o fali kulistej.

Wielkości charakteryzujące falę to:

- amplituda fali

- okres fali

- częstotliwość fali

- prędkość fali (prędkość fali w danym ośrodku jest stała)

- długość fali (odległość między najbliższymi cząsteczkami drgającymi w zgodnych fazach)

2

Fala przebywa drogę równą swojej długości w czasie okresu.

Zasada Huygensa
Opis ruchu falowego komplikuje się z chwilą, gdy czoło fali dociera do granicy obszaru swobodnego
rozprzestrzeniania się fali, lub do granicy dwu ośrodków, w których prędkości rozchodzenia się fal są
różne. Metody opisu ruchu falowego w tym przypadku dostarcza zasada Huygensa.
U źródła zasady Huygensa leżą trzy obserwacje doświadczalne:

•

Drgające źródła punktowe wysyłają w ośrodku jednorodnym i izotropowym fale koliste.

•

Fale wysyłane przez różne źródła rozchodzą się w ośrodku niezależnie od siebie (zasada
superpozycji).

•

Fale nie rozchodzą się w ośrodku natychmiastowo, lecz ze skończoną prędkością - coraz to nowe
punkty ośrodka są pobudzane do drgań.
Na podstawie tych obserwacji Huygens wysunął hipotezę, że:

Każdy punkt ośrodka, do którego dochodzi fala, można traktować jako elementarne źródło wtórnej
fali kolistej.

Równanie fali

Aby wyprowadzić równanie fali posłużymy się wykresem zależności wychylenia od odległości od źródła.

- wychylenie

- odległość od źródła

Wykorzystujemy równanie ruchu drgającego na opisanie położenia punktów A i B.
Punkt A -

Punkt B -

- czas, w którym fala przebywa drogę

Podstawiamy za powyższy wzór i przekształcamy, aby otrzymać równanie fali w prostszej postaci:

Równanie fali można także wyrazić przy pomocy liczby falowej k, której wartość wstawiona do

3

otrzymanego wzoru da inną postać równania fali:

Interferencja fal mechanicznych

Podobnie, jak w ruchach punktu materialnego materialnego ciała sztywnego, w ruchu falowym
obowiązuje zasada niezależności ruchów. Jeżeli w ośrodku rozchodzi się kilka fal, wysyłanych
jednocześnie przez różne źródła, to wypadkowy ruch każdej cząstki ośrodka jest złożeniem ruchów, jakie
wykonywałaby ta cząstka przy rozchodzeniu się każdej fali z osobna. Zasada niezależności ruchów w
zastosowaniu do ruchu falowego nosi nazwę zasady superpozycji fal.

Zjawisko nakładania się dwu lub więcej fal harmonicznych tej samej długości, prowadzące do

powstania ustalonego w czasie rozkładu przestrzennego obszarów wzmocnienia i osłabienia fali,

nazywamy interferencją fal.

.

WZMOCNIENIE

Jeżeli obie fale będą miały takie same amplitudy to nastąpi maksymalne wzmocnienie.
Wzmocnienie następuje w takich przypadkach:

Maksymalne wzmocnienie fali następuje we wszystkich punktach, dla których różnica odległości od
źródeł równa się całkowitej wielokrotności długości fali.

WYGASZENIE

4

Wygaszenie następuje we wszystkich punktach, dla których różnica odległości od źródeł jest równa
nieparzystej wielokrotności połowy długości fali.

Wyprowadźmy warunki na wygaszenie i wzmocnienie fal mechanicznych (korzystając z równania
fali):

Korzystamy ze wzoru na sumę funkcji trygonometrycznych:

I.

Wygaszenie nastąpi, gdy amplituda będzie równa zero:

Zamiast k podstawiamy

i otrzymujemy:

II.

II. Wzmocnienie nastąpi, gdy:

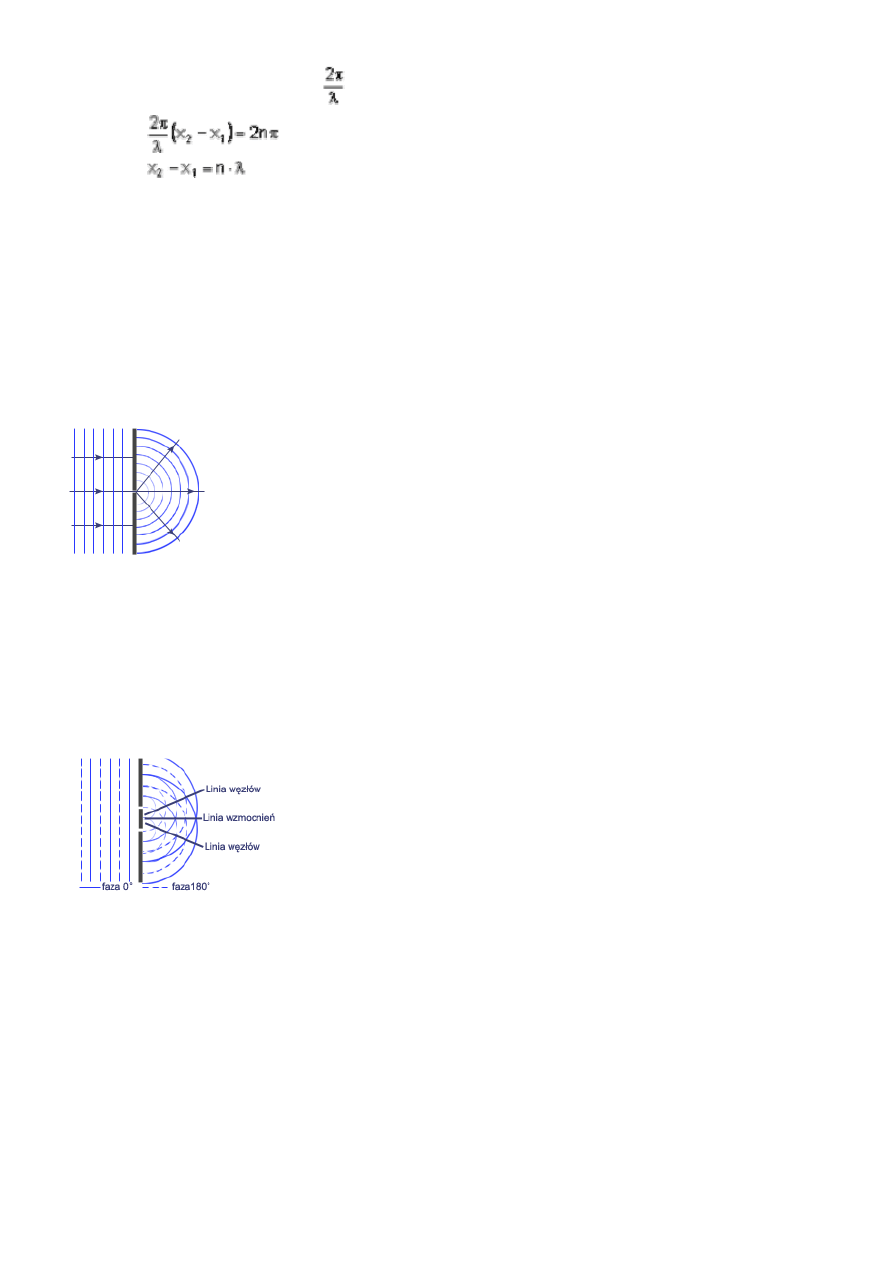
5

Zamiast k podstawiamy

i otrzymujemy:

Dyfrakcja fal mechanicznych

Dyfrakcją fali nazywamy ugięcie fali, czyli zmianę kierunku rozchodzenia się fali na szczelinach,

krawędziach, przeszkodach, itp.

Zjawisko dyfrakcji jest typowym dla fal. Tłumaczy je zasada Huygensa. Łatwo jest zaobserwować
dyfrakcję fal, ustawiając w zbiorniku z wodą przegrodę z wąską szczeliną i wytwarzając po jednej stronie
falę płaską. W chwili, gdy fala ta dojdzie do przegrody - szczelina staje się źródłem fali kołowej,
rozchodzącej się z niej we wszystkich kierunkach po drugiej stronie przegrody. Tą sytuację ilustruje
rysunek:

Umieszczając w zbiorniku z wodą przegrodę z dwiema szczelinami, równoległą do powierzchni
wytwarzanej fali płaskiej, możemy obserwować zarówno dyfrakcję jak i interferencję fal ugiętych.
Ponieważ powierzchnia fali płaskiej dochodzi do obydwu szczelin w tej samej chwili, stają się one,
zgodnie z zasadą Huygensa, źródłami elementarnych fal kołowych o jednakowych fazach i amplitudach.
amplitudach wyniku nakładania się fal w tych punktach powierzchni wody, do których dojdą fale o
jednakowych fazach, następuje wzmocnienie drgań i powierzchnia wody staje się silniej pofałdowana, w
innych zaś, do których dojdą fale o fazach przeciwnych , następuje wygaszenie drgań i powierzchnia
wody staje się gładka, tworząc charakterystyczne "linie węzłów".

Zasada Fermata

Fala biegnąca z jednego punktu do drugiego przebywa drogę, na której przebycie trzeba w porównaniu

z innymi sąsiednimi drogami minimum lub maksimum czasu.

Zasada ta prowadzi do prawa rozchodzenia się światła po liniach prostych w ośrodkach jednorodnych
oraz do praw odbicia i załamania fal.
Odbicie fal mechanicznych

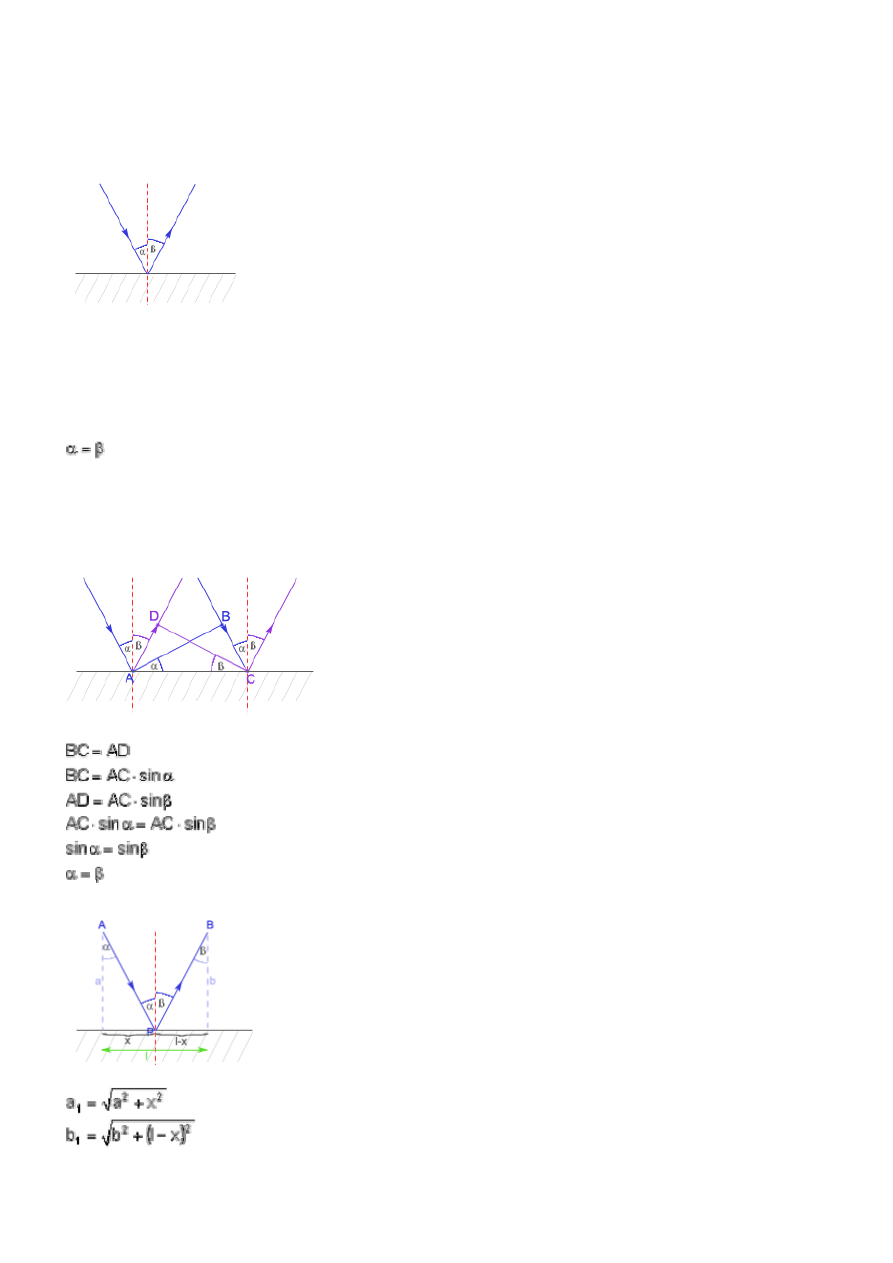
Kątem padania nazywamy kąt zawarty między promieniem fali padającej, a prostą prostopadłą

(normalną) do płaszczyzny odbijającej.

6

Kątem odbicia nazywamy kąt zawarty między promieniem fali odbitej, a prostą prostopadła (normalną)

do płaszczyzny odbijającej.

PRAWO ODBICIA

Kąt padania jest równy kątowi odbicia. Promień fali padającej, promień fali odbitej i prosta prostopadła

(normalna) płaszczyzny odbijającej leżą w jednej płaszczyźnie.

Przy odbiciu fali od ośrodka bardziej sztywnego następuje zmiana fazy na przeciwną.
Wyprowadzenie prawa odbicia:

I. geometrycznie

Odcinki BC i AD muszą być przebyte w tym samym czasie, więc:

II. z zasady Fermata

Z rysunku na podstawie twierdzenia Pitagorasa odczytujemy, że:

Drogę jaką przebyła fala od punktu A do B oznaczamy literą d:

7

Obliczamy czas, w którym fala pokonała drogę z punktu A do B:

Obliczamy pochodną z t:

Obliczoną pochodną przyrównujemy do zera, gdyż funkcja osiąga maksimum lub minimum, gdy jej
pochodna ma wartość zero.

Z rysunku odczytujemy wartość funkcji sinus dla obu kątów zaznaczonych na rysunku:

A następnie wstawiamy je do wyżej otrzymanego wzoru i uzyskujemy:

Załamanie fal mechanicznych

Fala ulega załamaniu, gdy przechodzi z jednego ośrodka do drugiego.
PRAWO ZAŁAMANIA

Stosunek sinusa kąta padania do sinusa kąta załamania, zwany współczynnikiem załamania n ośrodka

drugiego względem pierwszego, jest równy stosunkowi prędkości rozchodzenia się fali w ośrodku

pierwszym do prędkości rozchodzenia się fali w ośrodku drugim. w obu ośrodkach. Promień fali

padającej, promień fali załamanej i prosta prostopadła (normalna) do granicy ośrodków leżą w jednej

płaszczyźnie.

Wyprowadzenie prawa załamania:

I. geometrycznie

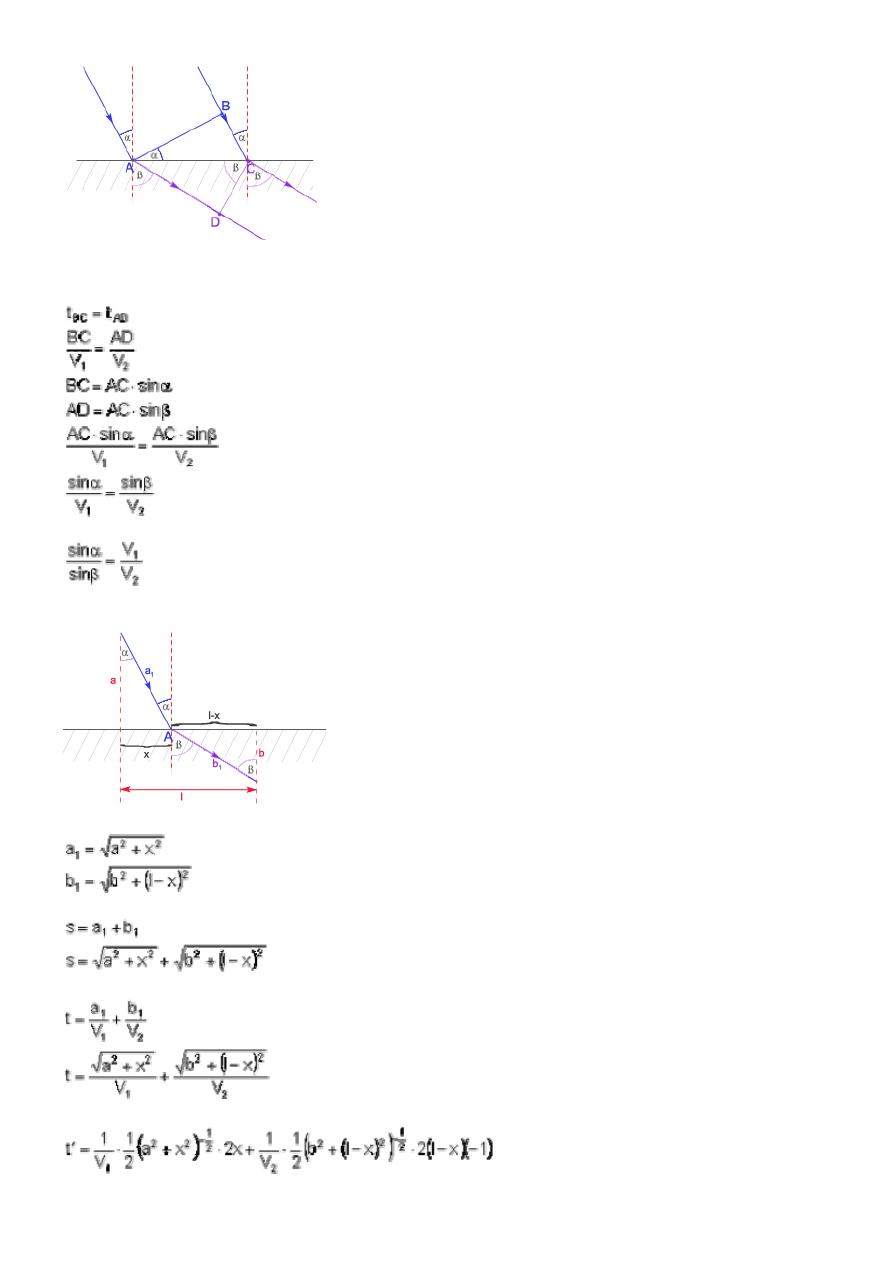
8

Fala musi pokonać drogę BC w jednym ośrodku w tym samym czasie co drogę AD w drugim ośrodku.

Przekształcamy równanie i otrzymujemy:

II. z zasady Fermata

Z rysunku na podstawie twierdzenia Pitagorasa odczytujemy, że:

Drogę jaką przebyła fala od punktu A do B oznaczamy literą s:

Obliczamy czas, w którym fala pokonała drogę z punktu A do B:

Obliczamy pochodną z t:

9

Obliczoną pochodną przyrównujemy do zera, gdyż funkcja osiąga maksimum lub minimum, gdy jej
pochodna ma wartość zero.

Z rysunku odczytujemy wartość funkcji sinus dla obu kątów zaznaczonych na rysunku:

A następnie wstawiamy je do wyżej otrzymanego wzoru i uzyskujemy:

Fala stojąca

Szczególnym przypadkiem interferencji fal jest powstawanie fali stojącej, będącej wynikiem nakładania
się dwóch fal o jednakowych amplitudach, częstościach i prędkościach, rozchodzących się w
przeciwnych kierunkach.
Falę stojącą można otrzymać najprościej na naciągniętym sprężystym sznurze. Jeśli jeden z jego końców
tego sznura wprawimy w ruch drgający harmoniczny, to biegnąca wzdłuż niego fala, po dotarciu do
punktu zamocowania sznura odbije się od niego, przy czym fala odbita ma tę samą częstotliwość i
amplitudę, co pierwotna fala, lecz porusza się w przeciwnym kierunku. W wyniku nakładania się fali
pierwotnej i fali odbitej cząsteczki sznura uzyskują, w zależności od ich położenia wzdłuż kierunku
rozchodzenia się fali, różne amplitudy drgań, zawarte w granicach od zera do wartości podwójnej
amplitudy fali pierwotnej. Drgania te nazywamy właśnie falą stojącą.

10

Długość ośrodka musi być równa całkowitej wielokrotności połowy długości fali.

Strzałki fali stojącej to punkty o największej amplitudzie drgań.

Węzły fali stojącej to punkty niedrgające (nie wykonujące drgań).

Wyprowadźmy równanie fali stojącej oraz warunki na strzałki i węzły. Skorzystamy z równania fali:

Zgodnie z definicją fali stojącej dodajemy równania obu fal:

Korzystamy ze wzoru na sumę funkcji trygonometrycznych:

Otrzymaliśmy wzór równania fali stojącej, z którego możemy wyprowadzić warunki na węzeł i strzałkę
fali stojącej.
WĘZEŁ

Fala stojąca jest węzłem, gdy odległość jest równa nieparzystej wielokrotności ćwiartki długości fali.
Wykażmy, że między dwoma sąsiednimi węzłami jest zawsze połowa długości fali.

Korzystając z powyższych równań uzyskamy wzór na różnicę odległości między dwoma sąsiednimi
węzłami.

11

STRZAŁKA

Fala stojąca jest strzałką, gdy odległość jest równa całkowitej wielokrotności połowy długości fali.
Wykażmy, że między dwoma sąsiednimi strzałkami jest zawsze połowa długości fali.

Energia fali

Fala przenosi energię od źródła drgań, które ją wysyła, przy czym energia ta równoważna jest pracy
zużytej na zakłócenie równowagi cząsteczek ośrodka, w którym rozchodzi się fala (pomijając straty
na pokonanie oporów ośrodka).
Badania wykazały, że energia E przenoszona przez falę jest wprost proporcjonalna do kwadratu
amplitudy i kwadratu częstotliwości fali. Stosunek przepływającej energii E do iloczynu powierzchni
fali S i czasu t, w którym przepływa jest miarą natężenia fali I.

Jednostką natężenia fali w układzie SI jest W/m

2

.

W przypadku fali płaskiej rozchodzącej się w ośrodku sprężystym i wysyłanej przez źródło drgań o

stałej mocy (

), natężenie fali ma wartość stałą, gdyż jej powierzchnia S jest stała.

W przypadku fali kulistej natężenie fali w punkcie P odległym o r od źródła drgań O wynosi:

skąd wynika, że dla źródła drgań o stałej mocy

natężenie fali kulistej jest odwrotnie

proporcjonalne do kwadratu odległości od źródła drgań.
W ośrodkach materialnych, czyli w rzeczywistych gazach, cieczach i ciałach stałych, w których
występuje tarcie międzycząsteczkowe, energia, jaką niesie ze sobą fala, ulega rozproszeniu, jest
bowiem zużywana na pokonanie tarcia i zamienia się na ciepło. Wskutek rozpraszania energii
amplituda fali maleje ze wzrostem odległości od źródła drgań. Taka fala nosi nazwę fali zanikającej
lub gasnącej.