1

00503 Kinematyka D

TEORIA

00503

Podstawy kinematyki D

Część 3

Przyspieszenie.

Droga i prędkość w ruchu jednostajnym.

Wektorowy charakter prędkości

i przyspieszenia.

Twierdzenie o prędkości i drodze

Instrukcja dla zdającego

1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 10
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Kwiecień

ROK 2008

Dane osobowe właściciela arkusza

2

00503 Kinematyka D

TEORIA

Temat: 9 Przyspieszenie w ruchu prostoliniowym.

1.

Wszyscy w jakościowy sposób rozumiemy co to jest przyspieszenie. Możemy wywołać
przyspieszenie samochodu naciskając pedał gazu. Im więcej pedał ten naciskamy, tym
większe jest przyspieszenie. Gdy trwa przyspieszenie prędkość rośnie, a oparcia siedzeń
popychają plecy pasażerów. Ta ilość popychania jest ilościową miarą przyspieszenia. Na-
ciśniecie na pedał hamulca daje ten sam efekt, tyle tylko, że teraz mamy ujemne przyspie-
szenie (nazywane opóźnieniem). Przyspieszenie jest miarą zmiany prędkości.

2.

Przyspieszenie jednostajne. Z definicji ciało porusza się z jednostajnym, czyli stałym
przyspieszeniem, gdy jego prędkość rośnie jednostajnie z czasem. Przyspieszenie a jest
stałe, gdy:

(1)

v v

0

= a·t, czyli:

(2) a

v

v

t

=

−

0

, gdzie v - v

0

jest przyrostem prędkości

w czasie t.

3.

Przyspieszenie chwilowe. Jeżeli przyspieszenie zmienia się z czasem, musimy wtedy
mierzyć zmianę prędkości

∆

v w ciągu krótkiego czasu

∆

t. Wtedy:

(3) a

v

t

dv

dt

t

=

=

→

∆

∆

∆

0

lim

4.

Przyspieszenie grawitacyjne. Jest godnym uwagi faktem doświadczalnym, że w pobliżu
powierzchni Ziemi każdy przedmiot upuszczony swobodnie spada ku środkowi Ziemi z
przyspieszeniem równym:

g

m

s

=

9 81

2

,

Zadziwiające jest, że to przyspieszenie jest niezależne od masy ciała, jego składu ani prędko-
ś

ci (chyba, że jest znaczny opór powietrza, wtedy przyspieszenie będzie mniejsze).

Suplement*:

Wartość 9 81

2

,

m

s

jest wartością przybliżoną.

Przy uwzględnianiu dalszych cyfr znaczących ujawnia się zależność g od szerokości geogra-
ficznej i wysokości punktu nad poziomem morza, w szczególności dla Nowego Jorku

g

m

s

=

9 82067

2

,

, dla Warszawy g

m

s

=

9 8123

2

,

.Będziemy zawsze przyjmować wielkość g jako

dodatnią. Jeżeli więc oś x skierujemy w górę, to przyspieszenie będzie równe a = -g.

3

00503 Kinematyka D

TEORIA

Temat: 10

Droga i prędkość w ruchu jednostajnym prostoliniowym.

1.

Jeżeli punkt materialny porusza się po linii prostej ruchem jednostajnym , to droga poko-
nywana w dowolnym czasie t, liczonym od chwili rozpoczęcia obserwacji (t

0

= 0), jest

wprost proporcjonalna do czasu trwania ruchu, co oznacza, że w równych, dowolnie ma-
łych odstępach czasu, punkt materialny przebywa równe drogi .

2.

Wiemy już, że stosunek dwóch wielkości, które są do siebie wprost proporcjonalne ma
wartość stałą. A więc i stosunek drogi s do odpowiadającego jej czasu t w ruchu jedno-
stajnym prostoliniowym ma wartość stałą. Zatem ruch jednostajny prostoliniowy, to ruch
odbywający się ze stałą prędkością (v = const. )

(1)

v

s

t

=

3.

Jeżeli punkt materialny porusza się ruchem jednostajnym prostoliniowym z prędkością v
w czasie t, to wartość przebytej drogi wyraża równanie:

(2)

s = v·t

zwane

równaniem ruchu jednostajnego prostoliniowego.

4.

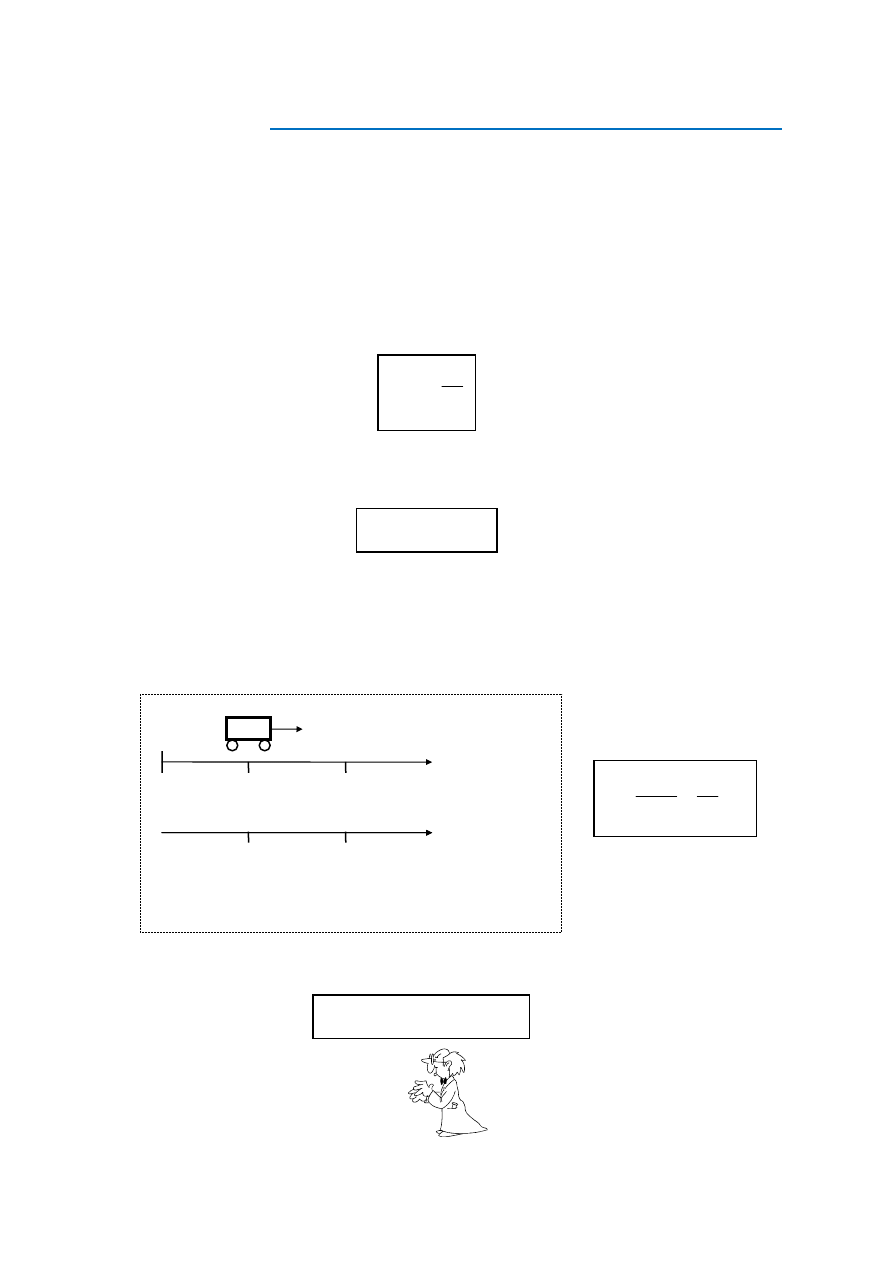
Jeżeli obserwację ciała poruszającego się ruchem jednostajnym prostoliniowym rozpoczę-
to w chwili t

0

, w której znajdowało się ono w odległości s

0

od przyjętego punktu odnie-

sienia (rys. 1), to wartość prędkości określamy wzorem (3):

0

s

0

s droga [metr]

(3)

v

s

s

t

t

s

t

=

−
−

=

0

0

∆
∆

0

t

0

t czas [sekunda]

Rys. 1

5.

Ze wzoru (3) otrzymujemy bardziej ogólne równanie ruchu jednostajnego prostoliniowe-
go:

(4)

s

s

v t

t

= +

−

0

0

(

)

4

00503 Kinematyka D

TEORIA

6.

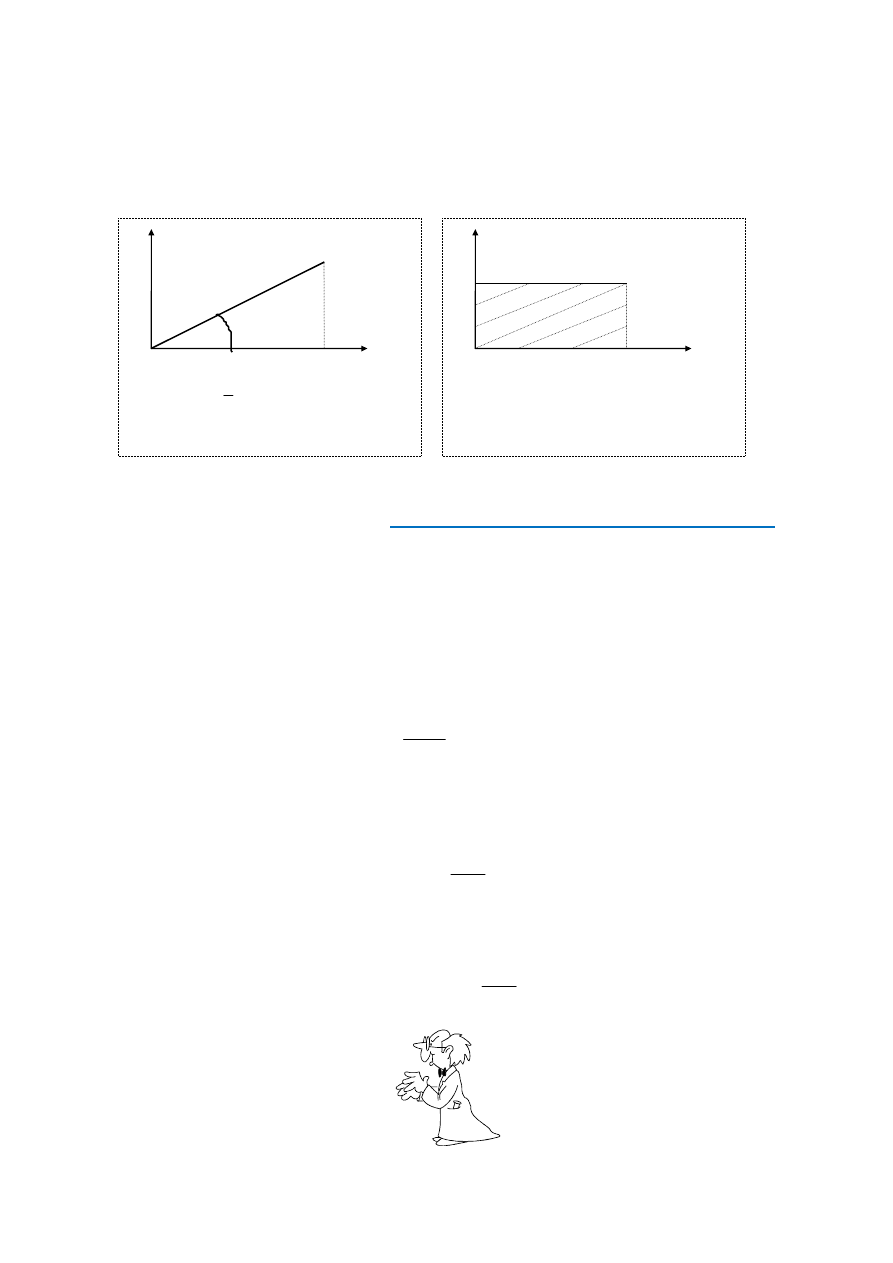
Ruchy punktów materialnych mogą być ilustrowane graficznie za pomocą wykresów.
Najczęściej są stosowane wykresy prędkości w układzie współrzędnych v,t oraz drogi w
układzie współrzędnych s,t co przedstawiono na rysunkach 2 i 3.

S v

α

s = v·t

0 t 0 t

v

s

t

==

= tg

α

Rys. 2 rys. 3

Temat: 11

Ruch jednostajnie przyspieszony.

1.

Dotychczas korzystaliśmy ze związku, który określał nam jaka jest prędkość, gdy znamy
przyspieszenie i czas. Często jednak chcemy znać położenie punktu materialnego, a nie
jego prędkość. Chcemy więc uzyskać równanie, które wyraża drogę s przez przyspiesze-
nie a i czas t, a także przez prędkość początkową v

0

.

2.

Drogę przebytą ruchem prostoliniowym jednostajnie zmiennym w czasie t można wyrazić
graficznie jako pole trapezu OABC (rys. 1) Pole to ma wartość:

(1) s

v

v

t

=

+

0

2

Podstawiając zamiast v wyrażenie

(2)

v

v

a t

= + ⋅

0

,

mamy

(3)

s

v t

a t

= ⋅ +

⋅

0

2

2

3.

Jeżeli w chwili rozpoczęcia obserwacji punkt materialny przebył już drogę s

0

, wtedy

równanie ruchu jednostajnie zmiennego prostoliniowego przyjmuje postać:

(4)

s

s

v t

a t

= + ⋅ +

⋅

0

0

2

2

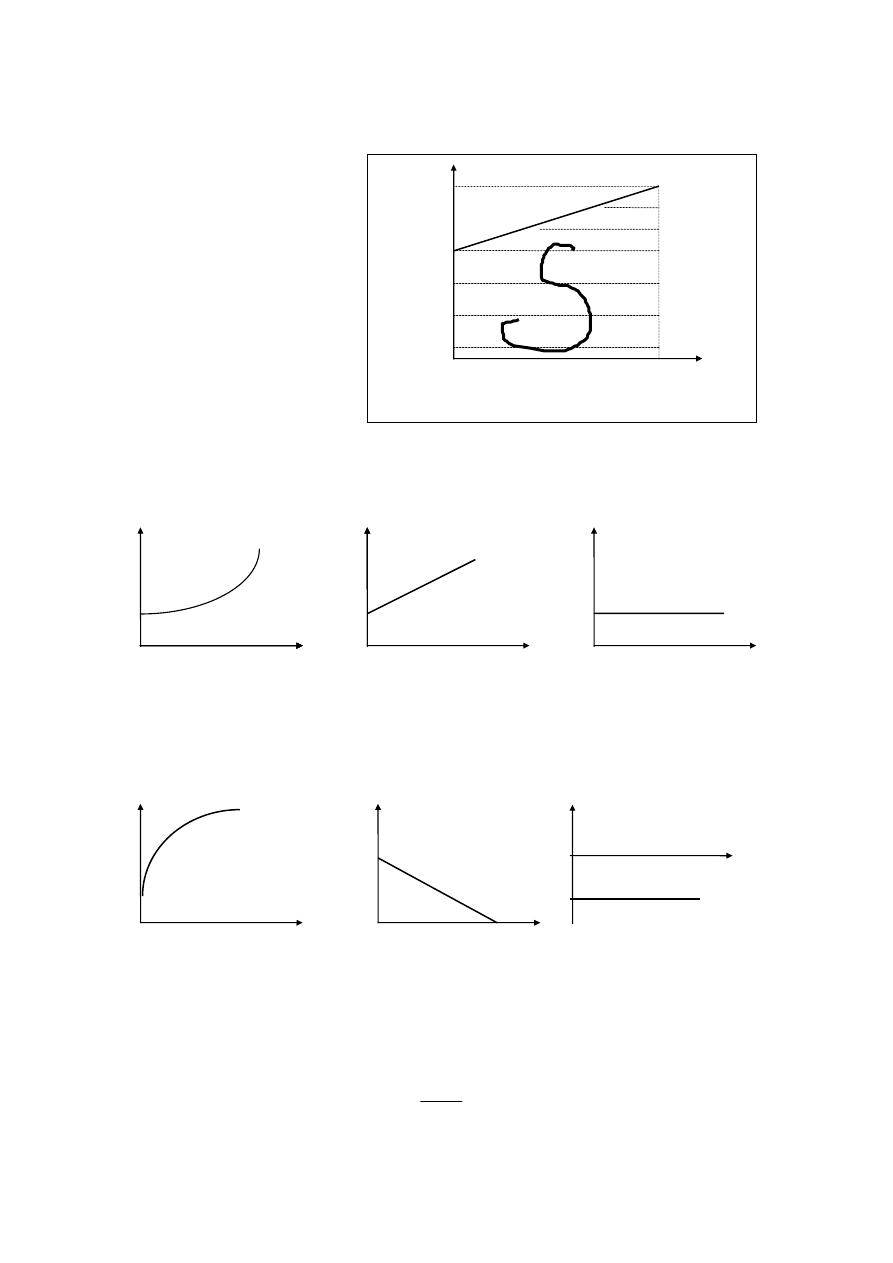
5

00503 Kinematyka D

TEORIA

Widzimy, że droga przebyta przez punkt materialny, który na początku był w spoczynku
i który ulega stałemu przyspieszeniu, rośnie jak kwadrat czasu.

v

v

0

Ruch jednostajnie przyspieszony,
to ruch, w którym w jednakowych
odstępach czasu punkt materialny
doznaje jednakowych przyrostów
prędkości.

0 t

Rys. 1

4.

Na rysunku 2 wykreślono równanie (4), na rysunku 3 - równanie (2), wreszcie na rysunku
4 przedstawiono zależność przyspieszenia od czasu w opisywanym rodzaju ruchu.

s v a


s

0

v

0

a

0

0 t 0 t 0 t

Rys. 2 Rys. 3 Rys. 4

O ile rysunki 2, 3 i 4 opisują graficznie

ruch jednostajnie przyspieszony, tak za pomocą

rysunków 5, 6 i 7 można zilustrować

ruch jednostajnie opóźniony:

s v a

v

0

0

t

s

0

-a

0 t 0 t

Rys. 5 Rys. 6 Rys. 7

5.

Związek między prędkością a odległością. Wygodnie jest nieraz znać zależność między
odległością i prędkością. Można to uzyskać rozwiązując równanie

(5)

a

v

v

t

=

−

0

6

00503 Kinematyka D

TEORIA

względem czasu t i podstawiając wynik do równania (4):

(6)

s

s

v

v

v

a

a

v

v

a

s

v

v

a

= + ⋅

−

+

⋅

−











= +

−

0

0

0

0

2

0

2

0

2

1

2

2

.

Zatem przy stałym a mamy:

(7)

v

v

a s

s

2

0

2

0

2

−

=

⋅ −

(

)

Często stawiać będziemy s

0

= 0

(8)

v

v

as

2

0

2

2

−

=

To warto wiedzieć:

⇒

ruch po linii prostej ze stałą prędkością opisuje równanie

s

s

v t

= + ⋅

0

,

⇒

*prędkość chwilowa wynosi

v

ds

dt

=

,

⇒

*przyspieszenie określamy według wzoru a

dv

dt

d s

dt

=

=

2

2

,

⇒

przy stałym przyspieszeniu, czyli a = const., mamy:

s

s

v t

at

o

= + ⋅ +

0

2

2

oraz

v

v

a s

s

2

0

2

0

2

−

=

⋅ −

(

) ,

7

00503 Kinematyka D

TEORIA

Temat:12 Wektorowy charakter prędkości i przyspieszenia.

1.

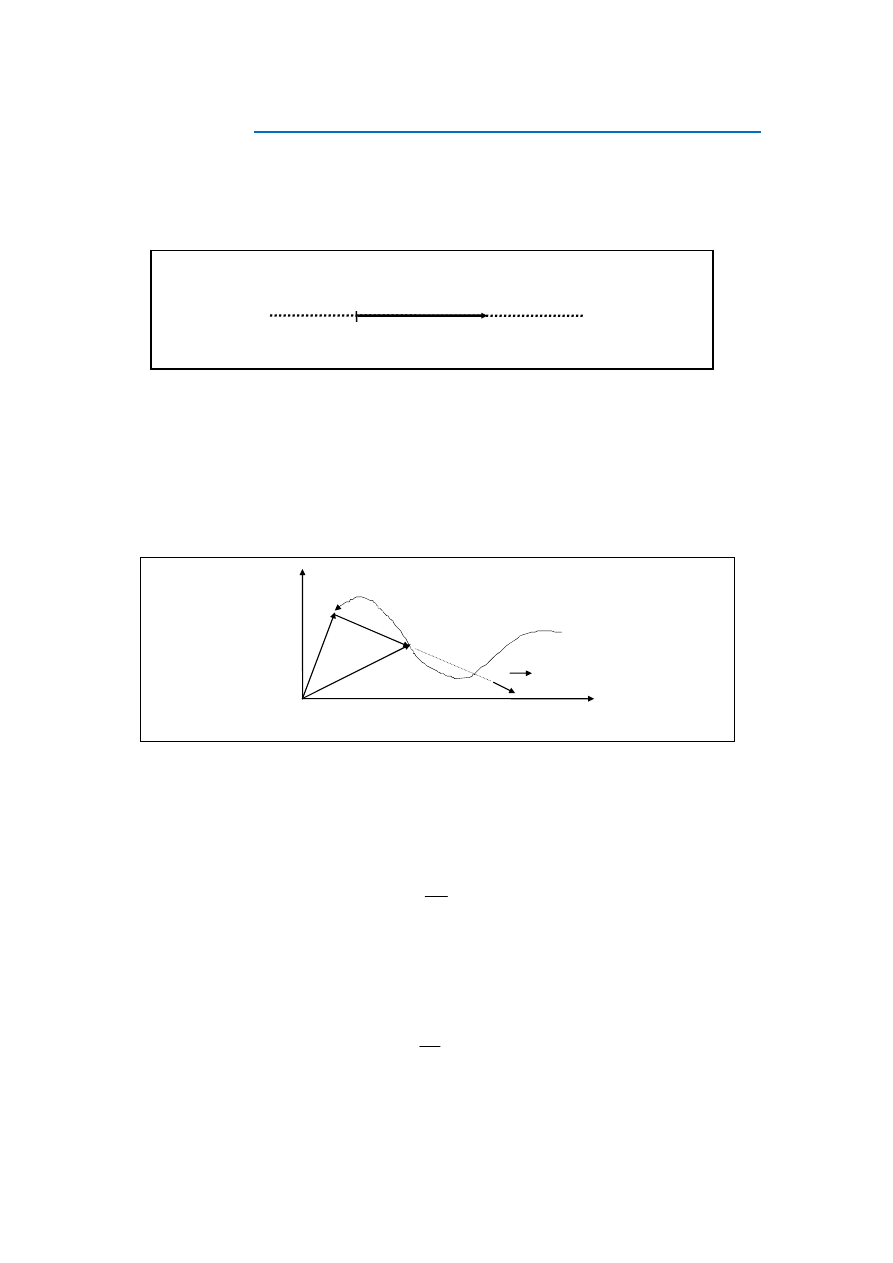
Wektor prędkości w ruchu prostoliniowym. Rozważając takie wielkości jak prędkość i
przyspieszenie należy pamiętać, że są to wielkości wektorowe. W ruchu prostoliniowym
prędkość jest oczywiście skierowana wzdłuż toru (rys. 1).

a A

r

v

B

Rys. 1

Prędkość w ruchu prostoliniowym jednostajnym jest stała zarówno co do wartości jak i

kierunku i zwrotu. W ruchu prostoliniowym zmiennym kierunek i zwrot wektora prędkości
jest stały, ale jego wartość ulega zmianie.

2.

Prędkość w ruchu krzywoliniowym. Stopniując trudności w rozważaniach kinematycz-
nych przejdziemy od ruchu prostoliniowego do krzywoliniowego płaskiego. Rozpatrzmy
ruch krzywoliniowy płaski przedstawiony na rysunku 2.

y

A

∆

s

B

r

r

1

Rys. 2

r

r

2

v

O

x

Niech wektory

r

r

1

i

r

r

2

przedstawiają promienie wodzące odpowiednio w chwilach t

1

i t

2.

Wektor

∆

r

r

r

r

r

r

= −

2

1

jest przyrostem wektora promienia wodzącego w czasie

∆

t = t

2

- t

1

.

Długość tego wektora tym mniej różni się od długości przebytej drogi s, im krótszy jest
czas obserwacji

∆

t (rys. 2). Wyrażenie:

(1)

r

r

v

r

t

=

∆

∆

przedstawia wektor prędkości średniej zgodny co do kierunku z wektorem

∆

r

r

.

Analogicznie jak poprzednio, wektor prędkości chwilowej w ruchu krzywoliniowym
( i w każdym innym ruchu) wyrażamy jako:

(2)

r

r

v

dr

dt

ch

=

8

00503 Kinematyka D

TEORIA

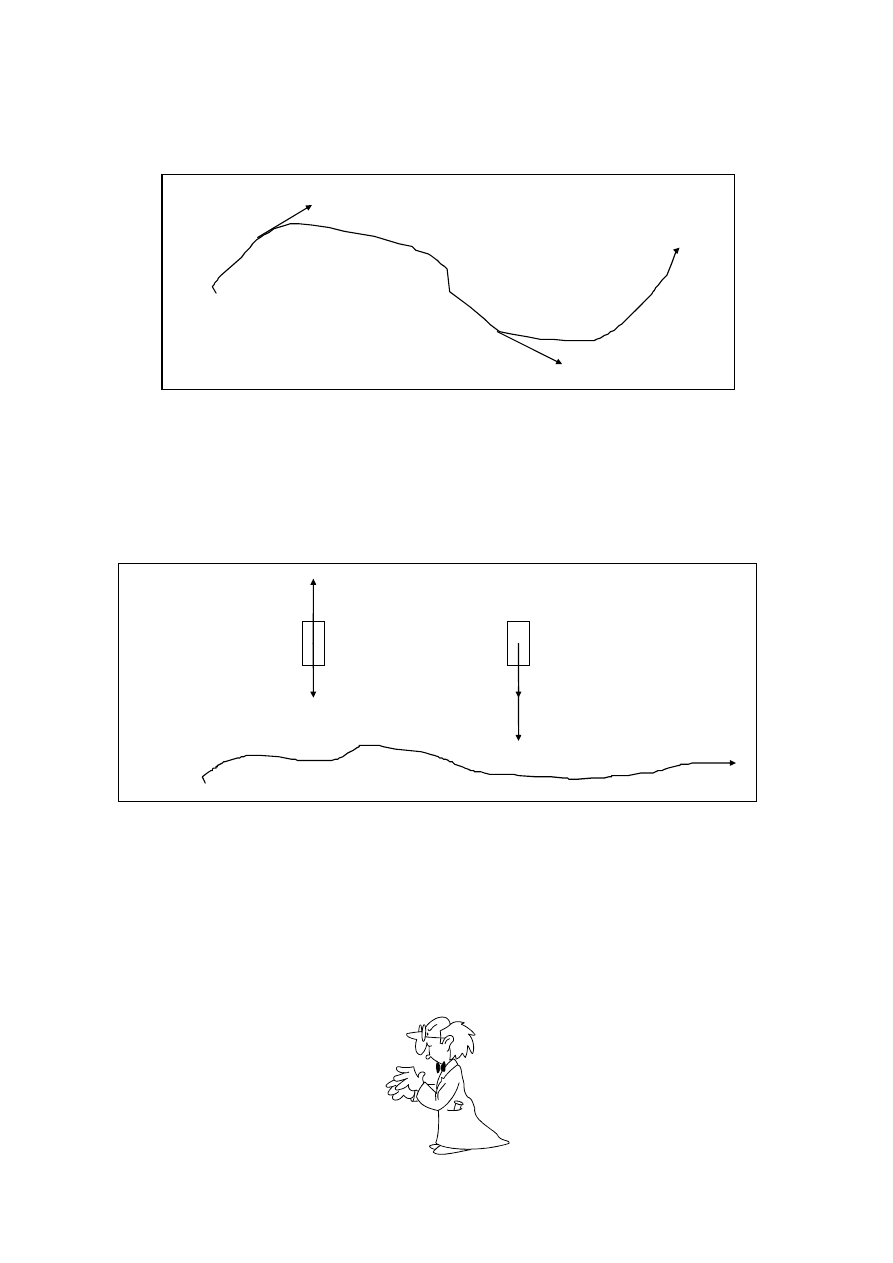
Zatem wektor prędkości chwilowej w danym punkcie toru jest wektorem stycznym z krzywą
określającą tor w tym punkcie (rys. 3).

r

v

1

Rys. 3

r

v

2

3.

Przyspieszenie w ruchu prostoliniowym. W ruchu prostoliniowym zmiennym występuje
przyspieszenie mające zwrot zgodny ze zwrotem prędkości w ruchu przyspieszonym, a
przeciwny w ruchu opóźnionym. Tak na przykład w rzucie pionowym do góry prędkość
jest stale skierowana pionowo w górę, a przyspieszenie (grawitacyjne) - stale pionowo w
dół. Podczas swobodnego spadku ciała prędkość i przyspieszenie są skierowane zgodnie
w dół (rys. 4).

r

v

a) b)
Ciało porusza się zaczyna spadać
pionowo do góry pionowo w dół.
i ...

r

g

r

v

r

g

Rys. 4

Powierzchnia Ziemi

4.

Przyspieszenie w ruchu krzywoliniowym. W ruchu krzywoliniowym jednostajnym dłu-
gości wektorów prędkości w różnych punktach toru są jednakowe, kierunki ich jednak
ciągle zmieniają się, czyli nawet w ruchu krzywoliniowym jednostajnym wektor prędko-
ś

ci nie jest stały.

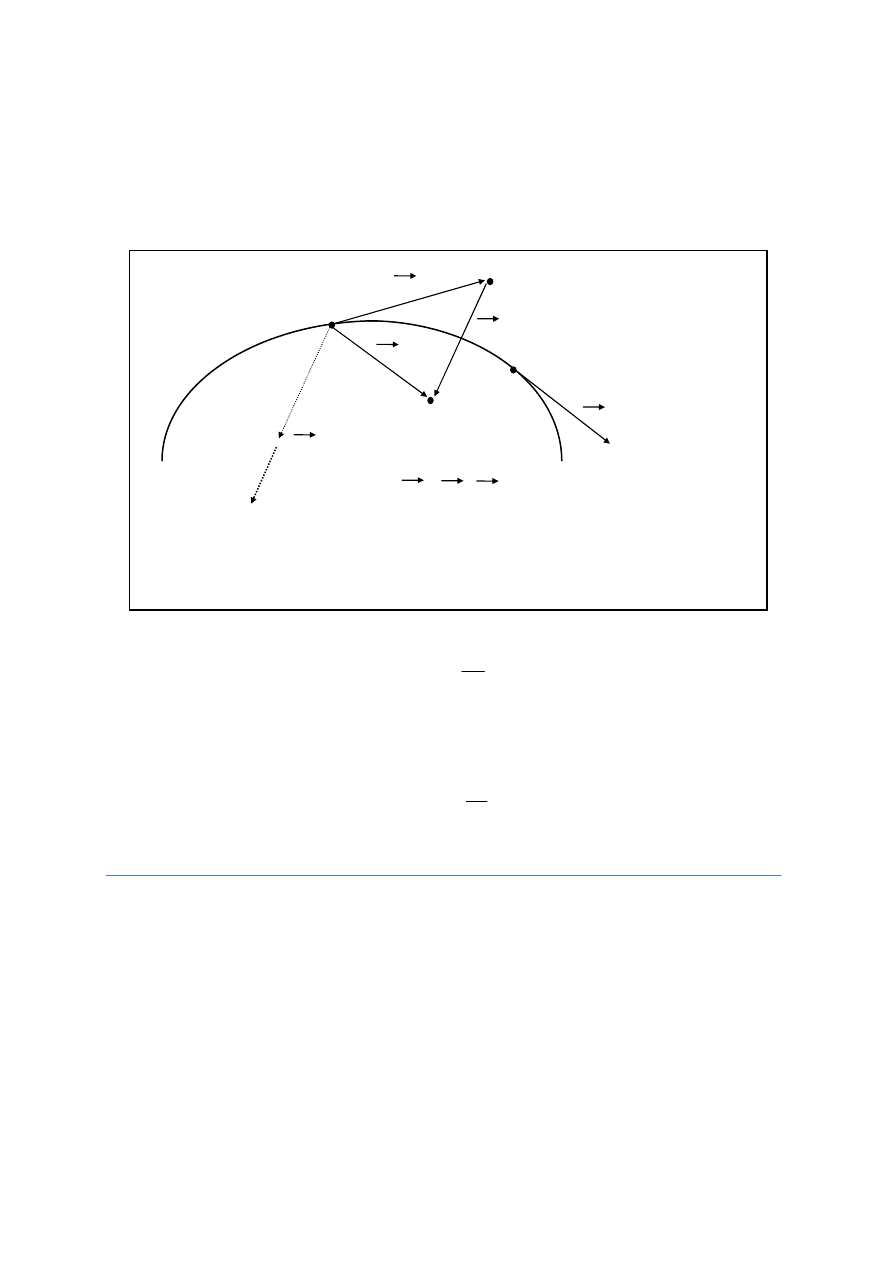
Zatem w każdym ruchu krzywoliniowym (jednostajnym i niejedno-

stajnym) można wyznaczyć wektorowy przyrost prędkości, a co za tym idzie przy-
spieszenie. Sposób określania graficznego przyspieszenia pokazuje rysunek 5. Widać, że
wektor przyspieszenia średniego różni się od przyspieszenia chwilowego zarówno warto-
ś

cią, kierunkiem, jak i zwrotem.

9

00503 Kinematyka D

TEORIA

Wniosek:

Prędkość stała oznacza, że przyspieszenie jest równe zeru, lecz stała wartość

prędkości może lub nie odpowiadać przyspieszeniu równemu zeru .Prędkość ciała poruszają-
cego się po krzywej ze stałą co do wartości prędkością zmienia jednak kierunek i zwrot, a
więc ma ono przyspieszenie. Działanie przyspieszenia odczuwamy, np. gdy samochód mija
szybko zakręt.

v

1

A

∆

v

v

2

B

v

2

∆

v

r

a

∆

v = v

2

- v

1

Rys. 5

Wyrażenie:

(3)

r

r

a

v

t

=

∆

∆

przedstawia wektor przyspieszenia średniego zgodny co do kierunku z wektorem

∆

r

v

.

Z kolei wektor przyspieszenia chwilowego wyrazimy za pomocą wzoru (4):

(4)

r

r

a

dv

dt

=

Koniec

10

00503 Kinematyka D

TEORIA

Notatki