1

00501 Kinematyka D

TEORIA

00501

Podstawy kinematyki D

Część 1

Przedmiot fizyki i metody badań.

Wielkości fizyczne i ich miary. Wektory.

Matematyka w fizyce.

Instrukcja dla zdającego

1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 10
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Kwiecień

ROK 2008

Dane osobowe właściciela arkusza

2

00501 Kinematyka D

TEORIA

Temat: 1

Przedmiot fizyki i metody badań.

1.

Fizyka należy do nauk przyrodniczych. Przedmiotem jej badań są zjawiska zachodzące w przyrodzie
martwej, celem - poznanie w sposób możliwie najbardziej wszechstronny praw rządzących tymi zjawi-
skami. Wśród podstawowych bodźców, które przyczyniły się do rozwoju fizyki wymienić należy
przemożny instynkt poznawania świata, jak również - a może przede wszystkim - praktyczne potrzeby
ludzi. Warto na wstępie podkreślić swoiste powiązanie fizyki z techniką, można tu mówić o sprzężeniu
zwrotnym: potrzeby techniki prowadzą do odkryć fizycznych , a te z kolei niejednokrotnie umożliwiają
dalsze osiągnięcia techniczne. O powiązaniu fizyki z innymi dziedzinami nauki często mówią same na-
zwy : geofizyka, biofizyka, chemia fizyczna, astrofizyka itp. Fizyka jest nauką ścisłą: prawa fizycz-
ne rządzące zjawiskami zachodzącymi w otaczającym nas świecie podawane są w postaci matema-
tycznych zależności. W fizyce doświadczalnej do poznania tych praw prowadzą obserwacje i do-
ś

wiadczenia, w fizyce teoretycznej - odpowiednio interpretowane wyniki analizy matematycznej.

2.

Stosowanie w fizyce naukowych metod badawczych o charakterze doświadczalnym datuje się od cza-
sów Galileusza (wiek XVI ). W przeciwieństwie do metod obserwacyjnych, w których badacz tylko re-
jestruje wyniki obserwacji, w metodach badawczych rola badacza jest czynna. Stwarza on mianowicie
określone warunki decydujące o przebiegu zjawiska, wywołuje jego powstanie, wykonuje pomiary,
powtarza takie badania wielokrotnie i korzystając ze stałości przebiegu zjawiska w danych warunkach
- zestawia wyniki pomiarów i z takich zestawień wyciąga wnioski formułując je początkowo w posta-
ci hipotez. Jeśli liczne badania potwierdzą słuszność hipotez, często przyjmują one postać praw lub
teorii ( na przykład: prawo ciążenia powszechnego, prawa Kirchhoffa, teoria falowa i kwantowa świa-
tła, teoria względności). Prawa o podstawowym znaczeniu niekiedy są nazywane zasadami (np. zasada
zachowania energii, zasada zachowania pędu). W wielu przypadkach prawa fizyczne ustalane są do
ciał wyidealizowanych, modelowych. Wprowadzane są takie pojęcia jak ciało doskonale sztywne, do-
skonale sprężyste, punkt materialny, gaz doskonały. Prawa fizyczne wyprowadzane w odniesieniu do
ciał modelowych mają uproszczoną postać matematyczną. Oczywiście są one tylko w przybliżeniu
spełnione dla ciał rzeczywistych, lecz niezależnie od tego w zastosowaniach technicznych często od-
dają cenne usługi zapewniając wymagany stopień dokładności.

3.

Rozwój nauki - ulepszanie metod badawczych i odkrywanie nowych zjawisk - prowadzi często do
stwierdzenia, że poprzednio ustalone prawa nie są dokładne, że wymagają zastąpienia nowymi prawa-
mi, lub też wprowadzenia granicy stosowalności. Tak np. znane ogólnie równanie wyrażające matema-
tycznie II zasadę dynamiki F = ma, gdzie F oznacza siłę, m. - masę, a - przyspieszenie, jest równa-
niem przybliżonym spełnionym tym dokładniej, im mniejsza jest prędkość poruszającego się ciała.
Gdy bowiem prędkość zbliża się do prędkości światła (co może występować na przykład w świecie
mikrocząstek) masa coraz szybciej rośnie: zamiast mechaniki niutonowskiej należy stosować mechani-
kę relatywistyczną.

O tym warto wiedzieć !!!

A)

Fizyka jest nauką przyrodniczą. Przedmiotem jej badań są zjawiska zachodzące w przyrodzie
martwej, celem - poznanie praw rządzących tymi zjawiskami.

B)

Fizyka jest nauką ścisłą: prawa fizyczne rządzące zjawiskami zachodzącymi w otaczającym
nas świecie podane są w postaci matematycznych zależności.

C)

Metody badań: a) obserwacyjne, b) doświadczalne.

D)

W celu uproszczenia matematycznej postaci praw - wprowadza się ciała wyidealizowane
(modelowe).

E)

Poznawane prawa są prawami obowiązującymi na danym etapie rozwoju nauki.

3

00501 Kinematyka D

TEORIA

Temat: 2 Wielkości fizyczne. Układy jednostek. Układ SI.

1.

Mianem wielkości fizycznej (albo wielkości mierzalnej) metrologia obejmuje każdą mie-
rzalną cechę zjawiska lub ciała. Przy stosowaniu metody doświadczalnej w badaniach fi-
zycznych poszczególne wielkości mierzone są z większą lub mniejszą dokładnością,
zawsze jednak z pewnym błędem. Wyniki pomiarów powinny być podawane w ogólnie
przyjętych dokładnie określonych jednostkach

2.

Dokonując przeglądu jednostek służących do wyrażania powszechnie znanych wielkości
fizycznych, np. takich jak długość, masa, ciśnienie, łatwo można się przekonać, że w tej
dziedzinie istnieje jeszcze duża dowolność. Tak np. w Europie do wyrażania długości sto-
suje się około 20 różnych jednostek, do wyrażania masy - jeszcze więcej. W wyniku
braku unifikacji powstawały w przeszłości różne układy jednostek. Dla przykładu: CGS,
MKS, MKSA, elektrostatyczny CGS, elektromagnetyczny CGS, techniczny i inne. Wzory
definiujące poszczególne wielkości fizyczne miały różną postać, a współczynniki i stałe
fizyczne różne wartości liczbowe. Utrudniało to bardzo wymianę informacji oraz szybkie
zapoznawanie się z literaturą i dokumentacją.

3.

Wielkim krokiem naprzód w dziedzinie unifikacji jednostek miar było zaproponowanie w
1960 roku przez XI Konferencję Generalną Miar jednolitego międzynarodowego układu
jednostek miar zwanego układem SI (Systeme International d’Unites) i zalecenie jego sto-
sowania. Zalety tego układu wiążą się nie tylko z jego międzynarodowym charakterem.
Układ ten jest tak pomyślany, że może być stosowany do wyrażania prawie wszystkich
wielkości w różnych dziedzinach wiedzy: ma on zatem ważną cechę uniwersalności.

4.

Układ SI opiera się na siedmiu wielkościach podstawowych i dwóch uzupełniających.
Układ SI ma dużo wspólnego z szeroko stosowanymi dawniej układami CGS i MKSA.
Układ jednostek mechanicznych opiera się na tych samych co układ SI wielkościach me-
chanicznych, a mianowicie na długości, masie i czasie. Inne są jednak w obu układach
jednostki podstawowe. Jeszcze więcej ze sobą mają wspólnego układy SI i MKSA. Układ
MKSA pokrywa się całkowicie z układem SI w dziedzinie podstawowych wielkości me-
chanicznych i elektrycznych oraz ich podstawowych jednostek. Wielkości podstawowe i
uzupełniające układu SI nazywamy wielkościami bazowymi.

Tabela wielkości podstawowych układu SI:

Wielkości fizyczne

Nazwa

jednostki

Oznaczenie

jednostki

Masa

kilogram

[kg]

Długość

metr

[m]

Czas

sekunda

[s]

Natężenie prądu elektrycznego

amper

[A]

Temperatura termodynamiczna

kelwin

[K]

Ś

wiatłość

kandela

[cd]

Liczność materii (ilość substancji)

mol

[mol]

4

00501 Kinematyka D

TEORIA

Tabela wielkości uzupełniających układu SI:

Wielkości fizyczne

Nazwa jednostki

Oznaczenie

jednostki

Kąt płaski

radian

rad

Kąt bryłowy

steradian

sr

5.

W układzie SI, jak zresztą w każdym układzie jednostek, obok wielkości bazowych wystę-
pują wielkości pochodne. Wielkości pochodne są określane na podstawie równań defini-
cyjnych bezpośrednio lub pośrednio za pomocą wielkości bazowych danego układu.

Przykłady:

Prędkość v definiujemy bezpośrednio za pomocą długości (drogi) s i czasu t:

v

s
t

=

Siłę definiujemy pośrednio, gdyż prędkość jest wielkością pochodną:

F

ma

m v v

t t

o

=

=

−

−

(

)

0

Podobnie postępujemy z jednostkami:

[ ]

v

m

s

=







oraz

[ ]

[ ]

[

]

[ ]

F

kg m s

N

kg

s

m

s

=

= ⋅ ⋅

=

⋅

−

2

Jednostki pochodne układu SI można podzielić na takie, które nie mają nazw specjalnych (np.
jednostka prędkości) oraz takie, którym nadano nazwy specjalne (np. jednostkę siły nazywa-
my niutonem, jednostkę pracy - dżulem).

6.

Tabela przedrostków jednostek metrycznych:

Przedrostek

Skrót

Potęga

dziesięciu

tera

T

10

12

giga

G

10

9

mega

M

10

6

kilo

K

10

3

centy

C

10

2

−

mili

m

10

3

−

mikro

µ

10

6

−

nano

n

10

9

−

piko

p

10

12

−

femto

f

10

15

−

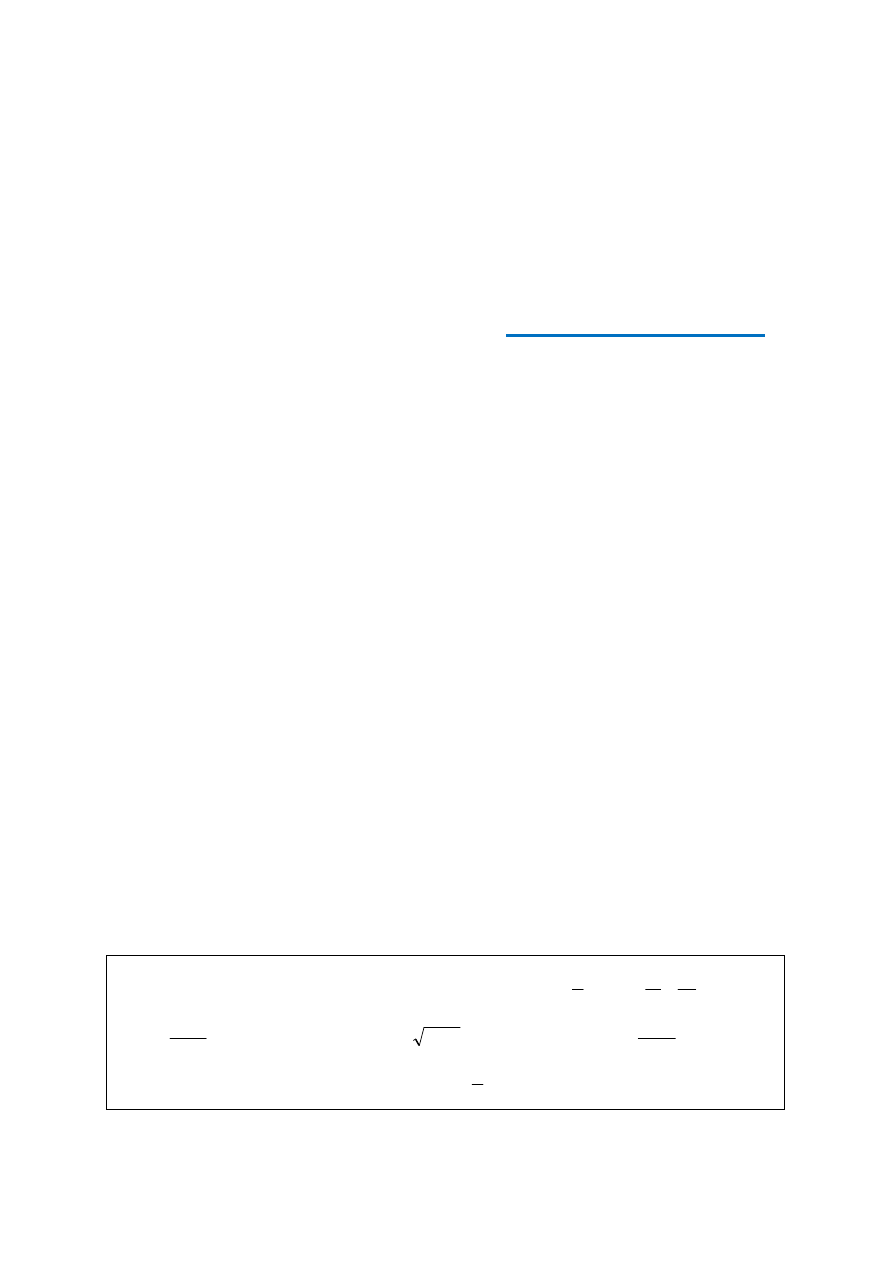
5

00501 Kinematyka D

TEORIA

Ćwiczenia:

1.

Wyraź wymienione jednostki za pomocą jednostek bazowych układu SI:

1 niuton, 1 dżul, 1 farad, 1 tesla, 1 wat.

2.

Podaj 8 nazw jednostek pochodzących od nazwisk zasłużonych badaczy. Czym różni się
pisownia tych jednostek od pisowni nazwisk uczonych?

Temat: 3

Matematyka w fizyce .

1.

Głównym celem fizyki jest poszukiwanie i poznawanie podstawowych praw przyrody, od
których zależą wszystkie zjawiska fizyczne. Historia nauki wykazuje postęp do coraz to
głębszych i głębszych poziomów pojmowania. Na każdym z kolejnych poziomów pod-
stawowe prawa i teorie stają się prostsze i jest ich coraz mniej. Na przykład, liczba cząstek
fundamentalnych i oddziaływań na ogół zmniejszała się w miarę upływu czasu. To histo-
ryczne spostrzeżenie, że im bardziej zbliżamy się do prawdy , tym prostsze stają się pod-
stawowe prawa, zostało sformułowane w XIV wieku przez filozofa Wilhelma Ockhama i
nazywa się brzytwą Ockhama.

2.

Uważa się, że fizyka posługuje się trudną matematyką wyższą. Na szczęście tak nie jest,
jeśli chodzi o prawa podstawowe. Działa tu brzytwa Ockhama: im bardziej podstawowe
prawo, tym jest ono prostsze pojęciowo i matematycznie . Trudniejsza matematyka
wchodzi w grę wtedy, kiedy próbujemy policzyć coś, co nie jest podstawowe, jak na
przykład problem trzech ciał ( ruch trzech wzajemnie oddziałujących ciał). Problem
trzech ciał nie jest podstawowy, gdyż w istocie jest superpozycją trzech wzajemnie po-
wiązanych problemów dwóch ciał. Przed kilkuset laty Issac Newton rozwiązał naprawdę
podstawowy problem - problem orbit dwóch ciał oddziałujących ze sobą siłą odwrotnie
proporcjonalną do kwadratu odległości. Problem dwóch ciał w astronomii można rozwią-
zać stosując matematykę elementarną, ale problem trzech ciał wymaga bardzo dobrego
komputera.

3.

Ucząc się fizyki używamy prostej algebry, geometrii i elementów trygonometrii (oczywi-
ś

cie w szkole średniej). Stopniowo pojawiać się będzie rachunek różniczkowy i całkowy,

przydatne będą również pochodne funkcji sinus i kosinus.

4.

Poniżej lista działań, w których pojawiają się najczęściej błędy uczniowskie:

Ćwiczenie: 1

a)

(

)

?

a

b

+

=

2

e) podziel liczbę 4 przez

1

2

h)

A

B

X

Y

+

=

?

b)

1

a

b

+

=

? f) 16ab

=

?

i)

10

10

10

5

−

−

=

?

c)

podaj połowę z liczby 10

10

−

g) podaj

1

2

z liczby 10

8

−

6

00501 Kinematyka D

TEORIA

5. Szczególnie użyteczna jest znajomość poniższych tożsamości:

a)

sin

cos

2

2

1

α

α

+

=

,

b)

2

2

sin

cos

sin

α

α

α

=

,

c)

y = sin x, wtedy x = arcsin y ,

d)

x

x

x

x

x

n

i

i

n

1

2

3

1

+ + + ⋅⋅⋅+

=

=

∑

.

6.

Wielkości występujące w fizyce są w większości albo znacznie większe od 1 albo znacznie
mniejsze od 1. Dla wygody przyjęło się ogólnie zapisywać daną wartość, wszystko jedno
czy bardzo dużą czy bardzo małą, jako liczbę między 1 a 10 (nazywaną mantysą) pomno-
ż

oną przez odpowiednią potęgę dziesięciu. Taki zapis jest ogólnie przyjęty.

Na przykład masa elektronu wynosi:

m

kg

e

=

⋅

−

9 11 10

31

,

mantysą jest tu liczba 9,11, wykładnikiem potęgi

liczba - 31

.

Masa Słońca wynosi:

m

kg

S

=

⋅

1 99 10

30

,

mantysa teraz wynosi 1,99, wykładnik: +30

.

Widać, że zakres wartości mas wynosi 10

60

, w fizyce odległości rozciągają się na podob-

ny zakres.
Proponowany formalizm matematyczny daje bardziej czytelny zapis wielkości fizycznych
i zmniejsza możliwość popełnienia błędu rachunkowego.

Ćwiczenie: 2

a)

Wyznacz z poniższego równania parametr a:

a b

c d

fgh

+

+

=

b)

Oblicz sumę:

1

1

1

A

B

C

+ + =

?

7

00501 Kinematyka D

TEORIA

c) Z poniższego wzoru wyznacz parametr r:

F

k

Q Q

r

=

⋅

1

2

2

d)

Zastosuj skróconą notację:

b

b

b

b

b

b

b

1

2

3

4

5

6

+ + + + + =

e)

Zastosuj skróconą notację:

m = 500[ton],
l = 0,00000016[m],

F = 2000[kN].

Nie zapomnij wyrazić powyższych jednostek w układzie SI.

f)

Oblicz wyrażenie dla

α

=

30

0

:

2 sin

cos

?

α

α

=

Temat: 4

Podstawowe wiadomości o wektorach.

1.

Wielkości fizyczne dzielimy na wielkości kierunkowe (wektorowe) i wielkości
bezkierunkowe (skalarne). Podczas opisywania wielkości wektorowych powinna
być podawana ich bezwzględna wartość liczbowa, zwana też modułem, kierunek,
zwrot i punkt przyłożenia.

2.

Wielkość wektorową można przedstawić geometrycznie jako odcinek skierowany,
tj. odcinek leżący na określonej prostej, mający określony początek i koniec (a
więc określony zwrot), jak również określoną długość wyrażającą w pewnej skali
bezwzględną wartość danego wektora (rys. 1).

A

r

a

B

Rys. 1

początek koniec

8

00501 Kinematyka D

TEORIA

3.

Skalarami są wielkości, których opis ogranicza się do podania wartości
liczbowej. Do skalarów zaliczamy np. czas, temperaturę, pracę, energię, ładunek
elektryczny itp.

4.

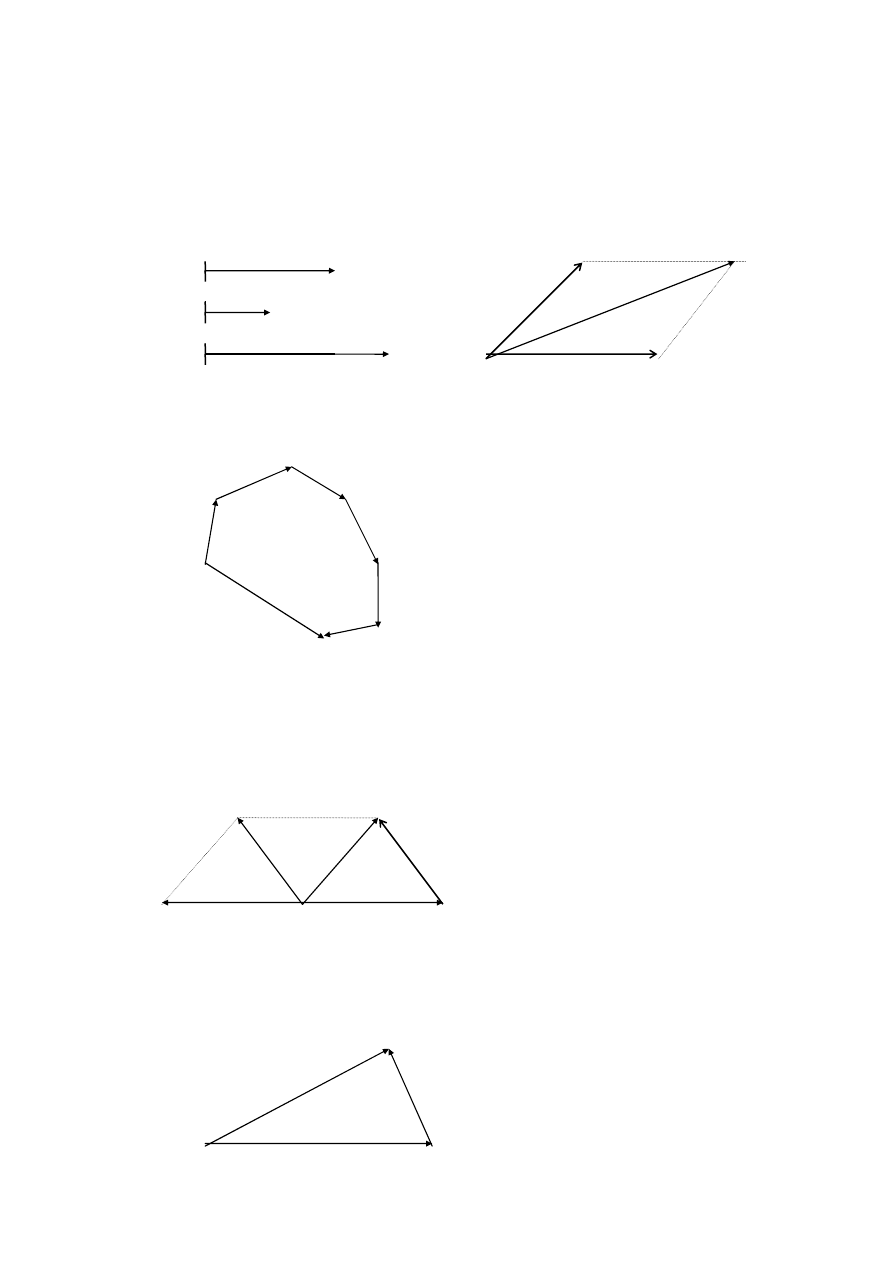
Dodawanie wektorów.

Poniższe rysunki ilustrują graficzne dodawanie wektorów:

r

a

r

b

r

a

r

r

a

b

+

r

r

a

b

+

r

b

Rys. 2 Rys. 3

r

a

2

r

a

3

r

r

r

r

r

r

r

a

a

a

a

a

a

a

1

2

3

4

5

6

+ + + + + =

r

a

1

r

a

4

r

a

5

r

a

r

a

6

Rys. 4

5.

Odejmowanie wektorów przedstawiono na rysunkach 5 i 6, przy czym metoda pokazana na
rys. 6 nazywa się metodą trójkąta.

r

r

a

b

−

r

a

r

r

a

b

−

−

r

b

r

b

Rys. 5

Rysunek 5 tłumaczy nam, że odjąć od wektora

r

a

wektor

r

b

, to znaczy dodać do wektora

r

a

wektor przeciwny do

r

b

, czyli wektor

−

r

b

r

a

r

r

a

b

−

r

b

Rys. 6 Metoda trójkąta.

9

00501 Kinematyka D

TEORIA

6.

W wyniku mnożenia wektora

r

a

przez liczbę otrzymujemy nowy wektor

na

r

o wartości

liczbowej n razy powiększonej i o zwrocie zgodnym lub przeciwnym do wektora

r

a

zależnie

od tego, czy liczba n jest dodatnia, czy też ujemna

Przykład: W ruchu jednostajnym zachodzi równość.

∆

∆

r

r

r

v

t

= ⋅

Zatem mnożenie wektora (w tym przypadku prędkości) przez skalar (czas) daje w wyniku złoże-
nia zupełnie inny wektor (przesunięcie), a zatem inny mamy tu efekt od mnożenia wektora przez
liczbę.

Koniec

10

00501 Kinematyka D

TEORIA

Notatki: