1

00508 Kinematyka bryły sztywnej D

TEORIA

00508

Kinematyka bryły sztywnej D

Określenie pojęcia i ruchu.

Kinematyczne wielkości kątowe i ich związek z

w wielkościami liniowymi.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 6
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

śyczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Maj

ROK 2008

Dane osobowe właściciela arkusza

2

00508 Kinematyka bryły sztywnej D

TEORIA

Temat: 36

Określenie pojęcia i ruchu bryły sztywnej.

1.

Dotychczas zajmowaliśmy się jedynie kinematyką i dynamiką punktu materialnego.
Obecnie zajmiemy się problemami bardziej złożonymi i bardziej zbliżonymi do stanu rze-
czywistego. Aby jednak nadmiernie nie komplikować sytuacji będziemy rozważać tylko
ciało sztywne (bryłę sztywną).

2.

Bryła sztywna, to ciało, które pod działaniem dowolnie wielkich sił nie ulega ani od-
kształceniu postaci (zmiana kształtu) ani odkształceniu objętości.

Zatem odległość dwóch dowolnych punktów bryły sztywnej pozostaje niezmienna.
Bryła sztywna jest tworem wyidealizowanym o własnościach odbiegających od własności
ciał spotykanych w praktyce. Podobnie jak pojęcie punktu materialnego, tak i pojęcie bry-
ły sztywnej jest pewnego rodzaju abstrakcją (modelem). Pozwala ono na skupienie uwagi
tylko na własnościach ciała, które są istotne dla przebiegu ruchu, a zapomnieniu o własno-
ś

ciach nieistotnych na naszym etapie badań (np. o niewielkich deformacjach ciał stałych

pod wpływem przyłożonych sił).
Bryła sztywna stanowi szczególny rodzaj układu punktów materialnych, w którym odległo-
ś

ci między punktami są stałe.

3.

Zatem położenia poszczególnych punktów bryły sztywnej są od siebie zależne. Wystarczy
podać położenie trzech punktów nie leżących na jednej prostej, aby w zupełności określić
położenie pozostałych punktów bryły:

a)

przy ustalonym jednym punkcie bryła może obracać się wokół tego punktu,

b)

przy ustalonych dwóch punktach bryła może obracać się wokół prostej łączącej te
punkty,

c)

ustalenie trzech niewspółliniowych punktów wyznacza już jednoznacznie położenie
bryły.

4.

Jak dotychczas było stwierdzone, bryła sztywna jest zbiorem wielkiej liczby punktów
materialnych znajdujących się w stałych odległościach wzajemnych. Fakt ten powoduje,
ż

e ruch bryły sztywnej może przybierać bardziej skomplikowane formy niż ruch punktu

materialnego. Dowolny, nawet bardzo skomplikowany ruch bryły sztywnej można złożyć
z ruchów prostszych, które będą albo ruchami postępowymi albo ruchami obrotowymi.

5.

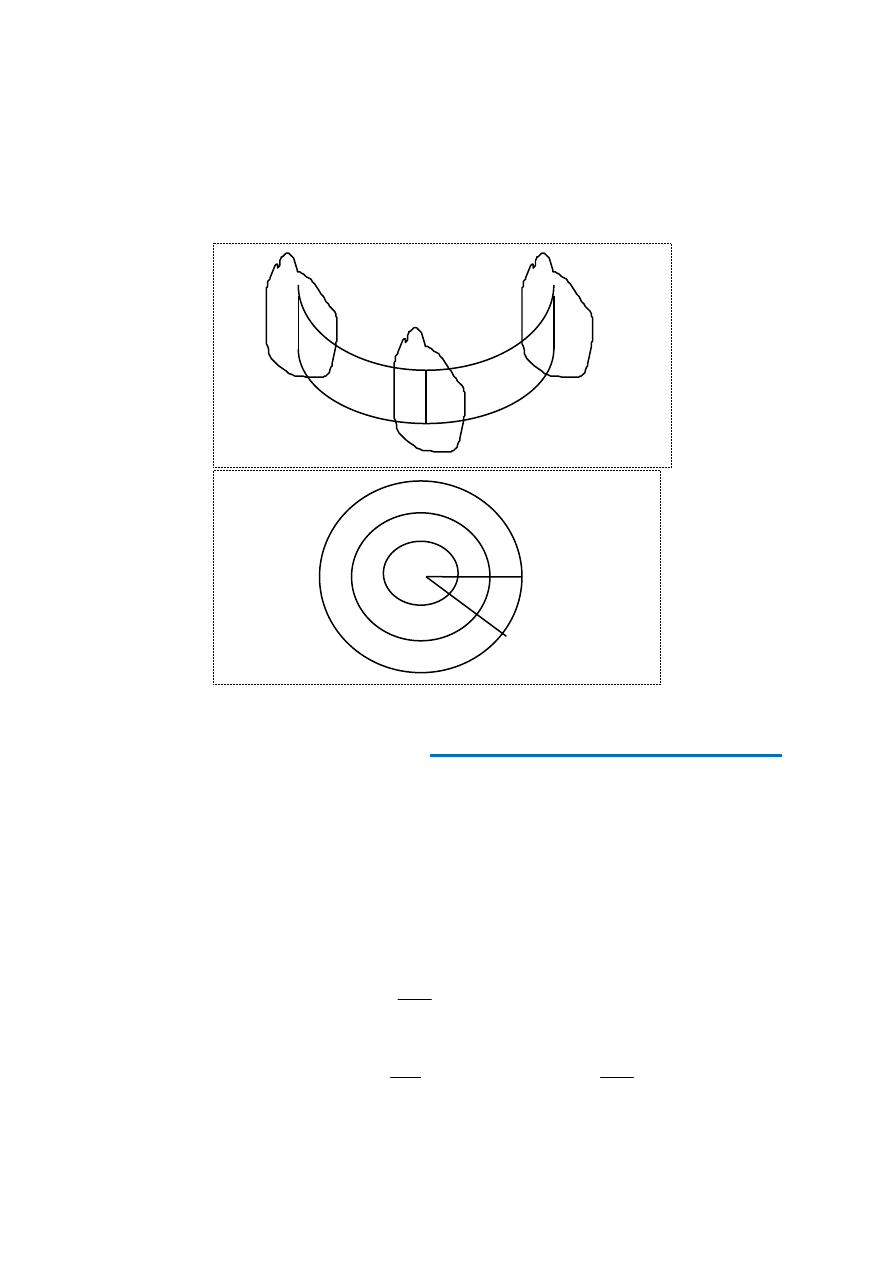
Ruch postępowy bryły sztywnej jest to taki ruch, przy którym dowolny odcinek łączący
dwa punkty bryły sztywnej, np. A i B (rys. 1),zachowuje stale do siebie położenie równo-
ległe. Wszystkie punkty bryły sztywnej, odbywającej ruch postępowy, zakreślają drogi
równe i mają jednakowe prędkości oraz przyspieszenia. W związku z tym badanie ruchu
postępowego bryły sztywnej sprowadza się do badania jakiegokolwiek wybranego punktu
bryły, a do tego wystarczają metody analizowane w kinematyce punktu materialnego.
Ruch postępowy nie musi odbywać się po linii prostej. Ruch samochodu na zakręcie sta-
nowi również przykład ruchu postępowego, tzw. koło diabelskie znane z wesołego mia-
steczka to kolejny przykład ruchu postępowego.

6.

Ruchem obrotowym bryły nazywamy taki ruch, w którym punkty materialne tworzące tę
bryłę poruszają się po okręgach współśrodkowych, których środki leżą na jednej prostej
zwanej osią obrotu. Oś obrotu nie bierze udziału w ruchu obrotowym ! Przykład ruch ob-
rotowego pokazano na rys. 2. Ważną cechą ruchu obrotowego jest to, że punkty material-
ne obracającej się bryły, leżące w różnych odległościach od osi obrotu, w jednakowym
czasie zakreślają łuki okręgów o różnej długości. Punkty te mają więc różne prędkości li-

3

00508 Kinematyka bryły sztywnej D

TEORIA

niowe. Jednocześnie promienie wodzące łączące wszystkie punkty bryły ze środkami za-
kreślanych okręgów obracają się w tym samym czasie o taki sam kąt

∆α

. Gdyby tak nie

było zmieniałaby się odległość między różnymi punktami bryły, co byłoby sprzeczne z
założeniem sztywności bryły. Te dwie cechy ruchu obrotowego powodują, że przy bada-
niu kinematycznych właściwości ruchu obrotowego bryły posługujemy się wyłącznie ki-
nematycznymi wielkościami kątowymi, a nie wielkościami liniowymi

A A’’

B B’’

A’

Rys. 1 B’

A A’ A’’
0
B
B’
B’’
Rys. 2

Temat: 37

Kinematyczne wielkości kątowe.

1.

Do kinematycznych wielkości kątowych należą: kąt obrotu (zwany drogą kątową)

α

, prędkość

kątowa

ω

i przyspieszenie kątowe

ε

.

2.

Kąt obrotu

α

zakreślony w czasie obrotu bryły przez promień leżący w płaszczyźnie prosto-

padłej do osi obrotu i łączący dowolny punkt bryły z tą osią odgrywa przy opisie ruchu obro-
towego rolę drogi. Dlatego też nazywa się go często drogą kątową bryły.

3.

Stosunek przyrostu drogi kątowej do czasu nazywamy prędkością kątową. Można przy tym
wyróżnić średnią prędkość kątową:

(1)

ω

α

ś

r

t

=

∆

∆

oraz *chwilową prędkość kątową:

(2)

ω

α

ω

α

=

=

→

d

dt

czyli

t

t

,

lim

∆

∆

∆

0

4

00508 Kinematyka bryły sztywnej D

TEORIA

4.

W podobny sposób można również zdefiniować przyspieszenie kątowe. Wartość średniego
przyspieszenia kątowego określa wzór:

(3)

ε

ω

ś

r

t

=

∆

∆

Natomiast *wartość chwilową:

(4)

ε

ω

=

d

dt

5.

Zdefiniowane powyżej kinematyczne wielkości kątowe mają następujące jednostki w układzie
SI:

droga kątowa [

α

] = radian [rad]

prędkość kątowa [

ω

] = radian na sekundę

rad

s







przyspieszenie kątowe [

ε

] = radian na sekundę do kwadratu

rad

s

2







6.

Kinematyczne wielkości kątowe są wielkościami wektorowymi. Są one wszystkie skierowane
prostopadle do płaszczyzny obrotu wyznaczonej przez tory punktów materialnych obracającej
się bryły.

Zwrot tych wektorów można określić za pomocą reguły śruby prawoskrętnej: jeżeli prawo-
skrętną śrubę będziemy wkręcać zgodnie z kierunkiem obiegu punktów materialnych bryły po
okręgach wokół osi obrotu, to powstający w wyniku tego przesuw śruby będzie zgodny ze
zwrotem wektorów drogi kątowej i prędkości kątowej tej bryły, a gdy ruch bryły będzie ru-
chem przyspieszonym (wartość prędkości kątowej będzie wzrastała w miarę upływu czasu), to
również ze zwrotem przyspieszenia kątowego.

7.

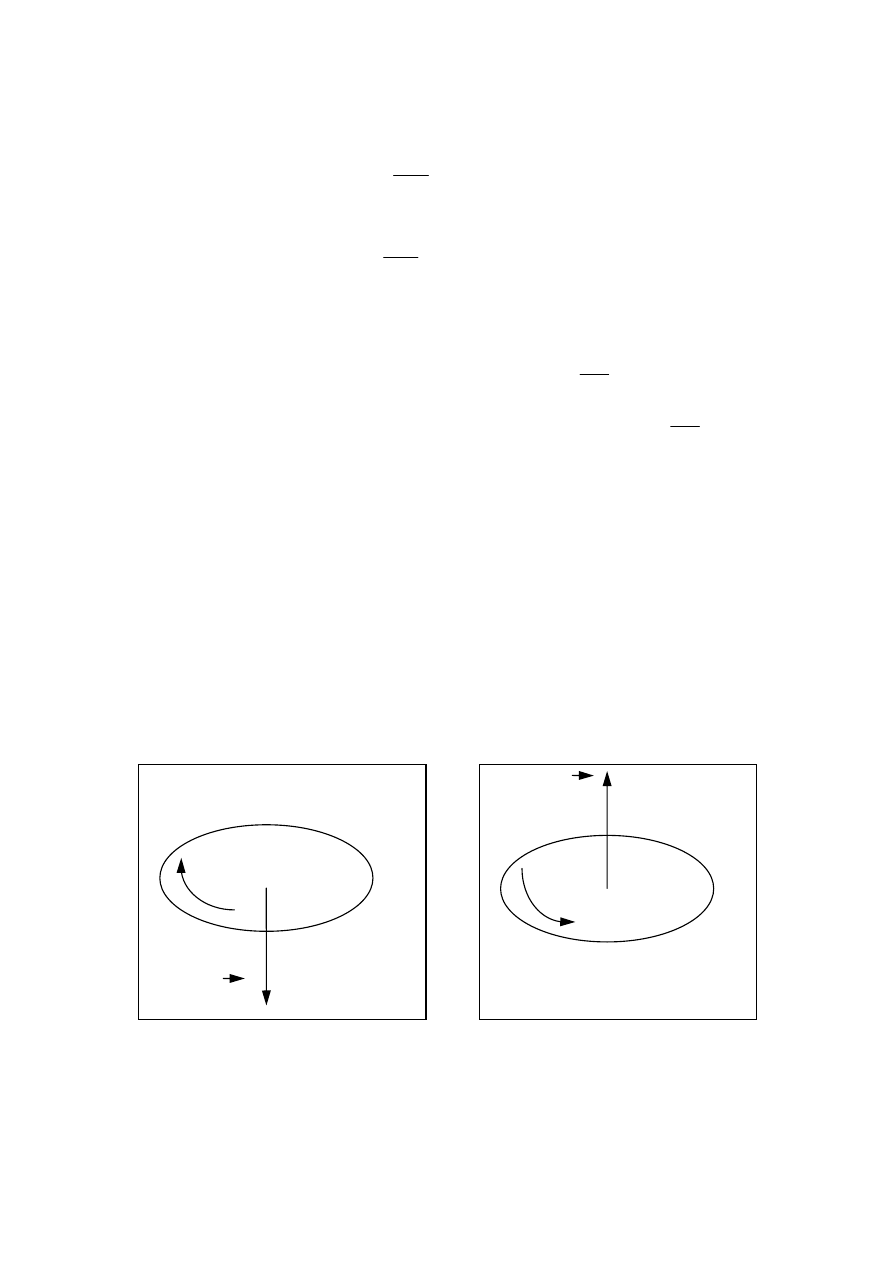
Inne określenia zwrotu wektora prędkości kątowej: prędkość kątowa jest wektorem leżącym
na osi obrotu i skierowanym do dołu, jeżeli ciało obraca się zgodnie z kierunkiem ruchu
wskazówek zegara (rys. 1), albo też do góry, jeżeli obraca się w kierunku przeciwnym do ru-
chu wskazówek zegara (rys. 2).

Rys. 1

ω

Rys. 2

-

ω

8.

*Należy zwrócić uwagę na to, ze tylko mały (elementarny) przyrost kąta d

α

jest wektorem.

Duży przyrost kąta

∆α

nie jest wektorem, gdyż nie spełnia właściwych reguł matematycz-

nych, jakim podlegają wielkości wektorowe.

9.

*Wektorowy opis ruchu obrotowego należy stosować wówczas, gdy oś obrotu bryły zmienia
swoje położenie w przestrzeni. Takich przypadków nie będziemy rozważać.

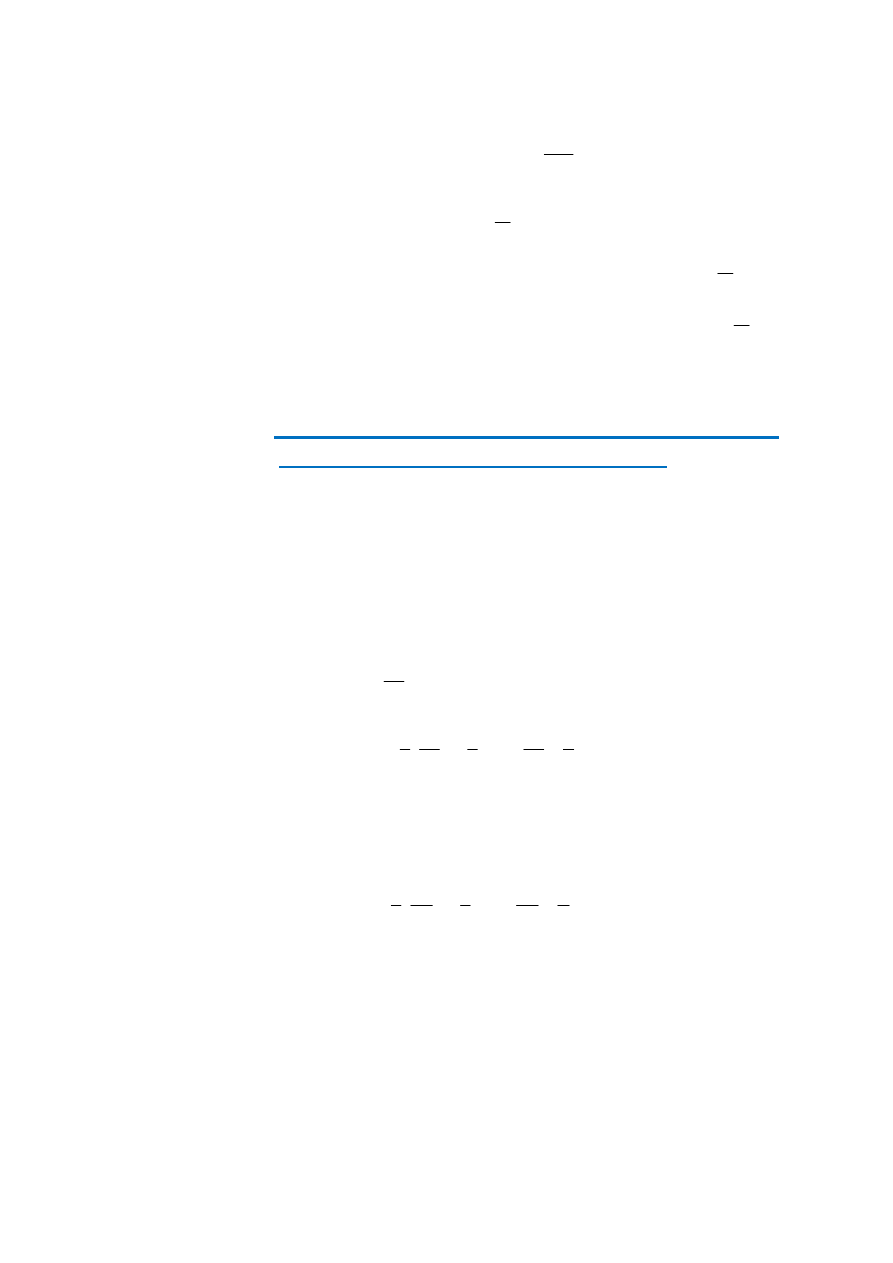
5

00508 Kinematyka bryły sztywnej D

TEORIA

Zadania:

1.

Koło o promieniu R = 10[cm] wiruje z prędkością kątową

ω

= 628













s

rad

. Znajdź czas pełnego obiegu T

oraz prędkość liniową punktu znajdującego się na obwodzie koła. Oblicz, ile obrotów wykona koło w ciągu

jednej minuty.

(Odp. T =0,0[ ]s, v = 62,8













s

m

, n = 6000)

2.

Oblicz promień koła zamachowego, jeżeli przy prędkości liniowej punktów na obwodzie v

1

= 6













s

m

,

punkty znajdujące się o l = 15 cm bliżej osi poruszają się z prędkością liniową wynoszącą v

2

= 5,5













s

m

.

(Odp. R = 1,8 [m])

Temat: 38

Związki między kinematycznymi wielkościami

kątowymi i wielkościami liniowymi.

1.

Kinematyczne wielkości kątowe mogą być również stosowane przy opisie ruchu punktu mate-
rialnego po okręgu. W tym jednak przypadku stosowanie tych wielkości nie jest konieczne,
jak to ma miejsce w opisie ruchu obrotowego bryły, a często podyktowane jest wyłącznie
względami wygody obliczeń.

2.

Między kinematycznymi wielkościami kątowymi i liniowymi istnieją proste związki matema-
tyczne. Wyprowadzimy je korzystając z geometrii, a ściślej - z zależności między wartością
kąta środkowego

∆α

, a długością

∆

s okręgu o promieniu r, na którym ten kąt jest oparty:

(1)

∆

∆

α

=

s

r

Wstawiając zależność (1) do wzoru na prędkość kątową, mamy:

(2)

ω

ω

=

⋅











= ⋅

=

⇒

= ⋅

→

→

∆

∆

∆
∆

∆
∆

t

t

r

s

t

r

s

t

v

r

v

r

0

0

1

1

lim

lim

Dla prędkości średnich (liniowej i kątowej) postępujemy podobnie i dostajemy:

(3)

v

r

ś

r

ś

r

=

⋅

ω

oraz między przyrostami wartości tych prędkości

(4)

∆

∆

v

r

=

⋅

ω

Wstawiając wzór (5) do wzoru definiującego przyspieszenie kątowe, otrzymujemy

(6)

ε

ω

=

⋅











= ⋅

=

⇒

= ⋅

→

→

∆

∆

∆

∆

∆

∆

t

t

r

v

t

r

v

t

a

r

a

r

0

0

1

1

lim

lim

skąd otrzymujemy:

(7)

a

r

= ⋅

ε

3.

*Zależności między wektorami kinematycznych wielkości kątowych i liniowych można wy-
razić przy pomocy iloczynów wektorowych:

(8)

d

x r

dr

r

r

r

α

=

(9)

r

r

r

ω

x r

v

=

(10)

r

r

r

ε

x r

a

=

6

00508 Kinematyka bryły sztywnej D

TEORIA

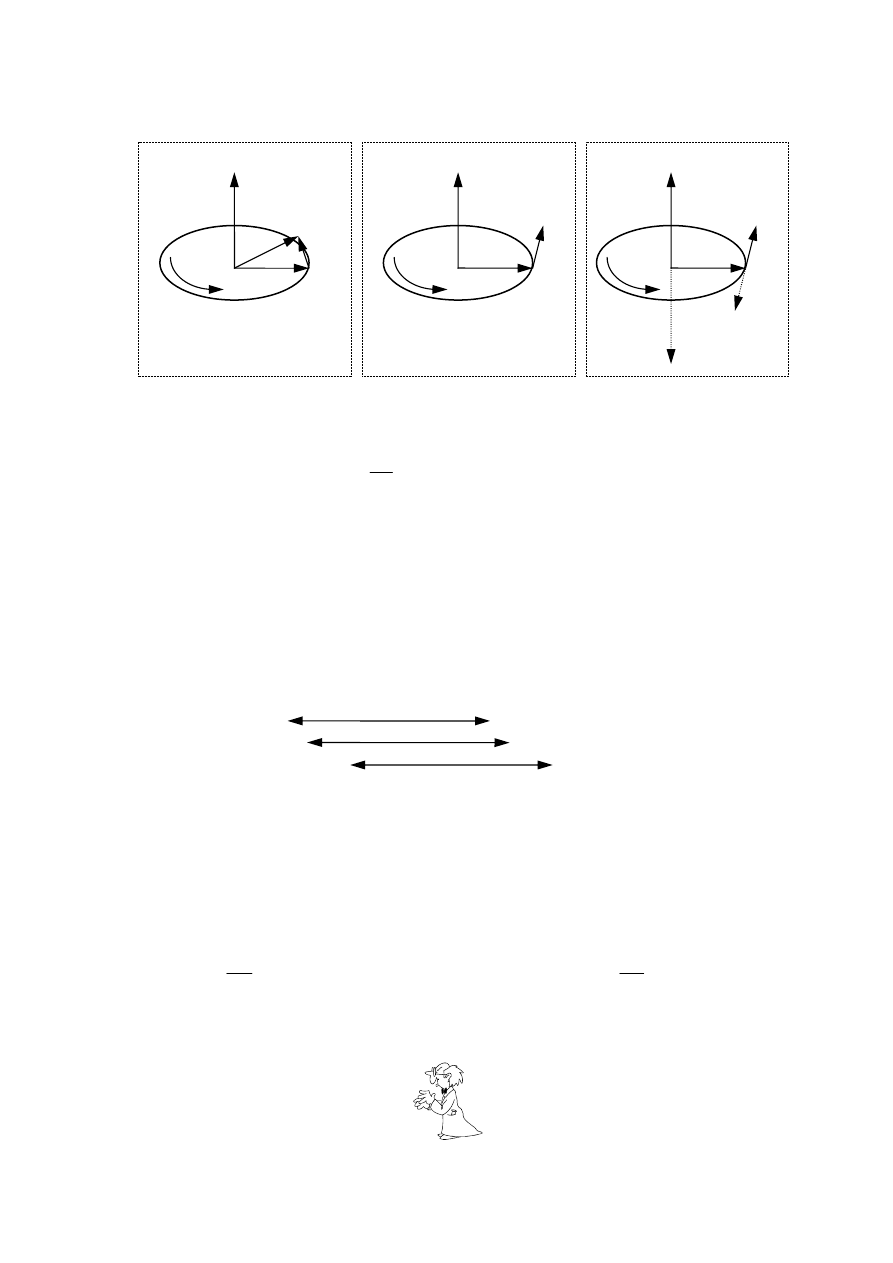
Usytuowanie przestrzenne wektorów określonych wzorami (8), (9) i (10) pokazują rysunki:

d

r

α

r

ω

r

ε

r

r dr

r

r

v

r

a

r

r

r

r

r

r

-

r

a

Rys. 1 Rys. 2 Rys. 3 -

r

ε

4.

Przy rozwiązywaniu zadań dotyczących ruchu po okręgu często korzysta się również z nastę-
pujących (i poznanych wcześniej) zależności wiążących prędkość kątową z okresem (często-
tliwością) ruchu jednostajnego po okręgu:

(11)

ω

π

=

2

T

, gdzie T - okres obrotu,

(12)

ω

π

=

2 f

, gdzie f - ilość obrotów w ciągu 1 sekundy.

Oraz z przyspieszeniem dośrodkowym:

(13)

a

r

=

⋅

ω

2

.

5.

Oprócz przedstawionych zależności między wielkościami kątowymi i liniowymi istnieją
także ścisłe zależności analogiczne do wyprowadzonych wcześniej, a opisujących ruch po
prostej i ruch obrotowy.

Zapamiętajmy regułę: wzory kinematyczne opisujące ruch po prostej i ruch obrotowy ma-
jące podobne postaci matematyczne - przejdą odpowiednio w siebie (staną się identyczne),
gdy zastąpimy w nich:
a) drogę kątową

α

drogą liniową s,

b) prędkość kątową

ω

prędkością liniową v,

c) przyspieszenie kątowe

ε

przyspieszeniem liniowym a.

*Powyższą regułę ilustruje poniższe zestawienie obok siebie najważniejszych wzorów ki-
nematycznych, czyli równań drogi i prędkości dla ruchu prostoliniowego i obrotowego:

Ruch po prostej (jednostajny) i obrotowy (jednostajny)

s

s

v t

= + ⋅

0

α α ω

=

+ ⋅

0

t

Ruch po prostej (zmienny) i obrotowy (zmienny)

v

v

a t

= + ⋅

0

ω ω ε

=

+ ⋅

0

t

s

s

v t

at

= +

+

0

0

2

2

α α ω

ε

=

+

+

0

0

2

2

t

t

v

v

as

2

0

2

2

−

=

ω

ω

εα

2

0

2

2

−

=