1

00509 Dynamika bryły sztywnej D

TEORIA

00509

Dynamika bryły sztywnej D

Momenty: bezwładności, siły i pędu.

Praca, moc i energia w ruchu obrotowym.

Zasada zachowania momentu pędu.

Przykładowe zadania.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 10
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

śyczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Maj

ROK 2008

Dane osobowe właściciela arkusza

2

00509 Dynamika bryły sztywnej D

TEORIA

Temat: 39

Ruch obrotowy bryły sztywnej

pod działaniem stałego momentu siły.

1.

Po krótkiej analizie kinematyki bryły sztywnej przechodzimy do dynamicznego opisu ruchu obro-
towego bryły sztywnej.

2.

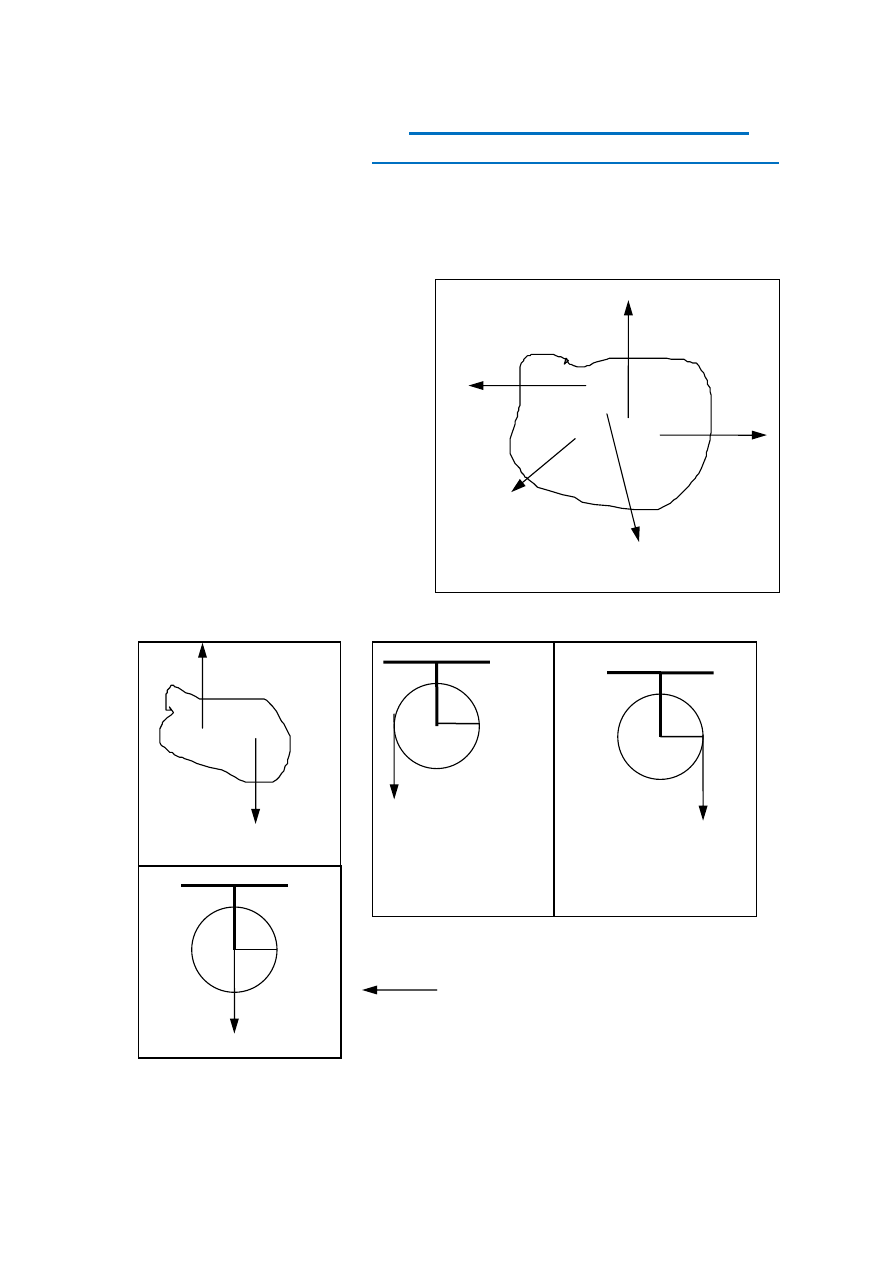
Rozpatrzmy bryłę sztywną, do której w różnych punktach przyłożone są różne siły (rys. 1). Jakie
warunki muszą być spełnione, aby ta bryła pozostawała w równowadze ?

Pierwszy z warunków jest identyczny z do-
tyczącym punktu materialnego (I zasada
dynamiki): wypadkowa wszystkich sił dzia-
łających na bryłę musi być równa zeru:

(1)

r

r

r

r

F

F

F

F

n

n

i

n

1

2

1

0

+

+ ⋅⋅⋅+

=

=

=

∑

Rysunek 2 wyjaśnia, że ten warunek nie
jest wystarczający.
Zatem skutek działania sił na bryłę sztywną
zależy nie tylko od wartości działających
sił, ale również od położenia linii działania
sił względem określonego punktu (osi obro-
tu), W przypadku pokazanym na rysunku
3a oraz 3b mówimy, że istnieje moment si-
ły względem siły obracającej krążek. W przypadku widocznym na rys. 3c - moment siły nie wy-
stępuje (jest równy zeru).

r

F

1

r
r

r

F

Rys. 2

r

F

2

Rys. 3a Rys. 3b

r

F

Krążek obraca się Krążek obraca się
w prawo w lewo

r

Rys. 3c Krążek pozostaje nieruchomy

r

F

Zatem: momentem siły

r

M

względem dowolnego punkt 0 lub momentem obrotowym nazywamy

wektor, którego wartość równa jest iloczynowi wartości siły

r

F

i jej ramienia r, a więc odległości

linii działania siły

r

F

od punkt 0.

r

F

2

r

F

1

r

F

3

r

F

4

Rys. 1

5

F

r

3

00509 Dynamika bryły sztywnej D

TEORIA

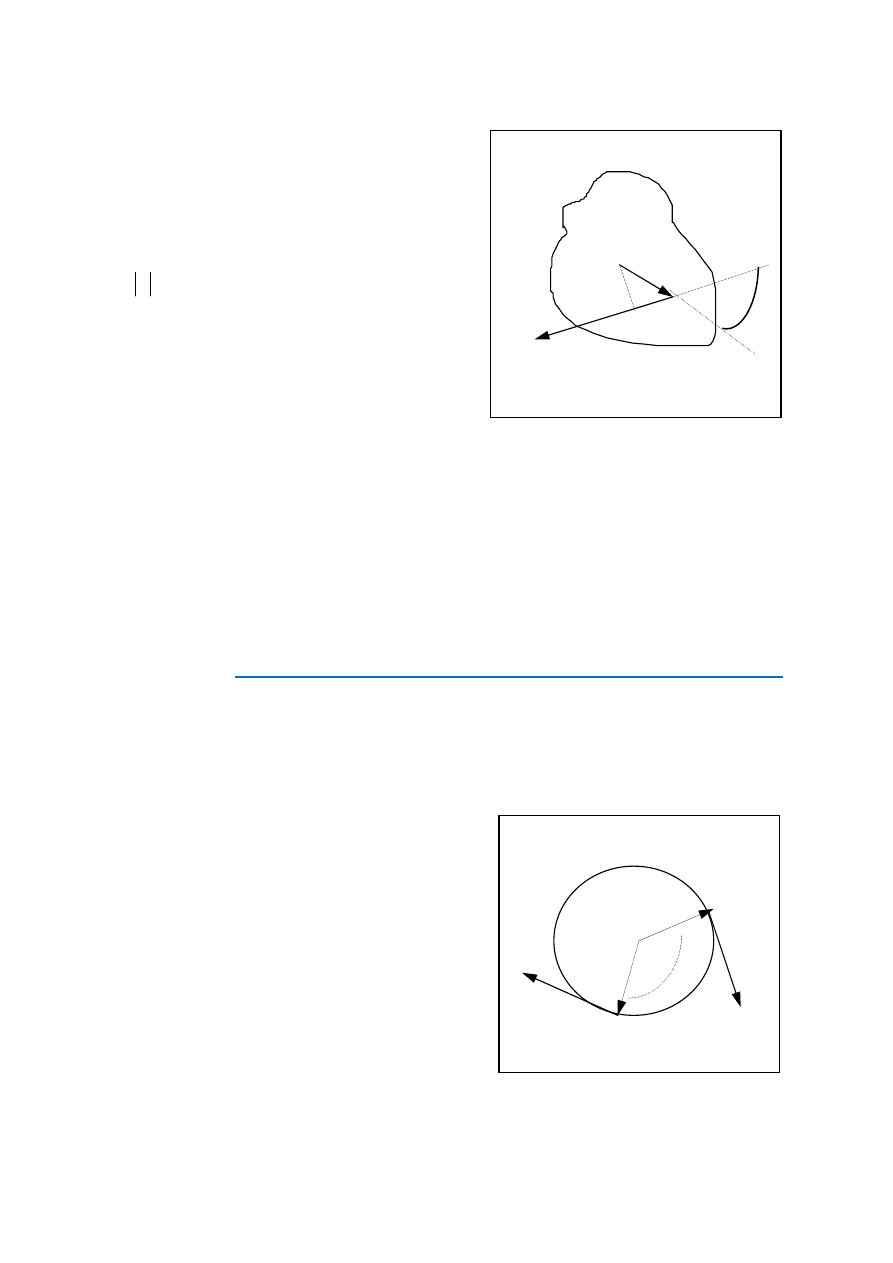
*Zgodnie z rys. 4 mamy:

(2)

M

F r

F r

= ⋅ = ⋅

sin

α

lub wektorowo:

(3)

r

r

r

M

R

F

= ×

.

Ponieważ na rys. 3a,b,c

r

r

R

F

⊥

, dlatego

(4)

M

F R

F R

= ⋅

= ⋅

sin 90

0

.

Również dla przypadku

r

r

R

F

⊥

zachodzi równość

r

R

r

=

i wtedy możemy zapisać:

(5)

M

F r

= ⋅

.

3.

*Teraz możemy podać drugi warunek równowagi
ciała sztywnego:

(6)

r

r

R

F

i

i

i

× =

∑

0

.

4.

Moment siły względem punktu 0 jest wektorem prostopadłym do płaszczyzny, w której leży punkt

i linia działania siły

r

F

(zresztą wynika to z określenia iloczynu wektorowego), przy czym ma on

znak dodatni, gdy siła jest skierowana tak względem punktu 0, że obraca bryłę zgodnie z kierun-
kiem ruchu wskazówek zegara (rys. 3c), lub ujemny, gdy kierunek obrotu bryły jest przeciwny

(rys. 3a). Jeżeli natomiast linia działania siły

r

F

przechodzi przez punkt 0, to ramię siły r = 0, a

więc i moment siły

r

M

jest równy zeru (rys.3b ). Jak już było stwierdzone, rysunki 3a,b,c dotyczą

przypadku

r

r

R

F

⊥

. Tylko takimi przypadkami będziemy się zajmować na dalszych stronach ni-

niejszego kursu.

Temat: 40 Praca i moc w ruchu jednostajnym obrotowym.

1.

Wprawienie ciała w ruch obrotowy jest związane z nadaniem mu przyspieszenia, a więc z
wykonaniem określonej pracy. Również utrzymanie ciała w stanie ruchu obrotowego jed-
nostajnego w warunkach, w których występują siły przeciwdziałające mu, wymaga wyko-
nania niezbędnej pracy do ich pokonania.

Załóżmy, że na obwodzie tarczy obracającej się
jednostajnie dookoła osi (rys. 1) działa stała co
do wartości siła

r

F

prostopadła do promienia

wodzącego

r

r

pokonująca opory ruchu. Jeżeli po

czasie t punkt przyłożenia siły przebędzie drogę
liniową

s

r

= ⋅

α

, to wykonana przez tę siłę praca

pokonywania oporów ruchu wyrazi się wzorem:

(1)

W

F s

= ⋅

,

lub
(2)

W

F r

= ⋅ ⋅

α

.

Iloczyn F r

⋅

jest momentem siły względem osi

obrotu, zatem:
(3)

W

M

=

⋅

α

.

0

•

r

r

R

α

r

F

Rys. 4

r

r

r

F

0

α

r

r

r

F

Rys. 1

4

00509 Dynamika bryły sztywnej D

TEORIA

Wniosek: I

Jeśli moment M utrzymuj cy cia o w ruchu obrotowym zachowuje sta

wartość

ą

ł

łą

,

to wykonana przez niego praca jest równa iloczynowi momentu M i drogi k towej

ą

.

α

2.

Za pomocą prostego rozumowania możemy wyznaczyć moc:

(4)

P

W

t

M

t

M

=

=

⋅

=

⋅

α

ω

, bowiem

ω

α

=

t

w rozpatrywanym rodzaju ruchu.

Wniosek: II

Miar mocy w ruchu obrotowym jednostajnym jest iloczyn dzia aj cego na

ą

ł ą

cia o momentu obrotowego M i jego prędkości k towej

ł

ą

ω

.

Temat: 41

Energia kinetyczna w ruchu obrotowym.

Moment bezwładności.

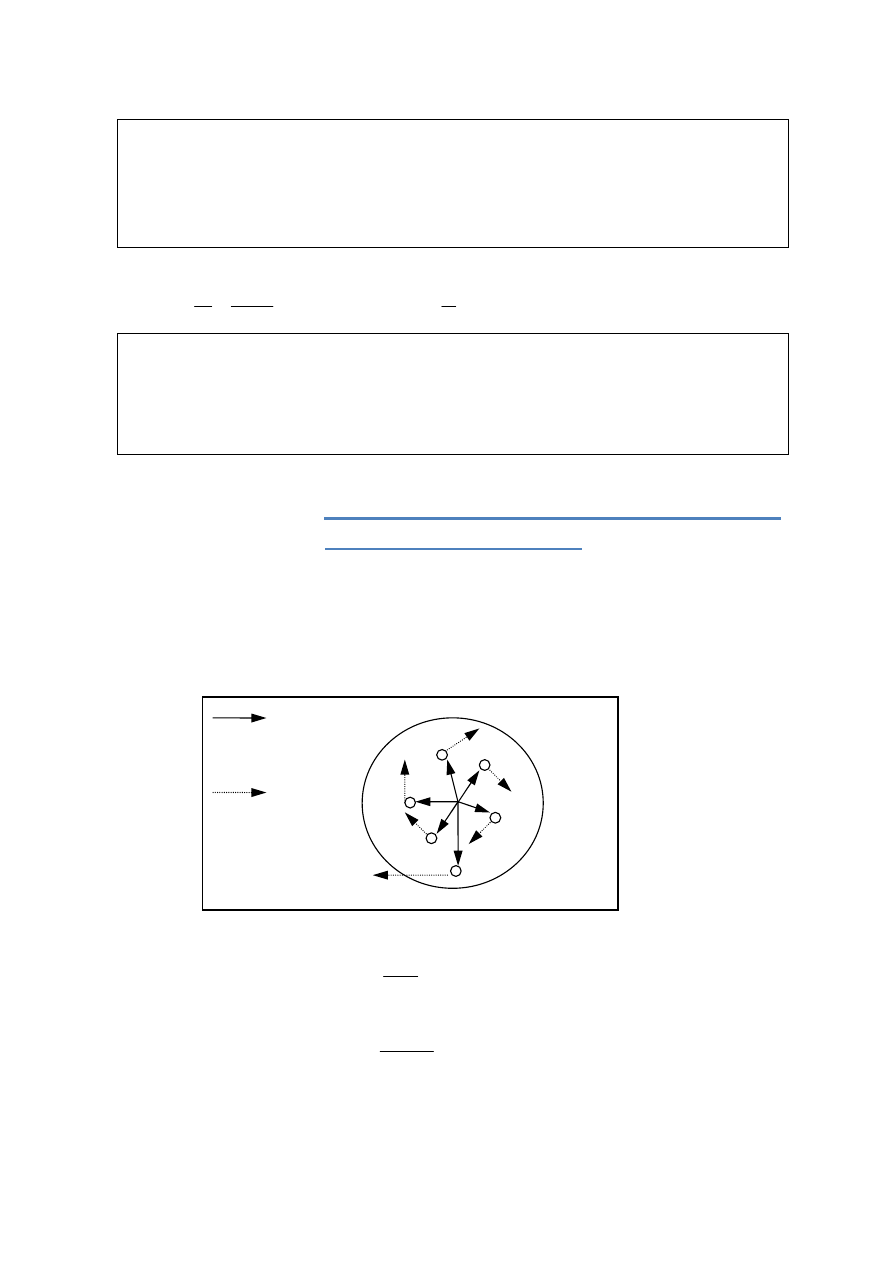
1.

Tematem analizy będzie energia kinetyczna bryły sztywnej znajdującej się w ruchu obro-
towym jednostajnym. Dla prostoty rozważań - bryłę stanowić będzie tarcza o masie m
składająca się z bardzo dużej liczby elementów o masach m

1

, m

2

, ... m

n

tak małych, że

można przyjąć je za punkty materialne obracające się dokoła osi przechodzącej przez jej
ś

rodek ciężkości (masy) ze stałą prędkością kątową (rys. 1).

r

r

Wektor wodzący m

1

punktu tarczy m

2

r

v m

3

m

4

Wektor prędkości m

5

punktu tarczy

m

n

Rys. 1

Energia kinetyczna pojedynczego elementu wynosi:

(1)

E

m v

k

i i

i

=

2

2

lub po podstawieniu

v

r

i

i

= ⋅

ω

(pamiętamy, że dla każdego punktu tarczy

ω

jest jednakowe)

(2)

E

m

r

k

i

i

i

=

ω

2

2

2

.

5

00509 Dynamika bryły sztywnej D

TEORIA

Energia kinetyczna całej tarczy jest równa sumie energii jej poszczególnych elementów:

(3)

E

E

m

r

m r

k

k

i

n

i

i

i

n

i i

i

n

i

=

=

=

=

=

=

∑

∑

∑

1

2

2

1

2

2

1

2

2

ω

ω

Zastanowimy się teraz nad wyrażeniem, które pozostało pod znakiem sumy, a mianowicie:

(4)

m r

i i

i

n

2

1

=

∑

Suma iloczynów mas poszczególnych cząstek bryły i kwadratów ich odległości od osi ob-
rotu jest miarą bezwładności bryły i nosi nazwę momentu bezwładności I bryły względem

danej osi obrotu: (5a) I =

m r

i i

i

n

2

1

=

∑

.

*W przypadku ciała sztywnego o ciągłym rozkładzie masy dzielimy je w myśli na nie-
skończenie małe elementy masy dm i sumowanie we wzorze (5a) zastępujemy całkowa-
niem. Wtedy moment bezwładności wyraża się wzorem:

(6)

I

r dm

=

∫

2

,

przy czym całkowanie rozciągnięte jest na całą objętość ciała.
Ze wzoru (6) widać, że o bezwładności obracającej się bryły nie decyduje suma mas po-
szczególnych cząstek bryły. Zasadnicze znaczenie ma rozmieszczenie mas względem osi
obrotu.


Wracamy teraz do równania (4), które zapiszemy:

(7)

E

I

k

=

⋅

ω

2

2

Wniosek:
Energia kinetyczna E

k

obracającego się ciała dokoła osi przechodzącej przez jej środek

masy jest równa połowie iloczynu momentu bezwładności tego ciała (moment ten ozna-
czamy literą I ) względem osi obrotu i kwadratu jej prędkości kątowej

ω

.

2.

Jednostką momentu bezwładności jest iloczyn jednostki masy i kwadratu jednostki długo-
ś

ci, a więc w układzie SI mamy:

(8)

[ ]

[

]

I

kg m

=

⋅

2

6

00509 Dynamika bryły sztywnej D

TEORIA

3.

Momenty bezwładności ciał geometrycznie określonych oblicza się zazwyczaj za pomocą
wzorów wyprowadzonych przy użyciu rachunku całkowego. Oto kilka wyników takich
obliczeń:

a)

kula jednorodna o promieniu R i masie m, oś obrotu przechodzi przez środek kuli

I

m R

=

⋅

2

5

2

b)

krążek (walec lub dysk) względem osi obrotu przechodzącej przez środek masy
wzdłuż długości krążka

I

m R

=

⋅

1

2

2

c)

pręt względem osi przechodzącej przez jego koniec i do niego prostopadłej:

I

m L

=

⋅

1

3

2

, gdzie L oznacza długość pręta.

Temat: 42

I i II zasada dynamiki dla ruchu obrotowego.

1.

Bezwładność, czyli samoistne podtrzymywanie stanu spoczynku lub ruchu jednostajnego, jest
cechą ciał, która przejawia się nie tylko w ruchu postępowym Liczne doświadczenia prowa-
dzą do wniosku, że i w ruchu obrotowym ciała (bryły) wykazują bezwładność. Można więc
analogicznie, jak to miało miejsce w dynamice punktu materialnego, podać I zasadę dynamiki
dla ruchu obrotowego brył. Pamiętając o tym, że przyspieszenie kątowe bryły wywołują nie-
zrównoważone momenty sił, można tę zasadę sformułować następująco:

W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem
jednostajnym, gdy nie działają na nią żadne momenty sił lub działające momen-
ty sił równoważą się wzajemnie:

(1)

r

r

r

r

r

r

M

M

M

M

M

M

i

i

n

n

=

∑

=

+

+

+

+ ⋅⋅⋅+

=

1

1

2

3

4

0

2.

Podany powyżej warunek równowagi dla ruchu obrotowego nie określa jednak całkowicie
równowagi bryły, która może jednocześnie wykonywać ruch obrotowy i postępowy. Dlatego
też dopiero łączne spełnienie warunków równowagi obu rodzajów ruchu daje pewność, że
bryła uprzednio spoczywająca pozostanie w spoczynku. Podstawą statyki bryły są następu-
jące dwa równania, które łącznie wzięte określają równowagę bryły:

r

r

r

r

r

r

M

M

M

M

M

M

i

i

n

n

=

∑

=

+

+

+

+ ⋅⋅⋅+

=

1

1

2

3

4

0

,

(2)

r

r

r

r

r

r

F

F

F

F

F

F

i

i

n

n

=

∑

= +

+ +

+ ⋅⋅⋅+

=

1

1

2

3

4

0

.

7

00509 Dynamika bryły sztywnej D

TEORIA

3.

Rozpatrzymy teraz przypadek, gdy na bryłę sztywną działa niezrównoważony moment siły.
W tym celu załóżmy, że na ciało sztywne o masie m związane z osią obrotu i mogące poru-
szać się wokół niej po torze kołowym o promieniu r, działa stała co do wartości siła obwodo-
wa

r

F , której wartość momentu

r

M wynosi M

F r

= ⋅

.

Pod wpływem działania tej siły bryła uzyska przyspieszenie

r

a , którego wartość spełnia rów-

nanie słuszne dla każdego jej punktu:

(3)

F

m a

= ⋅

.

Podstawiając do (3)

a

r

= ⋅

ε

i mnożąc obie strony równania przez r, otrzymamy dla każdego

punktu bryły:

(4)

F r

m

r

⋅ = ⋅ ⋅

ε

2

,

Pamiętając, że

M

F r

= ⋅

możemy napisać:

(5)

M

m

r

= ⋅ ⋅

ε

2

Przejdziemy teraz od poszczególnych punktów bryły sztywnej do bryły jako całości sumując
wszystkie elementarne momenty M

i

dające moment całkowity M

C

bryły

(6)

M

M

m r

I

C

i

i

n

i i

i

n

=

=

= ⋅

=

=

∑

∑

1

2

1

ε

ε

.

lub

ε

=

M

I

[w zapisie wektorowym: (7a)

r

r

ε

=

M

I

]

Zależność (7), a dokładniej (7a) stanowi podstawowe równanie dynamiki ruchu obrotowego
bryły sztywnej:

Niezrównoważony moment siły

r

M działając na bryłę nadaje jej przyspieszenie

kątowe

r

ε

, którego wartość jest wprost proporcjonalna do wartości tego mo-

mentu i odwrotnie proporcjonalna do momentu bezwładności I bryły, przy czym
jest ono skierowane tak samo jak moment

r

M .

Ze wzoru (7) widać, że moment bezwładności w ruchu obrotowym spełnia tę samą rolę co
masa w ruchu postępowym - jest mianowicie miarą bezwładności bryły, natomiast moment si-
ły odgrywa w ruchu obrotowym taką rolę jak siła w ruchu postępowym.

Zadanie:

1.

Wirnik silnika elektrycznego o mocy 10[kW] i prędkości obrotowej 2800









min

obr

ma moment

bezwładności równy 0,025

[

]

2

m

kg

⋅

. Oblicz moment obrotowy i energię kinetyczną wirnika

oraz czas rozruchu silnika.

(Odp. M = 34[N·m], E

k

= 1100 [J], t = 0,22[s])

8

00509 Dynamika bryły sztywnej D

TEORIA

Temat: 43

Wnioski z zasady zachowania krętu.

1.

*W każdym nie odosobnionym układzie ciał możemy wyróżnić siły wewnętrzne i zewnętrzne.
Siły wewnętrzne działające między poszczególnymi częściami układu występują parami,
zgodnie z III zasadą dynamiki. Jako równe i przeciwnie skierowane dają one w układzie wy-
padkową siłę równą zeru. Wykażemy, że ich moment wypadkowy względem dowolnego
punktu też się równa zeru (rys. 1).

-

r

F

r

F

r

R

2

r

R

1

r


0
Rys. 1

Momenty sił

r

F i -

r

F względem punktu 0 równają się F·r i -F·r. Są więc sobie liczbowo rów-

ne, mają kierunki jednakowe, lecz zwroty przeciwne: moment siły -

r

F skierowany jest przed

płaszczyznę rysunku, moment siły

r

F - za płaszczyznę rysunku.

Zatem: Siły wewnętrzne nie mają wypadkowego momentu siły, czyli nie mogą powodować

zmiany momentu pędu (krętu).

2.

Czy to jednak dowodzi, że w układzie odosobnionym ( a więc takim, w którym nie działają
siły zewnętrzne) nie mogą zajść żadne zmiany w ruchu obrotowym ciała ?

Stałości wypadkowego momentu pędu L odpowiada stałość iloczynu

I

⋅

ω

.Jeżeli mamy moż-

liwość zmieniania momentu bezwładności układu pod działaniem sil wewnętrznych, to zmia-
nom tym muszą towarzyszyć takie zmiany prędkości kątowej

ω

, aby iloczyn

I

⋅

ω

był stały.

3.

Jeśli łyżwiarz wykonuje piruet na lodzie, to rozsuwając szeroko ręce zwiększa swój moment
bezwładności, a tym samym zmniejsza prędkość kątową obrotu. I odwrotnie - „skupiając”
możliwie najbardziej całą swoją masę dokoła osi obrotu zmniejsza swój moment bezwładno-
ś

ci, co powoduje wzrost prędkości kątowej

ω

.

4.

Analogiczne spostrzeżenie poczynimy obserwując człowieka siedzącego na stołku kręcącym
się dokoła osi pionowej i trzymającego w rękach ciężkie kule. Składanie rąk na piersi, a na-
stępnie rozkładanie ich możliwie szeroko powoduje zmianę momentu bezwładności, a równo-
cześnie zmianę prędkości kątowej układu.

5.

Niech człowiek stojący na nieruchomym stołku trzyma w ręku oś pionową, na której jest
zamocowane koło rowerowe. Jeżeli człowiek wprawi w ruch obrotowy trzymane nad sobą ko-
ło, to stołek zacznie obracać się przy tym w przeciwną stronę, aby utrzymać wypadkowy mo-
ment pędu jako nadal zerowy.

9

00509 Dynamika bryły sztywnej D

TEORIA

6.

Rozpatrzone powyżej przykłady dają wyniki zgodne z zasadą zachowania momentu pędu. W
ostatnim przykładzie kręt początkowy układu wynosił zero i musiał zachować swoją wartość:
zatem kręt koła

I

k

k

⋅

ω

musi być równoważony przeciwnym co do znaku, lecz równym co do

wartości krętem

I

s

s

⋅

ω

stołka i stojącego na nim człowieka.

7.

Podobnie przemieszczanie się warstw powietrza w pobliżu powierzchni Ziemi związane z
różnicami ciśnień powoduje zmiany momentu bezwładności układu Ziemia - atmosfera, co
pociąga za sobą małe, ale mierzalne zmiany prędkości kątowej

ω

. Zmniejszanie rozmiarów

podczas stygnięcia jej skorupy również miało wpływ na wartość prędkości kątowej Ziemi.

Temat: 44

Zestawienie podstawowych wielkości i wzorów

obowiązują-

cych w ruchu postępowym i obrotowym brył sztywnych.

Ruch postępowy Ruch obrotowy

v

ds

dt

=

prędkość

ω

α

=

d

dt

a

dv

dt

=

przyspieszenie

ε

ω

=

d

dt

m

masa / moment bezwładności

I

F

siła / moment siły

M

F

m a

= ⋅

II zasada dynamiki

M

I

= ⋅

ε

p

m v

= ⋅

pęd / moment pędu

L

I

= ⋅

ω

F

dp

dt

=

ogólna postać

II zasady dynamiki

M

dL

dt

=

E

m v

k

=

⋅

2

2

energia kinetyczna

E

I

k

=

⋅

ω

2

2

Temat: 45

Zadania.

1.

Koło w postaci dysku o masie 3[kg] toczy się bez poślizgu po płaszczyźnie poziomej z pręd-

kością 3









s

m

. Na jakiej drodze może być ono zatrzymane, jeżeli do obwodu koła przyłożymy

siłę o wartości 1,5[N] ?

(Odp. s = 13,5 m)
2.

Z jaką prędkością stoczy się bez poślizgu pełny walec po równi pochyłej o wysokości 3[m] ?

(Odp. v = 6,26

m

s

)

3.

Moment bezwładności koła napędowego silnika wynosi I =

[

]

2

2

,

0

m

kg

⋅

. W jakim czasie uzy-

ska ono prędkość kątową n = 1800[obr/min], jeżeli moc silnika wynosi P = 200[W]?

(Odp. t = 17,74 s)
4.

Ile razy wzrośnie energia kinetyczna ciała obracającego się, jeżeli częstość obrotów wzrośnie
dwukrotnie ?

(Odp. n = 4)

10

00509 Dynamika bryły sztywnej D

TEORIA

5.

Jak i ile razy zmieni się częstotliwość obrotów łyżwiarki, jeżeli poprzez zmianę układu ciała
jej moment bezwładności względem osi obrotu zmniejszy się trzykrotnie ?

( n = 3 )
6.

Po równi pochyłej nachylonej do poziomu pod kątem

α

stacza się bez poślizgu jednorodny

walec o masie m. Oblicz wartość działającej w tym ruchu siły tarcia. Moment bezwładności

walca względem jego osi obrotu wyraża się wzorem

I

m r

=

⋅

1

2

2

. Przyspieszenie ziemskie

wynosi g.

(Odp.

T

mg

=

⋅

1

3

sin

α

)

7.

Na lekkiej belce, spoczywającej na dwóch podporach odległych o 6[m], trzeba zawiesić ciało
o ciężarze 1200[N]. W którym miejscu belki należy je zawiesić, aby nacisk belki na jedną z
podpór wynosił 500[N]?

(Odp. x = 3,5[m] od belki, na którą nacisk wynosi 500[N])

8.

Koło zamachowe wykonujące początkowo 12 obrotów na sekundę zatrzymuje się po 6 s. Ob-
licz średnie przyspieszenie kątowe.

(Odp.

ε

ś

r

rad

s

=

12 56

2

,

)

9.

Walec i cienkościenna rurka o tych samych masach i promieniach oraz momentach bezwład-

ności wynoszących odpowiednio

I

m R

1

2

1

2

=

⋅

(walec) i

I

m R

2

2

= ⋅

(rurka) wtaczają się z

jednakową prędkością na równię pochyłą. Które z tych ciał osiągnie większą wysokość ?
(Odp. rura)

10.

Koło zamachowe o momencie bezwładności I = 245

[

]

2

m

kg

⋅

obraca się wykonując w chwili

początkowej n = 20









s

obr

i po pewnym czasie zatrzymuje się wykonując N = 1000[obrotów].

Oblicz moment sił tarcia oraz czas, po którym koło zatrzymało się

(Odp. M = 308

[

]

m

N

⋅

, t = 100[s])

11.

Kula o masie m = 150[g] toczy się po płaszczyźnie poziomej z prędkością 8









s

m

. Jaką siłą F na

drodze s =12[m] można ją zahamować aż do zatrzymania się ?

(Odp. F = 0,56 N)

12.

Oblicz moment siły hamującej M, który zatrzyma w czasie t = 15[s] dysk o masie m = 10[kg] i o

promieniu r = 12[cm] obracający się z prędkością n = 1800









min

obr

.

(Odp. M = 0,9

[

]

m

N

⋅

)

13.

Oblicz, jaką część energii kinetycznej stanowi energia obrotu w przypadku toczących się bez
poślizgu po poziomej płaszczyźnie

a) obręczy (

I

m r

= ⋅

2

), b) pełnego walca, c) kuli.

14.

Oblicz moment obracający koło napędowe silnika, jeżeli przy rozwijanej mocy P = 5 kW daje on

n = 2880









min

obr

.

(Odp. M = 16,6

[

]

m

N

⋅

)