
1
Metoda siecznych

2
Metoda siecznych
Zakłada się, że występująca w równaniu (1) funkcja
()
⋅
f jest ciągła na zadanym przedziale
[ ]
b
a, i spełnia w punktach krańcowych warunek
f (x) = 0
(1)
( ) ( )
0
<
⋅
b
f
a
f
Należy znaleźć przedział
[ ]
b
a,
Ustalić liczby ε, δ (większe od błędu zaokrąglenia
wynikającego ze skończonej precyzji zapisu liczb w komputerze)

3
Przebieg oblicze
ń
Wyznaczamy punkt przeci
ę
cia prostej (siecznej) przechodz
ą
cej przez
punkty a, f (a) i b, f (b) z osi
ą
x
)
a
(
f
)
b
(
f
)
a
b
(
)
b
(
f
b
x
)
(
−
−
⋅
−
=
1
Sprawdzamy, czy
,
)
x
(
f
)
(
δ
<
1
Je
ż
eli TAK, to
)
(
x
1
jest rozwi
ą
zaniem
*
x
x
)
(
=
1
Je
ż
eli NIE, to liczymy dalej, ale najpierw musimy okre
ś
li
ć
, który z punktów
b
ę
dzie stanowił punkt odniesienia - punkt wykre
ś
lania kolejnych siecznych

4
Ustalenia
)
(
x
0
Je
ż
eli
b
x
to
b
f
x
f
=
<
⋅
)
0
(
)
1
(
0
)
(
)
(
Je
ż
eli NIE, to
a
x
)
(
=
0
Wyznaczamy punkt przeci
ę
cia prostej (siecznej) przechodz
ą
cej przez
punkty
)
x
(
f
,
x
),
x
(
f
,
x
)
(
)
(
)
(
)
(
1
1
0
0
z osi
ą
x

5
)
x
(
f
)
x
(
f
)
x
x
(
)
x
(
f
x
x
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
1
0
1
1
1
2
−
−
⋅
−
=
Sprawdzamy, czy
,
)
x
(
f
)
(
δ
<
2
Je
ż
eli TAK, to
)
2
(
x
jest rozwi
ą
zaniem
*
)
2
(
x
x
=
Je
ż
eli NIE, to liczymy dalej zgodnie z zale
ż
no
ś
ci
ą
)
x
(
f
)
x
(
f
)
x
x
(
)
x
(
f
x
x
)
k
(
)
k
(
)
k
(
)
k
(
)
k
(
)
k
(
)
k
(
1
1
1
−
−
+
−
−
⋅
−
=
k = 2, 3, …,

6
Po ka
ż
dej iteracji sprawdzamy, czy
δ
<
+
)
x
(
f
)
k
(
1
Koniec oblicze
ń
, gdy
δ
<
+
)
x
(
f
)
k
(
1
wtedy
*
x
x
)
k
(
=
+
1
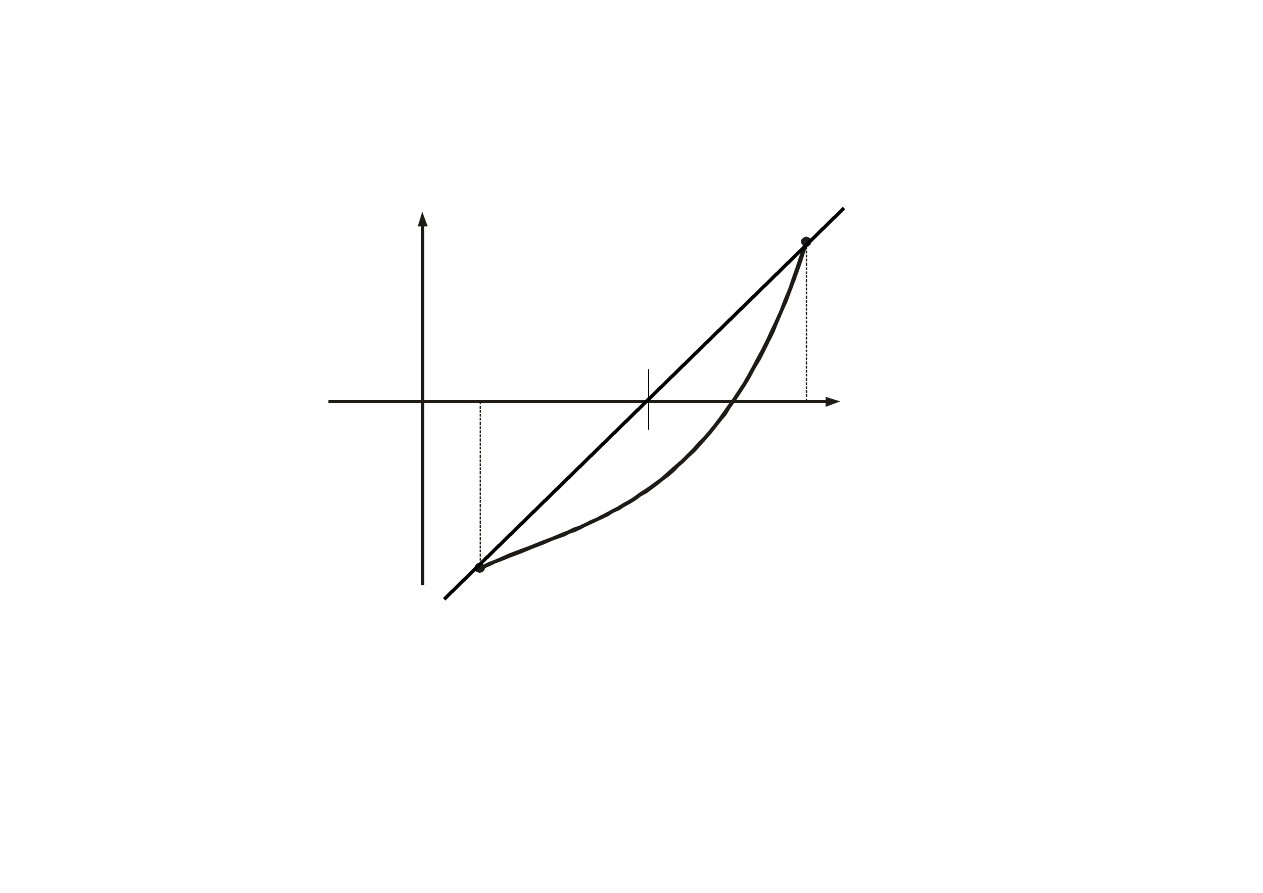
7
f(x)
x
f(b)
f(a)
a
b
0
Ilustracja graficzna
x
(1)
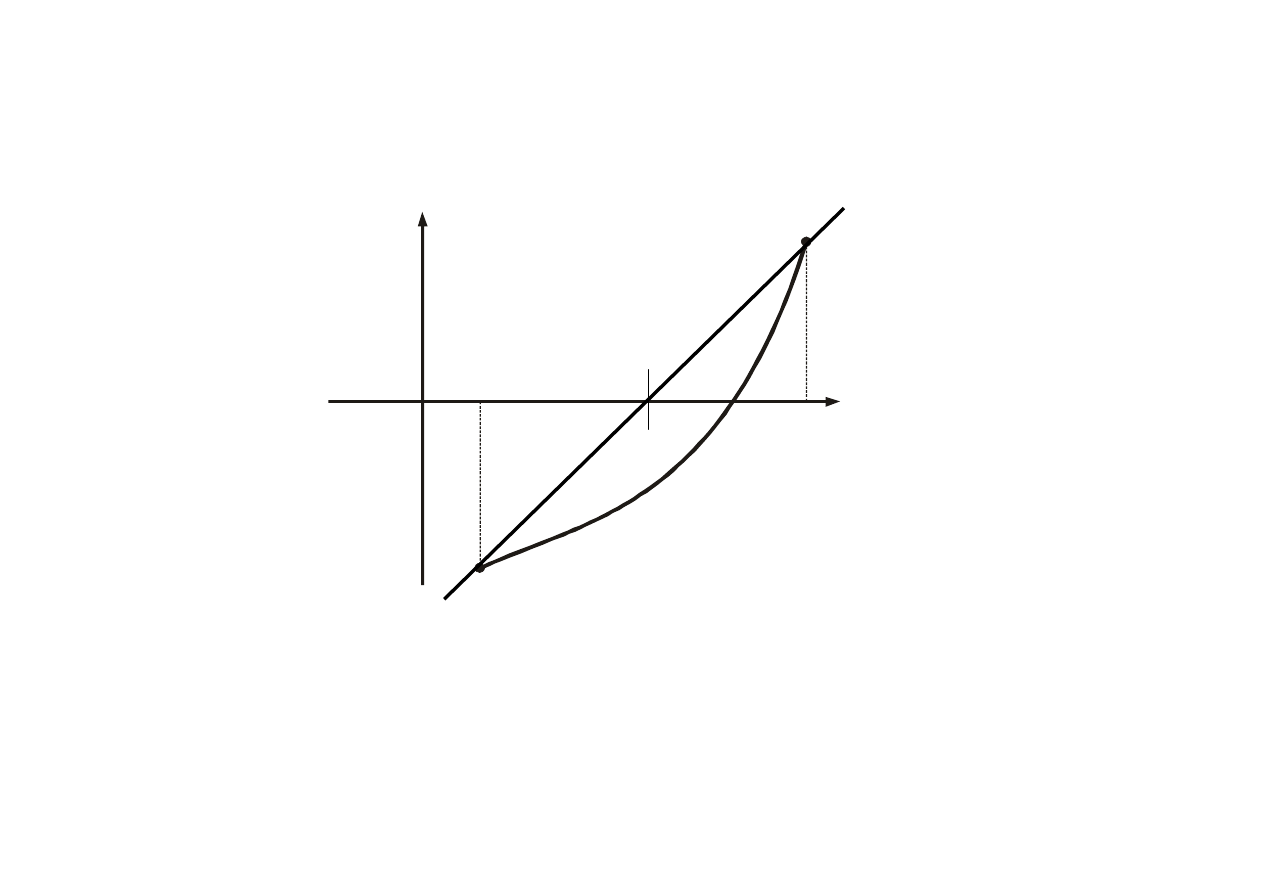
8
Ilustracja graficzna
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
f (x
(1)
) ·f (b) < 0
x
(0)
= b
x
(0)
│
f(x
(1)
)
│
<
δ
TAK
koniec oblicze
ń
x
(1)
= x
*
NIE
liczymy dalej
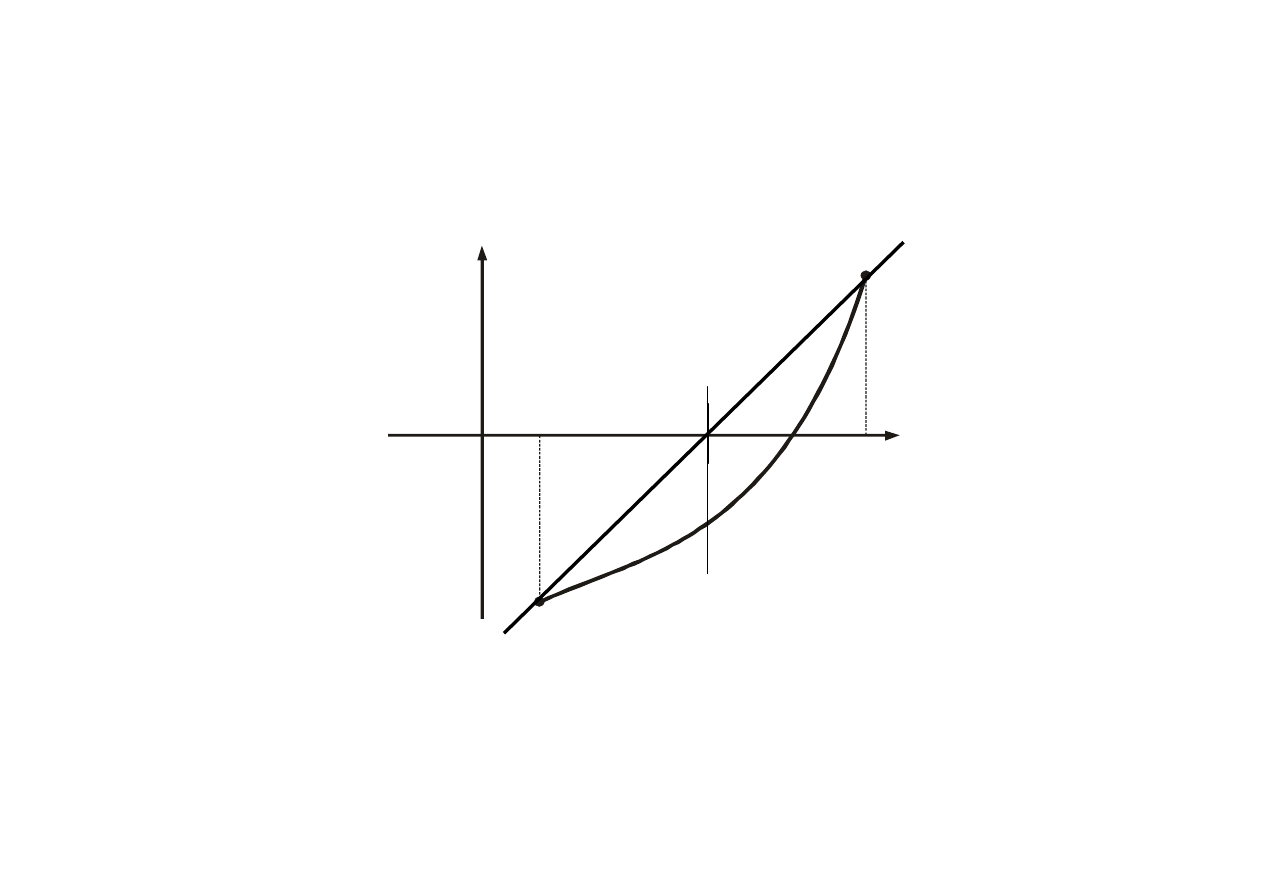
9
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
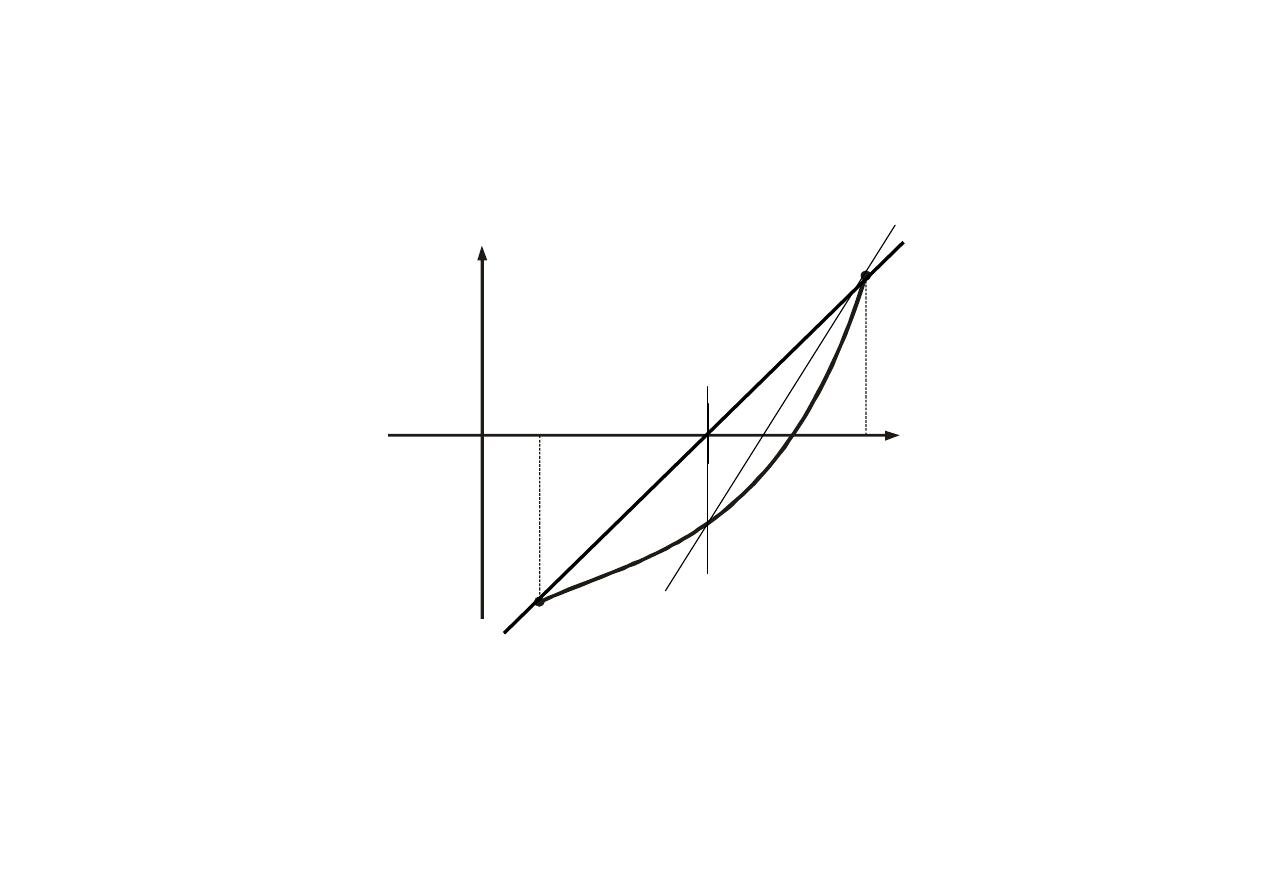
10
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
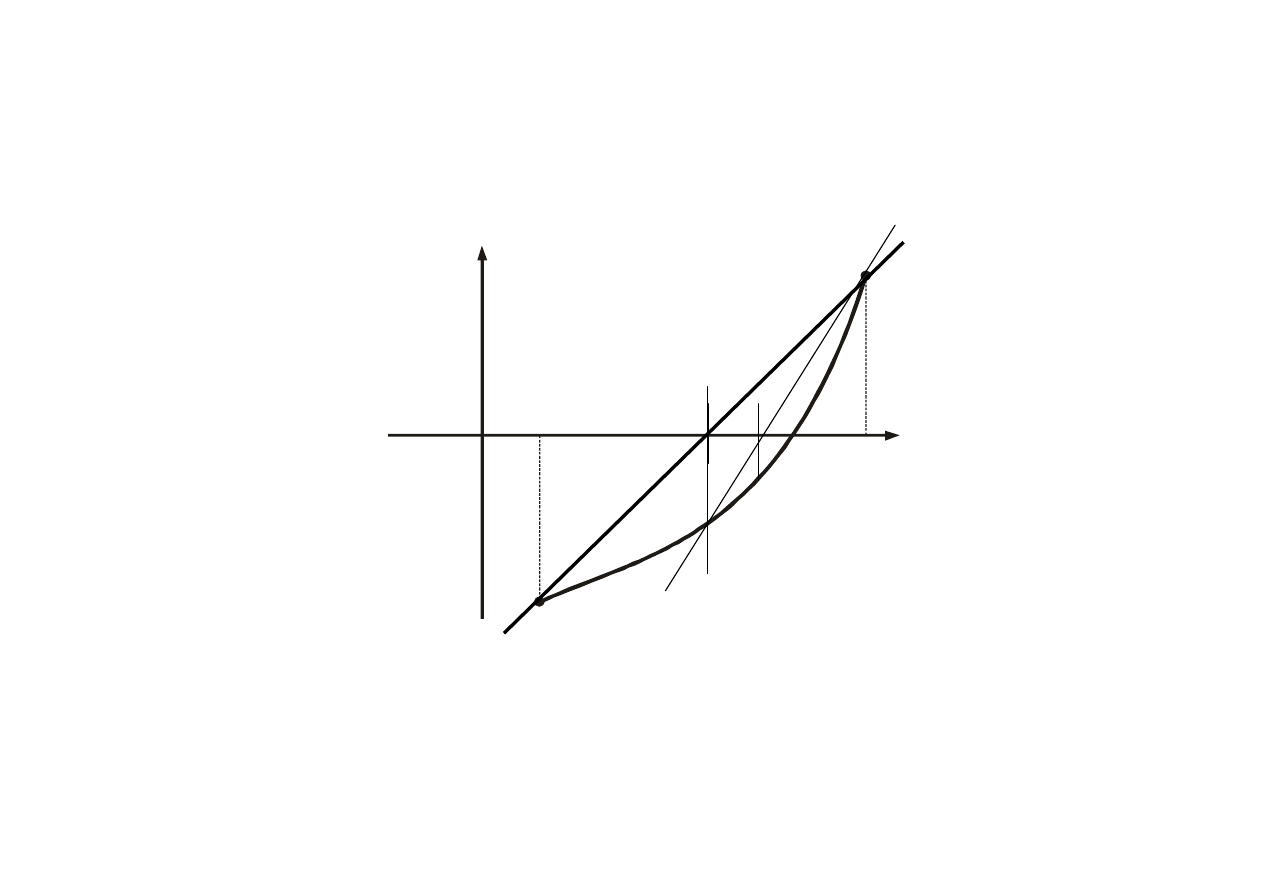
11
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
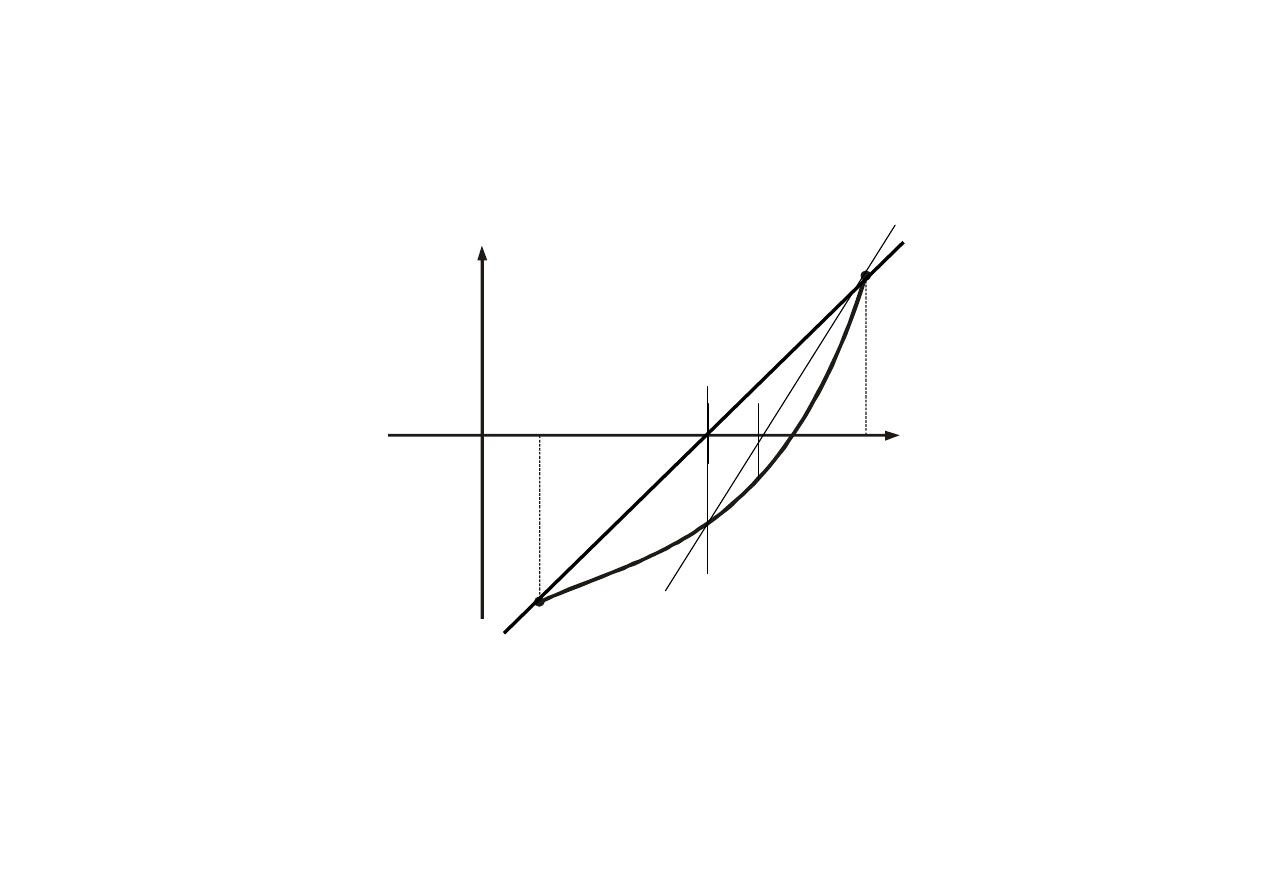
12
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
x
(2)
│
f (x
(2)
)
│
<
δ
TAK
ko
ń
czymy obliczenia
x
(2)
= x
*
NIE
liczymy dalej
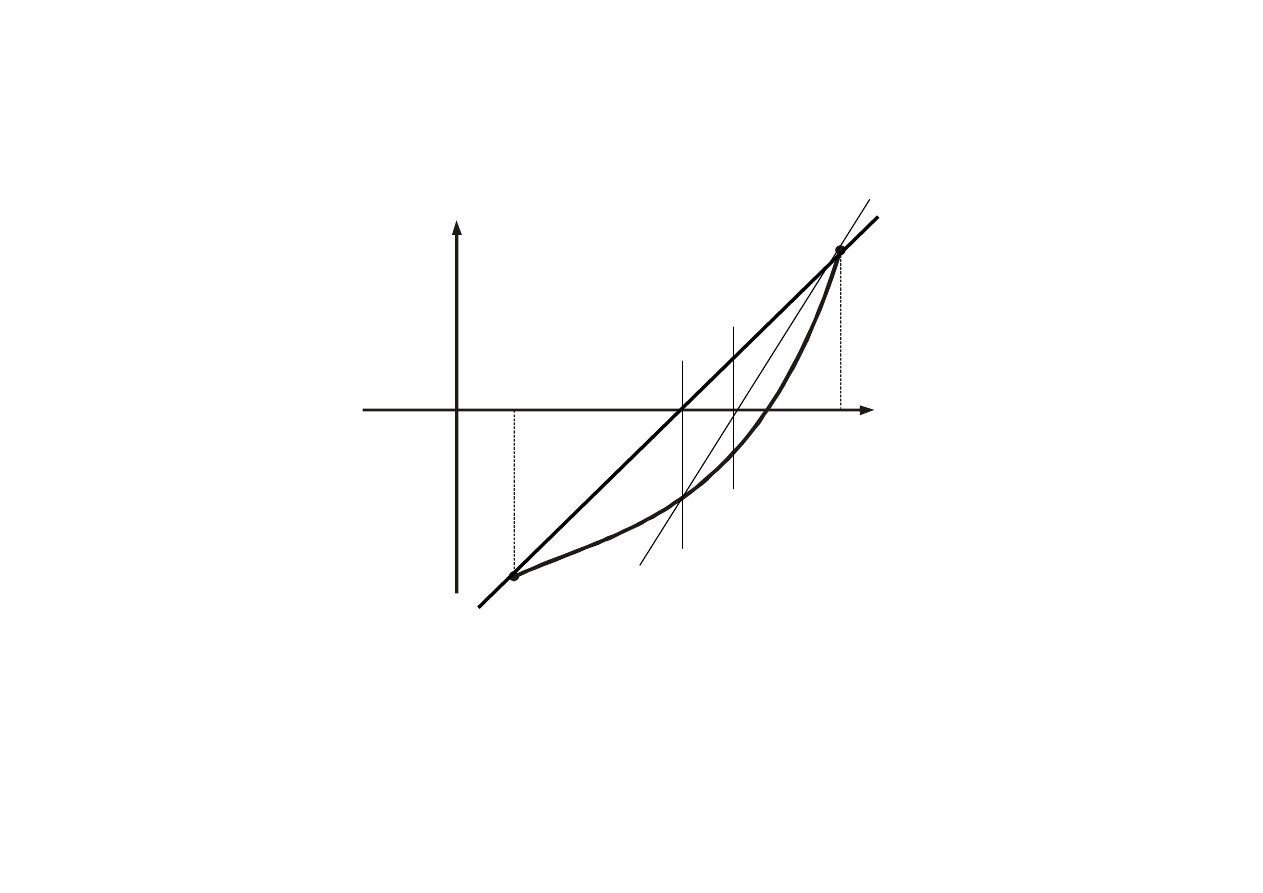
13
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
x
(2)
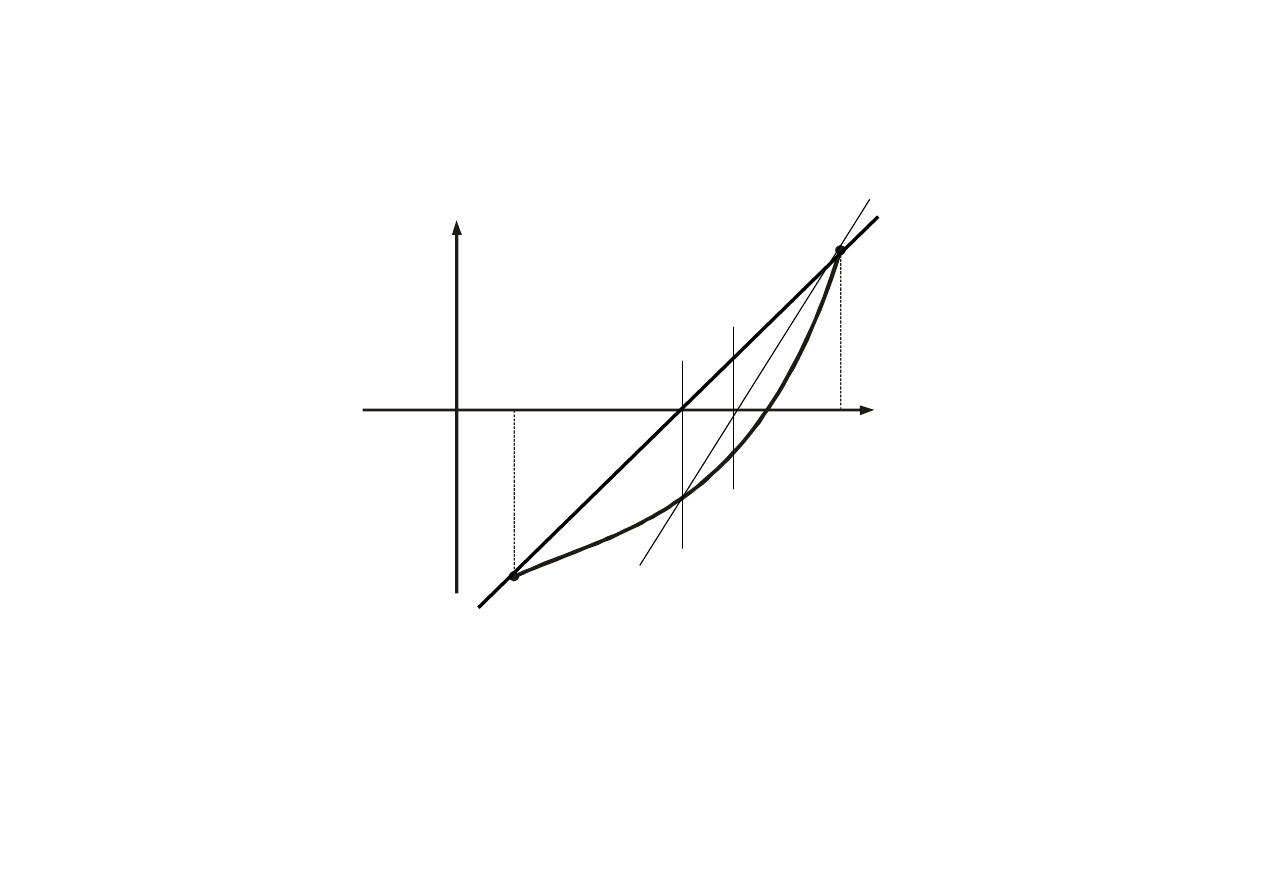
14
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
x
(2)
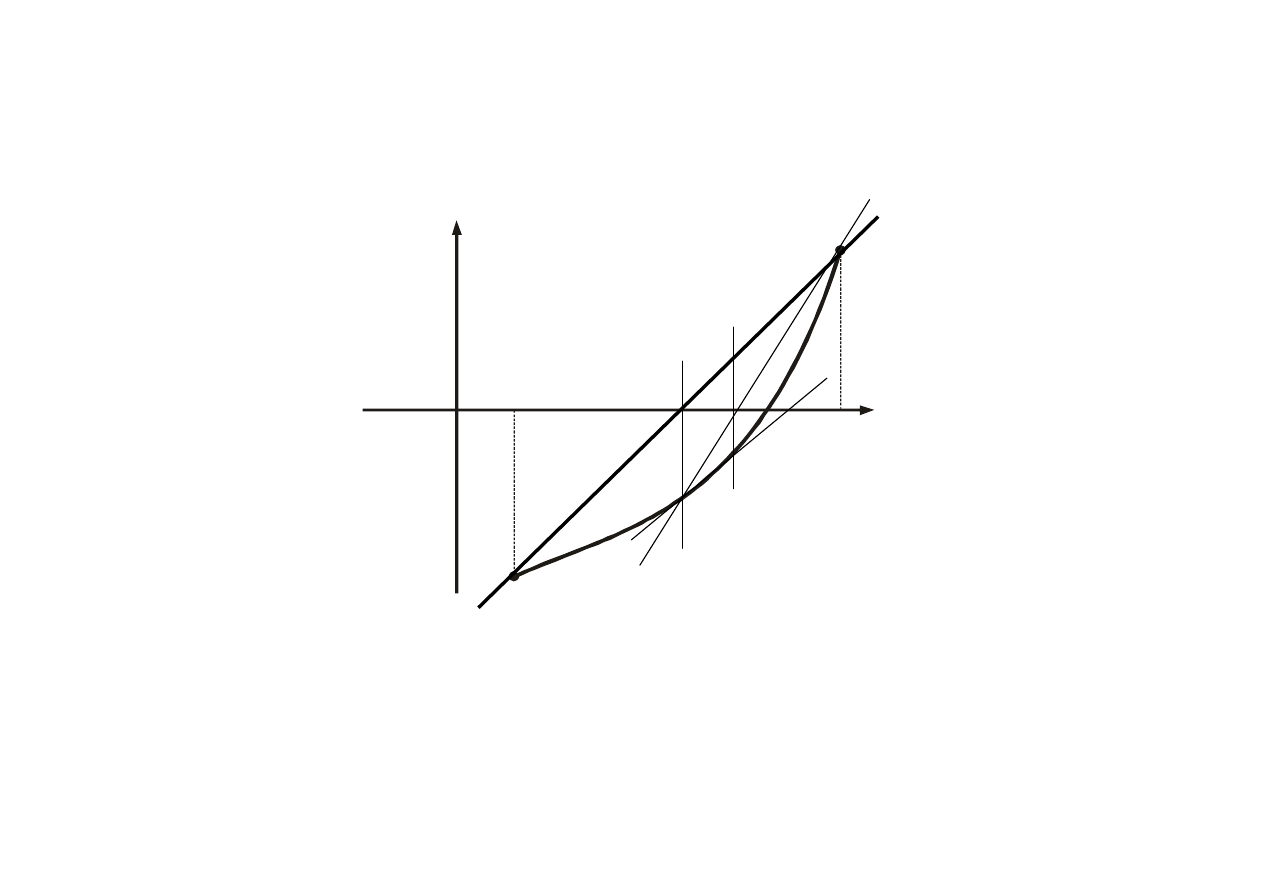
15
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
x
(2)
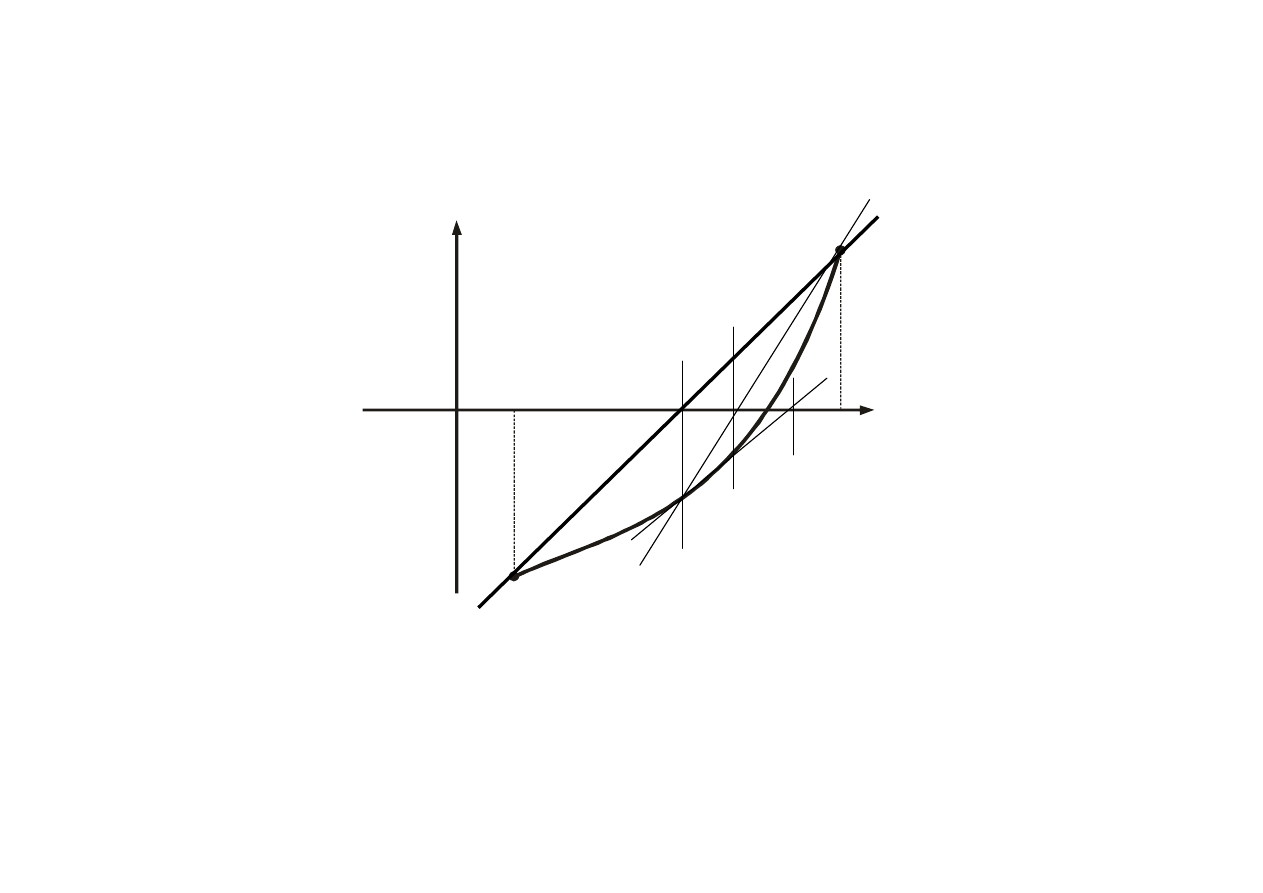
16
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
x
(0)
x
(2)
x
(3)
│
f (x
(3)
│
<
δ
TAK
ko
ń
czymy obliczenia
x
(3)
= x
*
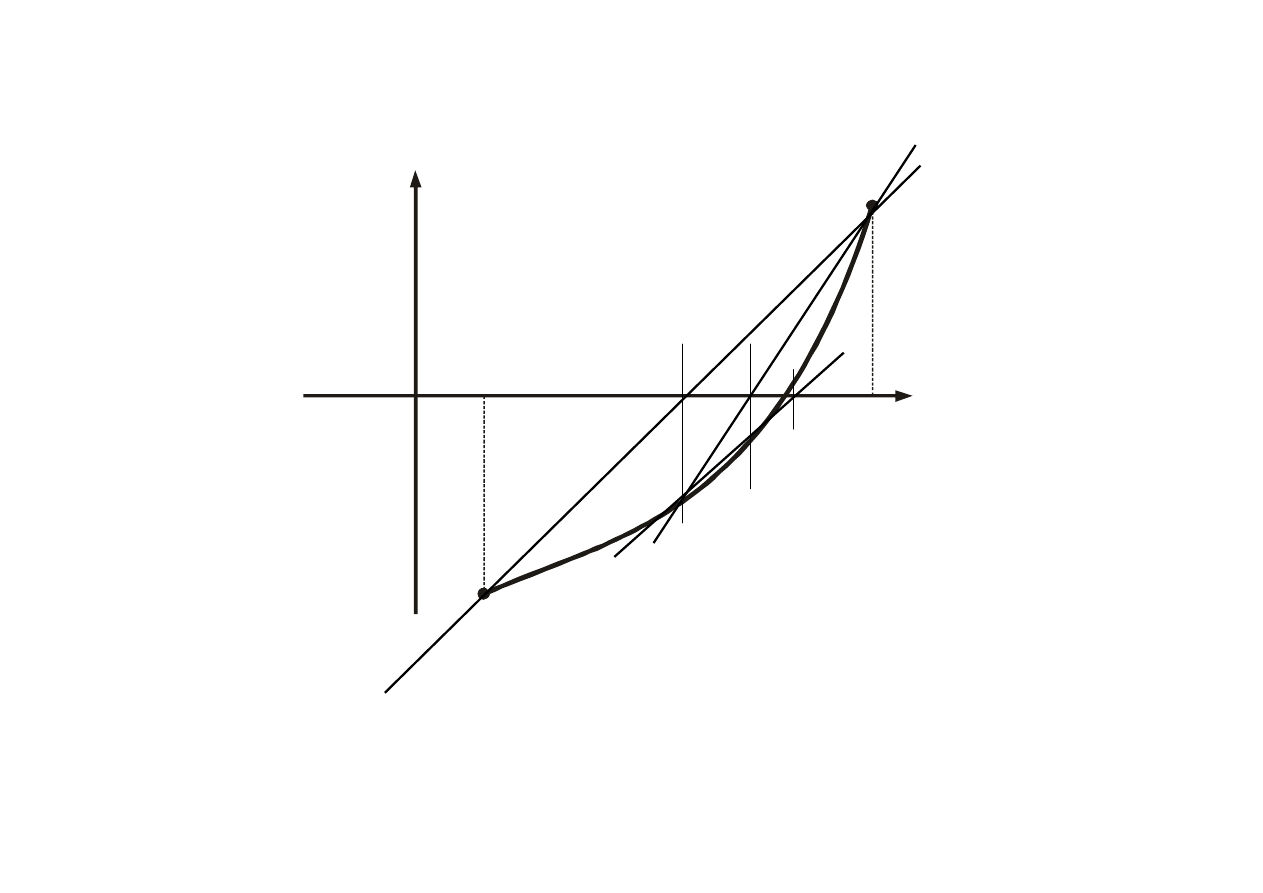
17
Ilustracja graficzna
f(x)
x
f(b)
f(a)
a
b
0
x
(1)
f (x
(1)
) ·f (b) < 0
x
(0)
= b
x
(0)
x
(2)
x
(3)

18
Przykład
0
6
2
3
=
−
−
x
x
Wyszukiwarka
Podobne podstrony:
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
Reguła?lsi i metoda siecznyc1
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
rozwiazywanie rownan metoda siecznych
metoda stycznych, siecznych, bisekcji
Metoda magnetyczna MT 14
Metoda animacji społecznej (Animacja społeczno kulturalna)
Metoda Weroniki Sherborne[1]
Metoda Ruchu Rozwijajacego Sherborne
Projet metoda projektu
METODA DENNISONA
PFM metodaABC
Metoda z wyboru usprawniania pacjentów po udarach mózgu
metoda sherborne
Metoda symultaniczno sekwencyjna
więcej podobnych podstron