70

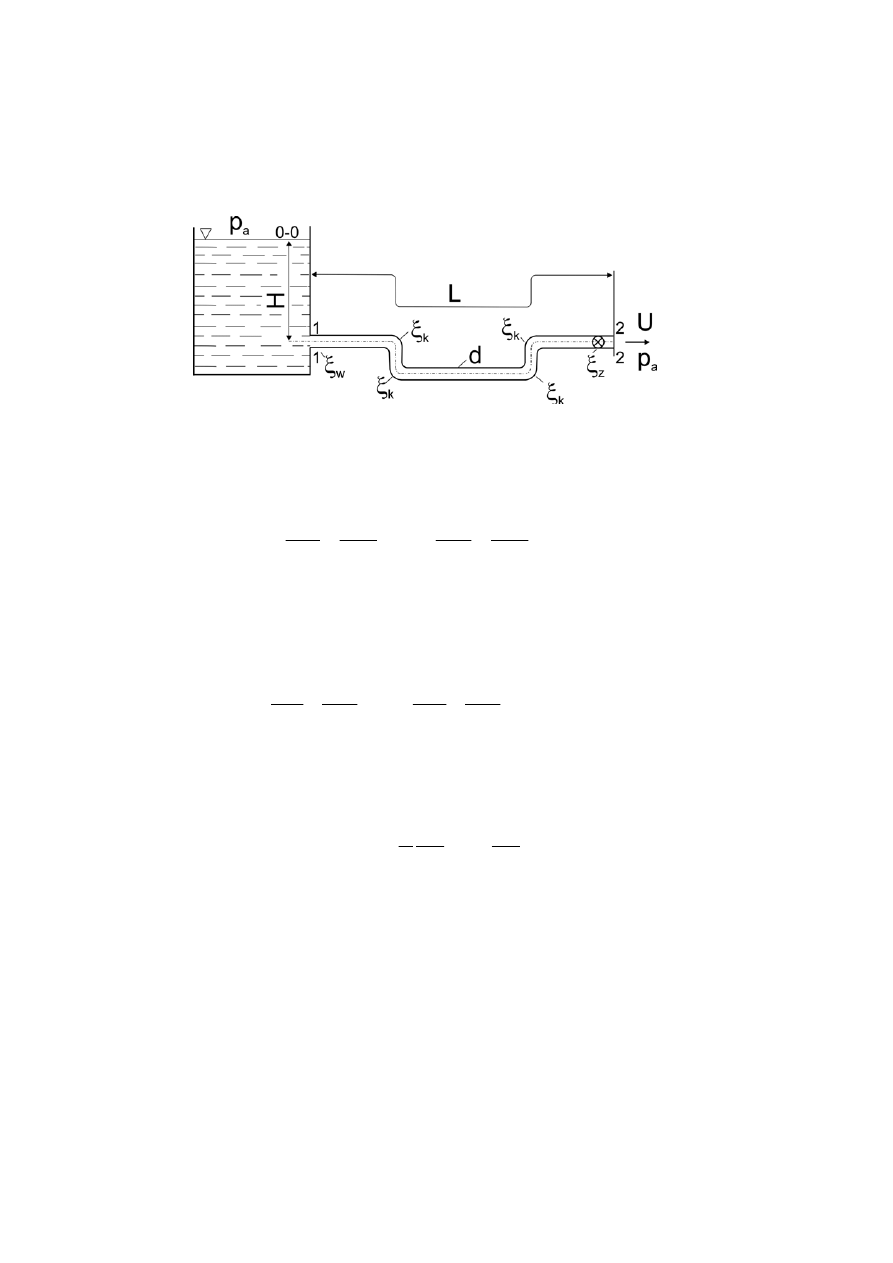
5. Równanie Bernoulliego dla przepływu płynów rzeczywistych

Prostota równania Bernoulliego sprawia że stosowane jest ono również dla przepływu płynu

lepkiego, mimo że w tym przypadku wszystkie przemiany energii są nieodwracalne.

W przepływie między przekrojami 1-1 i 2-2 płyn lepki traci energię na skutek tarcia wewnętrznego
jak i tarcia o ściankę kanału, tak więc całkowita energia przepływającego płynu w przekroju 1-1 jest
większa od całkowitej energii w przekroju 2-2 i relację pomiędzy całkowitymi energiami w tym
przypadku można zapisać:

2

2

2

2

1

1

2

1

z

g

ρ

p

2g

U

z

g

ρ

p

2g

U

+

⋅

+

>

+

⋅

+

Jeżeli w powyższej zależności znak ">" zastąpimy przez "=” wówczas dla zachowania równości
energii występującej po obu stronach równania konieczne jest zwiększenie prawej strony o energię
straconą wskutek lepkości płynu, w wyniku czego otrzymamy równanie Bernoulliego dla płynu
lepkiego:

str

2

2

2

2

1

1

2

1

h

z

g

ρ

p

2g

U

z

g

ρ

p

2g

U

+

+

⋅

+

=

+

⋅

+

Człon h

str

oznacza wysokość strat energii pomiędzy rozpatrywanymi przekrojami, które są sumą

strat tarcia na długości rurociągu i wszystkich strat miejscowych na poszczególnych elementach
rurociągu:

g

2

U

g

2

U

d

L

h

2

2

str

∑ξ

+

⋅

λ

=

gdzie:

λ

- współczynnik strat tarcia

λ

= f(Re, prędkości, chropowatości),

ξ

- współczynnik strat lokalnych

ξ

= f(rodzaju przeszkody, prędkości).

71

PRZYKŁADOWE ZADANIA

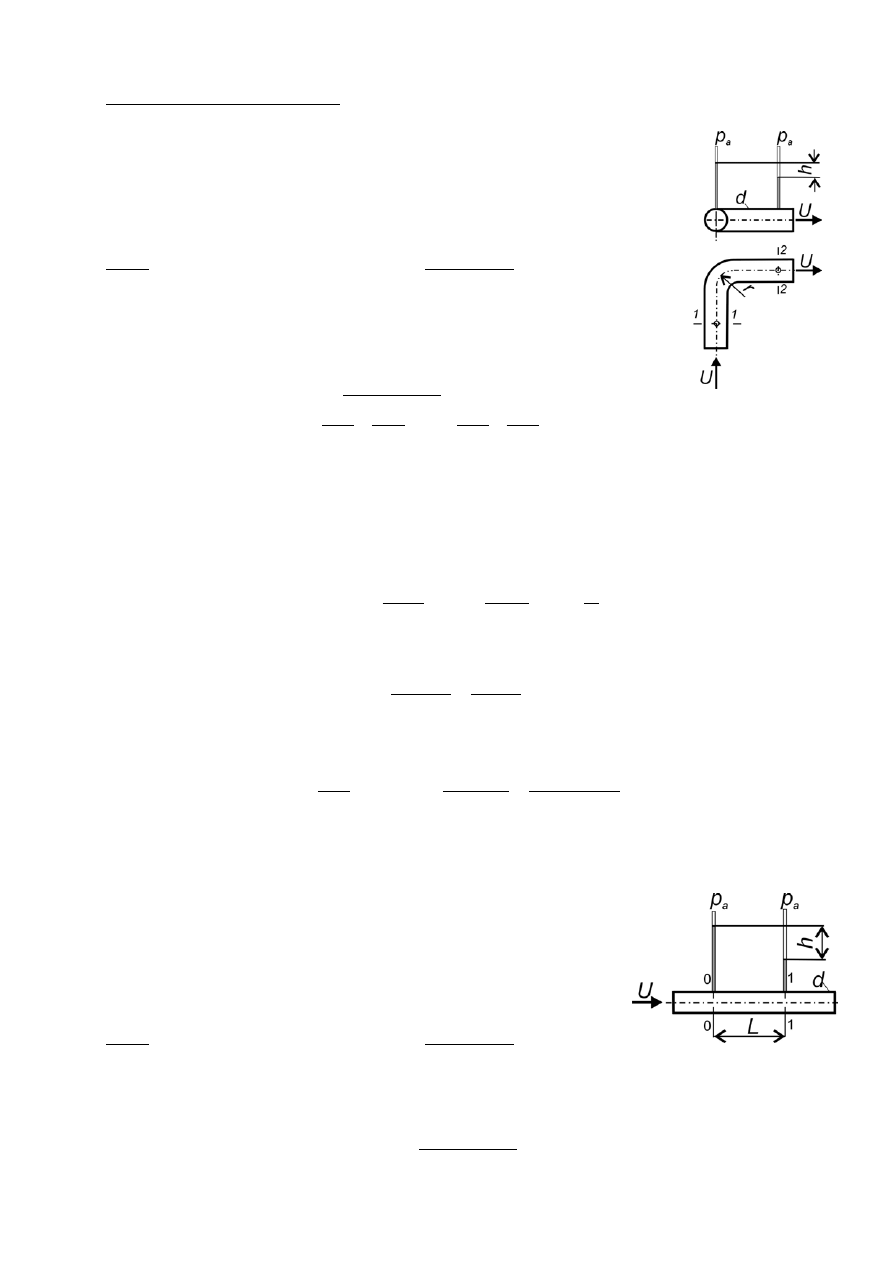
Zadanie 5.1 (poz. bibl. [3], zad. 6.4.2, str. 113)
Przez przewód z poziomym kolanem przepływa woda. Zmierzona różnica
poziomów wody w rurkach piezometrycznych przed i za kolanem wynosiła
h = 20 mmH

2

O. Średnica przewodu d = 30 mm, strumień objętości przepływu

Q = 1.5 dm

3

/s. Obliczyć wartość współczynnika straty lokalnej kolana.

Dane:

Wyznaczyć:

h = 20 mmH

2

O

ξ

d = 30 mm
Q

= 1.5 dm

3

/s

Rozwiązanie:

str

2

2

2

2

1

1

2

1

h

z

g

ρ

p

g

2

U

z

g

ρ

p

g

2

U

+

+

⋅

+

⋅

=

+

⋅

+

⋅

1-1 – przekrój, w którym wpływa czynnik do kolana
2-2 – przekrój, w którym wypływa czynnik z kolana

U

1

= U

2

= U

z

1

= z

2

= 0

4

d

U

Q

2

⋅

π

=

⇒

s

m

2.12

d

π

Q

4

U

2

=

⋅

⋅

=

Z równania Bernoulliego po uproszczeniu otrzymujemy stratę ciśnienia, spowodowaną zmianą
kształtu geometrycznego kolana:

m

0.02

g

ρ

g

ρ

h

g

ρ

p

p

h

2

1

str

=

⋅

⋅

⋅

=

⋅

−

=

którą możemy wyrazić wzorem:

g

2

U

h

2

str

⋅

⋅

ξ

=

⇒

087

.

0

12

.

2

02

.

0

81

.

9

2

U

h

g

2

2

2

str

=

⋅

⋅

=

⋅

⋅

=

ξ

Otrzymujemy:

ξ

= 0.087

Zadanie 5.2 (poz. bibl. [3], zad. 6.4.3, str. 113)

W poziomym przewodzie o średnicy

d = 25 mm zmierzono ciśnienie

w dwóch przekrojach odległych o

L = 8 m. Na podstawie różnicy

wysokości ciśnień, która wynosiła

h = 770 mmH

2

O, obliczyć

współczynnik strat tarcia

λ

, jeśli prędkość wody w przewodzie

U = 1.5 m/s.

Dane:

Wyznaczyć:

d = 25 mm

λ

L = 8 m
h = 770 mmH

2

O

U = 1.5 m/s

Rozwiązanie:

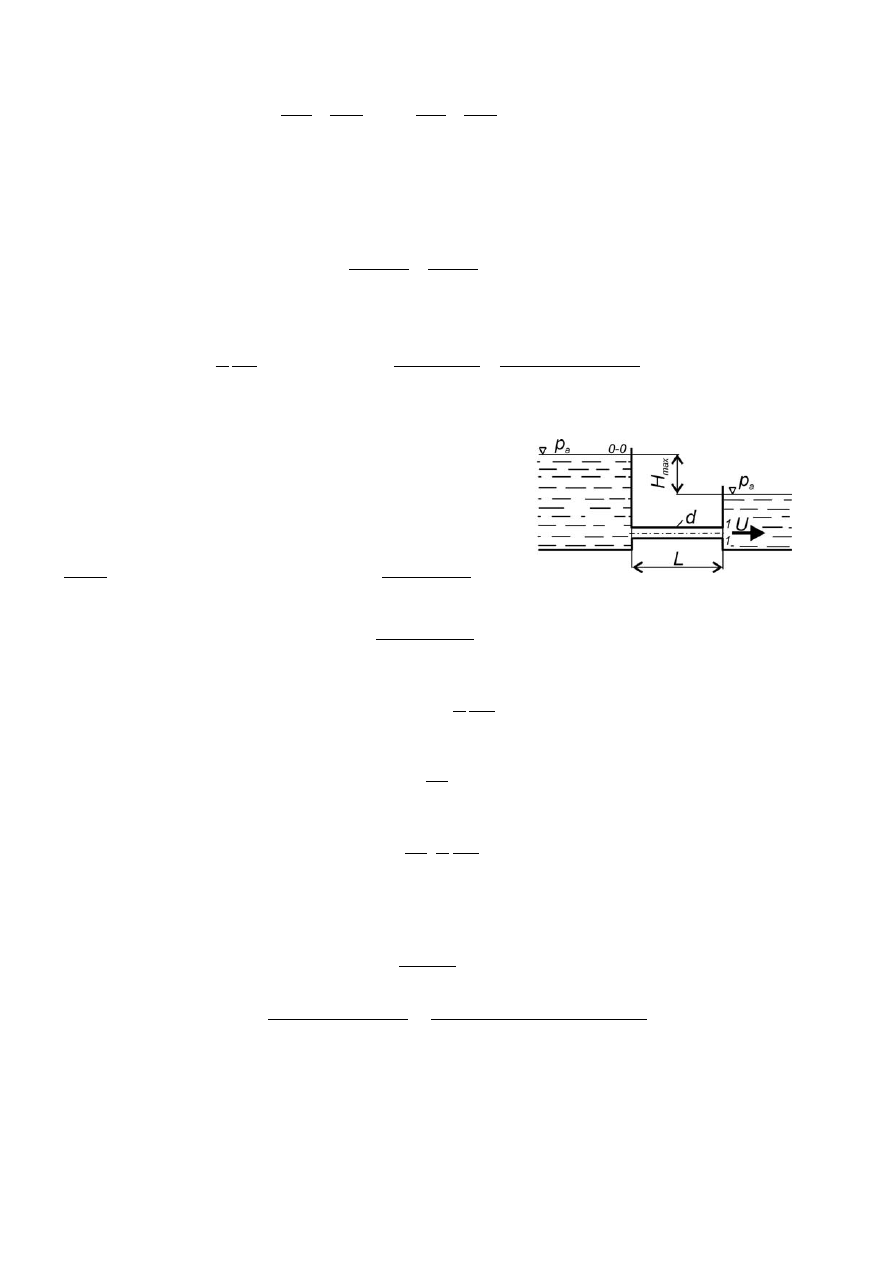
72

str

1

1

2

1

0

0

2

0

h

z

g

ρ

p

2g

U

z

g

ρ

p

2g

U

+

+

⋅

+

=

+

⋅

+

U

0

=

U

1

=

U

z

0

=

z

1

= 0

Z równania Bernoulliego po uproszczeniu otrzymujemy różnicę ciśnień, określającą stratę ciśnienia
na długości przewodu:

m

77

.

0

g

g

h

g

p

p

h

1

0

str

=

⋅

ρ

⋅

ρ

⋅

=

⋅

ρ

−

=

którą możemy wyrazić wzorem:

g

2

U

d

L

h

2

str

⋅

λ

=

⇒

021

.

0

5

.

1

8

025

.

0

77

.

0

81

.

9

2

U

L

d

h

g

2

2

2

str

=

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

λ

Otrzymujemy:

λ

= 0.021

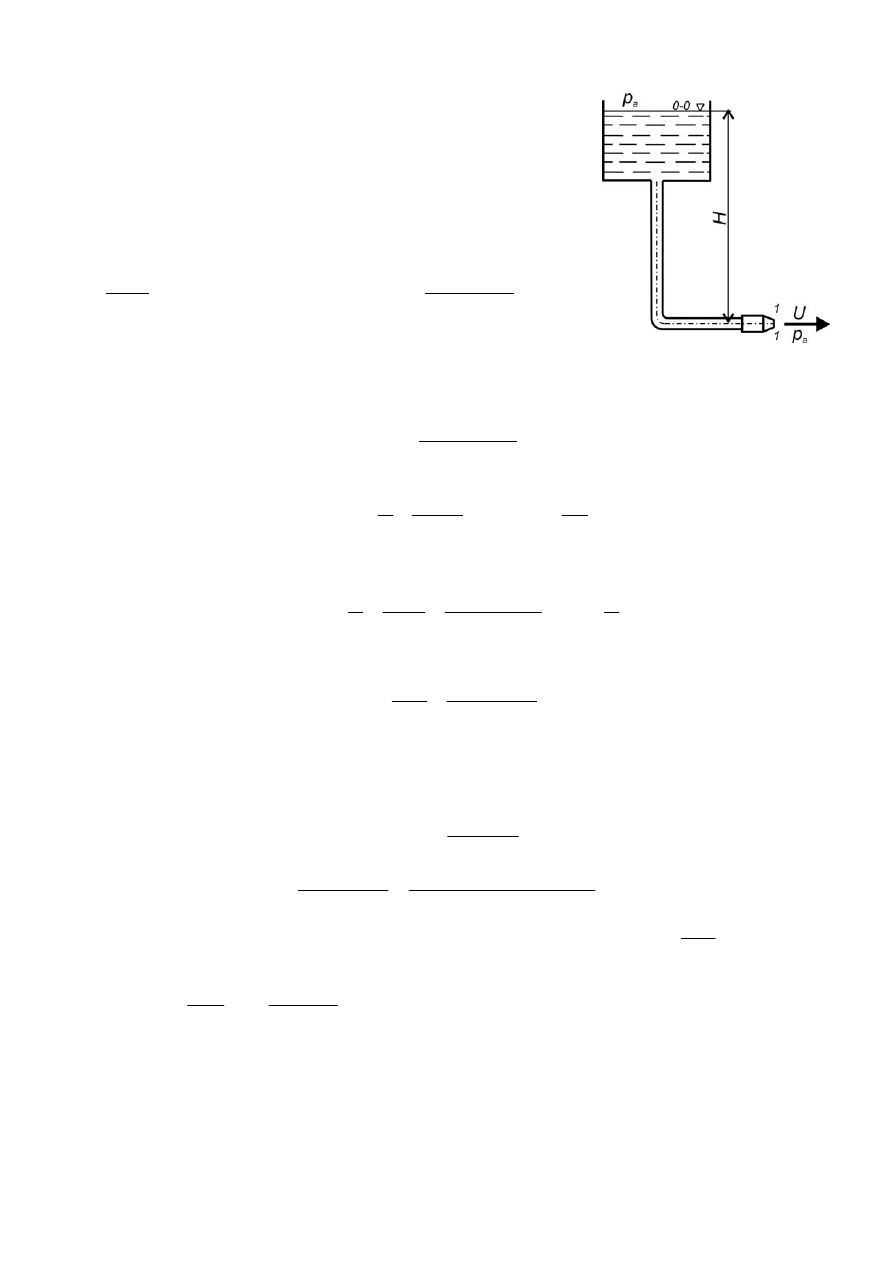
Zadanie 5.3 (poz. bibl. [3], zad. 6.4.4, str. 114)
Przewodem o średnicy

d = 1 cm i długości L = 2 m przepływa

woda z lewego zbiornika do prawego na skutek różnicy
poziomów cieczy w zbiornikach. Jaka może być maksymalna
wysokość

H

max

, aby w przewodzie był przepływ laminarny?

Uwzględnić tylko straty tarcia.
Dane:

Wyznaczyć:

d = 1 cm

H

max

L = 2 m

Rozwiązanie:

Dla uproszczenia pomijamy energię kinetyczną przepływającego płynu w przewodzie i zakładamy,
że rozporządzalna wysokość

H zostaje w całości zużyta na pokonanie straty tarcia w przewodzie:

g

2

U

d

L

H

h

2

str

⋅

λ

=

=

W przepływie laminarnym współczynnik strat tarcia określamy zależnością:

Re

64

=

λ

,

wtedy:

g

U

d

L

Re

32

H

2

⋅

=

W tym przypadku

H

max

odpowiada prędkości

U

max

dla której liczba

Re

max

wyniesie Re = 2300:

2300

U

d

Re

max

max

=

ν

⋅

=

3

2

7

3

max

2

max

01

.

0

81

.

9

2300

)

10

8

.

9

(

2

32

d

g

Re

L

32

H

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

ν

⋅

⋅

=

−

Po podstawieniu otrzymujemy:

H

max

= 0.015 m

73

Zadanie 5.4 (poz. bibl. [3], zad. 6.4.5, str. 114)
Hartowniczy piec jest opalany olejem opałowym, zużycie którego
wynosi

m&

= 300 kg/h. Gęstość oraz kinematyczny współczynnik

lepkości oleju wynoszą odpowiednio:

ρ

r

= 880 kg/m

3

i

ν

= 0.25 cm

2

/s. Określić ciśnienie oleju w przewodzie przed

rozpylaczem, jeśli zbiornik z olejem opałowym znajduje się na
wysokości

H = 8 m nad osią rozpylacza. Długość przewodu

L = 30 m, średnica d = 25 mm.

Dane:

Wyznaczyć:

m&

= 300 kg/h = 0.0833 kg/s

p

ρ

= 880 kg/m

3

ν

= 0.25 cm

2

/s = 0.25

⋅ 10

-4

m

2

/s

H = 8 m
L = 30 m
d = 25 mm

Rozwiązanie:

Strumień objętości wypływającej ropy:

s

m

m

Q

3

5

10

46

.

9

880

0833

.

0

−

⋅

=

=

=

ρ

&

Prędkość średnia:

s

m

193

.

0

025

.

0

14

.

3

10

46

.

9

4

d

Q

4

S

Q

U

2

5

2

=

⋅

⋅

⋅

=

⋅

π

⋅

=

=

−

Liczba Reynoldsa:

193

10

25

.

0

025

.

0

193

.

0

d

U

Re

4

=

⋅

⋅

=

ν

⋅

=

−

Liczba

Re wskazuje na przepływ laminarny. Stratę ciśnienia na wskutek tarcia na długości L

obliczamy z prawa Hagena-Poiseuille’a:

L

128

d

p

Q

4

⋅

µ

⋅

⋅

∆

⋅

π

=

Pa

.

.

.

.

d

L

Q

p

6509

025

0

14

3

30

022

0

10

46

9

128

128

4

5

4

=

⋅

⋅

⋅

⋅

⋅

=

⋅

π

⋅

µ

⋅

⋅

=

∆

−

gdzie dynamiczny współczynnik lepkości

s

m

kg

⋅

=

⋅

⋅

=

⋅

=

−

022

.

0

880

10

25

.

0

4

ρ

ν

µ

Wysokość ciśnienia przed rozpylaczem:

m

g

p

H

H

o

25

.

7

81

.

9

880

6509

8

=

⋅

−

=

⋅

∆

−

=

ρ

słupa oleju opałowego

74

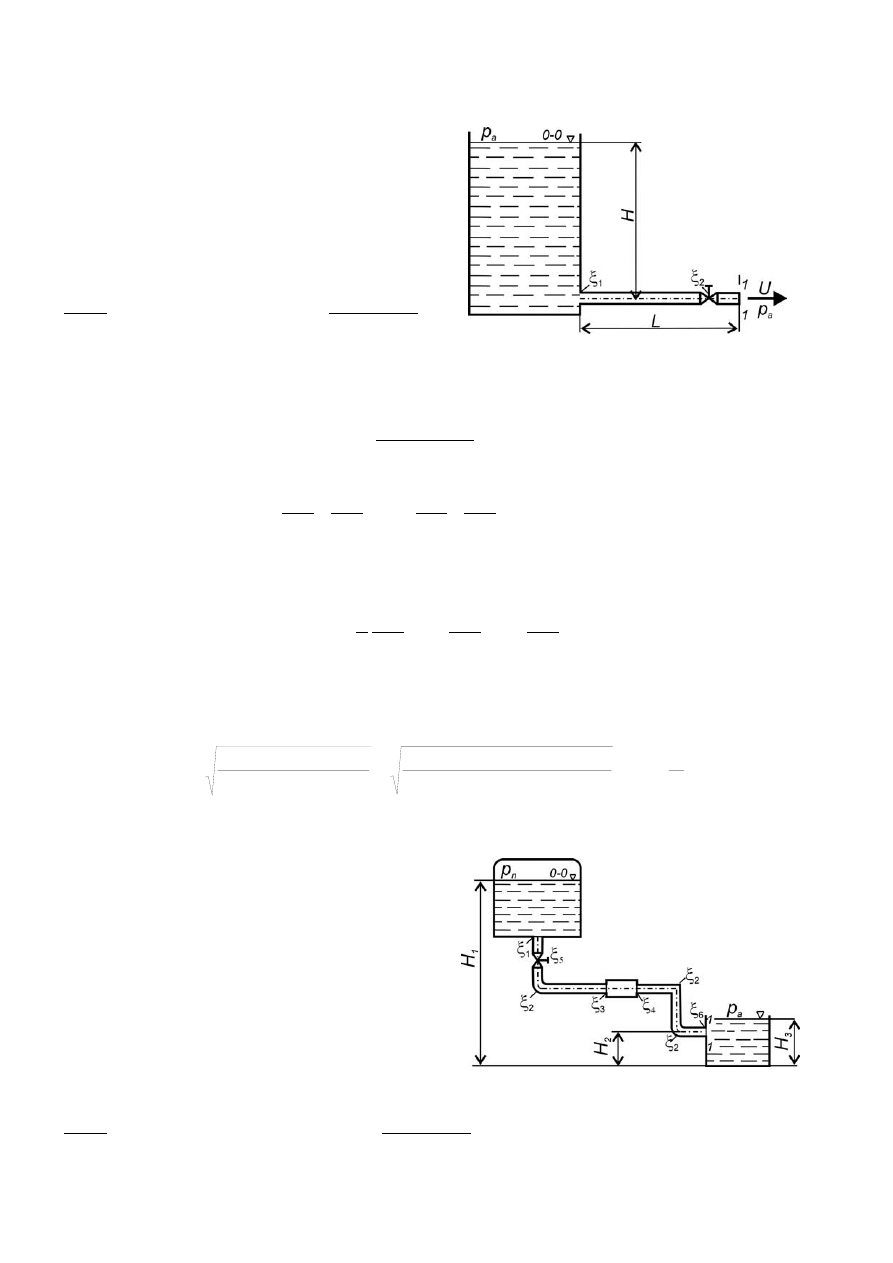
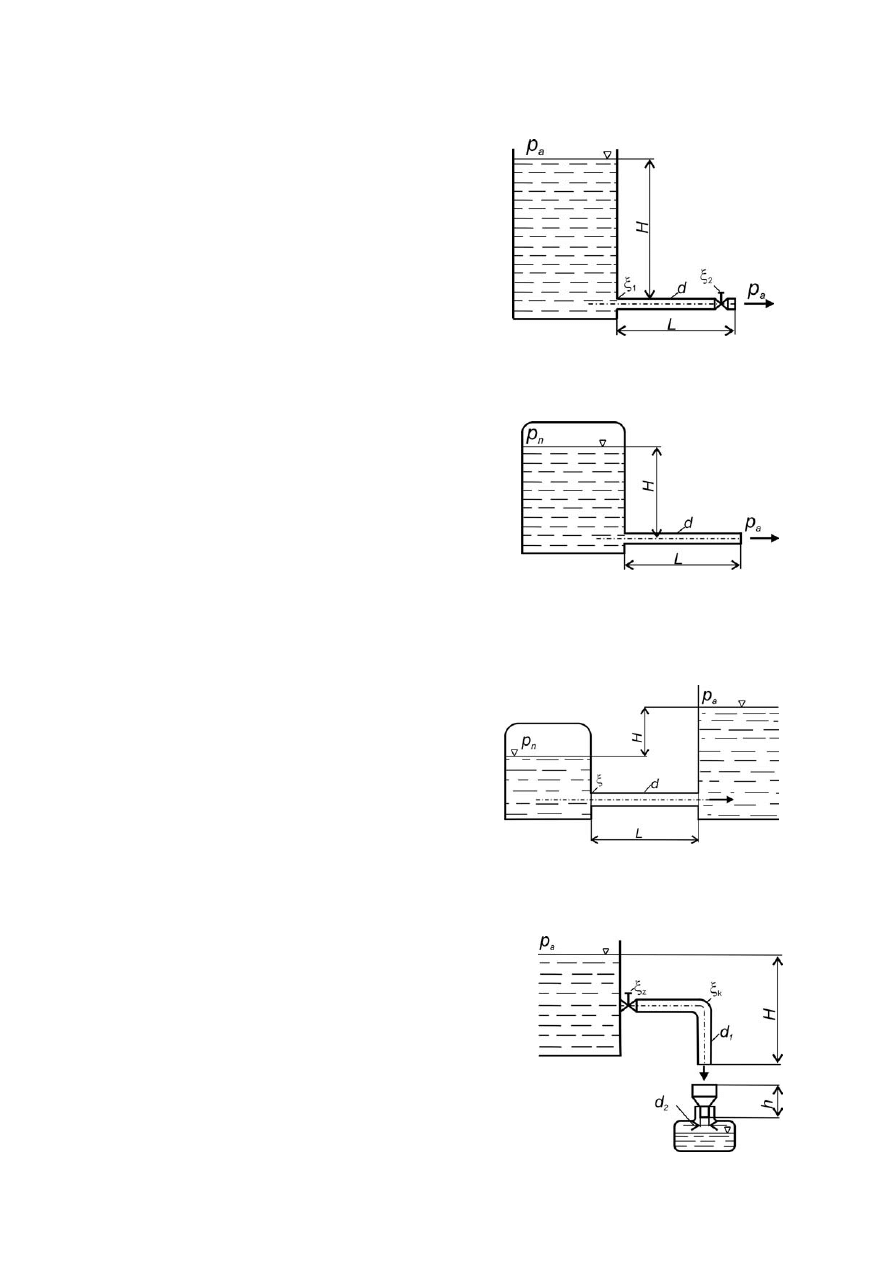
Zadanie 5.5

(poz. bibl. [3], zad. 6.4.9, str. 115)

Do otwartego zbiornika wypełnionego wodą
podłączony jest przewód o średnicy d = 50 mm i
długości L = 25 m. Obliczyć prędkość wypływu
wody z przewodu, jeśli H = 5 m. Uwzględnić straty
lokalne i tarcia, przyjąć:

ξ

1

= 0.5 (strata na wypływie

ze zbiornika),

ξ

2

= 4 (strata na zaworze),

λ

= 0.03.

Dane:

Wyznaczyć:

d

= 50 mm

U

L

= 25 m

H

= 5 m

ξ

1

= 0.5,

ξ

2

= 4

λ

= 0.03

Rozwiązanie:

Równanie Bernoulliego dla przekrojów 0-0 i 1-1:

str

1

1

2

1

0

0

2

0

h

z

g

ρ

p

2g

U

z

g

ρ

p

2g

U

+

+

⋅

+

=

+

⋅

+

zakładając: U

0

= 0, p

0

= p

1

= p

a

, z

0

= H

g

2

U

g

2

U

g

2

U

d

L

h

2

1

2

2

1

1

2

1

str

⋅

ξ

+

⋅

⋅

ξ

+

⋅

λ

=

Podstawiając powyższe zależności do równania Bernoulliego, możemy określić wartość prędkości
w przekroju wylotowym

s

m

18

.

2

)

05

.

0

/

25

(

03

.

0

4

5

.

0

1

5

81

.

9

2

d

/

L

1

H

g

2

U

2

1

1

=

⋅

+

+

+

⋅

⋅

=

⋅

λ

+

ξ

+

ξ

+

⋅

⋅

=

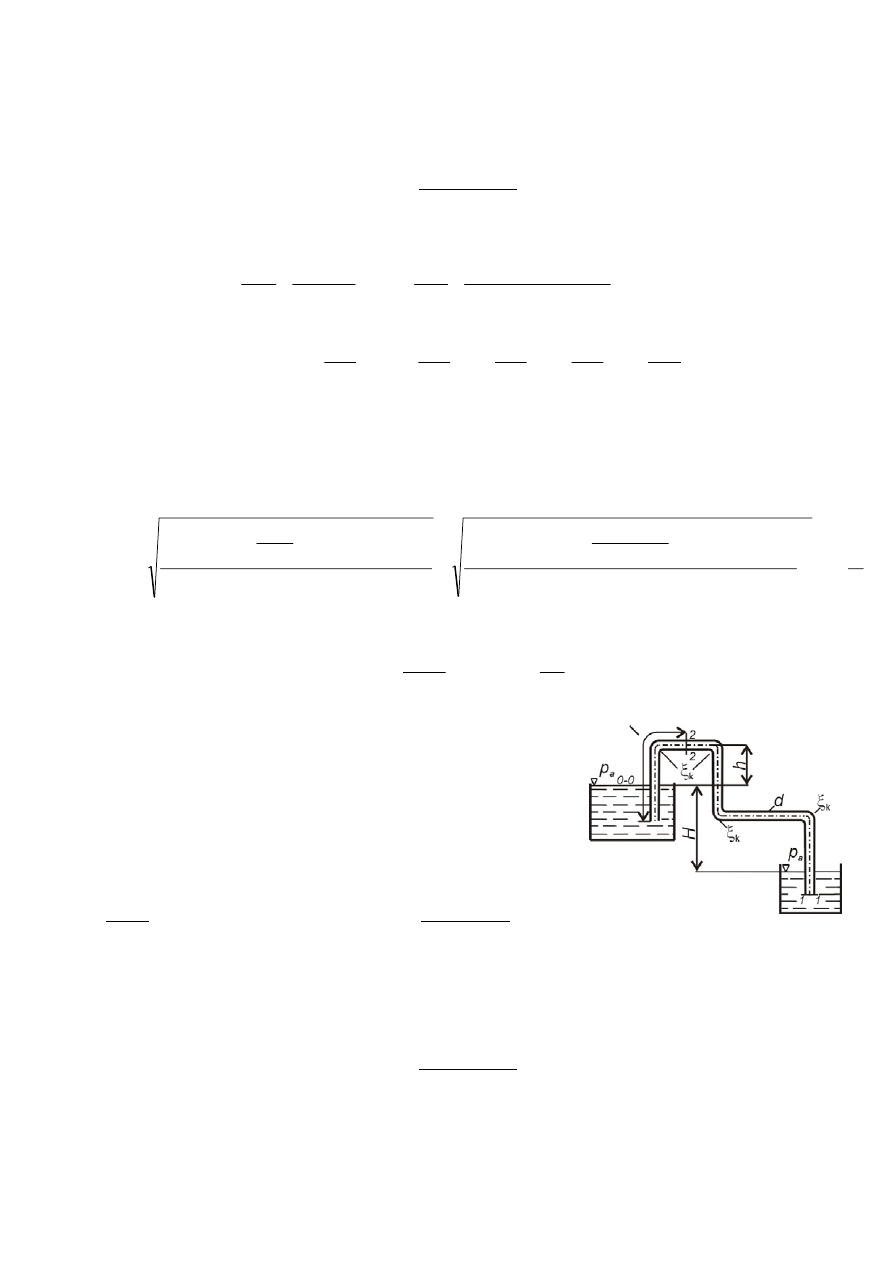
Zadanie 5.6

(poz. bibl. [3], zad. 6.4.11, str. 115)

Woda znajdująca się w górnym zamkniętym
zbiorniku pod ciśnieniem

p

n

= 10000 N/m

2

przepływa do dolnego, otwartego zbiornika.
Określić strumień objętości wody, jeśli H

1

= 10 m,

H

2

= 1 m, H

3

= 2 m, średnica przewodu d = 100 mm,

średnica odstojnika D = 200 mm, współczynnik
straty lokalnej zaworu

ξ

5

= 4, promień kolan

R

= 100 mm. Straty tarcia w rurociągu pominąć.

Współczynniki strat miejscowych wynoszą:

ξ

1

= 0.5,

ξ

2

= 0.29 dla R/d = 1,

ξ

3

= [1-(f/F)]

2

= [1

−(1/4)]

2

=

0.56,

ξ

4

= 0.37 dla f/F = 1/4,

ξ

6

= 1.

Dane:

Wyznaczyć:

p

n

= 10000 N/m

2

Q

H

1

= 10 m, H

2

= 1 m, H

3

= 2 m

75

d

= 100 mm, D = 200 mm

R =

100 mm

ξ

1

= 0.5,

ξ

2

= 0.29,

ξ

3

= 0.56,

ξ

4

= 0.37,

ξ

5

= 4,

ξ

6

= 1

Rozwiązanie:

Obieramy przekrój 0-0 na powierzchni zwierciadła w lewym zbiorniku i przekrój 1-1 na wylocie z
przewodu do prawego zbiornika. Równanie Bernoulliego dla tych przekrojów:

str

a

2

1

1

n

a

2

0

h

H

g

ρ

g

)ρ

H

(H

p

2g

U

H

g

ρ

p

p

2g

U

+

+

⋅

⋅

−

+

+

=

+

⋅

+

+

2

2

3

Sumaryczna strata energii wyraża się wzorem:

g

2

U

g

2

U

g

2

U

g

2

U

3

g

2

U

h

2

2

3

2

1

4

2

1

5

2

1

2

2

1

1

str

⋅

⋅

ξ

+

⋅

⋅

ξ

+

⋅

⋅

ξ

+

⋅

⋅

ξ

⋅

+

⋅

⋅

ξ

=

zakładamy:
U

0

= 0, U

2

= U

1

(d/D)

2

Podstawiając powyższe zależności do równania Bernoulliego, możemy określić wartość prędkości
w przekroju 1-1:

s

m

D

d

H

H

g

p

g

U

n

12

.

5

)

2

.

0

/

1

.

0

(

56

.

0

4

37

.

0

29

.

0

3

5

.

0

1

2

10

81

.

9

1000

10000

81

.

9

2

)

/

(

3

1

)

(

2

4

4

3

5

4

2

1

3

1

1

=

⋅

+

+

+

⋅

+

+













−

+

⋅

⋅

⋅

=

+

+

+

⋅

+

+

−

+

⋅

⋅

⋅

=

ξ

ξ

ξ

ξ

ξ

ρ

Strumień objętości natomiast wynosi:

s

m

041

.

0

U

4

d

Q

3

1

2

=

⋅

⋅

π

=

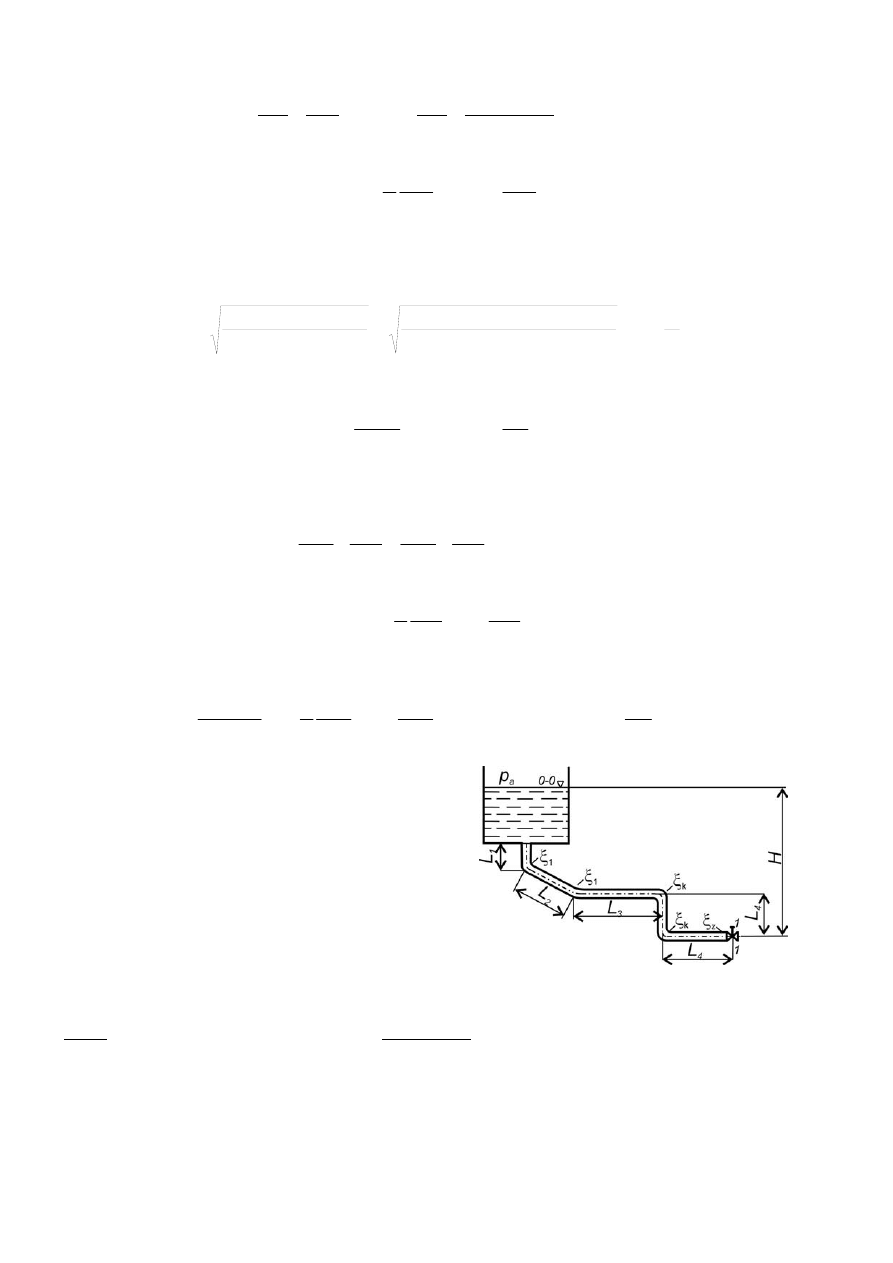
Zadanie 5.7

(poz. bibl. [3], zad. 6.4.12, str. 116)

Woda przepływa z górnego zbiornika do dolnego przez lewar o
średnicy d = 50 mm i całkowitej długości L = 30 m. Określić:
strumień objętości przepływu oraz podciśnienie w najwyższej
część lewara, jeśli różnica poziomów wody w zbiornikach
wynosi H = 4.5 m. Położenie górnego kolana h = 2.5 m,
współczynniki strat tarcia

λ

= 0.03, kolan

ξ

k

= 0.29. Dane:

l

= 12 m. Gęstość wody przyjąć ρ = 1000 kg/m

3

.

Dane: Wyznaczyć:
d

= 50 mm

Q, p

a

-

p

2

L =

30 m, l

= 12 m

H

= 4.5 m, h = 2.5 m

λ

= 0.03

ξ

k

= 0.29

ρ

= 1000 kg/m

3

Rozwiązanie:

Obieramy przekrój 0-0 na zwierciadle w lewym zbiorniku i przekrój 1-1 na wylocie z przewodu do
prawego zbiornika. Równanie Bernoulliego dla tych przekrojów:

76

str

a

2

1

a

2

0

h

g

ρ

g

ρ

x

p

2g

U

x

H

g

ρ

p

2g

U

+

⋅

⋅

⋅

+

+

=

+

+

⋅

+

g

U

g

U

d

L

h

k

str

⋅

⋅

⋅

+

⋅

⋅

=

2

4

2

2

1

2

1

ξ

λ

zakładamy: U

0

= 0, x - głębokość zanurzenia wylotu.

Podstawiając powyższe zależności do równania Bernoulliego, możemy określić wartość prędkości
w przekroju 1-1:

s

m

1

.

2

)

05

.

0

/

30

(

03

.

0

29

.

0

4

1

5

.

4

81

.

9

2

)

d

/

L

(

4

1

H

g

2

U

k

1

=

⋅

+

⋅

+

⋅

⋅

=

λ

+

ξ

⋅

+

⋅

⋅

=

Strumień objętości wynosi:

s

m

U

d

Q

3

1

2

0041

.

0

4

=

⋅

⋅

=

π

Aby obliczyć ciśnienie w najwyższym punkcie przewodu, obieramy przekroje 0-0 i 2-2, dla których
zapisujemy równanie Bernoulliego:

str

2

2

2

a

2

0

h

h

g

ρ

p

2g

U

g

ρ

p

2g

U

+

+

⋅

+

=

⋅

+

g

U

g

U

d

l

h

k

str

2

2

2

2

2

2

⋅

ξ

+

⋅

λ

=

U

0

= 0, U

2

= U

1

Po uproszczeniu i przekształceniu równania Bernoulliego otrzymujemy:

2

m

N

42000

O

mH

4.2

h

2g

U

ξ

2g

U

d

l

λ

g

ρ

p

p

2

2

2

k

2

2

2

a

≈

=

+

⋅

+

⋅

=

⋅

−

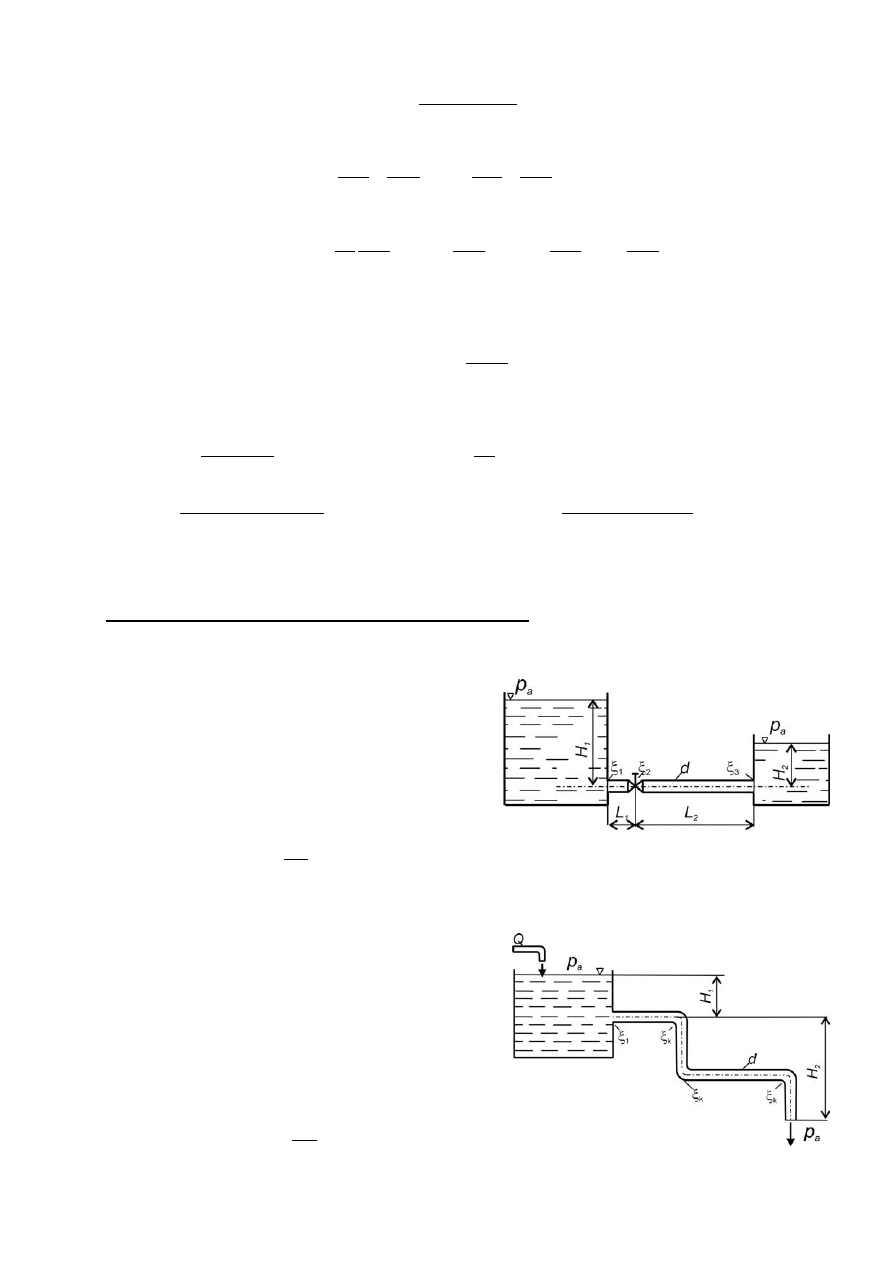
Zadanie 5.8

(poz. bibl. [3], zad. 6.4.16, str. 116)

Przez przewód o średnicy d = 75 mm wypływa woda
ze zbiornika do atmosfery (na skutek różnicy
poziomów H) w ilości Q = 8.1 dm

3

/s. Określić różnicę

H

i między poziomem cieczy w zbiorniku a wylotem z

przewodu, jeśli długości odcinków wynoszą: L

1

= 1 m,

L

2

= 6 m, L

3

= 60 m, L

4

= 3 m, L

5

= 70 m; współczynnik

straty lokalnej zaworu

ξ

z

= 4, współczynnik straty

lokalnej kolana

ξ

k

= 0.29; współczynnik straty lokalnej

kolana o mniejszej krzywiźnie

ξ

1

= 0.5; współczynnik

strat tarcia

λ

= 0.028.

Dane:

Wyznaczyć:

d

= 75 mm

H

Q

= 8.1 dm

3

/s

L

1

= 1 m, L

2

= 6 m, L

3

= 60 m,

L

4

= 3 m, L

5

= 70 m

ξ

z

= 4,

ξ

k

= 0.29,

ξ

1

= 0.5

λ

= 0.028

77

Rozwiązanie:

Układamy równanie Bernoulliego dla przekrojów 0-0 i 1-1:

str

1

2

1

0

2

0

h

g

ρ

p

2g

U

H

g

ρ

p

2g

U

+

⋅

+

=

+

⋅

+

,

gdzie suma strat energii wynosi:

g

2

U

g

2

U

2

g

2

U

2

g

2

U

d

L

h

2

1

z

2

1

k

2

1

1

2

1

c

str

⋅

⋅

ξ

+

⋅

⋅

ξ

⋅

+

⋅

⋅

ξ

⋅

+

⋅

⋅

λ

=

,

przy czym całkowita długość rurociągu: L

c

= L

1

+ L

2

+ L

3

+ L

4

+ L

5

.

Zakładamy że : U

0

= 0, ciśnienia w obu przekrojach kontrolnych są jednakowe p

0

= p

1

= p

a

.

Prędkość U

1

obliczamy natomiast z równania ciągłości:

2

1

d

Q

4

U

⋅

π

⋅

=

Podstawiając powyższe zależności do równania Bernoulliego, po przekształceniach znajdujemy
wysokość H:

m

82

.

5

075

.

0

70

3

60

6

1

028

.

0

4

29

.

0

2

5

.

0

2

1

81

.

9

075

.

0

14

.

3

0081

.

0

4

d

L

2

2

1

g

d

Q

4

H

4

2

2

c

z

k

1

4

2

2

=













+

+

+

+

⋅

+

+

⋅

+

⋅

+

⋅

⋅

⋅

=

=













⋅

λ

+

ξ

+

ξ

⋅

+

ξ

⋅

+

⋅

⋅

π

⋅

=

ZADANIA DO SAMODZIELNEGO ROZWIĄZANIA


Zadanie 5.9

(poz. bibl. [3], zad. 6.4.10, str. 115)

Poziomy przewód o średnicy d = 150 mm i
długości L = l

1

+ l

2

(l

1

= 10 m, l

2

= 40 m) łączy dwa

otwarte zbiorniki. W zbiornikach jest woda do
wysokości H

1

= 6 m, H

2

= 2 m. Określić strumień

objętości wody przepływającej z lewego zbiornika
do prawego. Uwzględnić straty lokalne i tarcia:

ξ

1

= 0.5,

ξ

2

= 4,

ξ

3

= 1,

λ

= 0.03.

Odpowiedź:

s

m

039

.

0

Q

3

=

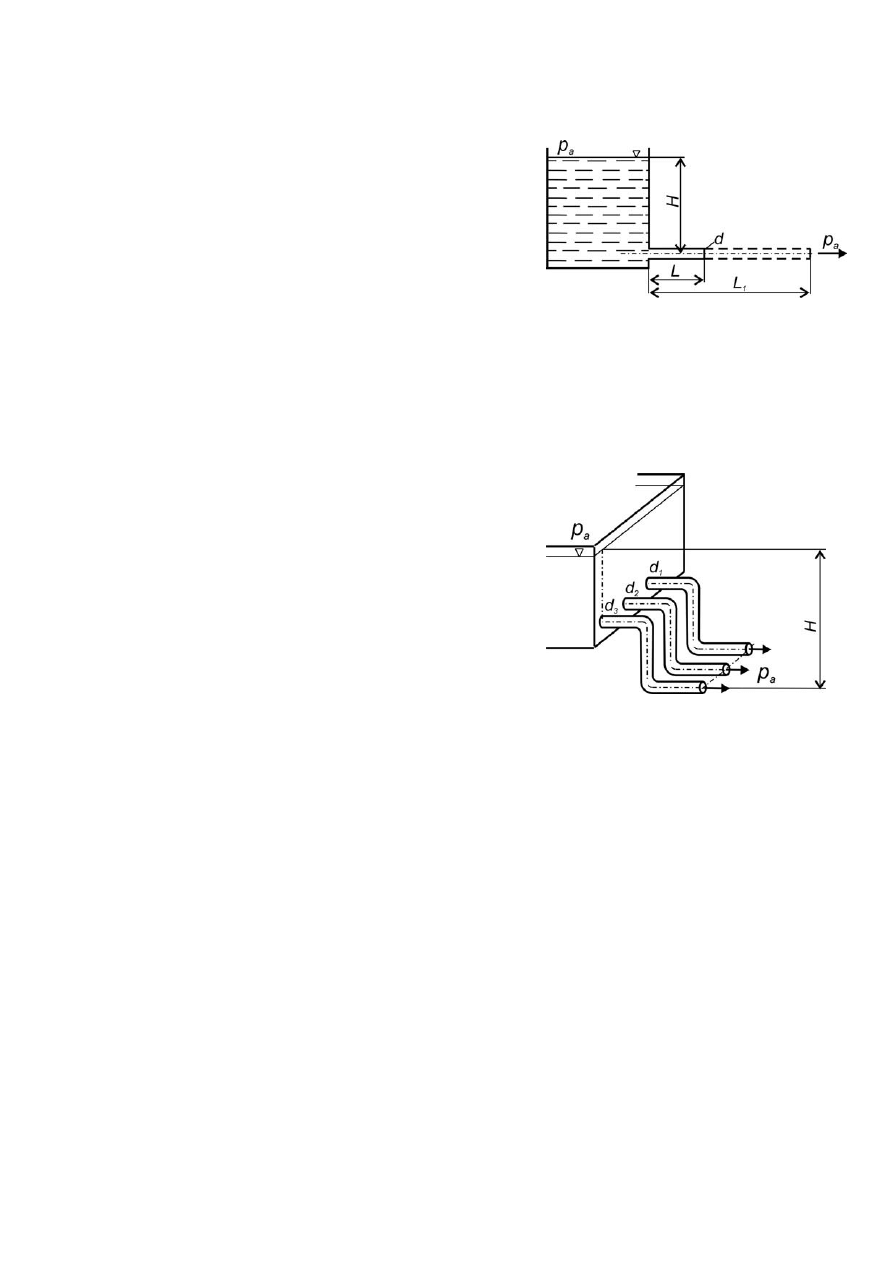
Zadanie 5.10

(poz. bibl. [3], zad. 6.4.13, str. 116)

Określić maksymalny strumień objętości wody
przepływającej przez rurę przelewową, jeśli
H

1

= 0.2 m, H

2

= 5 m, współczynnik strat tarcia

λ

= 0.03, średnica przewodu d = 100 mm, długość

przewodu L = 18 m,

ξ

k

= 0.29,

ξ

1

= 0.5 (H

1

-

odległość od osi rury przelewowej do górnej krawędzi
zbiornika).

Odpowiedź:

s

m

0285

.

0

Q

3

=

78

Zadanie 5.11
Do otwartego zbiornika wypełnionego wodą do poziomu
H

= 30 m podłączony jest przewód o długości L i

średnicy d = 50 mm. Obliczyć ile wynosi długość
przewodu L jeżeli prędkość wypływu wody z przewodu
do atmosfery wynosi 2 m/s. Uwzględnić straty lokalne i
tarcia, przyjmując:

ξ

1

= 0.5,

ξ

2

= 4,

λ

=

0.03. Ciśnienie

powietrza nad lustrem wody i w miejscu wypływu wody
z przewodu do otoczenia wynosi 760 mmHg.

Odpowiedź:

L

= 236 m.

Zadanie 5.12

(poz. bibl. [3], zad. 6.4.23, str. 119)

W zamkniętym zbiorniku zawierającym wodę, nad
powierzchnią zwierciadła znajduje się gaz o ciśnieniu
p

n

= 200 kN/m

2

. Na stałej głębokości H = 1 m pod

zwierciadłem wody dołączono do zbiornika przewód o
długości L = 15 m. Jaka jest średnica przewodu, jeśli
strumień objętości wypływającej wody wynosi
Q

= 7.36 dm

3

/s?. Przyjąć współczynnik strat tarcia równy

λ

= 0.0144. Straty lokalne oraz energię kinetyczną

wylotową pominąć jako małe w stosunku do strat tarcia.

Odpowiedź:

d

= 0.034 m.

Zadanie 5.13

(poz. bibl. [3], zad. 6.4.24, str. 119)

Woda przepływa z lewego zbiornika do prawego rurą o
średnicy d = 40 mm i długości L = 50 m. Nadciśnienie w
lewym zbiorniku p

n

= 120 kN/m

2

, różnica poziomów

cieczy w zbiornikach wynosi H = 3 m. Jaki jest strumień
objętości wody Q, jeżeli współczynnik strat lokalnych na
wejściu wynosi ξ = 0.5 a współczynnik strat tarcia wynosi
λ

= 0.018.

Odpowiedź:

Q

= 0.00357 m

3

/s.

Zadanie 5.14

(poz. bibl. [3], zad. 6.4.26, str. 119)

Przez przewód o średnicy d

1

= 20 mm i przy różnicy wysokości

H

= 1.5 m wypływa benzyna ze zbiornika do lejka

umieszczonego na beczce. Wysokość lejka h = 100 mm,
średnica wylotu rurki lejka d

2

= 30 mm. Określić, czy przy

pełnym otwarciu zaworu benzyna będzie wylewać się z lejka
przez jego górną krawędź. Współczynnik straty lokalnej
zaworu ξ

z

= 3, kolanka ξ

k

= 3. Straty tarcia pominąć.

Odpowiedź:

Q

1

= 0.82 dm

3

/s, Q

2

= 1 dm

3

/s, a więc benzyna

nie będzie się wylewać z lejka.

79

Zadanie 5.15

Ze zbiornika z wodą o stałym poziomie H = 1.5 m
wyprowadzony jest poziomo przewód o średnicy D = 7.5
cm i długości l = 5 m, przez który woda wypływa do
atmosfery. Obliczyć strumień objętości przepływu z
uwzględnieniem strat przepływu.
Jak zmieni się strumień objętości przepływu gdy
przewód zostanie przedłużony do l

1

= 35 m ?.

Jaki musi być poziom wody w zbiorniku aby przy
dłuższym przewodzie utrzymać poprzedni strumień
objętości przepływu ?. W obliczeniach zastosować metodę kolejnych przybliżeń przy założeniu, że
błąd względny obliczenia prędkości nie może przekraczać 3%.

Odpowiedź:

Q

= 17.4 dm

3

/s, Q

1

= 8.1 dm

3

/s, H

1

= 5.7 m.

Zadanie 5.16

(poz. bibl. [3], zad. 6.6.6, str. 123)

Woda z górnego zbiornika jest doprowadzana do
zbiornika dolnego trzema przewodami o średnicach
d

1

= 20 mm, d

2

= 30 mm, d

3

= 60 mm i długościach

l

1

= l

2

= l

3

= 60 m, przy czym wysokość rozporządzalna

H

= 5 m. Jaka musi być średnica przewodu zastępczego

aby jego strumień objętościowy przepływu był równy
sumie strumieni objętościowych wody przepływającej
przez poszczególne przewody?.
Wartość współczynnika strat tarcia

λ

uzależniona jest od

liczby Reynoldsa Re, natomiast straty miejscowe oraz
energię wylotową wody pominąć. Przy obliczaniu
prędkości przepływu zastosować metodę kolejnych
przybliżeń przy założeniu, że błąd względny obliczenia nie może przekraczać 3%.


Odpowiedź:

d

z

= 65 mm, Q

z

= 8.65 dm

3

/s.