
X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Jan KARCZEWSKI
1
Henryk KRÓ L
2
PROPOPOZYCJA METODY PROJEKTOWANIA
SPRĘ Ż YSTO-PLASTYCZNEJ BELKI SPRĘ Ż ONEJ
1. Wprowadzenie
Dotychczas w sprężysto-plastycznej analizie belek wstępnie sprężonych cięgnem zakłada
się, punktową formę przegubó w plastycznych. Takie podejś cie może dawać oszacowania
zbyt optymistyczne, a niekiedy niebezpieczne.
W rzeczywistoś ci strefy plastyczne rozwijają się wzdłuż belki redukując sztywnoś ć w ob-
szarze częś ciowo uplastycznionym. Zjawisko to powoduje, że stan graniczny noś noś ci jest osią-
gany dużo wcześ niej niż wynika to przy założeniu punktowej formy przegubó w plastycznych.
W pracy przedstawiono propozycję metody projektowania belek sprężonych cięgnami
przy założeniu rozprzestrzeniania się strefy plastycznej. Wykorzystano tutaj plastyczną
rezerwę noś noś ci w stadium eksploatacji.
Przedmiotem rozważań jest pełnoś cienna, belka wolnopodparta, obciążona siłą
skupioną przyłożoną w ś rodku rozpiętoś ci, sprężona cięgnem prostoliniowym na całej
długoś ci, umieszczonym w bezpoś rednim sąsiedztwie pasa dolnego.
2. Zał
oż enia
W proponowanej metodzie przyjęto następujące założenia :
- cięgno sprężające gwarantuje, że belka nie ulega zniszczeniu po uformowaniu się w jej
częś ci ś rodkowej przegubu plastycznego, lecz jedynie przechodzi z układu wewnętrznie
statycznie niewyznaczalnego w układ statycznie wyznaczalny zachowując jednocześ nie
możliwoś ć przenoszenia dalszego przyrostu obciążenia.
- Zniszczenie układu konstrukcyjnego belka-cięgno następuje po transformacji przegubu
plastycznego z chwilą, gdy oś plastyczna belki pokryje się z osią cięgna,
- wykorzystanie rezerwy plastycznej dopuszcza się wyłącznie w jednym stadium pracy
belki. W omawianej metodzie jest to stadium eksploatacji,
- praktyczne wykorzystanie plastycznej rezerwy noś noś ci przewidziano do chwili
uformowania się przegubu plastycznego. Drugim warunkiem jaki musi spełniać belka
jest fakt nieprzekroczenia w przekroju ś rodkowym wartoś ci ugięć dopuszczalnych,
1
Profesor, Politechnika Warszawska, Instytut Konstrukcji Budowlanych
2
Mgr inż. (doktorant), Politechnika Warszawska, Instytut Konstrukcji Budowlanych
200
- interakcja uogó lnionych sił wewnętrznych występujących w przekroju belki
modelowana jest krzywą graniczną pomiędzy momentem zginającym i siłą podłużną a
wspó łdziałanie siły poprzecznej z tymi siłami uwzględnione jest wg. hipotezy
Biezuchowa [1], zgodnie z któ rą huberowskie naprężenia zastępcze, w strefach
uplastycznionych przez naprężenia normalne i na osi obojętnej w stanie sprężysto-
plastycznym są ró wne granicy plastycznoś ci (rys. 1),
- krzywa plastyczna, tj. linia rozgraniczająca strefy sprężyste od strefy plastycznej
przyjmuje (licząc do osi symetrii) kształt paraboli (rys. 2) o ogó lnym ró wnaniu:
( )
n
1
n
3
n
3
2
n
2
1
n
1
a
z
a
...
z
a
z
a
z
a
z
+
+
+
+
+
=
-
-
-
-
j
(1)
- fragment belki, w któ rym występuje strefa odkształceń plastycznych traktuje się jako
częś ć o zredukowanej sztywnoś ci odpowiednio do przebiegu funkcji redukujących
moment bezwładnoś ci w tym obszarze (rys. 3),
- całkowite ugięcie stanowi sumę ugięcia od momentu zginającego u(x)
m
i siły
poprzecznej u(x)
t
, stąd ró wnania linii ugięcia w poszczegó lnych przedziałach (rys. 4)
przyjmują postać:
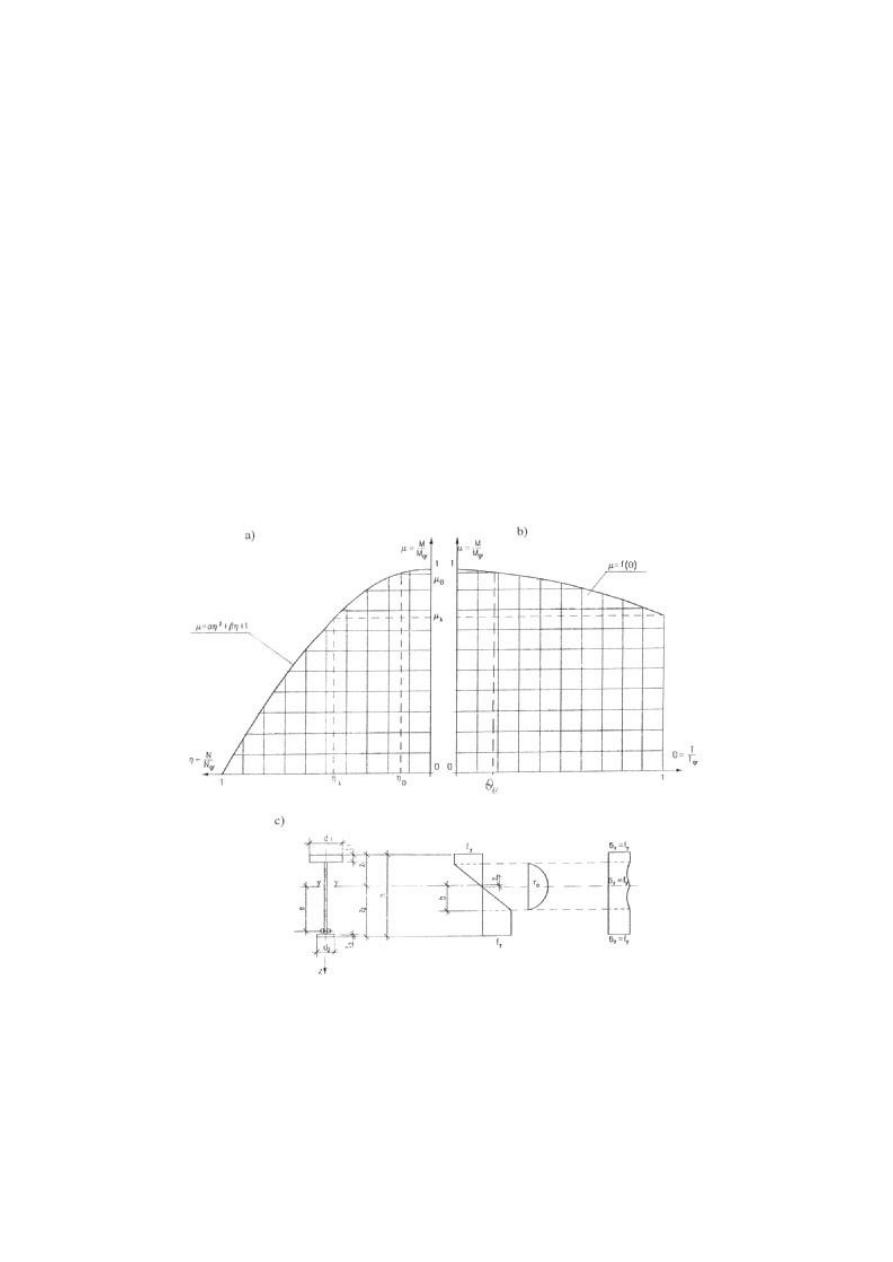
Rys. 1. Model interakcji uogó lnionych sił wewnętrznych z uwzględnieniem hipotezy
Biezuchowa :a) krzywa graniczna
m
= f(
h
); b) krzywa graniczna
m
= f(
q
); c) rozkład
naprężeń normalnych i ś cinających wg hipotezy Biezuchowa
201
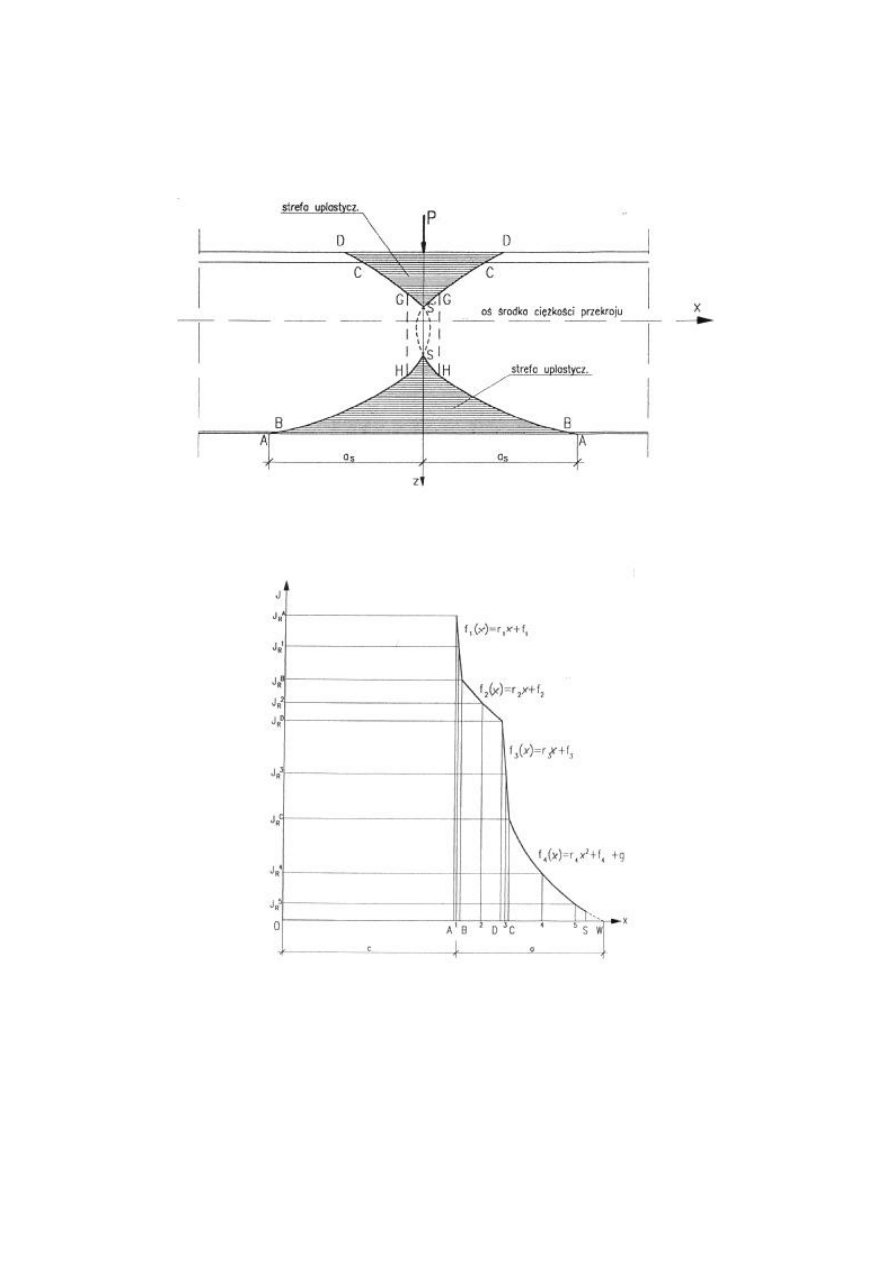
Rys. 2. Kontur strefy uplastycznienia wg przyjętego modelu
A, B, D, C, S – punkty charakterystyczne strefy uplastycznienia
Rys. 3. Wykres funkcji momentu bezwładnoś ci w obszarze uplastycznienia
J
r
A
, J
r
B , J
R
D
, J
R
C
– wartoś ci momentu bezwładnoś ci w punktach charakterystycznych
strefy uplastycznienia
202
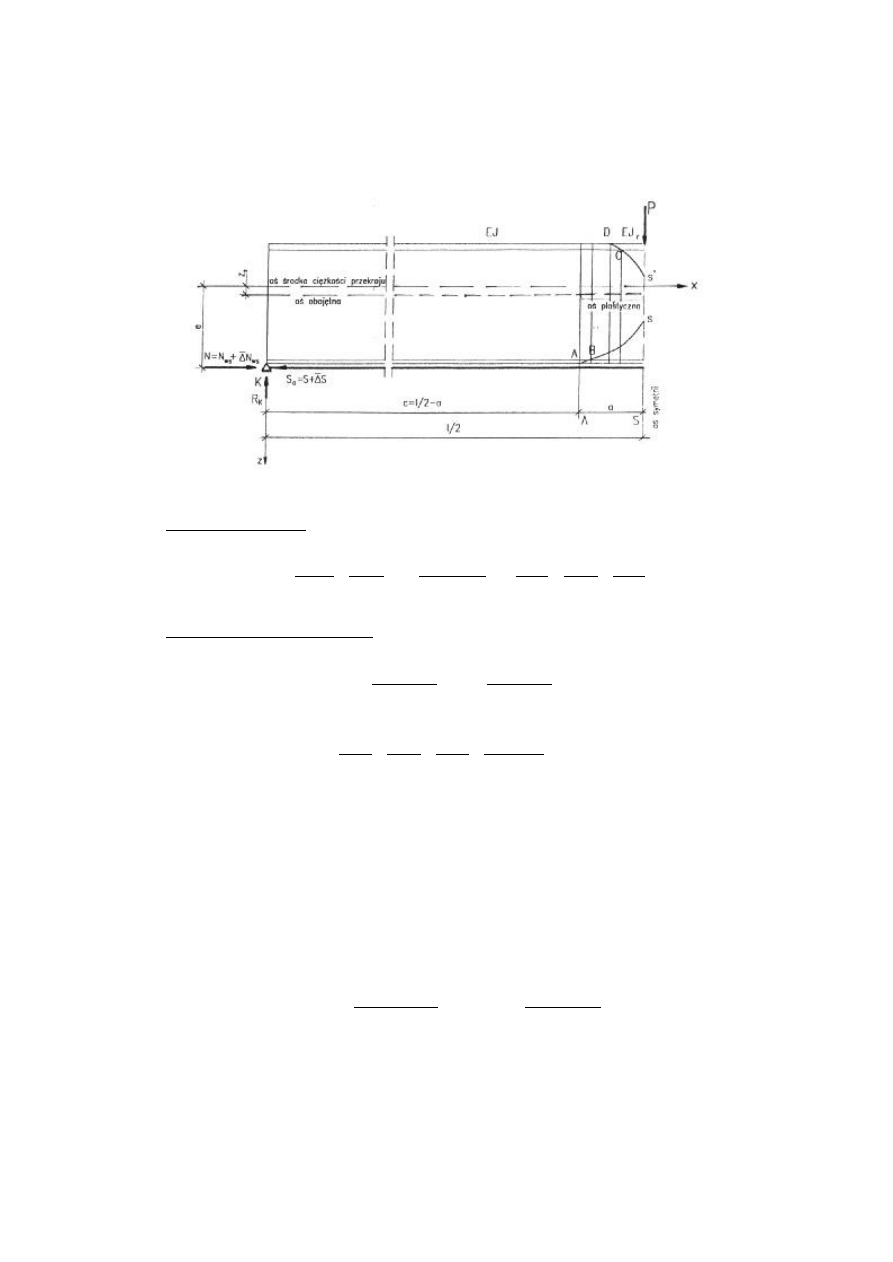
Rys. 4. Przedziały całkowania: KA – sprężysty, AS – sprężysto-plastyczny
przedział sprężysty KA
( )
2GA
x
P
EJ
x
Nec
4EJ
x
Pc
x
d
x
EJ
Ne
x
P/2
2EJ
x
Ne
12EJ
x
P
u
y
y
2
l/2
c
r
y
2
y
3
KA
k
+
+
+
+
+
-
-
=
ò
x
x
(2)
przedział sprężysto-plastyczny AS
( )
( )
( )
+
+
+
+
-
=
ò
òò
x
d
x
EJ
Ne
x
P/2
x
x
d
x
EJ
Ne
x
P/2
u
l/2
c
r
x
c
r
AS
x
(3)
(
)
( )
x
2GA
c
x
P
κ
2GA
Pc
κ
2EJ
Nec
6EJ
Pc
r
y
2
y
3
-
+
+
+
gdzie: J
r
(x) – zredukowany moment bezwładnoś ci okreś lony odpowiednimi funkcjami
w zależnoś ci od zakresu uplastycznienia belki,
k
– wspó łczynnik uwzględniający kształt przekroju belki (przyjęto
k
= 12).
3. Ograniczenia projektowe obszaru uplastycznionego
i przykł
ady obliczeniowe
Zgodnie z przyjętym kształtem i zasięgiem strefy uplastycznienia w belce obciążenie
towarzyszące zakończeniu stanu sprężystego oraz powstaniu przegubu plastycznego
przyjmuje zgodnie z rys. 5 wartoś ci:
(
)
l
e
N
M
4
P
P
A
A
A
spr
-
=
=
(
)
l
e
N
M
4
P
s
s
s
-
=
(4)
203
gdzie: M
A
i N
A
– wartoś ci momentu zginającego i siły podłużnej występujące w przekroju
belki na zakończenie stanu sprężystego,
M
s
i N
s
– wartoś ci momentu zginającego i siły podłużnej w chwili powstania
przegubu plastycznego w ś rodku belki
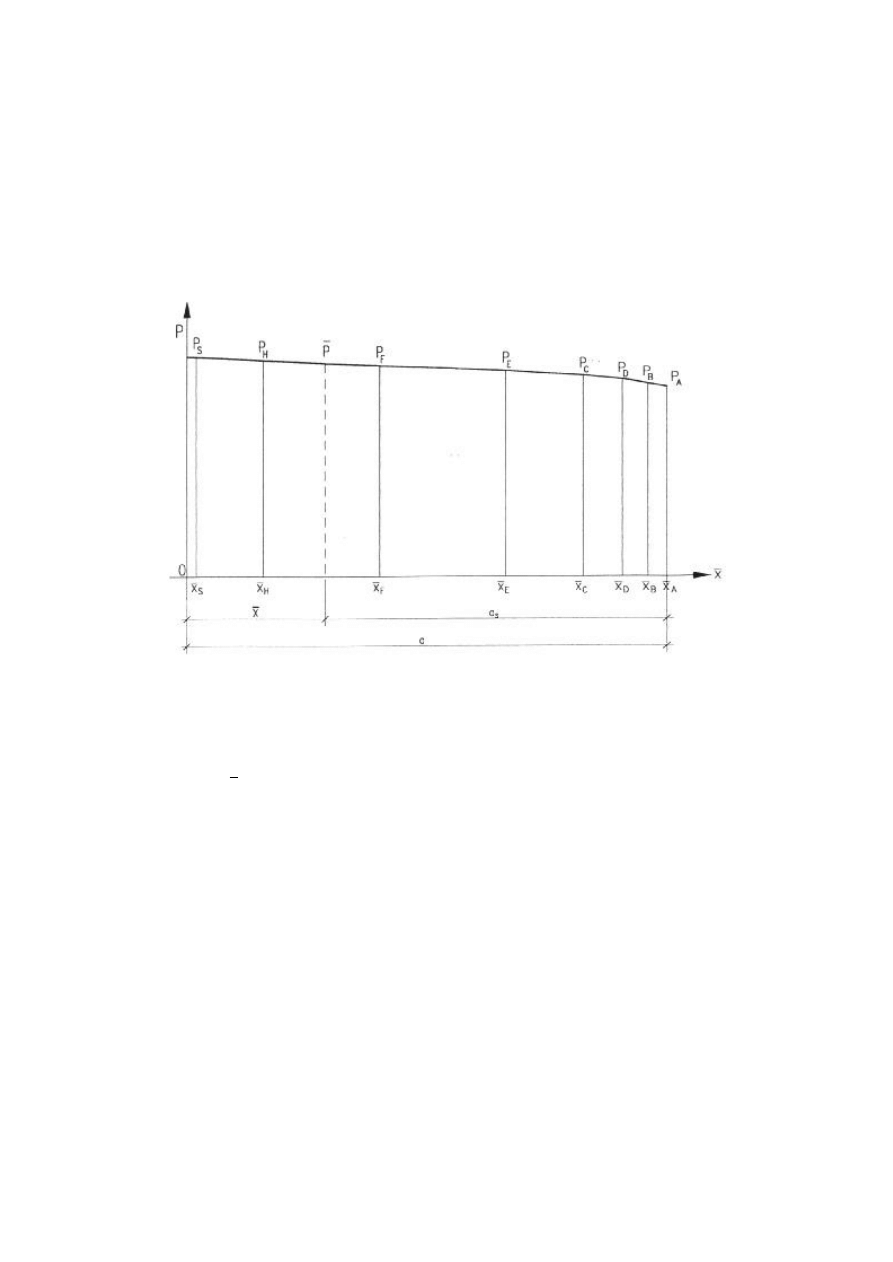
Rys. 5. Punkty odzwierciedlające wartoś ci obciążenia eksploatacyjnego
powodującego uplastycznienie belki zgodnie z krzywą plastyczną:
P
A
, P
B
, P
D
, P
C
, P
S
– obciążenie odpowiadające uplastycznieniu się kolej-
nych punktó w charakterystycznych strefy uplastycznienia;
P
E
, P
F
, P
H
– obciążenie odpowiadające uplastycznieniu się dowolnych
punktó w w strefie uplastycznienia;
P – rzeczywiste obciążenie eksploatacyjne
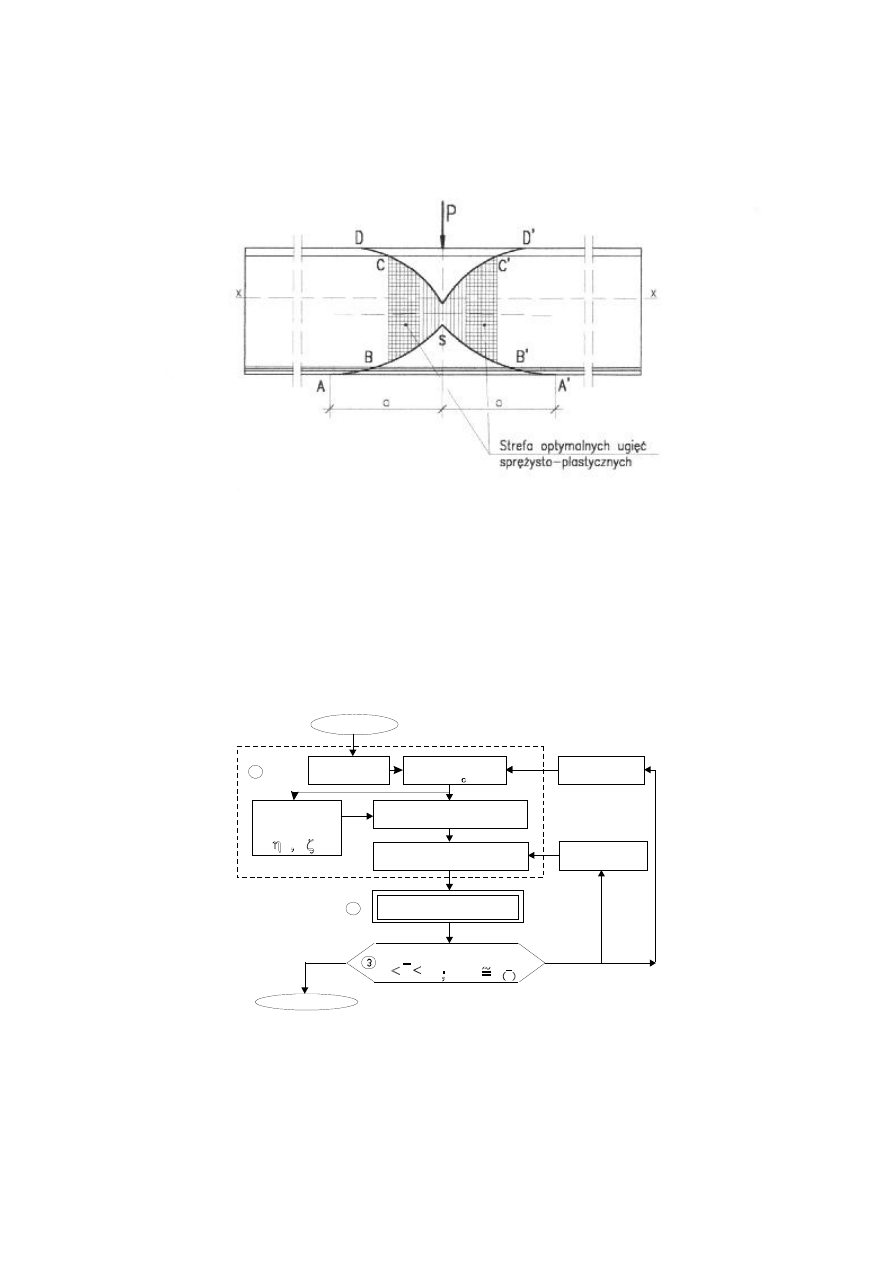
Kierując się zasadą optymalnego wykorzystania materiału ustalono, że wynikający z
analizy obszar odkształceń trwałych dla potrzeb projektowania powinien być zawężony do
przedziału C-S (rys. 6). Przyjęto, że najkorzystniejsze wykorzystanie rezerwy plastycznej
może nastąpić wó wczas, gdy siła eksploatacyjna P przyjmuje wartoś ć co najmniej ró wną P
c
,
tj. odpowiadającą uplastycznieniu się pierwszego, gó rnego włó kna przekroju ś rodnika
(rys. 6). Jednocześ nie z przeprowadzonych badań wynika, że ugięcie towarzyszące
powstaniu przegubu plastycznego jest kilkakrotnie większe od dopuszczalnego. Oznacza to,
że prawidłowo zaprojektowana belka powinna spełniać jednocześ nie dwa warunki
P
c
< P < P
s
oraz
( )
dop
p
u
u
@
(5)
któ re ilustruje rys. 6.
204
Rys. 6. Strefa uplastyczniona przy bezpiecznym wykorzystaniu
plastycznej rezerwy noś noś ci
Opracowany dla proponowanej metody program obliczeniowy składa się z trzech
podstawowych blokó w (rys. 7). W bloku głó wnym (ś rodkowym) wykorzystano wcześ -
niej sporządzony program obliczeniowy [2], w któ rym obliczone są wartoś ci wszystkich
parametró w strefy odkształceń plastycznych, niezbędnych do ustalania wartoś ci ugięć
i uogó lnionych sił wewnętrznych w dowolnym przekroju belki. Natomiast bloki pierw-
szy i trzeci obejmują proces poszukiwania wymiaró w belki i cięgna oraz właś ciwoś ci
Rys. 7. Uproszczony schemat blokowy programu
START
DANE WST
Ę PNE
L , P
CHARAKT. STALI
CHARAKT. STALI
KOREKTA
KOREKTA
WYZNACZENIE WST
Ę PNEJ
POWIERZCHNI PRZEKROJU
PROJEKTOWANIE WYMIAR
Ó W
PRZEKROJU BELKI I CI
Ę GNA
WYM. PRZEKROJU
BLOK G
ŁÓ WNY
KONIEC OBLICZE
Ń
WYZNACZENIE
PARAMETR
Ó W
POMOCNICZYCH
SPRAWDZENIE WARUNK
Ó W
1
2
E ,
f y
E
,
,
fyc
TAK
NIE
P
P
c P
s
u
u
dop
p
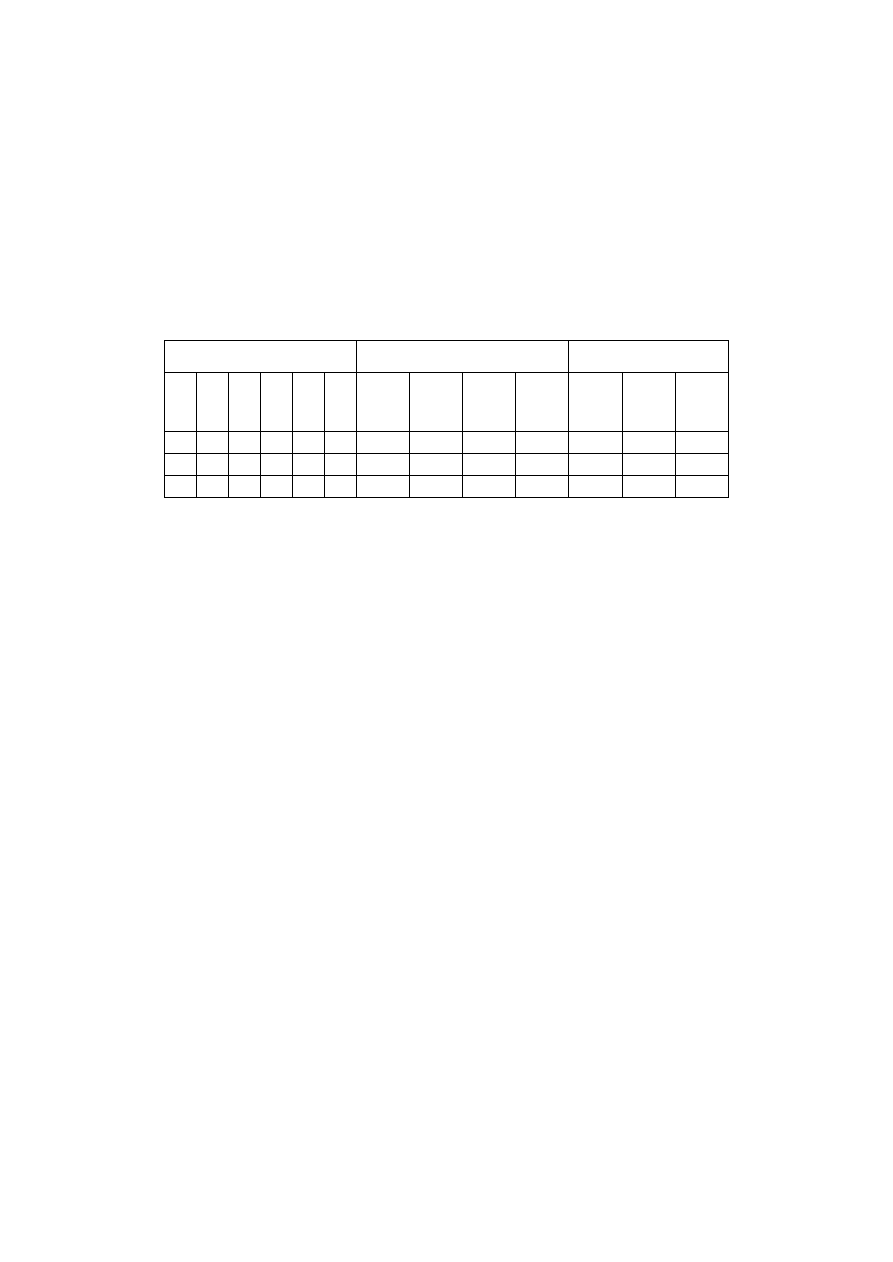
205
mechanicznych stali spełniających warunki (5). W tab. 1 zamieszczono wyniki
projektowania trzech belek, przyjmując dla poró wnania jednakowe wielkoś ci takie jak:
-
rozpiętoś ci – 12,0 m
-
obciążenie eksploatacyjne – 350,0 kN
-
właś ciwoś ci mechaniczne stali belki – E = 205,0 GPa; f
y
= 235,0 MPa
-
właś ciwoś ci mechaniczne stali cięgna – E
c
= 195,0 GPa; f
y
= 1070,0 MPa
Tablica 1
PROJEKTOWANE WYMIARY
[mm]
OBCIĄ Ż ENIE [kN]
UGIĘ CIE [mm]
s
h
1
d
1
t
2
d
2
t
3
t
spr
P
c
P
-
P
s
P
dop
u
÷÷
÷
ø
ö
çç
ç
è
æ
-
p
u
R
910 300 18 98
8
7
2383,5 3027,4 3609,4 3835,6
48
47,91
1,9
840 254 22 91
1
7
2208,6 2561,8 3612,3 3718,0
48
48,15
-3,1
880 268 20 116 8
8
2542,5 3251,1 3615,6 3938,3
48
47,59
8,5
Odmienne natomiast przyjęto smukłoś ci ś rodnika. Zakładając jego gruboś ć ró wną
7 mm założono dla pierwszej belki
l
= 130, dla drugiej
l
= 120 oraz dla trzeciej
l
= 110.
Przy czym w przypadku belki trzeciej z uwagi na brak możliwoś ci spełnienia obu warunkó w
(5) przyjęto gruboś ć ś rodnika ró wną 8 mm.
Wykonując poró wnania uzyskanych wartoś ci otrzymano zależnoś ci:
- ró żnica pomiędzy obciążeniem odpowiadającym ugięciu dopuszczalnemu a
obciążeniem maksymalnym dla fazy sprężystej wynosi kolejno: 51,4 %, 63,6%,
42,2%.
- ró żnica pomiędzy wytrzymałoś cią obliczeniową a naprężeniami w pasie dolnym
belki, liczonymi wg. stosowanych dla fazy sprężystej wzoró w [3] wynosi kolejno:
14,4%, 32,2%, 8%.
- mniejsza smukłoś ć ś rodnika przy stałej jego gruboś ci pozwala na lepsze
wykorzystanie odkształceń trwałych.
5. Wnioski koń cowe
*
Wydaje się możliwe praktyczne zastosowanie metody projektowania belek
sprężonych cięgnami z wykorzystaniem odkształceń trwałych w stadium
eksploatacji. Po wykonaniu prac związanych z wdrażaniem dodatkowych badań
należy przystąpić do opracowania szczegó łowej metody projektowania.
*
W ostatecznej wersji metody poza innymi, należy uwzględnić wpływ zjawisk
reologicznych stali na noś noś ć i odkształcalnoś ć belki. Będzie to możliwe po
opracowaniu tzw. map Frosta-Ashby’ego okreś lających właś ciwoś ci mechaniczne
gatunkó w stali produkowanych w Polsce, pracujących w warunkach wysokich
naprężeń. Wydaje się niezbędne opracowanie optymalnych dla danej belki
charakterystyk geometrycznych i mechanicznych.
Literatura
[1] BIEZUCHOW N. J., K teorii płasticzieskowo rasczieta na izgib, Westi. Inż . i Techn.
1936.10.

206
[2] KRÓ L H., Modelowanie stalowej belki spręż onej cięgnem z wykorzystaniem plastycznych
właś ciwoś ci stali. Rozprawa doktorska, Warszawa 2001, Biblioteka P.W.
[3] BOGUCKI W., Budownictwo stalowe, cz.1, str. 343
¸
357, Arkady, Warszawa 1976.
PROPOSED METHOD OF DESIGNING IN ELASTIC-PLASTIC
PHASE OF PRESTRESSED BEAMS
Summary
The paper deal with proposed method of designing of prestressed bean with utilising plastic
reserve of load carrying capacity in phase of exploitation.
The plastic zone spreading along longitudinal axis the beam was taken into
consideration. The special numerical program to enable obtain exemplary results was worked
out. The numerical examples are presented too.
Wyszukiwarka
Podobne podstrony:
Propozycja metody projektowania sprężysto plastycznej belki sprężonej
Projekt belki spreżonej
Metody komputerowe w teorii sprężystości i plastyczności
Projekt wdrożenia metody montażu nawisowego betonowych mostów sprężonych
37 Uproszczone metody projektowania przekroju sprężonego
Na teczkę z żelbetu 2, Projekt belki sprężonej
Na teczkę z muru, Projekt belki sprężonej
Na teczkę z żelbetu, Projekt belki sprężonej
Projekt belki spreżonej
44 Uproszczone metody projektowania przekroju sprężonego
Metody Projektowania 2
Prezentacja Teoria Sprężystości i Plastyczności
AS Projektowanie swobodnie podpartej belki zespolonejczęste
Moje logo Projekt znaku plastycznego
3 METODY PROJEKTOWANIA
19 Nosnosc sprezysto plastycznych ustrojow pretowych
Teoria sprężystości i plastyczności, Dok1
Teoria sprężystości i plastyczności zadania (2)
więcej podobnych podstron