ROZDZIAŁ 12

TABELE WIELODZIELCZE

I. Pojęcia i analizy wprowadzające

W poprzednich rozdziałach opisywaliśmy, poza nielicznymi wyjątkami, zmienne mierzalne
oraz procedury służące do ich statystycznej analizy. Poznaliśmy podstawowe testy
i jednoczynnikową analizę wariancji. W badaniach biologicznych i medycznych mamy

jednak do czynienia nie tylko ze zmiennymi mierzalnymi. Bardzo często stosujemy

klasyfikację o charakterze jakościowym, a także analizujemy (np. rozpatrując różnorodne
ankiety medyczne) wielokrotne dychotomie czy wielokrotne odpowiedzi. Do ich
opracowania potrzebne są specyficzne metody. W niniejszym rozdziale omówimy ten typ
zmiennych oraz przedstawimy sposoby wnioskowania statystycznego w takich
przypadkach. Testom nieparametrycznym związanym z analizą zmiennych jakościowych
i porządkowych poświęcony będzie drugi tom. Obecnie przedstawimy najważniejsze
zagadnienia i analizy dotyczące takich zmiennych. Poznamy bliżej:

1) Zmienne Jakościowe (Kategoryzujące)

Stosujemy je wówczas, gdy dane chcemy zgrupować w rozłączne kategorie, np. płeć, kolor

oczy, umowna skala natężenia choroby itd. Każdy element próby jest sklasyfikowany ze
względu na podane kryterium. Podziału możemy dokonać na dwa lub więcej podgrup.
Przykładowo: badając grupę dzieci możemy podzielić ją na trzy rozłączne podgrupy ze
względu na wielkość migdałków:
• migdałki bardzo powiększone,
• migdałki powiększone,
• migdałki nie powiększone.

2) Wielokrotne Odpowiedzi

Zmienne tego typu spotykamy najczęściej przy analizie danych pochodzących z ankiet lub
badań opinii publicznej. Przypuśćmy, że w ankiecie dotyczącej badania stanu zdrowia
pewnej populacji zadano osobom pytanie o trzy ostatnio przebyte ciężkie choroby.
Należało podać ich nazwy spośród 25 wymienionych w ankiecie. Otrzymane ankiety będą
zawierały od 0 do 3 odpowiedzi na to pytanie oraz będą zawierały różne nazwy schorzeń.

Są to tzw. zmienne wielokrotnych odpowiedzi:

Odpowiedź 1 Odpowiedź 2 Odpowiedź 3
choroba A choroba B choroba C

choroba K choroba C choroba P
------------ ------------- ------------

221

Przystępny kurs statystyki

Zazwyczaj chcemy podsumować odpowiedzi i podać frakcje (procent) osób z badanej
grupy, które chorowały na dane schorzenia.

3) Wielokrotne Dychotomie

Analogicznie jak poprzednio, zmienne tego typu spotykamy najczęściej przy analizie
danych pochodzących z ankiet lub badań opinii publicznej. Zilustrujemy je przy pomocy
kolejnego przykładu. Tym razem w ankiecie pytamy o pobyt w ciągu ostatniego roku
w jednym ze szpitali. Przypuśćmy, że interesują nas tylko trzy szpitale: Klinika A, Klinika
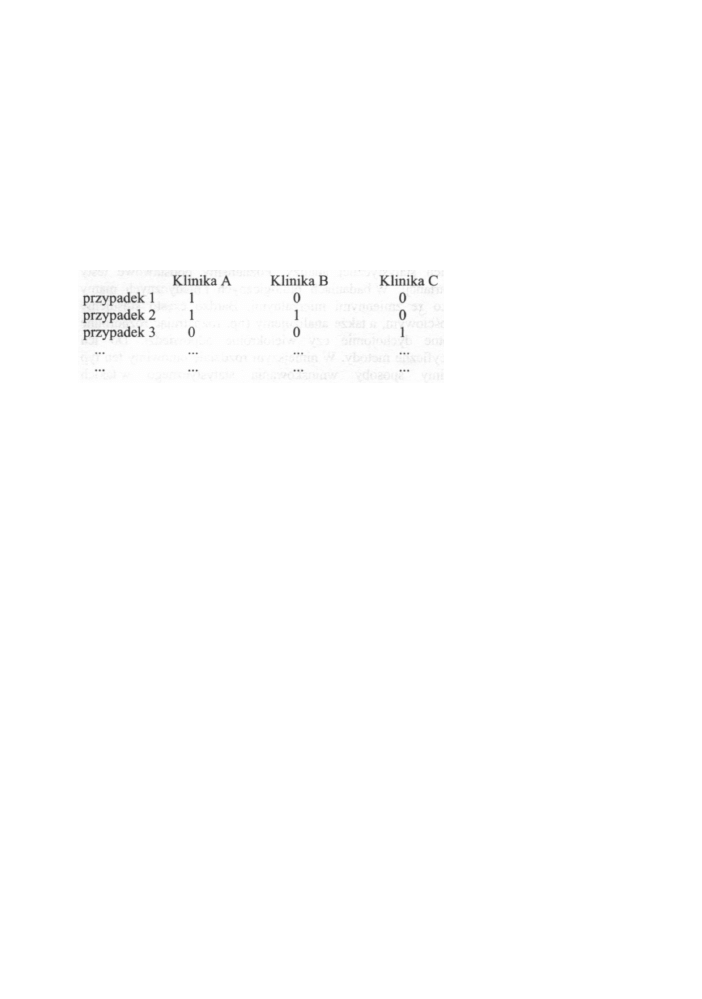
B i Klinika C. Jednym ze sposobów kodowania danych w tej sytuacji może być
następujący:

Dla każdej kliniki zarezerwowano jedną zmienną i wpisuje się 1, jeśli ankietowany podał,
że przebywał ostatnio w tej klinice, oraz 0 - jeśli nie. Każda zmienna reprezentuje więc
dychotomię, to znaczy dopuszczalne są tylko 1 i nie 1 (wpisujemy 1 i 0, ale moglibyśmy
równie dobrze wpisywać 1 i zostawiać pole puste zamiast 0). Mamy tu więc do czynienia
z tzw. wielokrotnymi dychotomiami. Przy opisywaniu takich zmiennych chcielibyśmy
mieć zestawienia jak poprzednio, to znaczy procenty dla każdej kliniki w stosunku do
liczby odpowiedzi i w stosunku do liczby ankietowanych.

Pragniemy też dokonać oceny zależności pomiędzy zmiennymi tego typu. Np.

zależność pomiędzy rodzajem ostatnio przebytego schorzenia a pobytem w różnych
klinikach, czy też powiązanie chorób z płcią ankietowanych. Jak tego dokonać? Jakie
narzędzia mamy do dyspozycji? Przeprowadzaniu takich analiz poświęcony będzie cały ten
rozdział. Opiszemy najważniejsze techniki. Większość metod tu przedstawionych służy do
wykrywania i oceny natężenia zależności (skojarzenia) dwóch cech jakościowych.
Pierwszym krokiem w takich analizach jest przedstawienie zebranych danych
indywidualnych w postaci tablicy wielodzielczej (kontyngencji). Wymaga to zliczenia

jednostek w odpowiednich komórkach tabeli z danymi. Zliczanie to bez użycia komputera
jest żmudne i męczące zwłaszcza dla dużej ilości przypadków. Tablice wielodzielcze

stanowią podstawę do obliczania pozostałych statystyk określających siłę związku.

Tablica wielodzielcza przedstawia nam rozkład obserwacji ze względu na kilka

cech jednocześnie. Załóżmy, że dysponujemy n obserwacjami dla jakościowej cechy
X (posiadającej kategorie X

1

, X

2

,... X

k

) i jakościowej cesze Y (o kategoriach Y

1

Y

2

, ...Y

p

).

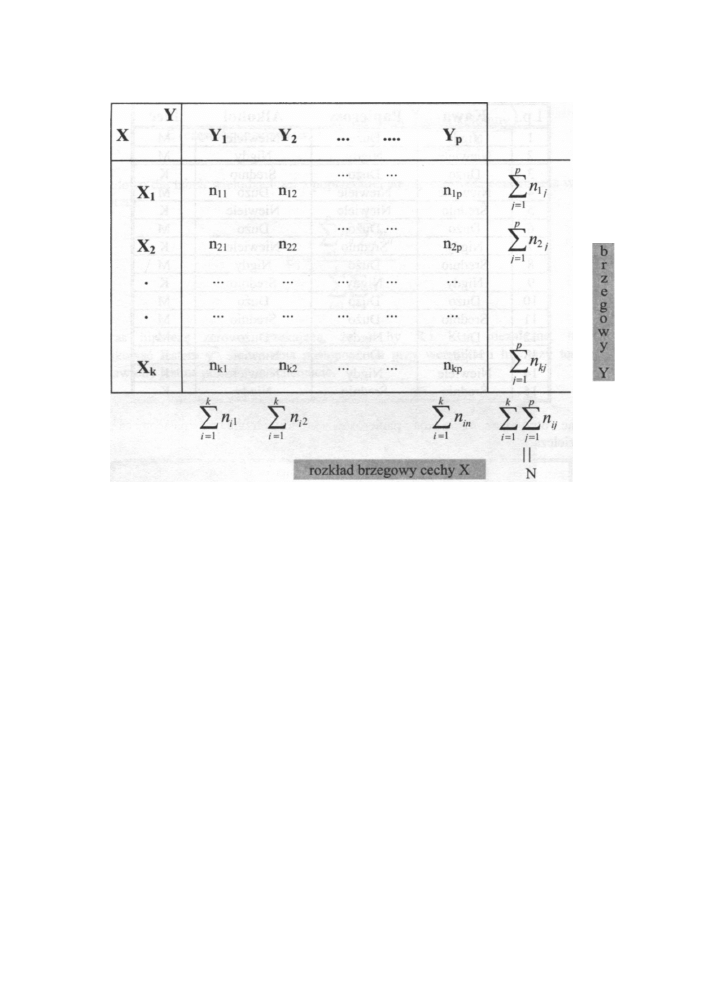
Wówczas tablica wielodzielcza przedstawia się następująco:

222

Tabele wielodzielcze

Liczebności n

ij

określają liczbę elementów próby, dla których cecha X ma wariant X

i

i jednocześnie cecha Y - wariant Y

j

. Tablica wielodzielcza pokazuje więc określony łączny

rozkład obu cech. Liczebności w ostatnim wierszu i w ostatniej kolumnie nazywamy
empirycznymi brzegowymi rozkładami, odpowiednio cechy Y i cechy X.

Przykładowo: chcąc ocenić wpływ używek (papieros, kawa, alkohol) na pewną

chorobę, zebraliśmy dane na temat ich używania w grupie 90-osobowej. Zastosowano
podział na cztery kategorie:

Nigdy - nie używano nigdy;
Niewiele - używano w niewielkich ilościach;

Średnio - używano w średnich ilościach;
Dużo - używano w dużych ilościach.

W badaniach brano również pod uwagę płeć respondentów. Początkowy fragment danych
(zapisanych w 4 kolumnach - 4 zmienne) przedstawia tabela przedstawiona poniżej:

223

Przystępny kurs statystyki

L p . Kawa Papierosy Alkohol Płeć

1

Nigdy

Dużo

Niewiele

M

2

Niewiele

Nigdy

Nigdy

M

3

Dużo

Dużo

Średnio

K

4

Niewiele

Niewiele

Dużo

M

5

Średnio

Niewiele

Niewiele

K

6

Dużo

Dużo

Dużo

M

7

Nigdy

Średnio

Niewiele

K

8

Średnio

Dużo

Nigdy

M

9

Nigdy

Nigdy

Średnio

K

10

Dużo

Dużo

Dużo

M

11

Średnio

Dużo

Średnio

M

12

Dużo

Nigdy

Dużo

M

13

Nigdy

Dużo

Niewiele

K

14

Niewiele

Nigdy

Niewiele

K

15

Średnio

Średnio

Nigdy

K

Zliczając otrzymane dane dla papierosów i płci otrzymamy następującą tablicę
wielodzielcza:

Płeć

Papieros

Nigdy

Papieros

Niewiele

Papieros

Średnio

Papieros

Dużo

Kobieta

11

8

6

5

30

Mężczyzna

4

4

28

24

60

15

12

34

29

90

W tabeli zacieniowano rozkłady brzegowe. Z tabeli widać wyraźną przewagę mężczyzn
w grupie palących duże lub średnie ilości papierosów. Za to około trzykrotnie więcej kobiet
niż mężczyzn nigdy nie paliło w rozpatrywanej przez nas grupie. Informacje byłyby
bogatsze po dołączenie danych procentowych. Stosuje się procenty liczone względem
ostatniej kolumny (względem płci), względem ostatniego wiersza (względem ilości
wypalanych papierosów) oraz względem całkowitej liczby respondentów.

Następny etap analizy statystycznej tak zebranych danych, to próba weryfikacji

hipotezy, że dwie jakościowe cechy w populacji są niezależne. Najczęściej stosowanym
„narzędziem" jest test χ.

2

Został on (test χ.

2

) opracowany przez Karla Pearsona w 1900 r.

i jest

metodą, dzięki której można się upewnić, czy dane zawarte w tablicy wielodzielczej

dostarczają wystarczającego dowodu na związek tych dwóch zmiennych. Test χ.

2

polega na

porównaniu częstości zaobserwowanych z częstościami oczekiwanymi przy założeniu
hipotezy zerowej (o braku związku pomiędzy tymi dwiema zmiennymi). Częstości
oczekiwane obliczamy wykorzystując częstości marginalne (z tablicy wielodzielczej)
według następującego wzoru:

224

Tabele wielodzielcze

Przykładowo dla tabeli wielodzielczej z poprzedniej strony częstości oczekiwane wyrażają
się wzorem:

Niepalący Palący mało

Palący duże

ilości

Suma

Zmiany występują

51

250

560

861

Zmian nie ma

370

210

59

639

Suma

421

460

619

1500

225

Wówczas hipotezę zerową orzekającą, że cechy X i Y są niezależne, możemy
zweryfikować testem χ

2.

Pełny opis postępowania przy weryfikacji hipotezy testem χ

2

przedstawiony jest na

poniższym schemacie.

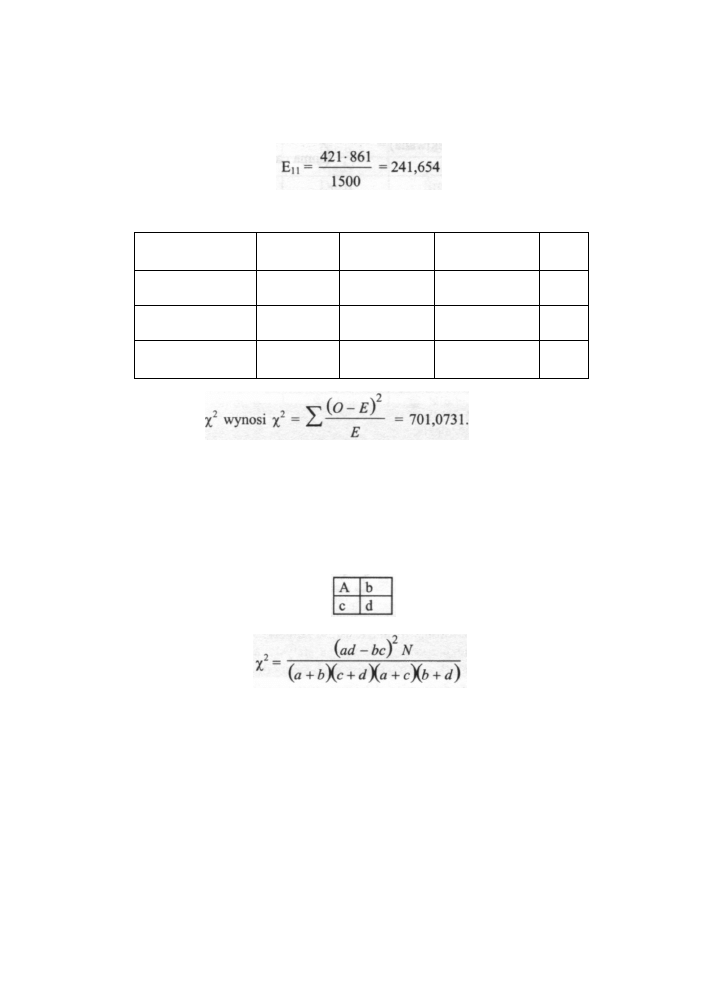
Przykład 1
Badano zależność pomiędzy ilością wypalanych papierosów a wystąpieniem pewnych
niekorzystnych zmian w płucach w grupie 1500 osób. Zebrane dane przedstawiono
w poniższej wielodzielczej tabeli:

Przystępny kurs statystyki

Wyniki obliczeń pozostałych wartości oczekiwanych przedstawiono w poniższej tabeli
w nawiasach obok wartości obserwowanych.

Niepalący

Palący mało

Palący duże

ilości

Suma

Zmiany występują

51

(241,654)

250

(264,04)

560

(353,306)

861

Zmian nie ma

370

210

59

639

(179,346)

(195,96)

(263,694)

Suma

421

460

619

1500

Wartość statystyki

Z kolei wartość krytyczna

odczytana z tablic dla poziomu istotności α = 0,001 wynosi χ.

2α

= 13,817. Pozwala

więc

nam odrzucić hipotezę zerową (χ.

2

> χ.

2α

) i

stwierdzić, że na poziomie istotności α = 0,001

istnieje

zależność pomiędzy ilością papierosów wypalanych dziennie a wystąpieniem

niekorzystnym zmian w płucach.

Zauważmy, że bardzo duże wartości oznaczają dużą różnicę pomiędzy

częstościami obserwowanymi a oczekiwanymi i jest to dowód istnienia zależności.
Przeciwnie - mała wartość χ.

2

(zwłaszcza bliska 0) nie daje dowodu na istnienie korelacji.

Dla tabel dwudzielczych 2x2 postaci
według prostszego, praktycznego wzoru:

wartość statystyki χ.

2

wyznaczamy

Przykład 2
W próbie liczącej 100 mężczyzn w wieku 50 - 60 lat zbadano częstość występowania
choroby wieńcowej i podwyższonego ciśnienia tętniczego. Chcemy ocenić, czy choroba
wieńcowa współistnieje z podwyższonymi wartościami ciśnienia tętniczego.

226

Przykładowo wyliczymy wartość oczekiwaną E

11

.

Zgodnie z definicją mamy

Tabele wielodzielcze

Ciśnienie

nie podwyższone

Ciśnienie

podwyższone

Razem

Choroba wieńcowa

nie występuje

37

17

54

Choroba wieńcowa

występuje

8

38

46

Razem

45

55

100

Współczynnik ten jest miarą korelacji pomiędzy dwiema zmiennymi jakościowymi
w tabeli 2x2. Przyjmuje on wartości od 0 (brak powiązania między zmiennymi) do 1
(całkowite powiązanie pomiędzy zmiennymi).

227

odrzucamy hipotezę zerową o niezależności zmiennych odrzucamy, a tym samym
wnioskujemy, że choroba wieńcowa występuje częściej u osób z podwyższonym
ciśnieniem tętniczym.

UWAGA !
Dla tabeli 2x2 przedstawionej wyżej statystyka χ.

2

jest

często modyfikowana w celu

utworzenia bardziej odpowiedniego testu. W większości komputerowych programów
statystycznych mamy możliwości obliczenia tych poprawek.

Najbardziej popularna jest poprawka Yatesa postaci:

gdzie N liczebność całej próby

Stosujemy ją, jeżeli 20 < N <40 i którakolwiek z liczebności oczekiwanych jest mniejsza
od 5. Dokładne omówienie wszystkich poprawek nastąpi później w tym rozdziale, przy
okazji omawiania, jak analizy tego typu obliczane są w pakiecie

STATISTICA.

Statystyka χ.

2

sprawdza, czy dwie zmienne

są ze sobą powiązane. Jednakże oprócz

sprawdzenia czy pomiędzy zmiennymi zachodzi związek, interesuje nas, jak silne jest to
powiązanie. Samej wartości χ.

2

jako pomiaru

siły związku nie możemy stosować, zależy

ona bowiem od liczebności grupy N i rośnie wraz z jej wzrostem. Tym niemniej w oparciu
o tę wartość zbudowano szereg miar siły związku. Do najczęściej stosowanych należą:

Przystępny kurs statystyki

2. Współczynnik V - Cramera postaci

gdzie k i p wymiary

tablicy wielodzielczej.
Współczynnik ten również przyjmuje wartości od 0 (brak relacji między zmiennymi) do 1.

3. Współczynnik kontyngencji Pearsona postaci

Gdy zmienne są niezależne, wówczas C = 0. Jego maksymalna wartość jest zawsze
mniejsza od 1 i zależy od liczby wierszy i kolumn. Przykładowo dla tabeli 3x3 wartość

jego wynosi 0,816. Ogranicza to jego zastosowanie do tablic kwadratowych (o
jednakowych wymiarach).

Interpretacja wszystkich tych współczynników jest taka sama:

• jeżeli posiada on wartość zero, to cechy X i Y są niezależne,
• im bliższa jedynki jest wartość tych współczynników, tym silniejsze jest

powiązanie pomiędzy analizowanymi cechami X i Y.

Przykład 2 (ciąg dalszy)
Obliczymy siłę zależności dla tablicy z przykładu 2. Współczynnik Φ = V =0,51 zaś
współczynnik kontyngencji wynosi C = 0,46. Pomiędzy rozpatrywanymi zmiennymi
zachodzi więc wysoka korelacja.
Graficznie zależność ta przedstawiona jest na poniższym rysunku.

Rys. 12.1 Trójwymiarowy wykres częstości dla danych z drugiego przykładu

Z analizą statystyczną zmiennych jakościowych związany jest też test istotności zmian
McNemara. Test ten służy do określenia istotności różnic w wynikach, które zaszły pod

228

Tabele wielodzielcze

wpływem jakiegoś oddziaływania. Zastosowanie testu McNemara wymaga uprzedniego
zestawienia wyników uzyskanych w badaniach w tabeli 2x2 o poniższym schemacie:

Po oddziaływaniu

Suma

—

+

Suma

Przed

+

A

B

A+B

oddziaływaniem —

C

D

C+D

Suma

A+C

B+D

N

W powyższej tabelce kolejne litery oznaczają odpowiednio:

A - liczbę osób, u których w wyniku zastosowania określonych oddziaływań doszło do

zmiany wyniku z „+" na „_",

B - liczbę osób, u których doszło do zmiany wyniku z"_" na „+",
C i D liczbę osób, u których nie stwierdzono zmiany wyniku.

Opis postępowania przy weryfikacji hipotezy testem McNemara przedstawiony jest na
poniższym schemacie.

Przykład 3
Przebadano 195 pacjentów na wystąpienie pewnych bakterii. Stwierdzono ich
występowanie u 103 osób. Po upływie 6 miesięcy leczenia przeprowadzono ponowne
badanie. Bakterie wykryto u 47, osób z czego 39 to pacjenci, u których wcześniej też
występowały bakterie. Czy można powiedzieć, że leczenie ma istotny wpływ na
zmniejszenie się liczby osób z bakteriami?

229

Przystępny kurs statystyki

Dla analizy statystycznej uzyskane wyniki przedstawimy w poniższej czteropolowej tabeli:

Po oddziaływaniu

—

+

Suma

Przed

+

8

84

92

oddziaływaniem

39

64

103

Suma

47

148

195

Ponieważ χ

2

=42,014 > χ

2 a

=6,64 przy poziomie

istotności 0,99 stwierdzamy, że odrzucamy

hipotezę zerową, zatem leczenie ma istotny wpływ na ilość osób, u których stwierdzono
występowanie bakterii.

II. A jak to się liczy w programie

STATISTICA

W programie

STATISTICA

do analizy tablic wielodzielczych i tabel zbiorczych służy opcja

Tabele wielodzielcze w module Podstawowe statystyki i tabele. Po wybraniu tej opcji
i naciśnięciu OK (lub po dwukrotnym kliknięciu na nazwie opcji) otwiera się okno Określ
tabelę przedstawione poniżej.

Rys. 12.2 Okno dialogowe - Określ tabelę

W powyższym oknie możemy wybrać dwie grupy statystycznych analiz dotyczących:

1. tablic zbiorczych (Stub-and-banner table),

2. tablic wielodzielczych i wielokrotnych odpowiedzi (Multivay crosstabulation tables).

O tym, w której z tych grup statystycznych będziemy przeprowadzać analizy, decyduje
wybór dokonany na liście rozwijalnej Analiza.

230

Teraz możemy dokonać obliczenia

Tabele wielodzielcze

Po jej rozwinięciu możemy wybrać:
• Tabele wielodzielcze - wybór tej opcji umożliwia rozwiązanie problemów związanych

z tabelaryzacją zmiennych jakościowych. Możemy utworzyć tabele wielodzielcze
i zbiorcze oraz obliczyć różne statystyki związane z takimi tabelami. Opcja ta
wybierana jest domyślnie.

• Tabele dla wielu odpowiedzi - wybór tej opcji umożliwia specyfikowanie i analizę

statystyczną wielokrotnych odpowiedzi i wielokrotnych dychotomii. Okno podstawowe
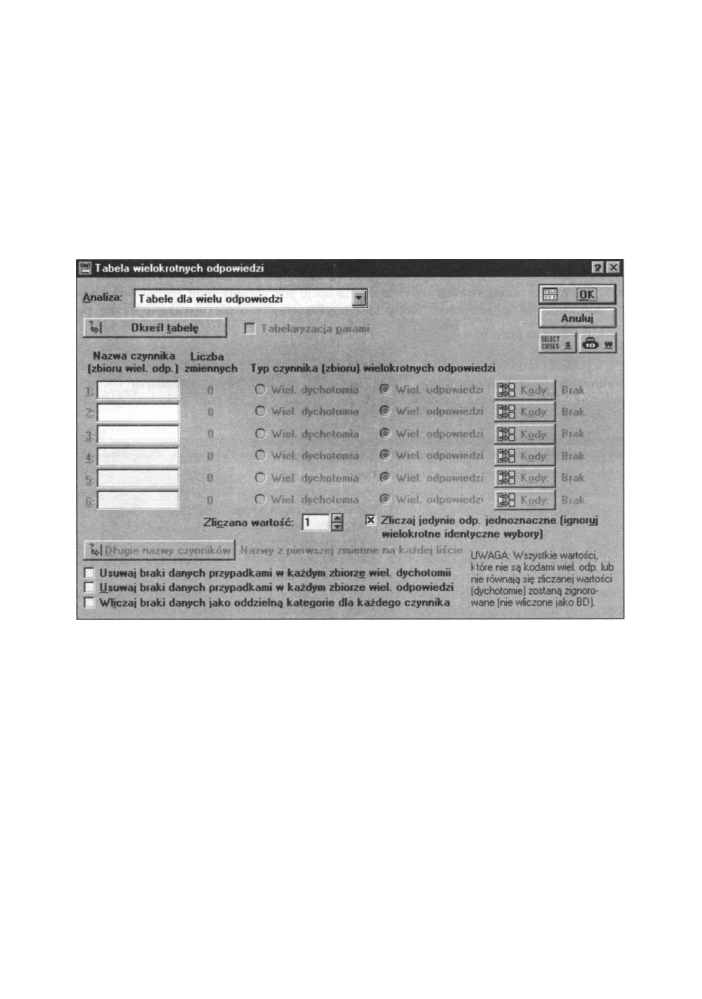
dla takich analiz widoczne jest na poniższym rysunku.

Rys. 12.3 Okno dialogowe - Tabele wielokrotnych odpowiedzi

Omówimy obie grupy po kolei ilustrując przykładami. Rozpoczniemy od tablic
wielodzielczych.

Tabele wielodzielcze

Dla wprowadzania danych służą dwa przyciski:
• Określ tabelę w polu Tabele wielodzielcze - przycisku tego używamy dla wyboru

zmiennych do tabeli wielodzielczej. Po kliknięciu na nim otworzy się okno
umożliwiające wybór sześciu list zmiennych. Po wyborze zmiennych możemy obliczyć
tabele wielodzielcze dla wszystkich możliwych kombinacji zmiennych z wybranych
list. Możemy również przeglądać i zmieniać aktualnie analizowaną tabelę. W tym celu
należy użyć opcji Przeglądaj lub usuń tabelę.

231

Przystępny kurs statystyki

• Określ tabelę w polu Tabela zbiorcza - po kliknięciu tego przycisku otwiera się okno

dla wyboru dwóch list zmiennych. Dla wybranych danych możemy obliczyć tabele
zbiorcze. W tabeli zbiorczej zmienna z pierwszej listy będzie fabularyzowana
w kolumnach, a z drugiej listy - w wierszach (poziomo). Ustawienia tu dokonane
anulują ustawienia z poprzedniego punktu.

O tym, jakie kody zostaną użyte do tabelaryzacji danych, decydują ustawienia w dolnej
części okna. Do wyboru mamy:
• Użyj wszystkich kodów całkowitych dla wybranej zmiennej - wybieramy tę opcję,

gdy chcemy, aby wszystkie wartości całkowite zmiennej były użyte do tabelaryzacji.

• Użyj kodów użytkownika - wybieramy tą opcję gdy chcemy sami zdefiniować kody

potrzebne do tabelaryzacji. Kody te specyfikujemy w oknie otwierającym się po

Rys. 12.4 Okno z opcjami dla wyników tabelaryzacji

Grupa opcji [1] to zespół najważniejszych przycisków uruchamiających tabelaryzację
i analizę statystyczną zebranych danych. Należą do nich:
• przycisk Tabela zbiorcza - wywołuje obliczenia tablic zbiorczych dwudzielczych,

gdzie zmienna wybrana na pierwszej liście tabelaryzowana jest w kolumnach,

232

kliknięciu na przycisku

Po wybraniu zmiennych i kliknięciu przycisku OK otwiera się pośrednie okno, w którym
wybieramy jakie podsumowania i jakie statystyki dla wybranych zmiennych chcemy
policzyć. Okno to wraz z zaznaczonymi najważniejszymi opcjami pokazane jest na
poniższym rysunku.

Tabele wielodzielcze

a zmienna wybrana na drugiej liście - w wierszach. Opcja ta jest aktywna, gdy wybrano
wprowadzanie danych przy pomocy przycisku Określ tabelę w polu Tabela zbiorcza;

• przycisk Przegląd tabeli zbiorczej - wywołujący obliczanie tabel sumarycznych dla

tablic wielodzielczych. Jeżeli zdefiniowaliśmy więcej niż jedną tablicę, otworzy się
okno dialogowe, w którym wybieramy właściwą tabelę. W tabeli sumarycznej ostatnia
wybrana zmienna będzie tabelaryzowana w kolumnach, a wszystkie pozostałe zmienne
w wierszach. Jeśli tych ostatnich jest więcej niż dwie zmienne, wówczas nasza tabela
sumaryczna wygląda jak sklejenie wielu tablic dwudzielczych. Takim sposobem
w jednym arkuszu wyników możemy oglądać nawet tablice sześciodzielcze. O tym, co
będzie wyświetlone w tabeli zbiorczej, decydują ustawienia dokonane przez nas
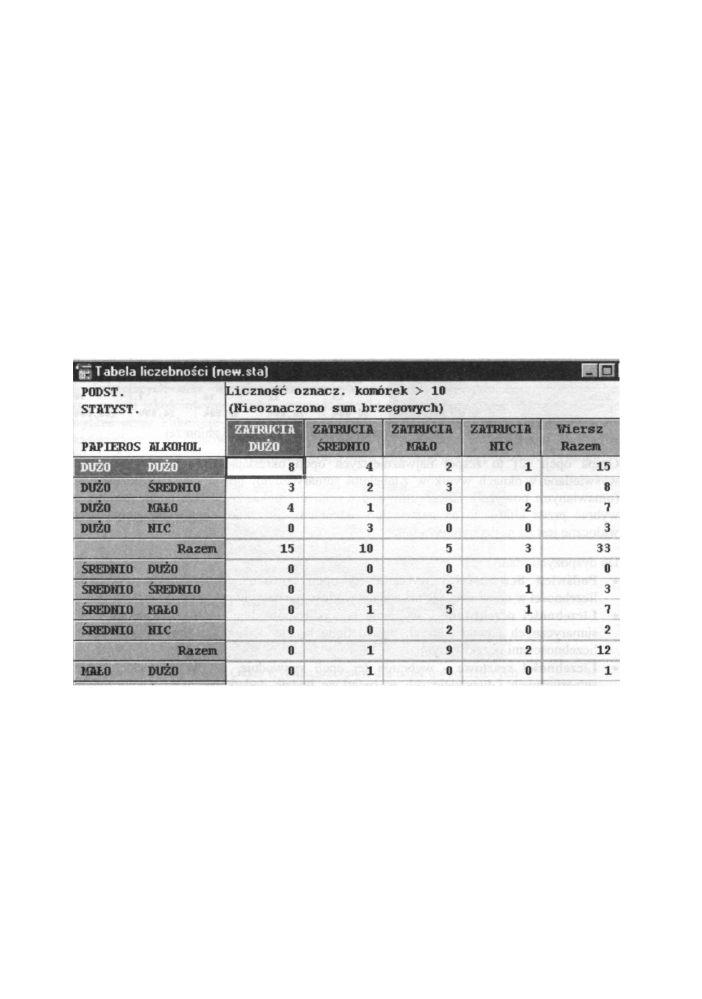
w oknie Tabele. Okno to omówimy później w tym rozdziale. Przykładowa tabela
sumaryczna dla trzech zmiennych jakościowych (papieros, alkohol, zatrucia) pokazana

jest na poniższym rysunku;

Rys. 12.5 Okno wynikowe z tabelą liczebności

• przycisk Dokładne tabele dwudzielcze - wywołuje okno wynikowe z tabelą

dwudzielczą. Jeżeli zdefiniowaliśmy więcej niż jedną tabelę, to otworzy się okno
dialogowe, w którym wybieramy tabelę, o którą nam chodzi. Jeżeli analizujemy tablice
z więcej niż dwiema zmiennymi, wówczas utworzona zostanie kaskada okien
wynikowych z tablicami dwudzielczymi (dla wszystkich par wybranych z grupy
badanych zmiennych). O tym, co jeszcze będzie wyświetlone w tabeli zbiorczej,
decydują ustawienia dokonane przez nas w oknie Tabele. Okno to omówimy później
w tym rozdziale. Jeżeli wybraliśmy dodatkowo jakieś statystyki dla tablic
dwudzielczych, to arkusz wyników ze statystykami wywołamy tym właśnie
przyciskiem. Pojawi się on jako następne okno wynikowe po wyświetleniu okna

233

Przystępny kurs statystyki

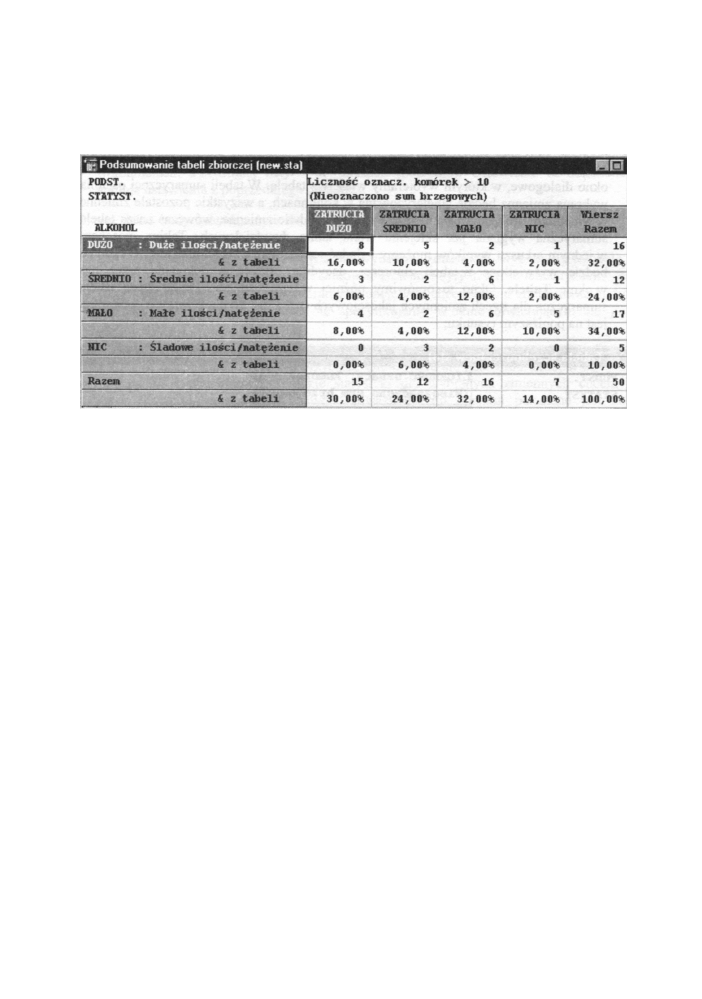
z tabelą dwudzielczą. Na poniższym rysunku mamy przykładową tabelę dwudzielczą
wraz z procentami obliczonymi względem całej grupy.

Rys. 12.6 Okno wynikowe - Podsumowanie tabeli zbiorczej

Grupa opcji [2] to zespół najważniejszych opcji określających szczegóły wyników
wyświetlane w oknach wyników z tabelami sumarycznymi lub tabelami dwudzielczymi
(omawianymi powyżej). Chcąc otrzymać wyniki dla pokazanych tam opcji, musimy je

wybrać przez kliknięcie na nazwie lub okienku opcji. Okno z omawianą grupą opcji
widoczne jest na następnym rysunku.

Do dyspozycji mamy:
• Podświetl liczebności - wybranie tej opcji powoduje podświetlenie wszystkich

liczebności w tabeli większe niż zadana wartość (na naszym rysunku wynosi ona 10).

• Liczebności oczekiwane - wybranie tej opcji spowoduje, że dla wszystkich tablic

sumarycznych i dwudzielczych wyświetlone będzie dodatkowe okno z wyliczonymi
liczebnościami oczekiwanymi.

• Liczebności resztowe - wybranie tej opcji spowoduje, że dla wszystkich tablic

sumarycznych i dwudzielczych wyświetlone będzie dodatkowe okno z wyliczonymi
liczebnościami resztowymi (liczebności obserwowane minus oczekiwane).

• Procenty z całości - wybranie tej opcji powoduje wyświetlenie w każdej komórce

w tabeli sumarycznej i dwudzielczej procentów obliczonych względem całkowitej
liczebności próby.

• Procenty w wierszach - wybranie tej opcji powoduje wyświetlenie w każdej komórce

w tabeli sumarycznej i dwudzielczej procentów obliczonych względem liczebności
w bieżącym wierszu tabeli.

• Procenty w kolumnach - wybranie tej opcji powoduje wyświetlenie w każdej komórce

w tabeli sumarycznej i dwudzielczej procentów obliczonych względem liczebności
w bieżącej kolumnie tabeli.

234

Tabele wielodzielcze

Rys. 12.7 Opcje dla tabel sumarycznych i dwudzielczych

W każdej tabeli sumarycznej lub dwudzielczej wyświetlone też mogą być długie nazwy
(etykiety) zmiennych. Osiągniemy to poprzez wybranie opcji Pokaż długie etykiety
wartości.

Grupa opcji [3] to zespół opcji umożliwiający wybór statystyk do analizy tabel
wielodzielczych oraz współczynników opisujących siłę powiązania miedzy dwoma
zmiennymi jakościowymi. Chcąc otrzymać wyniki dla pokazanych tam opcji, musimy je
wybrać przez kliknięcie na nazwie lub okienku opcji. Wartości tych statystyk zostaną
wyświetlone w dodatkowym oknie wynikowym po kliknięciu na przycisku Dokładne
tabele dwudzielcze. Okno z omawianą grupą opcji widoczne jest na poniższym rysunku.

235

Rys. 12.8 Okno wyboru statystyk dla tabel dwudzielczych

Do dyspozycji mamy:
• χ

2

Pearsona - jest najbardziej rozpowszechnionym testem

istotności dla zmiennych

jakościowych. Statystyka ta wykorzystuje liczebności oczekiwane obliczone dla tabeli

dwudzielczej. Gdyby nie było żadnej zależności pomiędzy zmiennymi, wówczas
powinniśmy oczekiwać mniej więcej takich samych liczebności oczekiwanych
i obserwowanych. W miarę odchodzenia od tego rośnie wartość testu χ

2

.

Dokładne

omówienie tego testu przedstawiliśmy na początku tego rozdziału.

Uwaga - Wartość testu χ

2

zależy od liczby obserwacji i liczby komórek w tabeli. Jeśli

bowiem jakieś liczebności teoretyczne będą poniżej 5, to wartość testu może być
wysoce nieprecyzyjna.

Przystępny kurs statystyki

• χ

2

największej wiarygodności - χ

2

największej wiarygodności sprawdza tę samą

hipotezę co test χ

2

Pearsona, ale jego

sposób obliczania oparty jest na teorii największej

wiarygodności. Wartości tych testów są do siebie zbliżone.

• χ

2

poprawką Yatesa - Jest to poprawka statystyki χ

2

dla

małych tabel o rozmiarach

2x2. Poprawka ta stosowana jest, jeżeli liczebności w tabeli są małe tak, że wówczas
liczebności oczekiwane są mniejsze od 5. Poprawka ta została dokładniej omówiona na
początku tego rozdziału.

• dokładny test Fishera - ten test jest obliczany tylko dla tabel 2x2. Oblicza on przy

założeniu hipotezy zerowej dokładne prawdopodobieństwo otrzymania tabeli
o liczebnościach obserwowanych. Podawane jest zarówno prawdopodobieństwo jedno -

jak i dwustronne. Dokładny test Fishera stosujemy, jeżeli całkowita liczebność

obserwacji jest mała lub jeśli bardzo małe są liczebności oczekiwane.

Dokładne omówienie wszystkich poprawek testu x

2

przedstawione będzie w rozdziale

czternastym, poświęconym testom nieparametrycznym. Obecnie aby nie zgubić się
w gąszczu tych poprawek, podamy jedynie wskazówkę - kiedy i jaką poprawkę
zastosować.

• test McNemary - ten test stosujemy, jeśli liczebności w tabeli 2x2 reprezentują

zmienne zależne. Dokładne omówienie tego testu wraz z przykładem przedstawiliśmy
wcześniej w tym rozdziale. Obliczać możemy:

1. test Mcnemara A/D (testujemy hipotezę, że liczebności w komórkach

A i D są identyczne) dla danych zapisanych w tabeli postaci:

Po oddziaływaniu

Suma

—

+

Suma

Przed

+

A

B

A + B

oddziaływaniem

—

C

D

C + D

Suma

A + C

B + D

N

2. test Mcnemara B/C (testujemy hipotezę, że liczebności w komórkach

B i C są identyczne) dla danych zapisanych w tabeli postaci:

236

Tabele wielodzielcze

Po oddziaływaniu

Suma

+

—

Suma

Przed

+

A

B

A+B

oddziaływaniem —

C

D

C+D

Suma

A+C

B+D

N

• współczynnik Φ - współczynnik ten jest miarą korelacji między dwiema zmiennymi

w tabeli 2x2. Jego wartość zmienia się od 0 (brak zależności między zmiennymi) do 1
(całkowita zależność między zmiennymi). Dokładne omówienie tego współczynnika
wraz z przykładem przedstawiliśmy wcześniej w tym rozdziale.

• współczynnik kontyngencji C - współczynnik ten zaproponowany przez Pearsona

(twórcę testu χ

2

) jest

miarą zależności między zmiennymi. Podstawą do obliczeń jest

wartość test χ

2.

Jego

postać omówiona była wcześniej w tym rozdziale. Jego największą

wadą jest to, że jego maksymalna wartość zależy od rozmiaru tabeli (osiąga wartość 1

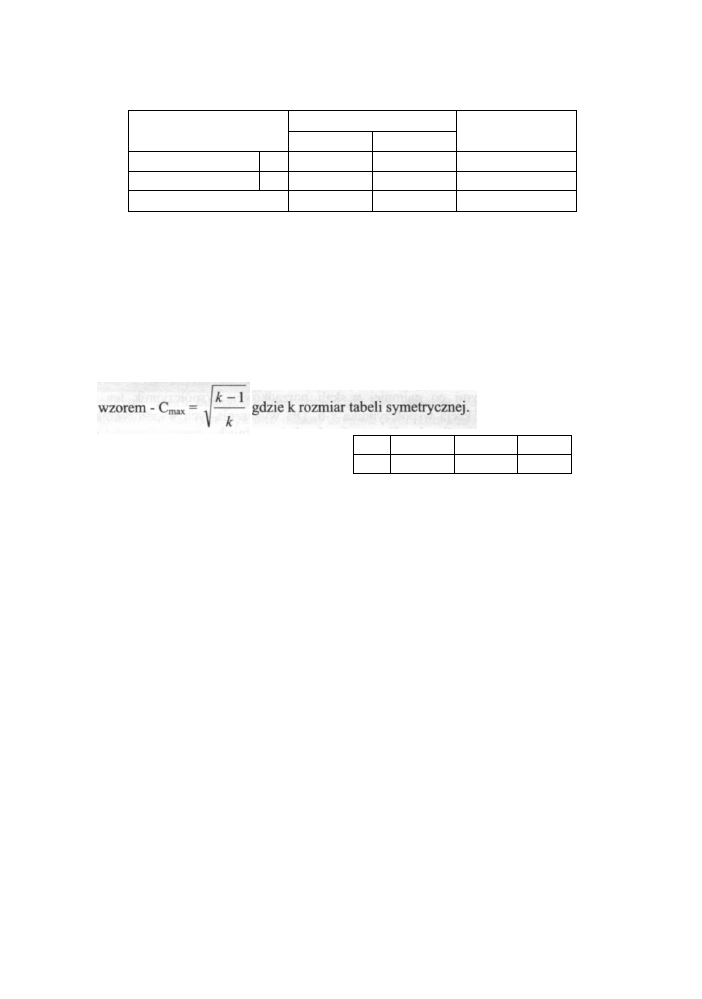
jedynie dla nieskończonej liczby kategorii). Ta maksymalna wartość wyraża się

Przykładowo -

k

2

3

Cmax

0,707

0,816

0,866

• współczynnik V Cramera - współczynnik ten jest miarą zależności między dwiema

zmiennymi w tabeli 2x2. Współczynnik ten również przyjmuje wartości od 0 (brak
relacji między zmiennymi) do 1. Im bliższa jedynki jest wartość tego współczynnika,
tym silniejsze jest powiązanie pomiędzy analizowanymi cechami.

• współczynnik korelacji tetrachorycznej - jest to miara stosowana do tablic 2x2.

Korelacja tetrachoryczna jest korelacją dwuwymiarowego rozkładu normalnego
wynikającą ze sztucznego podziału zmiennych na dwie kategorie. Współczynnik
korelacji tetrachorycznej daje ocenę tej tak sztucznie otrzymanej korelacji.
Współczynnik ten jest tym mniej rzetelny, im bardziej służące za podstawę do
wyliczenia rozkłady wartości zmiennych odbiegają od rozkładu normalnego.
Szacunkową wartością współczynnika korelacji tetrachorycznej jest cosinus pewnego
kąta (zależnego od wartości występujących w tabeli 2x2). Przykład zastosowania
współczynnika τ Kendalla przedstawiono w przykładzie.

• współczynniki τ Kendalla - współczynniki τ Kendalla dają ocenę podobieństwa

uporządkowań zbioru danych dla dwóch zmiennych mierzonych na skali porządkowej.
Można go stosować nawet wtedy, gdy w wielu komórkach pojawią się wartości małe
lub równe zero. Współczynniki te, zaproponowane przez Kendalla (1955 r.) przyjmują
wartości z przedziału <-l, 1>. Wartość 1 oznacza pełną zgodność uporządkowań,
wartość 0 brak zgodność a wartość -1 pełną ich przeciwstawność. Współczynniki
Kendalla wskazują więc nie tylko siłę, lecz również kierunek zależności.
Współczynniki te dostarczają ponadto więcej informacji niż powszechnie stosowany
współczynnik korelacji rang Spearmana. Współczynnik Spearmana nie może być

237

Przystępny kurs statystyki

stosowany do oceny podobieństw uporządkowań, bo nie zapewnia on wyników
niezmiennych przy dopuszczalnych przekształceniach na skali porządkowej. Również
porządkowanie za pomocą rang (liczb naturalnych) zakłada, że odległości między
sąsiednimi wartościami na skali porządkowej są sobie równe, a w rzeczywistości na
dowolnej skali porządkowej odległości pomiędzy dwiema wartościami są nie znane.
Wyliczane są dwa warianty τ oznaczane jako τ-b (tau-b) stosowany dla tablic
kwadratowych i Τ-C (tau-c) stosowany do tablic,

które nie są kwadratowe. Zastosowania

współczynnika τ Kendalla przedstawiono w przykładzie 5.

• współczynnik korelacji rang Spearmana - współczynnik rang Spearmana możemy

uważać za zwyczajny współczynnik korelacji Pearsona z tą jednak różnicą, że
obliczamy go wykorzystując rangi, a nie same wartości. Stosujemy go, gdy jedna lub
dwie zmienne mierzone są na skali porządkowej lub nie posiadają rozkładu
normalnego. Współczynnik ten przyjmuje wartości z przedziału <-l, 1>. Im bliższy jest
współczynnik korelacji rang Spearmana liczbie 1 lub -1, tym silniejsza jest analizowana

zależność. Dokładniej współczynnik ten będzie omówiony w drugim tomie.

• współczynniki d Sommera - jest to kolejna miara zależności pomiędzy dwoma

zmiennymi mierzonymi co najmniej w skali porządkowej. Współczynnik ten jest
asymetryczną modyfikacją współczynnika τ-b. Dla wyliczenia tych współczynników
wykorzystywana jest liczebność zgodnych i niezgodnych uporządkowań obu
zmiennych. Obliczane są dwie asymetryczne miary:

• d(X|Y) - zmienna zależna reprezentowana przez wiersze
• d(Y|X) - zmienna zależna reprezentowana przez kolumny

Współczynniki d-Somera przyjmują wartości z przedziału <-l, 1> i wskazują nie tylko
siłę, lecz również kierunek zależności. Wartość 1 oznacza doskonałą zgodność, wartość
0 oznacza niezależność, zaś wartość -1 wskazuje na doskonałą niezgodność (odwrotne
uporządkowanie elementów).

• współczynnik Gamma - współczynnik ten ma podobną konstrukcję i interpretację jak

współczynniki d-Somera i τ-Kendalla. Wymaga też podobnych założeń. Stosuje się go
w przypadku, gdy dane zawierają wiele przypadków „powiązanych par obserwacji"
(obserwacji reprezentujących ten sam wariant cechy).

• współczynniki niepewności - są to wskaźniki korelacji stochastycznej, których

koncepcja pochodzi od zastosowania teorii informacji w analizie statystycznej.
Współczynniki niepewności wykorzystują bowiem w swej konstrukcji pojęcie
niepewności związanej z rozkładem i jej miary entropii. Mają one następującą ogólną
konstrukcję:

238

Omawiane miary informują, w jakim stopniu znajomość wartości zmiennej niezależnej
zmniejszają naszą niepewność związaną z rozkładem zmiennej zależnej. Współczynniki
niepewności przyjmują wartość od 0 (znajomość zmiennej niezależnej nie zmniejsza

Tabele wielodzielcze

nieokreśloności zmiennej zależnej) do 1 (nieokreśloność zmiennej zależnej zanika).
Wyliczane są trzy współczynniki:

• S(X|Y) (zmienna zależna reprezentowana przez wiersze) i S(Y|X) (zmienna

zależna reprezentowana przez kolumny) asymetryczne - próbujemy bowiem
przewidzieć jedną zmienną (zależną) za pomocą innej zmiennej
(niezależnej).

• S(Y, X) symetryczna - w przypadku symetrii związku.

Grupa opcji [4] to zespół przycisków uruchamiających interpretacją graficzną
analizowanych problemów. Należą do nich:

- umożliwia tworzenie wykresu interakcji pomiędzy trzema

zmiennymi. Jeżeli mamy wybrane więcej niż trzy zmienne, powstanie kaskada takich
wykresów. Na każdym wykresie ostatni czynnik reprezentowany jest przez różne wzory
linii lub kolory, pozostałe zaś reprezentowany jest przez etykiety osi X-ów. Przykładowy
wykres interakcji pokazany jest na poniższym rysunku.

wybranych tabel. Jest to interpretacja graficzna szczegółowych tablic dwudzielczych.

239

- umożliwia sporządzenie skategoryzowanych histogramów

dla wybranych tablic. Każdy wykres może podsumowywać do trzech zmiennych, dlatego
dla więcej niż trzech zmiennych powstanie kaskada histogramów.

Rys. 12.9 Wykres interakcji zmiennych Papieros i Alkohol

- umożliwia tworzenie trójwymiarowych histogramów dla

Przystępny kurs statystyki

Rozważania teoretyczne zilustrujemy przykładami.

Przykład 4
W grupie 40 chorych na pewną chorobę zawodową przeanalizowano (na podstawie historii
choroby oraz ankiety) następujące dane:

1. Palenie papierosów z podziałem na kategorie

• dużo - palący dużą ilość papierosów
• średnio - palący przeciętną ilość papierosów
• mało - palący minimalne ilości papierosów

2. Picie alkoholu z podziałem na kategorie

• dużo - pijący duże ilości alkoholu
• średnio - pijący przeciętną ilość alkoholu
• mało - pijący minimalne ilości alkoholu

• nic - nie pijący w ogóle alkoholu

3. Narażenie na substancje toksyczne w pracy zawodowej z podziałem na kategorie

• dużo - narażeni na duże ilości substancji szkodliwych dla zdrowia
• średnio - narażeni na średnie ilości substancji szkodliwych dla zdrowia
• mało - narażeni na minimalne ilości substancji szkodliwych dla zdrowia
• nic - nie mający kontaktu z substancjami szkodliwymi dla zdrowia

4. Umowną skalę natężenia choroby z podziałem na kategorie

• I - najlżejsza postać choroby
• II - ostra postać choroby
• III - przewlekła, ostra postać choroby

Zebrane dane przedstawiono w poniższej tabeli:

Lp.

Skala

Papierosy

Alkohol

Zatrucia

chorobowa

przemysłowe

1

III

DUZO

DUZO

DUZO

2

I

DUŻO

MAŁO

DUŻO

3

III

DUŻO

DUŻO

DUŻO

4

III

DUŻO

DUŻO

DUŻO

5

III

DUŻO

MAŁO

DUŻO

6

I

MAŁO

DUŻO

ŚREDNIO

7

III

ŚREDNIO

DUŻO

DUŻO

8

II

DUŻO

DUŻO

MAŁO

9

III

MAŁO

MAŁO

NIC

10

II

DUŻO

DUŻO

NIC

11

III

DUŻO

ŚREDNI

DUŻO

12

I

MAŁO

MAŁO

ŚREDNIO

13

III

DUŻO

ŚREDNIO

DUŻO

14

III

DUŻO

MAŁO

DUŻO

15

III

DUŻO

MAŁO

DUŻO

16

III

DUŻO

ŚREDNIO

DUŻO

17

I

MAŁO

NIC

ŚREDNIO

18

II

MAŁO

MAŁO

NIC

19

III

DUŻO

DUŻO

DUŻO

240

Tabele wielodzielcze

Lp.

Skala

Papierosy

Alkohol

Zatrucia

chorobowa

przemysłowe

20

II

MAŁO

DUZO

ŚREDNIO

21

I

DUŻO

NIC

ŚREDNIO

22

II

DUŻO

MAŁO

NIC

23

I

DUŻO

NIC

ŚREDNIO

24

III

DUŻO

ŚREDNIO

ŚREDNIO

25

I

DUŻO

ŚREDNIO

ŚREDNIO

26

II

ŚREDNIO

ŚREDNIO

NIC

27

I

DUŻO

ŚREDNIO

MAŁO

28

II

MAŁO

ŚREDNIO

MAŁO

29

III

DUŻO

ŚREDNIO

MAŁO

30

III

DUŻO

MAŁO

NIC

31

III

DUŻO

DUŻO

MAŁO

32

II

ŚREDNIO

MAŁO

MAŁO

33

I

ŚREDNIO

ŚREDNIO

MAŁO

34

II

ŚREDNIO

NIC

MAŁO

35

I

ŚREDNIO

MAŁO

MAŁO

36

II

DUŻO

ŚREDNIO

MAŁO

37

II

ŚREDNIO

NIC

MAŁO

38

I

ŚREDNIO

MAŁO

MAŁO

39

II

ŚREDNIO

MAŁO

NIC

40

1

MAŁO

MAŁO

NIC

Postaramy się odpowiedzieć, czy istnieje zależność między skalą natężenia choroby
a wymienionymi w tabeli cechami jakościowymi (palenie papierosów, picie alkoholu,
narażenie na substancje szkodliwe dla zdrowia). Naszą analizę rozpotrzynamy od
wprowadzenia danych tak, że każda rozpatrywana cecha zajmuje osobną kolumnę
(zmienną). Fragment tak wprowadzonego zbioru widoczny jest na poniższym rysunku.

22

SKALA

23

PAPIEROS

24

ALKOHOL

25

ZATRUCIA

I I I

DUŻO

DUŻO

DUŻO

I

DUŻO

MAŁO

DUŻO
DUŻO

I I I

DUŻO

DUŻO

DUŻO
DUŻO

I I I

DUŻO

DUŻO

DUŻO

I I I

DUZO

MAŁO

DUŻO

I

DUŻO

DUŻO ŚREDNIO

I I I ŚREDNIO

DUŻO

DUŻO

I I

DUŻO

DUŻO

MAŁO

I I I

DUŻO

MAŁO

NIC

I I

DUŻO

DUŻO

NIC

I I I

DUŻO

ŚREDNI

DUŻO

Rys. 12.10 Fragment arkusza danych z przykładu 4

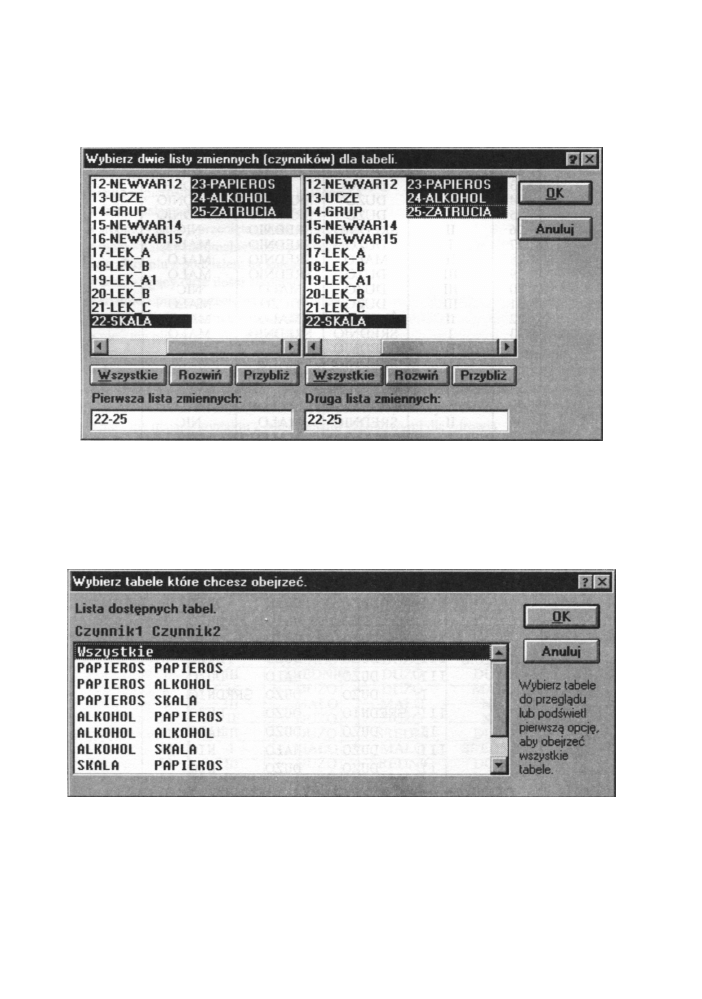
Następnie zmienne do analizy wybieramy w oknie otrzymanym po kliknięciu na przycisku

Określ tabelę w polu Tabele zbiorcze. Na obu listach zaznaczamy rozpatrywane zmienne.

241

Przystępny kurs statystyki

Konkretne tablice dwudzielcze będziemy mogli wybrać później. Okno to wraz
z wybranymi danymi widoczne jest na poniższym rysunku.

Rys. 12.11 Okno wyboru zmiennych

Po zamknięciu okna wyboru zmiennych (OK) klikamy przycisk OK otwierając okno
z wyborem analiz pokazane na rysunku. Analizę rozpoczniemy od przeglądnięcia tabel
zbiorczych. Wybieramy w polu Tabele opcję Procenty w kolumnach oraz Procenty
w wierszach a następnie klikamy na przycisku Przegląd tabeli zbiorczej. Otworzy się
okno widoczne na poniższym rysunku, w którym możemy wybrać interesującą nas tabelę.

Rys. 12.12 Okno wyboru tablicy do dalszej analizy

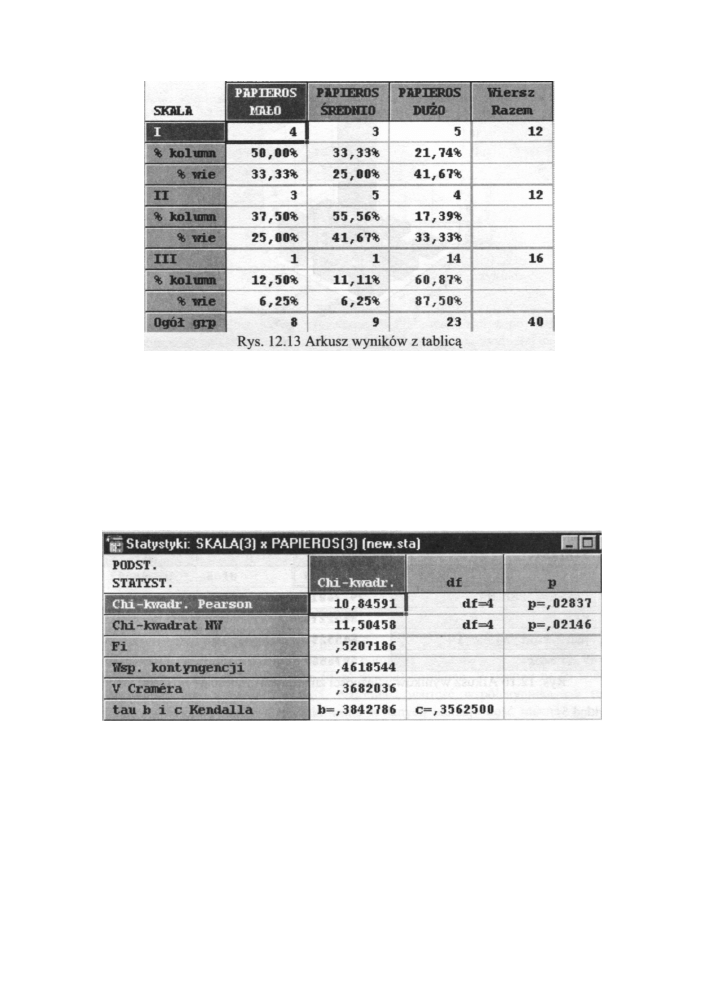
Wybieramy zmienne SKALA i PAPIEROS. Otrzymujemy następującą tablicę
dwudzielczą.

242

Tabele wielodzielcze

Z tabeli wynika, że ponad 60% osób palących duże ilości papierosów ma III stopień
natężenia choroby oraz spośród osób, którym przypisano III stopień natężenia choroby aż

85 % pali dużą ilość papierosów. Tabela więc podpowiada, że pomiędzy ilością
wypalanych papierosów a skalą natężenia choroby (większa ilość wypalanych papierosów

przyczynia się prawdopodobnie do ostrzejszej postaci choroby) istnieje korelacja.
Potwierdźmy nasze przypuszczenia głębszą analizą statystyczną. W tym celu w polu

Statystyki dla tabel dwudzielczych wybieramy dla dalszej analizy testy %

2

oraz

współczynnik kontyngencji oraz x Kendall. W wyniku obliczeń otrzymujemy arkusz
wynikowy widoczny w poniższym oknie.

Rys. 12.14 Arkusz wyników z obliczonymi statystykami

Wyniki testu χ

2

(χ

2

= 10,8459 przy p= 0,028)

potwierdzają nasze poprzednie

przypuszczenia. Istnieje korelacja o przeciętnej sile (C = 0,4619 iV = 0,368) pomiędzy
ilością wypalanych papierosów a stopniem natężenia choroby. Graficznie interpretacja
takiej sytuacji widoczna jest na poniższym rysunku:

243

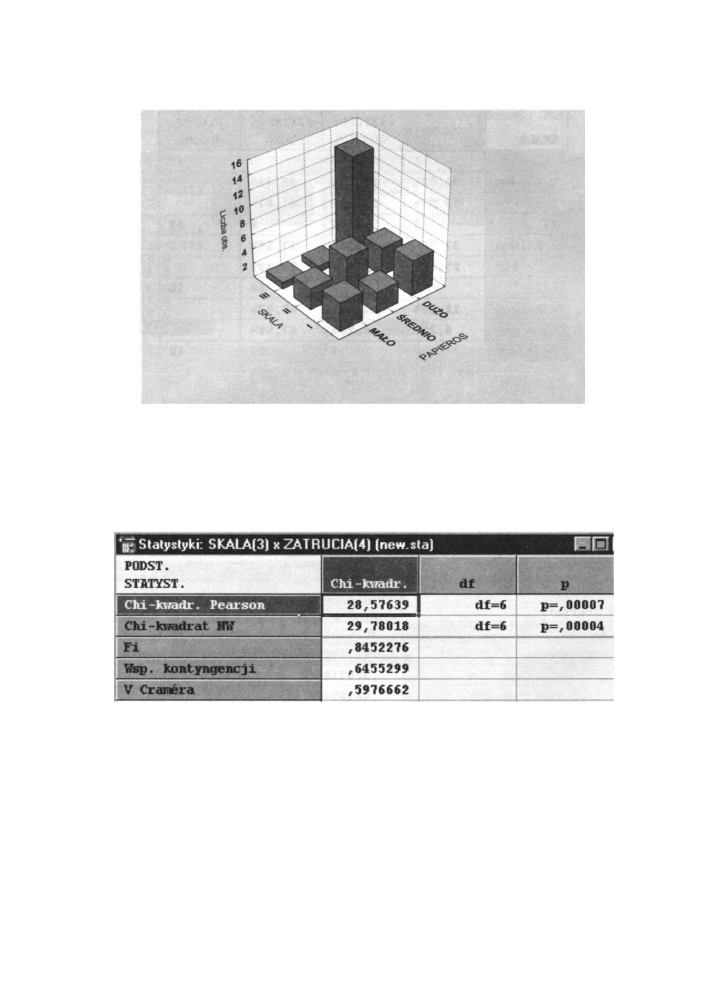
Przystępny kurs statystyki

Rys. 12.15 Interpretacja graficzna zależności zmiennych „Papieros" i „Skala"

Jeszcze mocniejsza jest zależność pomiędzy wielkością narażenia na czynniki toksyczne
w pracy a skalą natężenia przebiegu schorzenia. Wartość test wynosi x

2

= 28,576 przy

niskim poziomie p = 0,00007. Współczynnik kontyngencji opisujący siłę zależności
osiągną wartość C = 0,646. Informuje nas o tym arkusz wynikowy widoczny poniżej.
Analizę pozostałych powiązań zostawiam Czytelnikowi.

Rys. 12.16 Arkusz wyników zależności zmiennych „Zatrucia" i „Skala

Przykład 5
W grupie 40 chorych na pewną chorobę przeprowadzono badania poziomu hormonu
insuliny oraz wielkości glukozy w surowicy krwi. Otrzymane wyniki pogrupowano
w trzech kategoriach - I poniżej normy, II - w normie oraz III - powyżej normy. Po
wprowadzeniu danych wyliczamy tabele wielodzielcza, która przyjmuje postać:

244

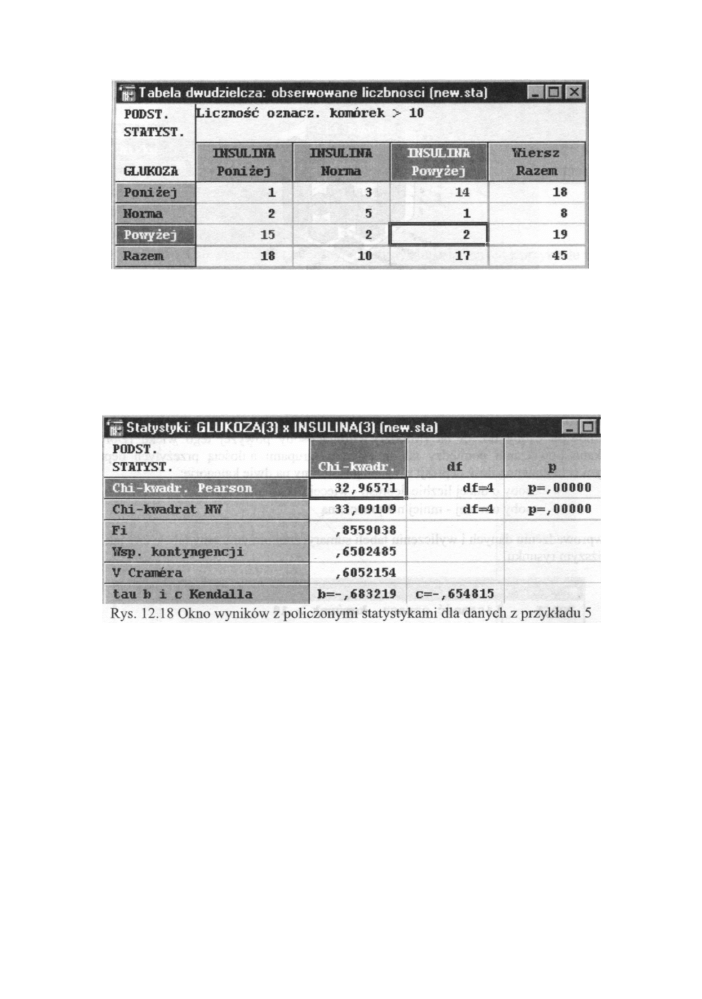
Tabele wielodzielcze

Rys. 12.17 Tablica dwudzielczą dla zmiennych z przykładu 5

W tabeli na czerwono zaznaczono w komórkach liczebności powyżej 10. Ułożenie
większych wartości wzdłuż jednej z przekątnych i ich wielkości zopowiadają istnienie
korelacji pomiędzy analizowanymi zmiennymi. Sprawdzamy to wybierając wśród opcji
Statystyki dla tabel dwudzielczych test χ

2

do analizy oraz

współczynniki kontyngencji

i współczynniki Kendalla dla poznania siły tej zależności. Po wykonaniu obliczeń

uzyskujemy następujące okno z arkuszem wynikowym.

Otrzymane wyniki potwierdzają nasze przypuszczenia. Przy dowolnie małym (mniejszym
niż 0,000001) poziomie istotności istnieje pomiędzy poziomem insuliny a poziomem
glukozy we krwi istotna statystycznie (dość mocna) korelacja. Wskazuje na to wielkość
współczynnika kontyngencji C = 0,65. Natomiast wartość współczynnika τ-b (tabela
kwadratowa),

wykorzystując uporządkowanie w danych ukazuje dość mocną negatywną

korelację. Zwiększenie poziomu insuliny u chorych wpływa na szybkie zmniejszenie się
poziomu glukozy w surowicy krwi.

Również trójwymiarowy wykres doskonale potwierdza wyniki statystycznej analizy.
Najwyższe słupki biegnące wzdłuż drugiej przekątnej potwierdzają istnienie negatywnej
korelacji.

245

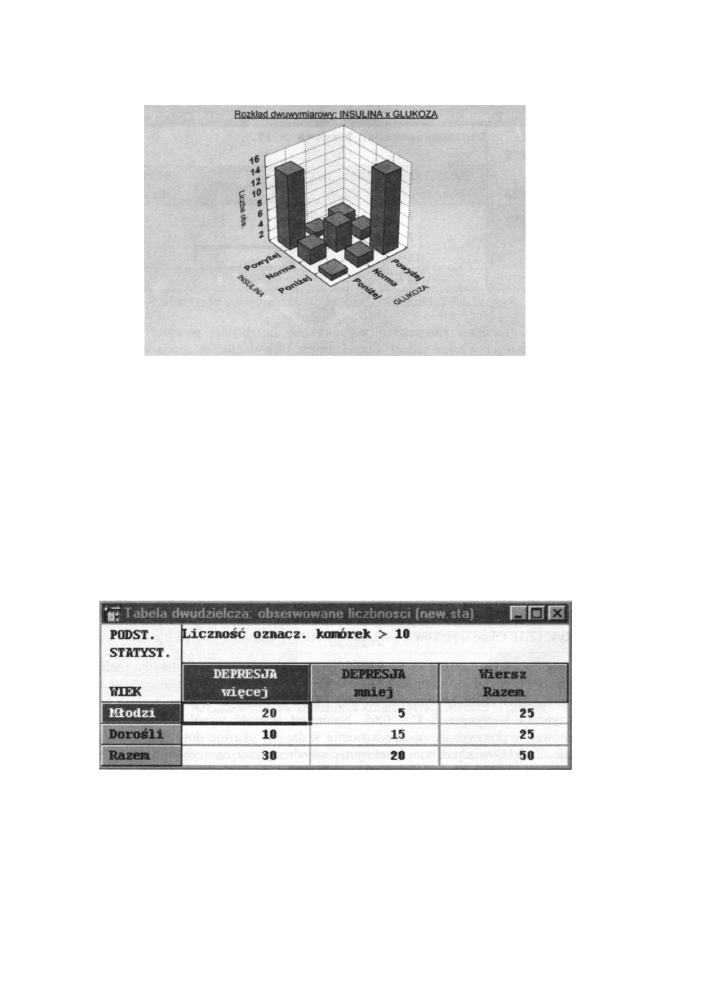
Przystępny kurs statystyki

Rys. 12.19 Interpretacja graficzna zależności zmiennych z przykładu 5

Przykład 6
W klinice psychiatrycznej wśród licznych danych zebranych na temat pacjenta
analizowano również wiek pacjenta oraz liczbę depresji w określonym czasie. Zmienne te
miały rozkład normalny. Zmienną wiek podzielono na dwie kategorie. Pierwsza
obejmowała osoby do 35 lat (Młodzi) a druga osoby powyżej tego wieku (Dorośli).
Szukano powiązania pomiędzy tak powstałymi grupami a ilością przeżytych depresji.
W tym celu zmienną ilość depresji również podzielimy na dwie kategorię:

• osoby o dużej liczbie depresji - więcej ponad przeciętną
• osoby o małej - mniej niż przeciętną

Po wprowadzeniu danych i wyliczeniu tabeli sumarycznej otrzymujemy tabelę 2x2 jak na
poniższym rysunku.

Rys. 12.20. Tablica dwudzielczą dla zmiennych z przykładu 6

Przeprowadzimy analizę statystyczną (test χ

2

i

współczynnik kontygencji) prostej tabeli

2x2. Wyniki obliczeń pokazuje poniższy arkusz.

246

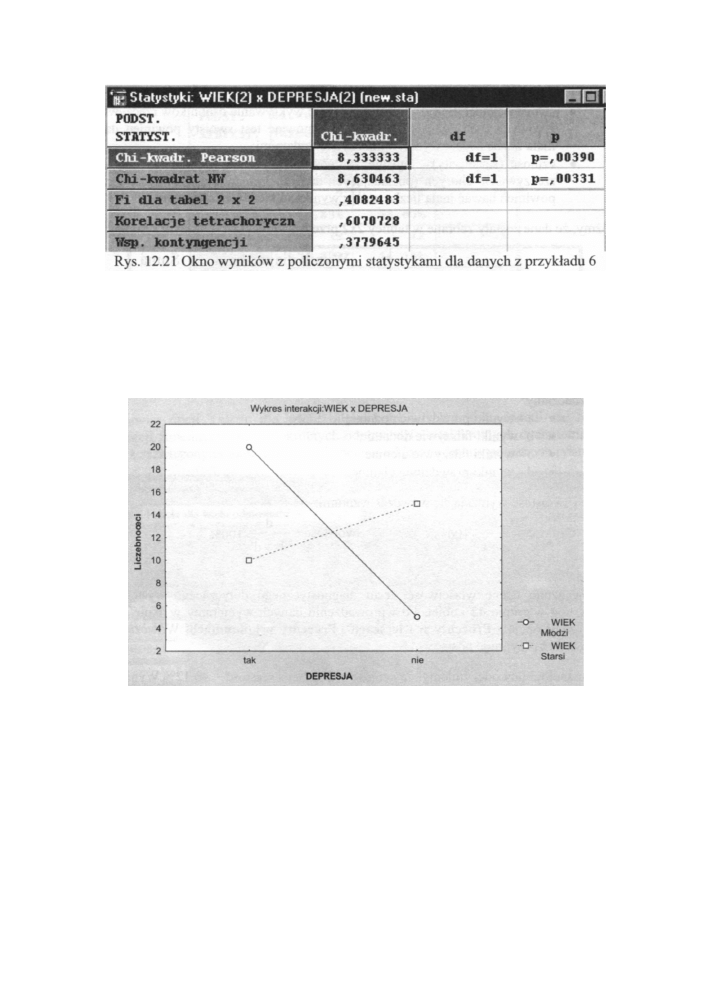
Tabele wielodzielcze

Wyniki testu χ

2

wskazują na istnienie powiązania między przynależnością do grupy

wiekowej a ilością przeżytych depresji. Warto zwrócić uwagę na obliczony tu
współczynnik korelacji tetrachorycznej (bo taka tu ma miejsce). Wartość jego (0,607)
najlepiej więc określa siłę zależności. Pacjenci „młodzi" przeżywają więcej depresji niż
pacjenci „starsi". Uzupełnieniem naszych obliczeń będzie wykres interakcji podkreślający
istnienie omawianej zależności.

DEPRESJA

Rys. 12.22 Wykres interakcji dla zmiennych z przykładu 6

Z wyników analiz tu przeprowadzanych mogą skorzystać również epidemiologowie. W ich
głównym nurcie badań jest ocena trafności testu. Chodzi o to, by podział na chorych

i zdrowych był podziałem realnym. Oznacza to, że po weryfikacji innymi testami
i różnorodnymi badaniami lekarskimi w obu grupach było jak najmniej fałszywie chorych
(sklasyfikowanie zdrowych jako chorych) i jak najmniej fałszywie zdrowych (tj.
sklasyfikowanie chorych jako zdrowych). Stosowane są dwie miary oceny trafności testu.

247

Przystępny kurs statystyki

Są to:

• swoistość (specificity) - opisuje zdolność wykrywania osobników rzeczywiście

zdrowych (bez danej cechy). Inaczej mówiąc test swoisty powinien dawać
mała liczbę osób z wynikami fałszywie dodatnimi;

• czułość (sensitivity) - opisuje zdolność wykrywania wszystkich osobników

rzeczywiście chorych (posiadających daną cechę). Inaczej mówiąc test czuły
powinien dawać małą liczbę osób z wynikami fałszywie ujemnymi.

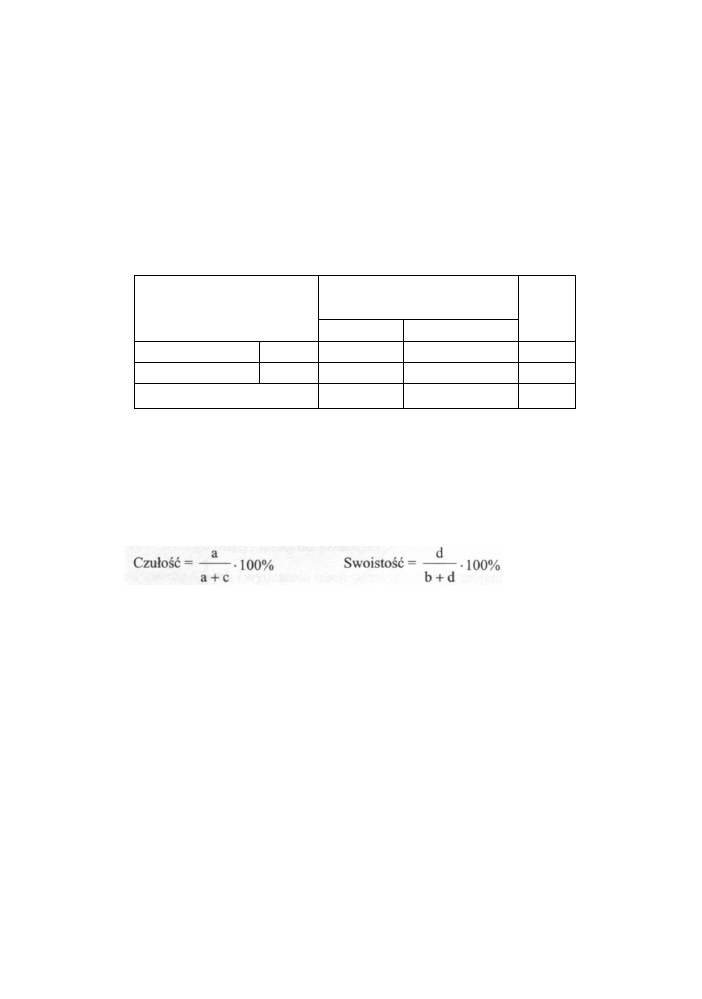
Załóżmy, że dane zostały zebrane w tablicy 2x2 przedstawionej na poniższym rysunku:

Wynik diagnozy

klinicznej

Suma

chorzy

zdrowi

Wynik testu

+

a

b

a+b

przesiewowego

-

c

d

c+d

Suma

a+c

b+d

N

gdzie oznaczamy:

• a - wyniki prawdziwie dodatnie
• b -wyniki fałszywie dodatnie
• c - wyniki fałszywie ujemne
• d - wyniki prawdziwie ujemne

Czułość i swoistość wyrażają się wówczas wzorami:

248

Przykład 7
Przeprowadzono ocenę właściwości testu diagnostycznego dotyczącego występowania
żylaków nóg w grupie 42 kobiet. Po wprowadzeniu danych wybieramy w oknie Wyniki
tabelaryzacji opcje - Procenty w wierszach i Procenty w kolumnach. Wówczas tabela
wynikowa 2x2 przyjmuje postać:

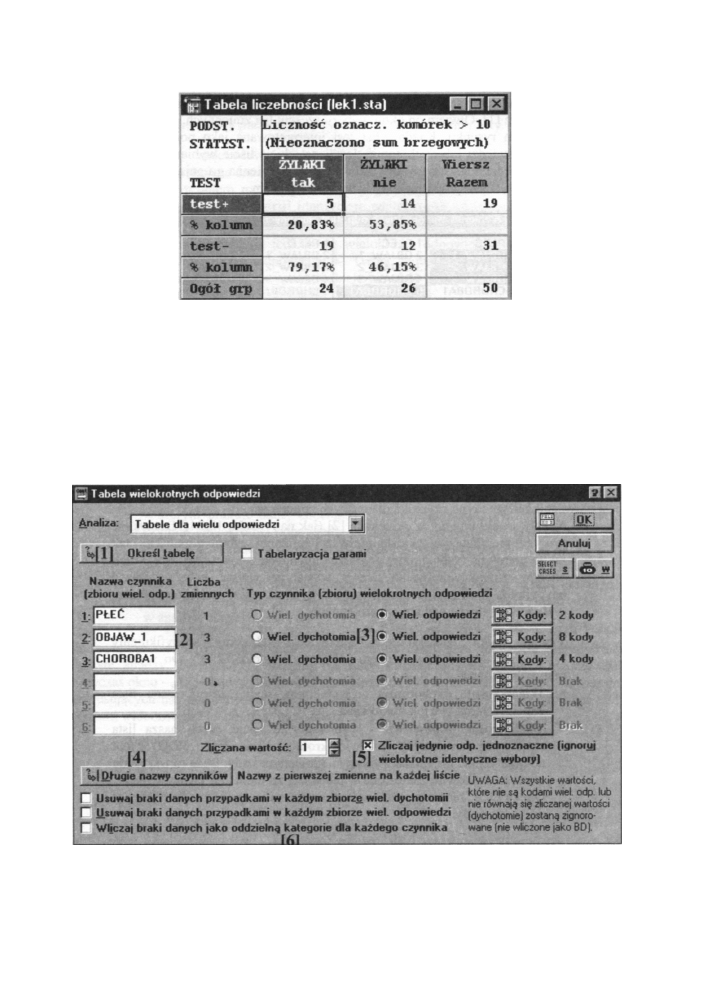
Z otrzymanej tablicy odczytujemy, że czułość = 20,8% i swoistość = 46,12%. Wynika stąd,
że rezultaty testu nie są zachęcające. Z ogólnej liczby 24 chorych test ma wartości dodatnie
tylko w 21%.

Tabele wielodzielcze

Rys. 12.23 Tabela liczebności dla danych z przykładu 7

Omówimy obecnie drugą grupę analiz poświęconą wielokrotnym odpowiedziom
i wielokrotnym dychotomiom.

Wielokrotne odpowiedzi i dychotomie

Po wybraniu opcji Tabele dla wielu odpowiedzi na ekranie wyświetli się okno do
specyfikacji zmiennych dla wielokrotnych odpowiedzi i wielokrotnych dychotomii. Okno
to wraz z zaznaczonymi najważniejszymi opcjami widoczne jest na poniższym rysunku.

Rys. 12.24 Okno opcji Tabele wielokrotnych odpowiedzi

Przystępny kurs statystyki

Do wyboru danych do analizy służy przycisk Określ tabelę oznaczony na powyższym
rysunku symbolem [1]. Otwiera on okno wyboru sześciu list zmiennych. Okno to pokazane

jest na poniższym rysunku. Każda z list jest interpretowana jako pojedyncza zmienna

wielokrotnej odpowiedzi lub dychotomii. Jeżeli na jakiejś liście wybierzemy tylko jedną
zmienną, wtedy będzie ona traktowana jako tradycyjna zmienna grupująca. Dokładny opis
wyboru zmiennych został przedstawiony w rozdziale trzecim.

Rys. 12.25 Okno wyboru zmiennych.

Następnym ważnym krokiem w opracowywaniu wielokrotnych odpowiedzi/dychotomii

jest określenie nazwy i typu czynnika dla naszych zmiennych.

Nazwy specyfikujemy w okienkach [2] (jak na rysunku 12.24). Domyślnie
program bierze nazwy z każdej pierwszej zmiennej wybranej na liście - tak

jak to mamy na rysunku przy wyborze zmiennych z powyższej listy. Jeżeli

chcemy zmienić domyślne nazwy wystarczy wpisać nowe w polach
edycyjnych obok odpowiedniego czynnika. Obok nazwy zmiennych mamy
wyświetloną liczbę wybranych zmiennych.

Typ czynnika wielokrotnych odpowiedzi/dychotomii specyfikujemy
w polach oznaczonym symbolem [3] (patrz rysunek 12.24). Do wyboru
mamy dwie opcje:
• Wielokrotna dychotomia - wybieramy opcję, jeżeli nasza lista

zmiennych ma być tak traktowana.

• Wielokrotne odpowiedzi - wybieramy tę opcję, jeżeli nasza lista

aktualnych zmiennych to wielokrotne odpowiedzi. STATISTICA
automatycznie przypisze wybranym zmiennym kody. Będą to wszystkie
wartości całkowite znalezione w pierwszej zmiennej na wybranej liście.
Oczywiście możemy dokonać zmiany wybranych kodów klikając
przycisk Kody.

Możemy także przy pomocy przycisku Długie nazwy czynników (oznaczonego numerem

[4] na rysunku 12.24) wprowadzić długie nazwy zmiennych używanych jako nazwy

250

Tabele wielodzielcze

zbiorów wielokrotnych odpowiedzi. Domyślnie jako długie nazwy zmiennych są

przyjmowana długie nazwy pierwszych zmiennych z odpowiedniej listy.

Następnie musimy zadecydować, jak mają być analizowane jednakowe wielokrotne
odpowiedzi oraz brakujące dane (tzn. brak odpowiedzi respondenta).

Pierwszy problem rozstrzygniemy przy pomocy pola wyboru „Zliczaj jedynie

odpowiedzi jednoznaczne (ignoruj identyczne wielokrotne odpowiedzi)" oznaczonego
numerem [5] na rysunku 12.24. Jeżeli opcja ta jest wybrana, wówczas zgodnie z jej nazwę
STATISTICA

pomija w analizie jednakowe wielokrotne odpowiedzi. Przykładowo: jeśli

ankietowany w wielokrotnej odpowiedzi - Twoja największa dolegliwość (o trzech
możliwościach) odpowiedział trzy razy jednakowo „ból głowy", wówczas STATISTICA
policzy tę odpowiedź jako jeden przypadek.

Jeżeli chodzi o braki danych, to mamy do dyspozycji trzy pola wyboru (oznaczone
numerem [6] na rysunku 12.24):

• Usuwaj braki danych przypadkami w ramach każdego zbioru

wielokrotnej dychotomii - jeżeli to pole jest wybrane, wtedy jako brak
odpowiedzi (przypadek brakujący) będzie przyjmowany każdy przypadek,
w którym brakuje danej chociażby w jednej zmiennej zawierającej odnośny
czynnik wielokrotnej dychotomii. „Porządny" przypadek to ten który ma dane
we wszystkich zmiennych wielokrotnych dychotomii.

• Usuwaj braki danych przypadkami w ramach każdego zbioru

wielokrotnych odpowiedzi - jeżeli to pole jest wybrane, wtedy jako brak
odpowiedzi (przypadek brakujący) będzie przyjmowany każdy przypadek,
w którym brakuje danej chociażby w jednej zmiennej zawierającej odnośny
czynnik wielokrotnej odpowiedzi. „Porządny" przypadek to taki, który co ma
dane we wszystkich zmiennych wielokrotnych odpowiedzi.

• Włączaj braki danych jako oddzielną kategorię dla każdego czynnika -

jeżeli to pole będzie wybrane, wówczas STATISTICA będzie zliczać brakujące

dane w dodatkowej kategorii. Domyślnie program pomija braki danych
w analizie statystycznej.

Po wybraniu zmiennych i ustawieniu odpowiednich opcji czas na tabele sumaryczne
i proste analizy danych. Przechodzimy do nich klikając przycisk OK. Otworzy się
wówczas okno - „Wynikowa tabela wielokrotnych odpowiedzi" umożliwiające wybranie
interesujących nas podsumowań i analiz. Okno to wraz z zaznaczonymi najważniejszymi
opcjami widoczne jest na poniższym rysunku.

251

Przystępny kurs statystyki

Rys. 12.26 Okno „Wynikowa tabela wielokrotnych odpowiedzi"

Przed rozpoczęciem dokładniejszej analizy klikamy przycisk Podsumowanie specyfikacji
tabeli (oznaczony numerem [5] na powyższym rysunku), by dokonać, jak podaje przycisk,
podsumowania wszystkich specyfikacji dotyczących danej tabeli. Dostajemy informację o:
• nazwach aktualnych zmiennych,
• liczbie poziomów i nazwie każdego czynnika,
• typie każdego czynnika.

Rodzaj dalszej analizy lub podsumowań wybieramy wykorzystując grupę przycisków [1].
Do dyspozycji mamy:

1. Przegląd tabel sumarycznych - kliknięcie tego przycisku wywołuje tablice

sumaryczne dla tablic wielodzielczych. W tabeli sumarycznej ostatnia wybrana zmienna
będzie tabelaryzowana w kolumnach, a wszystkie pozostałe zmienne w wierszach. Jeśli
tych ostatnich jest więcej niż dwie wówczas nasza tabela sumaryczna wygląda jak
sklejenie wielu tablic dwudzielczych. Takim sposobem w jednym arkuszu wyników
możemy oglądać nawet tablice sześciodzielcze. O tym, co będzie wyświetlone w tabeli
zbiorczej, decydują ustawienia dokonane przez nas w oknie Tabele wielodzielcze.

2. Tabele liczebności - kliknięcie tego przycisku wywołuje kaskadę okien z tabelami

liczebności dla każdego czynnika w tabeli. W prezentowanych tabelach liczebności dla
każdej kategorii zmiennej wyświetlone są w kolejnych kolumnach następujące dane:

• liczebność odpowiedzi,
• procent odpowiedzi liczony w stosunku do całkowitej liczby odpowiedzi,
• procent odpowiedzi liczony w stosunku do liczby respondentów (jest to

procent ankietowanych, którzy udzielili danej odpowiedzi - o ile pomijamy

jednakowe wielokrotne odpowiedzi).

Uwaga. Ponieważ każdy respondent może udzielić wielokrotnych odpowiedzi
i wielokrotnych dychotomii to ostatnia kolumna w tabeli liczebności nie musi w sumie
dawać 100%!

3. Szczegółową tablicę dwudzielczą - kliknięcie tego przycisku wywołuje arkusz

wyników z tablicami dwudzielczymi. Jeżeli analizujemy tablice z więcej niż dwiema
zmiennymi, wówczas utworzona zostanie kaskada okien wynikowych z tablicami
dwudzielczymi (dla wszystkich par wybranych z grupy badanych zmiennych). O tym,

252

Tabele wielodzielcze

co będzie wyświetlone w tabeli zbiorczej, decydują ustawienia dokonane przez nas
w oknie Tabele wielodzielcze. Okno to omówimy poniżej.

O tym, co zostanie wyświetlone w powyżej omawianych oknach wynikowych tabel
dwudzielczych i sumarycznych, decydują ustawienia przyjęte przez nas w oknie Tabele
wielodzielcze [2] i [3] na rysunku 12.26). Szczegółowo ustawić możemy:

• Podświetlaj liczebności > - po wybraniu tej opcji w tabelach zostaną wyróżnione

liczebności większe od wartości podanej w tym oknie.

• Procenty z całości - po wybraniu tej opcji w tabelach wynikowych sumarycznych

i dwudzielczych wyświetlone zostaną procenty obliczone w stosunku do liczby
respondentów. Jeżeli dodatkowo wybraliśmy opcję Wyświetl % w oddzielnych
tabelach, to wyliczone procenty pojawią się w oddzielnych arkuszach wyników.

• Procenty w kolumnach - po wybraniu tej opcji w tabelach wynikowych

sumarycznych i dwudzielczych wyświetlone zostaną procenty obliczone w stosunku
do całkowite liczby odpowiedzi w bieżącym wierszu. Jeżeli dodatkowo wybraliśmy
opcję Wyświetl % w oddzielnych tabelach, to wyliczone procenty pojawią się
w oddzielnych arkuszach wyników.

• Procenty w wierszach - po wybraniu tej opcji w tabelach wynikowych

sumarycznych i dwudzielczych wyświetlone zostaną procenty obliczone w stosunku
do całkowitej liczby odpowiedzi w kolumnach tabeli. Jeżeli dodatkowo wybraliśmy
opcję Wyświetl % w oddzielnych tabelach, to wyliczone procenty pojawią się
w oddzielnych arkuszach wyników.

• Obliczaj procenty względem ([5] na rysunku 12.26) - tu decydujemy, czy

obliczane liczebności i procenty opierają się na liczbie odpowiedzi lub na liczbie
przypadków (respondentów) w odpowiedniej liczebności brzegowej. Musimy
wprowadzić takie rozróżnienie, bowiem każdy respondent może przyczynić się do
więcej niż jednej odpowiedzi i przez to może być liczony więcej niż jeden raz.

Dokonane podsumowania i analizy możemy zinterpretować graficznie. W tym celu
klikamy przycisk Wykresy interakcji liczebności ([4] na rysunku 12.26). Zostanie
wyświetlony liniowy wykres interakcji maksymalnie pomiędzy trzema zmiennymi.
W przypadku wybrania więcej niż trzech czynników utworzona zostanie kaskada
wykresów interakcji dla każdej kombinacji poziomów. Na każdym wykresie ostatni
czynnik będzie powiązany z różnymi wzorami linii i kolorami, przedostatni z etykietami
górnymi osi x-ów, ostatni zaś z czynników reprezentowany będzie przez etykiety dolne osi
x-ów. Przykładowy wykres interakcji dla trzech zmiennych pokazany jest na rysunku

12.27.

253

Przystępny kurs statystyki

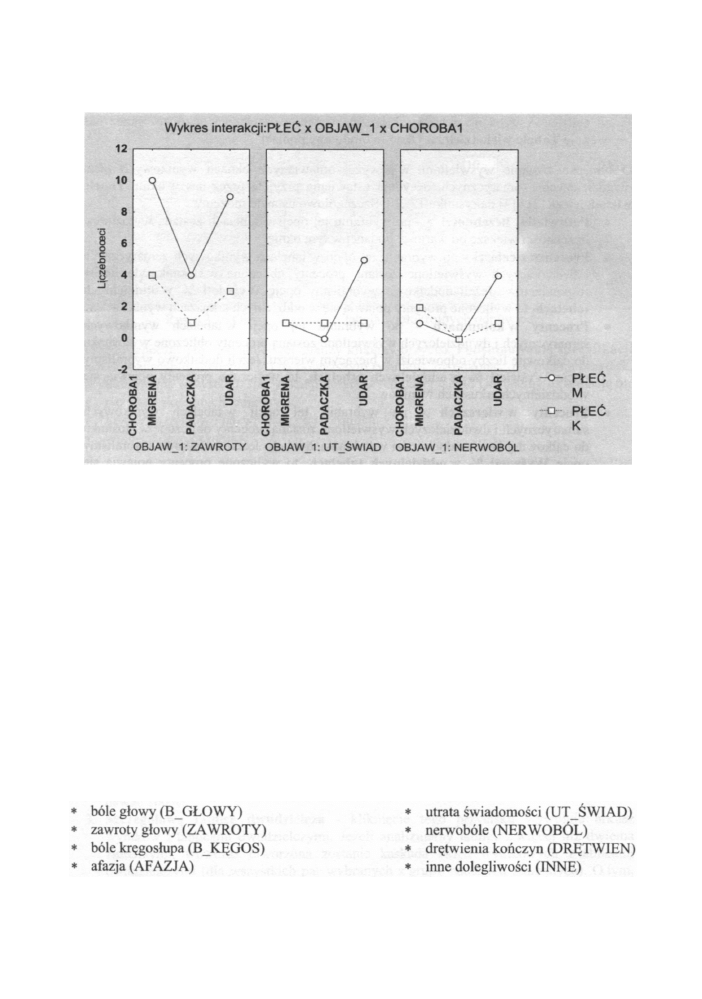
Rys. 12.27 Wykres interakcji trzech zmiennych Płeć, Objaw-1, Choroba

Przykład 8
Rozważmy zbiór danych będący rezultatem hipotetycznej ankiety. Przypuśćmy, że
przeprowadziliśmy badanie grupy pacjentów leczonych neurologicznie. Interesowały nas
największe dolegliwości, przebyte choroby neurologiczne oraz szpitale, w których ci
chorzy byli leczeni. Dodatkowo notowaliśmy płeć respondentów. Zebrane dane
zapisaliśmy w arkuszu danych wprowadzając następujące zmienne:

PŁEĆ - (pierwsza zmienna) - jest to prosta zmienna jakościowa o dwóch kategoriach K -
kobieta i M - mężczyzna.

OBJAW_l OBJAW_2 OBJAW_3 - (trzy następne zmienne) - są to wielokrotne zmienne
odpowiedzi.

W ankiecie użytej do badań proszono ankietowanych o wybór ich największych

trzech ostatnich dolegliwości z zaprezentowanych listy 8 różnych możliwości. Lista
zawierała:

254

Tabele wielodzielcze

Trzy wybrane przez każdego respondenta możliwości zawarto we wspomnianych wyżej
trzech zmiennych. Pierwszą odpowiedź zawarto w zmiennej OBJAW_1, drugą
w OBJAW_2, a trzecią w zmiennej OBJAW_3. Wielokrotne identyczne odpowiedzi były
niedozwolone. Musimy więc tratować zmienne OBJAW_1 - OBJAW_3 jako wielokrotne

zmienne odpowiedzi.

CHOROBA_1 CHOROBA_2 CHOROBA_3 - (kolejne trzy zmienne) to druga grupa
wielokrotnych odpowiedzi.

Poproszono każdego z respondentów o wpisanie 3 ostatnio przebytych chorób

neurologicznych. Odpowiedzi zostały podzielone na cztery grupy:

* migrena (MIGRENA)
* udar niedokrwienny mózgu (UDAR)
* krwotok podpajęczynówkowy (KRWOTOK)
* padaczka (PADACZKA)

Podobnie jak poprzednio, odpowiedzi respondentów zawarto w zmiennych CHOROBA_1
CHOROBA_2 CHOROBA_3. W tym wypadku jednak osoby mogły powtórzyć tę samą
odpowiedź trzy razy (tzn. mogły wymienić 3 te same choroby jako przebyte).

KLINIKA1 KLINIKA2 KLINIKA3 - (ostatnie trzy zmienne) to wielokrotne dychotomie.

Każdego z ankietowanych poprosiliśmy także o wskazanie, w którym z trzech

podanych szpitali był w ostatnim roku leczony. Odpowiedzi te zawarto w trzech zmiennych
KLLNIKAl KLINIKA2 KLINIKA3 oznaczających umownie nazwy szpitali). Jeżeli
ankietowany podał, że był ostatnio leczony w pierwszej, drugiej lub trzeciej klinice,
w odpowiedniej kolumnie wpisywano 1, w przeciwnym przypadku komórka pozostawała
pusta. Tak więc jest to wielokrotna dychotomia (zmienne przyjmują tylko dwa stany).

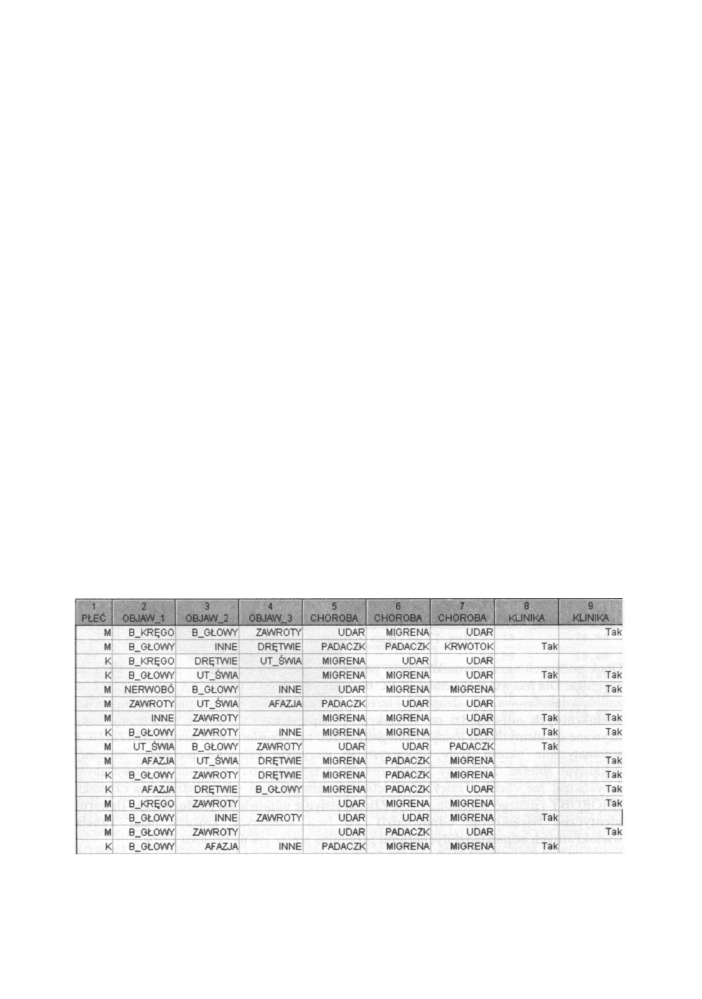
W sumie w ankiecie brało udział 125 respondentów. Poniżej pokazano fragment (15
pierwszych odpowiedzi) tak przygotowanego arkusza danych.

Rys. 12.28 Fragment arkusza danych dla przykładu 8

255

Przystępny kurs statystyki

Analizę rozpoczniemy od wyliczeń prostych tabel liczebności dla zmiennej PŁEĆ i dla
wielokrotnych odpowiedzi. Ponieważ zmienne KLINIKA1, KLINIKA2 oraz KLINIKA3
zawierają braki danych (respondent nie leczył się w żadnej z tych klinik), więc zmienne te
będziemy analizować później osobno. Po otwarciu okna Tabela wielokrotnych
odpowiedzi/dychotomii klikamy na przycisku Określ tabelę, by wyspecyfikować
odpowiednie zmienne. Zmienne określamy tak jak pokazano to na rysunku 12.25.

W pierwszej kolumnie wybraliśmy tylko zmienną PŁEĆ, a wówczas program

będzie ją interpretował jak pojedynczą zmienną jakościową (kategorialną). W drugiej
kolumnie wybrano zmienne OBJAW_1 - OBJAW_3, a w trzeciej - zmienne CHOROBA1 -
CHOROBA3. Po kliknięciu OK zamykamy okno wyboru danych i wracamy do okna
Tabela wielokrotnych odpowiedzi/dychotomii. W kolumnie po lewej stronie możemy
(jak to było omawiane wcześniej) określić nazwy dla czynników wielokrotnych
odpowiedzi. Program domyślnie dla każdego czynnika nadaje nazwy brane od pierwszej
zmiennej na odpowiedniej liście. Jeżeli chcemy to zmienić, klikamy przycisk Nazwa
czynnika (zbioru) wielokrotnych odpowiedzi i w otwierającym się oknie wpisujemy
własne nazwy (krótkie lub długie), które będą użyte do identyfikacji czynników

w kolejnych tabelach. Przykładowo zmieńmy domyślną nazwę CHOROBA1 na
CHOROBY i wprowadzając długą nazwę jak na rysunku poniżej.

Rys. 12.29 Okno określania długich nazw

Obok podanych nazw czynników przy pomocy przycisków opcji ustawiamy typ każdego
czynnika. Dla pierwszej zmiennej PŁEĆ nie mamy żadnego wyboru, jest to bowiem prosta
zmienna jakościowa. Dla drugiego i trzeciego czynnika ustawiamy opcje Typ czynnika
wielokrotnych odpowiedzi na Wielokrotne odpowiedzi. Na koniec wybieramy kody
używane do identyfikacji różnych kategorii. Jeżeli nie określimy tych kodów STATISTICA
automatycznie określi kody wykorzystując wszystkie kategorie pierwszej zmiennej
w każdym zbiorze. Zalecamy jednak określić wszystkie kody samemu. W rozważanym
przykładzie nie chcemy zawyżać liczebności identycznymi odpowiedziami w czynniku
CHOROBY i dlatego włączamy opcję Zliczaj jedynie odpowiedzi jednoznaczne (ignoruj
identyczne wielokrotne odpowiedzi). Po tych wstępnych krokach okno Tabela
wielokrotnych odpowiedzi/dychotomii przyjmuje postać jak na rysunku 12.24.

256

Tabele wielodzielcze

Klikamy OK w oknie Tabele wielokrotnych odpowiedzi/dychotomii dla

kontynuacji analizy. Otworzy się wówczas omawiane już okno Wynikowa tabela
wielokrotnych odpowiedzi. Ustawimy opcję Podświetl liczebności na 40 i klikamy na
przycisku Tabele liczebności dla obliczenia prostych tabel liczebności. Pojawią się tablice
frekwencji dla zmiennej płeć i dla pozostałych dwóch wielokrotnych odpowiedzi. Poniższe
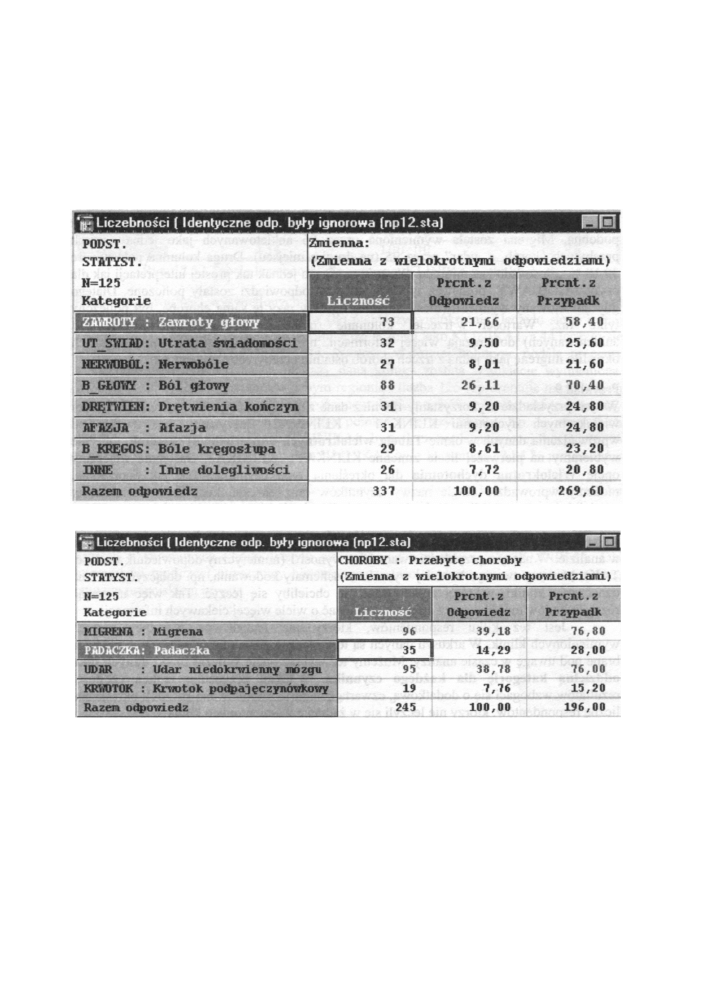
rysunki pokazują tablice liczebności dla czynnika OBJAWY i CHOROBY.

Rys. 12.30 Tabela liczebności dla zmiennej OBJAWY

Rys. 12.31 Tabela liczebności dla zmiennej CHOROBY

W sumie ankietowanych było 125 osób, co potwierdza liczba pokazana w górnym lewym
rogu tabel na powyższych rysunkach. W pierwszej kolumnie tabeli dla czynnika OBJAWY
mamy wyliczoną liczbę respondentów, którzy wymienili odpowiedni rodzaj dolegliwości

jako jeden z trzech najbardziej dokuczliwych. Ponieważ tylko pojedyncze odpowiedzi były

liczone, dlatego każdy respondent jest liczony w tej kolumnie tylko raz. Z wyliczonej tabeli
(rysunek 12.30) możemy wywnioskować, że „bóle głowy" były najczęstszą dolegliwością
wymienianą na pierwszym, drugim lub trzecim miejscu przez 88 ankietowanych. „Zawroty

257

Przystępny kurs statystyki

głowy" były na drugim miejscu najczęstszych dolegliwości (73 osoby). Pozostałe
dolegliwości zostały wymienione tylko przez 30-40 ankietowanych. Druga kolumna
wyświetla procenty wyliczane w stosunku do wszystkich odpowiedzi. Możemy więc
powiedzieć, że ze wszystkich dolegliwości 26,11 % (100*88/337) stanowiły „bóle głowy".
Z kolei trzecia pokazuje procent ankietowanych, którzy wymienili odpowiedni typ
dolegliwości jako pierwszą, drugą lub trzecią. Możemy więc zobaczyć, że „bóle głowy"
zostały określone jako największa dolegliwość przez 70,4 % ankietowanych (100*88/125).

Interpretacja tablicy liczebności dla czynnika CHOROBY (rysunek 12.31) jest

podobna. Migrena została wymieniona przez 96 ankietowanych jako jedna z trzech
przebytych chorób, a „udar" przez 95 (na drugim miejscu). Druga kolumna pokazuje że
39,18 % „głosowało" za migreną. Wartość ta nie ma jednak tak prostej interpretacji jak dla
czynnika OBJAWY, ponieważ tylko pojedyncze odpowiedzi zostały policzone. Dlatego
gdy ankietowany wymienił (nieświadomie) np. trzy razy tę samą chorobę, był policzony
tylko raz. Wartości w trzeciej kolumnie (procenty względem przypadków, tj.
ankietowanych) dostarczają więcej informacji, np. 76,8 % wszystkich ankietowanych

określiło migrenę jako jedną z trzech chorób ostatnio przebytych.

Przykład 9
W tym przykładzie wykorzystamy również dane z naszej ankiety. Tym razem do analizy
wielokrotnych dychotomii KLINKA1 - KLINIKA2. Zaczynamy jak zwykle od
wprowadzenia danych w oknie Tabela wielokrotnych odpowiedzi/dychotomii. Obecnie
wybieramy na pierwszej liście zmienne KLINKA1 - KLINIKA2. Następnie włączamy
opcję Wielokrotna dychotomia dla określenia typu czynnika. Tak jak poprzednio,
możemy wprowadzić długie nazwy czynników oraz określić kod, który został użyty

w wielokrotnym czynniku dychotomicznym dla określenia, czy ankietowany przebywał
w ciągu ostatniego roku w którejś klinice czy też nie. Kod ten podajemy w okienku
Zliczana wartość. Wszystkie wartości niezgodne z wartością zliczaną będą pomijane
w analizie. W naszym przykładzie wartość ta wynosi 1 (numeryczny odpowiednik wartości
TAK). Możemy tworzyć bardziej wyszukane schematy kodowania, np. dołączyć kod 2 na
oznaczanie kliniki, w której ankietowani nie chcieliby się leczyć. Tak więc używając
różnych kodów moglibyśmy z ankiety wyciągnąć o wiele więcej ciekawych informacji.

Jest też kilku respondentów, którzy nie leczyli się w żadnej z trzech

wymienionych klinik. W arkuszu danych są to widoczne puste miejsca. Osoby te nie będą
brane pod uwagę w czasie analizy. Możemy też wybrać opcję Wliczaj braki danych jako
oddzielną kategorię dla każdego czynnika. W takim przypadku tablica częstości
rezultatów wzbogaci się o dodatkową, czwartą kategorię zatytułowaną BRAKI, określającą
liczbę respondentów, którzy nie leczyli się w żadnej z wymienionych klinik.

Klikamy OK by przejść do okna Wynikowa tabela wielokrotnych odpowiedzi.

W oknie tym klikamy ponownie na przycisku Tabele liczebności dla wyliczenia tabel
frekwencji. Tabela ta pokazana jest na poniższym rysunku.

258

Tabele wielodzielcze

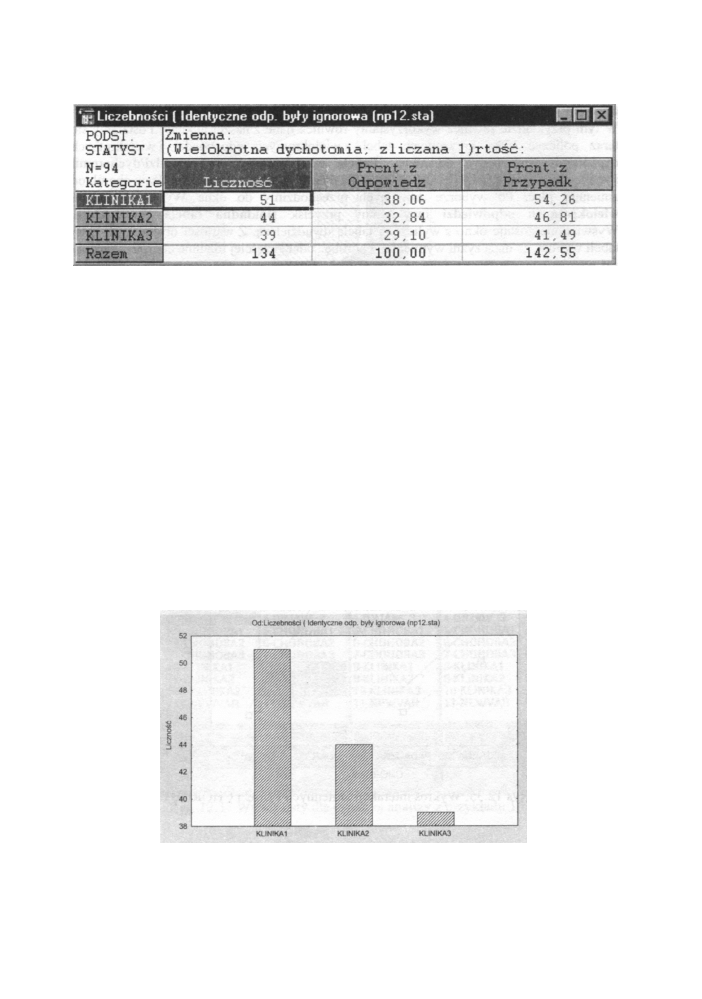
Rys. 12.32 Tabela liczebności dla zmiennej KLINIKA z przykładu 9

Interpretacja wartości wyświetlonych w tej tablicy jest analogiczna jak dla wielokrotnych
odpowiedzi. W sumie 134 respondentów (bo niektórzy wielokrotnie) leczyło się w jednej
z klinik, 51 spośród nich leczyło się w klinice oznaczonej jako KLINIKA1, a 44 leczyło się
klinice oznaczonej jako KLINIKA2 itd. Wartości w drugiej kolumnie podają procenty
w stosunku do liczby mówiącej, ile razy dana klinika została w ankiecie wymieniona.
Gdyby te szpitale były jedynymi w danym regionie i liczba 125 reprezentuje mniej więcej
całkowitą liczbę cierpiących na dolegliwości neurologiczne, wówczas wartości te (procenty
z drugiej kolumny) dają podział pacjentów pomiędzy te trzy kliniki. Np. ze wszystkich
klinik w klinice oznaczonej jako KLINIKA1 było leczonych najwięcej bo 38,06 %
przypadków. W klinice oznaczonej jako KLINIKA2 było leczonych 32,84 % przypadków
itd.

Trzecia kolumna tej tabeli podaje procent respondentów, którzy w ostatnim roku

leczyli się w odpowiednich klinikach. Procenty te są wyliczane w stosunku do liczby, tzn.
w stosunku do liczby respondentów, którzy leczyli się choć w jednej z wymienionej klinik.
Tak więc wiemy, że 54,26 % tych respondentów, którzy leczyli się w którejkolwiek
z trzech wymienionych klinik, leczyło się w klinice oznaczonej jako KLINIKA 1. Dla
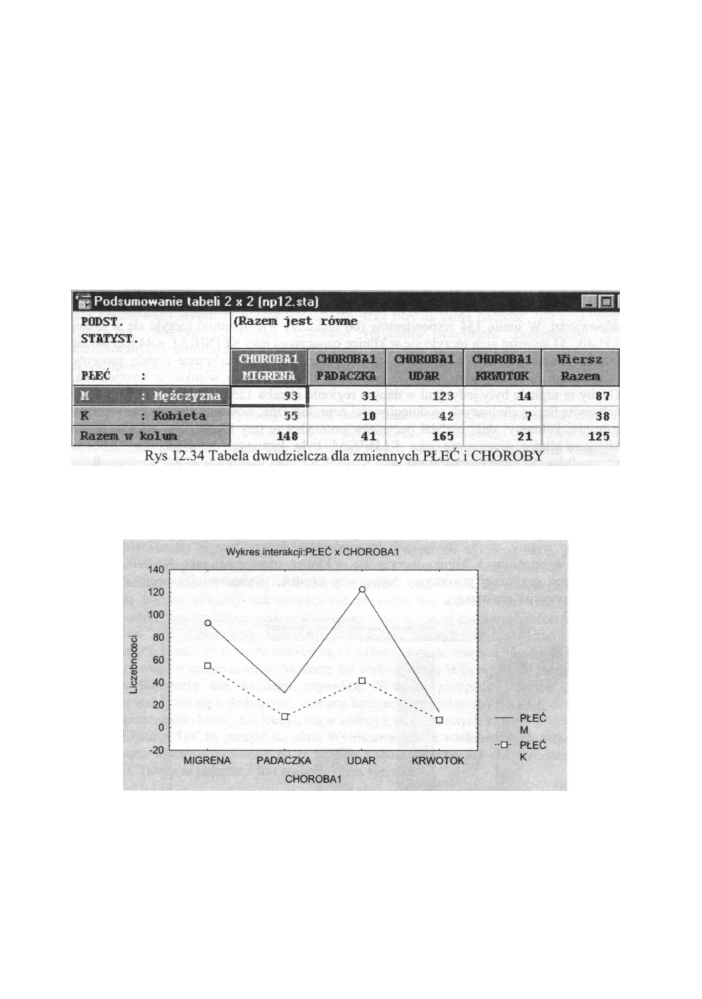
interpretacji graficznej utworzymy histogramy częstości wykorzystując opcję wywołaną
prawym przyciskiem myszy.

Rys. 12.33 Histogram dla zmiennej KLINIKA z przykładu 9

259

Przystępny kurs statystyki

Przykład 10
W tym przykładzie również wykorzystamy również dane z naszej ankiety. Postaramy się
teraz policzyć kilka krzyżowych tabel z wielokrotnych odpowiedzi i wielokrotnych
dychotomii. Powróćmy do okna Tabela wielokrotnych odpowiedzi/dychotomii
i wybierzmy zmienne PŁEĆ i CHOROBY dla dalszej analizy zależności rodzaju chorób od
zmiennej płeć. Po wyborze zmiennych przechodzimy do okna Wynikowa tabela
wielokrotnych odpowiedzi i wybieramy przycisk Dokładna tabela dwudzielczą.
Wyświetlone zostaje okno z wyliczoną tabelą dwudzielczą. Z wartości obliczonych w tej
tabeli wynika, że mężczyźni wymieniali chorobę „udar" częściej niż inne choroby. Kobiety
zaś wymieniały migrenę częściej od pozostałych.

Otrzymane dane możemy zinterpretować graficznie, klikając przycisk Wykresy interakcji
liczebności oraz tworząc trójwymiarowy histogram. Oba wykresy potwierdzają wnioski
wyciągnięte z tabeli dwudzielczej.

CHOROBA1

Rys 12.35. Wykres interakcji zmiennych PŁEĆ i CHOROBY

260

Tabele wielodzielcze

Rys 12.36. Trójwymiarowy histogram dla zmiennych PŁEĆ i CHOROBY z przykładu 10

Na zakończenie sprawdźmy, czy istnieją preferencje dla różnych klinik między
ankietowanymi płci męskiej i żeńskiej, jeśli wymienili szczególny rodzaj dolegliwości.
Inaczej mówiąc: chcemy policzyć krzyżową tabelę dla zmiennych PŁEĆ, OBJAWY
i KLINIKA. W oknie Tabela wielokrotnych odpowiedzi/dychotomii wybieramy trzy
listy z tymi zmiennymi, jak pokazano to na poniższym rysunku.

Rys. 12.37 Wybór listy dla ostamiej analizy z przykładu 10

261

Przystępny kurs statystyki

Następnie klikamy OK i przechodzimy do okna Wynikowa tabela wielokrotnych

odpowiedzi. W oknie tym włączamy opcje:

• Procenty z całości
• Obliczaj procenty względem liczby respondentów
• Wybrane procenty w oddzielnych tabelach

Ustawienia te pozwolą nam łatwiej podsumować potrójną tablicę, wyświetlając podwójne
tabele najpierw dla mężczyzn, potem dla kobiet. Ponadto obliczone procenty zostaną
wyświetlone w oddzielnych tabelach. Klikamy następnie przycisk Dokładna tabela
dwudzielczą dla uruchomienia obliczeń. Wyświetlona zostanie kaskada okien
z wynikowymi tabelami.

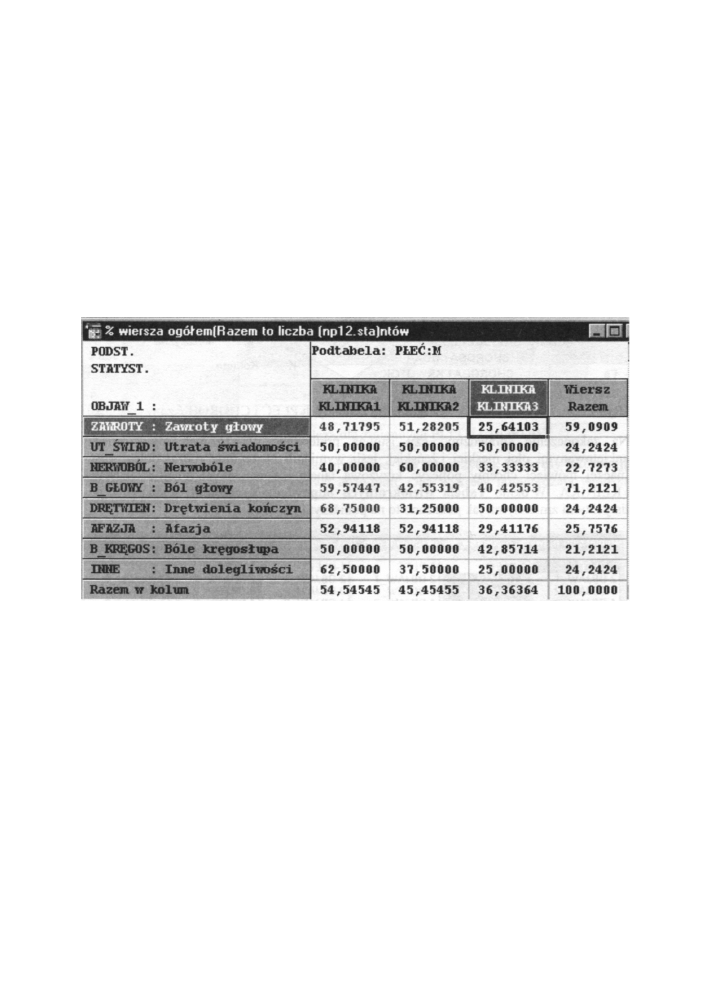
Przykładowa tablica z procentami dla mężczyzn przedstawiona jest na poniższym

rysunku.

Rys. 12.38 Wynikowa tabela z procentami dla mężczyzn (przykład 10)

Patrząc na tą podwójną tablicę dla mężczyzn zauważamy, że 68,75 % mężczyzn
skarżących się na drętwienie kończyn leczyło się w klinice oznaczonej symboliczną nazwą
KLINIKA1 oraz 59,57 % mężczyzn skarżących się na bóle głowy leczyło się w szpitalu
KLINIKA1. Po przeglądnięciu wszystkich procentów zauważamy, że mężczyźni
w większości przypadków (poza skarżącymi się na nerwobóle) leczyło się w szpitalu
KLINIKA1. Podobną analizę można przeprowadzić dla kobiet. Oczywiście wszystkie
wyniki liczbowe można zinterpretować graficznie.

Tablice krzyżowe i podsumowywujące dla wielokrotnych zmiennych

i wielokrotnych dychotomii na początku mogą wydawać się skomplikowane. Warto je
poznać i opanować stanowią bowiem jedyne doskonałe narzędzie dla analizy dużej liczby
różnorodnych ankiet.

262