Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Tabelaryczna i graficzna prezentacja struktury zbiorowości

Wstępna analiza statystyczna obejmuje szereg czynności związanych z porządkowaniem, prezentacją i

opisową charakterystyką zbioru danych. Polega ona, najogólniej mówiąc, na przekształceniu szczegółowych
danych dotyczących poszczególnych osób (rzeczy, zjawisk, procesów) na syntetyczną informację o całej badanej
zbiorowości, czyli na przedstawieniu i opisie struktury tej zbiorowości.

Tabela wyników surowych – arkusz danych

Dane zebrane wpisz w arkusz danych,
aby porządek był zachowany

Zgromadzony w trakcie badań materiał – wypełnione ankiety, rozwiązane testy, dane z przeprowadzonych

wywiadów, itp. musi zostać uporządkowany w tabeli wyników surowych.

Tabela wyników surowych to zapisane - w uporządkowaniu wyznaczonym schematem tabeli - dane z badań.

A więc, na przykład, dane dotyczące płci, wykształcenia, odpowiedzi poszczególnych osób na pytania ankiety,
kwestionariusza, wyniki wykonywanych lub rozwiązywanych przez nich testów, jak też inne wyznaczone celem
badań pomiary.

Identy-
fikator

ZMIENNE

Cechy fizyczne

Środowisko rodzinne

Sprawność

PŁEĆ

WZROST ......

....

Liczba
RODZ.

......

......

........

TEST1

TEST2

.......

1
2
3
...

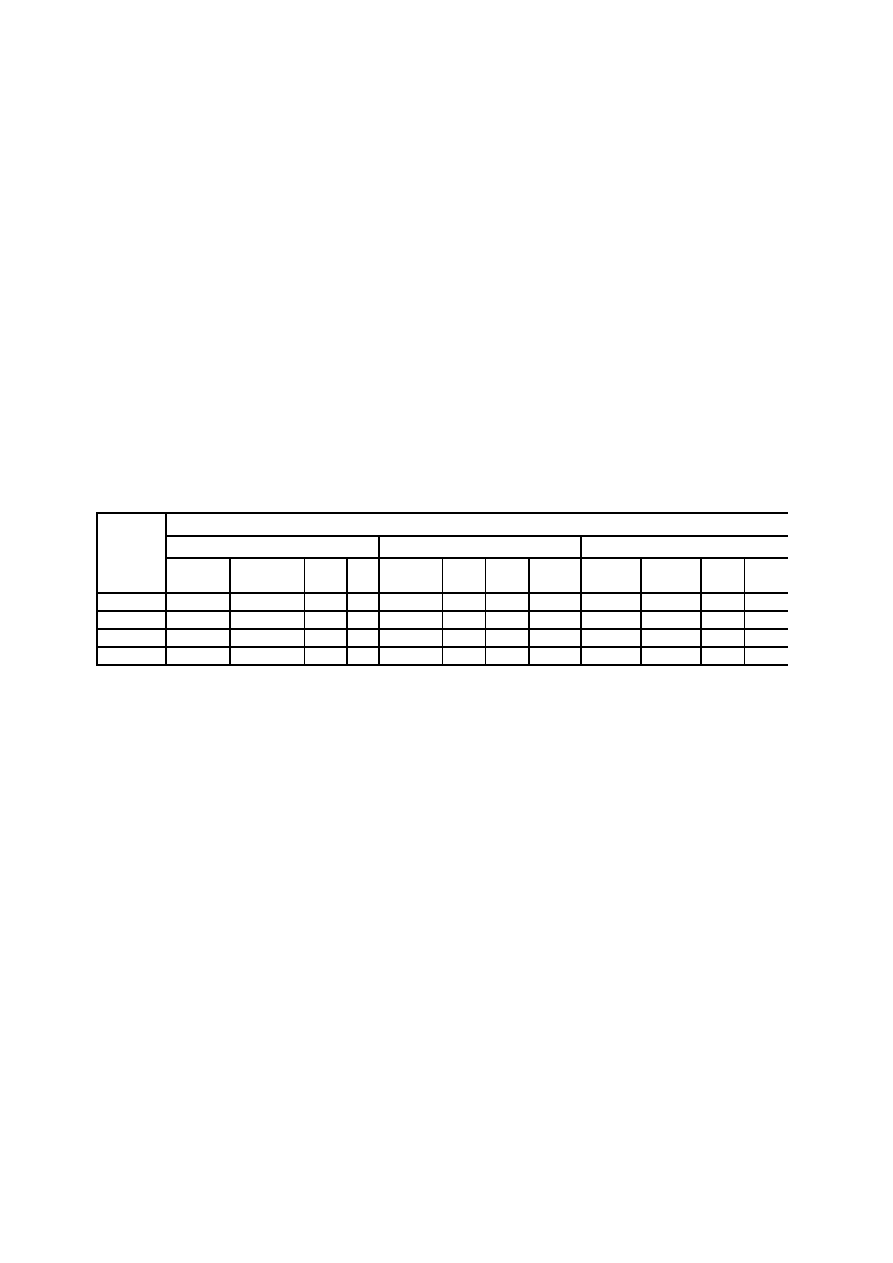
Rys.1. Schemat tabeli wyników surowych – przykład

Pierwsza kolumna tabeli wyników surowych – boczek tabeli – zawiera identyfikatory jednostek badania.

Identyfikatorem mogą być dowolne nazwy lub symbole pozwalające rozróżnić poszczególne jednostki. Mogą to
być, na przykład, po prostu liczby porządkowe.

W główce tabeli wyników surowych zapisujemy w hierarchicznym uporządkowaniu właściwości

wyznaczone przedmiotem badań (zmienne badane). Zmiennymi są na przykład takie właściwości osób jak: płeć,
wzrost, liczba rodzeństwa, poziom wykształcenia, preferowany rodzaj wypoczynku, poziom inteligencji.

W komórki tabeli wyników surowych wpisujemy zaobserwowane wartości wyróżnionych zmiennych. I tak

wartości zmiennej płeć, to: płeć męska (mężczyzna), płeć żeńska (kobieta); wartości zmiennej preferowany
rodzaj wypoczynku, to na przykład: wypoczynek bierny, wypoczynek czynny; wartości zmiennej liczba
rodzeństwa, to liczby: 0 rodzeństwa, 1 rodzeństwo, 2 rodzeństwa, ......

Każdy wiersz tabeli zawiera te wartości wyróżnionych zmiennych, które charakteryzują osobę (jednostkę)

oznaczoną identyfikatorem w tym wierszu umieszczonym. Jeżeli, na przykład, identyfikator 1 został
przyporządkowany Annie Abackiej, to w wierszu o numerze 1 wpiszemy wszystkie zebrane dane dotyczące
Anny Abackiej. W kolumnie natomiast umieszczamy dane zebrane od wszystkich osób, ale dotyczące tylko
jednej z badanych właściwości, np. liczby rodzeństwa.

Tabela rozkładu jednej zmiennej

Zgromadzenie i uporządkowanie w tabeli wyników surowych materiału z badań to, można powiedzieć,

wstępny etap wstępnej analizy statystycznej. Kolejnym etapem jest rozpoznanie struktury danych, a tym samym
struktury badanej zbiorowości ze względu na różne, interesujące nas zmienne. Szukamy na przykład odpowiedzi
na pytania: Ile w badanej zbiorowości uczniów jest dziewcząt, a ilu chłopców?; Jaki procent badanej
zbiorowości stanowią dziewczęta, a jaki chłopcy? (jest to pytanie o wskaźniki struktury); Jak licznie
reprezentowane są poszczególne postawy dzieci względem rodziców?; Która z tych postaw jest reprezentowana
najczęściej? (jest to pytanie o wartość modalną, dominantę); Jaki jest rozkład wyników testu sprawności w
badanej grupie młodzieży?

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Odpowiedzi na te i podobne pytania można uzyskać poddając zgromadzone dane odpowiedniemu

grupowaniu. Czynność ta prowadzi do wyodrębnienia w badanej zbiorowości względnie jednorodnych grup, tzn.
takich, że osoby (jednostki) zaliczone do jednej grupy mają co najmniej jedną własność wspólną, bądź różnią się
ze względu na tę własność nieznacznie. Tak więc wyróżnimy, na przykład, grupę chłopców i grupę dziewcząt,
jeżeli za podstawę wyodrębnienia grup przyjmiemy zmienną „płeć”; albo grupy młodzieży, które uzyskały w
teście sprawności wyniki 0p-5p, 6p-10p, itd.; albo grupy chłopców o wynikach odpowiednio 0p-5p, 6p-10p, itd.
i grupy dziewcząt o takichże wynikach. Ogólnie, jakie to mają być grupy wynika przede wszystkim z celów
badań. Natomiast samo grupowanie musi spełniać określone warunki formalne. Po pierwsze, otrzymane grupy
muszą być rozłączne, czyli nie mogą mieć elementów wspólnych. Po drugie, wszystkie podlegające grupowaniu
elementy muszą zostać przyporządkowane do tworzonych grup.

STRUKTURĘ danych
przedstawisz najlepiej
w tabeli lub na wykresie.

Taka struktura, ROZKŁADEM ZMIENNEJ zwana,
prezentuje zbiorowość
pod względem cechy wybranej do badania.

Po utworzeniu grup określamy liczebność każdej grupy, tzn. zliczamy ile jednostek do każdej z grup należy.

Ustalamy tym samym następujące przyporządkowanie:

1.

wartość zmiennej x

1

→ liczba n

1

danych równych wartości x

1

2.

wartość zmiennej x

2

→ liczba n

2

danych równych wartości x

2

.

3........

Takie przyporządkowanie nazywamy rozkładem liczebności badanej zbiorowości według wartości

zmiennej, krótko: rozkładem empirycznym zmiennej

. Rozkład zmiennej obrazuje strukturę badanej

zbiorowości pod względem badanej zmiennej (cechy) i może być przedstawiony w tabeli liczebności lub na
wykresie.

Wartość

zmiennej

X

Liczebność

n

i

Liczebność

względna

p

i

%

x

1

n

1

p

1

x

2

n

2

p

2

..

....

.....

Σ

N

100

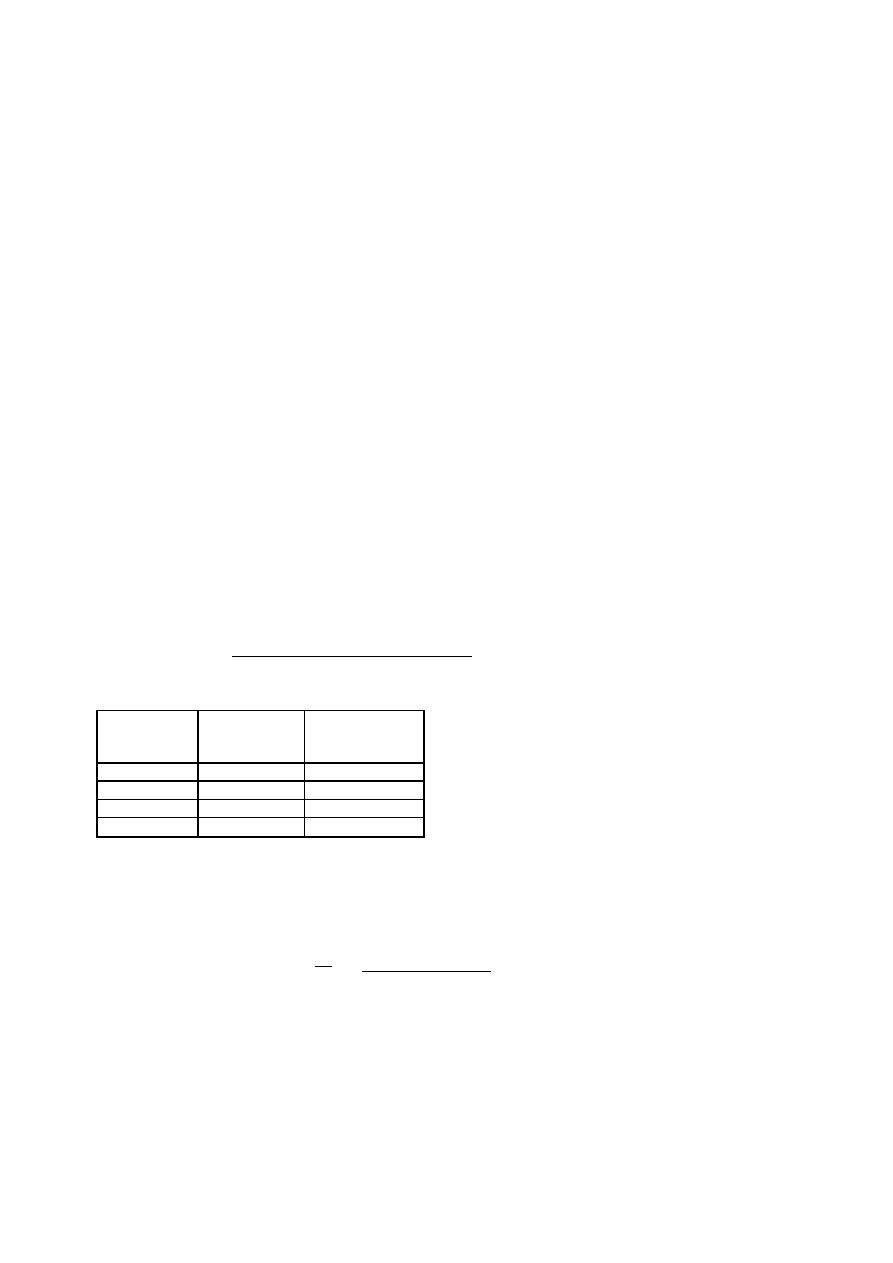
Rys. 2. Schemat tabeli przedstawiającej rozkład zmiennej

Symbol N oznacza tu liczebność badanej zbiorowości, zaś n

i

liczebności wyodrębnionych grup. Suma

liczebności wyodrębnionych grup równa jest liczebności badanej zbiorowości:

n

1

+ n

2

+ .... + n

k

= N, gdzie k oznacza tu liczbę wartości zmiennej.

Liczebności względne

N

n

p

i

i

=

, to wskaźniki struktury. Wskaźnik struktury informuje o tym, jaka część

zbiorowości charakteryzuje się własnością (wartością zmiennej), dla której wskaźnik struktury został obliczony.
Dla wskaźników struktury spełniona jest równość:

p

1

+ p

2

+ .... + p

k

= 1

Wskaźniki struktury można też podawać w procentach. Wówczas mamy równość:

p

1

+ p

2

+ .... + p

k

= 100%

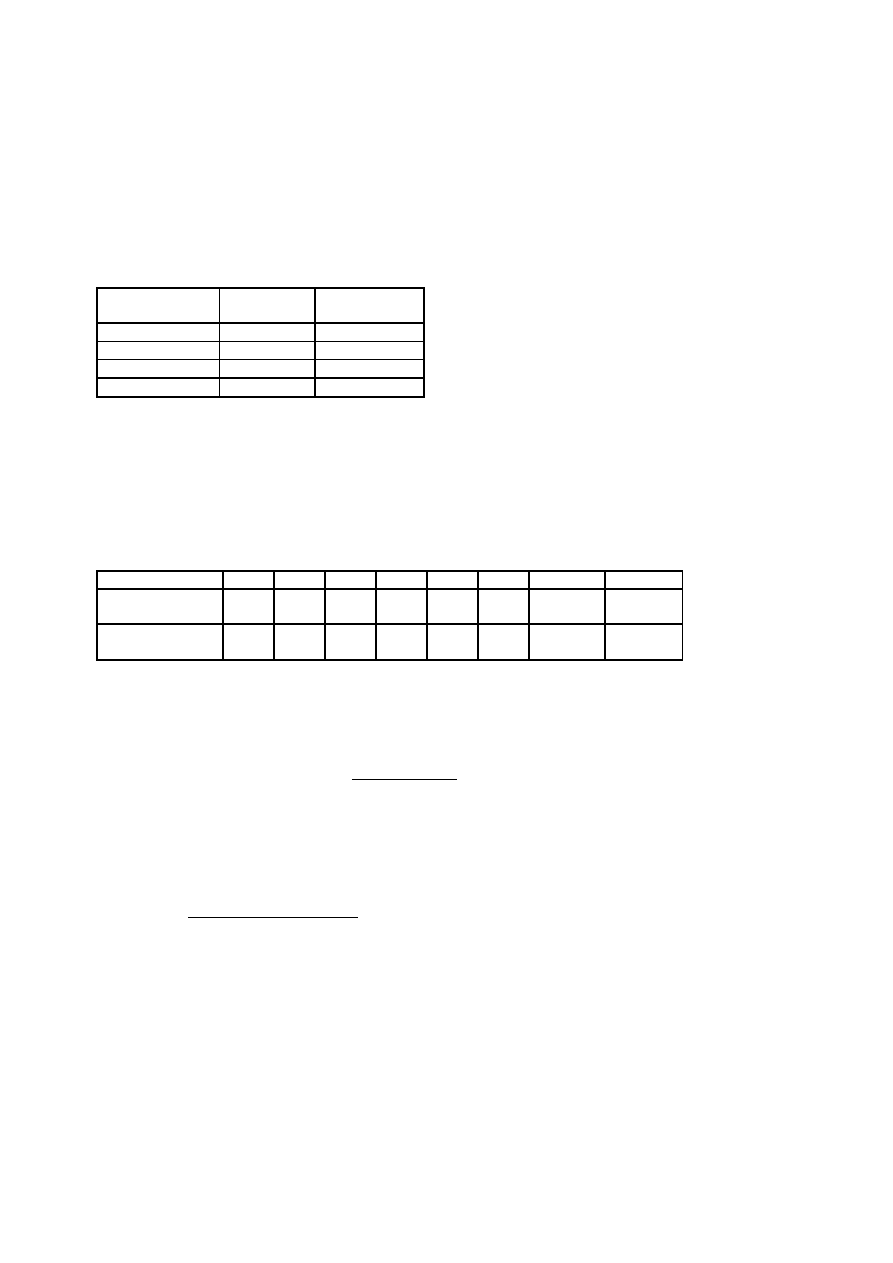
Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Przykład 1: W ramach prac związanych z przygotowaniem projektu przeciwdziałania bezrobociu w pewnym

regionie, należało poznać strukturę wykształcenia osób bezrobotnych. Pobrano 500-osobową próbę osób
zarejestrowanych w urzędach pracy tego regionu i sprawdzono, jaki poziom wykształcenia ma każda z nich.

Tabela 1. przedstawia otrzymany szereg rozdzielczy (rozkład zmiennej: poziom wykształcenia w badanej

grupie osób).

Tabela 1. Wykształcenie osób bezrobotnych zarejestrowanych w ......

Poziom
wykształcenia

Liczebność

n

i

Liczebność

względna p

i

Zawodowe

335

0,670

Średnie

121

0,242

Wyższe

44

0,088

Σ

n

i

500

1,000

Źródło: Dane umowne

Dla wartości „wykształcenie średnie” wskaźnik struktury wynosi 0,242 co oznacza, że 24,2% badanej

zbiorowości stanowią osoby z wykształceniem średnim.

Przykład 2: W celu ustalenia norm empirycznych testu ortograficznego dla uczniów kończących klasę III

szkoły podstawowej przeprowadzono badania. Losowo wybrani na początku czerwca z populacji
trzecioklasistów uczniowie wypełniali test. Rozkład liczby popełnionych błędów przedstawiony jest w tabeli 2.

Tabela2. Liczba błędów w teście ortograficznym

Liczba błędów

0

1

2

3

4

5

ponad 6

Razem

Częstość

12

37

64

93

71

32

11

330

Częstość
względna %

7

11

19

28

22

10

3

100

W badanej grupie 330 uczniów bezbłędnie test ortograficzny napisało 12 dzieci, tj. 7% wszystkich uczniów
piszących test. Najczęściej uczniowie popełniali 3 błędy – 93 uczniów na 330, co stanowi 28 % wszystkich
biorących udział w badaniu.

Jeżeli grupowaniu podlegają zmienne o wartościach liczbowych strukturę badanej zbiorowości można

przedstawić również w postaci rozkładu kumulowanego

.

W rozkładzie kumulowanym wartościom zmiennej przyporządkowane są liczebności kumulowane. Przez

liczebność kumulowaną rozumiemy liczbę jednostek l

k

, dla których wartość zmiennej nie przekracza danej

wartości x

k

:

∑

=

=

k

i

i

k

n

l

1

Gdy wartościom zmiennej przyporządkowane zostają liczebności kumulowane względne otrzymany szereg

przedstawia dystrybuantę empiryczną. Liczebność kumulowana względna określa, jaką część badanej
zbiorowości stanowią te jednostki, dla których wartość zmiennej nie przekracza danej wartości x

k

:

∑

=

=

k

i

i

k

p

q

1

Gdy analizowana zmienna jest zmienną o wartościach liczbowych, jak na przykład liczba rodzeństwa,

liczba popełnionych błędów, itp. lub na przykład wiek, wzrost, czas wykonania zadania i mamy dużo danych,
należy ustalić najpierw pewne przedziały wartości zmiennej a następnie zliczyć ile danych w tych przedziałach
się „mieści”.

Liczbę przedziałów, ich szerokość oraz granice ustalamy tak, aby otrzymany rozkład czytelnie przedstawiał

strukturę badanej zbiorowości. Odpowiedź na pytanie ile przedziałów ma być w konkretnym przypadku, zależy
głównie od tego, jak liczna jest badana zbiorowość. Nie ma jednak algorytmu, którego zastosowanie
zapewniałoby otrzymanie optymalnego, z punktu widzenia celu badań, obrazu struktury zbiorowości. W

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

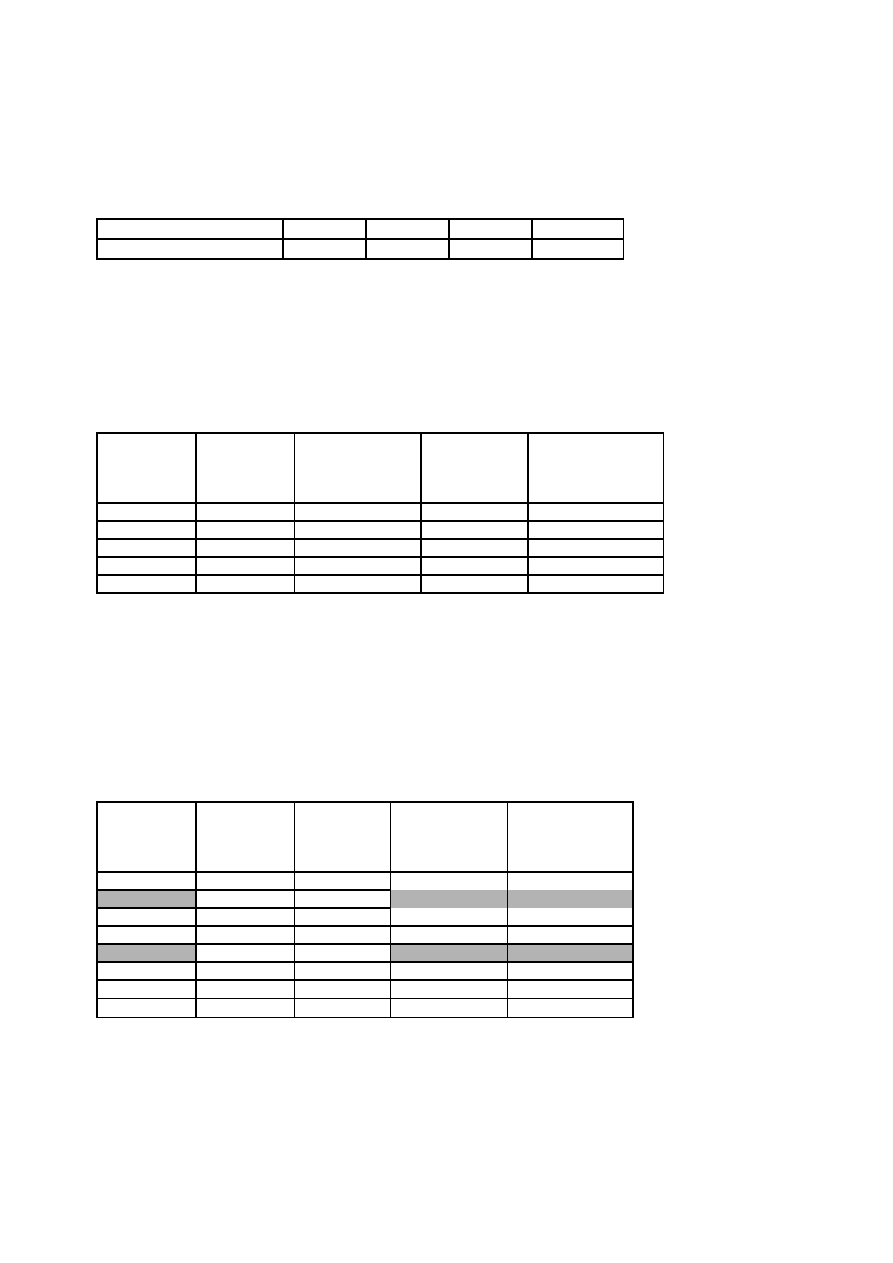
literaturze można znaleźć różne propozycje ustalania liczby przedziałów klasowych, z których jedna
przedstawiona jest na rys. 4.

Liczebność zbiorowości

40 - 60

60 – 100

100 – 200

200 – 500

Liczba klas

6 -8

7 – 10

9 – 12

12 – 17

Źródło: Z.Zając, Zarys metod statystycznych, PWE, 1988
Rys.4. Proponowana liczba przedziałów klasowych w zależności od liczby danych

Szerokości przedziałów ustalamy tak, aby wyodrębnione w ten sposób grupy były w miarę jednorodne. Z

pewnych względów najlepiej jest gdy szerokości przedziałów są równe, ale nie jest to wymóg konieczny.
Czasem zasadnym jest ustalenie przedziałów o różnej szerokości.

Rozkład zmiennej według przedziałów wartości zmiennej przedstawiamy w tabeli o następującym

schemacie.

Przedziały
klasowe
wartości
zmiennej X

Liczebność

n

i

Liczebność

względna

p

i

%

Liczebność

kumulowana

l

k

Liczebność

kumulowana

względna
%

(x

1

; x

2

]

(x

2

; x

3

]

(x

3

; x

4

]

.....

100

suma

100

-

-

Rys. 3. Schemat tabeli przedstawiającej rozkład zmiennej według przedziałów wartości zmiennej

Rozkład kumulowany zawiera inną informację o badanej zbiorowości niż szereg rozdzielczy prosty.

Liczebność kumulowana informuje nas o tym, u ilu osób badanej zbiorowości zaobserwowano wartości
zmiennej nie wyższe niż ta, dla której tę liczebność obliczyliśmy. Liczebność względna kumulowana wskazuje,
jaka część badanej zbiorowości charakteryzuje się wartościami zmiennej nie wyższymi od tej, dla której tę
liczebność ustaliliśmy.
Rozkładu kumulowanego można nie uwzględniać jeżeli tego nie potrzebujemy. Pomijamy wówczas w tabeli
kolumny „liczebność kumulowana” oraz „liczebność kumulowana względna”.

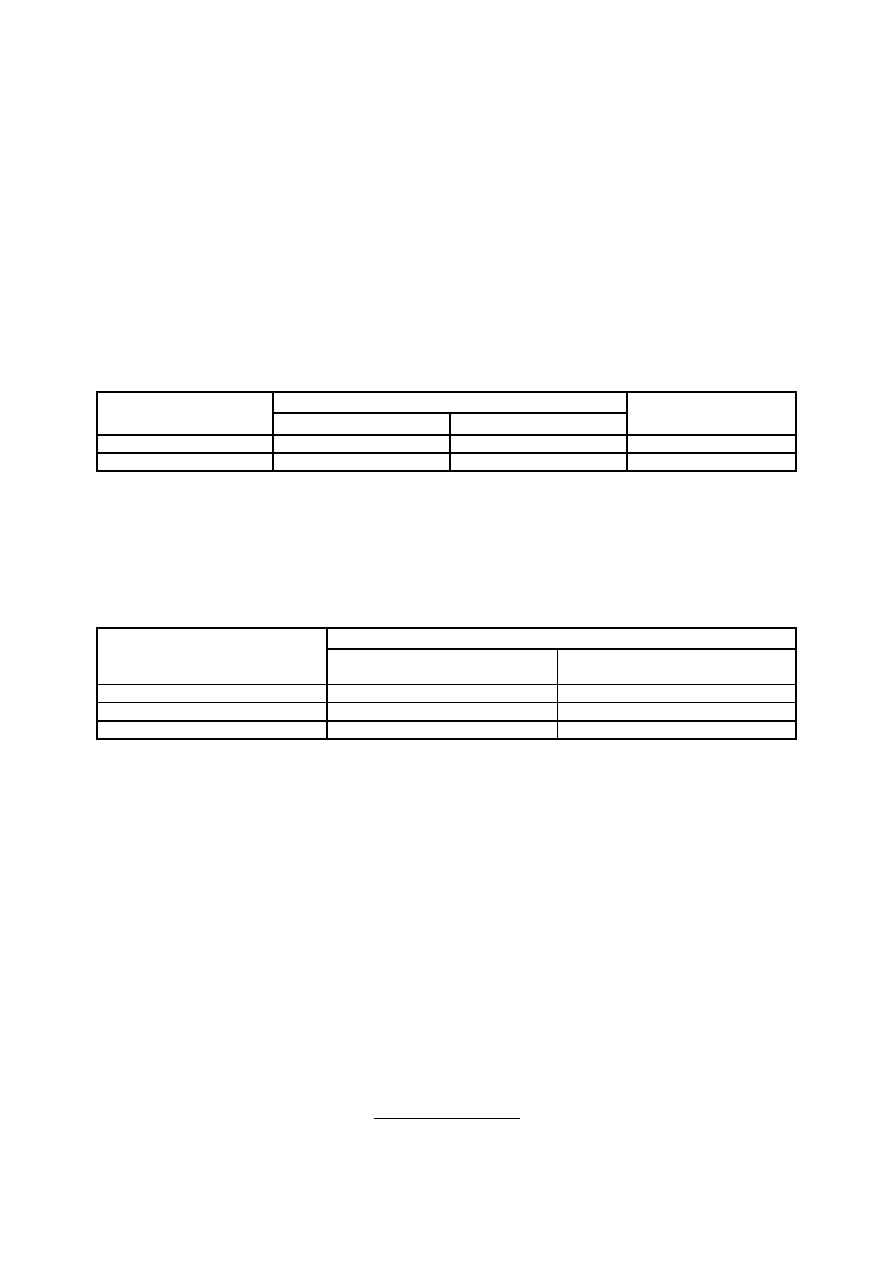
Tabela 3.

Wzrost uczniów Szkoły Podstawowej nr 55 w Zabeziu w roku szkolnym 1999/2000

Wzrost

(cm)

Liczebność

Liczebność

względna

%

Liczebność

kumulowana

Liczebność

kumulowana

względna

%

(136 – 140]

10

2

10

2

(140 – 145]

30

6

40

8

(145 – 150]

100

20

140

28

(150 – 155]

200

40

340

68

(155 – 160]

120

24

460

92

(160 – 165]

30

6

490

98

(165 – 170]

10

2

500

100

∑

500

100

-

-

Źródło: Dane umowne

W powyższym przykładzie liczba uczniów, których wzrost nie przekracza 145 cm równa jest 40 (liczebność

kumulowana równa 40), co stanowi 8% badanej zbiorowości. Uczniów o wzroście nie większym niż 160 cm jest
460, czyli 92% zbiorowości.

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Tabele rozkładu jednej zmiennej w wyodrębnionych grupach

W jednej tabeli można również przedstawić dwa rozkłady tej samej zmiennej w wyodrębnionych grupach.

Taka prezentacja ułatwia porównawcze omówienie struktury badanej zbiorowości, uwypuklenie podobieństw i
różnic w strukturze grup ze względu na badaną właściwość.

Przykład: Jeżeli chcemy porównać rozkład wykształcenia w grupach według miejsca zamieszkania, to tabela
może mieć taką np. formę.

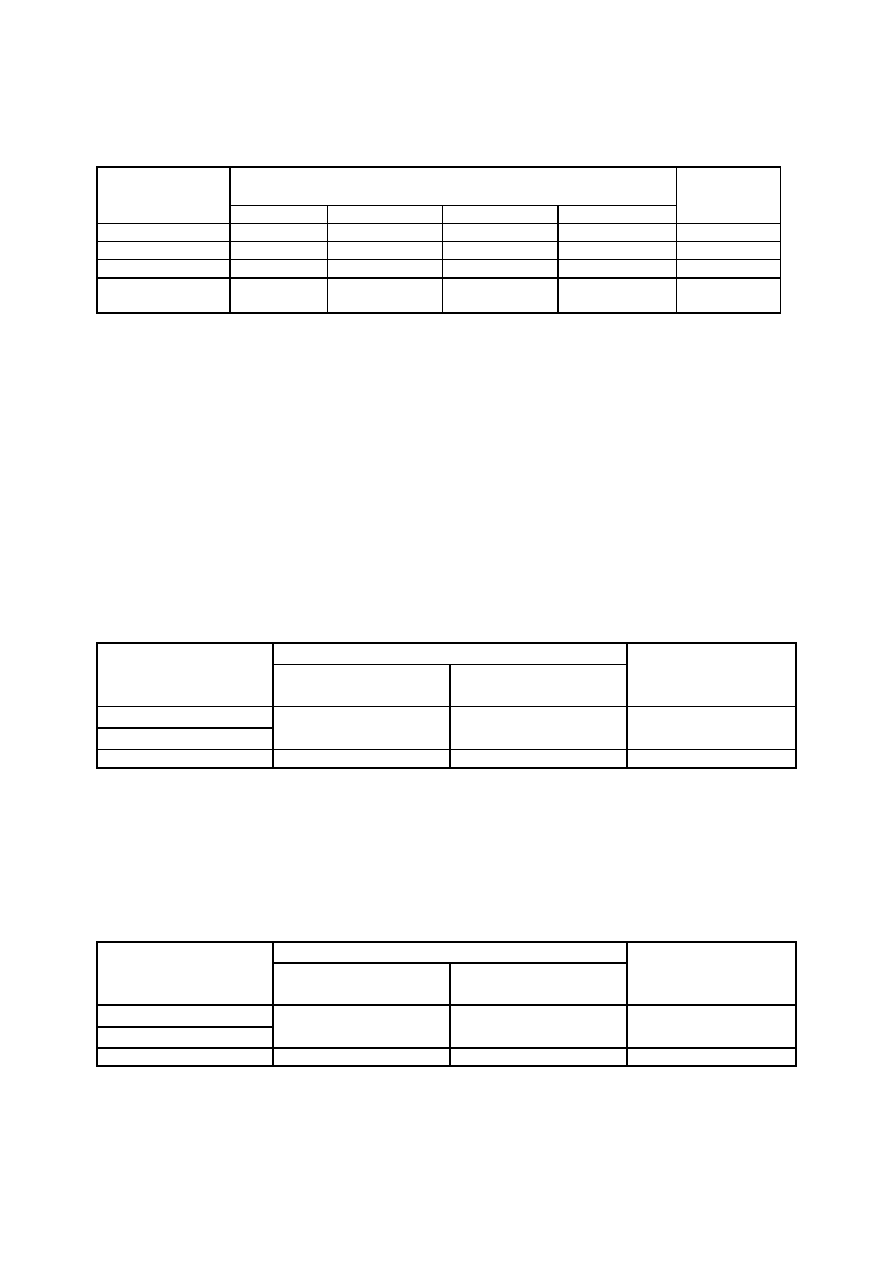
Tabela 4.

Wykształcenie osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w roku 2005 według miejsca

zamieszkania (w procentach)

Miejsce

zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

razem

wieś

57

43

100

miasto

26

74

100

W grupie osób bezrobotnych mieszkających na wsi przeważają osoby o wykształceniu niższym niż średnie
(57%). Odwrotnie jest w grupie osób bezrobotnych mieszkających w mieście, tu przeważają bezrobotni o
wykształceniu średnim lub wyższym (74%).

Jeżeli natomiast chcemy porównać rozkład miejsca zamieszkania w grupach według wykształcenia, to tabela
może przybrać taką formę.

Tabela 5 .

Miejsce zamieszkania osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w roku 2005 według

wykształcenia (w procentach)

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

wieś

70

39

miasto

30

61

razem

100

100

W grupie osób bezrobotnych mających wykształcenie niższe niż średnie więcej osób mieszka na wsi (70%) niż
w mieście (30%). Inaczej jest w grupie bezrobotnych posiadających wykształcenie średnie lub wyższe – więcej
osób z tej grupy mieszka w mieście (61%) niż na wsi (39%).

Tabele rozkładu wielozmiennej

Wyniki grupowania, które przebiegało w ten sposób, że każda jednostka badania została zaliczona do grupy

ze względu na to, jaką wartość przyjmuje ze względu na więcej niż jedną zmienną, tworzą rozkład
wielozmiennej. Jeżeli, na przykład, interesować nas będzie struktura bezrobotnych ze względu na wykształcenie
(zmienna X) i miejsce zamieszkania (zmienna Y) jednocześnie, tworzymy grupy w ten sposób: określamy
wykształcenie i miejsce zamieszkania każdej osoby i zliczamy ile jest osób o wykształceniu niższym niż średnie
i mieszkających na wsi, ile jest osób o wykształceniu średnim lub wyższym i mieszkających na wsi, ile jest osób
o wykształceniu niższym niż średnie i mieszkających w mieście, itd. Otrzymamy w ten sposób rozkład
dwuzmiennej (wykształcenie X, miejsce zamieszkania Y), czyli rozkład dwuzmiennej (X,Y).
Rozkład dwuzmiennej przedstawiamy w tabelach dwudzielczych, zwanych też tabelami korelacyjnymi lub
krzyżowymi.

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Zmienna Y

Zmienna X

Sumy
brzegowe

x1

x2

x3

.........

(zmienna Y)

y1
y2

......

Sumy brzegowe
(zmienna X)

Liczebność
zbiorowości

Rys.6. Schemat tabeli dwudzielczej

W główce tabeli umieszczamy nazwę jednej zmiennej (X) oraz wartości tej zmiennej lub przedziały

wartości zmiennej (x1, x2, x3, x4), w boczku tabeli nazwę drugiej zmiennej oraz jej wartości lub przedziały
wartości. W komórki tabeli wpisujemy liczebności wyodrębnionych grup, tzn. liczebności grup, dla których
zmienna X przyjmuje wartość x1 a zmienna Y wartość y1, dalej – zmienna X przyjmuje wartość x2 a zmienna Y
wartość y1, itd. Ostatnia kolumna, w której umieszczone są sumy liczebności kolejnych wierszy i ostatni wiersz,
w którym mamy sumy liczebności kolejnych kolumn przedstawiają rozkłady brzegowe. Ostatnia kolumna (wraz
z pierwszą, gdzie są wyszczególnione wartości zmiennej Y) - rozkład zmiennej Y, ostatni wiersz (wraz z
pierwszym, gdzie są wyszczególnione wartości zmiennej X) - rozkład zmiennej X.

W tabeli wielodzielczej możemy umieszczać dodatkowo lub zamiast liczebności bezwzględnych,

liczebności względne.

Poniżej (tabela ) pokazany jest przykład tabeli dwudzielczej przedstawiającej rozkład dwuzmiennej

(wykształcenie, miejsce zamieszkania) w populacji osób bezrobotnych zarejestrowanych w Urzędzie Pracy w
Paradyżu w roku 2005.

Tabela 6.

Wykształcenie a miejsce zamieszkania osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w

roku 2005.

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

razem

wieś
miasto

56
24

43
67

99
91

razem

80

110

190

Spośród 190 przebadanych osób 56 ma wykształcenie niższe niż średnie i mieszka na wsi a 67 ma wykształcenie
średnie lub wyższe i mieszka w mieście. Jak widać bezrobotni o wykształceniu średnim lub wyższym
przeważają w mieście.

W tabeli możemy również podać wartości procentowe.

Tabela 7.

Wykształcenie a miejsce zamieszkania osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w

roku 2005 (w procentach).

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

razem

wieś
miasto

29
13

23
35

52
48

razem

42

58

100

Spośród przebadanych osób 29% stanowią bezrobotni, którzy mają wykształcenie niższe niż średnie i mieszkają
na wsi a 35% bezrobotni, którzy mają wykształcenie średnie lub wyższe i mieszkają w mieście. Jak widać
bezrobotni o wykształceniu średnim lub wyższym przeważają w mieście.

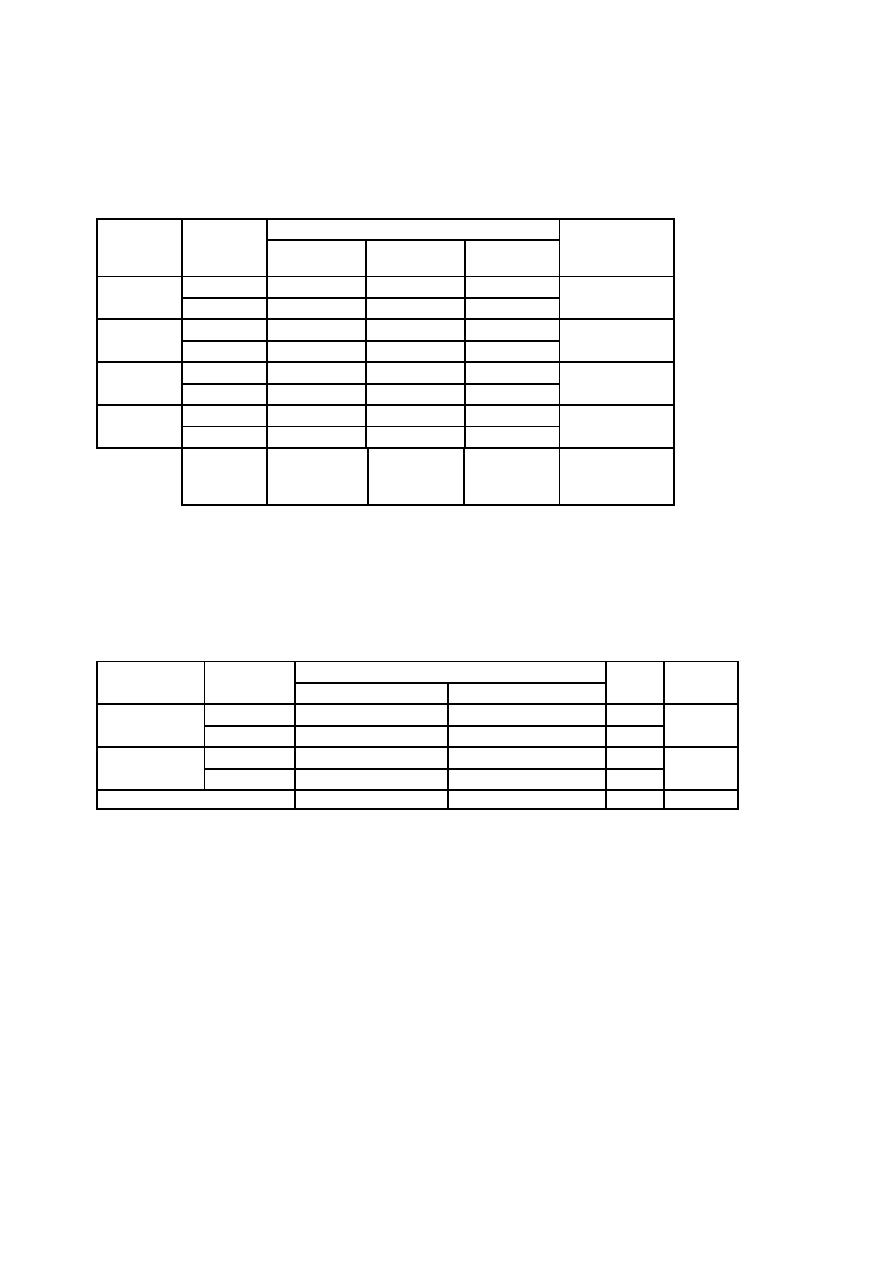
Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Czasem zachodzi potrzeba przedstawienia struktury badanej zbiorowości z uwzględnieniem więcej niż dwu
zmiennych. Rozkład trójzmiennej przedstawiamy w tabeli o następującym schemacie:

Zmienna Y

Zmienna Z

Zmienna X

x1

x2

.......

Sumy brzegowe
(zmn Y)

y1

z1
z2

y2

z1
z2

y3

z1
z2

........

.....
.....

Sumy
brzegowe
(Zmn X)

Liczebność

zbiorowości

Rys.7. Schemat tabeli trójdzielnej

Prezentację struktury badanej grupy bezrobotnych z uwzględnieniem oprócz miejsca zamieszkania oraz
wykształcenia również płci przedstawia tabela poniżej.

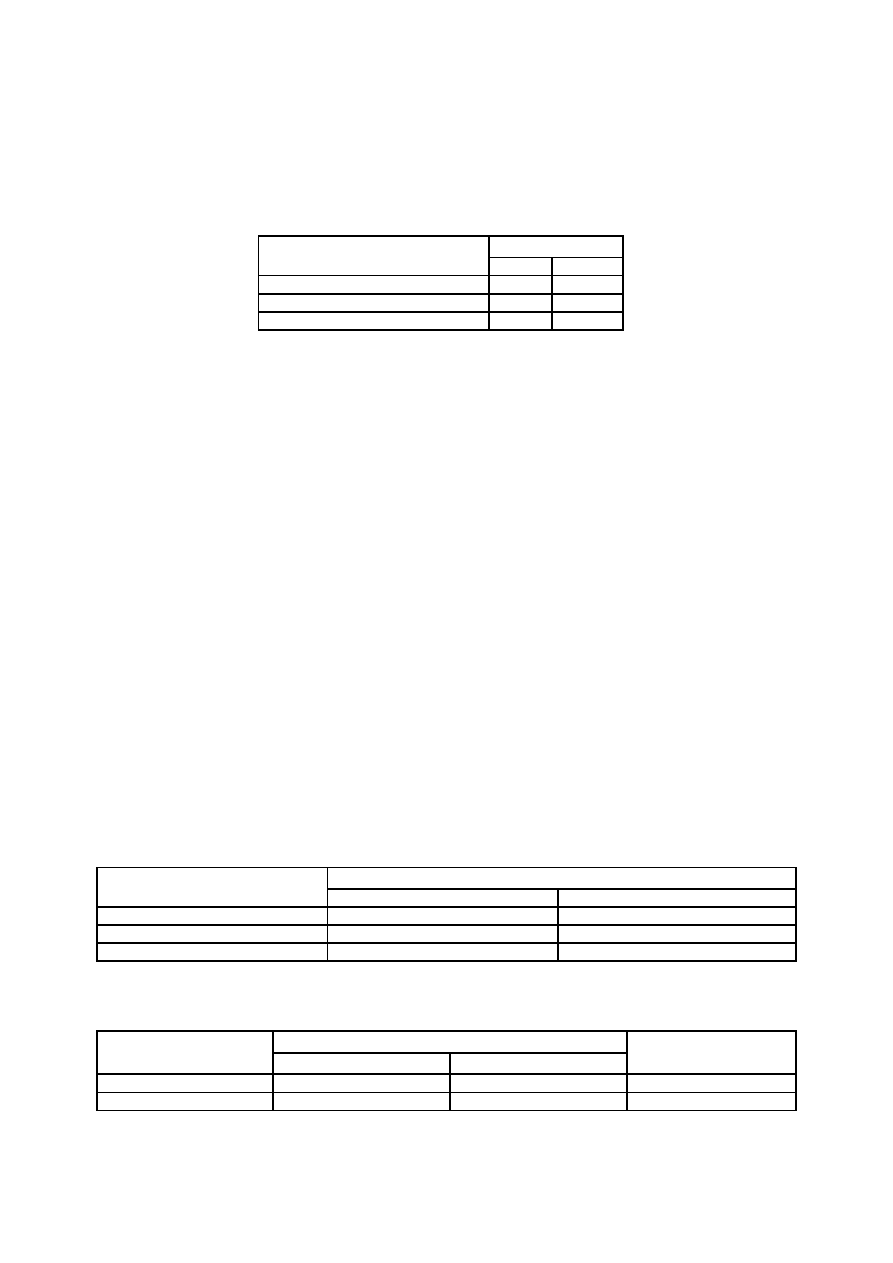
Tabela 8. Bezrobotni zarejestrowani w Urzędzie Pracy w Paradyżu w roku 2005 ze względu na wykształcenie,

miejsce zamieszkania i płeć (w procentach)

Miejsce

zamieszkania

Płeć

Wykształcenie

niższe niż średnie

średnie lub wyższe

∑

płeć

∑

miejsce

wieś

kobieta

10

13

23

mężczyzna

19

10

29

52

miasto

kobieta

7

20

27

mężczyzna

6

15

21

48

∑

wykształcenie

42

58

100

100

Proponuję, aby interpretacji powyższej tabeli czytelnik dokonał samodzielnie.
Interpretacja!!!!! Jako zadanie na koniec rozdziału

Tytułowanie tabel i wykresów

Badania empiryczne statystyczne mogą być badaniami populacji ograniczonej lub nieograniczonej. Jeżeli
badaniu podlega populacja ograniczona, to badanie może być wyczerpujące – gdy badaniu został poddany każdy
element populacji lub częściowe – gdy badaniu zostały poddane tylko elementy próbki populacji. Tytuł tabeli lub
wykresu przedstawiającej rozkład analizowanej przez badacza zmiennej powinien być tak sformułowany, aby
wynikało z niego, jakie to było badanie. I tak, gdy przeprowadzono:

1. Badania całościowe populacji ograniczonej - tytuł tabeli zawiera:

nazwę zmiennej (cechy, właściwości), której rozkład przedstawiony jest w tabeli

co?

nazwę populacji i

kto

jej przestrzenne

gdzie

i czasowe ograniczenie

kiedy?

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Przykład:

Tabela 1.

Wykształcenie osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu

w roku 2005.

Wykształcenie

Liczebność

n

%

niższe niż średnie

80

średnie lub wyższe

110

suma

190

2. Badania częściowe populacji ograniczonej - tytuł tabeli zawiera:

nazwę zmiennej (cechy, właściwości), której rozkład przedstawiony jest w tabeli

nazwę

populacji i

jej przestrzenne
i czasowe ograniczenie

oraz informację, że badania nie są całościowe

Przykład:
Tabela 2. Wykształcenie badanej grupy osób bezrobotnych zarejestrowanych w Urzędzie Pracy w

Paradyżu w roku 2005.
lub

Tabela 2. Wykształcenie bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w roku 2005

(próba 30 osób).

W pierwszym z powyższych przykładów na to, że badania są częściowe wskazuje zwrot „badanej grupy osób”, w
drugim informacja podana w nawiasie.

3. Badania populacji nieograniczonej – tytuł tabeli zawiera:

nazwę zmiennej (cechy, właściwości), której rozkład przedstawiony jest w tabeli

nazwę

populacji, którą reprezentuje badana próbka
Przykład:
Tabela 1. Rozkład wieku uczniów w grupie eksperymentalnej

Jeżeli w jednej tabeli przedstawiamy dwa rozkłady jednej zmiennej w wyodrębnionych grupach, to tytuł tabeli
zawiera informację taką jak w przypadku, gdy prezentowany jest rozkład jednej zmiennej (czyli uwzględniająca
rodzaj badania) wraz z dodatkiem „według...”

Przykład:

Tabela 3. Miejsce zamieszkania osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w roku

2005 według wykształcenia(w procentach)

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

wieś

70

39

miasto

30

61

razem

100

100

Przykład:

Tabela 4. Wykształcenie osób bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu w roku 2005

według miejsca zamieszkania(w procentach)

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

razem

wieś

57

43

100

miasto

26

74

100

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Jeżeli w tabeli przedstawiamy rozkład dwuzmiennej, w tytule tabeli podajemy nazwę tej dwuzmiennej w formie
„nazwa cechy 1 a nazwa cechy 2” oraz informację pozwalającą określić typ badania.
Przykład:
Tabela 5. Wykształcenie a miejsce zamieszkania osób bezrobotnych zarejestrowanych w Urzędzie Pracy w

Paradyżu w roku 2005.

Miejsce zamieszkania

Wykształcenie

niższe niż średnie

średnie lub wyższe

razem

wieś

56

43

99

miasto

24

67

91

razem

80

110

190

Wykresy statystyczne

Strukturę badanej zbiorowości można przedstawić graficznie na wykresach statystycznych. Poprawnie i

czytelnie sporządzone wykresy pozwalają na szybką orientację w strukturze danych, obrazowo ujmują różnice
między rozkładami zmiennej w różnych zbiorowościach, co ułatwia dalszą tych różnic analizę statystyczną.
Umożliwiają wstępne rozpoznanie zgodności otrzymanego rozkładu empirycznego z rozkładem teoretycznym,
itd. O wartości wykresu decyduje wybór odpowiedniego do charakteru danych typu wykresu, jak również
właściwy dobór i opis skali oraz właściwa legenda. Przesądzają one często w ogóle o wykresu czytelności.

W literaturze spotykamy wiele rozróżnień typów wykresów statystycznych a odpowiadające rozróżnionym

typom nazwy nie są spójnie stosowane przez różnych autorów. Podobnie rzecz się ma w przypadku
komputerowych programów umożliwiających sporządzanie wykresów statystycznych. W tym skrypcie
ograniczymy się do podania bardzo ogólnych wskazówek dotyczących doboru typu wykresu, w zależności od
rodzaju właściwości (zmiennej), której rozkład ma być przedstawiony graficznie.

Rozróżnimy dwa podstawowe typy wykresów przydatnych do obrazowania rozkładu zmiennej w

zbiorowości:
1.Wykresy, w których wykorzystuje się metodę podziału powierzchni wybranej figury zamkniętej (np. koła,
prostokąta) na części w proporcjach odpowiadających proporcjom podziału badanej zbiorowości na grupy;

2.

Wykresy, w których wykorzystuje się układ odniesienia (np. układ współrzędnych kartezjańskich); w tym

przypadku informację o rozkładzie zmiennej w zbiorowości odczytuje się z odpowiednio oznaczonych i
wyskalowanych osi układu odniesienia.
Pośrednim typem są wykresy, w których wykorzystuje się jedną oś odniesienia.

Wykresy pierwszego typu stosujemy przede wszystkim do prezentacji rozkładu zmiennej nominalnej, bo

tylko taki w tym przypadku jest odpowiedni, choć można je również wykorzystać do prezentacji rozkładu
dowolnej zmiennej. Wykresy drugiego typu stosujemy wyłącznie do prezentacji rozkładu zmiennych
mierzonych na skalach z jednostką miary.

Wykres kołowy i kolumnowy

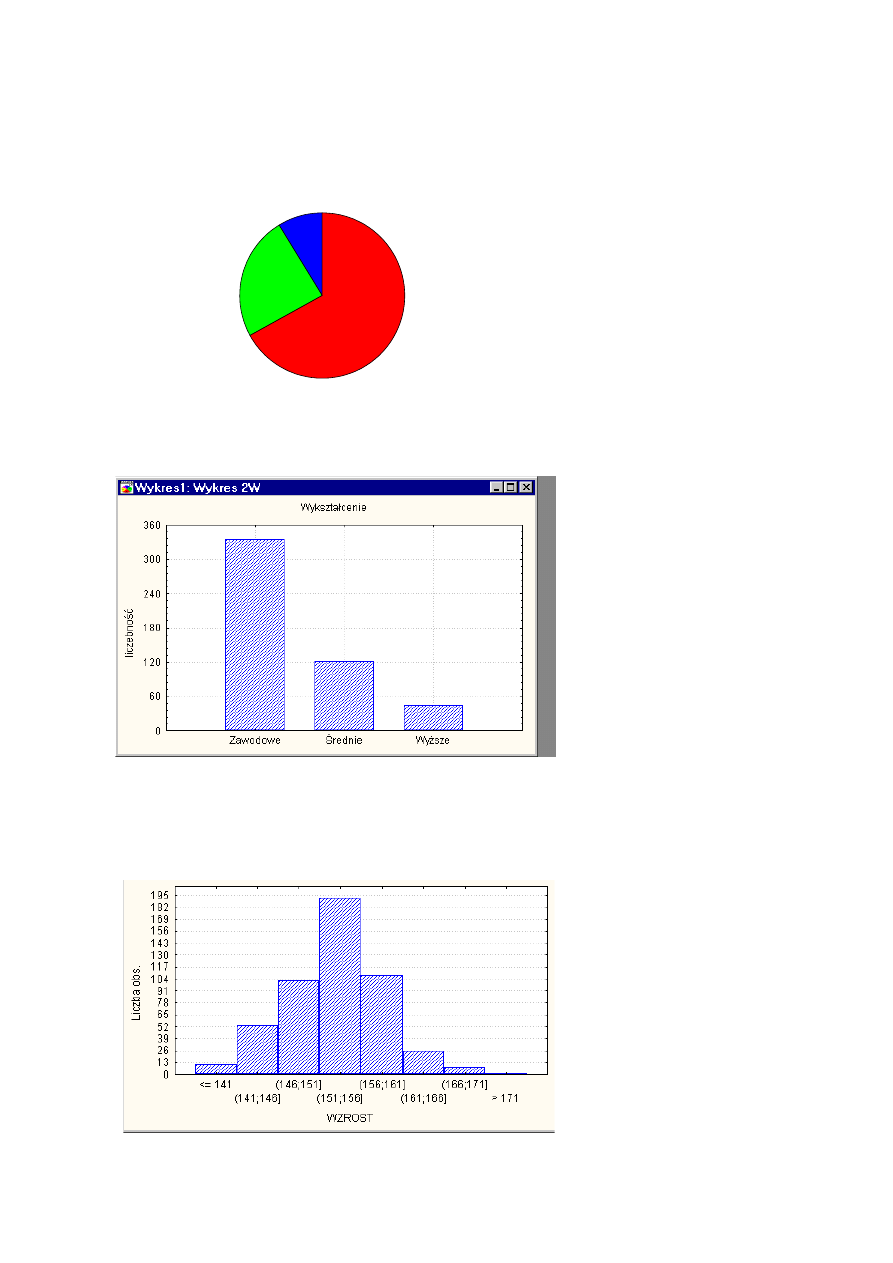
Przykładem wykresu typu I jest wykres kołowy. Koło – reprezentujące całą zbiorowość - dzielimy tak, aby

poszczególne wycinki koła były proporcjonalne do liczebności rozróżnionych grup.

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Rys. Wykształcenie osób bezrobotnych zarejestrowanych w .................

Wyższe, 8,8 %

Średnie, 24,2 %

Zawodowe, 67,0 %

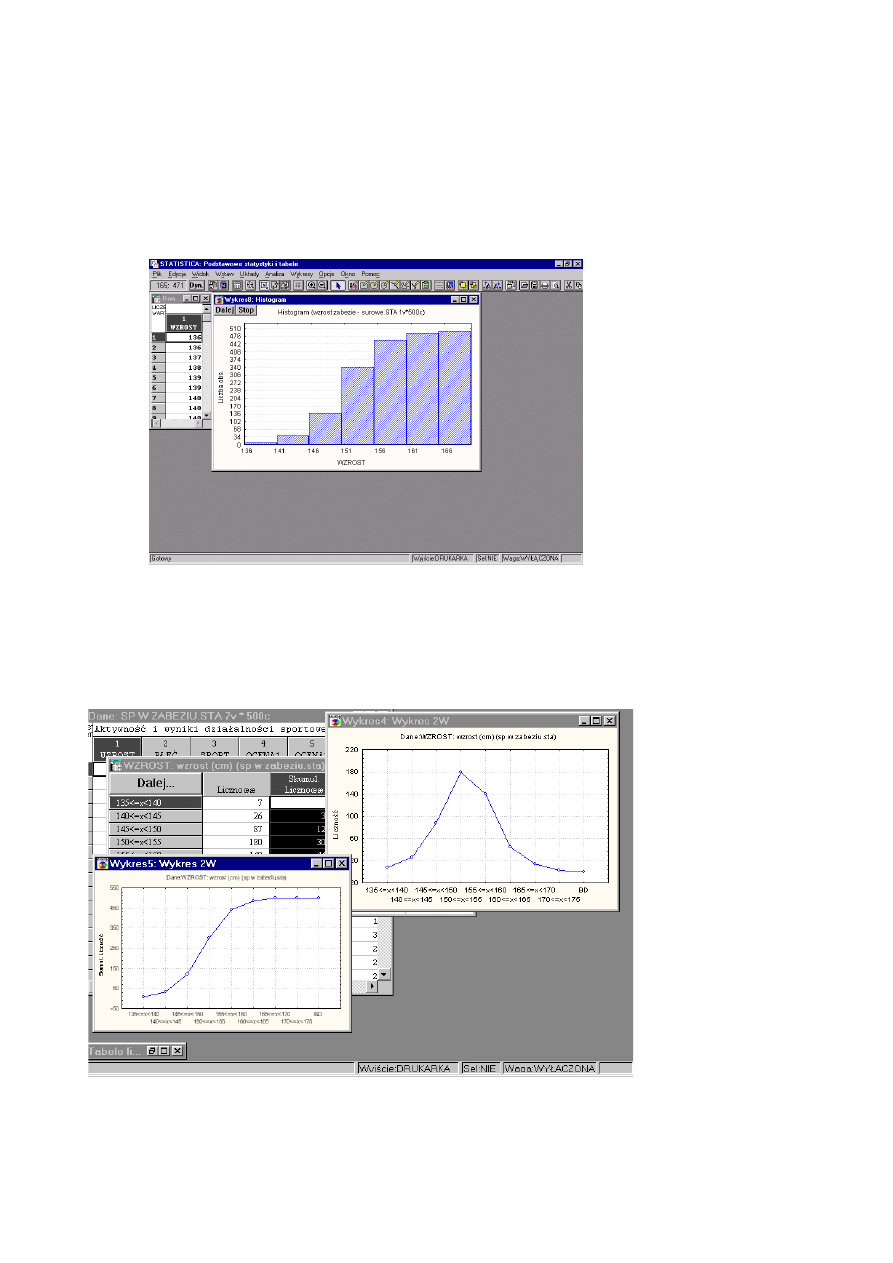
Tę samą informację możemy przedstawić na wykresie kolumnowym:

Histogram

Przykładem wykresu typu II. jest histogram zmiennej ciągłej. Struktura zbiorowości obrazowana jest na

histogramie poprzez szereg prostokątów umieszczonych w odpowiednio opisanym i wyskalowanym układzie
dwu osi liczbowych; na jednej osi reprezentowane są wartości zmiennej, na drugiej - liczebności lub liczebności
względne (wskaźniki struktury).

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Jeżeli obrazujemy szereg rozdzielczy kumulowany, na drugiej osi reprezentowane są liczebności

kumulowane lub liczebności względne kumulowane, a otrzymany wykres to histogram kumulowany.

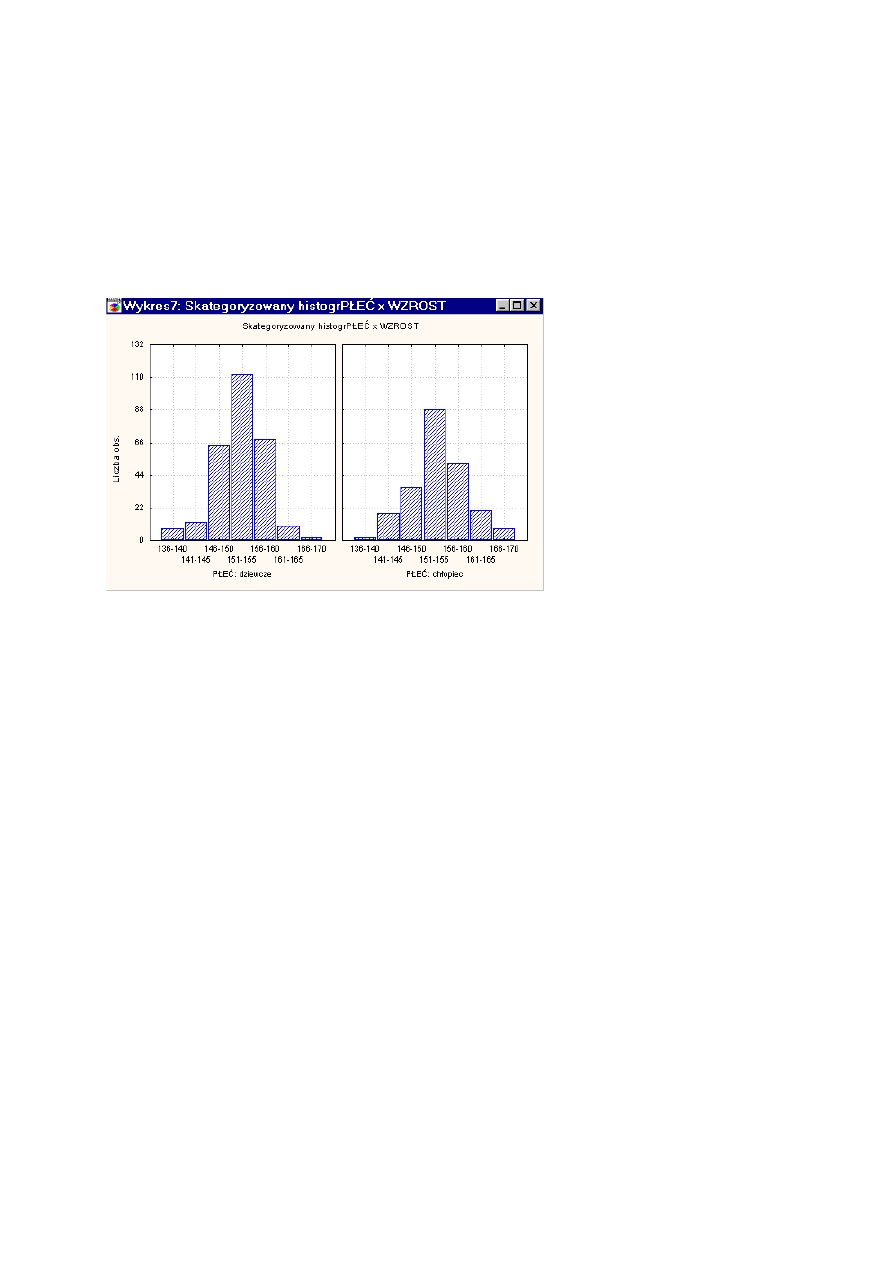
Wykres liniowy

Rozkład zmiennej ciągłej przedstawiony może być graficznie na wykresie liniowym zwanym wielobokiem

liczebności. Wielobok liczebności otrzymamy, gdy połączymy odcinkami punkty, których współrzędne
wyznaczone są przez środek przedziału klasowego i odpowiadającą temu przedziałowi liczebność.

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Wykres złożony

Wykresy złożone przedstawiają strukturę zbiorowości względem więcej niż jednej zmiennej. Tutaj

pokażemy pewną odmianę wykresu złożonego – układ wykresów skategoryzowanych. Układ taki przedstawia
rozkład według np. dwu zmiennych na tylu osobnych wykresach, ile wartości ma jedna ze zmiennych
grupujących..

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

Zadania i ćwiczenia
1. Zapisz następujące liczby w postaci procentów:

0,2 = 20%
0,02 = 2%
0,30 =
0,24 =
0,05 =
0,004 =
0,256 =
1,00 =
1,25 =

2. Wyniki :egzaminu z matematyki w grupie studentów przedstawiają się następująco:

ndst, dst, dst, db, ndst, bdb, bdb, db, db, dst, dst, dst, db, bd, bd, ndst, dst, dst, dst, db, dst, db, bdb, dst, db, bdb,
bdb, dst, db, db, db, dst, dst, bdb, db, db, dst, dst, bdb, db, db, dst, bdb, dst, dst, db, db, db, dst, bdb, dst, db, db

Ile było ocen” ndst”, ile „dst”, ile „db”, ile „bdb”? Utwórz odpowiednią tabelę liczebności przedstawiającą
rozkład ocen w grupie studentów.
Ilu studentów zdawało egzamin?
Oblicz wskaźniki struktury otrzymanego rozkładu dla każdej oceny.

3. Na podstawie tabeli 8 odpowiedz na następujące pytania:

Ile procent bezrobotnych zarejestrowanych w Urzędzie Pracy w Paradyżu mieszka na wsi?
Ile procent bezrobotnych ma wykształcenie niższe niż średnie?
Ile, w procentach, jest kobiet wśród badanych?
Ile, w procentach, jest mężczyzn o wykształceniu średnim lub wyższym?
Jaki procent badanych bezrobotnych

Tabela 8. Bezrobotni zarejestrowani w Urzędzie Pracy w Paradyżu w roku 2005 ze względu na wykształcenie,

miejsce zamieszkania i płeć (w procentach)

Miejsce

zamieszkania

Płeć

Wykształcenie

niższe niż średnie

średnie lub wyższe

∑

płeć

∑

miejsce

wieś

kobieta

10

13

23

mężczyzna

19

10

29

52

miasto

kobieta

7

20

27

mężczyzna

6

15

21

48

∑

wykształcenie

42

58

100

100

Statystyka w badaniach. Tabele i wykresy

Urszula Augustyńska

4. Przeprowadź statystyczną analizę danych zawartych w poniższej tabeli według podanych poleceń:

Identyfikator

Wynik testu

(„odporność” na

stres)

Ocena z

egzaminu

Płeć

A.Z.

28

db

K

A.C.

26

db

K

B.D.

29

dst

K

B.S.

30

bdb

M

C.R.

27

dst

M

C.G.

28

db

K

T.U.

28

dst

M

D.T.

32

db

K

F.O.

29

bdb

K

H.I.

32

dst

K

N.O.

29

dst

M

M.E.

33

bdb

M

L.D.

31

bdb

M

S.W.

25

dst

K

S.B.

24

dst

M

G.G.

30

db

K

K.L.

28

db

M

K.I.

29

db

K

R.A.

27

bdb

K

G.I.

24

dst

K

J.F.

31

bdb

M

L.W.

23

db

M

T.A.

33

bdb

M

W.A.

26

dst

K

C.M.

25

dst

M

M.C.

34

db

K

B.O.

27

db

M

D.R.

22

dst

M

W.P.

23

dst

K

Przedstaw tabelarycznie i graficznie rozkład zmiennej płeć oraz rozkład zmiennej ocena z egzaminu.
Pamiętaj o tytułach tabel i wykresów oraz o zamieszczeniu legendy. W tabeli umieść również liczebności
względne (w procentach).

Przedstaw w tabeli dwudzielczej strukturę grupy:

•

wynik testu a płeć

•

wynik testu a ocena

Pamiętaj o tytułach tabel i legendzie.

Sporządź histogram (zwykły i kumulowany) zmiennej wynik testu (podziel wyniki testu na pięć klas). Naszkicuj
wielobok liczebności oraz dystrybuantę empiryczną.

Oblicz lub odczytaj ze sporządzonych wykresów:

•

Jaki procent grupy stanowią osoby, które osiągnęły w teście wynik 30 punktów lub więcej?

•

Jaki procent grupy stanowią osoby, które osiągnęły w teście wynik 23 punktów lub mniej?