Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
Współzależność zmiennych
Analiza współzależności między zmiennymi dotyczy, najogólniej mówiąc, poszukiwania odpowiedzi na
pytanie, czy dwie lub więcej zmiennych jest ze sobą związanych, czy i w jakiej wzajemnej relacji pozostają.
Inaczej: czy między zbiorem danych będących wynikiem pomiaru jednej zmiennej a zbiorem danych będących
wynikiem pomiaru drugiej zmiennej istnieje zależność i jaka ona jest.
Związek ten wyraża się różnie w zależności od tego na jakich skalach mierzone są analizowane zmienne. W
przypadku zmiennych mierzonych na skali nominalnej mówimy o współwystępowaniu (koincydencji), w
przypadku zmiennych mierzonych na skalach porządkowych mówimy o współuporządkowaniu (koordynacji), w
przypadku zmiennych mierzonych na skali z jednostką miary mówimy o współzmienności (korelacji).
Związek między zmiennymi może być analizowany dwojako. Interesować może nas siła tego związku w
badanej próbce populacji
lub możliwość przewidywania wartości jednej zmiennej na podstawie wartości innych zmiennych dla
dowolnego elementu populacji.
Analiza współzależności – zmienne nominalne
Analiza współzależności (inaczej: ścisłości związku) między zmiennymi nominalnymi polega na ocenie częstości
współwystępowania określonych wartości zmiennych, których związek chcemy badać. Zacznijmy od przypadku,
gdy obie interesujące nas zmienne są dwuwartościowe. Wówczas rozkład dwuzmiennej (X,Y) można
przedstawić w tabeli czteropolowej o schemacie (rys. 1):
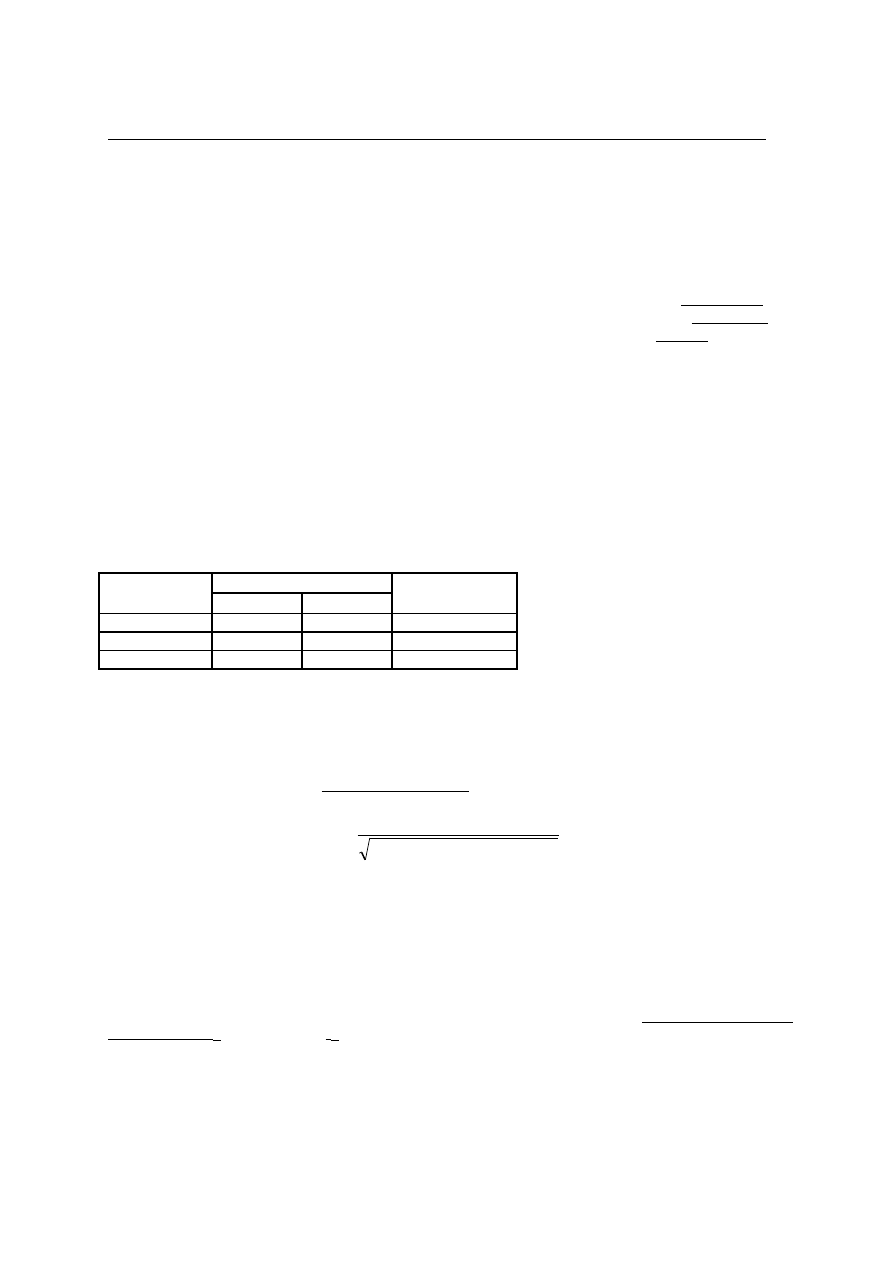
Zmienna Y
Zmienna X
x
1
x
2
Razem
y
1
a
b
a+b
y
2
c
d
c+d
Razem
a+c
b+d
a+b+c+d=n
Rys.1. Schemat tabeli czteropolowej
Liczba a w tabeli jest liczbą przypadków (obserwacji), dla których zmienna X przybiera wartości x
1
i
jednocześnie zmienna Y przybiera wartość y
1
, analogicznie pozostałe liczby w tabeli. Ostatni wiersz przedstawia
rozkład brzegowy zmiennej X, a ostatnia kolumna rozkład brzegowy zmiennej Y.
Jednym z mierników ścisłości związku zmiennych dwuwartościowych jest współczynnik korelacji punktowo-
czteropolowej Yule'a, zwany krótko współczynnikiem φ (fi):
(
)(
)(
)(
)
d
a
d
c
c
b
b
a
bc
ad
+
+
+
+
−
=
ϕ
,
gdzie a, b, c, d to liczebności w odpowiednich polach tabeli czteropolowej. Uwaga: we wzorze jest błąd -
popraw
Współczynnik ten jest odpowiedni dla zmiennych nominalnych, których wartości stanowią dwie rozłączne klasy.
Może zmieniać się on od –1 do 1, ale znak zależy od tego, w jakim porządku wpisane zostały do tabeli
poszczególne klasy wartości zmiennych X i Y. Dla zmiennych nominalnych jest to w zasadzie kwestią wygody i
stąd informację co do ścisłości związku opieramy na bezwzględnej wartości tego współczynnika.
Innym miernikiem ścisłości związku między zmiennymi dwuwartościowymi jest współczynnik korelacji
tetrachorycznej r
tet
. Współczynnik r
tet
ma zastosowanie wówczas, gdy klasy wartości zostały wyznaczone z
podziału zmiennych ciągłych o rozkładzie normalnym. Współczynnik ten dostarcza najbardziej pewnych
oszacowań, gdy obie rozróżnione klasy zawierają w przybliżeniu takie same liczebności, czyli gdy rozkłady
brzegowe są równomierne (G.Clauss, H.Ebner, s.297). Stosuje się go najczęściej, gdy można uznać, że założenie
1
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
o ciągłości zmiennych i ich normalnym rozkładzie oraz liniowej zależności w populacji jest spełnione, ale
pomiar zmiennych został dokonany z dokładnością skali nominalnej.
Gdy przynajmniej jedna z analizowanych zmiennych jest więcej niż dwuwartościowa mamy do wyboru
współczynnik kontyngenji C-Pearsona oraz współczynnik V-Cramera.
Jeżeli chcemy wypowiadać się o populacji interpretację obliczonej siły związku poprzedzamy sprawdzeniem
istotności statystycznej tego związku między analizowanymi zmiennymi. Korzystamy tu z testu niezależności χ
2
(patrz Zeszyt 1 przewodnika).
Warto w tym miejscu może jeszcze zwrócić uwagę na fakt, że interpretacja współczynników siły związku między
zmiennymi jakościowymi wymaga odniesienia do całości analizowanego zagadnienia, w szczególności do
rozkładu analizowanej dwuzmiennej (J.P.Guilford, s.351). Współczynniki te nie dają się interpretować prosto w
terminach prawdopodobieństwa, czy też w terminach proporcji zmienności, jak ma to miejsce w przypadku
współczynników korelacji zmiennych ilościowych. Z tego też względu interpretację współczynnika należy
poprzedzić opisem rozkładu odpowiedniej dwuzmiennej oraz, ewentualnie, przyjętymi założeniami co do typu
rozkładu zmiennych w populacji.
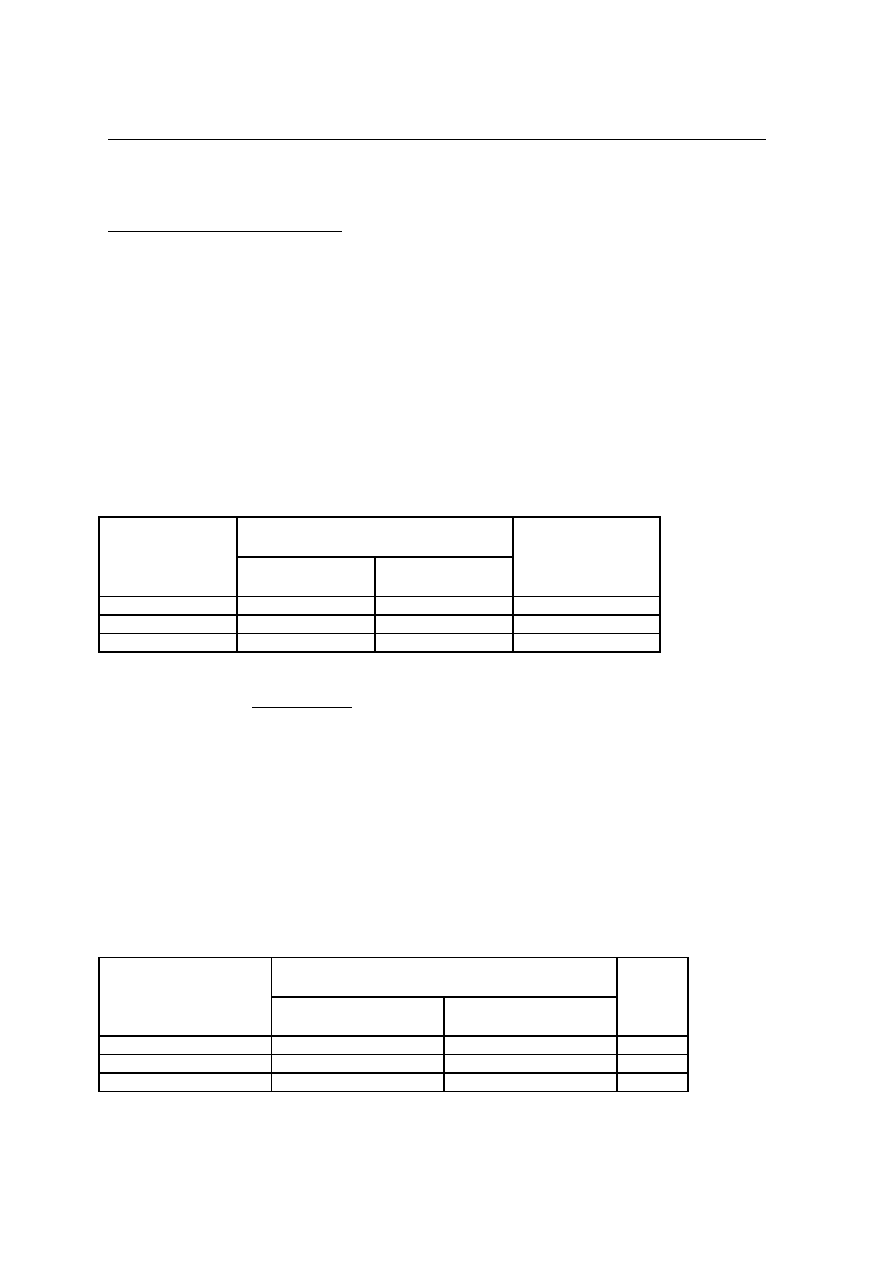
Przykład: W badaniach dojrzałości szkolnej dzieci postawiono pytanie o związek poziomu dojrzałości szkolnej
dziecka z wykształceniem matki. Wyróżniono dwa poziomy dojrzałości: A - dziecko spełnia wszystkie wymagania
dojrzałości szkolnej, B – dziecko nie spełnia wszystkich wymagań dojrzałości szkolnej oraz dwa poziomy
wykształcenia matki: N - niższe niż średnie, W - średnie lub wyższe.
Wykształcenie matki
Kategoria spełnienia wymagań dojrzałości
Nie spełnia
wszystkich
Spełnia wszystkie
Razem
Niższe niż średnie
22
2
25
Średnie lub wyższe
3
22
24
Razem
24
25
49
Ponieważ dane ujęte są w tablicy czteropolowej, do określenia siły związku posłużymy się współczynnikiem φ:
φ = (22 · 22 – 3 · 2) /
24 · 25 · 25· 24
= 0,80
Opis: Wartość „wykształcenie niższe niż średnie” współwystępuje z wartością „nie spełnia wszystkich wymagań
dojrzałości szkolnej” a wartość „wykształcenie średnie lub wyższe” z wartością „spełnia wszystkie wymagania
dojrzałości szkolnej” częściej niż pozostałe pary wartości. Rozkłady brzegowe są przy tym równomierne.
Współczynnik fi przyjmuje wartość, φ=0,80.
Interpretacja: Dzieci matek z wykształceniem średnim lub wyższym częściej spełniają wszystkie wymagania
dojrzałości szkolnej niż dzieci matek z wykształceniem niższym niż średnie. Współzależność ta jest wysoka,
φ=0,80.
Przykład: W badaniach uwarunkowań postaw twórczych nauczycieli nauczania początkowego postawiono
pytania o stopień zadowolenia z wyboru zawodu oraz stopień zadowolenia z życia osobistego. Należy ocenić siłę
związku między tymi cechami.
Czy jest Pani zadowolona
ze swojego życia
osobistego?
Czy jest Pani zadowolona z wykonywanego zawodu?
Nie
Tak
Razem
Nie
23
11
34
Tak
13
53
66
Razem
36
64
100
2
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
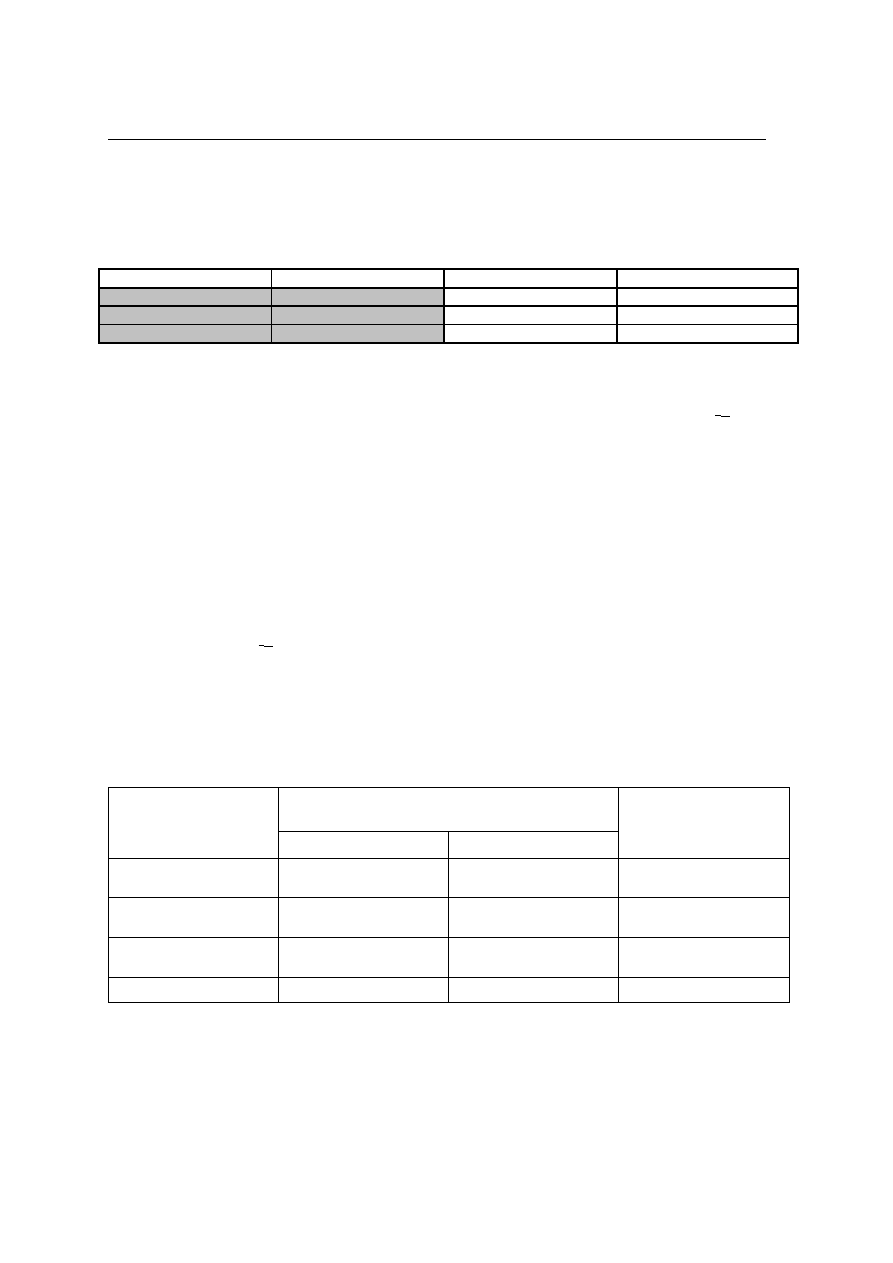
Tym razem posłużymy się programem komputerowym do wyliczenia różnych miar siły związku między
analizowanymi zmiennymi: zadowolenie z życia osobistego i zadowolenie z wykonywanego zawodu.
Statystyki: ZADOWOLE(2) x P16(2) (ankieta.sta)
Chi^2 Pearsona
22,39336
df=1
p=,00000
Fi dla tabel 2 x 2
,4732162
Korelacje tetrachoryczn
,6866131
Wsp. Kontyngencji
,4277408
W pierwszym wierszu wydruku podana jest informacja pozwalająca ocenić, czy analizowany związek jest
statystycznie istotny. W kolejnych wierszach mamy wyliczone wartości trzech współczynników siły związku:
współczynnik
fi,
współczynnik
korelacji
tetrachorycznej
r
tet
i wspólczynnik kontyngencji C.
Wartości współczynników fi φ i współczynnika kontyngencji C są podobne i niezbyt wysokie, natomiast
współczynnik korelacji tetrachorycznej jest prawie półtora razy wyższy. Współczynnik korelacji tetrachorycznej
jest dobry o ile zasadnym jest założenie o ciągłym charakterze korelowanych właściwości oraz ich normalnym
rozkładzie w populacji oraz liniowej zależności. Założenie ciągłości analizowanych zmiennych można uzasadnić
następująco (por. Guilford, s.343): analizowane właściwości zostały zmierzone na skali nominalnej (kategorie
odpowiedzi: Tak, Nie), ale można przyjąć, że stopień „potwierdzenia” przy wyborze odpowiedzi „Tak” jak i
stopień przeczenia przy wyborze odpowiedzi „Nie” jest różny u różnych osób i rozciąga się od mocnego
potwierdzenia z jednej strony do silnego przeczenia z drugiej. Brak też argumentów przeciw tezie o normalnym
rozkładzie tych właściwości w populacji zatrudnionych i liniowej zależności między nimi, co może być uznane
za wystarczające uzasadnienie przyjęcia takowego założenia. Rozkłady brzegowe są wystarczająco
równomierne, aby uznać r
tet
za miarodajne oszacowanie współczynnika korelacji liniowej r.
Interpretacja: między zadowoleniem z wykonywanego zawodu a zadowoleniem z życia osobistego w populacji
nauczycieli nauczania początkowego występuje statystycznie istotna (χ
2
=22,39; df=1, p<0,0001) wysoka
(r
tet
=0,7) korelacja dodatnia.
Przykład: W pomiarze początkowym poziomu samodzielności dziecka zastosowano test, którego wyniki można
traktować jako dane nominalne. Pomiar przeprowadzono w trzech typach przedszkoli. Należy sprawdzić, czy
między typem przedszkola a wynikiem testu zachodzi związek oraz, jeżeli tak, jaka jest jego siła.
PLACÓWKA
Wynik testu Szafa
0
1
Razem
przedszkole
Montessori
5
10
15
przedszkole
waldorfskie
2
13
15
przedszkole
standardowe
14
1
15
Razem
21
24
45
Tu również do obliczenia miar siły związku wykorzystamy program komputerowy:
3
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
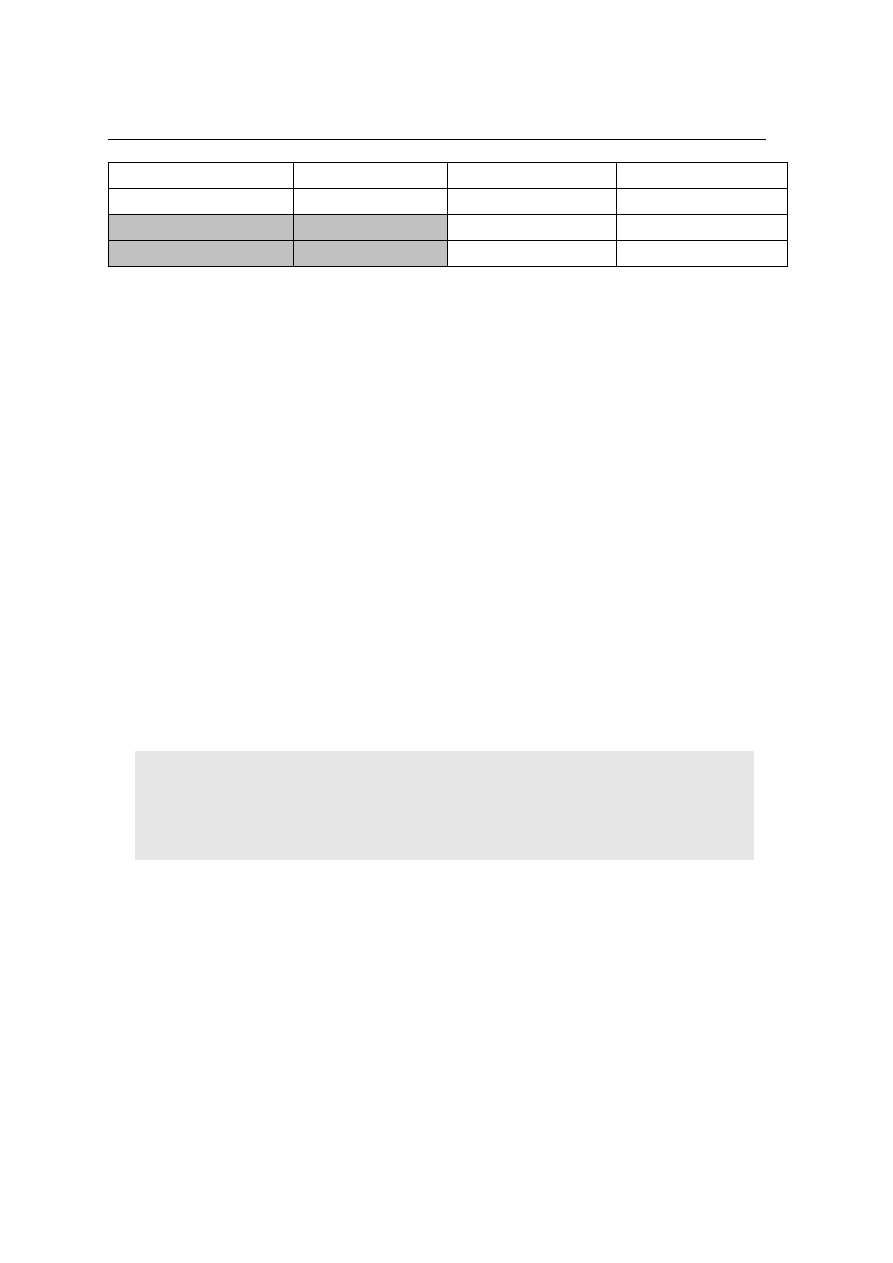
Chi^2 Pearsona
20,89286
df=2
p=,00003
Fi
0,6813852
wsp.kontyngencji
0,5630925
V Craméra
0,6813852
W pierwszym wierszu wydruku podana jest informacja pozwalająca ocenić, czy analizowany związek jest
statystycznie istotny.
Chociaż program wylicza wartość współczynnika fi, jego wartości nie bierzemy pod uwagę ponieważ wyniki
badania ujęte są w tabeli 3 wiersze x 2 kolumny, a pamiętamy, że wspólczynnik fi nadaje się określenia siły
związku, gdy wyniki badania przedstawione są w tabeli dwudzielczej (2 wiersze x
2 kolumny).
Interpretacja: W przedszkolu Montessori oraz przedszkolu waldorfskim rozkład wyników testu „szafa” jest
podobny - przeważają wyniki pozytywne wykonania testu. W przedszkolu standardowym obserwujemy natomiast
przewagę wyników negatywnych.
Wartość statystyki χ
2
daje podstawę do przyjęcia hipotezy o zależności między wynikiem testu „szafa” a typem
placówki przedszkolnej. Zależność ta jest statystycznie istotna (χ
2
= 20,9; p<0,001) i umiarkowana (φ=0,68; C=
0,56; V=0,68).
Analiza współzależności – zmienne porządkowe
Badanie związku między właściwościami w przypadku, gdy analizowane zmienne zmierzone zostały na skali
porządkowej sprowadza się do odpowiedzi na pytanie: w jakim stopniu uporządkowanie jednostek badania
według wartości jednej zmiennej odpowiada uporządkowaniu według wartości drugiej zmiennej, czyli, można
powiedzieć, na pytanie o zgodność uporządkowania jednostek badania według dwu różnych kryteriów. Do
określenia siły związku między zmiennymi porządkowymi odpowiednią miarą jest współczynnik Kendalla τ.
Współczynnik Kendalla jest miarą bazującą na informacji o liczbie przypadków dla których występuje zgodność
(niezgodność) uporządkowań w odpowiadających sobie parach wyników. Wartość τ = 1 oznacza pełną
zgodność uporządkowań w odpowiadających sobie parach wyników, czyli pełną zgodność uporządkowań
przypadków według obu zmiennych. Wartość τ = -1 oznacza pełną przeciwstawność uporządkowań, a τ = 0 brak
jakiejkolwiek zgodności uporządkowań, czyli brak związku między zmiennymi.
Często stosowaną miarą określania siły związku między zmiennymi porządkowymi bywa współczynnik korelacji
rang Spearmana. Współczynnik ten daje dobre oszacowanie współczynnika korelacji Pearsona dla dużych
szeregów pomiarów i był stosowany jako mniej „pracochłonny” sposób szacowania współczynnika r
(J.P.Guilford, s..322). Obecnie, ze względu na możliwości obliczeniowe programów komputerowych takie jego
wykorzystanie w analizie danych przestaje mieć znaczenie. Natomiast konstrukcja współczynnika Spearmana,
wykorzystująca operacje odejmowania rang (a więc liczb porządkowych) jest od strony teoretycznej dyskusyjna.
Przykład: W badaniach uwarunkowań powodzenia w studiowaniu postawiono pytanie o związek między
średnią oceną końcową a stopniem satysfakcji z wybranego kierunku studiów.
Stopień satysfakcji z wybranego kierunku mierzono na 10 punktowej skali porządkowej. (Cz.Lewicki, s.115).
4
Współczynnik τ Kendalla przybiera wartości z przedziału [-1; 1].
Wartość τ = 1 określa pełną zgodność uporządkowań w odpowiadających sobie parach
wyników, wartość τ = - 1 pełną przeciwstawność uporządkowań, a τ = 0 brak
jakiejkolwiek zgodności uporządkowań, czyli brak związku między zmiennymi..
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
Identyfikator
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Ocena
3,6
4,5
3,0
4,1
3,2
3,6
4,7
3,1
3,9
3,5
5,0
4,4
3,0
4,2
4,6
Satysfakcja
5
9
3
2
2
8
10
7
6
4
1
3
9
8
2
Ponieważ obie zmienne mierzone są na skali porządkowej właściwą miarą związku między oceną a satysfakcją
będzie współczynnik tau Kendalla..
Do obliczenia miary siły związku wykorzystamy program komputerowy:
Para zmiennych
N
ważnych
Tau
Kendalla
Z
poziom p
OCENA & ZADOWOLE
15
-,049515
-,257286
,796958
Interpretacja: Współczynnik tau Kendalla dla wprowadzonych par pomiarów jest praktycznie równy zeru.
Wartość statystyki Z testu istotności i odpowiadający jej poziom istotności p (p>0,7) wskazuje na brak związku
między uzyskaną oceną a satysfakcją z wybranego kierunku studiów w populacji studentów, dla której to
populacji pobrana próbka studentów jest próbką reprezentatywną.
Analiza współzależności – zmienne ilościowe
Związek między zmiennymi ilościowymi może być analizowany dwojako. Interesować może nas 1) siła tego
związku albo 2) możliwość przewidywania wartości jednej zmiennej na podstawie wartości innych zmiennych.
W pierwszym przypadku mamy do czynienia z analizą korelacyjną, w drugim z analizą regresji.
Nie trzeba szczególnych badań, żeby zauważyć, że istnieje związek między masą ciała a wzrostem. Osoby
wyższe mają zazwyczaj większą masę niż osoby niskie. I odwrotnie, można się spodziewać, że osoba o większej
masie będzie też wyższa. Nie jest to jednak zależność bezwyjątkowa. Może się zdarzyć, że z dwu osób właśnie
ta wyższa będzie ważyła mniej niż ta niższa. Jednak, ogólnie rzecz biorąc, wyższym wartościom wzrostu
odpowiada przeciętnie wyższa wartość masy ciała. Siłę tego związku określa współczynnik korelacji.
Przewidywać, jaki wzrost może mieć osoba o danej masie ciała, albo odwrotnie, jaką masę ciała może mieć
osoba o danym wzroście, pozwala równanie regresji.
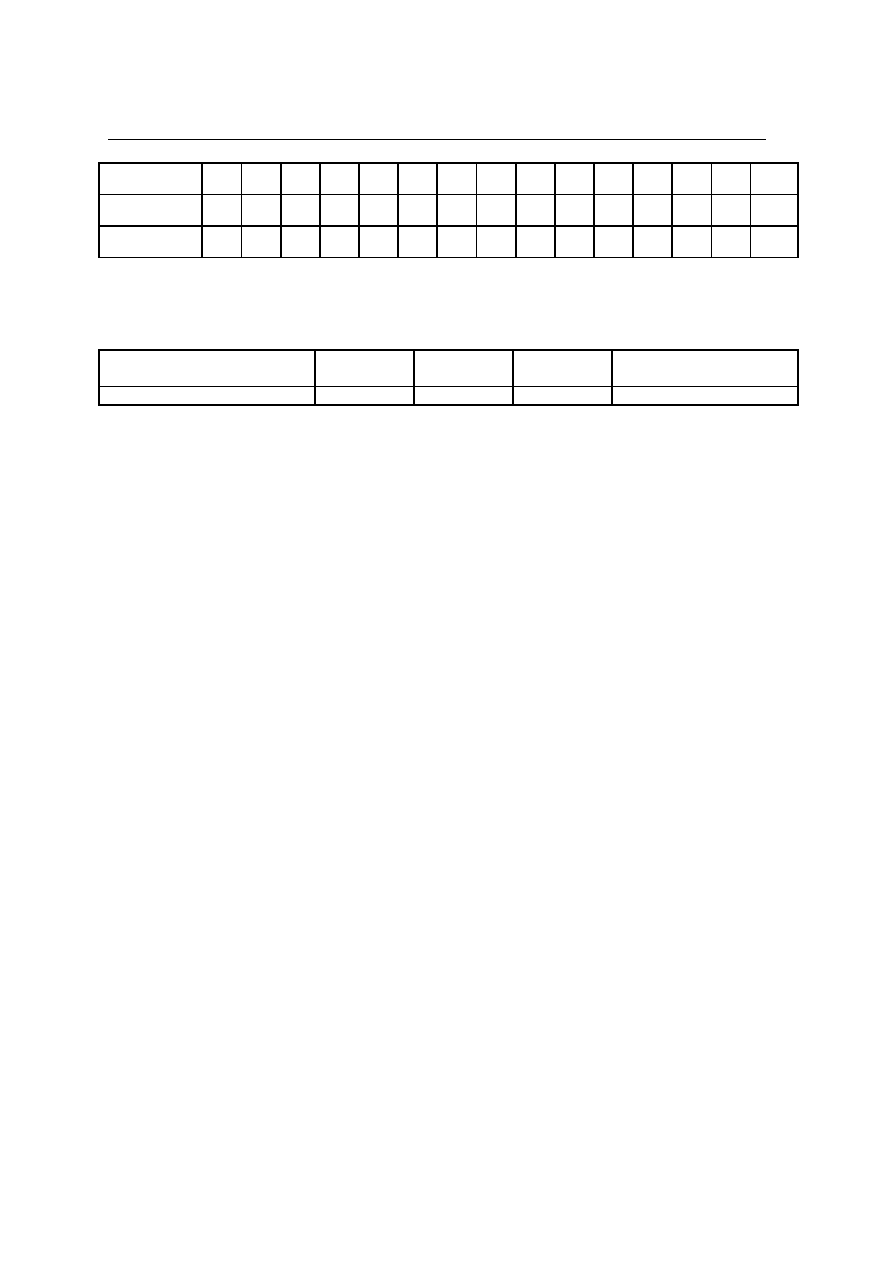
Związek między dwiema zmiennymi, zmienną X i zmienną Y w konkretnej zbiorowości można przedstawić
na wykresie zwanym wykresem korelacyjnym lub wykresem rozrzutu. Niech, na przykład, zmienna X oznacza
wynik testu sprawności manualnej, a zmienna Y wynik testu koncentracji uwagi w zbiorowości próbnej 6-latków.
Wówczas punkt wykresu określa jaki wynik osiągnęło konkretne dziecko w teście sprawności oraz w teście
koncentracji. Ogólnie, wykres tworzą pary pomiarów (x, y) dla każdego elementu badanej zbiorowości.
5
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
korelacja dodatnia
zmienna X
z
mien
n
a
Y
4
8
12
16
20
24
28
32
8
12
16
20
24
28
32
korelacja ujemna
zmienna X
z
mien
na
Y
4
8
12
16
20
24
28
32
-2
2
6
10
14
18
22
26
Przykładem korelacji dodatniej jest zależność między wzrostem a masą ciała. Przykładem korelacji ujemnej
jest zależność między czasem trwania wykładu a koncentracją uwagi studenta.
Im bardziej rozproszone są punkty wykresu tym słabszego związku między zmiennymi możemy się
spodziewać.
Miarą siły związku między dwiema zmiennymi ilościowymi, gdy związek jest liniowy jest współczynnik
korelacji liniowej Pearsona r. Współczynnik korelacji liniowej z próby może być wyznaczony według
poniższego wzoru:
(
)
(
)
(
)
(
)
∑
∑
∑
=
=
=
−
−
−
−
=
n
i
n
i
y
i
x
i
n
i
y
i
x
i
M
y
M
x
M
y
M
x
r
1
1
2
2
1
,
gdzie x
i
oraz y
i
oznaczają pomiary odpowiednio zmiennej X i zmiennej Y, a M
x
oraz M
y
odpowiednio średnią
rozkładu zmiennej X i średnią rozkładu zmiennej Y.
Podany powyżej współczynnik korelacji Pearsona ma zastosowania wówczas, gdy związek między zmiennymi
jest liniowy. O ile próbka nie jest zbyt mała, każde większe odchylenie od liniowości można wykryć analizując
6
Korelacja jest dodatnia jeżeli większym wartościom jednej zmiennej odpowiadają
przeciętnie wyższe wartości drugiej zmiennej lub, co na jedno wychodzi, niższym
wartościom jednej zmiennej odpowiadają przeciętnie niższe wartości drugiej
zmiennej.
Korelacja jest ujemna, jeżeli wyższym wartościom jednej zmiennej odpowiadają
przeciętnie niższe wartości drugiej zmiennej lub, co na jedno wychodzi, niższym
wartościom jednej zmiennej odpowiadają przeciętnie wyższe wartości drugiej
zmiennej.
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
wykres rozrzutu. Jeżeli punkty układają się wzdłuż innej krzywej (nie linii prostej) obliczona wartość r zaniża
siłę związku między zmiennymi, w skrajnym przypadku nawet do zera. Współczynnik r jest też „wrażliwy” na
dane odstające. Kilka wyraźnie odległych punktów może spowodować, że otrzymamy dużą wartość r, choć w
rzeczywistości brak jest związku między analizowanymi zmiennymi.
Na wykresie rozrzutu pełną korelację przedstawiają punkty układające się dokładnie wzdłuż linii prostej.
Niektórzy autorzy wprowadzają jakościowe oceny siły związku na podstawie wartości współczynnika r.
Tabela Ocena jakościowa siły związku
Wartość współczynnika korelacji
R
Ocena jakościowa siły związku
0,0< r < 0,2
słaba
0,2 ≤ r < 0,4
niska
0,4 ≤ r < 0,7
umiarkowana
0,7 ≤ r < 0,9
wysoka
0,9 ≤ r < 1
bardzo wysoka
Źródło: J.G.Guilford, Podstawowe metody statystyczne w psychologii i pedagogice, Warszawa 1964, s.157
Należy jednak podkreślić, że znaczenie przy interpretacji współczynnika ma nie tylko jego wartość lecz również
jego statystyczna istotność. Nawet stosunkowo duża wartość r w próbce nie musi świadczyć o istnieniu związku
między zmiennymi w populacji, jeżeli okaże się ona statystycznie nieistotnie różna od zera.
Przykład: W badaniach postaw nauczycieli nauczania początkowego postawiono pytania o związek między
stażem pracy nauczyciela a takimi postawami jak: konformizm – nonkonformizm, postawa twórcza – postawa
odtwórcza. Wyniki badania postaw spełniają warunki pomiaru ze skali przedziałowej.
Do obliczenia miary siły związku wykorzystamy program komputerowy:
PODST.
STATYST.
Zmienna
Oznaczone wsp. korelacji są istotne z p < 0,0500
(Braki danych usuwano przypadkami) N=97
KONFORM
NONKONF
POST_ODT
POST_TWO
STAŻ
0,021
0,025
0,019
-0,003
p=0,842
p=0,811
p=0,855
p=0,974
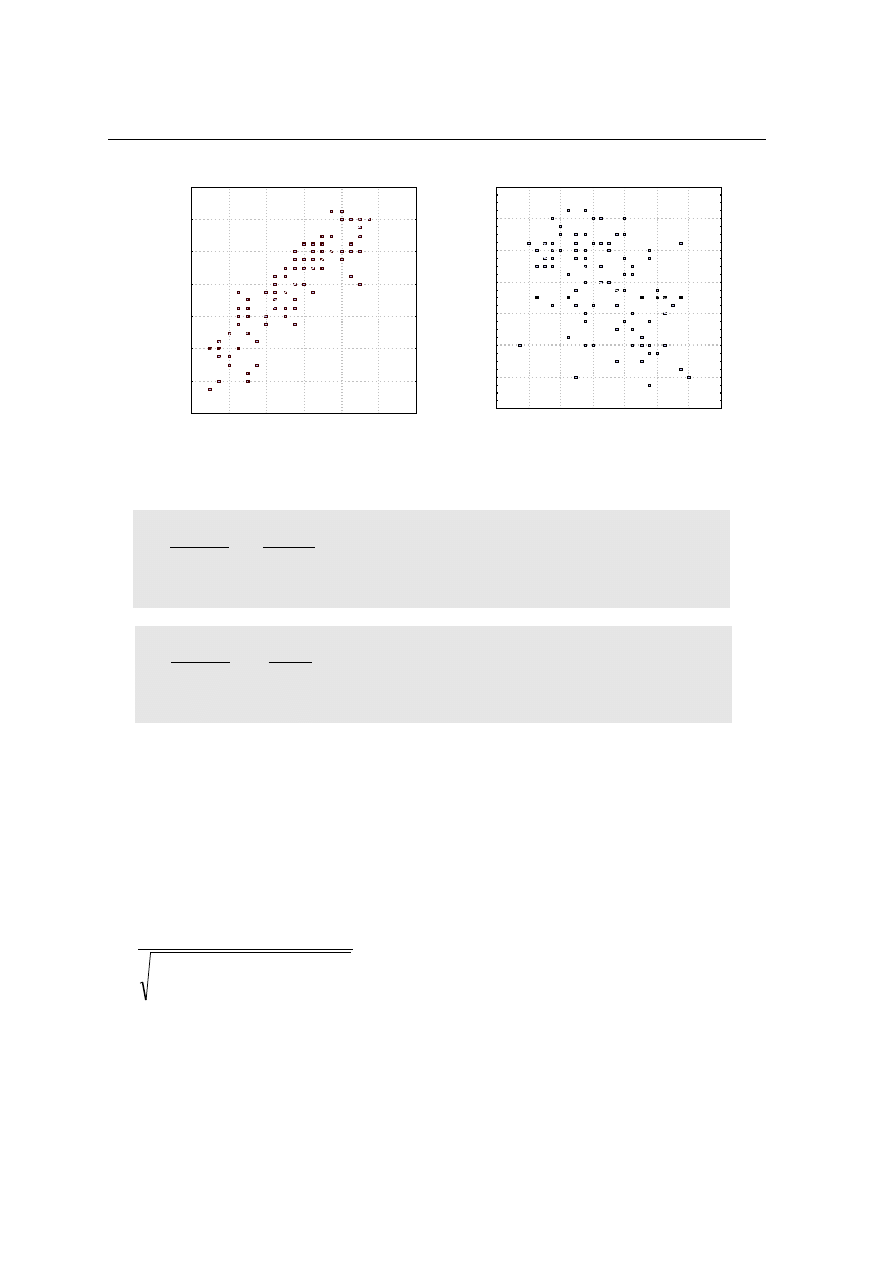
Żaden z policzonych współczynników korelacji nie okazał się statystycznie istotny (p>0,05). Przed
wyciągnięciem ostatecznych wniosków rzućmy okiem na wykresy rozrzutu badanych zależności.
7
Współczynnik korelacji liniowej Pearsona r informuje nas o „sile” i kierunku zależności między
analizowanymi zmiennymi.
Współczynnik r przybiera wartości z przedziału [-1; 1]. Wartość r = –1 określa pełną korelację
ujemną, wartość r = 1 pełną korelację dodatnią, a wartość r = 0 brak związku między zmiennymi.
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
Korelacje (KNAH.STA 84v*100c)
WIEK
KONFORM
NONKONF
POST_ODT
POST_TWO
Ponieważ nie obserwujemy, aby związki były krzywoliniowe możemy stwierdzić brak zależności między,
kolejno, poziomem konformizmu, poziomem nonkonformizmu oraz poziomem postawy twórczej i postawy
odtwórczej a stażem pracy w badanej populacji nauczycieli nauczania początkowego.
Aby zbadać zależność między poziomem konformizmu-nonkonformizmu a poziomem postawy (odtwórcza –
twórcza) należy obliczyć współczynniki korelacji dla każdej pary zmiennych.
Tu również skorzystamy z programu komputerowego; wyniki analizy podane są w tabeli poniżej.
PODST.
STATYST.
Zmienna
Oznaczone wsp. korelacji są istotne z p < ,05000
(Braki danych usuwano przypadkami) N=97
KONFORM
NONKONF
POST_ODT
,942
-,382
p=0,00
p=,000
POST_TWO
-,463
,965
p=,000
p=0,00
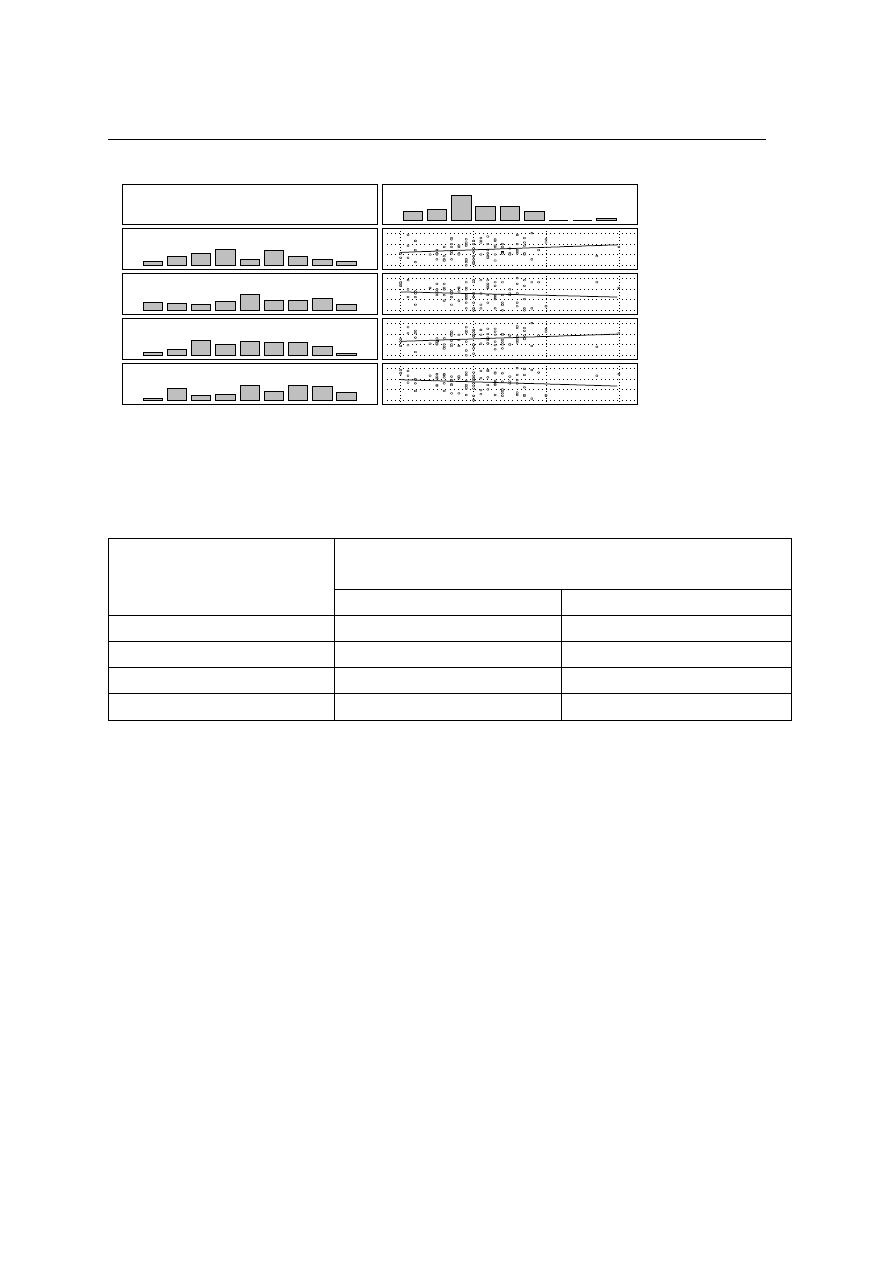
Wszystkie współczynniki korelacji okazały się statystycznie istotne (p<0,05). Najsilniejszy, dodatni związek
obserwujemy między poziomem konformizmu a nasileniem postawy odtwórczej (r=0,942) oraz między
poziomem nonkonformizmu i nasileniem postawy twórczej (r=0,968), tzn. im wyższy poziom konformizmu tym
większe, przeciętnie, nasilenie postawy odtwórczej, im wyższy poziom nonkonformizmu, tym większe, przeciętnie,
nasilenie postawy twórczej. Umiarkowany, ujemny związek obserwujemy zaś między poziomem konformizmu a
nasileniem postawy twórczej (r=-0,492) oraz między poziomem nonkonformizmu a nasileniem postawy
odtwórczej (r=-0,395).
Analiza regresji
Wykres korelacyjny przedstawia faktyczny stan rzeczy w próbce, tzn. obrazuje jaką wartość przyjmuje zmienna
Y gdy zmienna X przyjmuje wartość x, dla każdego elementu zbiorowości próbnej. Zadaniem analizy regresji
jest znalezienie funkcji pozwalającej na przewidywanie tej zależności dla dowolnego elementu zbiorowości
generalnej. Jeżeli można zasadnie się spodziewać, że zależność jest liniowa, funkcją tą jest prosta regresji o
ogólnym równaniu Y’=bX+a. Współczynniki b i a są tak dobrane, żeby prosta była jak najlepiej dopasowana do
punktów empirycznych, czyli tak, aby błąd przewidywania był najmniejszy.
8
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
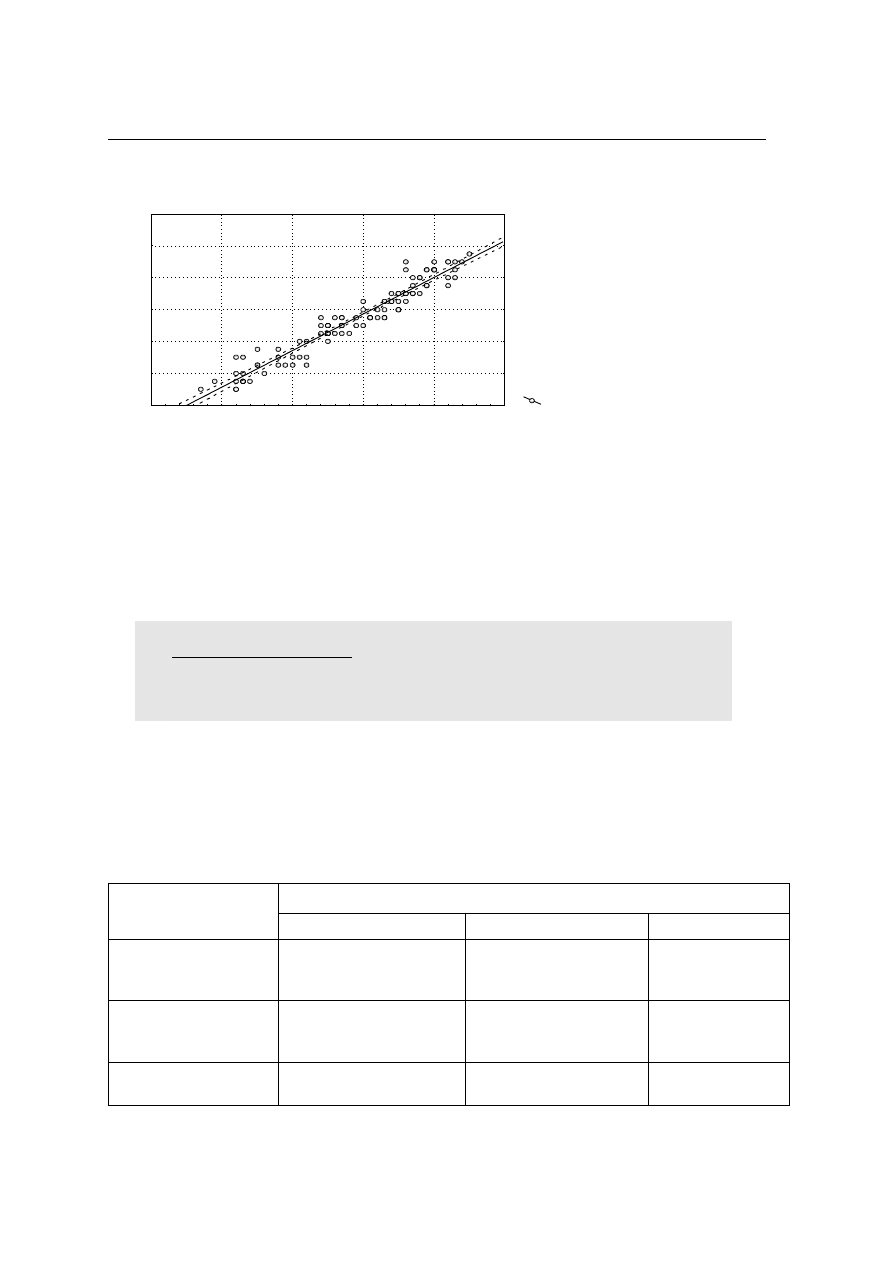
Regresja
95% p.ufności
POST_TWO vs. NONKONF (BD usuwano przypadk.)
NONKONF = 1,0755 + ,45911 * POST_TWO
Wsp. korelacji = ,96518
POST_TWO
N
O
N
KO
N
F
8
12
16
20
24
28
32
10
20
30
40
50
60
Równanie regresji dla związku przedstawionego na powyższym wykresie ma postać:
NONOKONF=1,1+0,46*POST_TWO. Pozwala ono oszacować poziom nonkonformizmu na podstawie wyniku
uzyskanego w teście postawy twórczej. Na przykład można się spodziewać, że osoba, która w teście postawy
twórczej uzyskała wynik 40, w teście badającym poziom nonkonformizmu osiągnie wynik 1,1+0,46*40≈20
punktów, przy czym przewidywanie obarczone jest 5% błędem (prawdopodobieństwo, że tak właśnie będzie
wynosi 95%, że tak nie będzie – 5%).
Widać z przeprowadzonej analizy, że poziom postawy twórczej (mierzony użytym w badaniu narzędziem) wiąże
się w wysokim stopniu z poziomem nonkonformizmu. Można zapytać w jakiej części zmienność zmiennej
„postawa twórcza” wyjaśniona została w tym badaniu zmiennością zmiennej „poziom nonkonformizmu”.
Odpowiednią miarą jest tu kwadrat współczynnika korelacji, r
2
, który nosi nazwę współczynnika determinacji.
W omawianym przykładzie r
2
= 0,965
2
= 0,93. Oznacza to, że nasilenie postawy twórczej wyjaśnione może być
w 93% poziomem nonkonformizmu. Jest to bardzo dużo, ale trzeba pamiętać, że ten związek dotyczy zmiennych
wskaźnikowych (zoperacjonalizowanych). Przy innej operacjonalizacji zmiennych procent wyjaśnionej
zmienności może być inny.
Poniższa tabela porządkuje omówione miary siły związku według skal pomiaru zmiennych, dla których ten
związek jest określany.
Skala pomiaru
Zmiennej X
Skala pomiaru zmiennej Y
nominalna
porządkowa
z jednostką miary
nominalna
1.Współczynnik φ (fi)
2. wsp. kontyngencji C
3. wsp. V Cramera
porządkowa
1. wsp. Kendalla τ (tau)
2. wsp. korelacji rang
Spearmana
z jednostką miary
1. wsp. korelacji
liniowej Pearsona r
9
Współczynnik determinacji r
2
informuje w jakim stopniu zmienność jednej zmiennej
wyjaśniona może być zmiennością drugiej zmiennej, co można rozumieć, że
współczynnik determinacji informuje o „wielkości” powiązania analizowanych
zmiennych.
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
Zadania i ćwiczenia
1. W badaniach uwarunkowań postaw twórczych nauczycieli nauczania początkowego postawiono pytania o
stopień zadowolenia z wyboru zawodu oraz stopień zadowolenia z życia osobistego. Oceń siłę związku między
tymi cechami. Podaj interpretację.
Czy jest Pani zadowolona
ze swojego życia
osobistego?
Czy jest Pani zadowolona z wykonywanego zawodu?
Nie
Tak
Razem
Nie
23
11
34
Tak
13
53
66
Razem
36
64
100
Uwaga: we wzorze podanym w materiałach jest błąd – popraw wzór
2. Narysuj wykresy punktowe dla podanych zbiorów par pomiarów.
a)
Osoba 1
Osoba 2
Osoba 3
Osoba 4
Osoba 5
Osoba 6
Wynik testu X:
2
4
5
9
12
13
Wynik testu Y:
2
4
5
9
12
13
b)
Osoba 1
Osoba 2
Osoba 3
Osoba 4
Osoba 5
Osoba 6
Wynik testu X:
10
7
6
9
9
11
Wynik testu Y:
8
2
4
5
7
10
c)
Osoba 1
Osoba 2
Osoba 3
Osoba 4
Osoba 5
Osoba 6
Osoba 7
Wynik testu X:
1
2
3
5
7
2
9
Wynik testu Y:
7
5
9
4
8
3
1
3. Określ siłę związku miedzy zmienną X i Y dla przykładu a) i c) z zadania 2 (oblicz współczynnik korelacji
rang ρ (ro) Spearmana oraz współczynnik korelacji liniowej Pearsona (r)). Podaj interpretację.
4. Określ współczynnik determinacji dla związku przedstawionego w przykładzie a) i c) i podaj jego
interpretację (skorzystaj z obliczeń z zadania 3).
5. Badając związek pomiędzy płcią uczniów a ich hierarchią wartości zastosujesz:
a) Współczynnik fi
b) Współczynnik kontyngencji C
c) Współczynnik korelacji r Pearsona
d) Współczynnik
τ Kendalla
Odpowiedź uzasadnij.
10
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
Wskazówka 1. Jak rangować zbiory wyników
Celem rangowania jest przypisanie wynikom – pomiarom zmiennej - pewnych liczb (rang) odzwierciedlających
miejsce danego wyniku w uporządkowanym zbiorze wyników. Jest to operacja podobna do „ponumerowania”,
przy czym najmniejszemu wynikowi przypisuje się zwykle rangę 1.
Porangujmy pomiary zmiennej X z przykładu b) zadania 1.
Krok 1: wypisujemy wyniki w porządku od najmniejszego do największego:
6, 7, 9, 9, 10, 11 i liczymy ile jest wyników (w naszym przypadku jest ich 6)
Krok 2: każdej liczbie w uporządkowanym ich zbiorze przypisujemy liczbę naturalną począwszy od liczby 1
(numerujemy)
6, 7, 9, 9, 10, 11
1 2 3 4 5 6
ostatnie liczba w uporządkowanym zbiorze pomiarów ma mieć numer odpowiadający liczbie pomiarów
(wyników).
Krok 3: jeżeli w zbiorze pomiarów są liczby, które się powtarzają, to nazywają się one liczbami „związanymi” i
należy przyporządkować im rangi tak, aby tej fakt odzwierciedlić. W powyższym przykładzie mamy dwie liczby
9 o rangach 3 i 4. Odzwierciedleniem tego faktu będzie przypisanie im wspólnej rangi, będącej średnią
arytmetyczną rang dotychczasowych, czyli rangi (3 + 4)/2 = 3,5.
Krok 4: wypisujemy w 2 kolumnach końcowy efekt rangowania wyników:
wyniki rangi
6
1
7
2
9
3,5
9
3,5
10
5
11
6
Wkazówka 2: Jak obliczyć współczynnik korelacji rang Spearmana
Obliczanie współczynnika korelacji rang ρ Spearmana (zadanie 2b)
ρ =
)
1
(
6
1
2
1
2
−
⋅
−
∑
n
n
R
n
i
, gdzie n jest liczbą par pomiarów, R – różnica rang pomiarów zmiennej X i rang pomiarów
zmiennej Y
Pomiarom zmiennej X przyporządkowujemy rangi, czyli liczby określające pozycję danej liczby w
uporządkowanym tych liczb zbiorze (kolumna 2). Następnie przyporządkowujemy rangi pomiarom zmiennej Y
(pamiętając o tym, że mają być to pomiary od pary z X) i obliczamy różnice tych rang (kolumna 5), a dalej
kwadraty różnic (kolumna 6):
Tabela 1: Obliczanie współczynnika ro- Spearmana
1
pomiary
zmiennej X
2
rangi pomiarów
zmiennej X
3
pomiary
zmiennej Y
(od pary z X)
4
rangi
pomiarów
zmiennej Y
5
różnice rang
6
różnice rang
do kwadratu
6
1
4
3
-2
4
7
2
2
2
0
0
9
3,5
5
4
-0,5
0,25
9
3,5
7
5
1,5
2,25
10
5
1
1
4
16
11
6
10
6
0
0
suma kwadratów różnic rang
22,5
11
Statystyka w badaniach. Współzależność zmiennych
Urszula Augustyńska
ρ = 1 – 6(22,5 : 6(6
2
-1)) = 1 – 6(22,5 : 210) = 1 – 0,66 = 0,34
Wkazówka 4: Jak obliczyć współczynnik r Pearsona
Obliczanie współczynnika korelacji liniowej r Pearsona (zadanie 2b)
(
)
(
)
(
)
(
)
∑
∑
∑
=
=
=
−
−
−
−
=
n
i
n
i
y
i
x
i
n
i
y
i
x
i
M
y
M
x
M
y
M
x
r
1
1
2
2
1
M
x
= (6 + 7 + 9 + 9 + 10 + 11) : 6 = 8,7
M
y
= (1 + 2 + 4 + 5 + 7 + 10) : 6 = 4,8
Tabela 2: Obliczanie współczynnika r Pearsona
pomiary
zmiennej X
pomiary
zmiennej Y
x
i
- M
x
(x
i
- M
x
)
2
y
i
- M
y
(y
i
- M
y
)
2
(x
i
– M
x
) ·(y
i
- M
y
)
Osoba 3
6
4
6 – 8,7 =
-2,7
7,29
4 – 4,8
= -0,8
0,64
2,16
Osoba 2
7
2
7 – 8,7 =
-1,7
2,89
2 – 4,8
= -2,8
7,84
4,76
Osoba 4
9
5
9 – 8,7 =
0,3
0,09
5 – 4,8 =
0,2
0,04
0,01
Osoba 5
9
7
9 – 8,7 =
0,3
0,09
7 – 4,8
= 2,2
4,84
0,66
Osoba 1
10
1
10 – 8,7
= 1,3
1,69
1 – 4,8
= - 3,8
14,44
- 4,94
Osoba 6
11
10
11 – 8,7
= 2,3
5,29
10 – 4,8
= 5,2
27,04
11,96
Razem
17,34
54,84
14,612
r
=
14,61
17,34⋅54,84
=
0,48
12