PEŁZANIE
Pełzanie – zespół zjawisk, które można wyjaśnić przyjmując, że w zależności między
naprężeniem a odkształceniem występuje czas. Jest to zatem proces reologiczny.
Reologia -
nauka zajmująca się powstawaniem odkształceń w materiałach i zmianą tych
odkształceń wraz z upływem czasu. Reologiczne równanie stanu, sformułowane dla
jednoosiowego rozciągania, zgodnie z jedną z klasycznych teorii pełzania - teorią starzenia,
ma postać:
F(
,
, t)
T=const.
= 0
gdzie:
-
naprężenie,
-
odkształcenie, t - czas, T – temperatura.
Równanie to odpowiada założeniu, że w określonej temperaturze istnieje pewna
powierzchnia we współrzędnych
,
, t. Po przecięciu tej powierzchni płaszczyznami
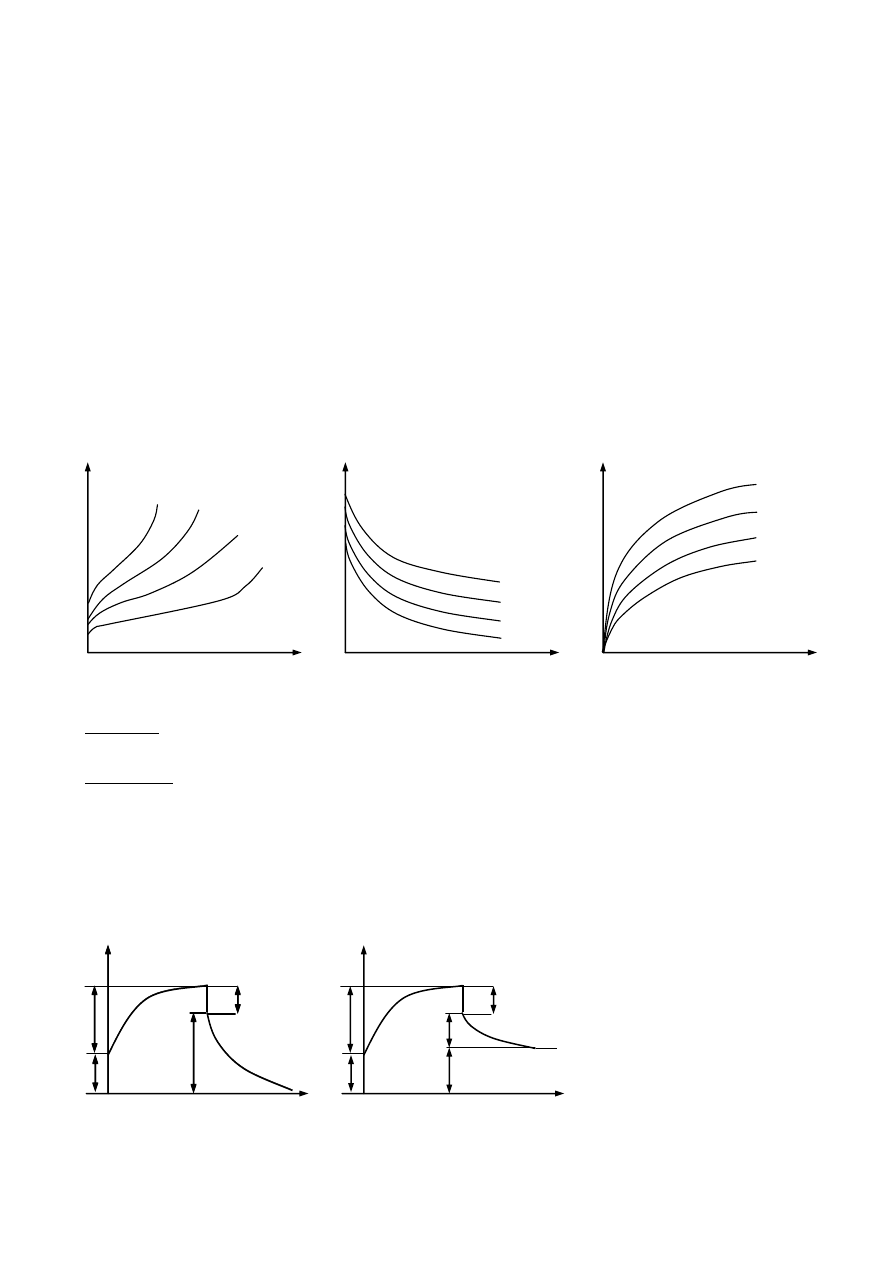
prostopadłymi do poszczególnych współrzędnych otrzymuje się trzy różne rodzaje krzywych:
a)
– krzywe pełzania – przecięcie powierzchni F(
,
, t) płaszczyznami
= const.,
b)
– krzywe relaksacji - przecięcie powierzchni F(
,
, t) płaszczyznami
= const.,
c)
– izochroniczne krzywe pełzania - przecięcie F(
,
, t) płaszczyznami t = const.,
Pełzanie i relaksacja to dwa podstawowe procesy reologiczne
Pełzanie jest to zjawisko zmiany odkształcenia elementu w czasie pod wpływem stałego
naprężenia działającego w stałej temperaturze.
Relaksacja
jest to zmniejszanie się naprężeń w elementach poddanych długotrwałemu
działaniu obciążeń przy stałej wartości odkształcenia całkowitego.
Pełzanie
W temperaturze pokojowej pełzanie uwidacznia się w tworzywach sztucznych i w stopach
metali lekkich, w temperaturach wysokich i podwyższonych także w stalach.
Pełzanie może być a) - sprężyste lub b) - plastyczne.
0A=
s
=
/E
–odkszt. sprężyste
AB=
p
– odkszt. pełzania
BC=
s
=
/E
–nawrót sprężysty
CD=
e
– nawrót niesprężysty
t
– odkształcenie trwałe
W metalach zachodzi przede wszystkim pełzanie plastyczne, w tworzywach sztucznych –
sprężyste i plastyczne w zależności od stanu tworzywa.
0
t
1
t
t
0
0
1
2
>
1
3
>
2
4
>
3
1
2>
1
3>
2
4>
3
t
2>
t
1
t
3>
t
2
t
4>
t
3
a)
b)
c)
A
B
C
D
t
p
s
s
e
0
A
B
C
D
t
p
s
s
e
0
t
A
B
C
D
t
p
s
s
e
0
a)
b)
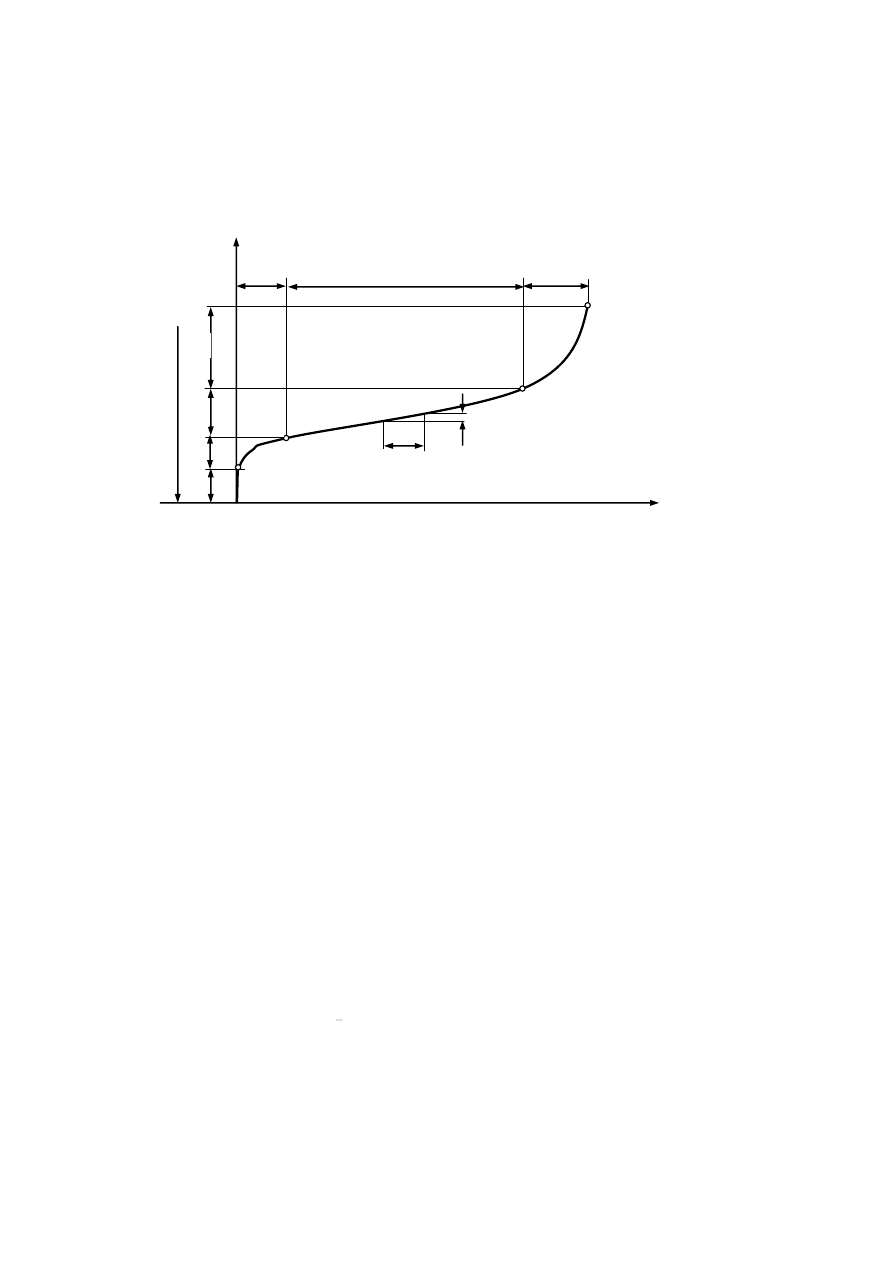
Wykres pełzania
Prawidłowa ocena warunków bezpiecznej pracy wymaga znajomości zmian odkształcenia i
naprężenia. Wymaga to ustalenia następujących zależności:
I.
.
)
(
const
dla
t
II.
)
,
(
T
0
– odkształcenie początkowe (sprężyste lub sprężyste i plastyczne),
p
– odkształcenie pełzania (składa się z trzech części odpowiadających trzem zakresom
pełzania:
pI
,
pII
,
pIII
).
I.
– okres pełzania nieustalonego, charakteryzujący się ciągłym zmniejszaniem prędkości
pełzania (odcinek AB).
II.
– okres pełzania ustalonego, o stałej prędkości pełzania (odcinek BC),
III.
– okres pełzania przyśpieszonego, w którym prędkość pełzania zwiększa się, co prowadzi
do złomu (odcinek CD).
Całkowite odkształcenie podczas pełzania:
=
0
+
p
=
0
+
t
⅓
+ Kt
Odkształcenie pełzania:
p
=
t
⅓
+ Kt
obejmuje odkształcenie w I i II okresie pełzania, przy czym pierwszy człon tego równania
opisuje tę część procesu (pełzanie nieustalone), które zachodzi ze zmniejszającą się w czasie
prędkością, a drugi człon – proces zachodzący ze stałą prędkością (pełzanie ustalone).
Różniczkując to równanie względem czasu otrzymamy zależność prędkości pełzania od czasu
K
At
3
2
stała prędkość pełzania K = const. (w II okresie) jest minimalną prędkością pełzania.
Ustalenie zależności prędkości pełzania od naprężenia i temperatury określa się
doświadczalnie. Najbardziej znaną jest zależność Nortona – Baileya:
n
pII
k
gdzie: k, n
– stałe zależne od materiału i temperatury
A
B
C
D
I
II
III
t
p
0
0
p
I
p
II
p
III
p
II
t
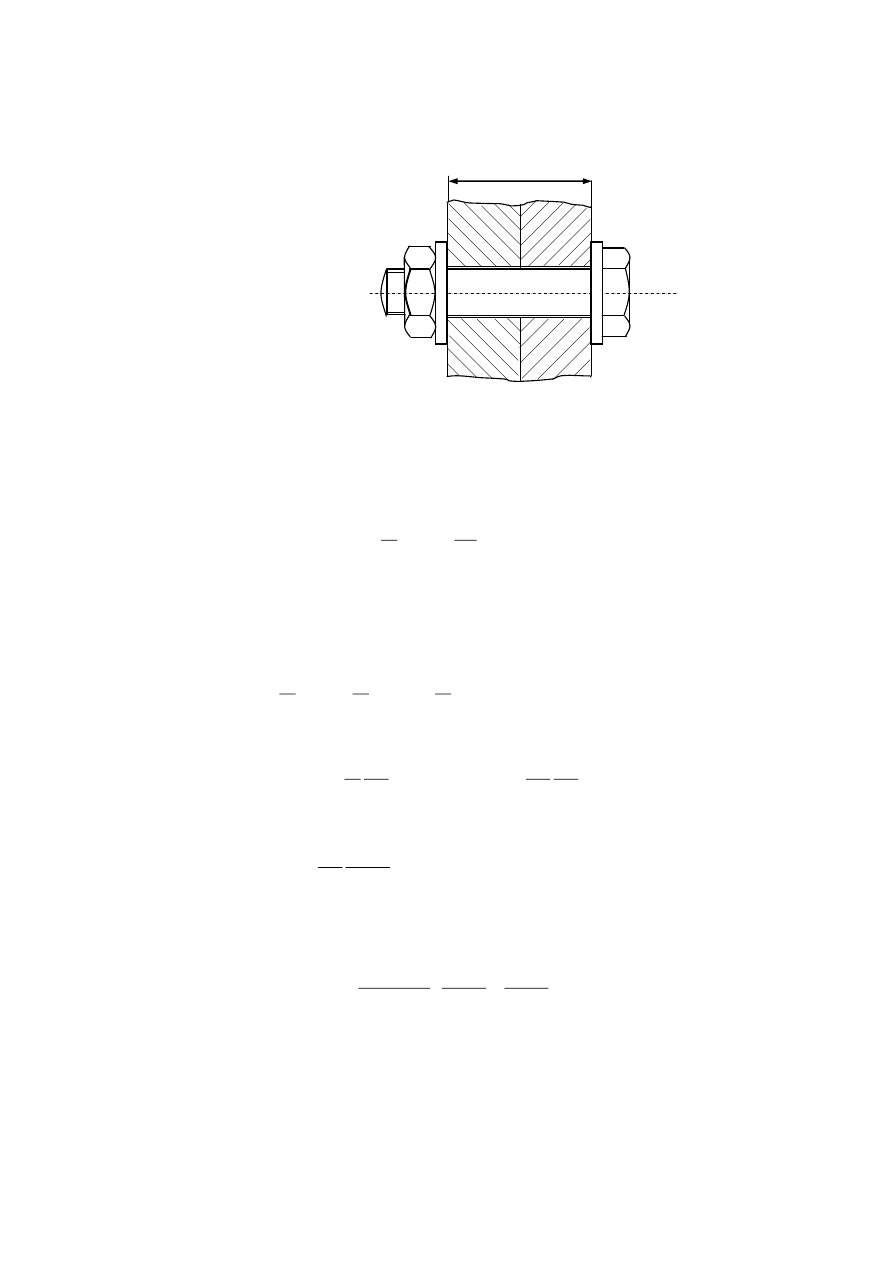
Relaksacja naprężeń
Typowym przypadkiem relaksacji jest zmniejszanie się naprężeń w śrubach łączących różne
elementy, szczególnie pracujących w wysokich lub podwyższonych temperaturach.
Rozpatrzmy taką śrubę:
Zakładamy sztywne połączenie – odległość między zewnętrznymi powierzchniami podkładek
(l=const).Uwzględniamy tylko pełzanie samej śruby – obliczenia uproszczone.
Suma odkształcenia sprężystego (
s
=
/E) i odkształcenia pełzania
p
nie zmieni się, gdyż
odkształcenie całkowite
jest stałe i równe odkształceniu początkowemu
0
=
0
/E
E
E
p
p
s
0
Jeżeli uwzględnimy tylko zakres pełzania ustalonego
n
pII
k
Po zróżniczkowaniu równania wyrażającego odkształcenie całkowite względem czasu mamy:
0
n
pII
p
k
E
E
E
Po przekształceniu otrzymamy:
n
n
d
kE
dt
dt
d
E
k
1
1
Całkując względem czasu otrzymamy:
C
n
kE
t
n
1
1
)
1
(
Stałą całkowania C otrzymamy z warunku:
=
0
dla t = 0.
Po podstawieniu stałej całkowania otrzymamy zależność między naprężeniem a czasem:
)
1
(
0
)
1
(
1
1
)
1
(
1
n
n
kE
n
t
l
Wyszukiwarka
Podobne podstrony:
18 FALA TETNAid 17717 Nieznany (2)
18 Silnik uniwersalnyid 17837 Nieznany
17 18 GPW102 Rocznik2012 Miedzy Nieznany (2)
18 Opracowanie programu i reali Nieznany (2)
18 Prowadzenie dzialalnosci rol Nieznany (2)
18 rabiega tadlaid 17832 Nieznany
18 pomoc spolid 17808 Nieznany (2)
Cw 17 18 Energia wiatru ver1 1 Nieznany
18 Tyczenie i inwentaryzacja ob Nieznany
18 Wykonywanie izolacji przeciw Nieznany
18 Prowadzenie prac zwiazanych Nieznany (2)
18 rozdzial 17 obddadd7lgo54zmd Nieznany (2)
18 Planowanie i analiza dzialal Nieznany (2)
18 Specyficzne rodzaje zdanid Nieznany (2)
18 Technologia strugania wyrown Nieznany
18 rozdzial 17 UXCTXEQZKIEB67R3 Nieznany (2)
18 rozdzial 17 vmtc3jege7kyyouu Nieznany (2)
18 05 2011id 17575 Nieznany (2)
18 Sporzadzanie dokumentacji te Nieznany
więcej podobnych podstron