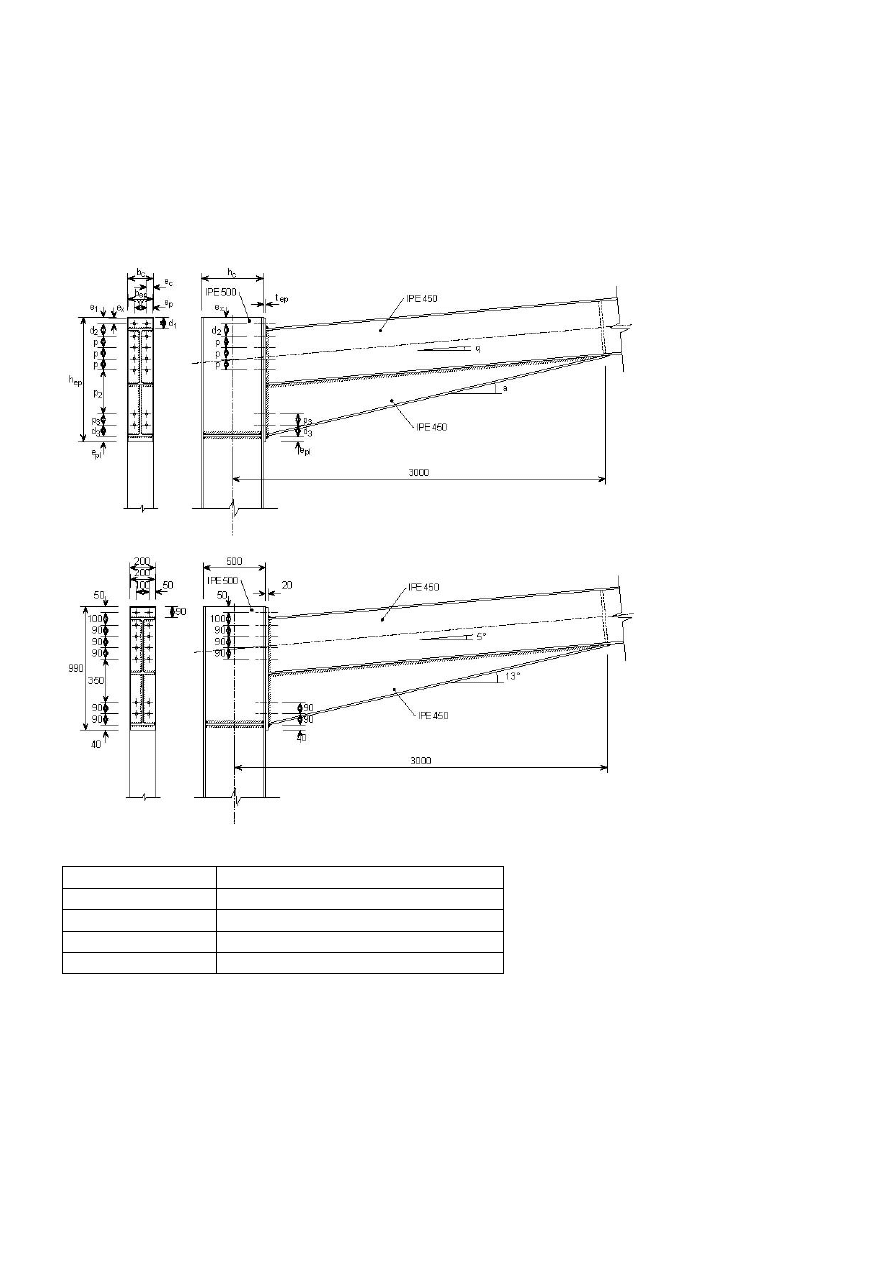
Przykład obliczeniowy
UWAGA: W obliczeniach uwzględnić postanowienia Załącznika Krajowego oraz aktualne
poprawki do normy.
Połączenie doczołowe ramy portalowej w okapie
1. Dane
Podstawowe parametry połączenia
Słup
IPE 500 stal S355
Rygiel
IPE 450 stal S355
Typ połączenia Doczołowe na śruby zwykłe (kat. A)
Blacha czołowa
990 × 200 × 20 stal S355
Śruby
M24, kl. 8.8
Słup IPE 500, stal S355
Wysokość profilu h
c
= 500 mm
Szerokość stopki b
c
= 200 mm
Grubość środnika t
wc
= 10,2 mm
Grubość pasa t
fc
= 16,0 mm
Promień wyokrąglenia r
c
= 21 mm
Pole pow. A
c
= 116 cm
2
Moment bezwładności I
y,c
= 48200 cm
4
Wysokość środnika między wyokrągleniami d
c,c
= 426 mm
Granica plastyczności f
y,c
= 355 N/mm
2
Wytrzymałość na rozciąganie f
u,c
= 510 N/mm
2
Rygiel IPE 450, stal S355
Wysokość profilu h
b
= 450 mm
Szerokość stopki b
b
= 190 mm
Grubość środnika t
wb
= 9,4 mm
Grubość pasa t
fb
= 14,6 mm
Promień wyokrąglenia r
b
= 21 mm
Pole pow. A
b
= 98,8 cm
2
Moment bezwładności I
y,b
= 33740 cm
4
Wysokość środnika między wyokrągleniami d
c,b
= 378,8 mm
Wysokość środnika w świetle pasów h
i,b
= 420,8 mm
Granica plastyczności f
y,b
= 355 N/mm
2
Wytrzymałość na rozciąganie f
u,b
= 510 N/mm
2
Skos IPE 450, stal S355
Wysokość profilu h
h
= 450 mm
Szerokość stopki b
h
= 190 mm
Grubość środnika t
wh
= 9,4 mm
Grubość pasa t
fh
= 14,6 mm
Promień wyokrąglenia r
h
= 21 mm
Granica plastyczności f
y,h
= 355 N/mm
2
Wytrzymałość na rozciąganie f
u,h
= 510 N/mm
2
Blacha czołowa 990 × 200 × 20, stal S355
Wysokość h
p
= 990 mm
Szerokość b
p
= 200 mm
Grubość t
p
= 20 mm
Granica plastyczności f
y,p
= 355 N/mm
2
Wytrzymałość na rozciąganie f
u,p
= 510 N/mm
2
Liczba rozciąganych szeregów śrub n
t
= 5
Liczba ścinanych szeregów śrub n
s
= 2
Odległość od górnej krawędzi blachy do pierwszego szeregu śrub e
x
= 50 mm
Odległość od krawędzi słupa do pierwszego szeregu śrub e
1
= 50 mm
Rozstaw szeregów w strefie rozciągania p = 90 mm
Odległość pomiędzy ostatnim szeregiem śrub rozciąganych a pierwszym szeregiem śrub ścinanych
p
2
= 90 mm
Rozstaw szeregów w strefeie ścinania p
3
= 90 mm
Odległość od górnej powierzchni rygla do górnej krawędzi blachy czołowej d
1
= 90 mm
Odległość między pierwszym szeregiem śrub rozciąganych a szeregiem śrub pod pasem górnym rygla
d
2
= 100 mm
Odległość od ostatniego szeregu śrub ścinanych do dolnej powierzchni pasa skosu d
3
= 90 mm
Odległość pomiędzy dolną powierzchnią pasa skosu a dolną krawędzią blachy czołowej e
pl
= 40 mm
Odległość od bocznej krawędzi blachy czołowej do linii śrub e
p
= 50 mm
Odległość od krawędzi pasa słupa do linii śrub e
c
= 50 mm
Rozstaw linii śrub w = 100 mm
Śruby M24, kl.8.8
Pow. czynna rdzenia śruby A
s
= 353 mm
2
Nominalna średnica śruby d = 24 mm
Średnica otworu d
0
= 26 mm
Granica plastyczności f
yb
= 640 N/mm2
Wytrzymałość na rozciąganie f
ub
= 800 N/mm2
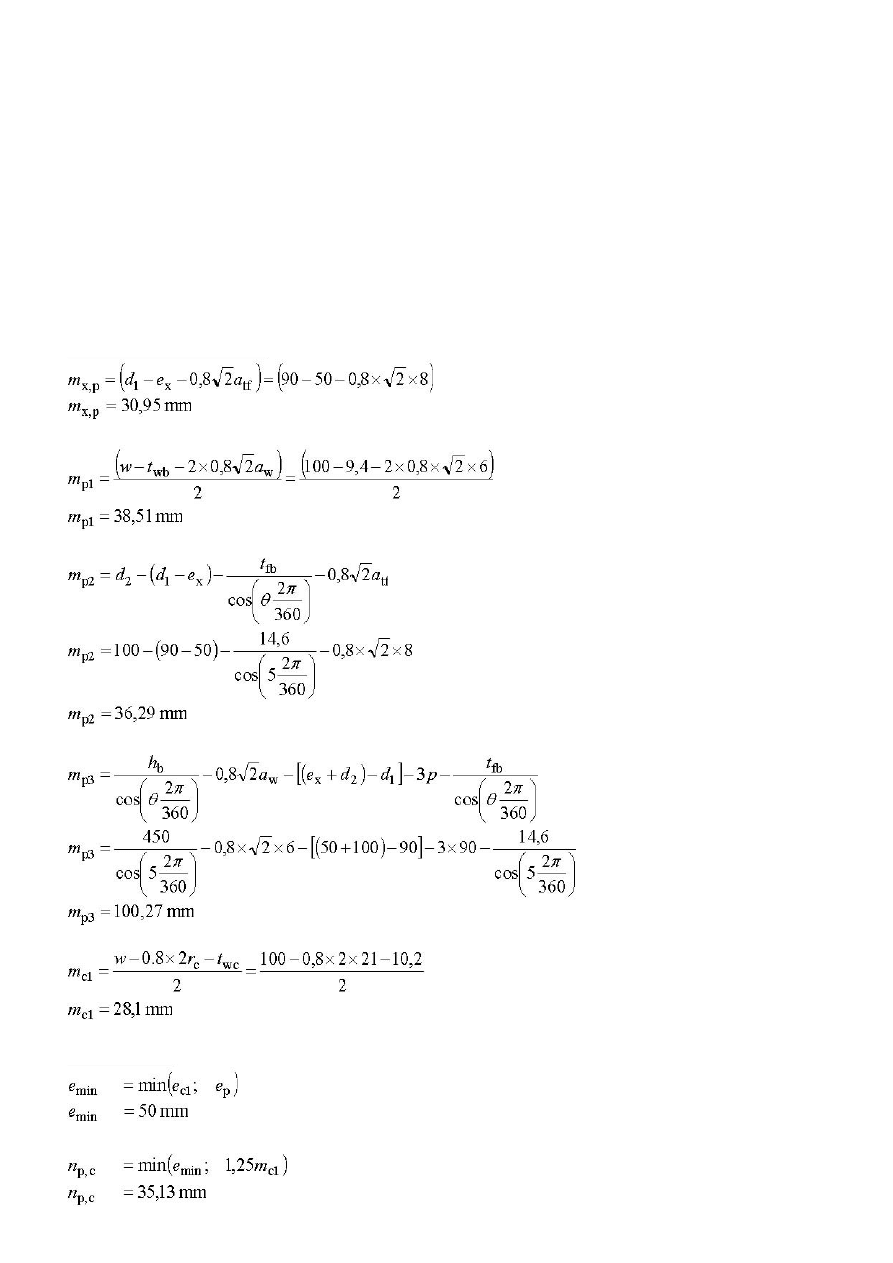
Częściowe współczynniki bezpieczeństwa PN-EN 1993-1-1 §6.1 , Uwaga 2B + NA.14
γ
M0
= 1,0
γ
M,1
= 1,0
γ
M,2
= 1,25 (przy ścinaniu w SGN)
Parametry stali
Moduł sprężystości E = 210000 N/mm
2
Siły obliczeniowe w połączeniu
M
Ed
= 880 kNm
N
Ed
= 175 kN
V
Ed
= 200 kN
Dodatkowe dane geometryczne (wg PN-EN 1993-1-8, rys. 6.2)
Odległości od krawędzi
Pole pow. słupa (wg PN-EN 1993-1-1 §6.2.6 (3))
Nośność śruby (PN-EN 1993-1-8 Tabl. 3.4) .
= 203 kN (dla jednej śruby)
2. Spoiny
2.1 Spoina pomiędzy pasem rozciąganym a blachą czołową
Potrzebną grubość spoiny można wyznaczyć na podstawie wzoru przybliżonego
przyjęto
2.2 Spoina pomiędzy blachą czołową a środnikiem rygla
Potrzebną grubość spoiny można wyznaczyć na podstawie wzoru przybliżonego
przyjęto,
2.3 Spoiny pasa ściskanego
Zakładając zapewnienie docisku pomiędzy pasem dolnym rygla (ew.skosu) a powierzchnią blachy
czołowej grubość spoiny można przyjąć konstrukcyjnie. Grubość pasa skosu wynosi 14,6 mm, zatem
należy zastosować spoinę o gr. 6 mm (dla pasów o gr. poniżej 12mm przyjmuje się spoiny o gr. 5mm).
3 Potencjalna nośność szeregów śrub na rozciąganie
3.1 Szereg nr 1
3.1.1 Strona słupa
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
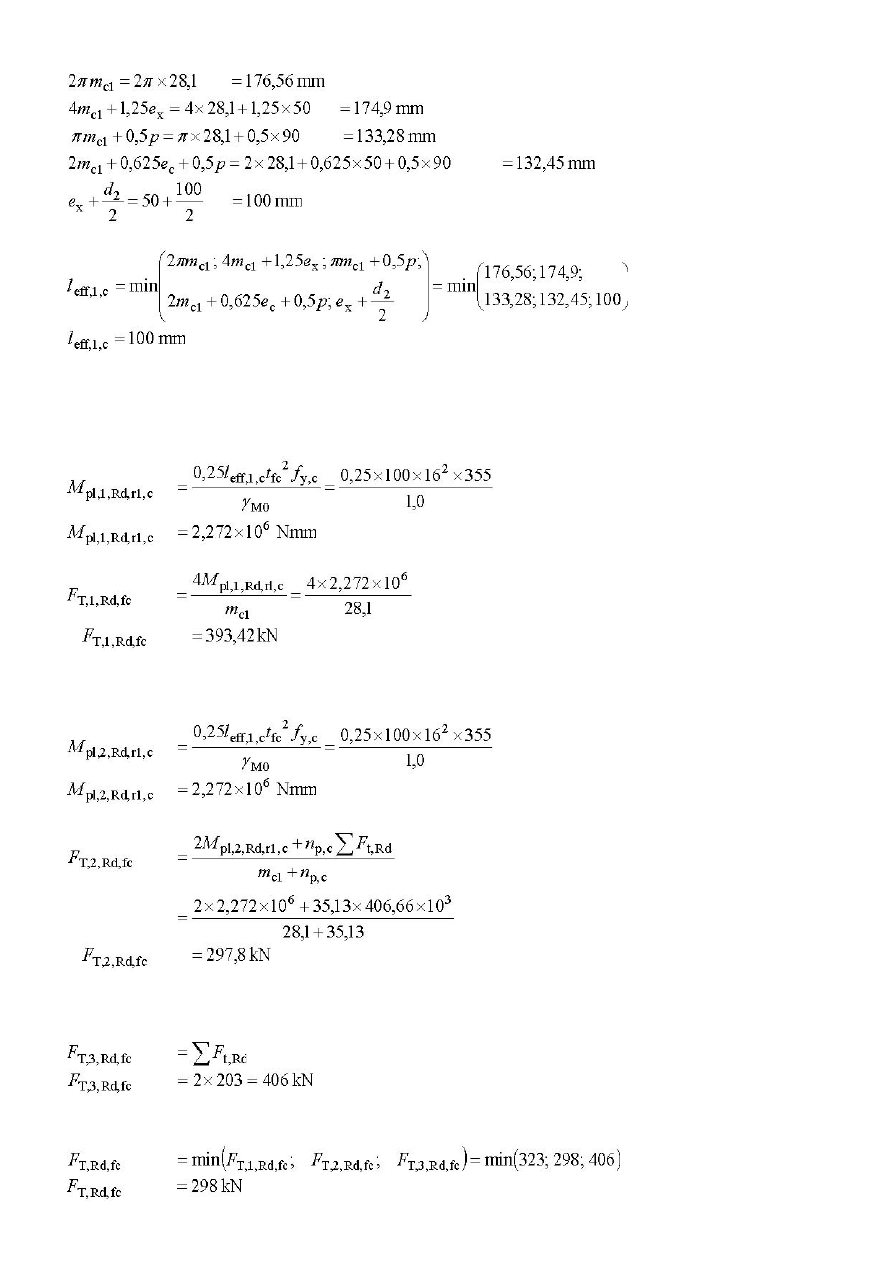
Pas słupa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność pasa słupa przy zginaniu wynosi:
Środnik słupa przy rozciąganiu porzecznym
Zgodnie z geometrią połączenia (PN-EN 1993-1-8 Tabl. 5.4)
stąd,
(PN-EN 1993-1-8 Tabl. 6.3)
(PN-EN 1993-1-8 §6.2.6.3 (3))
3.1.2 Strona rygla
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Blacha czołowa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność blachy czołowej przy zginaniu wynosi,
3.2 Szereg nr2
3.2.1 Strona słupa
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Pas słupa przy zginaniu
Forma 1; Metoda 1
Forma 2
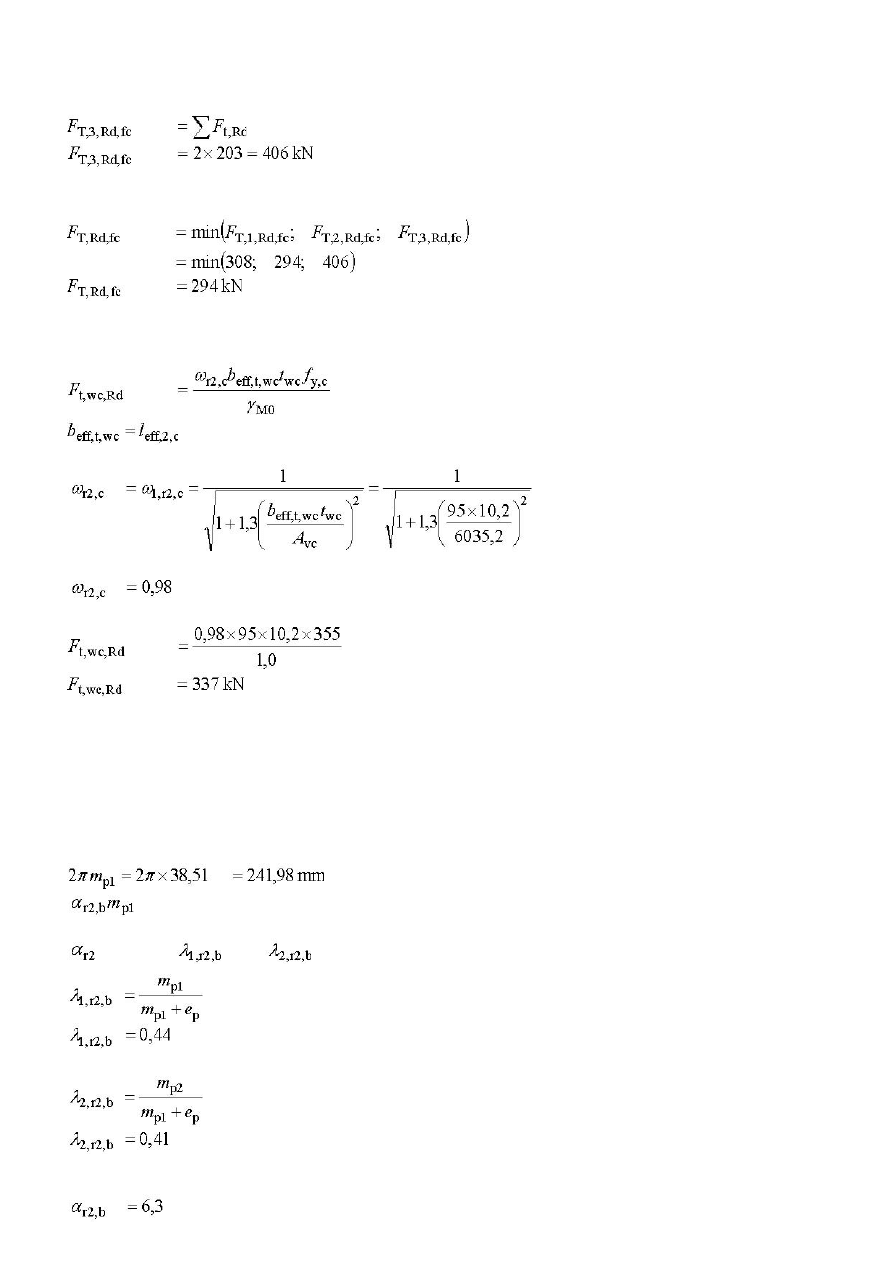
Forma 3
Zgodnie z powyższym nośność pasa słupa przy zginaniu wynosi:
Środnik słupa przy rozciąganiu poprzecznym
3.2.2 Strona rygla
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
zależy od
oraz
, zdefiniowanych następująco (por. PN-EN 1993-1-8, rys. 6.11):
stąd,
Blacha czołowa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność blachy czołowej przy zginaniu wynosi,
Środnik rygla przy rozciąganiu
3.3 Szereg nr 3
3.3.1 Strona słupa
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Pas słupa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność pasa słupa przy zginaniu wynosi,
.
Środnik słupa przy rozciąganiu poprzecznym
3.3.2 Strona rygla
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Blacha czołowa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność blachy czołowej przy zginaniu wynosi,
.
Środnik rygla przy rozciąganiu
3.4 Szereg nr 4
3.4.1 Strona słupa
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Pas słupa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność pasa słupa przy zginaniu wynosi,
Środnik słupa przy rozciąganiu poprzecznym
3.4.2 Strona rygla
Blacha czołowa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Nośność blachy czołowej przy zginaniu wynosi,
Środnik rygla przy rozciąganiu
3.5 Szereg nr 5
3.5.1 Strona słupa
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Pas słupa przy zginaniu
Forma 1; Metoda 1
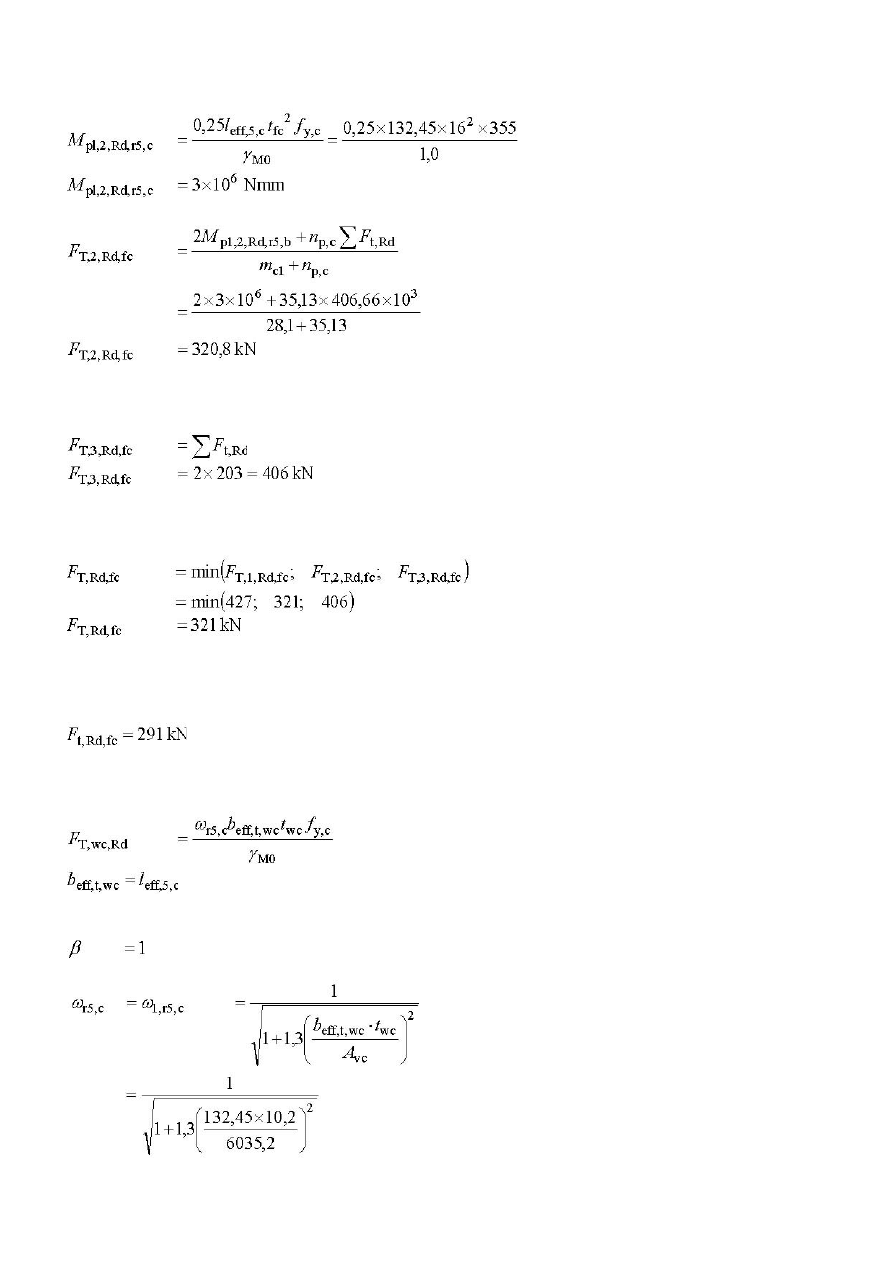
Forma 2
Forma 3
Zgodnie z powyższym nośność pasa słupa przy zginaniu wynosi,
Otrzymana nośność szeregu śrub nr 5 jest większa niż jakiegokolwiek porzedniego szeregu. Nośność
szeregu należy zatem ograniczyć do nośności szeregu nr 4.
Przyjęto,
Środnik słupa przy rozciąganiu poprzecznym
Zgodnie z geometrią połączenia
stąd,
3.5.2 Strona rygla
Długość efektywna
Długość efektywna zastępczego króćca teowego może być wyznaczona jako wartość minimalna z
podanych poniżej wyrażeń:
Blacha czołowa przy zginaniu
Forma 1; Metoda 1
Forma 2
Forma 3
Zgodnie z powyższym nośność blachy czołowej przy zginaniu wynosi,
Środnik rygla przy rozciąganiu
W ostatnim szeregu śrub potencjalna nośność na rozciąganie zostanie ograniczona do nośności
poprzedniego szeregu, stąd
Podsumowując.
.
4. Oszacowanie nośności strefy ściskania
Warunek nośności ma postać,
.
Działająca siła ściskająca jest sumą obliczeniowych nośności szeregów śrub na rozciąganie,
Obliczeniowa nośność na ściskanie strefy ściskania jest mniejszą z wartości obliczeniowych nośności:
- środnika słupa na ściskanie,
- pasa i środnika skosu na ściskanie,
tj.,
4.1 Środnik słupa przy ściskaniu poprzecznym
Nośność środnika można wyznaczyć za pomocą formuły,
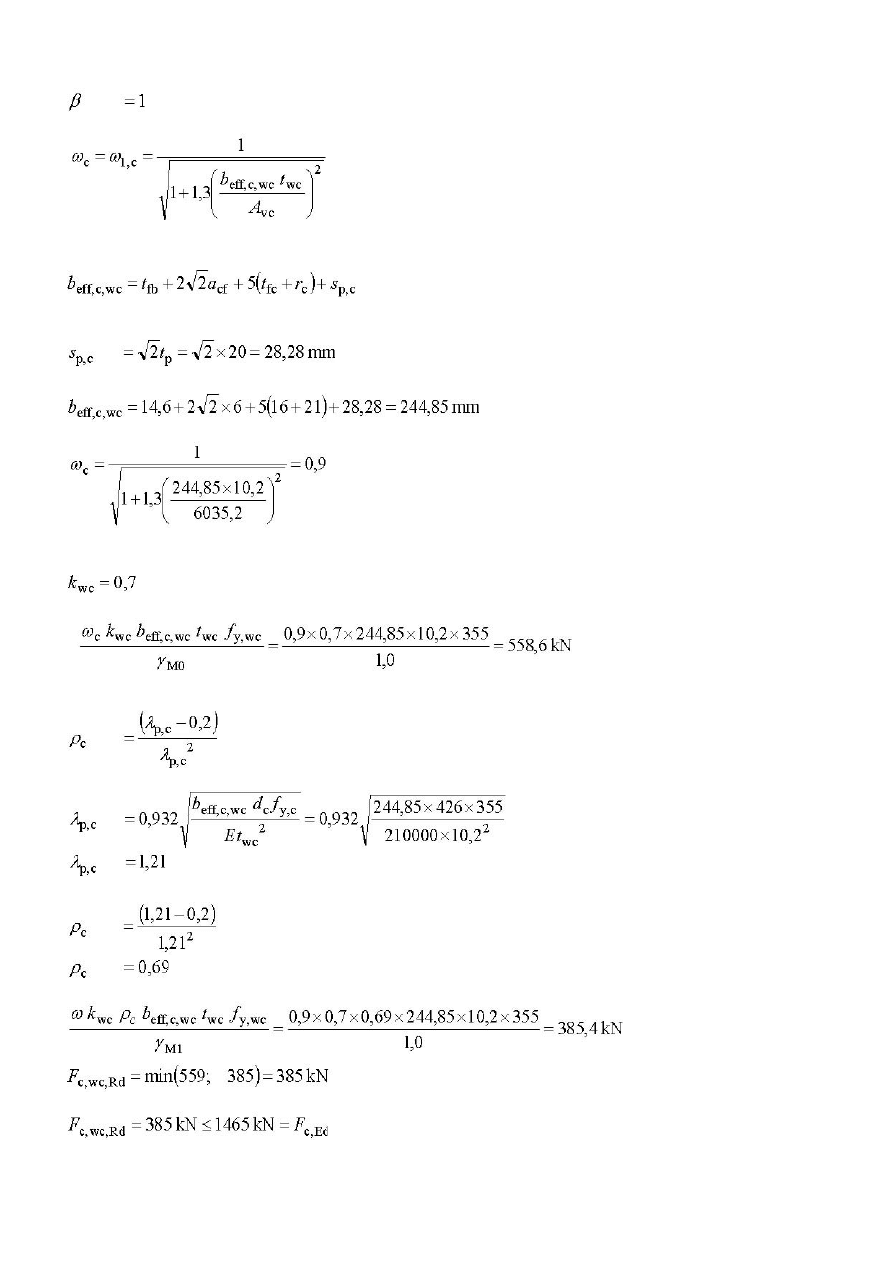
Zgodnie z geometrią połączenia
stąd,
gdzie,
oraz
Conservatively:
gdzie,
Nośność środnika słupa na ściskanie jest bardzo niewielka w porównaniu do działającej siły; należy
zastosować żebro usztywniające w poziomie pasa skosu.
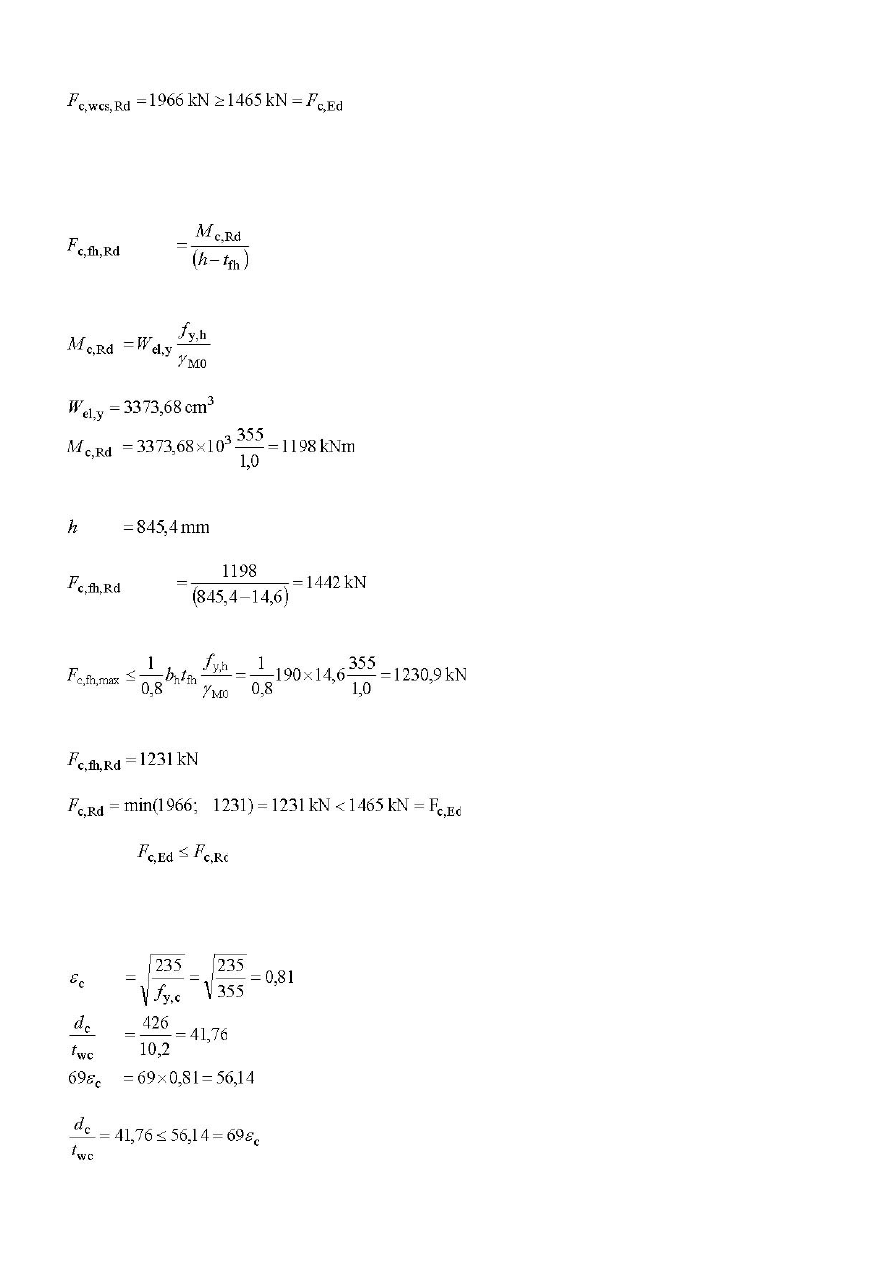
Nośność obliczeniowa żebra na ściskanie została obliczona zgodnie z §9.1(3) normy PN-EN 1993-1-5.
Przy uwzględnieniu nośności żebra usztywniającego warunek nośności strefy ściskania jest spełniony.
4.2 Pas i środnik skosu przy ściskaniu
Warunek nośności
gdzie,
Sprężysty wskaźnik wytrzymałości wynosi,
Ramię sił h jest równe,
Pas może przenieść siłę o wartości maks. (por. EN 1993-1-8 §6.2.6.7 (1))
,
stąd nośność na ściskanie skosu jest mniejszą z dwóch podanych niżej wartości:
Warunek
nie został spełniony, należy dokonać redystrybucji sił w szeregach śrub.
W p.7 niniejszego opracowania przedstawiono szczegóły dotyczące w/w redystrybucji.
5. Panel środnika słupa przy ścinaniu
stąd nośność panelu środnika słupa przy ścinaniu wynosi,
W celu uniknięcia ograniczania nośności śrub na rozciąganie na skutek nadmiernego wytężenia panelu
środnika słupa wywołanego ścinaniem, środnik słupa w obrębie węzła wzmacnia się dodatkową blachą o
gr. 10mm (tzn.pogrubiamy środnik), por. PN-EN 1993-1-8 §6.2.6.1.
Nośność wzmocnionego panelu środnika na ścinanie,
Powiększone pole środnika (pole czynne przy ścinaniu)
gdzie,
dla blachy wzmacniającej środnik o gr. 10mm,
6. Środnik rygla przy ściskaniu (oddziaływanie pasa skosu)
Procedura wyznaczania nośności na ściskanie środnika rygla jest taka sama jak procedura wyznaczania
nośności ściskanego środnika słupa bez udziału żebra wzmacniającego. Obliczeń wyznaczania nośności
środnika rygla na ściskanie nie zamieszczono w niniejszym opracowaniu.
Siłę działającą na środnik rygla można wyznaczyć rozpatrując poniższy trójkąt sił.
Stąd,
Nośność środnika rygla na ściskanie jest większa niż działająca siła, warunek nośności jest spełniony. Jeśli
warunek nie byłby spełniony to należałoby wzmocnić środnik za pomocą żebra tak jak to zrobiono w
słupie.
7. Dystrybucja sił w szeregach śrub
Pierwszym warunkiem jakie muszą spełniać efektywne nośności obliczeniowe szeregów śrub na
rozciąganie jest warunek,
gdzie,
Ponieważ
To należy zastosować następującą redystrybucję sił,
Warunek nośności panelu środnika na ścinanie ma postać,
w tym przypadku
zatem,
Warunek jest spełniony, nie musimy dokonywać dalszej redystrybucji.
Efektywne nośności szeregów śrub na rozciąganie muszą również spełniać następujący warunek,
Biorąc pod uwagę najniekorzystniejszy możliwy przypadek otrzymujemy,
Warunek jest spełniony, wymienione wyżej nośności szeregów śrub są zatem efektywnymi nośnościami
szeregów śrub na rozciąganie.
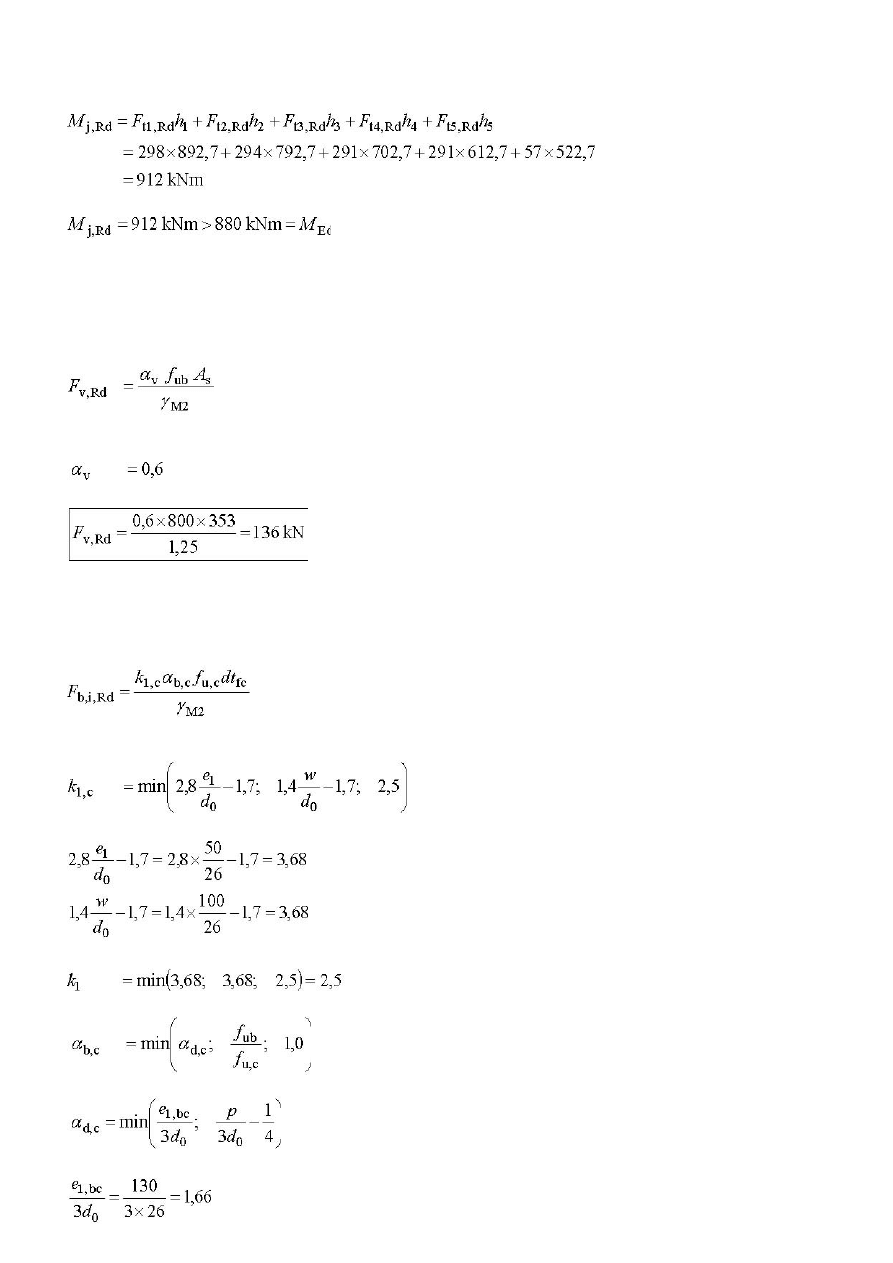
8. Nośność połączenia na moment zginający
Nośność jest większa od działającego momentu, warunek nośności został spełniony.
9. Oszacowanie nośności połączenia na ścinanie
9.1 Nośność pojedynczej śruby na ścinanie
Nośność trzpienia śruby na ścinanie określona jest wzorem,
gdzie dla śrub kl. 8.8
(patrz PN-EN 1993-1-8 Tabl. 3.4)
9.2 Nośność pojedynczej śruby na docisk do pasa słupa
Nośność śruby na docisk do pasa słupa można wyznaczyć za pomocą formuły,
gdzie,
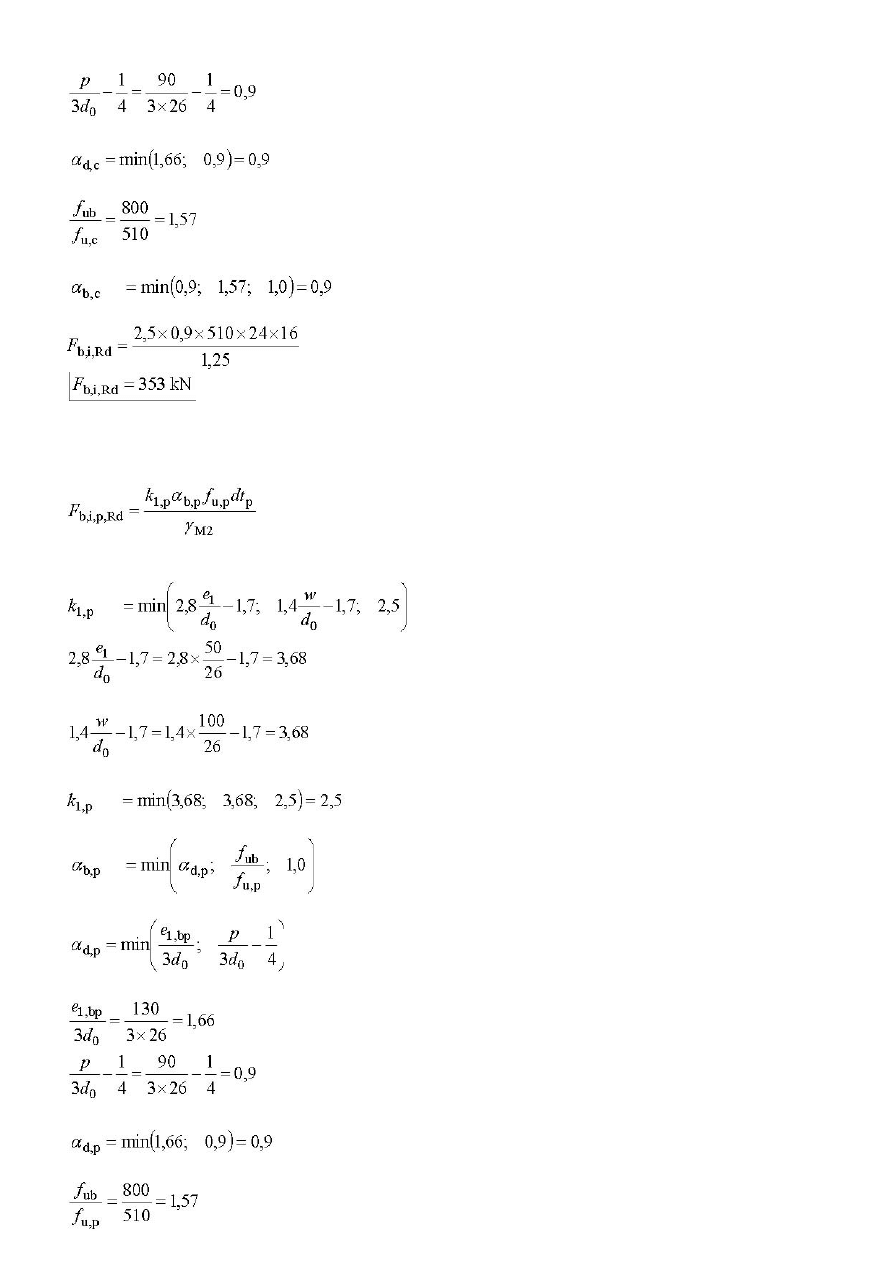
9.3 Nośność pojedynczej śruby na docisk do blachy czołowej rygla
Nośność śruby na docisk do blachy czołowej rygla można wyznaczyć za pomocą formuły,
gdzie,
Obliczeniowa nośność na ścinanie pojedynczej śruby jest wartością minimalną z trzech wyznaczonych
powyżej nośności, tj.
.
Liczba śrub potrzebna do przeniesienia siły poprzecznej,
,czyli wystarczą dwie śruby.
Zgodnie z powyższymi obliczeniami wystarczy jeden szereg śrub ścinanych. Obliczeniowa nośność
połączenia na ścinanie wynosi,