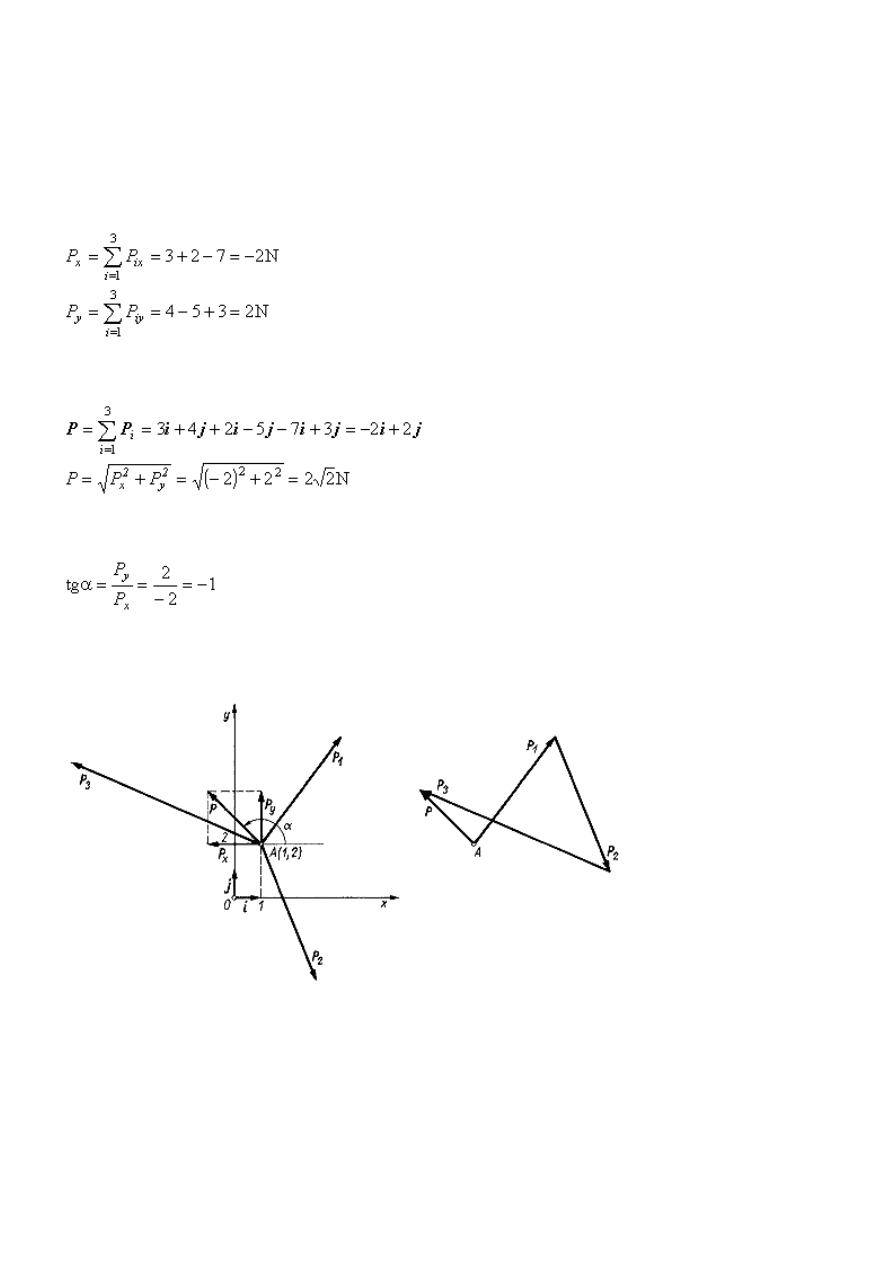
Przykład 1
Dane są trzy siły: P

1

= 3i + 4j, P

2

= 2i + 5j, P

3

= 7i + 3j (składowe sił wyrażone są w niutonach),

przecinające się w punkcie A (1, 2). Wyznaczyć wektor wypadkowej i jej wartość oraz kąt nachylenia
linii działania względem osi Ox układu.

Rozwiązanie
Przy zastosowaniu sposobu analitycznego należy wyznaczyć składowe wypadkowej P

x

i P

y

Wektor i wartość wypadkowej wynoszą

Kierunek wypadkowej określa kąt , który wyznaczamy z następującego wzoru

Ponieważ składowe wypadkowej są następujące: P

x

< 0, P

y

> 0, to kąt = 135 . Linia działania

wypadkowej przechodzi przez punkt A pod kątem = 135 do osi Ox.

Przykład 2
Wzdłuż dwóch boków i głównej przekątnej sześcianu działają siły P

1

, P

2

,P

3

. Wartości tych sił są

równe: P

1

= P

2

= Q, P

3

= 3Q. Wyznaczyć ich wypadkową.

R o z w i ą z a n i e
Cosinusy kierunkowe sił P

1

, P

2

, P

3

wynoszą

Wyznaczamy składowe wypadkowej

Wartość wypadkowej wyznaczamy z następującego wzoru

a jej cosinusy kierunkowe i kąty wynoszą odpowiednio

Linia działania wypadkowej przebiega przez punkt przecięcia się linii działania sił P

1

, P

2

, P

3

pod

kątami

i

do osi układu współrzędnychOxyz.

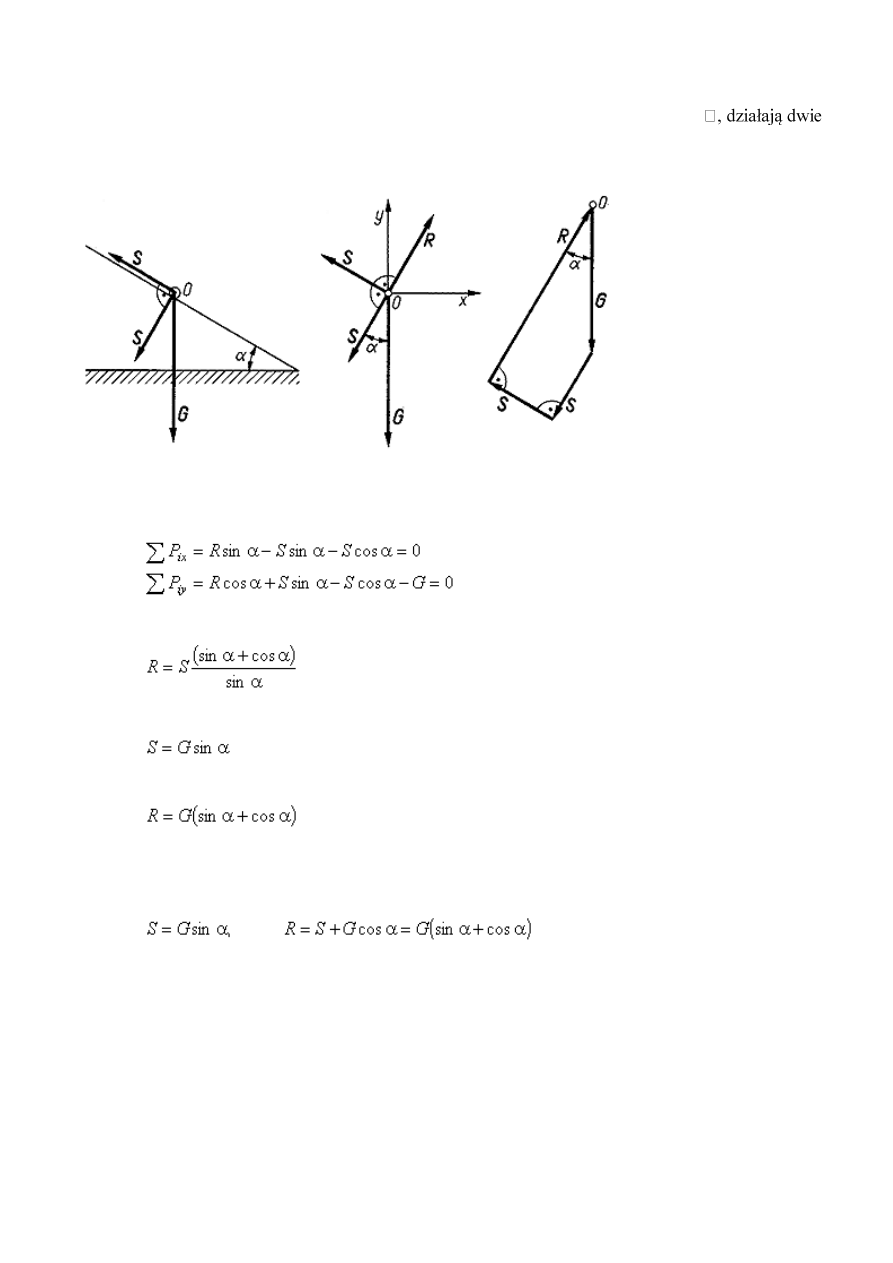
Przykład 3
Na punkt materialny o ciężarze G, leżący na gładkiej równi pochyłej o kącie pochylenia
siły S tak, jak przedstawiono na rysunku. Wyznaczyć siłę S oraz reakcję równi, jeżeli punkt znajduje się
w spoczynku.

R o z w i ą z a n i e
Metoda analityczna. Na punkt materialny działają cztery siły, które są w równowadze. Na podstawie
warunków równowagi sił zbieżnych można napisać następujące równania równowagi

Z równania pierwszego otrzymamy

Po podstawieniu do drugiego równania

Stąd

Metoda geometryczna. Na rysunku przedstawiono zamknięty wielobok sił utworzony z czterech sił
działających na punkt materialny, z którego wyznaczono wartości siły S i reakcji R

Przykład 4
Nieważka belka AB o długości l opiera się jednym końcem A na stałej podporze przegubowej A. Drugi
koniec B tej belki jest zamocowany na podporze przegubowej przesuwnej (rysunek). Wyznaczyć reakcje
podpórA i B, jeżeli belka jest obciążona w punkcie C siłą P.

R o z w i ą z a n i e
Metoda analityczna. Na rysunku b belka została uwolniona od więzów i przyłożone zostały
reakcje R

Ax

, R

Ay

i R

B

. Ponieważ belka jest obciążona trzema siłami R

A

, R

B

i P, wobec tego ich linie

działania muszą przecinać się w jednym punkcie D, zaś trójkąt sił musi być zamknięty (rys. c).
W przyjętym układzie współrzędnych Axy równania równowagi będą następujące

Ponadto

gdzie

Z rozwiązania powyższego układu trzech równań otrzymamy

Metoda geometryczna. Na rysunku c przedstawiono trójkąt sił R

A

, R

B

i P. Na podstawie twierdzenia

równań sinusów otrzymamy

Stąd

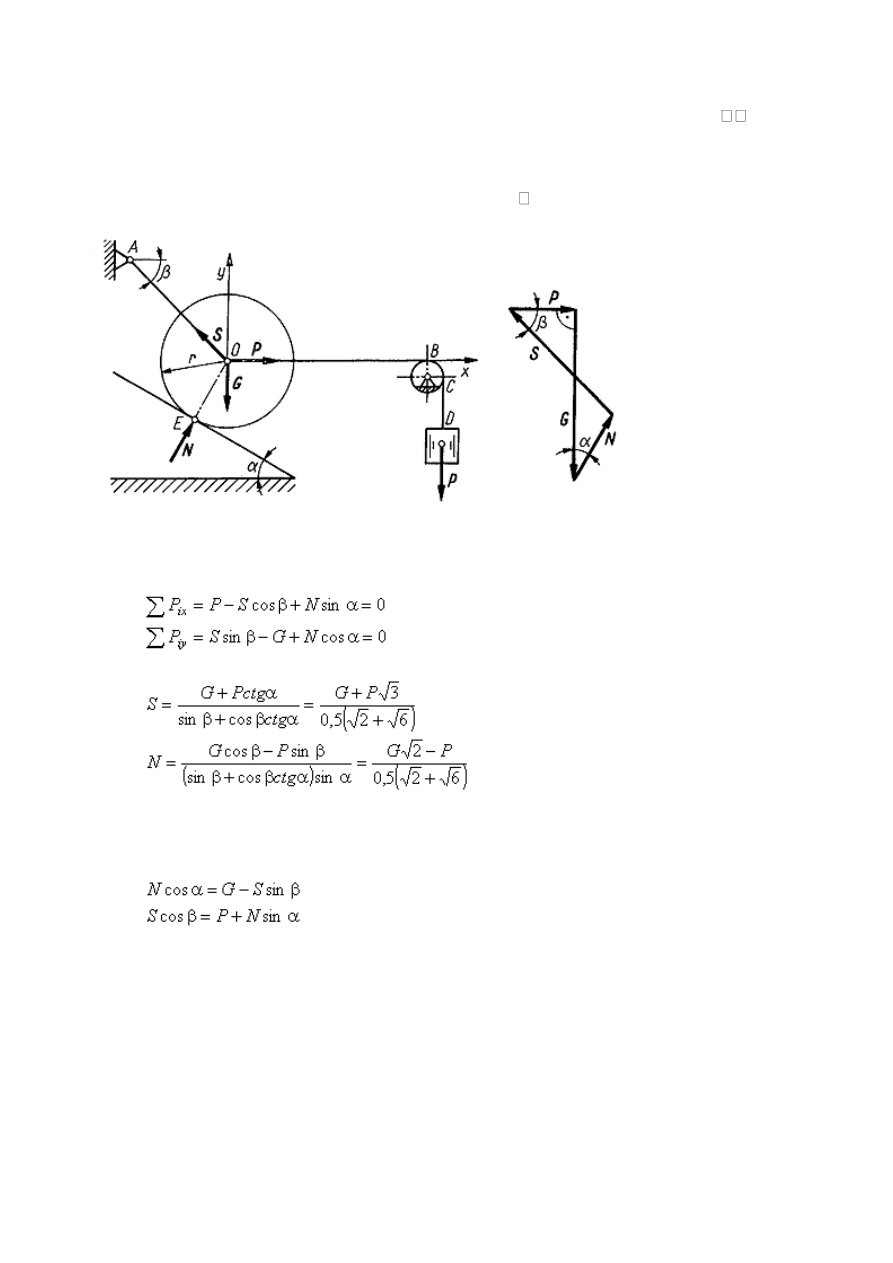
Przykład 5
Walec o promieniu r i ciężarze G spoczywa na gładkiej równi pochyłej o kącie pochylenia

= 30º i

jest utrzymywany w położeniu równowagi za pomocą liny OA, zgodnie z rysunkiem. Do środka walca
zamocowano drugą linę, którą przerzucono przez nieważki krążek. Na końcu tej liny zawieszono
ciężar P. Obliczyć wartość reakcji N w punkcie E zetknięcia się walca z równią oraz napięcie w linie OA,
jeżeli lina OB jest pozioma, a lina OA tworzy z poziomem kąt = 45º.

R o z w i ą z a n i e
Metoda analityczna. Na walec działają siły P, G, S i N. Równania równowagi walca są następujące

Stąd

Metoda geometryczna. Na rysunku b przedstawiono zamknięty wielobok sił, utworzony ze wszystkich sił
działających na walec. Korzystając z odpowiednich trójkątów otrzymamy

Z rozwiązania tych równań otrzymamy takie same wartości sił S i N, jak przy zastosowaniu metody
analitycznej.

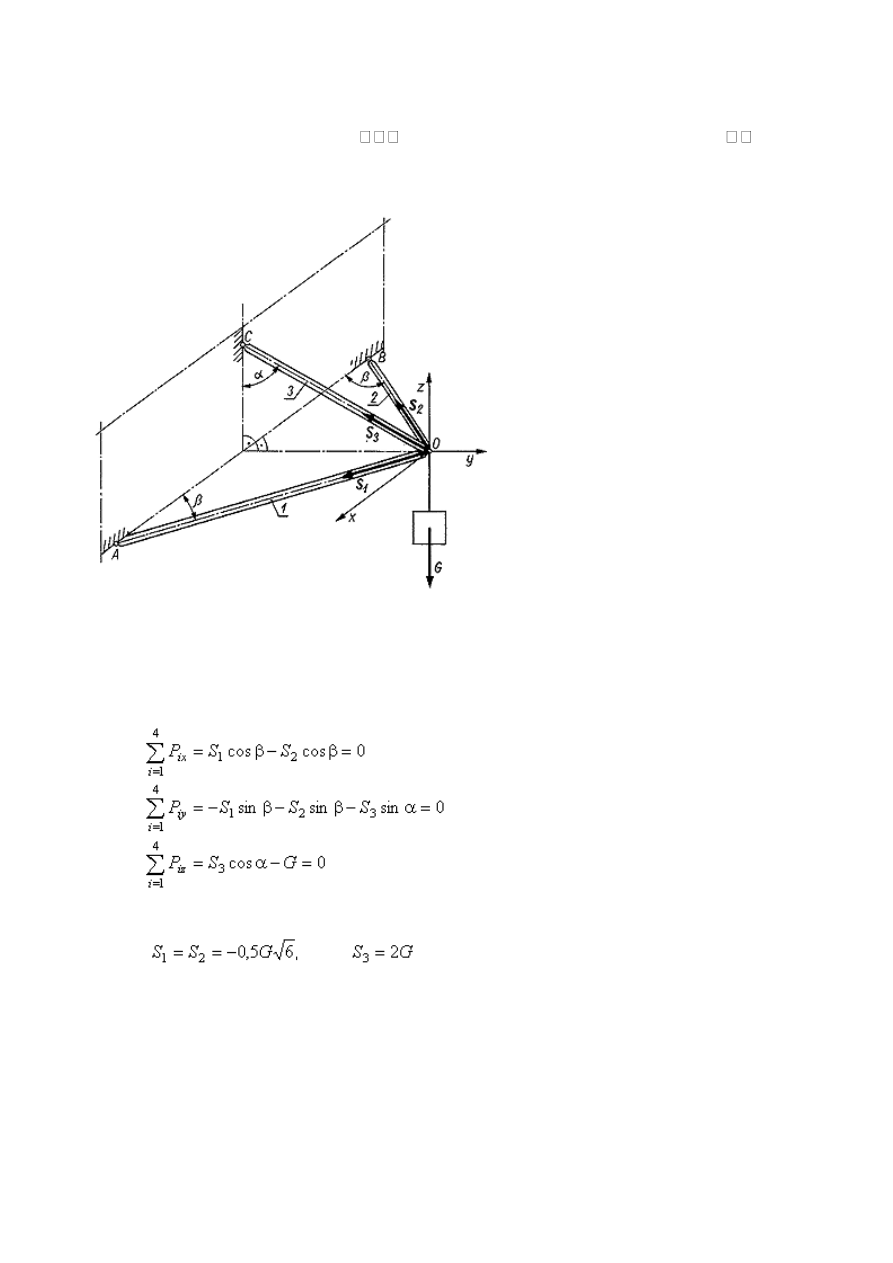
Przykład 6
Ciało o ciężarze G jest zawieszone na wsporniku składającym się z trzech prętów połączonych
przegubowo w sposób pokazany na rysunku. Pręty AO i BO, leżące w płaszczyźnie prostopadłej do
pionowej ściany, tworzą z tą ścianą kąty

= 45º. Pręt CO tworzy z pionową ścianą kąt

= 60º i

również leży w płaszczyźnie prostopadłej do tej ściany. Obliczyć siły w prętach, pomijając ich ciężary
własne oraz tarcie w przegubach.

R o z w i ą z a n i e
Metoda analityczna. Na przegub O działają siły wynikające z oddziaływania
prętów OA, OB i OC: S

1

, S

2

i S

3

oraz ciężar G. Na podstawie warunków równowagi otrzymujemy

następujące równania

Po rozwiązaniu powyższego układu równań otrzymamy

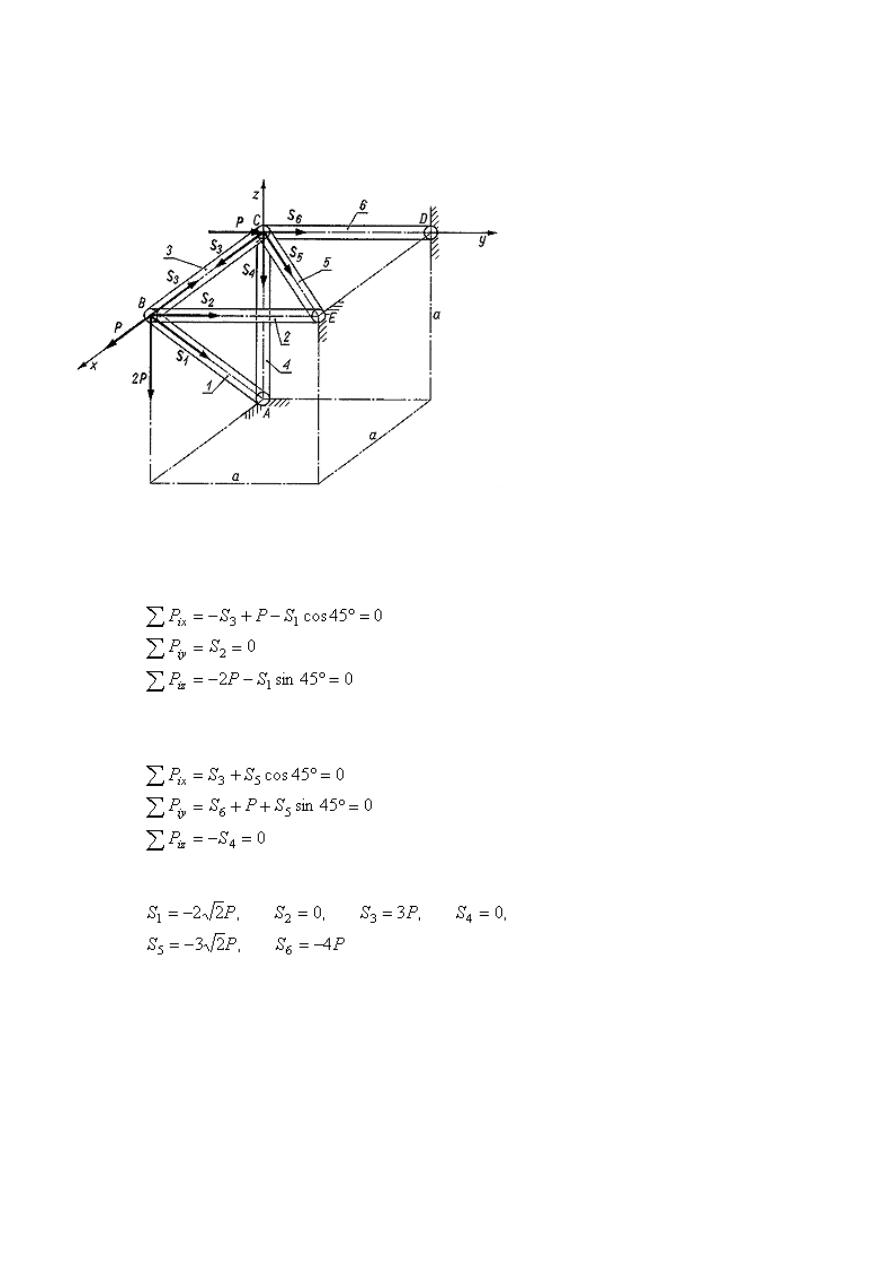
Przykład 7
Wyznaczyć siły w prętach konstrukcji pokazanej na rysunku. Nieważkie
pręty AB, AC, BC, BE, CE i CD są połączone przegubowo w węzłach A, B,C, D i E. W węźle B działają
dwie siły: 2P w kierunku pionowym i siła P w kierunku pręta BC.

R o z w i ą z a n i e
Metoda analityczna. Na węzeł B działają reakcje S

1

, S

2

i S

3

, wynikające z oddziaływania

prętów AB, BE i BC oraz siły P i 2P. Równania równowagi tego węzła są następujące

Na węzeł C działają reakcje S

3

, S

4

, S

5

i S

6

oraz siła P. Równania równowagi rozpatrywanego węzła są

równe

Po rozwiązaniu powyższego układu równań otrzymamy